Topology optimization of 2D in-plane single mass MEMS gyroscopes

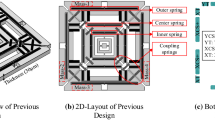
Abstract

In this paper, we apply the topology optimization method to the design of MEMS gyroscopes, with the aim of supporting traditional trial and error design procedures. Using deterministic, gradient-based mathematical programming, the approach is here applied to the design of 2D in-plane single mass MEMS gyroscopes. We first focus on a benchmark academic case, for which we present and compare three different formulations of the optimization problem, considering typical industrial requirements. These include the maximization of the response of the sensor’s structure to the external angular rate, target resonant frequencies and minimum or constrained material usage. Also, a minimum length scale is imposed to the geometric features in order to ensure manufacturability, and an explicit penalization of grey elements is proposed to improve convergence to black and white layouts. Once the suitability of the method has been assessed, the formulation associated with the lowest computational cost, i.e. the one considering static estimations of the resonant frequencies, is applied to the design of a real-world MEMS gyroscope, targeting different resonant frequencies.

Appendices

Appendix: 1: Adjoint sensitivity analysis of the sense response

In order to compute the sensitivities of the sense response ψ₁ (12) with respect to the projected field, we first consider the corresponding harmonic response problem:

$$ (-\alpha^{2}{\omega_{s}^{2}}\boldsymbol{M}+i\alpha\omega_{s}\boldsymbol{G_{C}}({\Omega}_{z})+\boldsymbol{K}) \boldsymbol{u_{h}} = \boldsymbol{f_{h}} $$

(32)

and rewrite it introducing the dynamic stiffness matrix S as well as expliciting the dependencies on the projected field and on the sense resonant frequency:

$$ \boldsymbol{S}(\overline{\tilde{\gamma}}_{e},\omega_{s}) \boldsymbol{u_{h}} = \boldsymbol{f_{h}} $$

(33)

Considering that:

$$ \begin{array}{@{}rcl@{}} &&\boldsymbol{S}=\boldsymbol{S_{r}}+i\boldsymbol{S_{i}} \\ &&\boldsymbol{u_{h}}=\boldsymbol{u_{h,r}}+i\boldsymbol{u_{h,i}}\\ &&\boldsymbol{f_{h}}=\boldsymbol{f_{h,r}}+i\boldsymbol{f_{h,i}} \end{array} $$

(34)

Equation (33) can be split into its real and imaginary parts as:

$$ \begin{array}{@{}rcl@{}} &&\boldsymbol{S_{r}}\boldsymbol{u_{h,r}}-\boldsymbol{S_{i}}\boldsymbol{u_{h,i}}=\boldsymbol{f_{h,r}}\\ &&\boldsymbol{S_{r}}\boldsymbol{u_{h,i}}+\boldsymbol{S_{i}}\boldsymbol{u_{h,r}}=\boldsymbol{f_{h,i}} \end{array} $$

(35)

Referring to Eq. 12, the sense response ψ₁ can be expressed as a function of the projected field and of the real and imaginary parts of the harmonic displacements vector:

$$ \psi_{1}=\psi_{1}(\overline{\tilde{\gamma}}_{e},\boldsymbol{u_{h,r}},\boldsymbol{u_{h,i}}) $$

(36)

As usual for adjoint sensitivity analysis, we add to this function extra (vanishing) terms that are related to the harmonic response to the sense eigenvalue problem and to the normalization of the sense modal shape:

$$ \begin{array}{@{}rcl@{}} \widehat{\psi}_{1} &= & \psi_{1} + \boldsymbol{\lambda_{1}}^{T} (\boldsymbol{S_{r}}\boldsymbol{u_{h,r}} -\boldsymbol{S_{i}}\boldsymbol{u_{h,i}}-\boldsymbol{f_{h,r}}) + \\ && - \boldsymbol{\lambda_{2}}^{T} (\boldsymbol{S_{r}}\boldsymbol{u_{h,i}}+\boldsymbol{S_{i}}\boldsymbol{u_{h,r}}-\boldsymbol{f_{h,i}}) + \\ && + \boldsymbol{\lambda_{3}}^{T} (\boldsymbol{K}-{\omega_{s}^{2}}\boldsymbol{M})\boldsymbol{{\Phi}_{s}} + \lambda_{4} (\boldsymbol{{\Phi}_{s}}^{T}\boldsymbol{M}\boldsymbol{{\Phi}_{s}}-1) \end{array} $$

(37)

We now compute the sensitivities of the above function with respect to the projected field that after rearranging the terms become:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \widehat{\psi}_{1}}{\partial \overline{\tilde{\gamma}}_{e}} &= & \boldsymbol{\lambda_{1}}^{T} \frac{\partial \boldsymbol{S_{r}}}{\partial \overline{\tilde{\gamma}}_{e}}\boldsymbol{u_{h,r}} - \boldsymbol{\lambda_{1}}^{T} \frac{\partial \boldsymbol{S_{i}}}{\partial \overline{\tilde{\gamma}}_{e}}\boldsymbol{u_{h,i}} + \\ & -& \boldsymbol{\lambda_{2}}^{T} \frac{\partial \boldsymbol{S_{r}}}{\partial \overline{\tilde{\gamma}}_{e}}\boldsymbol{u_{h,i}} - \boldsymbol{\lambda_{2}}^{T} \frac{\partial \boldsymbol{S_{i}}}{\partial \overline{\tilde{\gamma}}_{e}}\boldsymbol{u_{h,r}} + \\ & +& \boldsymbol{\lambda_{3}}^{T} \left( \frac{\partial \boldsymbol{K}}{\partial \overline{\tilde{\gamma}}_{e}} - {\omega_{s}^{2}} \frac{\partial \boldsymbol{M}}{\partial \overline{\tilde{\gamma}}_{e}} \right) \boldsymbol{{\Phi}_{s}} + \\ & +& \lambda_{4} \boldsymbol{{\Phi}_{s}}^{T} \frac{\partial\boldsymbol{M}}{\partial \overline{\tilde{\gamma}}_{e}} \boldsymbol{{\Phi}_{s}} + \\ & +& \left( \frac{\partial \psi_{1}}{\partial\boldsymbol{u_{h,r}}} + \boldsymbol{\lambda_{1}}^{T} \boldsymbol{S_{r}} - \boldsymbol{\lambda_{2}}^{T} \boldsymbol{S_{i}} \right) \frac{\partial\boldsymbol{u_{h,r}}}{\partial \overline{\tilde{\gamma}}_{e}} + \\ &+ &\left( \frac{\partial \psi_{1}} {\partial\boldsymbol{u_{h,i}}} - \boldsymbol{\lambda_{1}}^{T} \boldsymbol{S_{i}} - \boldsymbol{\lambda_{2}}^{T} \boldsymbol{S_{r}} \right) \frac{\partial\boldsymbol{u_{h,i}}}{\partial \overline{\tilde{\gamma}}_{e}} + \\ & +& \left( \vphantom{\frac{\partial \boldsymbol{S_{i}}}{\partial \omega_{s}}\boldsymbol{u_{h,r}}} \right. \boldsymbol{\lambda_{1}}^{T} \frac{\partial \boldsymbol{S_{r}}}{\partial \omega_{s}}\boldsymbol{u_{h,r}} - \boldsymbol{\lambda_{1}}^{T} \frac{\partial \boldsymbol{S_{i}}}{\partial \omega_{s}}\boldsymbol{u_{h,i}} + \\ & -& \boldsymbol{\lambda_{2}}^{T} \frac{\partial \boldsymbol{S_{r}}}{\partial \omega_{s}}\boldsymbol{u_{h,i}} - \boldsymbol{\lambda_{2}}^{T} \frac{\partial \boldsymbol{S_{i}}}{\partial \omega_{s}}\boldsymbol{u_{h,r}} + \\ & -& 2 \omega_{s} \boldsymbol{\lambda_{3}}^{T}\boldsymbol{M}\boldsymbol{{\Phi}_{s}} \left. \vphantom{\frac{\partial \boldsymbol{S_{i}}}{\partial \omega_{s}}\boldsymbol{u_{h,r}}} \right) \frac{\partial \omega_{s}}{\partial \overline{\tilde{\gamma}}_{e}} + \\ & +& \left( \boldsymbol{\lambda_{3}}^{T} (\boldsymbol{K} - {\omega_{s}^{2}} \boldsymbol{M} ) + \lambda_{4} 2 \boldsymbol{{\Phi}_{s}}^{T} \boldsymbol{M} \right) \frac{\partial\boldsymbol{{\Phi}_{s}}}{\partial \overline{\tilde{\gamma}}_{e}} \end{array} $$

(38)

In order to eliminate the expressions involving $\frac {\partial \boldsymbol {u_{h,r}}}{\partial \overline {\tilde {\gamma }}_{e}}$ and $\frac {\partial \boldsymbol {u_{h,i}}}{\partial \overline {\tilde {\gamma }}_{e}}$, we require the first two parentheses to vanish:

$$ \begin{array}{@{}rcl@{}} && \boldsymbol{\lambda_{1}}^{T} \boldsymbol{S_{r}} - \boldsymbol{\lambda_{2}}^{T} \boldsymbol{S_{i}} = - \frac{\partial \psi_{1}}{\partial\boldsymbol{u_{h,r}}} \\ && \boldsymbol{\lambda_{1}}^{T} \boldsymbol{S_{i}} + \boldsymbol{\lambda_{2}}^{T} \boldsymbol{S_{r}} = \frac{\partial \psi_{1}} {\partial\boldsymbol{u_{h,i}}} \end{array} $$

(39)

Multiplying the second equation in Eq. 39 by i and adding it to the first one yields:

$$ (\boldsymbol{\lambda_{1}}^{T} + i \boldsymbol{\lambda_{2}}^{T}) (\boldsymbol{S_{r}} + i \boldsymbol{S_{i}}) = - \left( \frac{\partial \psi_{1}}{\partial\boldsymbol{u_{h,r}}} - i \frac{\partial \psi_{1}}{\partial\boldsymbol{u_{h,i}}} \right) $$

(40)

that after introducing λ^∗ = λ₁ + iλ₂ and S = S_r + iS_i, and after transposing, gives (21) that allows to compute the adjoints λ₁ and λ₂.

In order to compute the adjoints λ₃ and λ₄, we instead eliminate the expressions involving $\frac {\partial \omega _{s}}{\partial \overline {\tilde {\gamma }}_{e}}$ and $\frac {\partial \boldsymbol {{\Phi }_{s}}}{\partial \overline {\tilde {\gamma }}_{e}}$, i.e. we require the last two parentheses in Eq. 38 to vanish. After transposing, this yields (23) that allows to compute λ₃ and λ₄.

The final expression of the sensitivities of ψ₁ (20) can be obtained from Eq. 38 by removing the four eliminated terms.

Appendix 2: Adjoint sensitivity analysis of the statically estimated modal stiffness and mass

The sensitivities of the statically estimated resonant frequencies (27) are obtained from the sensitivities of the statically estimated modal stiffness and mass (28).

In order to compute the sensitivities of the statically estimated modal stiffness $\tilde {k}_{m,i}$ with respect to the projected field, we first consider the correspondent static load case and partition it into the sets of free and constrained degrees of freedom (pedices f and c respectively):

$$ \begin{array}{@{}rcl@{}} \left[\begin{array}{cc} \boldsymbol{K_{ff}} & \boldsymbol{K_{fc}} \\ \boldsymbol{K_{cf}} & \boldsymbol{K_{cc}} \end{array}\right] \left[\begin{array}{cc} \boldsymbol{\tilde{\Phi}_{i,f}} \\ \boldsymbol{\tilde{\Phi}_{i,c}} \end{array}\right] = \left[\begin{array}{cc} \boldsymbol{f_{i,f}} \\ \boldsymbol{f_{i,c}} \end{array}\right] = \left[\begin{array}{cc} \boldsymbol{0} \\ \boldsymbol{f_{i,c}} \end{array}\right] \end{array} $$

(41)

Following the partition, the expression for $\tilde {k}_{m,i}$ becomes:

$$ \begin{array}{@{}rcl@{}} \tilde{k}_{m,i}& = &\boldsymbol{\tilde{\Phi}_{i,f}}^{T} \boldsymbol{K_{ff}} \boldsymbol{\tilde{\Phi}_{i,f}} + 2 \boldsymbol{\tilde{\Phi}_{i,c}}^{T} \boldsymbol{K_{cf}} \boldsymbol{\tilde{\Phi}_{i,f}} + \\ &+& \boldsymbol{\tilde{\Phi}_{i,c}}^{T} \boldsymbol{K_{cc}} \boldsymbol{\tilde{\Phi}_{i,c}} \end{array} $$

(42)

We then add to $\tilde {k}_{m,i}$ two vanishing terms related to the two sets of equations in Eq. 41:

$$ \begin{array}{@{}rcl@{}} \widehat{\tilde{k}}_{m,i}& = & \boldsymbol{\tilde{\Phi}_{i,f}}^{T} \boldsymbol{K_{ff}} \boldsymbol{\tilde{\Phi}_{i,f}} + 2 \boldsymbol{\tilde{\Phi}_{i,c}}^{T} \boldsymbol{K_{cf}} \boldsymbol{\tilde{\Phi}_{i,f}} +\\ &+& \boldsymbol{\tilde{\Phi}_{i,c}}^{T} \boldsymbol{K_{cc}} \boldsymbol{\tilde{\Phi}_{i,c}} + \boldsymbol{\nu_{1}}^{T}(\boldsymbol{K_{ff}}\boldsymbol{\tilde{\Phi}_{i,f}} + \\ &+ &\boldsymbol{K_{fc}}\boldsymbol{\tilde{\Phi}_{i,c}}) + \boldsymbol{\nu_{2}}^{T}(\boldsymbol{K_{cf}}\boldsymbol{\tilde{\Phi}_{i,f}} + \\ &+& \boldsymbol{K_{cc}}\boldsymbol{\tilde{\Phi}_{i,c}} - \boldsymbol{f_{i,c}}) \end{array} $$

(43)

The sensitivities of the above function with respect to the projected field, after rearranging the terms, become:

$$ \begin{array}{@{}rcl@{}} \frac{\partial\widehat{\tilde{k}}_{m,i}}{\partial \overline{\tilde{\gamma}}_{e}} &= & \boldsymbol{\tilde{\Phi}_{i,f}}^{T} \frac{\partial\boldsymbol{K_{ff}}}{\partial \overline{\tilde{\gamma}}_{e}} \boldsymbol{\tilde{\Phi}_{i,f}} + 2 \boldsymbol{\tilde{\Phi}_{i,c}}^{T} \frac{\partial\boldsymbol{K_{cf}}}{\partial \overline{\tilde{\gamma}}_{e}} \boldsymbol{\tilde{\Phi}_{i,f}} +\\ & + &\boldsymbol{\tilde{\Phi}_{i,c}}^{T} \frac{\partial\boldsymbol{K_{cc}}}{\partial \overline{\tilde{\gamma}}_{e}} \boldsymbol{\tilde{\Phi}_{i,c}} + \boldsymbol{\nu_{1}}^{T}\frac{\partial\boldsymbol{K_{ff}}}{\partial \overline{\tilde{\gamma}}_{e}}\boldsymbol{\tilde{\Phi}_{i,f}} + \\ & + &\boldsymbol{\nu_{1}}^{T} \frac{\partial\boldsymbol{K_{fc}}}{\partial \overline{\tilde{\gamma}}_{e}}\boldsymbol{\tilde{\Phi}_{i,c}} + \boldsymbol{\nu_{2}}^{T}\frac{\partial\boldsymbol{K_{cf}}}{\partial \overline{\tilde{\gamma}}_{e}}\boldsymbol{\tilde{\Phi}_{i,f}} + \\ &+& \boldsymbol{\nu_{2}}^{T} \frac{\partial \boldsymbol{K_{cc}}}{\partial \overline{\tilde{\gamma}}_{e}}\boldsymbol{\tilde{\Phi}_{i,c}} + \left( \vphantom{\frac{\partial \boldsymbol{S_{i}}}{\partial \omega_{s}}\boldsymbol{u_{h,r}}} \right. 2 \boldsymbol{\tilde{\Phi}_{i,f}}^{T} \boldsymbol{K_{ff}} + \\& +& 2 \boldsymbol{\tilde{\Phi}_{i,c}}^{T} \boldsymbol{K_{cf}} + \boldsymbol{\nu_{1}}^{T}\boldsymbol{K_{ff}} + \\ &+ &\boldsymbol{\nu_{2}}^{T}\boldsymbol{K_{cf}}\left. \vphantom{\frac{\partial \boldsymbol{S_{i}}}{\partial \omega_{s}}\boldsymbol{u_{h,r}}} \right) \frac{\partial\boldsymbol{\tilde{\Phi}_{i,f}}}{\partial \overline{\tilde{\gamma}}_{e}} - \boldsymbol{\nu_{2}}^{T} \frac{\partial\boldsymbol{f_{i,c}}}{\partial \overline{\tilde{\gamma}}_{e}} \end{array} $$

(44)

Requiring the terms that multiply $\frac {\partial \boldsymbol {\tilde {\Phi }_{i,f}}}{\partial \overline {\tilde {\gamma }}_{e}}$ and $\frac {\partial \boldsymbol {f_{i,c}}}{\partial \overline {\tilde {\gamma }}_{e}}$ to vanish, we get:

$$ \left[\begin{array}{cc} \boldsymbol{K_{ff}} & \boldsymbol{K_{fc}} \\ \boldsymbol{0} & \boldsymbol{I} \end{array}\right] \left[\begin{array}{cc} \boldsymbol{\nu_{1}} \\ \boldsymbol{\nu_{2}} \end{array}\right] = \left[\begin{array}{cc} -2 (\boldsymbol{K_{ff}}\boldsymbol{\tilde{\Phi}_{i,f}} + \boldsymbol{K_{fc}}\boldsymbol{\tilde{\Phi}_{i,c}}) \\ \boldsymbol{0} \end{array}\right] $$

(45)

Being the right-hand side null because of Eq. 41, we conclude that ν₁ = 0 and ν₂ = 0 that substituted in Eq. 44 gives the sensitivities of the statically estimated modal stiffness in Eq. 28.

The sensitivities of the statically estimated modal mass can be obtained by first expressing $\tilde {m}_{m,i}$ following the partition in Eq. 41 and then adding the vanishing terms related to the static load case as in Eq. 43. Thus:

$$ \begin{array}{@{}rcl@{}} \widehat{\tilde{m}}_{m,i} &= & \boldsymbol{\tilde{\Phi}_{i,f}}^{T} \boldsymbol{M_{ff}} \boldsymbol{\tilde{\Phi}_{i,f}} + 2 \boldsymbol{\tilde{\Phi}_{i,c}}^{T} \boldsymbol{M_{cf}} \boldsymbol{\tilde{\Phi}_{i,f}} +\\ &+& \boldsymbol{\tilde{\Phi}_{i,c}}^{T} \boldsymbol{M_{cc}} \boldsymbol{\tilde{\Phi}_{i,c}} + \boldsymbol{\mu_{1}}^{T}(\boldsymbol{K_{ff}}\boldsymbol{\tilde{\Phi}_{i,f}} + \\ &+ &\boldsymbol{K_{fc}}\boldsymbol{\tilde{\Phi}_{i,c}}) + \boldsymbol{\mu_{2}}^{T}(\boldsymbol{K_{cf}}\boldsymbol{\tilde{\Phi}_{i,f}} + \\ &+ &\boldsymbol{K_{cc}}\boldsymbol{\tilde{\Phi}_{i,c}} - \boldsymbol{f_{i,c}}) \end{array} $$

(46)

We now repeat the same procedure as before: we compute the sensitivities of Eq. 46 and we require the terms that multiply $\frac {\partial \boldsymbol {\tilde {\Phi }_{i,f}}}{\partial \overline {\tilde {\gamma }}_{e}}$ and $\frac {\partial \boldsymbol {f_{i,c}}}{\partial \overline {\tilde {\gamma }}_{e}}$ to vanish. We therefore obtain (29) that allows to compute the adjoint vector $\boldsymbol {\mu }=[\boldsymbol {\mu _{1}}^{T}, \boldsymbol {\mu _{2}}^{T}]^{T}$, and we get also the final expression of the sensitivities of the statically estimated modal mass (28) by removing the eliminated terms.