Locally D-optimal designs for heteroscedastic polynomial measurement error models

Abstract

This paper considers constructions of optimal designs for heteroscedastic polynomial measurement error models. Corresponding approximate design theory is developed by using corrected score function approach, which leads to non-concave optimisation problems. For the weighted polynomial measurement error model of degree p with some commonly used heteroscedastic structures, the upper bounds for the number of support points of locally D-optimal designs can be determined explicitly. A numerical example is given to show how heteroscedastic structures affect the optimal designs.

Introduction

Measurement error models, also referred to as errors-in-variables models, differ from the classical regression models in that one or more of the independent variables or covariates are subject to error. We note that the covariates are often measured with error in practice, due to human negligence, mechanical inaccuracy and systematic error. Overlooking these errors will potentially result in biased estimates, see Fuller (1987) and Carroll et al. (2006). Owing to the broad applicability of measurement error models, finding efficient experimental designs for such models is of great interest.

Recently, Konstantinou and Dette (2015) developed an approximate optimal design theory for local optimality criteria in error-in-variables models with the measurement error independent of the true covariates which is called classical errors. Konstantinou and Dette (2017) extended their previous work and provide a robust design strategy to parameter misspecification. For further references on optimal designs for measurement error models, we refer to Donev (2004), Doví et al. (1993), Keeler and Reilly (1992) and Pronzato (2002).

We note that the above-mentioned references focused on homoscedastic measurement error models. However, in practice, data occurs often with heteroscedastic errors in both response and covariates. Optimal design problems for various models with heteroscedastic errors in response have been widely studied in literature. Wong (1995) established the conditions for the Kiefer–Wolfowitz’s theorem to apply to linear models with heteroscedastic errors in response or that with the weight function $1/\lambda (\cdot )$ for some known positive functional $\lambda (\cdot )$ which is called the efficiency function. Dette and Trampisch (2010) derived the D-optimal design for the common weighted univariate polynomial regression model, which is available based on a differential equation for the logarithmic derivative of the efficiency function. Moreover, there are many results on optimal designs of multi-factor models with heteroscedastic errors under various optimality criteria, including Wong (1994), Rodríguez and Ortiz (2005), Rodríguez et al. (2016), He and Yue (2017) and among others. However, to our knowledge, there have been no reports about general methods for solving the optimal design problem under measurement error models with heteroscedasticity.

In this paper, we investigate optimal designs for the polynomial measurement error model with heteroscedasticity. Our focus is on classical errors which include the sampling and instrument recording errors frequently arising in practice. In Sect. 2, we introduce some basic notations of the weighted polynomial measurement error model of degree p and give a necessary condition for Kiefer’s $\Phi _{\ell }$-optimality criteria based on the corrected score function approach. Section 3 presents a construction of the locally D-optimal designs explicitly for the heteroscedastic polynomial measurement error model with partially specified heteroscedastic structures. The theoretical results are illustrated with a numerical example in Sect. 4, and finally, some concluding remarks are given in Sect. 5.

Estimation and optimal designs

In this section, we consider the approximate design problem in the context of univariate measurement error models with classical additive errors. The corrected score function approach (Nakamura 1990; Gimenez and Bolfarine 1997), which is called correction approach for abbreviation, is applied to correct for the effects of measurement error on parameter estimation. The information matrix of a design and a necessary condition for $\Phi _{\ell }$-optimality are obtained.

Models and estimation

Throughout the paper we consider the weighted polynomial measurement error model of degree p

$$\begin{aligned} y_{ij}=\beta _{0}+\beta _{1}x_{i}+\cdots +\beta _{p}x^{p}_{i}+e_{ij},\quad i=1,\ldots ,n,\quad j=1,\ldots ,r_{i} \end{aligned}$$

(2.1)

where $y_{ij}$ is a real-valued response, $\varvec{\beta }=(\beta _{0},\beta _{1},\ldots ,\beta _{p})^{T}$ is the vector of unknown model parameters, $x_{i}\in {\mathcal {X}}$ is a setting of the true covariate, with ${\mathcal {X}}\subset {\mathbb {R}}$ denoting the design space, n is the number of distinct experimental settings, $r_{i}$ is the number of repeated observations taken at the ith setting and $e_{ij}$ is the measurement error in the response $y_{ij}$. The unknown true value of the covariate $x_{i}$ is also subject to measurement error $u_{ij}$. In particular, it is assumed that we observe

$$\begin{aligned} z_{ij}=x_{i}+u_{ij},\quad i=1,\ldots ,n,\quad j=1,\ldots ,r_{i}. \end{aligned}$$

(2.2)

The vectors $\varvec{\varepsilon }_{ij}=(e_{ij},u_{ij})^{T}$ of response errors $e_{ij}$ and covariate errors $u_{ij}$ are assumed to be independent and normally distributed with means 0 and covariance matrix being of the form

$$\begin{aligned} \text{ Cov }(\varvec{\varepsilon }_{ij})=\left( \begin{array}{cc} \displaystyle \frac{1}{\lambda _{e}(x_{i})} &{} 0 \\ 0 &{} \displaystyle \frac{1}{\lambda _{u}(x_{i})} \\ \end{array} \right) , \quad i=1,\ldots ,n,\quad j=1,\ldots ,r_{i} \end{aligned}$$

for some known positive functions $\lambda _{e}(x)$ and $\lambda _{u}(x)$, which are called the efficiency functions and our interest here is when $\lambda _{e}(x)$ and $\lambda _{u}(x)$ are not constants on ${\mathcal {X}}$.

Definition 1

Let ${\mathcal {F}}$ be an open convex subset of a parameter space including $\varvec{\beta }$ and $l(\varvec{x},\varvec{y},\varvec{\beta })$ be the log-likelihood function. Substituting $\varvec{z}$ for $\varvec{x}$, $l(\varvec{z},\varvec{y},\varvec{\beta })$ is termed the naive log-likelihood function, considering $\varvec{x}$ is subject to error and $\varvec{z}$ is the observable value of $\varvec{x}$, then

$$\begin{aligned} U(\varvec{z},\varvec{y},\varvec{\beta })=\displaystyle \frac{\partial l(\varvec{z},\varvec{y},\varvec{\beta })}{\partial \varvec{\beta }} \end{aligned}$$

is called the naive score function.

As is well known that the naive score function $U(\varvec{z},\varvec{y},\varvec{\beta })$ leads to an inconsistent estimator of $\varvec{\beta }$ in general, when the covariates exist errors. Hence, we consider the estimation for $\varvec{\beta }$ in the measurement error model based on the correction approach.

Definition 2

A function $U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })$ is called a corrected score, if it satisfies

$$\begin{aligned} E^{*}\{U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })\}=U(\varvec{x},\varvec{y},\varvec{\beta }), \quad \varvec{\beta }\in {{{\mathcal {F}}}}, \end{aligned}$$

where $E^{*}$ denotes the conditional mean with respect to $\varvec{z}$ given $\varvec{x}$ and $\varvec{y}$. When $U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })$ is differentiable in ${\mathcal {F}}$, the quantity

$$\begin{aligned} I^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })=-\displaystyle \frac{\partial U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })}{\partial \varvec{\beta }} \end{aligned}$$

is called a corrected information. The value $\widehat{\varvec{\beta }}_{C}$ such that $U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })=0$ with $I^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })$ being positive definite is called the corrected estimator of $\varvec{\beta }$.

As in Nakamura (1990) and Gimenez and Bolfarine (1997), let $E^{+}$ denote the expectation with respect to the random variables $\varvec{y}$ and $E=E^{+}E^{*}$ denote the global expectation, then

$$\begin{aligned} E\{U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })\}=E^{+}E^{*}\{U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })\} =E^{+}\{U(\varvec{x},\varvec{y},\varvec{\beta })\}=0 \end{aligned}$$

which indicates that a corrected score function is an unbias score function.

For the measurement error model defined in (2.1) and (2.2), the corrected score function can be represented as follows

$$\begin{aligned} U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })=\sum ^{n}_{i=1}\sum ^{r_{i}}_{j=1}U^{*}_{C}(z_{ij},y_{ij},\varvec{\beta }), \end{aligned}$$

where

$$\begin{aligned} U^{*}_{C}(z_{ij},y_{ij},\varvec{\beta }) =\lambda _{e}(x_{i})\left( \begin{array}{c} y_{ij}t_{ij,0}-\sum ^{p}_{k=0}\beta _{k}t_{ij,k} \\ y_{ij}t_{ij,1}-\sum ^{p}_{k=0}\beta _{k}t_{ij,k+1} \\ \vdots \\ y_{ij}t_{ij,p}-\sum ^{p}_{k=0}\beta _{k}t_{ij,k+p} \end{array} \right) \end{aligned}$$

$t_{ij,k}$ is defined such that $E^{*}(t_{ij,k})=x^{k}_{i}$ and can be computed recursively from

$$\begin{aligned} t_{ij,0}=1,\quad t_{ij,1}=z_{ij},\quad t_{ij,k+1}=z_{ij}t_{ij,k}-\frac{kt_{ij,k-1}}{\lambda _{u}(x_{i})}, \end{aligned}$$

(2.3)

$i=1,\ldots ,n,~j=1,\ldots ,r_{i},~k=1,\ldots ,2p-1$, which was derived by Stefanski (1989) for the homoscedastic case, but his arguments go through also in the heteroscedastic case.

According to the recursive formulas (2.3), the conditional mean of the product of any two elements $t_{ij,k}$ and $t_{ij,l}$ can be expressed in the following form:

$$\begin{aligned} E^{*}(t_{ij,k}t_{ij,l})=\sum \limits _{q=0}^{k}\left( {\begin{array}{c}k\\ q\end{array}}\right) \displaystyle \frac{l!}{(l-q)!\lambda ^{q}_{u}(x_{i})}x^{l+k-2q}_{i}, \quad 1\le k\le l\le 2p. \end{aligned}$$

(2.4)

The limiting properties of the corrected estimator $\widehat{\varvec{\beta }}_{C}$ as the sample sizes increase are derived under the assumption

$$\begin{aligned} \lim _{r_{i}\rightarrow \infty }\displaystyle \frac{r_{i}}{r}=\omega _{i}>0 ,\quad i=1,\ldots ,n \end{aligned}$$

as $r_{i}\rightarrow \infty$, where $r=\sum _{i=1}^{n}r_{i}$ is the total number of trials. In this paper we collect the information provided by the different experimental conditions and the limiting relation above in the matrix

$$\begin{aligned} \xi =\left\{ \begin{array}{cccc} x_{1} &{} x_{2} &{} \cdots &{} x_{n} \\ \\ \omega _{1} &{} \omega _{2} &{} \cdots &{} \omega _{n} \\ \end{array} \right\} , \quad 0<\omega _{i}\le 1, \quad \sum ^{n}_{i=1}\omega _{i}=1. \end{aligned}$$

(2.5)

Note that $\xi$ defines a probability measure on the design space ${\mathcal {X}}$ and following Kiefer (1974), we call any probability measure of the form (2.5) an approximate design on ${\mathcal {X}}\subset {\mathbb {R}}.$

For illustrative purposes, two expressions are marked before describing the asymptotic covariance

$$\begin{aligned} I_{1}(x_{i},\varvec{\beta })&:= E\{I^{*}_{C}(z_{ij},y_{ij},\varvec{\beta })\}, \\ I_{2}(x_{i},\varvec{\beta })&:= E\{U^{*}_{C}(z_{ij},y_{ij},\varvec{\beta })U^{*}_{C}(z_{ij},y_{ij},\varvec{\beta })^{T}\}, \end{aligned}$$

where $i=1,\ldots ,n;~j=1,\ldots ,r_{i}.$

On account of Theorems 1 and 3 of Zavala et al. (2007), we can obtain the asymptotic properties of the corrected estimator $\widehat{\varvec{\beta }}_{C}$ for the model parameters $\varvec{\beta }$:

$$\begin{aligned} r^{1/2}(\widehat{\varvec{\beta }}_{C}-\varvec{\beta }_{0}){\mathop {\rightarrow }\limits ^{L}} N(0,M^{-1}_{C}(\xi , \varvec{\beta })), \end{aligned}$$

where $\varvec{\beta }_{0}$ is the true value of model parameters, ${\mathop {\rightarrow }\limits ^{L}}$ denotes convergence in distribution and the inverse of the asymptotic covariance matrix $M_{C}(\xi , \varvec{\beta })$ is called information matrix of the design $\xi$ (e.g., see Pukelsheim 2006). Here we assume that there exists a design $\xi$, such that $M_{C}(\xi , \varvec{\beta })$ is nonsingular. The information matrix $M_{C}(\xi , \varvec{\beta })$ is given by

$$\begin{aligned} M_{C}(\xi , \varvec{\beta })=D_{0}(\xi ,\varvec{\beta })D^{-1}_{1}(\xi ,\varvec{\beta })D_{0}(\xi ,\varvec{\beta }), \end{aligned}$$

(2.6)

where the matrices $D_{0}(\xi ,\varvec{\beta })$ and $D_{1}(\xi ,\varvec{\beta })$ are as below

$$\begin{aligned} \begin{aligned} D_{0}(\xi ,\varvec{\beta })&=\displaystyle \frac{1}{r}E\{I^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })\}\\&=\displaystyle \frac{1}{r}\sum _{i=1}^{n}\sum _{j=1}^{r_{i}}E\{I^{*}_{C}(z_{ij},y_{ij},\varvec{\beta })\}\\&=\displaystyle \frac{1}{r}\sum _{i=1}^{n}r_{i}I_{1}(x_{i},\varvec{\beta })\\&=\int _{{\mathcal {X}}}I_{1}(x,\varvec{\beta })d\xi (x) \end{aligned} \end{aligned}$$

(2.7)

and

$$\begin{aligned} \begin{aligned} D_{1}(\xi ,\varvec{\beta })&=\displaystyle \frac{1}{r}E\left\{ U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })U^{*}_{C}(\varvec{z},\varvec{y},\varvec{\beta })^{T}\right\} \\&=\displaystyle \frac{1}{r}\sum _{i=1}^{n}\sum _{j=1}^{r_{i}}E\left\{ U^{*}_{C}(z_{ij},y_{ij},\varvec{\beta }) U^{*}_{C}(z_{ij},y_{ij},\varvec{\beta })^{T}\right\} \\&=\displaystyle \frac{1}{r}\sum _{i=1}^{n}r_{i}I_{2}(x_{i},\varvec{\beta })\\&=\int _{{\mathcal {X}}}I_{2}(x,\varvec{\beta })d\xi (x). \end{aligned} \end{aligned}$$

(2.8)

For simplicity, we will consider the case where the ratio of two efficiency functions is constant over the design space, i.e., we assume that

$$\begin{aligned} \displaystyle \frac{\lambda _{e}(x)}{\lambda _{u}(x)}=c, \quad x\in {\mathcal {X}}, \end{aligned}$$

where c is a positive constant. It is remarkable that formula (2.6) evolves into the information matrix of heteroscedastic polynomial regression model, if $c=0$.

Optimal designs

In designs of experiments, an extremely useful tool for characterizing optimal designs and verifying the optimality of a candidate design is the general equivalence theorem, see Silvey (1980) and Atkinson et al. (2007). However, the mapping $\xi \rightarrow M_{C}(\xi ,\varvec{\beta })$ is in general not concave under the measurement error structure we consider here. The following Theorem 1 only provides a necessary condition for Kiefer’s $\Phi _{\ell }$-optimality which is of practical importance. As Dette and Trampisch (2012) point out, the optimal design problem is in fact an infinite-dimensional one, because there exists no upper bound on the number of support points of the designs under consideration. The necessary conditions make the infinite-dimensional optimization problem reduce to a finite-dimensional one, which is numerically tractable.

Kiefer’s $\Phi _{\ell }$-optimality criteria for the $(p+1)\times (p+1)$ information matrix $M_{C}(\xi ,\varvec{\beta })$ is defined by

$$\begin{aligned} \Phi _{\ell }(M_{C}(\xi ,\varvec{\beta })) =\left\{ \displaystyle \frac{1}{p+1}\text{ tr }[M^{\ell }_{C}(\xi ,\varvec{\beta })]\right\} ^{1/\ell }, \quad \ell \in [-\infty ,1), \end{aligned}$$

which includes the prominent D-, A- and E-optimality ($\ell =0$, $\ell =-1$, $\ell =-\infty$, respectively). A design $\xi ^{*}$ is called $\Phi _{\ell }$-optimal for the measurement error model defined in (2.1) and (2.2), if it maximizes $\Phi _{\ell }(M_{C}(\xi ,\varvec{\beta }))$ for a given $\ell \in [-\infty ,1)$. Note that the $\Phi _{\ell }$-optimal design depends on the values of unknown parameters $\varvec{\beta }$, which is called locally optimal design.

Theorem 1

If $\ell \in (-\infty ,1)$, any locally $\Phi _{\ell }$-optimal design $\xi ^{*}$ on ${\mathcal {X}}$ for estimating $\varvec{\beta }$ by the correction approach in any functional model defined by (2.1) and (2.2) satisfies the inequality

$$\begin{aligned} d_{C}(x,\xi ^{*},\varvec{\beta }):= 2d_{0}(x,\xi ^{*},\varvec{\beta })-d_{1}(x,\xi ^{*},\varvec{\beta })\le \text{ tr }\{M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })\} \end{aligned}$$

(2.9)

for all $x\in {\mathcal {X}}$, where

$$\begin{aligned} d_{0}(x,\xi ^{*},\varvec{\beta })&=\text{ tr }\{D^{-1}_{0}(\xi ^{*},\varvec{\beta })M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })I_{1}(x,\varvec{\beta })\}, \\ d_{1}(x,\xi ^{*},\varvec{\beta })&=\text{ tr }\{D^{-1}_{0}(\xi ^{*},\varvec{\beta })M^{\ell +1}_{C}(\xi ^{*},\varvec{\beta }) D^{-1}_{0}(\xi ^{*},\varvec{\beta })I_{2}(x,\varvec{\beta })\}. \end{aligned}$$

Furthermore, the maximum of $d_{C}(x,\xi ^{*},\varvec{\beta })$ is achieved at the support points $x^{*}$ of $\xi ^{*}$.

Proof

For the $\Phi _{\ell }$-optimal design $\xi ^{*}$ and any design $\xi$, let $\xi _{a}=(1-a)\xi ^{*}+a\xi$ with $a\in [0,1]$. Denote

$$\begin{aligned} \pi (\xi )=\log \{\Phi _{\ell }[M_{C}(\xi , \varvec{\beta })]\}=\displaystyle \frac{1}{\ell }\{\log \{\text{ tr }[M^{\ell }_{C}(\xi ,\varvec{\beta })]\}-\log (p+1)\}. \end{aligned}$$

The Fŕechet derivative of $\pi (\xi )$ at $\xi ^{*}$ is given by

$$\begin{aligned}&\displaystyle \frac{d}{da}\pi (\xi _{a})\mid _{a=0}\\&\quad =\displaystyle \frac{1}{\ell \text{ tr }\{M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })\}}\displaystyle \frac{d}{da}\text{ tr }\{M^{\ell }_{C}(\xi _{a}, \varvec{\beta })\}\mid _{a=0}\\&\quad =\displaystyle \frac{1}{\text{ tr }\{M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })\}}\text{ tr }\{M^{\ell -1}_{C}(\xi ^{*}, \varvec{\beta })\displaystyle \frac{d}{da}D_{0}(\xi _{a},\varvec{\beta })D^{-1}_{1}(\xi _{a},\varvec{\beta })D_{0}(\xi _{a},\varvec{\beta })\}\mid _{a=0}\\&\quad =\displaystyle \frac{1}{\text{ tr }\{M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })\}} \Big [2\text{ tr }\{D^{-1}_{0}(\xi ^{*},\varvec{\beta })M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })D_{0}(\xi ,\varvec{\beta })\}-\text{ tr }\{M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })\}\\&\qquad -\,\text{ tr }\{D^{-1}_{0}(\xi ^{*},\varvec{\beta })M^{\ell +1}_{C}(\xi ^{*}, \varvec{\beta })D^{-1}_{0}(\xi ^{*},\varvec{\beta })D_{1}(\xi ,\varvec{\beta })\}\Big ]. \end{aligned}$$

Now replacing $\xi$ by Dirac measures $\delta _{x}$ with weight 1 at the support points $x\in {\mathcal {X}}$ and noting expressions (2.7) and (2.8), we then have

$$\begin{aligned} d_{0}(x,\xi ^{*},\varvec{\beta })&=\text{ tr }\{D^{-1}_{0}(\xi ^{*},\varvec{\beta })M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })D_{0}(\delta _{x},\varvec{\beta })\}\\&=\text{ tr }\{D^{-1}_{0}(\xi ^{*},\varvec{\beta })M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })I_{1}(x,\varvec{\beta })\} \end{aligned}$$

and

$$\begin{aligned} d_{1}(x,\xi ^{*},\varvec{\beta })&=\text{ tr }\{D^{-1}_{0}(\xi ^{*},\varvec{\beta })M^{\ell +1}_{C}(\xi ^{*}, \varvec{\beta })D^{-1}_{0}(\xi ^{*},\varvec{\beta })D_{1}(\delta _{x},\varvec{\beta })\}\\&=\text{ tr }\{D^{-1}_{0}(\xi ^{*},\varvec{\beta })M^{\ell +1}_{C}(\xi ^{*}, \varvec{\beta })D^{-1}_{0}(\xi ^{*},\varvec{\beta })I_{2}(x,\varvec{\beta })\}. \end{aligned}$$

Since $\xi ^{*}$ is $\Phi _{\ell }$-optimal, $\displaystyle \frac{d}{da}\pi (\xi _{a})\mid _{a=0}$ is non-positive for any $\xi$ and then the inequality

$$\begin{aligned} d_{C}(x,\xi ^{*},\varvec{\beta })\le \text{ tr }\{M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })\} \end{aligned}$$

follows for all $x\in {\mathcal {X}}$.

For the proof of the equality part of Theorem 1, let us assume that

$$\begin{aligned} \max _{x\in {\mathcal {X}}}d_{C}(x,\xi ^{*},\varvec{\beta })<\text{ tr }\{M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })\}. \end{aligned}$$

Then

$$\begin{aligned} \int _{{\mathcal {X}}}d_{C}(x,\xi ^{*},\varvec{\beta })d\xi ^{*}(x)<\int _{{\mathcal {X}}}\text{ tr }\{M^{\ell }(\xi ^{*}, \varvec{\beta })\}d\xi ^{*}(x)=\text{ tr }\{M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })\}. \end{aligned}$$

Now for any design $\xi$, from the expression on the left side of (2.9), we have

$$\begin{aligned} \int _{{\mathcal {X}}}d_{C}(x,\xi ,\varvec{\beta })d\xi (x)&=2\text{ tr }\{D^{-1}_{0}(\xi ,\varvec{\beta })M^{\ell }_{C}(\xi ,\varvec{\beta })\int _{{\mathcal {X}}}I_{1}(x,\varvec{\beta })d\xi (x)\}\\&\quad -tr\{D^{-1}_{0}(\xi ,\varvec{\beta })M^{\ell +1}_{C}(\xi ,\varvec{\beta })D^{-1}_{0}(\xi ,\varvec{\beta }) \int _{{\mathcal {X}}}I_{2}(x,\varvec{\beta })d\xi (x)\}\\&=2\text{ tr }\{D^{-1}_{0}(\xi ,\varvec{\beta })M^{\ell }_{C}(\xi ,\varvec{\beta })D_{0}(\xi ,\varvec{\beta })\}\\&\quad -\text{ tr }\{D^{-1}_{0}(\xi ,\varvec{\beta })M^{\ell +1}_{C}(\xi ,\varvec{\beta })D^{-1}_{0}(\xi ,\varvec{\beta })D_{1}(\xi ,\varvec{\beta })\}\\&=\text{ tr }\{M^{\ell }_{C}(\xi ,\varvec{\beta })\}, \end{aligned}$$

which contradicts our initial assumption. Hence

$$\begin{aligned} \max _{x\in {\mathcal {X}}}d_{C}(x,\xi ^{*},\varvec{\beta })=\text{ tr }\{M^{\ell }_{C}(\xi ^{*}, \varvec{\beta })\} \end{aligned}$$

which is attained at the support of $\xi ^{*}$, and this completes the proof of Theorem 1. $\square$

In what follows, we focus on the most commonly used criterion of D-optimality which corresponds to $\ell =0$ in Kiefer’s $\Phi _{\ell }$-optimality.

Corollary 1

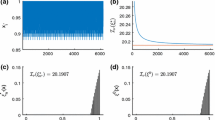
A locally D-optimal design $\xi ^{*}$ on ${\mathcal {X}}$ for estimating $\varvec{\beta }$ by the correction approach in the model defined by (2.1) and (2.2) satisfies the inequality$d_{C}(x,\xi ^{*},\varvec{\beta })\le p+1$ for all $x\in {\mathcal {X}}$. Moreover, at the points of the locally D-optimal design $\xi ^{*}$,

$$\begin{aligned} p+1-d_{C}(x,\xi ^{*},\varvec{\beta })=0, \end{aligned}$$

(2.10)

and the remaining points

$$\begin{aligned} p+1-d_{C}(x,\xi ^{*},\varvec{\beta })>0. \end{aligned}$$

(2.11)

Before ending this section, we provide an upper bound of the number of roots of the equation in (2.10), based on the property of the Chebycheff system (see Karlin et al. 1966).

Lemma 1

The left side of Eq. (2.10) can be represented by a linear combination of the following $4p^2$ functions:

$$\begin{aligned} x^{i-2j}\lambda _e^{1-j}(x),\quad j=0,1,\ldots ,2p-1; \quad i=2j,2j+1,\ldots ,4p-2. \end{aligned}$$

(2.12)

If functions (2.12) form a Chebycheff system, the equality (2.10) has no more than $4p^{2}-1$ roots.

Proof

Let $\lambda _{u}(x)=\lambda _{e}(x)/c$ and $\xi ^{*}$ be a locally D-optimal design for the correction approach in measurement error model defined by (2.1) and (2.2). Also let

$$\begin{aligned} D^{-1}_{0}(\xi ^{*},\varvec{\beta })=\big (a_{ij}\big )_{(p+1)\times (p+1)}, \quad D^{-1}_{1}(\xi ^{*},\varvec{\beta })=\big (b_{ij}\big )_{(p+1)\times (p+1)}, \end{aligned}$$

where the entries $a_{ij}$ and $b_{ij}\in {\mathbb {R}}$. In view of formula (2.9), the Eq. (2.10) becomes

$$\begin{aligned} p+1-2\text{ tr }\{D^{-1}_{0}(\xi ^{*},\varvec{\beta })I_{1}(x,\varvec{\beta })\} +\text{ tr }\{D^{-1}_{1}(\xi ^{*},\varvec{\beta })I_{2}(x,\varvec{\beta })\}=0. \end{aligned}$$

(2.13)

It can be shown by calculation that the left side of the equation in (2.13) is a linear combination composed of $4p^{2}$ functions given in (2.12), based on the formulas in (2.4). If the functions form a Chebycheff system, any nontrivial linear combination of these functions has at most $4p^{2}-1$ distinct zeros, which completes the proof. $\square$

Construction of locally D-optimal designs

In this section we focus on the locally D-optimal designs for the measurement error models defined in (2.1) and (2.2) and choose $\lambda _{e}(x)$ and $\lambda _{u}(x)$ to be one of several classes of efficiency functions commonly used for modeling heteroscedasticity; see, e.g., Fedorov (1972) and Dette and Trampisch (2012). They are given as follows:

• (i) $\lambda (x)=e^{-x}, \qquad x\in [0,+\infty );$

• (ii) $\lambda (x)=x^{-n},\qquad x\in (0,+\infty ), \; n=1, 2.$

Theorem 2

The locally D-optimal design on ${\mathcal {X}}=[x_{l},x_{u}]\subset [0,\infty )$ for the weighted polynomial measurement error model of degree p defined in (2.1) and (2.2) with efficiency functions in (i) has at most $2p^{2}$ support points. Moreover, if $p=1$, the locally D-optimal design for the linear measurement error model has exactly two support points including point $x_{l}$.

Proof

For the efficiency function in (i), we find that the left side of Eq. (2.10) is a linear combination composed of the following $4p^{2}$ functions:

$$\begin{aligned} x^{i-2j}e^{(j-1)x}, \quad j=0,1,\ldots ,2p-1 ; \quad i=2j,2j+1,\ldots ,4p-2. \end{aligned}$$

(3.1)

By simplifying, the linear combination is a not identically vanishing exponential polynomial $\sum ^{2p-2}_{i=-1}q_{i}(x)e^{ix}$, where $q_{-1}(x),q_{0}(x),\ldots ,q_{2p-3}(x),q_{2p-2}(x)$ is a real ordinary polynomial of degree $4p-2,4p-4,\ldots ,2,0$ respectively, admits at most $[(4p-2+1)+(4p-4+1)+\cdots +(2+1)+(0+1)]-1=4p^2-1$ zeros (see Pólya and Szegö 1925, Vol. II, p. 48, problem 75).

Now, we assume that the locally D-optimal design for the weighted polynomial measurement error model of degree p consists of at least $2p^{2}+1$ points and consider the function

$$\begin{aligned} \Psi (x):=p+1-d_{0}(x,\xi ^{*},\varvec{\beta })-\gamma , \end{aligned}$$

where $\gamma$ is a small positive number.

If all support points of the design are found inside ${\mathcal {X}}=[x_{l},x_{u}]$, then by (2.10) and (2.11) the number of distinct roots of the function $\Psi (x)$ is larger than or equal to $4p^{2}+2$. If one or two points of the design are at the end, then the number of distinct roots will be, respectively, no less than $4p^{2}+1$ or $4p^{2}$. In this way, for the weighted polynomial measurement error model of degree p the number of distinct roots of the function $\Psi (x)$ is $m\ge 4p^{2},$ which contradicts the previous conclusion. Therefore, the locally D-optimal design for the model (2.1) and (2.2) has at most $2p^{2}$ support points.

On the other hand, it is evident that the number of points of the design must be greater than or equal to $p+1$, otherwise the information matrix will be degenerate. Therefore, if $p=1$, the locally D-optimal design for the linear measurement error model has exactly two support points.

Using (2.6), the determinant of the information matrix of design $\xi =\{x_1, x_2; \omega _1,\omega _2\}$ with $\omega _1+\omega _2=1$ for the linear polynomial measurement error model is given by

$$\begin{aligned}&\det M_{C}(\xi ,\varvec{\beta })\\&\quad =[\det D_{0}(\xi ,\varvec{\beta })]^{2}[\det D_{1}(\xi ,\varvec{\beta })]^{-1}\\&\quad =\left[ \det \left( \sum _{i=1}^{2}\omega _{i}I_{1}(x_{i},\varvec{\beta })\right) \right] ^{2} \left[ \det \left( \sum _{i=1}^{2}\omega _{i}I_{2}(x_{i},\varvec{\beta })\right) \right] ^{-1}\\&\quad =\omega _1^{2}\omega _2^{2} \left( \displaystyle \frac{c\omega _1(1+\beta ^{2}_{1}c)(1+2\beta ^{2}_{1}c)e^{x_{1}+2x_{2}}}{(x_{2}-x_{1})^{4}} +\displaystyle \frac{c\omega _2(1+\beta ^{2}_{1}c)(1+2\beta ^{2}_{1}c)e^{2x_{1}+x_{2}}}{(x_{2}-x_{1})^{4}} \right. \\&\qquad +\left. \displaystyle \frac{\omega _1\omega _2(1+\beta ^{2}_{1}c)^{2}e^{x_{1}+x_{2}}}{(x_{2}-x_{1})^{2}}\right) ^{-1} \end{aligned}$$

It is straightforward to verify that $\det \{M_{C}(\xi ,\varvec{\beta })\}$ is decreasing with $x_{1}$, for fixed $\omega _1$ and $x_{2}$. Therefore, it is maximized at $x^{*}_{1}=x_{l}$. $\square$

Theorem 3

The locally D-optimal design on ${\mathcal {X}}=[x_{l},x_{u}]\subset (0,\infty )$ for the weighted polynomial measurement error model of degree p defined in (2.1) and (2.2) with efficiency functions in (ii) has at most 2p support points. Moreover, if $p=1$, the locally D-optimal design for the linear measurement error model is unique and has exactly two support points. This design is

$$\begin{aligned} \xi ^{*}=\left\{ \begin{array}{cc} x_{l} &{}\quad x_{u} \\ \omega _{1} &{}\quad \omega _{2} \end{array} \right\} . \end{aligned}$$

Proof

Firstly, we take $\lambda _{e}(x)=x^{-1}$ as an example to prove. It is readily to verify that the left side of the equality (2.10) is a linear combination composed of $4p-1$ functions $x^{-1},1,x,\ldots ,x^{4p-4},x^{4p-3}$, based on formulas (2.12).

Let $0\le x_{l}<x_{1}<\cdots <x_{4p-1}\le x_{u}$, then

$$\begin{aligned} V=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} x^{-1}_{1} &{} x^{-1}_{2} &{} \cdots &{} x^{-1}_{4p-1} \\ 1 &{} 1 &{} \cdots &{} 1 \\ x_{1} &{} x_{2} &{} \cdots &{} x_{4p-1} \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ x^{4p-4}_{1} &{} x^{4p-4}_{2} &{} \cdots &{} x^{4p-4}_{4p-1} \\ x^{4p-3}_{1} &{} x^{4p-3}_{2} &{} \cdots &{} x^{4p-3}_{4p-1} \\ \end{array} \right) , \end{aligned}$$

whose determinant is as follows

$$\begin{aligned} |V|=\frac{\prod _{1\le i<j\le 4p-1}(x_{j}-x_{i})}{\prod ^{4p-1}_{k=1}x_{k}}>0. \end{aligned}$$

Hence, $4p-1$ functions $x^{-1},1,x,\ldots ,x^{4p-4},x^{4p-3}$ form a Chebycheff system. According to the result of the Lemma 1, the equality (2.10) has no more than $4p-2$ roots.

Similarly, we assume that the locally D-optimal design for the weighted polynomial measurement error model of degree p consists of at least $2p+1$ points. Considering the function

$$\begin{aligned} \Psi (x):=p+1-d_{0}(x,\xi ^{*},\varvec{\beta })-\gamma , \end{aligned}$$

where $\gamma$ is a small positive number.

If all support points of the design are found inside ${\mathcal {X}}=[x_{l},x_{u}]$, then by (2.10) and (2.11) the number of distinct roots of the function $\Psi (x)$ is larger than or equal to $4p+2$. If one or two points of the design are at the end, then the number of distinct roots will be, respectively, no less than $4p+1$ or 4p. In this way, for the weighted polynomial measurement error model of degree p the number of distinct roots of the function $\Psi (x)$ is $m\ge 4p$, which contradicts the previous conclusion. Hence, the locally D-optimal design for the model (2.1) and (2.2) has at most 2p support points.

On the other hand, it is evident that the number of points of the design must be greater than or equal to $p+1$, otherwise the information matrix will be degenerate. Therefore, if $p=1$, the locally D-optimal design for the linear measurement error model has exactly two support points.

Therefore, using (2.6), the determinant of the information matrix of design $\xi =\{x_1, x_2; \omega _1,\omega _2\}$ with $\omega _1+\omega _2=1$ for the linear measurement error model is given by

$$\begin{aligned}&\det M_{C}(\xi ,\varvec{\beta })\\&\quad =[\det D_{0}(\xi ,\varvec{\beta })]^{2}[\det D_{1}(\xi ,\varvec{\beta })]^{-1}\\&\quad =\left[ \det \left( \sum _{i=1}^{2}\omega _{i}I_{1}(x_{i},\varvec{\beta })\right) \right] ^{2} \left[ \det \left( \sum _{i=1}^{2}\omega _{i}I_{2}(x_{i},\varvec{\beta })\right) \right] ^{-1}\\&\quad =\omega _1^{2}\omega _2^{2} \left( \displaystyle \frac{c\omega _1(1+\beta ^{2}_{1}c)(1+2\beta ^{2}_{1}c)x_{1}x^{2}_{2}}{(x_{2}-x_{1})^{4}} +\displaystyle \frac{f\omega _2(1+\beta ^{2}_{1}c)(1+2\beta ^{2}_{1}c)x^{2}_{1}x_{2}}{(x_{2}-x_{1})^{4}} \right. \\&\qquad +\left. \displaystyle \frac{\omega _1\omega _2(1+\beta ^{2}_{1}c)^{2}x_{1}x_{2}}{(x_{2}-x_{1})^{2}}\right) ^{-1}. \end{aligned}$$

It is easy to show that $\det \{M_{C}(\xi ,\varvec{\beta })\}$ is decreasing with $x_{1}$, for fixed $\omega _1$ and $x_{2}$. Likewise, Fixing $\omega _1$ and $x_{1}$, $\det \{M_{C}(\xi ,\varvec{\beta })\}$ is increasing with $x_{2}$ on the $[x_{l},x_{u}]$ and so $\det \{M_{C}(\xi ,\varvec{\beta })\}$ reaches its maximum at $(x_{l}, x_{u})$.

The proof for the case $\lambda _{e}(x)=x^{-2}$ can be conducted by means of a similar argument, and it is omitted here. $\square$

Numerical results

This section presents some numerical results of the locally D-optimal designs for the linear measurement error model

$$\begin{aligned} \begin{array}{l} y_{ij}=\beta _{0}+\beta _{1}x_{i}+e_{ij},\\ z_{ij}=x_{i}+u_{ij}, \end{array} \quad i=1,\ldots ,n, \quad j=1,\ldots ,r_{i}, \end{aligned}$$

(4.1)

where $(e_{ij},u_{ij})^{T}\sim N_{2}((0,0)^T, \text{ diag }(1/\lambda _e(x_{i}), c/\lambda _e(x_{i}))$, and the design space is ${\mathcal {X}}=[1,4]$. Suppose that a prior information regarding the model parameter value is available by preliminary experiments, e.g., $(\beta _{0},\beta _{1})=(1.1158,0.7516)$.

We calculate numerically the locally D-optimal designs for this model with various values of c and different efficiency function $\lambda _e(x)$ on ${\mathcal {X}}=[1,4]$ of the form in (i)–(ii). We note from the results that the D-optimal designs are effected by the values of c and $\beta _1$, but not sensitive to $\beta _0$. Therefore in what follows we will fix the value of $\beta _0$, i.e., $\beta _0=1.1158$. To compare the performance of different designs, we define a relative efficiency of a design $\xi$ with respect to a locally D-optimal design $\xi ^{*}$ for the measurement error model as follows:

$$\begin{aligned} RE(\xi ^{*}_{c,\beta _{1}})=\displaystyle \frac{\Phi (\xi ^{*}_{0})}{\Phi (\xi ^{*}_{c,\beta _{1}})}=\left( \displaystyle \frac{\det M_{C}(\xi ^{*}_{c,\beta _{1}})}{\det M_C(\xi ^{*}_{0})}\right) ^{1/2}, \end{aligned}$$

where $\xi ^*_0$ denotes the D-optimal design for model (4.1) with the efficiency function $\lambda _e(x)$ and $c=0$. Note that the case of $c=0$ means that $u_{ij}=0$ in (4.1), and then $\xi ^*_0$ does not depend on the value of $(\beta _{0},\beta _{1})$. Let $\xi ^{*}_{c,\beta _{1}}$ represents the locally D-optimal design for model (4.1) with the efficiency function $\lambda _e(x)$ under values of c and $\beta _{1}$ while $\beta _0=1.1158$ is fixed.

Table 1 lists the relative efficiencies of $\xi ^{*}_{0}$ compared to $\xi ^{*}_{c,\beta _1}$ with efficiency functions $\lambda _e(x)$ in (i)–(ii) under the given c and $\beta _{1}$, respectively.

Table 1 Relative efficiencies of $\xi ^{*}_0$ compared to the locally D-optimal designs $\xi ^{*}_{c,\beta _1}$ for model (4.1) with efficiency function $\lambda _e(x)$ on ${\mathcal {X}}=[1,4]$ for fixed $\beta _0=1.1158$

From Table 1 we observe that the optimal design $\xi ^{*}_{c,\beta _1}$ is sensitive to the ratio c of two efficiency functions and the model parameter $\beta _{1}$. This is particularly true for c, where a small change can result in an enormous loss in efficiencies. If the value of $\beta _{1}$ is correctly specified, the relative efficiency obtained by using correction approach only depends on the ratio c of two efficiency functions, and $RE(\xi ^{*}_{c,\beta _1})$ decreases quickly as c increases.

For the model with higher degrees, a practical way to find the locally D-optimal saturated designs is to proceed numerically. Through a large number of simulations, we find that the results of relative efficiencies are similar to those in the case $p=1$.

Concluding remarks

This paper extends the work of Konstantinou and Dette (2015) to heteroscedastic cases. We first develop the necessary optimality condition for Kiefer’s $\Phi _{\ell }$-criteria based on the correction approach for the weighted polynomial measurement error model of degree p, and then the upper bounds for the number of support points for the model with partially typical heteroscedastic structures are depicted explicitly, especially, the locally D-optimal design is unique and can be constructed for the linear measurement error model. Moreover, our numerical results show that the optimal designs under the heteroscedastic assumption are sensitive to the ratio of efficiency functions and the parameters in the model. It is of particular importance to take measurement errors into account for the planning of experiments in the presence of measurement error in variables.