Experimental characterization of the hypersonic flow around a cuboid

Abstract

Understanding the hypersonic flow around faceted shapes is important in the context of the fragmentation and demise of satellites undergoing uncontrolled atmospheric entry. To better understand the physics of such flows, as well as the satellite demise process, we perform an experimental study of the Mach 5 flow around a cuboid geometry in the University of Manchester High SuperSonic Tunnel. Heat fluxes are measured using infrared thermography and a 3D inverse heat conduction solution, and flow features are imaged using schlieren photography. Measurements are taken at a range of Reynolds numbers from ${40.0 \times 10^3}$ to ${549 \times 10^3}$. The schlieren results suggest the presence of a separation bubble at the windward edge of the cube at high Reynolds numbers. High heat fluxes are observed near corners and edges, which are caused by boundary-layer thinning. Additionally, on the side (off-stagnation) faces of the cube, we observe wedge-shaped regions of high heat flux emanating from the windward corners of the cube. We attribute these to vortical structures being generated by the strong expansion around the cube’s corners. We also observe that the stagnation point of the cube is off-centre of the windward face, which we propose is due to sting flex under aerodynamic loading. Finally, we propose a simple method of calculating the stagnation point heat flux to a cube, as well as relations which can be used to predict hypersonic heat fluxes to cuboid geometries such as satellites during atmospheric re-entry.

Graphic abstract

1 Introduction

A half century of human space flight and exploitation has resulted in approximately 6000 satellites being placed in orbit around the Earth. Due to their limited operational lifespan, fewer than one in six of those satellites are still operational, leaving a large number of decommissioned satellites in orbit around the Earth (ESA’s Annual Space Environment 2019). Due to the limited availability of Earth orbits, the presence of decommissioned satellites in space increases the risk of in-orbit collisions and the associated risks of space debris. To address these problems, satellites must be disposed of at their end-of-life. The method of disposal generally depends on the orbit the satellite is placed in. Due to their high altitudes, satellites in Geostationary Earth Orbit (GEO) are often raised to a graveyard orbit well away from the other common orbits. On the other hand, decommissioned satellites in Low Earth Orbit (LEO) are often left alone at the end of their life, as their low orbits will gradually decay due to the atmospheric drag experienced in LEO. Eventually this results in an uncontrolled atmospheric re-entry. For smaller satellites, a re-entry event will induce temperatures and forces large enough to destroy the satellite, with with only limited parts making groundfall. As the satellite size increases however it becomes more and more likely that significant satellite mass will hit the ground.

Satellite debris impacting the Earth carries with it a casualty risk which, although small for any given re-entry event, cannot be neglected due to the sheer number of satellites in orbit above the Earth. As a result, it is generally accepted that space users have a duty to minimize the risks associated with re-entry events (Merrifield et al. 2014). To this end, the European Space Agency issued an instruction in 2014 that the casualty risk for any re-entry event should be no greater than 1 in $10^{4}$ (Dordain 2014). A number of other national space agencies, including NASA, also adhere to this figure (IADC 2007). Estimates of the ground casualty risk associated with re-entry are calculated using dedicated tools (Koppenwallner et al. 2005; Martin et al. 2005) which must take into account the number of objects involved, their fragmentation and demise mechanisms, the effective cross-sections of the surviving components, their most likely locations as they hit the ground, as well as an accurate population density map of the Earth.

In particular, there remains considerable uncertainty in predictions of the aerothermodynamic heating rates induced by the hypersonic flow around satellites during re-entry. This is largely due to the fact that satellite geometries are significantly different from most other re-entry bodies—they are typified by sharp corners, facets, and multi-scale structures. These features cause strong expansions and compressions in the flow around the satellite, significantly thinning or thickening the boundary-layer and therefore increasing or decreasing local heating rates. Beyond the obvious importance of understanding what the maximum heat flux to a body is, some recent studies have suggested that satellite fragmentation mechanisms are driven by failure of fasteners and glues rather than melting of body panels (Soares and Merrifield 2018). As these components are often located near corners and edges, fully understanding the heating rates at these locations is particularly important.

The fundamental roadblock to a better understanding of the re-entry heating rates to satellites is that there is very little freely available high-fidelity data, either experimental or numerical, of hypersonic aerothermal heating to faceted shapes such as cuboids, plates, or cylinders. Heating rates to flat-ended cylinders were analysed experimentally and theoretically in Eaves (1968), Inouye et al. (1968), Klett (1964), Kuehn (1963), and Matthews and Eaves (1967). In particular, the work of Matthews and Eaves (1967) identified that, at certain conditions, a separation bubble can form immediately downstream of a cylinder’s expansion edge. Unfortunately, there are no data available for heating rates under the separation bubble. Nevertheless, the authors suggested that these heat fluxes, and the separation bubble formation, are highly dependent on the Reynolds number. A 2D CFD study investigating the effect of Reynolds number on the hypersonic flow around faceted shapes confirmed that the formation of such a separation bubble was dependent on Reynolds number (Rees et al. 2018), and that the presence of a separation could significantly decrease local heating rates. This reduction in local heating is especially significant in the context of satellite demise as it will result in an increased casualty risk. In recent free-flight experiments of a cube in a hypersonic flow (Seltner et al. 2019), the authors claimed the presence of a separation at the leading edge of the cube, but the resolution of the schlieren was not high enough to capture it in detail. In addition to cylinders, heating rates to cuboids have also been studied in the reports of Crosby and Knox (1980), and Laganelli (1980), who experimentally measured heat fluxes to a cube in a Mach 8 flow at discrete locations using thin-foil calorimeters. However, these studies only report results at one flow condition and at limited discrete locations on the model surface.

This scope of this work is the experimental study of the hypersonic flow around a cuboid shape, with emphasis placed on leveraging modern measurement techniques to obtain accurate heat flux measurements, especially near the corners and edges of the geometry. To achieve these high-fidelity heat flux measurements, the temperature field is measured over the entire surface of the wind tunnel model using InfraRed Thermography (IRT), and the heat flux is calculated by the solution of a three-dimensional inverse heat conduction problem (3D-IHCP). In this way, the Stanton number, $C_{\text{H}}$ is calculated at every point on the surface of the cube, including in the regions closest to the corners and edges. The use of IRT is advantageous due to the fact that it is a non-intrusive measurement technique, with a high spatial resolution, low response time, and high sensitivity. In addition to the IRT measurements, the flow structure around the cube is imaged with schlieren photography to further study the separation formation described in Matthews and Eaves (1967), Rees et al. (2018), and Seltner et al. (2019).

2 Flow facility, models, and test conditions

2.1 High SuperSonic tunnel (HSST)

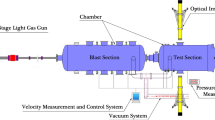
Experiments have been performed in the University of Manchester’s High SuperSonic Tunnel (HSST), based in the department of Mechanical, Aerospace and Civil Engineering. HSST is a long-duration blow-down facility with an electric resistive heater and a swappable nozzle. A schematic diagram of the wind tunnel is presented in Fig. 1, and a table of the achievable flow conditions with a Mach 5 nozzle are presented in Table 1. Optical access to the working section is provided by two parallel, rectangular quartz windows which span the full length of the useful test jet. Infrared access is afforded via a ${75 \ \text {mm}}$ diameter uncoated germanium window. Fixed model mounting positions are provided by an arc-balance sting, which allows the model to be mounted at angles of attack of $\pm 20^{\circ }$. Model orientation on the sting is afforded by a keyway and grub-screw arrangement. A detailed description of the tunnel and its operation can be found in Erdem (2011), and Fisher (2019).

Table 1 HSST characteristic flow conditions with a Mach 5 nozzle

Fig. 1

Schematic diagram of the HSST facility

2.2 Schlieren

Schlieren images were acquired through Töpler’s Z-type schlieren method. Two 12 in.diameter f/7.9 mirrors pass the light from a Newport optics model 66921 Xenon arc lamp, typically at 450 W, onto the knife-edge in the cut-off plane which is then focused though a ${500 \ \text {mm}}$ focal length achromatic doublet lens onto the camera sensor. The images are captured with a commercial Nikon D5200 24-megapixel DSLR camera.

2.3 Models, materials, and mounting

Two model geometries are tested: a ${30 \ \text {mm}}$ length cube and a ${30 \ \text {mm}}$ diameter hemisphere, with the hemisphere model being used to validate the IRT and heat flux calculation techniques (see Sect. 6.1). The models were mounted to a sting adaptor, which allows the model to fit to the arc-balance sting (Fig. 2). By swapping the sting adaptor, the models can be mounted in different roll orientations, allowing different facets of the cube to be imaged by the IR camera and schlieren. For IRT measurements, the cube model is oriented in a rolled ${45 ^{\circ }}$ orientation such that three surfaces of the cube are imaged simultaneously (see Fig. 5a for a sample IR image of a cube model). In this way, temperature data at a corner of the cube are obtained. For schlieren measurements, the cube is mounted in an unrolled orientation so that all relevant flow structures can be imaged.

The models are manufactured from MACOR^®, a machinable glass-ceramic. It was chosen due to its favourable thermal properties, high emissivity, success in previous experimental hypersonic IRT applications (Cardone et al. 2012), and ease of machining. Measurements of the temperature variation of MACOR’s thermal properties are known from Imbriale (2013), and are plotted in Fig 3. The directional emissivity variation of MACOR has been reported in Cardone et al. (2012). Imbriale (2013) correlated this data to find a correlation of the form

$$\begin{aligned} \varepsilon \left( \theta \right) = \left( \varepsilon _{0} \cos \left( \theta \right) \right) ^{\frac{a}{\cos ^{b}\left( \theta \right) }}, \end{aligned}$$

(1)

with coefficients ${\varepsilon _0 = 0.934}$, ${a = 0.0098}$, and ${b = 2.4}$. The temperature variation of the emissivity of MACOR is unknown, and is assumed to be negligible in the current tests. However, measurements of the emissivity temperature variation of similar ceramic materials such as fused silica glass (Clayton 1962) suggest that the emissivity variation of such materials is very small up to temperatures of the order of ${530 \ \text {K}}$.

The sting adaptors are manufactured from $\text {Rigur}^{\text{TM}}$, a 3D printed simulated polypropylene with a high thermal deformation temperature (Rigur Polyjet 2016).

Fig. 2

Experimental set-up in the HSST working section

Fig. 3

Temperature variation of MACOR thermal properties given by Corning Inc. and as reported in Imbriale (2013)

2.4 Test conditions

The conditions achievable in HSST (Table 1) are much less energetic than real re-entry flows, which generally have enthalpies on the order of tens of MJ/kg and Mach numbers on the order of 25–30 (for re-entry from LEO). Despite the divergence in total energy between the present tests and flight conditions, the higher density and lower velocity in HSST means that the Reynolds numbers achieved in the wind tunnel are still representative of re-entry Reynolds numbers, which are typically on the order of $10^4$ at 80 km. Furthermore, due to the exponential increase in the density of the Earth’s atmosphere during the initial stages of re-entry, the Reynolds number of re-entry flows can increase rapidly at altitudes around 80 km while the Mach number only varies weakly.

For these two reasons, the experimental flow conditions are specifically chosen to investigate the effect of Reynolds number on the flow field and surface heat fluxes, while maintaining a constant Mach number. The tested flow conditions are presented in Table 2. IRT measurements are taken at four conditions at Mach 5 with nominal ${T_0 = 800 \ \text {K}}$ and nominal $P_0$ varying from 200 to ${800 \ \text {kPa}}$. Further schlieren images are taken at a fifth condition with nominal ${T_0 = 350 \ \text {K}}$. Due to the fact that hypersonic flow field behaviour is relatively weakly dependent on Mach number (known as Mach number independence), these experimental conditions can still provide valuable insight into re-entry flow behaviour.

Table 2 Experimental flow conditions

3 Infrared measurements and data processing

3.1 Infrared camera and calibration

The calibration of the infrared camera follows the basic principles described in Carlomagno and Cardone (2010). The infrared camera used is a FLIR A655SC fitted with a $25 ^{\circ }$ FOV lens. The detector resolution is $640 \times 480$ pixels, and the frame rate is ${50 \ \text {Hz}}$. The IR calibration is performed using a Fluke 9132 portable infrared calibrator. The calibrator consists of a quasi-black-body target with $\varepsilon = 0.95$ which can be heated up to 500 °C in 0.1 °C increments. The calibration is performed in situ, that is with the calibrator placed in the tunnel working section with the camera viewing the calibrator through the germanium window. In this case, the total radiant intensity detected by the camera $I_{\text{D}}$, can be written as:

$$\begin{aligned}&I_{\text{D}} = \tau _\text{opt}\tau _\text{atm}\varepsilon I_\text{bb}^\text{obj} + \tau _\text{opt}\tau _\text{atm}(1-\varepsilon )I_\text{bb}^\text{amb} \nonumber \\& \qquad + (1-\tau _\text{atm})I_\text{bb}^\text{atm} + \tau _\text{atm}\varepsilon _\text{opt}I_\text{bb}^\text{opt}, \end{aligned}$$

(2)

where $\tau _\text{atm}$ and $\tau _\text{opt}$ are the transmissivities of the atmosphere and germanium window, $I_\text{bb}^{\text{obj}}$, $I_\text{bb}^\text{amb}$, and $I_\text{bb}^\text{opt}$ are the radiant intensities corresponding to a black body at the temperatures of the target, the atmosphere and the optical window respectively. The emissivities of the target and the window are denoted $\varepsilon$ and $\varepsilon _\text{opt}$ respectively. By substituting Planck’s law into Eq. 2, and assuming that the absorptivity of the atmosphere is negligible, that is that $\tau _\text{atm} = 1$, the following expression is obtained:

$$\begin{aligned} I_\text{D} & = \tau _\text{opt}\varepsilon \frac{R}{e^{B/T_\text{obj}} - F} + \tau _\text{opt}(1-\varepsilon )\frac{R}{e^{B/T_\text{amb}}-F} \\ & \quad + \varepsilon _{opt}\frac{R}{e^{B/T_\text{opt}}-F}, \end{aligned}$$

(3)

where $T_\text{obj}$, $T_\text{amb}$, and $T_\text{opt}$ refer to the temperatures of the object, the ambient environment, and the window, respectively, and R, B, and F are coefficients of radiation. Assuming that $\tau _\text{opt}$ is constant with temperature, then this coefficient multiplies into the calibration coefficient R. Furthermore, if $\varepsilon _\text{opt}$ and $T_\text{opt}$ are constant (which is reasonable for the test facility in question) then the last term of Eq. 3 becomes a constant C which must be found during the calibration. The calibration equation, therefore, becomes:

$$\begin{aligned} I_{\text{D}} = \varepsilon \frac{R}{e^{B/T_{\text{obj}}} - F} + (1-\varepsilon )\frac{R}{e^{B/T_\text{amb}}-F} + C. \end{aligned}$$

(4)

The addition of a constant C to the calibration equation was proposed by Zaccara et al. (2019) as a way of taking the camera Non-Uniformity Correction (NUC) into account and regulate the different gains and zero offsets of each pixel of the Focal Plane Array. In our case, it simply represents and corrects for any emission of the germanium window. We are able to take the camera NUC into account by calibrating the camera to a NUC-corrected intensity value called the Object Signal, which is calculated by the FLIR A655SC’s firmware.

During the calibration, the signal of the calibration target is recorded at 55 evenly spaced data points between $293.6$ and $676.5 \ \text {K}$. The Levenberg-Marquardt nonlinear least squares algorithm is used to calculate the calibration coefficients R, B, F, and C in Eq. 4. The resulting calibration curve is shown in Fig. 4, while the calibration parameters, including the coefficient of determination and the RMS error are presented in Table 3.

Fig. 4

Camera calibration curve

Table 3 Summary of the infrared camera calibration

The camera is mounted to a Minitec frame fixed to the floor of the laboratory. It is positioned at a $48.5^{\circ }$ angle to the horizontal axis of the model (Fig. 2), which allows it to image three sides of the cube model.

3.2 Image processing

This section describes the image processing algorithm used to convert the raw IR data acquired by the camera (Fig. 5a) to temperature values suitable for input to the heat flux calculation. First, the raw data are filtered using a three-dimensional Savitsky-Golay filter in both space and time. Following filtering, the IR video is stabilised to remove the effect of model and sting vibration during tunnel start-up and shut-down. The image registration algorithm used to stabilise the IR video is the single-step discrete Fourier transform approach proposed by Guizar-Sicairos et al. (2008), which has already been used successfully on IR videos (Avallone et al. 2015). This algorithm calculates the displacement between two images to a sub-pixel accuracy by computing the upsampled cross-correlation between an image and a reference image by the fast Fourier transform.

Following image registration, the locations of the different surfaces of the cube in the IR image must be identified, and an affine transformation calculated to transform the perspective view of each of the faces to the square arrays corresponding to the mesh used in the heat flux calculation method described in Sect. 4. Previously, Cardone et al. (2012) produced a mapping between a surface mesh and an IR image by means of an optical calibration of the IR camera. Due to the simplicity of the geometry considered in this case, we take a much simpler approach. The edges of the cube in the IR image (Fig. 5b) are identified with a fuzzy-logic-based edge detection algorithm. Following this, the most likely location of the cube edges are extracted, and their intersections are used to define the corners of the cube. These corner locations are used to define the moving points of an affine transformation to a square (Fig. 5c). During the calculation of the affine transformation, the IR image is down-sampled to give a final spatial resolution of the cube temperature maps of ${2 \ \text {pix/mm}}$ (Fig. 5d). The sensitivity of the heat flux calculation to errors in both the edge detection algorithm as well as the down-sampling procedure are discussed in Sect. 6.5.

Once the affine transformation has been calculated for every IR frame, the temperature map on each surface of the cube can be calculated by applying the infrared calibration (Eq. 4) to each surface. By applying the calibration independently to each surface, the variation in emissivity of each surface (due to the directional emissivity effect) can be taken into account. To calculate the directional emissivity for each cube face, the viewing angle $\theta$ to each surface is calculated using knowledge of the camera viewing direction ${\mathbf {W}}$ (this is known from the camera’s orientation in its mounting position), and the normal vector to each of the cube’s faces ${\mathbf {n}}$ (which is known from the cube’s orientation on the sting):

$$\begin{aligned} \theta = \arccos \left|\frac{{\mathbf {W}}\cdot {\mathbf {n}}}{\left|{\mathbf {W}}\right|}\right|. \end{aligned}$$

(5)

The sensitivity of the computed heat flux values to errors in the model emissivity, both due to surface finish as well as directional effects, is discussed in Sect. 5.

Fig. 5

Image processing steps for the cube IR data

4 Hypersonic heat flux calculation

Once the temperature history of an object has been measured, the heat flux to the surface of the object can be calculated by a physical model—the heat conduction equation—of the heat transfer in the measurement area. Walker and Scott (1998) identified three different classes of such solutions:

• 1. Analytical techniques

• 2. Direct numerical techniques

• 3. Inverse techniques.

The first of Walker and Scott’s three solution classes uses a theoretical closed form solution to the 1D form of the heat equation, such as that proposed in Cook and Felderman (1966) and Kendall and Dixon (1996). If the boundary flux is piecewise constant and the body material properties are constant, this is a very simple and quick way of calculating the heat flux to a body. However, the restrictions on the form of the boundary conditions, as well as the requirement for the material properties to be constant are both strong limitations. The second of Walker and Scott’s techniques addresses the first’s drawbacks by numerically solving the heat conduction equation using numerical techniques. These could be a finite difference, finite volume, or finite element method with implicit or explicit time-stepping. The experimental temperature measurements are given as Dirichlet boundary conditions. This allows more flexibility in the solution, as it permits 2D and 3D conduction to be taken into account, as well as variable material thermal properties, such as described in Häberle and Gülhan (2007) and Henckels and Gruhn (2004). The primary drawback of this technique is that it involves differentiating the experimental data, thus magnifying any experimental error or noise.

The third, most sophisticated and robust method is to solve an inverse heat condution problem (IHCP). Typically, inverse problems involve the calculation of an object’s boundary conditions using knowledge of some internal conditions (Ozisik and Orlande 2000). In the context of measuring heat fluxes using IRT, the heat flux to the surface is estimated by considering the evolution of the surface temperature. IHCPs, while offering maximum flexibility in heat flux calculations (Avallone et al. 2015) also have their disadvantages, namely their significant complexity and computational cost. In addition to this, they are ill-posed problems as their solutions are not unique, meaning their solutions are extremely sensitive to small changes in input data (Ozisik and Orlande 2000).

Due to the fact that hypersonic heat fluxes tend to be extremely high, a common assumption made when calculating heat fluxes with any of the above techniques is that any transverse heat transfer within the body is small compared to the convective heat flux to the body. In this case, it is reasonable to neglect any transverse conduction and only consider the heat flux normal to the body surface. This assumption gains further justification when heat flux is being measured to a model with a low thermal diffusivity. However, in cases where significant transverse conduction is present, the dimensionality of the heat conduction equation must be increased in order to achieve an accurate solution. Previous applications of a 2D-IHCP in the context of hypersonic aerothermodynamics include Avallone et al. (2015) and Zaccara et al. (2019), where a 2D-IHCP solution was used to calculate the heat transfer caused by turbulent transition on a wedge and cone respectively. Both results showed very limited dependence on transverse conduction. Other authors (Nortershauser and Millan 2000; Sousa et al. 2012) have performed 3D-IHCP solutions on problems considering the heating of small test articles by flames and electric heaters, but they only considered relatively small computational domains (approximately 300 cells). In the case of the present work, any assumptions of 1D or 2D conduction cannot be made—the conduction in the model near the corners and edges will be strongly two or three-dimensional and therefore the 3D-IHCP solution must be solved.

In the remainder of this section, we briefly describe a method of solving the IHCP on the cuboidal domain by the conjugate gradient method with adjoint and sensitivity problems, a commonly used IHCP solution methodology (Huang and Wang 1999; Imbriale 2013). In the summary below, we follow the derivation of Ozisik and Orlande (2000).

4.1 Definition of the direct problem

We start by introducing the direct problem. Consider a cuboid domain $\varOmega$ with surfaces $S = {S_1,...,S_6}$. The heat equation on this domain, with Neumann boundary conditions can be written as:

$$\begin{aligned} \left\{ \begin{array}{l} \rho c_p(T)\frac{\partial T}{\partial t} = \nabla \left( k(T) \nabla T\right) , \ \forall \ {\mathbf {x}} \in \varOmega \\ T(\mathbf{x },t)=T_{i}(\mathbf{x },t), \ \forall \ {\mathbf {x}} \in \varOmega , \ t=0 \\ k(T) \frac{\partial T}{\partial n} = q(\mathbf{x },t), \ \forall \ {\mathbf {x}} \in S, 0<t<t_{f} \end{array} \right. \end{aligned}$$

(6)

where $\rho$, $c_p$, and k are the material density, specific heat capacity, and thermal conductivity respectively. The material temperature is T, q is the conductive heat flux, and ${\mathbf {x}}$ and t are the space and time variables.

4.2 Definition of the inverse problem

The inverse problem can be described as follows: find the value of q(S, t) which gives the known temperature evolution at each measurement point $Y_m$ on S (the details of the computational mesh are given in Sect. 4.6). In practise, this is every pixel of the IR image. Start by defining the cost functional for this problem:

$$\begin{aligned} f(q(S,t)) = \int ^{t_f}_0 \sum ^{M}_{m=1} \left( T_m(q(S,t))-Y_m\right) ^2 \text{d}t \end{aligned}$$

(7)

where $T_m$ is the solution to 6 for q(S, t) at each measurement point, and M is the total number of measurement points. The conjugate gradient method (CGM) attempts to iteratively construct a value of q(S, t) of the form:

$$\begin{aligned} q_{n+1}(S,t) = q_{n}(S,t) + \beta _n p_{n}(S,t) \end{aligned}$$

(8)

where the subscript n denotes the iteration count.

4.3 Calculation of the search step size and the sensitivity problem

The step size $\beta _{n}$ is taken to be the step size by which the cost functional $f_n$ reaches a minimum in the direction $p_n$. The expression for $\beta _n$ can therefore be found by minimising Eq. 7, giving:

$$\begin{aligned} \beta _{n} = \frac{\int _0^{t_f} \sum ^{M}_{m=1} \left( T_m-Y_m\right) \varDelta T {\text{d}}t}{\int _0^{t_f} \sum ^{M}_{m=1} (\varDelta T)^2 {\text{d}}t}. \end{aligned}$$

(9)

where $\varDelta T$ is defined as the directional derivative of the temperature T in the direction of q. To find an expression for the evolution of $\varDelta T$, it is assumed that a perturbation of $q + \varDelta q$ in Eq. 6 causes a perturbation $T + \varDelta T$ in the solution. Substituting these in the direct problem, subtracting the original direct problem from the resulting equations and ignoring 2nd order terms yields the sensitivity problem:

$$\begin{aligned} \left\{ \begin{array}{l} \rho c_p(T)\frac{\partial \varDelta T}{\partial t} = \nabla \left( k(T)\nabla \varDelta T\right) , \ \forall \ {\mathbf {x}} \in \varOmega \\ \varDelta T(\mathbf{x },t)=0, \ \forall \ {\mathbf {x}} \in \varOmega , \ t=0 \\ k(T)\frac{\partial \varDelta T}{\partial n} = \varDelta q(\mathbf{x },t), \ \forall \ {\mathbf {x}} \in S, 0<t<t_{f} \end{array} \right. \end{aligned}$$

(10)

4.4 Calculation of the conjugate direction and the adjoint problem

The conjugate direction, $p_{n}$ can be calculated by the equation

$$\begin{aligned} p_{n}(q_n) = -\nabla f_{n} + \gamma _{n} p_{n-1}, \end{aligned}$$

(11)

where $\nabla f$ is the gradient of the cost functional and $\gamma _n$ is called the conjugation coefficient, calculated using the Fletcher-Reeves formula:

$$\begin{aligned} \gamma _{n} = \frac{\int _0^{t_f}\int _S (\nabla f_{n}) ^2 {\text{d}}S {\text{d}}t}{\int _0^{t_f}\int _S (\nabla f_{n-1}) ^2 {\text{d}}S {\text{d}}t}. \end{aligned}$$

(12)

The only unknown quantity in Eqs. 11 and 12 is the gradient of the cost functional, $\nabla f$. The expression for the evolution of $\nabla f$ is known as the adjoint equation:

$$\begin{aligned} \left\{ \begin{array}{l} \rho c_p(T)\frac{\partial \lambda }{\partial t} = - \nabla \left( k(T) \nabla \lambda \right) , \ \forall \ {\mathbf {x}} \in \varOmega \\ \lambda (\mathbf{x },t)=0, \ \forall \ {\mathbf {x}} \in \varOmega , \ t=t_f \\ k(T)\frac{\partial \varDelta T}{\partial n} = 2 \left( T - Y \right) , \ \forall \ {\mathbf {x}} \in S, 0<t<t_{f} \end{array} \right. \end{aligned}$$

(13)

where $\lambda = \nabla f$. The derivation of the adjoint problem follows a process similar to the one used to derive the sensitivity problem. The details can be found in Ozisik and Orlande (2000).

Of note is the fact that, due to the nature of the final value problem (Eq. 13), the gradient of the cost functional at the final time is zero, that is, ${\nabla f(t_f) = \lambda (t_f) = 0}$ and, therefore, the conjugate direction will always be zero at the final time. To overcome this singularity, the gradient at the final time is modified as follows:

$$\begin{aligned} \nabla f(t_f) = \lambda (t-\varDelta t), \end{aligned}$$

(14)

where $\varDelta t$ is the time step used to solve the heat equation. In this way, the effect of the singularity is reduced. To further reduce the effect of the singularity, the IHCP solution calculation is extended beyond the end of the tunnel run by 50 time steps (during this time the heat flux to the cube is zero).

4.5 Stopping criterion

The stopping criterion of the CGM can be defined either by a tolerance criterion, or when the algorithm reaches a minimum, that is, when there is negligible change in the solution after a direction re-set. In other words, if there are no measurement errors, the stopping criterion can be defined as

$$\begin{aligned} f_n < \varepsilon , \end{aligned}$$

(15)

where $\varepsilon<< 1$. In practice, the temperature measurement error will place a constraint on how small $f_n$ can become. Following Huang and Wang (1999) and Ozisik and Orlande (2000), the temperature measurement residuals will be approximately equal to the standard deviation of the temperature measurement errors, that is:

$$\begin{aligned} T_m - Y_m \approx \sigma . \end{aligned}$$

(16)

Therefore, $\varepsilon$ in Eq. 15 can be expressed by:

$$\begin{aligned} \varepsilon = M\sigma ^2 t_f, \end{aligned}$$

(17)

which gives the appropriate value of $\varepsilon$ for the current problem.

4.6 Algorithm

In summary, the CGM for solving the IHCP can be described in the following steps at each iteration n:

• 1. Solve Eq. 6 with $q_n$ as the boundary conditions.

• 2. Check the stopping criterion (Eq. 15). If satisfied, exit the solution.

• 3. Solve the adjoint problem (Eq. 13) to obtain ${\lambda = \nabla f}$.

• 4. Calculate the conjugation coefficient $\gamma$ by the Fletcher-Reeves formula (Eq. 12).

• 5. Calculate the conjugate direction $p_n$ (Eq. 11).

• 6. Solve the sensitivity problem (Eq. 10) with ${\varDelta q = p_n}$.

• 7. Calculate the step length $\beta _n$ (Eq. 9).

• 8. Update the solution to obtain $q_{n+1}$ (Eq. 8).

Previous applications of the CGM (such as Imbriale 2013) to hypersonic problems did not take into account the temperature variation of the material thermal properties k(T) and $c_p(T)$. To do this, we calculate the values of these properties at every spatial point and time step during the solution of the direct problem (step 1 in Sect. 4.6). These values are then used at the corresponding locations and times in the solution of the adjoint and sensitivity problem on the same domain. In this sense, k and $c_p$ in Eqs. 10 and 13 could be written as functions of space ${\mathbf {x}}$ and time t rather than temperature T. These values are then updated at each iteration during the solution of the direct problem.

For this work, the algorithm has been implemented in Matlab. The direct, sensitivity, and adjoint problems are solved with the same forward-time central-space (FTCS) finite differencing scheme on an equally spaced, structured grid with ${dx = 0.5 \ \text {mm}}$. To reduce the computational expense of the IHCP, the flow around the cube is considered symmetrical and the IHCP is only solved over one quarter of the cube, that is ${-0.5 \le z/L \le 0.5 }$ and ${0 \le s/L \le 1.5}$ (see Fig. 5d for coordinates), giving a final grid size of $54 \times 10^3$ points. The boundary conditions at the three surfaces of the domain where temperatures are unknown are considered to be adiabatic. This is justified as the transverse conduction normal to the boundaries in these regions is likely to be small.

Once the conductive heat flux q has been evaluated, the modified Stanton number $C_{\text{H}}$ is calculated, defined as

$$\begin{aligned} C_\text{H} = \frac{q+q_\text{rad}}{\rho _\infty u _{\infty }\left( H_0 - h_w\right) }= \frac{q_\text{conv}}{\rho _\infty u _{\infty }\left( H_0 - h_w\right) }, \end{aligned}$$

(18)

where $q_\text{rad}$ is the total radiative heat flux away from a surface, given by the Stefan-Boltzmann equation, $q_\text{conv}$ is the convective heat flux to the surface, and $H_0$ is the total enthalpy of the free-stream flow, given by:

$$\begin{aligned} H_0 = h_\infty + u_\infty ^2/2. \end{aligned}$$

(19)

In the remainder of this work, any reference to Stanton number refers to the modified Stanton number as defined above. The wall and free-stream enthalpy values $h_w$ and $h_\infty$ are calculated using the HOT thermal database package for Matlab and Octave (Martin 2019).

5 Error sensitivity analysis

To validate the IHCP approach to calculating heat fluxes outlined in Sect. 4, as well as to estimate the errors associated with the calculations, it is important to investigate both the uncertainty inherent to the IHCP solution, as well as the sensitivity of the solution methodology to errors in the input data. To conduct such an analysis, it is necessary to use a synthetic (rather than experimental) dataset. In this way the precise difference between a true $C_{\text{H}}$ value (which is known for the synthetic dataset) and the IHCP-calculated value can be found.

For the sensitivity analysis in this study, the synthetic heat fluxes applied to the cube geometry are chosen such that they approximate the expected experimental values. On the stagnation surface of the cube, the heat fluxes are given by a modified version of the expression given by Klett (1964) for the heat flux to a flat-ended cylinder:

$$\begin{aligned} q(s,z) = q_0\left( 1+0.6\left( \frac{2r}{L}\right) ^{3.3}\right) \end{aligned}$$

(20)

where L is the cube length, s and z are the coordinates shown in Fig. 5d, and $r^2=s^2+z^2$. The conductive heat flux value at the stagnation point is chosen as $q_0=7\times 10^4 \ {\text {W/m}}^2$.

On the streamwise surfaces of the cube, the heat flux distribution is given by the Eckert reference temperature method for a flat plate hypersonic boundary layer. To include temporal variation in the sample data, the heat flux values are multiplied by a factor of $(1-e^{-t/\tau })$ where ${\tau = 8.1667}$.

Once the temperature maps on each surface have been calculated by a solution of the direct problem (Eq. 6), the temperatures are passed backwards through the IR calibration to obtain equivalent Object Signal values. This makes it possible to investigate how various errors (such as in emissivity and ambient temperature measurement) propagate through the calibration procedure.

When calculating the Stanton number values, the synthetic values of $H_0$, $\rho _\infty$, and $u_\infty$ are found from typical HSST total temperature and pressure data for a run at nominal conditions of ${T_0=800 \ \text {K}}$ and ${P_0 = 800 \ \text {kPa}}$.

Errors are assumed to enter the Stanton number calculation from the following sources:

• 1. Error inherent in the IHCP solver.

• 2. Error in the ambient temperature measurement.

• 3. Error in the camera calibration.

• 4. Error in assumed emissivity values.

• 5. Error in the initial temperature distribution over the model.

• 6. Error in the value of thermal conductivity.

• 7. Error in the value of specific heat capacity.

• 8. Error in measurement of the wind tunnel total temperature.

• 9. Error in measurement of the wind tunnel total pressure.

To investigate the sensitivity of the data processing procedure to each of these error sources, the inputs to the IHCP are perturbed by an amount approximately equal to the estimated measurement error $\varDelta$. The resulting error in the Stanton number $\varDelta C_{\text{H}}$ is then characterised using the normalized root mean squared error:

$$\begin{aligned} \varDelta C_{\text{H}} = \frac{\sqrt{M(t_{end}-t_{start})\sum ^{t_{end}}_{t=t_{start}} \sum _{m=1}^M (C_{\text{H}}({\mathbf {x}}_{m},t)-{\hat{C}}_{\text{H}}({\mathbf {x}}_{m},t))^2}}{\sum ^{t_{end}}_{t=t_{start}} \sum _{m=1}^M {\hat{C}}_H({\mathbf {x}}_{m},t)}, \end{aligned}$$

(21)

where ${\hat{C}}_\text{H}$ is the true value of the Stanton number, given by the synthetic data, and $t_\text{start}$ and $t_\text{end}$ are the time indices where a steady-state Stanton number is achieved. A summary of the error sources, their assumed error (and justification), and the resulting values of $\varDelta C_{\text{H}}$ can be found in Table 4.

Traditionally, the global accuracy of the calculated Stanton numbers could be estimated as the root sum of the squares of the $\varDelta C_{\text{H}}$ values. However, by this method, the error associated with the IHCP methodology will also be present in each approximation of the partial derivatives, and the total error will contain incidences of the IHCP error. To correct for this, we write the sum of squares error equation as

$$\begin{aligned}&\varDelta {C_{{\text{H}}_\text{tot}}}^2 = \left( \frac{\varDelta C_{{\text{H}}}}{\varDelta T_\text{amb}}\varDelta _{T_\text{amb}}\right) ^2 + \left( \frac{\varDelta C_{{\text{H}}}}{\varDelta T_{{\text{IR}}}}\varDelta _{T_{{\text{IR}}}}\right) ^2 \nonumber \\&\quad + \left( \frac{\varDelta C_{{\text{H}}}}{\varDelta \varepsilon } \varDelta _{\varepsilon }\right) ^2 + \left( \frac{\varDelta C_{{\text{H}}}}{\varDelta T_i} \varDelta _{T_i}\right) ^2 + \left( \frac{\varDelta C_{{\text{H}}}}{\varDelta k} \varDelta _{k}\right) ^2 \nonumber \\&\quad + \left( \frac{\varDelta C_{{\text{H}}}}{\varDelta c_p} \varDelta _{c_p}\right) ^2 + \left( \frac{\varDelta C_{{\text{H}}}}{\varDelta T_0} \varDelta _{T_0}\right) ^2 + \left( \frac{\varDelta C_{{\text{H}}}}{\varDelta P_0} \varDelta _{P_0}\right) ^2 \nonumber \\&\quad - 7\varDelta C_{{\text{H}}_{{\text{IHCP}}}}^2 \end{aligned}$$

(22)

so that only one incidence of $\varDelta C_{{\text{H}}_\text{IHCP}}$ is included in the final error value. This gives a global error in $C_{\text{H}}$ of 12%, which is dominated by the errors due to the material emissivity (see Table 4). It is important to note, however, that this value is not constant across the entire computational domain. Figure 6 shows how the error value changes across the computational domain. In this case, we define a time average error, $\delta C_{\text{H}}$ as:

$$\begin{aligned} \delta C_{\text{H}} = \frac{\sqrt{(t_{end}-t_{start})\sum ^{t_{end}}_{t=t_{start}}(C_{\text{H}}({\mathbf {x}}_{m},t)-{\hat{C}}_{\text{H}} ({\mathbf {x}}_{m},t))^2}}{\sum ^{t_{end}}_{t=t_{start}} {\hat{C}}_{\text{H}}({\mathbf {x}}_{m},t)}. \end{aligned}$$

(23)

For the flat faces of the model, the error is approximately 9%, below the global error of 12%, but in regions of strong multi-dimensional conduction the error can increase up to 15%. It is notable that the error is much higher near the edges and corners of the cube, where three-dimensional conduction is strongest.

Table 4 Error sources and sensitivity

Fig. 6

Contours of the error in Stanton number

The effect of the internal conduction and the magnitude of the error in the regions where the conduction is strongest could be directly experimentally assessed by placing thermocouples internally in the model. Unfortunately, the effect of installing such instrumentation would significantly complicate the infrared measurements and the IHCP solution. Due to the extremely low thermal diffusivity of MACOR, the thermocouples would have to be placed very near the surface of the cube. The placement of these instruments would affect the distribution of the cube material as well as the surface temperature of the cube. These factors would have to be corrected for in the solution of the IHCP which would require a much more complex mesh.

6 Results

6.1 Heat flux measurement validation with a hemisphere model

Taking IRT measurements of temperature histories and calculating heat fluxes with an IHCP solution are both complex processes with many possible sources of error in both experimental set-up (including IR calibration) and data reduction algorithms. Therefore, to validate the combined experimental set-up and the IHCP solver, they are used to calculate the experimental stagnation point heat flux to a hemisphere. This is a particularly useful geometry with which to validate the experimental set-up as the stagnation point heat flux on a hemisphere is well characterised, and can be accurately calculated using a number of different methods.

For this application, we obtain a theoretical value of the heat flux at the stagnation point of a sphere by solving the self similar form of the boundary layer equations (for their derivation see Anderson (2006)):

$$\begin{aligned} \left\{ \begin{array}{l} \left( Cf''\right) ' + ff'' = \left( f'\right) ^2 - g \\ \left( \frac{C}{Pr}g'\right) ' + fg'=0, \end{array} \right. \end{aligned}$$

(24)

where $f' = \partial f/ \partial \eta = u/u_e$, $g = g\left( \xi ,\eta \right) = h/h_e$, and $C = \rho \mu / \rho _e \mu _e$. In these relations, $\eta$ and $\xi$ are the Lees-Doronitsyn variables, subscripts $_e$ refer to flow variables at the edge of the boundary-layer, and Pr is the flow Prandtl number. The reader is referred to Anderson (2006) for more details about these equations as well their derivations. The equations are solved using the tridiagonal solution method described in Blottner (1979) and implemented in Adams (2002). This is preferred to using an existing correlation (such as the Fay and Riddell (1958) or Sutton and Graves (1971) correlations) due to the fact that the free-stream conditions used for these experiments lie outside of the range of validity of these correlations.

These theoretical heat flux values are compared to experimental values at the stagnation point of a ${30 \ \text {mm}}$ diameter hemisphere in a hypersonic flow with $M=5$, $T_0 = 805 \ \text {K}$, and $P_0 = 200 \ \text {kPa}$ (which corresponds to a free-stream Reynolds number of $Re/\text {m} = 1.23 \times 10^6$). The experimental heat flux values are calculated using both the IHCP solution described above, as well as the Cook and Felderman (1966) equation, a Class 1 method using the classification system described in Sect. 4. The IHCP is solved assuming 1D conduction only (i.e. neglecting any transverse conduction in the hemisphere model) at the stagnation point. A plot of experimental Stanton numbers at the stagnation point of the hemisphere during the run of the HSST is presented in Fig. 7, alongside the theoretical value. The time-averaged 1D-IHCP value during the wind-tunnel steady state $2<t<6$ is $C_{{\text{H}}_0} = 0.0275$, while the Cook and Felderman value is $C_{{\text{H}}_0} = 0.0281$, slightly higher likely due to its assumption of constant material thermal properties. The boundary-layer self similar solution gives a value of $C_{{\text{H}}_0} = 0.0259$, 6% smaller than the IHCP solution, and 8% smaller than the Cook and Felderman value. How much the difference between the theoretical and experimental heat flux values is due to the IRT measurement technique and heat flux calculation method, or due to errors in the free-stream flow parameter estimation could be ascertained by performing an additional test with a conventional heat flux probe, instrumented with a thin-film heat flux gauge. This was not performed in the present experimental campaign.

The RMS error of the IHCP solution is 1.7%, while for the Cook and Felderman solution it is 2.2%. These are slightly lower than the values of 3–4% calculated by Avallone et al. (2013), likely due to the slightly higher noise (${\sigma = 0.8 \ \text {K}}$) in the temperature histories gathered by Avallone et al.

The results described in this section, in combination with the error sensitivity analysis described in Sect. 5 gives further confidence in the cube results discussed below.

Fig. 7

Hemisphere stagnation point Stanton number evolution during a tunnel run

6.2 Cuboid schlieren results

Schlieren photographs of the cube model at high ($549\times 10^3$) and low ($40.0\times 10^3$) Reynolds numbers are presented in Fig. 8. The schlieren appears to confirm the appearance of different flow structures with increasing Reynolds number as predicted by Rees et al. (2018). Most notable is the appearance of an apparent separation shock at the windward edge of the cube at high Reynolds numbers (Fig. 9) which is not present at lower Reynolds numbers. This pattern is similar to that imaged by Matthews and Eaves (1967) around a cylinder, and supports the conclusion made in Rees et al. (2018) that a separation bubble can form on the sides of a cube at hypersonic speeds, as Reynolds number is increased, even if it was not present at lower Reynolds values. The free-stream total temperature was lowered significantly to achieve the high Reynolds number condition, and therefore it was not possible to take any high-quality IRT data at this condition. As a result the separation bubble’s effect on the heat flux could not be quantified.

Fig. 8

Schlieren images for a cuboid at $M=5$ at high and low Reynolds numbers

Fig. 9

Labelled schlieren at $M=5$ and $Re = 549\times 10^{3}$

6.3 Heat fluxes to the cube

The solutions to the 3D-IHCP for the cube model at the four-different free-stream conditions are plotted in Fig. 10. These are time-averaged Stanton numbers calculated by averaging over the steady-state portion of the tunnel run time ($2<t<6$ s). The trends in the contours are as expected, with heat flux increasing due to the thinning boundary layer as the edges and corners are approached. Notably, in addition to the increases of heat flux at the edges of the cube, there are also wedge-shaped regions of high $C_{\text{H}}$ along the streamwise edges of the cube. These appear to show some Reynolds number dependence, getting wider as the Reynolds number is increased. Figures 11 and 12 show plots of Stanton number normalised by the stagnation point Stanton number in both the streamwise (at the centreline of the cube, $z/L =0.50$) and spanwise (at $s/L=1.0$) directions. The identification of the stagnation point Stanton number is discussed in Sect. 7.1. Figure 11 shows that the wedges of increased Stanton number along the streamwise edges of the cube are bounded either side by a region of slightly decreased Stanton number. Furthermore, Fig. 12 shows that on the side face of the cube, the Stanton number tends to reach a maximum at $s/L =1.0$.

The solutions to the 1D-IHCP (neglecting any transverse conduction) for the cube model at the four free-stream conditions are presented in Fig. 13. Due to the nature of the 1D solution, the 1D-IHCP can be solved across the whole measurement surface of the cube (no symmetry assumption is necessary) and so results for the entire cube (rather than a quarter-cube as in Fig. 10) are shown. These results show broadly similar behaviour to the 3D-IHCP solutions, albeit with less-defined changes in heat flux near the corners and edges of the model.

One thing which is notable in the 1D-IHCP contours that is not immediately obvious in the 3D-IHCP contours is the presence of regions of lower Stanton number on the stagnation surface of the cube. These regions correspond to the low-temperature regions visible in the raw IR image (Fig. 5a). These regions are off-centre of the stagnation surface, and the relative strength of the reduction in heat flux appears to increase with Reynolds number. These regions are also present in the 3D-IHCP solution, however, due to the noisier nature of the 3D solution, they are not as clear.

Fig. 10

Stanton number contours calculated using a 3D-IHCP solution for a cube at Mach 5 and at four different Reynolds numbers

Fig. 11

Spanwise Stanton number profiles at $s/L = 1.0$

Fig. 12

Streamwise Stanton number profiles at $z/L = 0.5$

Fig. 13

Stanton number contours calculated using a 1D-IHCP solution for a cube at Mach 5 and at four different Reynolds numbers

6.4 Effects of three-dimensional conduction

The transverse (conductive) heat transfer within the model is time-dependent. As different parts of the model heat up at different rates the temperature gradients (and therefore internal conduction rates) will vary with time. A comprehensive analysis of the effect of internal conduction on the accuracy of the 1D versus the 3D-IHCP solution would take this variation into account. However, for the purposes of this analysis, we will simply compare the time-averaged difference between the $C_{\text{H}}$ values obtained with the 3D and 1D conduction assumptions. We define contours of the difference due to dimensionality as

$$\begin{aligned} \varepsilon _{\text{D}} = \frac{|C_{{\text{H}}_{1{\text{D}}}}-C_{{\text{H}}_{3{\text{D}}}}|}{C_{{\text{H}}_{3{\text{D}}}}}, \end{aligned}$$

(25)

which are plotted in Fig. 14. The results show that, although the effect of high-dimensional conduction is unimportant on the stagnation surface and large parts of the side-faces of the cube, failing to account for 3D conduction in the regions near the corners and edges of the cube can result in errors up to 500%. These errors are likely lower at the start of the tunnel run time and higher towards the end. Furthermore, there are regions of significant high-dimensional conduction around the edges of the hot wedges described above. Despite these errors associated with the 1D-IHCP, the 3D-IHCP solutions also have some limitations. First, the 3D results are noisier than the 1D results. This noise is captured by the error contours shown in Fig. 6. More importantly, the 3D solutions rely on an accurate image-to-IHCP input perspective transformation. If the location of the edge of a cube is assumed to be even slightly wrong the $C_{\text{H}}$ calculation can be significantly affected.

Fig. 14

Percent errors due to inappropriate conduction assumption

6.5 Sensitivity to image processing and quality

To investigate the sensitivity of the 3D-IHCP solution to errors in the identification of the edge locations of the cube, seven analyses of solution’s sensitivity to the edge location were performed. For this analysis, the four corners defining the cube’s stagnation surface (see Fig. 5c) were moved up and down by 3 pixels (in the raw IR image), to give a total of 6 different edge locations, in addition to the baseline location used in the main results. Furthermore, to investigate the effect of the down-sampling of the IR image, another analysis was performed where the image was processed with minimal down-sampling, resulting in a solution with a spatial resolution of 3.7 pix/mm rather than 2.0 pix/mm.

The results of these sensitivity analyses on the Case 4 (high Re) results can be seen by examining the cube centreline Stanton numbers (Fig. 15). As the corners get moved up the IR image (that is, away from the stagnation surface), there a region of non-physical negative Stanton number that appears after moving the edge location only 2 pixels. These negative Stanton numbers were reported in Rees et al. (2019), but were not identified as being caused by errors in the image processing method. As the corners get moved down the IR image, that is towards the stagnation surface, the increase in Stanton number across the cube edge becomes non-monotonic after a movement of 3 pixels. The non-physicality of this behaviour suggests that the current image processing algorithm can locate the edge of the cube in the IR image to within $\pm 2.5$ pixels. However, Fig. 15c suggests that the spatial resolution of the image, as well as the down-sampling during the image processing could also affect the accuracy of the edge location. Although the 2 pix/mm and 3.7 pix/mm lines in Fig. 15c look very similar, we note that the extra noise present in the high-resolution solution may be causing a non-monotonic change in heat flux through the cube edge at $s/L = 0.5$. Finally, we note that the down-sampling does not otherwise affect the 3D-IHCP solution, suggesting that down-sampling process does not significantly affect the results.

Obviously, accurate identification of the cube’s edge locations in the infrared image is a crucial aspect of obtaining accurate heat fluxes using the 3D-IHCP solution. Edge detection algorithms generally rely on the assumption that edges are locations of high gradient (even if they may not place the edge at the region of highest gradient). This assumption is not true in the case of the windward edge ($s/L = 0.5$) of the cube. Therefore, the localisation of this edge of the cube, as well as the streamwise edge at $z/L = 0.0$ relies on the assumption that the edge is located at the region of highest temperature, which is not justified a priori. This problem could be mitigated by performing an optical calibration of the camera and then fitting the IHCP cube mesh mapped to its surface (as discussed in Sect. 3.2 and by Cardone et al. (2012)).

Fig. 15

Centreline Stanton number profiles for the Edge Sensitivity analyses for Case 4

7 Discussion

7.1 Stagnation surface behaviour

The most striking result of the stagnation surface contours in Figs. 10 and 13 is the presence of the regions of lower Stanton number. The variation in the Stanton number of the present experimental data due to these ‘cold spots’ is up to 30%. The cold spot location and strength also appears to show a Reynolds number dependence, getting stronger and further off-centre as the tunnel total pressure (and therefore Reynolds number) increases. Although this behaviour perhaps indicates that the cause of these regions is non-uniformity of the free-stream flow, previous studies of the flow uniformity of HSST (Erdem 2011; Fisher 2019) suggest that any non-uniformity across the test jet is negligible. Alternatively, an imperfection in the model surface conditions could cause such a behaviour. However, the tests were performed with two different cube models, ruling out this explanation.

Instead, we propose a different explanation: that these regions are in fact the stagnation points of the cube, which have been moved off-centre by the flex of the tunnel mounting sting. The stagnation point on the windward surface of the cube should manifest itself in the Stanton number contours as such a cold spot. This is due to the fact that as the flow accelerates away from the stagnation point on the windward surface, the boundary-layer will thin, increasing the heat flux, making the stagnation point the region of lowest heating on the stagnation surface. If the model is perfectly aligned in the free-stream flow direction, the stagnation point would be at the geometric centre of the stagnation surface. However, due to the planar nature of the stagnation surface of a cube (in other words, the radius of curvature is infinite), the location of the stagnation point is likely to be highly sensitive to the cube attitude—a small change in the cube attitude may result in a significant change in the stagnation point location. The flexure of the sting during a run will change the cube attitude slightly, causing the stagnation point to move. As the Reynolds number of the flow, and therefore the aerodynamic force on the cube increases with the increase in flow total pressure, the sting flex will get larger, making the change in stagnation point location and strength stronger. This off-set stagnation point would explain why the plots in Fig. 12 do not collapse exactly, and why the Stanton number at the geometric centre of the cube does not correspond to the stagnation point Stanton number.

To investigate the stagnation point Stanton numbers measured in these experiments, they are compared to correlations for the stagnation point heating to a flat surface at similar flow conditions. Previous studies (Matthews and Eaves 1967; Trimmer 1968) have measured the stagnation point heat flux to a flat-ended cylinder and compared it to the stagnation point heating to a hemisphere. These studies related the relative heating rates between these two geometries to the effective stagnation point velocity gradient at the edge of the boundary layer:

$$\begin{aligned} \beta = \frac{{\text{d}}u_e}{{\text{d}}x}. \end{aligned}$$

(26)

We know from many stagnation point correlations that the Stanton number at a stagnation point is directly proportional to the square root of $\beta$:

$$\begin{aligned} C_{\text{H}} \propto \sqrt{\beta }. \end{aligned}$$

(27)

Assuming that the only difference between an equivalent stagnation point flow on a round surface and a flat face is the velocity gradient, then:

$$\begin{aligned} C_{H_{{\text{FF}}}} \propto C_{H_{{\text{SS}}}}, \end{aligned}$$

(28)

where $C_{H_{{\text{FF}}}}$ is the stagnation point Stanton number to a flat face and $C_{H_{{\text{SS}}}}$ is the stagnation point Stanton number to an equivalent spherical geometry. It should therefore be possible, using knowledge of the difference in velocity gradient between the two geometries, to find a correspondence between the stagnation point heat flux to a flat surface and an equivalent sphere.

Trimmer (1968) and Matthews and Eaves (1967) performed experiments to measure the velocity gradient to an end-on cylinder in hypersonic flow. Cylinders of various bluntness were tested, from a hemispherically-capped cylinder to a flat-ended cylinder. By comparing the non-dimensionalised velocity gradients measured in these two studies, the constant of proportionality in Eq. 28 is found to be 0.54 (from the Matthews and Eaves data) and 0.57 (from the Trimmer data). Klett (1964) found similar results, suggesting a proportionality constant of 0.5, although did not report what data this value was based on. The Reynolds number variation of these results (Klett, Trimmer, and Matthews and Eaves) are presented in Fig. 16, as well as the current experimental data for a cube. The combined data show significant scatter, although the current experimental data are generally lower than the earlier data. The average ratio of the stagnation point Stanton numbers measured on the cube geometries to an equivalent hemisphere value (where $R_n = L/2$) (found using the same self-similar solution used in Sect. 6.1) is found to be 0.44 on average across conditions. This is not surprising as the cube will naturally have an effective nose radius slightly larger than L/2 due to the presence of the corners. In this sense, a better way of defining the effective nose radius of a cube would be to use the diagonal distance across the corners: $R_n = \sqrt{2}L/2$. Using this definition, the average constant of proportionality for the current experimental data becomes 0.52, closer to the values reported in the earlier references.

It should be remarked that the previous experimental data were collected using thin-film heat flux gauges at discrete locations on the model stagnation surface. Therefore, it would not have been possible for the authors to capture the variation in heat flux occurring in the current experimental data. It is therefore possible that the stagnation point heat fluxes measured in the earlier data may be larger than the true stagnation values.

Fig. 16

Comparison of flat-surface stagnation point values for different datasets

7.2 Off-stagnation behaviour

In the off-stagnation regions, that is the side faces of the cube, the most notable flow feature are the regions of high heat flux, or wedges, which appear to emanate from the windward corners of the cube. Such flow phenomena have already been observed in CFD simulations of hypersonic flow around faceted shapes, such as in Gülhan et al. (2016), but have not been studied experimentally. The angles of these wedges appear to show dependence on Reynolds number, suggesting that they are a viscous, rather than inviscid flow effect. This is in contrast to similar results presented in Rees et al. (2019), which indicated no Reynolds number dependence, leading to the opposite conclusion. The likely reason for this discrepancy is that the results in Rees et al. (2019) only considered a 2D-IHCP in the spanwise direction, which resulted in less spatially accurate wedge shapes. The shapes of the wedges in the high and low Reynolds number cases are compared in Fig. 17. These profiles were obtained by thresholding the Stanton number contours on the side faces so that only regions where the heat flux was higher than $0.1\%$ of the average heat flux on the surface were visible. The edges of these thresholded images were then extracted to produce the profile. The wedge spreading angles for all the tested conditions are reported in Table 5. The heat fluxes under the wedges can be significant, with regions of peak heating reaching up to $100 \%$ of the stagnation point heat flux value. The average values of the increased Stanton number caused by these wedges, $C_{\text{H}_\text{w}}$ (defined as the average value of the Stanton number bound by the contours in Fig. 17) are reported in Table 5.

Notably, the regions of high heat flux wedges are bounded on either side by a similar region of lower heat flux (see Fig. 11). Such a pattern is often seen in the presence of vortical structures, suggesting that the wedges are generated by vortices being shed by the corner of the cube. The Reynolds number dependence of the wedge angle is further evidence that these wedges are a viscous flow effect.

Away from these wedges, the heat flux on the side faces of the cube is much lower than anywhere else. The average values of the Stanton number along the centreline of the cube, $C_{\text{H}_\text{c}}$ (that is along $z/L=0.5$ for $s/L>0.5$) are reported in Table 5, and are between 15 and 18% of the stagnation point value.

Fig. 17

Experimental Wedge shapes at high and low Reynolds numbers

7.3 Comparison to satellite demise heating models

Object-oriented satellite demise tools such as DRAMA (Martin et al. 2005) prescribe heat fluxes to simple shapes such as cuboids and cylinders through the use of a heating shape factor $F_\text{sh}$, defined as:

$$\begin{aligned} F_\text{sh} = \frac{{\hat{q}}}{q_\text{ss}} \end{aligned}$$

(29)

where ${\hat{q}}$ is the space-averaged heat flux to the object:

$$\begin{aligned} {\hat{q}} = \frac{\int _S q \text{d}S}{S} \end{aligned}$$

(30)

and $q_{ss}$ is the stagnation point heat flux to a sphere with radius equivalent to the effective nose radius of the object being considered. By convention, the equivalent nose radius is taken to be $R_n = L/2$, rather than $R_n = \sqrt{2}L/2$ as suggested above. In this way, the heat load to an object can be calculated by finding $q_\text{ss}$, which is trivial to calculate using any number of correlations [such as Sutton and Graves (1971) or Fay and Riddell (1958)], and multiplying by the shape factor (which is stored in a library containing factors for multiple different primitive shapes at many different orientations and attitudes). The shape factors for the experimental data are presented in Table 5. Although the shape factors show very little dependence on Reynolds number, they hide the strong spatial variations in heat flux which exist in reality. The fact that the highest heat fluxes occur near the edges of the cube means that these are the regions which are likely to fail or melt first during destructive re-entry. As a result, the fragmentation and demise of a satellite is most likely to be driven by the heat fluxes in these regions.

To take the important spatial variations of heat flux into account, we propose that shape factors $F_\text{sh}$ should instead be presented as edge-specific shape factors, where the average in Eq. 30 only includes the cube regions near the edges. There are two ways of doing this. Either all of the edges of the cube can be included in the average, or the edges can be separated into three categories: windward ($s/L = 0.5$), streamwise ($z/L = 0.5$), and leeward ($s/L = 1.5$, the data for which are not available from the current experiments), and then three different heat flux averages ${\hat{q}}$ and shape factors can be calculated. To illustrate this, shape factors for all these different definitions have been plotted in Fig. 18. In this case, the definition of the ‘edge’ is the region of the cube surface within 0.1L of the spatial discontinuity. Only this region is used in the calculation of Eq. 30. This definition is slightly arbitrary and the factor of 0.1 could be increased or decreased depending on the context. For example, if it is known that the epoxy joints holding the satellite panel together have a length of $\delta$ then $\delta /L$ would be the most appropriate factor to use for edge definition.

The above results are presented with an implicit assumption that the current methodologies used for modelling satellite demise (broadly outlined in the Introduction) are the most appropriate way of modelling demise. We implicitly assume that fragmentation is driven by melting or other catastrophic failure in regions of maximum heat flux. While this is a seemingly intuitive model, any model of satellite demise is extremely challenging to validate experimentally. Due to the complexity of the demise process, it is possible that demise is driven by other failure modes, for example delamination of the aluminium honeycomb sandwich panels. Alternatively, studies of Thermal Protection System (TPS) materials have looked at possible TPS failure mechanisms which are initiated by damage to the TPS caused by micrometeoroid impacts (Agrawal et al. 2013). Such micro-damages could very well be a nucleation point for satellite demise and failure. If it can be shown that satellite fragmentation is driven by a phenomenon other than melting at corners and edges then the results presented in the current study must be re-interpreted with that in mind.

Table 5 Summary of Stanton number patterns

Fig. 18

The evolution of different shape factors with Reynolds number

Finally, as briefly discussed in Sect. 2.4, these results are based on a free-stream flow with a fraction of the enthalpy of a real re-entry flow. To further confirm the applicability of these results to real re-entry flows, the current results should be compared against and supplemented with additional data from CFD, high energy (shock tube) experiments, or even flight data. The higher free-stream enthalpies considered in these datasets will cause much higher absolute values of heat flux, and possibly different heating patterns which could affect the values of the different shape factors calculated above.

8 Conclusions

The Mach 5 flow-field around a cube has been studied experimentally, using both schlieren photography to visualize the flow-field as well as infrared thermography and an IHCP data reduction method to measure the surface heat fluxes to the cube. The schlieren images revealed the presence of a separation bubble on the side surface of the cube at certain Reynolds numbers. This structure was imaged at a Reynolds number of $549\times 10^3$. Unfortunately, due to the low free-stream total temperature required to achieve this Reynolds number, it was not possible to take any high-quality IRT data, and therefore the separation bubble’s effect on the heat flux could not be quantified.

A detailed error sensitivity analysis of the inverse heat conduction method for heat flux calculation used showed that the Stanton numbers calculated by the data reduction method have an error of 12%, which is dominated by errors in the material emissivity. These errors appear to be highest near the regions of the cube where internal transverse conduction in the cube is strongest, such as corners and edges.

On the stagnation surface of the cube, the heat flux measurement results show broad agreement with existing data for stagnation point heating to flat axisymmetric surfaces. However, experimental heat flux contours to the stagnation surface of the cube shows the presence of distinct off-centred regions of lower heat flux, which we have termed ‘cold spots’. The Stanton number in these regions can be as much as 30% lower than the Stanton number to the geometric centre of the cube. Furthermore, their strength appears to show some dependence on Reynolds number. We deduce that the cause of these cold spots is due to sting flex during the tunnel run, causing a misalignment of the stagnation point. To confirm this hypothesis, a valuable future study would be to perform an oil flow visualisation of the flow around the cube. Such an experiment would also confirm the presence of a separation bubble on the side face of the cube at higher Reynolds numbers. We propose that the stagnation point heat flux to a cube can be estimated by calculating the stagnation point heat flux to a sphere with a nose radius of $R_n=\sqrt{2}L/2$, and multiplying the resulting value by 0.52, a coefficient very similar to those used to estimate the heat flux to a flat-ended cylinder. However, the stagnation point heat flux may be as much as 30% lower compared to other regions on the stagnation surface. The most notable flow feature on the off-stagnation (side) faces of the cube are wedge-shaped regions of increased heat flux emanating from the windward corners of the cube. The heat flux under these wedges can be very high, with regions of peak heating reaching stagnation point values. The spreading angle of these wedges show Reynolds number dependence and we therefore attribute them to the presence of vortical structures that are shed from the corners of the cube. Using the experimentally measured heat fluxes to the surface of the cube, we calculated different shape-factors describing the average heating to the cube as a whole as well as edges and corners, where heating is highest.

Finally, we draw attention to what we believe to be the two most important weaknesses of the current study. Firstly, as discussed extensively in Sect. 2.4 the flow conditions considered in this study are very low-energy when compared to true flight conditions. Taking equivalent experimental infrared measurements at flows corresponding to flight conditions would be challenging, as the infrared data capturing would need to take into the account the transmissivity of the reacting shock layer, the strongly varying material properties (including emissivity), and the very short test times. Preliminary arcjet and plasmatron studies of the re-entry flows around CubeSats (Masutti et al. 2018) have identified regions of high heating and temperature using uncalibrated IR measurements. Repetitions of these high-enthalpy studies using carefully calibrated IR measurements would provide valuable data with which the current measurements could be extrapolated to flight conditions. The second weakness of the current study is that it only considers one orientation of the model with respect to the free-stream. In reality, a satellite during re-entry will be tumbling rather than maintaining one attitude, constantly changing the heat flux distribution over the geometry. The time scale of the satellite tumbling motion is much larger than the time-scale of the hypersonic flow. As a result, when calculating heat fluxes for a tumbling geometry, only steady state flow-fields need to be considered. Even with this simplification, it is impractical to gather experimental data at a sufficiently fine-grained range of attitude orientations. Therefore, future research which considers the effect of tumbling on the heat fluxes to a satellite would have to be largely CFD based, with judiciously chosen conditions and orientations at which validation experiments can be performed.