Partial Justification of the Peregrine Soliton from the 2D Full Water Waves

Abstract

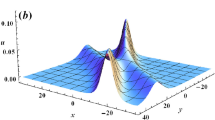
The Peregrine soliton $Q(x,t)=e^{it}(1-\frac{4(1+2it)}{1+4x^2+4t^2})$ is an exact solution of the 1d focusing nonlinear Schrödinger equation (NLS) $iB_t+B_{xx}=-2|B|^2B$, having the feature that it decays to $e^{it}$ at the spatial and time infinities, and with peaks and troughs in a local region. It is considered as a prototype of the rogue wave by the ocean waves community. The 1D NLS is related to the full water wave system in the sense that asymptotically it is the envelope equation for full water waves. In this paper, working in the framework of water waves which decay non-tangentially, we give a rigorous justification of the NLS from the full water waves equation on long time scale in a regime that allows for the partial justification of the Peregrine soliton. As a byproduct, we prove the long time existence of solutions for the full water waves equation with small initial data in space of the form $H^s(\mathbb {R})+H^{s'}(\mathbb {T})$, where $s\geqq 4, s'>s+\frac{3}{2}$.

Appendices

Appendix A. Holomorphicity of Plane Waves

Let $\zeta (\alpha )=\alpha +ce^{ik\alpha }, \alpha \in \mathbb {R}$, c is a small constant, $k>0$, for simplicity, assume k is an integer. Let

$$\begin{aligned} \Gamma :=\{\zeta (\alpha ):\alpha \in \mathbb {R}\}. \end{aligned}$$

Then $\Gamma$ is a graph. Let $\Omega _+$ be the region above $\Gamma$, and $\Omega _-$ the region below $\Gamma$. On one hand, it is easy to prove

Lemma A.1

$\alpha$, $e^{-ik\alpha }$ and $e^{ik\alpha }$ are holomorphic in $\Omega _+$.

On the other hand, we’ll show that $e^{ik\alpha }$ cannot be a boundary value of a bounded holomorphic function in $\Omega _-$.

Lemma A.2

If $c\ne 0$, then $e^{ik\alpha }$ cannot be a boundary value of a holomorphic function in $\Omega _-$.

Proof

If $e^{ik\alpha }$ is a boundary value of a holomorphic function in $\Omega _-$, then $e^{ik\alpha }$ is complete, and so $\alpha$ is as well. Assume that $\alpha =\Phi (\zeta (\alpha ))$, $\Phi$ being complete. Let $\Psi (\zeta )=\zeta +ce^{ik\zeta }$. Then $\Psi$ is complete, and $\Psi (\alpha )=\zeta (\alpha )$. Thus we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \Psi \circ \Phi (\zeta (\alpha ))=\zeta (\alpha )\\ \Phi \circ \Psi (\alpha )=\alpha . \end{array}\right. } \end{aligned}$$

$\Psi \circ \Phi$ and $\Phi \circ \Psi$ are complete, so we must have $\Psi \circ \Phi (z)\equiv z, \Phi \circ \Psi (z)\equiv z$. Thus $\Psi$ and $\Phi$ are the inverse of each other.

If $c\ne 0$, then the function $z+ce^{ikz}$ has an essential singularity at $\infty$ because $ce^{ikz}$ does. By Picard’s theorem, $z+ce^{ikz}$ attains all values in $\mathbb {C}$ infinitely many times with at most one exception. Suppose $z_0$ is this exception, i.e., $z+ce^{ikz}=z_0$ has finitely many solutions (possibly none). Then $z+ce^{ikz}=z_0+2\pi$ has infinitely many solutions. Then

$$\begin{aligned} z-2\pi +ce^{ikz}=z_0 \quad \Rightarrow \quad z-2\pi +ce^{ik(z-2\pi )}=z_0. \end{aligned}$$

Thus $z+ce^{ikz}=z_0$ has infinitely many solutions, which is a contradiction.

In particular, $z+ce^{ikz}=0$ has infinitely many solutions. Thus $\Psi$ is not invertible, which is a contradiction. $\square$

Lemma A.3

If $e^{-ik\alpha }$ is boundary value of a holomorphic function in $\Omega _-$, then $e^{ik\alpha }$ is also holomorphic in $\Omega _-$.

Proof

Let $e^{-ik\alpha }=G(\zeta (\alpha ))$, where G is holomorphic in $\Omega _-$. Then the zeros of G are a discrete set, which we denote by S. We’ll show that $S=\emptyset$. Since $\zeta =\alpha +ce^{ik\alpha }$, we have

$$\begin{aligned} \alpha =\zeta (\alpha )-\frac{c}{e^{-ik\alpha }}=\zeta (\alpha )-\frac{c}{G(\zeta (\alpha ))}. \end{aligned}$$

Define$H(\zeta ):=\zeta -\frac{c}{G(\zeta )}, ~ \zeta \in \Omega _-$. Then H has boundary value $\alpha$. Thus $\alpha$ is boundary value of a meromorphic function in $\Omega _-$, with poles at S.

Note that $e^{-ikH(\zeta (\alpha ))}$ has boundary values $e^{-ik\alpha }$, and $e^{-ikH(\zeta )}$ is holomorphic in $\Omega _-\setminus S$, by uniqueness extension of holomorphic functions, we must have $e^{-ikH(\zeta )}=G(\zeta )$ on $\Omega _-\setminus S$.

If $S\ne \emptyset$, then take $z_0\in S$. Then since $G(z_0)$ is defined, $z_0$ must be a removable singularity of $e^{-ikH(\zeta )}$. However, since $z_0$ is a pole of $H(\zeta )$, so $z_0$ is an essential singularity of $e^{-ikH(\zeta )}$, which is a contradiction. Thus $S=\emptyset$.

We conclude that $\alpha$ is holomorphic in $\Omega _-$, and so $e^{ik\alpha }$ is holomorphic in $\Omega _-$. $\square$

Corollary A.1

$e^{-ik\alpha }$ cannot be the boundary value of a holomorphic function in $\Omega _-$ if $c\ne 0$.

Appendix B

As before, we use the periodic Hilbert transform to estimate the error term $r_0$. The nonlocal Hilbert transform $\mathcal {H}_{\omega }$ is used when we estimate the error term $r_1$. Let’s denote $\tilde{\mathfrak {H}}_p$ as the periodic Hilbert transform associated with $\tilde{\omega }$.

1.1 B.1 Governing Equation for $r_0$

We have

$$\begin{aligned}&((D_t^0)^2-iA_0\partial _{\alpha })(I-\mathfrak {H}_p)r_0\\&\quad = ((D_t^0)^2-iA_0\partial _{\alpha })(I-\mathfrak {H}_p)\tilde{\omega }-2\left[ D_t^0\omega ,\mathfrak {H}_p\frac{1}{\omega _{\alpha }}+\bar{\mathfrak {H}}_p\frac{1}{\bar{\omega }_{\alpha }}\right] \partial _{\alpha }D_t^0\omega \\&\qquad +\,\frac{1}{ 4\pi i}\int _{\mathbb {T}} \Big (\frac{D_t^0\omega (\alpha ,t)-D_t^0\omega (\beta ,t)}{\sin (\frac{\pi }{2}(\omega (\alpha ,t)-\omega (\beta ,t)))}\Big )^2(\omega -\bar{\omega })(\beta )\mathrm{d}\beta \\&\quad := \mathcal {G}. \end{aligned}$$

We split $\mathcal {G}$ as $\mathcal {G}=\mathcal {G}_1+\mathcal {G}_2+\mathcal {G}_3+\mathcal {G}_4$, where

$$\begin{aligned} \mathcal {G}_1&:=((D_t^0)^2-iA_0\partial _{\alpha })(I-\mathfrak {H}_p)\tilde{\omega }-((\tilde{D}_t^0)^2-i\tilde{A}_0\partial _{\alpha })(I-\tilde{\mathfrak {H}}_p)\tilde{\omega }. \end{aligned}$$

(485)

$$\begin{aligned} \mathcal {G}_2&:=-2\left[ D_t^0\omega ,\mathfrak {H}_{p}\frac{1}{\omega _{\alpha }}+\bar{\mathfrak {H}}_{p}\frac{1}{\bar{\omega }_{\alpha }}\right] \partial _{\alpha }D_t^0\omega +2\left[ \tilde{D}_t^0\tilde{\omega },\tilde{\mathfrak {H}}_{p}\frac{1}{\tilde{\omega }_{\alpha }}+\bar{\tilde{\mathfrak {H}}}_{p}\frac{1}{\bar{\tilde{\omega }}_{\alpha }}\right] \partial _{\alpha }\tilde{D}_t^0\tilde{\omega }, \end{aligned}$$

(486)

and

$$\begin{aligned} \mathcal {G}_3:=&\frac{1}{4\pi i}\int _{\mathbb {T}} \Big (\frac{D_t^0\omega (\alpha ,t)-D_t^0\omega (\beta ,t)}{\sin (\frac{\pi }{2}(\omega (\alpha ,t)-\omega (\beta ,t)))}\Big )^2(\omega -\bar{\omega })(\beta )\mathrm{d}\beta \nonumber \\&-\,\frac{1}{4\pi i}\int _{\mathbb {T}}\Big (\frac{\tilde{D}_t^0\tilde{\omega }(\alpha ,t)-\tilde{D}_t^0\tilde{\omega }(\beta ,t)}{\sin \Big (\frac{\pi }{2}(\tilde{\omega }(\alpha ,t)-\tilde{\omega }(\beta ,t))\Big )}\Big )^2 (\tilde{\omega }-\bar{\tilde{\omega }})(\beta )\mathrm{d}\beta , \end{aligned}$$

(487)

and

$$\begin{aligned} \mathcal {G}_4:=&(\tilde{D}_t^0)^2-i\tilde{A}_0\partial _{\alpha })(I-\mathfrak {H}_p)\tilde{\omega }-2\left[ \tilde{D}_t^0\tilde{\omega },\tilde{\mathfrak {H}}_p\frac{1}{\tilde{\omega }_{\alpha }}+\bar{\tilde{\mathfrak {H}}}_p\frac{1}{\bar{\tilde{\omega }}_{\alpha }}\right] \partial _{\alpha }\tilde{D}_t^0\tilde{\omega }\nonumber \\&+\,\frac{1}{4\pi i}\int _{\mathbb {T}}\Big (\frac{\tilde{D}_t^0\tilde{\omega }(\alpha ,t)-\tilde{D}_t^0\tilde{\omega }(\beta ,t)}{\sin (\frac{\pi }{2}(\tilde{\omega }(\alpha ,t)-\tilde{\omega }(\beta ,t)))}\Big )^2 (\tilde{\omega }-\bar{\tilde{\omega }})(\beta )\mathrm{d}\beta . \end{aligned}$$

(488)

1.2 B.2 Governing Equation for $D_t^0(I-\mathfrak {H}_p)r_0$

We need to derive an equation to control $D_t^0 r_0$ as well. We consider instead the quantity

$$\begin{aligned} \sigma _0:=(I-\mathfrak {H}_p)\Big \{D_t^0(I-\mathfrak {H}_p)(\omega -\alpha )-\tilde{D}_t^0(I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\alpha )\Big \}. \end{aligned}$$

We have

$$\begin{aligned}&((D_t^0)^2-iA_0\partial _{\alpha })(I-\mathfrak {H}_p)D_t^0(I-\mathfrak {H}_p)(\omega -\alpha )\nonumber \\&\quad = -[(D_t^0)^2-iA_0\partial _{\alpha },\mathfrak {H}_p]D_t^0(I-\mathfrak {H}_p)(\omega -\alpha )\nonumber \\&\qquad +\,(I-\mathfrak {H}_p)((D_t^0)^2-iA_0\partial _{\alpha })D_t^0(I-\mathfrak {H}_p)(\omega -\alpha )\nonumber \\&\quad =-2[D_t^0\zeta ,\mathfrak {H}_p]\frac{\partial _{\alpha }(D_t^0)^2(I-\mathfrak {H}_p)(\omega -\alpha )}{\omega _{\alpha }}\nonumber \\&\qquad +\,\frac{1}{4\pi i}\int _{\mathbb {T}} \Big (\frac{D_t^0\omega (\alpha )-D_t^0\omega (\beta )}{\sin (\frac{\pi }{2}(\omega (\alpha )-\omega (\beta )))}\Big )^2 \partial _{\beta }D_t^0 (I-\mathfrak {H}_p)(\omega (\beta )-\beta )\mathrm{d}\beta \nonumber \\&\qquad +\,(I-\mathfrak {H}_p)[(D_t^0)^2-iA_0\partial _{\alpha }, D_t^0](I-\mathfrak {H}_p)(\omega -\alpha )+(I-\mathfrak {H}_p)D_t^0 \mathcal {G}, \end{aligned}$$

(489)

and

$$\begin{aligned}&((D_t^0)^2-iA_0\partial _{\alpha })(I-\mathfrak {H}_p)\tilde{D}_t^0(I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\alpha )\nonumber \\&\quad = -[(D_t^0)^2-iA_0\partial _{\alpha },\mathfrak {H}_p]\tilde{D}_t^0(I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\alpha )\nonumber \\&\qquad +\,(I-\mathfrak {H}_p)((D_t^0)^2-iA_0\partial _{\alpha })\tilde{D}_t^0(I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\alpha )\nonumber \\&\quad =-2[D_t^0\omega ,\mathfrak {H}_p]\frac{\partial _{\alpha }D_t^0 \tilde{D}_t^0(I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\alpha )}{\omega _{\alpha }}\nonumber \\&\qquad +\,\frac{1}{4\pi i}\int _{\mathbb {T}} \Big (\frac{D_t^0\omega (\alpha )-D_t^0\omega (\beta )}{\sin (\frac{\pi }{2}(\omega (\alpha )-\omega (\beta )))}\Big )^2 \partial _{\beta }\tilde{D}_t^0 (I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\beta )(\beta )\mathrm{d}\beta \nonumber \\&\qquad +\,(I-\mathfrak {H}_p)((D_t^0)^2-iA_0\partial _{\alpha }) \tilde{D}_t^0(I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\alpha )\nonumber \\&\quad = -2[D_t^0\omega ,\mathfrak {H}_p]\frac{\partial _{\alpha }D_t^0 \tilde{D}_t^0(I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\alpha )}{\omega _{\alpha }}\nonumber \\&\qquad +\,\frac{1}{4\pi i}\int _{\mathbb {T}} \Big (\frac{D_t^0\omega (\alpha )-D_t^0\omega (\beta )}{\sin (\frac{\pi }{2}(\omega (\alpha )-\omega (\beta )))}\Big )^2 \partial _{\beta }\tilde{D}_t^0 (I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\beta )(\beta )\mathrm{d}\beta \nonumber \\&\qquad +\,(I-\mathfrak {H}_p)((\tilde{D}_t^0)^2-i\tilde{A}_0\partial _{\alpha }) \tilde{D}_t^0(I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\alpha )\nonumber \\&\qquad +\,(I-\mathfrak {H}_p)((D_t^0)^2-iA_0\partial _{\alpha }-(\tilde{D}_t^0)^2+i\tilde{A}_0\partial _{\alpha })\tilde{D}_t^0(I-\tilde{\mathfrak {H}}_p)(\tilde{\omega }-\alpha ). \end{aligned}$$

(490)

Using (489) and (490), we have that

$$\begin{aligned} ((D_t^0)^2-iA_0\partial _{\alpha })\sigma _0=\text {fourth order}. \end{aligned}$$

(491)