1 Introduction

Human African trypanosomiasis (HAT), also known as sleeping sickness, is a neglected tropical disease that continues to affect people living in world’s poorest communities. In particular, it is more prevalent in nations or communities with weak health infrastructure, scanty health information and low food security. Two forms of the disease exist depending on the parasite involved: Trypanosoma brucei gambiense, which is a chronic form of the disease present in western and central Africa, and Trypanosoma brucei rhodesiense, which is an acute disease located in eastern and southern Africa [1]. Of the HAT cases recorded in the last decade, approximately 98% are attributed to the gambiense form and the remainder to rhodesiense [1]. With such statistics, several researchers believe that the rhodesiense form is a zoonotic disease that affects mainly animals (livestock and wildlife), with humans being only accidentally infected [1].

Although the signs and symptoms of HAT are generally similar for both forms, their frequency, severity and kinetic appearance differ. The rhodesiense form is an acute disease that usually progresses to death within six months, whereas the gambiense form is usually a chronic progressive infection with an average duration of almost three years [1]. Furthermore, clinical signs and symptoms are unspecific in both forms of the disease, and their appearance varies between individuals and foci. Some of the main signs and symptoms of the first stage of infection are intermittent fever, headache, lymphadenopathies, weakness, asthenia, anemia, cardiac disorders, endocrine disturbances, musculoskeletal pains and hepatosplenomegaly [1]. Neuropsychiatric signs and symptoms, including sleep disturbances, are often presented by patients in the second stage of infection. It is worth noting that most of the symptoms of both stages overlap, rendering the distinction between the stages unclear [1].

HAT is transmitted by more than 20 species of Glossina tsetse flies. Prior studies have shown that all metabolic processes that occur in tsetse flies strongly depend on temperature. In particular, it was observed that the interlarval period, pupal period, adult lifespan and the period between successive feeds are reduced as temperature increases [2]. Phelps and Lovemore [3] noted that temperature does not only alter the different developmental periods of the vector but it also plays a huge role in the fly’s flight activity. Furthermore, for temperature below 17∘C it was noted that tsetse flies will rest in direct sunlight and when temperatures are above 32∘C the vectors will be inactive and they will seek artificial refuges, and in most cases these are cool shaded places [4].

According to Phelps and Burrow [5], temperatures above 40∘C are fatal to both small and large flies and pupae. Bursell [6] opines that temperature and the size of the fly affect the amount of fat reservation in the fly. Precisely, smaller flies have less fat than larger ones. This is one of the reasons why temperatures below 16∘C are known not to be suitable for the development of smaller flies, since the fat which would have been reserved during the larval periods will get exhausted before the pupa is fully matured. Thus fat reservation is integral for the development of the fly from pupa to adult as well as the survival of the fly till it gets its first blood-meal [6]. Phelps and Clarke [7] demonstrated that extreme temperature is associated with higher mortality among young flies, particularly in small male flies.

The above discussion clearly demonstrates that temperature has an integral role on tsetse population dynamics and can be one of the strongest abiotic determinants of tsetse distributions [8]. Hence, as opined by Leak [9], understanding the relationship between these factors and vector population dynamics is therefore a potential area for modelling and further development of the existing models. Mathematical modelling, as a powerful tool in quantifying the complex and numerous factors, has been widely used to understand the transmission and control of HAT [8, 10–32]. The aforementioned studies improved the existing knowledge on HAT dynamics. For example, the study of Hagrove et al. [10] demonstrated that treating cattle with insecticides could be useful on HAT management. Pandey et al. [11], Funk et al. [12], Ndondo et al. [13] and Rock et al. [14] among others explored the role of animals as reservoirs on HAT dynamics. Their studies demonstrated that animals play an integral role of HAT dynamics hence they need to be incorporated in the frameworks that seek to explore the intrinsic dynamics of HAT. Stone and Chitnis [15] utilised a mathematical model to explore the effects of heterogeneous biting exposure and animal hosts on Trypanosoma brucei gambiense transmission and control. Outcomes from their study highlighted that heterogeneity biting rates as well as ecological and environmental factors play a crucial role on Trypanosoma brucei gambiense transmission and control.

Recently, Lord et al. [16], Alderton et al. [17] and Ackley and Hagrove [18] explored the role of temperature on HAT dynamics. Alderton et al. [17] utilised an agent based model to explore the effects of temperature on seasonal HAT transmission. Among several other outcomes, their work suggested that mathematical models could strongly mirror the transmission dynamics of HAT. In particular, they found out that their model solutions were in agreement with reality. Lord et al. [16] developed a mathematical model for HAT that incorporated the effects of temperature on mortality, larviposition and emergence rates. Making use of the epidemiological data for infection in cattle they validated their framework, and findings from their work highlighted that temperature variations are key to tsetse distribution and abundance. Ackley and Hagrove [18] developed a dynamical model to simulate female tsetse populations and the associated changes in their age distribution. One of the key findings from their work is that for temperatures greater than 25∘C mortality among immature classes of the vector increases substantially.

As concerted efforts to “eliminate” HAT continue to increase, with the current set target being “the reduction of gambiense HAT incidence to less than 1 new case per 10,000 population at risk in at least 90% of foci with fewer than 2000 cases reportedly globally by 2020” and “to target zero incidence of the disease by 2030” [19], different modelling approaches need to be utilised to continue the characterisation of the relationship between temperature and HAT. In this paper, we utilise fractional calculus to explore the effects of temperature on Trypanosoma brucei rhodesiense.

Although the aforementioned studies improved our quantitative and qualitative knowledge on the relationship between temperature and HAT, most of the mathematical models of infectious diseases have been described by the ordinary differential equations (ODEs) in which the order of derivative is an integer. However, recent studies suggest that models that use integer-order differentiation do not adequately capture memory effects, long-rage interactions and hereditary properties, which govern many real world problems [33]. In contrast, it has been proved that models that utilise fractional differentiation provide “more reasonable” outcomes compared to those that use integer-order differentiation [33] since they can capture memory effects. Moreover, several researchers concur that many real world problems are influenced by history, suggesting that memory has a strong impact on the underlying dynamics. Based on this notion, fractional-order calculus has been widely and extensively used in many fields such as engineering, biochemistry, finance, chemistry, medicine, biology and so on, compared to the classical order [34, 35].

Prior studies suggest that evolution and control of epidemic processes in human societies cannot be considered without any memory effect [33–36]. In particular, they argue that whenever a disease spreads within a community, individuals gain knowledge or experience, which greatly influences their response [33]. Thus once people are aware of a certain disease and its impact they use suitable mitigation strategies to minimise contact between themselves and vectors, thereby minimising chances of being infected. Evidently, this results in some endogenous controlled suppression of the spreading, although other factors can help [33]. Based on this assertion, fractional-order derivative is more suited for modelling problems involving memory, which is the case in most biological systems [36]. Another advantage of using fractional-order derivative is that it enlarges the stability region of the dynamical systems [36]. Motivated by this discussion we believe that the memory has an effect on HAT dynamics. The framework proposed in this study includes the life cycle of tsetse flies, humans and animals. Furthermore, the model incorporates the formulae proposed by Artzrouni and Gouteux [25] to explore the role of human detection and vector control on short and long term dynamics of the disease at different temperature levels.

The rest of the paper is organised as follows. In Sect. 2, we present preliminaries on the Caputo fractional calculus. The proposed model and analytical results are presented in Sect. 3. In Sect. 4, the dynamical behaviour of the proposed model is investigated. Precisely, we compute the basic reproduction number and investigate the stability of the model’s steady states. In Sect. 5, numerical experiments are done in order to verify theoretical results presented in the study. Finally, a brief discussion rounds up the paper.

2 Preliminaries on the Caputo fractional calculus

We begin by introducing the definition of Caputo fractional derivative and stating related theorems (see [37–41]) that we will utilise to derive important results in this work.

Definition 2.1

Suppose that \(\alpha >0\), \(t>a\), \(\alpha , a,t\in \mathbb{R}\). The Caputo fractional derivative is given by

$$\begin{aligned} {}^{c}_{a}D^{\alpha }_{t}f(t) = \frac{1}{\varGamma (n-\alpha )} \int ^{t}_{a} \frac{f^{n}(\xi )}{(t-\xi )^{\alpha +1-n}}\,d\xi ,\quad n-1< \alpha ,n \in \mathbb{N.} \end{aligned}$$

Definition 2.2

(Linearity property [37])

Let \(f(t),g(t):[a,b]\rightarrow \mathbb{R}\) be such that \({}^{c}_{a}D^{\alpha }_{t}f(t)\) and \({}^{c}_{a}D^{\alpha }_{t}g(t)\) exist almost everywhere, and let \(c_{1},c_{2}\in \mathbb{R}\). Then \({}^{c}_{a}D^{\alpha }_{t}(c_{1}f(t))+{}^{c}_{a}D^{\alpha }_{t}(c_{2}g(t))\) exists everywhere, and

$$\begin{aligned} {}^{c}_{a}D^{\alpha }_{t} \bigl(c_{1}f(t)+c_{2}g(t)\bigr)=c_{1} {}^{c}_{a}D^{ \alpha }_{t}f(t)+ c_{2} {}^{c}_{a}D^{\alpha }_{t}g(t). \end{aligned}$$

Definition 2.3

(Caputo derivative of a constant [40])

The fractional derivative for a constant function \(f(t)=c\) is zero, that is,

$$\begin{aligned} {}^{c}_{a}D^{\alpha }_{t}c=0. \end{aligned}$$

Let us consider the following general type of fractional differential equations involving Caputo derivative:

$$\begin{aligned} {}^{c}_{t_{0}}D^{\alpha }_{t} x(t)=f \bigl(t,x(t)\bigr),\quad \alpha \in (0,1) \end{aligned}$$
(1)

with initial condition \(x_{0}=x(t_{0})\).

Definition 2.4

(see [37])

The constant \(x^{*}\) is an equilibrium point of the Caputo fractional dynamic system (1) if and only if \(f(t,x^{*})=0\).

Definition 2.5

(see [41])

For the system described by (1):

  1. (i)

    The trivial solution is said to be stable if, for any \(t_{0}\in \mathbb{R}\) and any \(\epsilon >0\), there exists \(\delta =\delta (t_{0},\epsilon )\) such that \(\|x(t_{0})\|<\delta \) implies \(\|x(t)\|<\epsilon \) for all \(t>t_{0}\).

  2. (ii)

    The trivial solution is said to be asymptotically stable if it is stable and, for any \(t_{0}\in \mathbb{R}\) and any \(\epsilon >0\), there exists \(\delta _{a}=\delta _{a}(t_{0},\epsilon )>0\) such that \(\|x(t)\|<\delta _{a}\) implies \(\lim_{t\rightarrow \infty } \|x(t)\|=0\).

  3. (iii)

    The trivial solution is said to be uniformly stable if it is stable and \(\delta =\delta (\epsilon )>0\) can be chosen independently of \(t_{0}\).

  4. (iv)

    The trivial solution is uniformly asymptotically stable if it is uniformly stable and there exists \(\delta _{a}.0\), independent of \(t_{0}\), such that if \(\|x(t_{0})\|<\delta _{a}\), then \(\lim_{t\rightarrow \infty } \|x(t)\|=0\).

  5. (v)

    The trivial solution is globally (uniformly) asymptotically stable if it is (uniformly) asymptotically stable and \(\delta _{a}\) can be an arbitrary large finite number.

Theorem 2.1

(Uniform asymptotic stability [37, 42])

Let\(x^{*}\)be an equilibrium point for the nonautonomous fractional-order system (1) and\(\varOmega \subset \mathbb{R}^{n}\)be a domain containing\(x^{*}\). Let\(L:[0,\infty )\times \varOmega \rightarrow \mathbb{R}\)be a continuously differentiable function such that

$$\begin{aligned} W_{1}(x)\leq L\bigl(t,x(t)\bigr)\leq W_{2}(x) \end{aligned}$$

and

$$\begin{aligned} {}^{c}_{a}D^{\alpha }_{t} L \bigl(t,x(t)\bigr)\leq -W_{3}(x) \end{aligned}$$

for all\(\alpha \in (0,1)\)and all\(x\in \varOmega \), where\(W_{1}(x)\), \(W_{2}(x)\)and\(W_{3}(x)\)are continuous positive definite functions onΩ. Then the equilibrium point of system (1) is uniformly asymptotically stable.

The following theorem summarises a lemma proved in [37], where a Volterra-type Lyapunov function is obtained for fractional-order epidemic systems.

Theorem 2.2

(see [37])

Let\(x(\cdot )\)be a continuous and differentiable function with\(x(t) \in \mathbb{R}_{+}\). Then, for any time instant\(t\geq t_{0}\), one has

$$\begin{aligned} {}^{c}_{t_{0}}D^{\alpha }_{t} \biggl(x(t)-x^{*}-x^{*}\ln \frac{x(t)}{x^{*}} \biggr) \leq \biggl(1-\frac{x^{*}}{x(t)} \biggr) {}^{c}_{t_{0}}D^{ \alpha }_{t}x(t), \quad x^{*}\in \mathbb{R}^{+}, \forall \alpha \in (0,1). \end{aligned}$$

Theorem 2.3

(see [43])

Let\(\alpha >0\), \(n-1<\alpha <n-\mathbb{N}\). Suppose that\(f(t)\), \(f^{\prime }(t)\), … , \(f^{(n-1)}(t)\)are continuous on\([t_{0},\infty )\)and the exponential order and that\({}^{c}_{t_{0}}D^{\alpha }_{t}f(t)\)is piecewise continuous on\([t_{0},\infty )\). Then

$$\begin{aligned} {\mathcal{L}}\bigl\{ {}^{c}_{t_{0}}D^{\alpha }_{t}f(t) \bigr\} = s^{\alpha } {\mathcal{F}} (s)- \sum^{n-1}_{k=0} s^{\alpha -k-1} f^{(k)}(t_{0}), \end{aligned}$$

where\({\mathcal{F}} (s)= {\mathcal{L}}\{f(t)\}\).

Theorem 2.4

(see [44])

Let\(\mathbb{C}\)be a complex plane. For any\(\alpha >0\)\(\beta >0\)and\(A\in \mathbb{C}^{n\times n}\), we have

$$\begin{aligned} {\mathcal{L}}\bigl\{ t^{\beta -1} E_{\alpha , \beta }\bigl(At^{\alpha } \bigr)\bigr\} = s^{ \alpha -\beta }\bigl(s^{\alpha }-A\bigr)^{-1} \end{aligned}$$

for\({\mathcal{R}}s>\|A\|^{\frac{1}{\alpha }}\), where\({\mathcal{R}}s\)represents the real part of the complex numbers, and\(E_{\alpha , \beta }\)is the Mittag-Leffler function [45].

3 Mathematical model

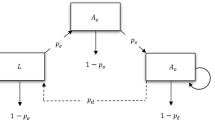
In this section, the Caputo fractional calculus has been used to formulate and explore the role of temperature on the transmission and control of Trypanosoma brucei rhodesiense. The proposed mathematical model demonstrates the interplay between the tsetse and two hosts, humans and animals. Furthermore, the proposed framework consists of two parts (i) the life cycle of the tsetse flies and (ii) the full model that governs HAT transmission dynamics when the tsetse fly population growth persists. Comprehensive details on the modelling of the early stages of the tsetse flies can be found in [13]. As proposed in [13], let the following system summarise the dynamical growth of the tsetse fly:

$$ \left . \textstyle\begin{array}{l} {}^{c}_{t_{0}}D^{\alpha }_{t} L(t)= b^{\alpha }_{l}W N_{v} (1-\frac{L}{K_{l}^{\alpha }} )-(\sigma _{l}^{\alpha }+\mu _{p}^{ \alpha })L, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} N_{v}(t)= \sigma _{l}^{\alpha }L-\mu _{v}^{ \alpha }N_{v}. \end{array}\displaystyle \right \} $$
(2)

The variable \(L(t)\) represent the pupal stage of the tsetse, and \(N_{v}(t)\) denotes the total adult vector population at time t, which is comprised of susceptible \(S_{v}(t)\) and infectious \(I_{v}(t)\). Thus, \(N_{v}=S_{v}+I_{v}\). In addition, all model parameters and variables in system (2) are considered to be positive, and the parameters are defined as follows: \(b_{l}\) represents the rate at which female flies give birth to larvae; W denotes a fraction of female flies in the population of adult flies; \(K_{l}\) is the pupal carrying capacity of the nesting site; \(\sigma _{l}\) is the transition from pupal stage into an adult fly, thus \(1/\sigma _{l}\) represents the average time a fly spends as a pupa; \(\mu _{p}\) and \(\mu _{v}\) account for mortality rate of pupae and adult flies, respectively.

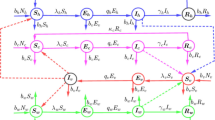
Assuming that the growth of the tsetse fly persists, we now present the full model that governs disease transmission. Thus, we subdivide the two host populations (humans and animals) into compartments of: the susceptible \(S_{i}(t)\), the infectious \(I_{i}(t)\) and the recovered \(R_{i}(t)\), \(i=a, h\). The subscripts a and h represent the animal and human populations, respectively. It follows that the total population of each host at time t is given by \(N_{i}(t)=S_{i}(t)+I_{i}(t)+R_{i}(t)\). The proposed fractional-order model has the form

$$ \left . \textstyle\begin{array}{l} {}^{c}_{t_{0}}D^{\alpha }_{t} S_{v}(t)=\sigma _{l}^{\alpha } L-(\beta _{hv}^{ \alpha }I_{h}+\beta _{av}^{\alpha }I_{a})S_{v}-\mu _{v}^{\alpha }S_{v}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} I_{v}(t)=(\beta _{hv}^{\alpha }I_{h}+ \beta _{av}^{\alpha }I_{a})S_{v}-\mu _{v}^{\alpha } I_{v}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} S_{h}(t)= \varLambda _{h}^{ \alpha }-\beta _{vh}^{\alpha }f(I_{v})S_{h}-\mu _{h}^{\alpha }S_{h}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} I_{h}(t)= \beta _{vh}^{ \alpha }f(I_{v})S_{h}-(\mu _{h}^{\alpha }+\gamma _{h}^{\alpha })I_{h}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} S_{a}(t)= \varLambda _{a}^{ \alpha }-\beta _{va}^{\alpha }f(I_{v})S_{a}-\mu _{a}^{\alpha }S_{a}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} I_{a}(t)= \beta _{va}^{ \alpha }f(I_{v})S_{a}-(\mu _{a}^{\alpha }+\gamma _{a}^{\alpha })I_{a}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} R_{h}(t)= \gamma _{h}^{ \alpha } I_{h} - \mu _{h}^{\alpha } R_{h}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} R_{a}(t)= \gamma _{a}^{ \alpha } I_{a} - \mu _{a}^{\alpha } R_{a}. \end{array}\displaystyle \right \} $$
(3)

All model parameters and variables in system (3) are considered to be positive, and the parameters are defined as follows: parameter \(\varLambda _{j}\), \(j=a,h\), represents the constant recruitment rate of the host population through birth and they are assumed to be susceptible, \(\mu _{i}\), \(i=a,h,v\), denotes natural mortality rate, \(\beta _{vk}\) represents the transmission rate of infection from an infected tsetse vector to a susceptible host k given that effective contact between the two species occurs, \(\beta _{kv}\) represents disease transmission from an infected host k to a susceptible vector given that effective contact between the two occurs, \(\gamma _{k}\) is the recovery rate for the host population. Furthermore, disease transmission from infectious vectors to susceptible hosts is modelled by a nonlinear incidence rate, and the function \(f(I_{v})\) is equivalent to

$$\begin{aligned} f(I_{v})=\frac{ I_{v}}{1+\theta I_{v}}, \end{aligned}$$

where θ is a positive constant.

As highlighted earlier, temperature plays a crucial role on Trypanosoma brucei rhodesiense transmission dynamics. To account for this effect, we now remodel parameters of system (2) and (3): \(b_{l}\) is the rate at which female flies give birth to larvae; \(\sigma _{l}\) denotes pupal development rate; \(\mu _{p}\) denotes pupal mortality rate and \(\mu _{v}\) is adult tsetse mortality rate; and functions of temperature. In particular, we adopted the following function [16, 46] to model the rate at which female flies give birth to larvae:

$$\begin{aligned} b_{l}=d_{1}+d_{2}(T-T_{0}), \end{aligned}$$
(4)

where \(T_{0}\) was set to 20∘C [16]. Function (4) was derived by Hargrove [46] when the author used ovarian dissection data from marked and released G. m. morsitans and G. pallidipes at Rekomitjie. Precisely, Hargrove’s work suggested that the larviposition rate per day increases linearly between 20∘C and 30∘C. Adult fly mortality rate \(\mu _{v}\) is now modelled by

$$ \mu _{v}= \textstyle\begin{cases} a_{1}& \text{for }T\leq 25, \\ a_{1}e^{a_{2}(T-25)}& \text{for } T> 25, \end{cases} $$

where T is the temperature in ∘C, \(a_{2}\) parameterises the increase at higher temperatures. Based on the laboratory experiments performed by Phelps [2], pupal survival to adulthood depends on temperature variations and is highest for temperatures between about 20∘C and 30∘C. As temperatures move from this range, the mortality rises sharply, leading to a U-shaped curve, and a suitable function to represent this relation is

$$\begin{aligned} \mu _{p}=b_{1}+b_{2}\exp \bigl(-b_{3}(T-T_{2})\bigr)+b_{4}\exp \bigl(b_{5}(T-T_{3})\bigr), \end{aligned}$$

where T is the temperature in ∘C, \(T_{2}\) and \(T_{3}\) are not parameters but are constants selected to ensure that the coefficients \(b_{3}\) and \(b_{5}\) are in a convenient range, and in our simulation these will be set to 16∘C and 32∘C as in [16].

Additional important result from Phelps’ work was the quantification of the daily rate of pupal development \(\sigma _{L}\) in G. m. morsitans as a function of constant temperature. The following function was considered to be the best representation of pupal emergence and temperature variations:

$$\begin{aligned} \sigma _{l}=\frac{c_{1}}{1+\exp (c_{2}+c_{3}T)}, \end{aligned}$$

where T represents the mean daily temperature and \(c_{1}\), \(c_{2}\) and \(c_{3}\) parametrise pupal hatching rate [16].

Remark 3.1

Note that, in order to avoid flaws regarding the time dimension, we introduced α in the model parameters (right-hand side) of both systems (2) and (3), so that the dimensions of these parameters become \((\mathrm{time})^{-\alpha }\), which is in agreement with the left-hand side of the model.

It is worth noting that there is need to derive the threshold quantity that determines the growth of the tsetse fly population. Thus, the analysis of the proposed model will begin with system (2). Once this threshold condition has been determined, one can then proceed to investigating the dynamical behaviour of system (3).

4 Analytical results of the proposed framework

4.1 The dynamical behaviour of system (2)

In this section, the dynamical behaviour of system (2) is investigated. The basic properties of the model and other fundamental results will be established.

4.1.1 Basic properties of the model

Theorem 4.1

Let\({\mathcal{X}}(t)=(L(t), N_{v}(t))\)be the unique of model (2) for\(t\geq 0\). Then the solution\({\mathcal{X}}(t)\)remains in\(\mathbb{R}^{2}_{+}\).

Proof

To demonstrate that the solution \({\mathcal{X}}(t)\) of model (2) is nonnegative, there is need to investigate the direction of the vector field given by the right-hand side of (2) on each space and determine whether the vector field points to the interior of \(\mathbb{R}^{2}_{+}\) or is tangent to the coordinate space. Since

$$\begin{aligned}& {}^{c}_{t_{0}}D^{\alpha }_{t} L(t)|_{L=0} = b^{\alpha }_{l}W N_{v} \geq 0, \\& {}^{c}_{t_{0}}D^{\alpha }_{t} N_{v}(t)|_{N_{v}=0} = \sigma _{l}^{\alpha }L \geq 0. \end{aligned}$$

The results presented imply that the vector field given by the right-hand side of (2) on each coordinate plane is either tangent to the coordinate plane or points to the interior of \(\mathbb{R}^{2}_{+}\). Hence, the domain \(\mathbb{R}^{2}_{+}\) is a positively invariant region. Moreover, if the initial conditions of system (2) are nonnegative, then it follows that the corresponding solutions of model (2) are nonnegative. □

Theorem 4.2

Let\({\mathcal{X}}(t)=(L(t), N_{v}(t))\)be the unique of model (2) for\(t\geq 0\). Then the solution\({\mathcal{X}}(t)\)is bounded above, that is, \({\mathcal{X}}(t)\in \varOmega \)whereΩdenotes the feasible region and is given by

$$\begin{aligned} \varOmega = \bigl\{ (L,N_{v} )\in \mathbb{R}^{2}_{+}| 0\leq L \leq K_{l}^{\alpha }, 0\leq N_{v}\leq C \bigr\} . \end{aligned}$$

Proof

For model (2) to be biologically meaningful, all model solutions need to be positive. Hence, from the first equation of model (2), one can easily note that for all solutions of this equation to remain positive the following condition must hold \(0\leq L(t)\leq K_{l}^{\alpha }\); otherwise, the solutions will be negative and biologically irrelevant. From the bounds of \(L(t)\), it follows that

$$\begin{aligned} {}^{c}_{t_{0}}D^{\alpha }_{t} N_{v}(t) =& \sigma _{l}^{\alpha }L-\mu _{v}^{ \alpha }N_{v} \\ \leq &\sigma _{l}^{\alpha }K_{l}^{\alpha }- \mu _{v}^{\alpha }N_{v}. \end{aligned}$$

By closely following Theorems 2.3 and 2.4, applying the Laplace transform leads to

$$\begin{aligned} s^{\alpha }{\mathcal{L}} \bigl(N_{V}(t)\bigr)-s^{{\alpha }-1} N_{v}(0)\leq \frac{\sigma _{l}^{\alpha }K_{l}^{\alpha }}{s}-\mu _{v}^{\alpha }{ \mathcal{L}}\bigl(N_{v}(t)\bigr). \end{aligned}$$

Combining the like terms, one gets

$$\begin{aligned} {\mathcal{L}}\bigl(N_{v}(t)\bigr) \leq &\sigma _{l}^{\alpha }K_{l}^{\alpha } \frac{s^{-1}}{s^{\alpha }+\mu _{v}^{\alpha }}+ N_{v}(0) \frac{s^{{\alpha }-1}}{s^{\alpha }+\mu _{v}^{\alpha }} \\ =&\sigma _{l}^{\alpha }K_{l}^{\alpha } \frac{s^{\alpha -(1+\alpha )}}{s^{\alpha }+\mu _{v}^{\alpha }}+ N_{v}(0) \frac{s^{{\alpha }-1}}{s^{\alpha }+\mu _{v}^{\alpha }}. \end{aligned}$$

Applying the inverse Laplace transform leads to

$$ \begin{aligned}[b] N_{v}(t)&\leq {\mathcal{L}}^{-1} \biggl\{ \sigma _{l}^{\alpha }K_{l}^{ \alpha } \frac{s^{\alpha -(1+\alpha )}}{s^{\alpha }+\mu _{v}^{\alpha }} \biggr\} + {\mathcal{L}}^{-1} \biggl\{ N_{v}(0) \frac{s^{{\alpha }-1}}{s^{\alpha }+\mu _{v}^{\alpha }} \biggr\} \\ &\leq \sigma _{l}^{ \alpha }K_{l}^{\alpha } t^{\alpha } E_{\alpha ,\alpha +1}\bigl(-\mu _{v} t^{\alpha }\bigr)+ N_{V}(0)E_{\alpha ,1}\bigl(- \mu _{v} t^{\alpha }\bigr) \\ &\leq \frac{\sigma _{l}^{ \alpha }K_{l}^{\alpha }}{\mu _{v}^{\alpha }}\mu _{v}^{ \alpha }t^{\alpha } E_{\alpha ,\alpha +1}\bigl(-\mu _{v} t^{\alpha }\bigr)+ N_{V}(0)E_{ \alpha ,1}\bigl(-\mu _{v} t^{\alpha }\bigr) \\ &\leq \max \biggl\{ \frac{\sigma _{l}^{ \alpha }K_{l}^{\alpha }}{\mu _{v}^{\alpha }}, N_{v}(0) \biggr\} \bigl( \mu _{v}^{\alpha }t^{\alpha } E_{\alpha ,\alpha +1}\bigl(- \mu _{v} t^{ \alpha }\bigr)+E_{\alpha ,1}\bigl(-\mu _{v} t^{\alpha }\bigr)\bigr) \\ &= \frac{C}{\varGamma (1)} = C, \end{aligned} $$
(5)

where \(C=\max \{ \frac{\sigma _{l}^{ \alpha }K_{l}^{\alpha }}{\mu _{v}^{\alpha }}, N_{v}(0) \}\). Thus, \(N_{V}(t)\) is bounded from above. Hence, one can conclude that the solution \(X_{1}(t)\) is bounded above. □

4.1.2 Equilibrium points and their stability

In what follows, we derive the fundamental results for model (2). Through direct calculations, one can note that model (2) has two equilibrium points, trivial \((L,N_{v})=(0,0)\) and nontrivial

$$\begin{aligned} \bigl\{ L^{*},N_{v}^{*}\bigr\} = \biggl\{ \biggl(1-\frac{1}{r} \biggr)K_{l}^{ \alpha }, \frac{\sigma _{l}^{ \alpha }}{\mu _{v}^{ \alpha }} \biggl(1-\frac{1}{r} \biggr)K_{l}^{ \alpha } \biggr\} , \end{aligned}$$

where

$$\begin{aligned} r= \frac{\sigma _{l}^{ \alpha }}{\sigma _{l}^{ \alpha }+\mu _{p}^{ \alpha }} \frac{b_{l}^{ \alpha }}{\mu _{v}^{ \alpha }}W, \end{aligned}$$

r is a threshold quantity that determines growth of the tsetse fly population. It is defined as the likelihood of the fly to survive the pupal stage multiplied by the surviving population of female flies [13].

Theorem 4.3

  1. (i)

    If\(r\leq 1\), then the equilibrium point\((0,0)\)is the sole equilibrium point of system (2) and it is globally (uniformly) asymptotically stable inΩ.

  2. (ii)

    If\(r>1\), then the equilibrium\((L^{*},N_{v}^{*})\)is globally (uniformly) asymptotically stable in\(\operatorname{int}(\varOmega )\).

Proof

We will use Lyapunov functionals to demonstrate that Theorem 4.3 holds.

  1. (i)

    To investigate the first part of Theorem 4.3, we consider the following Lyapunov function:

    $$\begin{aligned} U_{1}(t)=\frac{\mu _{v}^{ \alpha }}{b_{l}^{ \alpha }W}L(t)+N_{v}(t). \end{aligned}$$

    Observe that the function \(U(t)\) is defined, continuous and positive definite for all \(L(t)\) and \(N_{v}(t)\). It follows from Definition (2.2) that

    $$\begin{aligned} {}^{c}_{t_{0}}D^{\alpha }_{t} U_{1}(t) =&\frac{\mu _{v}^{ \alpha }}{b_{l}^{ \alpha }W} {}^{c}_{t_{0}}D^{\alpha }_{t}L(t)+ {}^{c}_{t_{0}}D^{\alpha }_{t} N_{v}(t) \\ =&\frac{\mu _{v}^{ \alpha }}{b_{l}^{ \alpha }W} \biggl[b_{l}^{ \alpha }W N_{v} \biggl(1-\frac{L}{K_{l}^{ \alpha }} \biggr)-\bigl(\sigma _{l}^{ \alpha }+ \mu _{p}^{ \alpha }\bigr)L \biggr]+\sigma _{l}^{ \alpha }L-\mu _{v}^{ \alpha }N_{v} \\ =&-\frac{\mu _{v}^{ \alpha } N_{v}L}{K_{l}^{ \alpha }}- \frac{\sigma _{l}^{ \alpha }}{r}(1-r) . \end{aligned}$$

    Since \({}^{c}_{t_{0}}D^{\alpha }_{t} U(t)<0\), for \(r<1\), we can conclude that the equilibrium point \((0,0)\) is globally (uniformly) asymptotically stable in Ω. Now, we proceed to demonstrating item (ii).

  2. (ii)

    Consider the following Lyapunov function:

    $$\begin{aligned} U_{2}(t) =&a_{1} \biggl[ L(t)-L^{*}-L^{*} \ln \biggl(\frac{L(t)}{L^{*}} \biggr) \biggr]+a_{2} \biggl[N_{v}(t)-N_{v}^{*}-N_{v}^{*} \ln \biggl( \frac{N_{v}(t)}{N_{v}^{*}} \biggr) \biggr], \end{aligned}$$

    where \(a_{1}\) and \(a_{2}\) are positive constants to be determined. Applying Lemma 2.2 leads to

    $$\begin{aligned} {}^{c}_{t_{0}}D^{\alpha }_{t} U_{2}(t) \leq &a_{1} \biggl(1- \frac{L^{*}}{L(t)} \biggr) {}^{c}_{t_{0}}D^{\alpha }_{t} L(t) +a_{2} \biggl(1-\frac{N_{v}^{*}}{N_{v}(t)} \biggr) {}^{c}_{t_{0}}D^{\alpha }_{t} N_{v}(t) \\ =&a_{1} \biggl(1-\frac{L^{*}}{L(t)} \biggr) \bigl(g(N_{v},L)-\bigl(\sigma _{l}^{ \alpha }+\mu _{p}^{\alpha }\bigr)L\bigr) \\ &{}+a_{2} \biggl(1-\frac{N_{v}^{*}}{N_{v}(t)} \biggr) \bigl(\sigma _{l}^{\alpha } L-\mu _{v}^{\alpha }N_{v} \bigr), \end{aligned}$$

    with \(g(N_{v},L)=b_{l}^{\alpha }W N_{v} (1- \frac{L}{K_{l}^{\alpha }} )\).

    Setting \(a_{1}=1\) and \(a_{2}=g(N_{v}^{*},L^{*})>0\), with \(g(N_{v}^{*},L^{*})=b_{l}^{\alpha }W N_{v} (1- \frac{L^{*}}{K_{l}^{\alpha }} )\). Furthermore, by utilising the identities \(g(N_{v}^{*},L^{*})=(\sigma _{l}^{\alpha }+\mu _{p}^{\alpha })L^{*}\) and \(\sigma _{l}^{\alpha } L^{*}=\mu _{v}^{\alpha }N^{*}_{v}\), one gets

    $$\begin{aligned} {}^{c}_{t_{0}}D^{\alpha }_{t} U_{2}(t) \leq & g\bigl(N_{v}^{*},L^{*} \bigr) \biggl( 2- \frac{N_{v}}{N_{v}^{*}} -\frac{L N^{*}_{v}}{L^{*}N_{v}} - \frac{L^{*}}{L}\frac{g(N_{v},L)}{g(N_{v}^{*},L^{*})}+ \frac{g(N_{v},L)}{g(N_{v}^{*},L^{*})} \biggr). \end{aligned}$$

    Let \(\varPhi (x)=1-x+\ln x\) for \(x>0\). It follows that \(\varPhi (x)\leq 0\), with the equality satisfied if and only if \(x=1\). Using this relation, we have

    $$\begin{aligned} &2-\frac{N_{v}}{N_{v}^{*}} -\frac{L N^{*}_{V}}{L^{*}N_{V}} - \frac{L^{*}}{L} \frac{g(N_{V},L)}{g(N_{V}^{*},L^{*})}+ \frac{g(N_{V},L)}{g(N_{V}^{*},L^{*})} \\ &\quad =\varPhi \biggl(\frac{L N^{*}_{V}}{L^{*}N_{V}} \biggr)+\varPhi \biggl( \frac{L^{*}}{L}\frac{g(N_{V},L)}{g(N_{V}^{*},L^{*})} \biggr)- \frac{N_{v}}{N_{v}^{*}}+ \frac{g(N_{V},L)}{g(N_{V}^{*},L^{*})} \\ &\qquad {}-\ln \biggl(\frac{ N^{*}g(N_{V},L)}{Ng(N_{V}^{*},L^{*})} \biggr) \\ &\quad \leq \ln \biggl(\frac{N_{v}}{N_{v}^{*}} \biggr)- \frac{N_{v}}{N_{v}^{*}}+ \frac{g(N_{V},L)}{g(N_{V}^{*},L^{*})}-\ln \biggl(\frac{g(N_{V},L)}{g(N_{V}^{*},L^{*})} \biggr) \\ &\quad \leq 0. \end{aligned}$$

    Hence, we can conclude that if \(r>1\), then the equilibrium \((L^{*},N_{v}^{*})\) is globally (uniformly) asymptotically stable in \(\operatorname{int}( \varOmega )\). From the above analytical results we can also deduce that if \(r<1\), then the tsetse vector population will go into extinction and for \(r>1\) it will persist. Thus, as we proceed to perform the analysis of (2), we will consider \(r>1\) implying the tsetse flies are at the equilibrium \((L^{*},N_{v}^{*})\). □

4.2 Analysis of the full model

We have noted that the tsetse population grows if \(r>1\) and the equilibrium \((L^{*},N_{V}^{*})\) will be globally (uniformly) asymptotically stable. Therefore, in this section, we explore the dynamics of the full model, and we will consider \(L=L^{*}\). Furthermore, as we can observe, the last two equations in system (3) do not influence the dynamics of the disease since all the other six equations do not depend on these equations. Hence, without loss of generality one can explore the dynamics of the disease based on a reduced system:

$$ \left . \textstyle\begin{array}{l} {}^{c}_{t_{0}}D^{\alpha }_{t} S_{v}(t) =\sigma _{l}^{\alpha } L^{*}-( \beta _{hv}^{\alpha }I_{h}+\beta _{av}^{\alpha }I_{a})S_{v}-\mu _{v}^{ \alpha }S_{v}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} I_{v}(t) =(\beta _{hv}^{\alpha }I_{h}+ \beta _{av}^{\alpha }I_{a})S_{v}-\mu _{v}^{\alpha } I_{v}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} S_{h}(t) = \varLambda _{h}^{ \alpha }-\beta _{vh}^{\alpha }f(I_{v})S_{h}-\mu _{h}^{\alpha }S_{h}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} I_{h}(t) = \beta _{vh}^{ \alpha }f(I_{v})S_{h}-(\mu _{h}^{\alpha }+\gamma _{h}^{\alpha })I_{h}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} S_{a}(t) = \varLambda _{a}^{ \alpha }-\beta _{va}^{\alpha }f(I_{v})S_{a}-\mu _{a}^{\alpha }S_{a}, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} I_{a}(t) = \beta _{va}^{ \alpha }f(I_{v})S_{a}-(\mu _{a}^{\alpha }+\gamma _{a}^{\alpha })I_{a}. \end{array}\displaystyle \right \} $$
(6)

4.2.1 Basic properties of the model

By closely following the approach in Sect. 4.1.1 one can easily verify the positivity and boundedness of solutions for system (6). For instance, we can note that all the solutions of system (6) are unique and positive since

$$ \left . \textstyle\begin{array}{l} {}^{c}_{t_{0}}D^{\alpha }_{t} S_{v}(t) =\sigma _{l}^{\alpha } L^{*} \geq 0, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} I_{v}(t) =(\beta _{hv}^{\alpha }I_{h}+ \beta _{av}^{\alpha }I_{a})S_{v}\geq 0, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} S_{h}(t) = \varLambda _{h}^{ \alpha }\geq 0, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} I_{h}(t) = \beta _{vh}^{ \alpha }f(I_{v})S_{h}\geq 0, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} S_{a}(t) = \varLambda _{a}^{ \alpha }\geq 0, \\ {}^{c}_{t_{0}}D^{\alpha }_{t} I_{a}(t) = \beta _{va}^{ \alpha }f(I_{v})S_{a}\geq 0. \end{array}\displaystyle \right \} $$
(7)

Moreover, by following the approach used earlier, it can determined that \(0\leq N_{i}(t) \leq \max \{ \frac{\varLambda _{i}^{\alpha }}{\mu _{i}^{\alpha }}, N_{i}(0)\}\) for \(i=a,h\) implying that all the solutions of system (6) are bounded above.

4.2.2 Equilibrium points and their stability

In the absence of the disease in the community, system (6) admits a trivial equilibrium point also known as the disease-free equilibrium (DFE) and given by

$$\begin{aligned} {\mathcal{E}}^{0}: \bigl(S^{0}_{h},I^{0}_{h},S^{0}_{a},I^{0}_{a},S^{0}_{v},I^{0}_{v} \bigr)= \biggl(\frac{\varLambda _{h}^{ \alpha }}{\mu _{h}^{ \alpha }},0, \frac{\varLambda _{a}^{ \alpha }}{\mu _{a}^{ \alpha }},0, \frac{\sigma _{l}^{ \alpha } }{\mu _{v}^{ \alpha }} \biggl(1- \frac{1}{r} \biggr)K_{l}^{ \alpha },0 \biggr). \end{aligned}$$

Following the next generation matrix approach [47, 48], it can easily be verified that the basic reproduction number of system (6) is

$$\begin{aligned} {\mathcal{R}}_{0} =&\sqrt{K_{l}^{ \alpha } \frac{\sigma _{l}^{ \alpha }}{\mu _{v}^{ \alpha }} \biggl(1- \frac{1}{r} \biggr) \biggl( \frac{\beta _{vh}^{ \alpha }\beta _{hv}^{ \alpha }\varLambda _{h}^{ \alpha }}{\mu _{v}^{ \alpha }\mu _{h}^{ \alpha }(\mu _{h}^{ \alpha }+\gamma _{h}^{ \alpha })}+ \frac{\beta _{av}^{ \alpha }\beta _{va}^{ \alpha }\varLambda _{a}^{ \alpha }}{\mu _{v}^{ \alpha }\mu _{a}^{ \alpha }(\mu _{a}^{ \alpha }+\gamma _{a}^{ \alpha })} \biggr)} . \end{aligned}$$
(8)

The basic reproduction number \({\mathcal{R}}_{0}\) is defined to be the expected number of secondary cases (vector or host) produced in a completely susceptible population by one infectious individual (vector or host, respectively) during its lifetime as infectious. The basic reproduction number is an integral epidemiological metric for understanding Trypanosoma brucei rhodesiense persistence and extinction. As we can observe, this metric depends on disease transmission parameters \(\beta _{ij}\) for \(i\neq j=a, h,v\), the average infectious period of the vector (host) \(\frac{1}{(\mu _{i}^{ \alpha }+\gamma _{i}^{ \alpha })}\), vector competence and survival \(\frac{\sigma _{l}^{ \alpha }}{\mu _{v}^{2 \alpha }} (1-\frac{1}{r} )K_{l}^{ \alpha }\).

Remark 4.1

From the expression of the basic reproduction number (8), one can observe that if \(r=1\), \({\mathcal{R}}_{0}=0\), and for \(r<1\), we have \({\mathcal{R}}_{0}\leq 1\). This implies that whenever \(r\leq 1\) the disease will not persist in the community since the tsetse fly population would naturally become extinct.

Next, we investigate the stability of the steady states of system (6). We will begin with the disease-free equilibrium (DFE).

Theorem 4.4

For\(\alpha \in (0,1)\), the disease-free equilibrium of system (6) is globally (uniformly) asymptotically stable for\({\mathcal{R}}_{0} < 1\).

Proof

Consider the following Lyapunov functional:

$$\begin{aligned} {\mathcal{L}}_{0}(t) =& c_{1} \biggl\{ S_{h}(t)-S^{0}_{h} -S^{0}_{h} \ln \frac{S_{h}(t)}{S_{h}^{0}} \biggr\} + c_{1} I_{h}(t) + c_{2} \biggl\{ S_{a}(t)-S^{0}_{a} -S^{0}_{a} \ln \frac{S_{a}(t)}{S_{a}^{0}} \biggr\} \\ &{}+ c_{2} I_{a}(t) +c_{3} \biggl\{ S_{v}(t)-S^{0}_{v} -S^{0}_{v} \ln \frac{S_{v}(t)}{S_{v}^{0}}+ I_{v}(t) \biggr\} , \end{aligned}$$

where \(c_{1}\), \(c_{2}\) and \(c_{3}\) are positive constants to be determined. Now, it follows from Definition 2.2 and Lemma 4.3 that

$$\begin{aligned} {}^{c}_{t_{0}}D^{\alpha }_{t} { \mathcal{L}}_{0}(t) \leq & c_{1} \biggl(1- \frac{S^{0}_{h}}{S_{h}} \biggr) {}^{c}_{t_{0}}D^{\alpha }_{t} S_{h} + c_{1} {}^{c}_{t_{0}}D^{\alpha }_{t}I_{h} + c_{2} \biggl(1- \frac{S^{0}_{a}}{S_{a}} \biggr) {}^{c}_{t_{0}}D^{\alpha }_{t} S_{a} \\ & {}+ c_{2} {}^{c}_{t_{0}}D^{\alpha }_{t}I_{a} + c_{3} \biggl(1- \frac{S^{0}_{v}}{S_{v}} \biggr) {}^{c}_{t_{0}}D^{\alpha }_{t} S_{v} + c_{3} {}^{c}_{t_{0}}D^{\alpha }_{t}I_{v}. \end{aligned}$$

Setting

$$\begin{aligned}& c_{1} = \mu _{v}^{\alpha }\beta _{hv}^{\alpha }\bigl(\mu _{a}^{\alpha }+ \gamma _{a}^{\alpha }\bigr),\qquad c_{2}=\mu _{v}^{\alpha }\beta _{av}^{ \alpha }\bigl(\mu _{h}^{\alpha } +\gamma _{h}^{\alpha } \bigr), \\& c_{3} = \biggl( \frac{\beta _{hv}^{\alpha }\beta _{vh}^{\alpha }\varLambda _{h}^{\alpha } (\mu _{a}^{\alpha }+\gamma _{a}^{\alpha })}{\mu _{h}^{\alpha }}+ \frac{\beta _{va}^{\alpha }\beta _{av}^{\alpha }\varLambda _{a}^{\alpha } (\mu _{h}^{\alpha }+\gamma _{h}^{\alpha })}{\mu _{a}^{\alpha }} \biggr) \end{aligned}$$

and simplifying one gets:

$$\begin{aligned} {}^{c}_{t_{0}}D^{\alpha }_{t}{ \mathcal{L}}_{0}(t) \leq & -\mu _{v}^{ \alpha } \mu _{h}^{\alpha }\beta _{hv}^{\alpha }\bigl(\mu _{a}^{\alpha }+ \gamma _{a}^{\alpha }\bigr) \frac{(S_{h}-S^{0}_{h})^{2}}{S_{h}}-\mu _{v}^{ \alpha }\mu _{a}^{\alpha }\beta _{av}^{\alpha }\bigl(\mu _{h}^{\alpha }+ \gamma _{h}^{\alpha }\bigr) \frac{(S_{a}-S^{0}_{a})^{2}}{S_{a}} \\ &{} - \biggl( \frac{\beta _{hv}^{\alpha }\beta _{vh}^{\alpha }\varLambda _{h}^{\alpha } (\mu _{a}^{\alpha }+\gamma _{a}^{\alpha })\mu _{v}^{\alpha }}{\mu _{h}^{\alpha }}+ \frac{\beta _{va}^{\alpha }\beta _{av}^{\alpha }\varLambda _{a}^{\alpha } (\mu _{h}^{\alpha }+\gamma _{h}^{\alpha })\mu _{v}^{\alpha }}{\mu _{a}^{\alpha }} \biggr) \frac{(S_{v}-S^{0}_{v})^{2}}{S_{v}} \\ &{} - \biggl( \frac{\beta _{hv}^{\alpha }\beta _{vh}^{\alpha }\varLambda _{h}^{\alpha } (\mu _{a}^{\alpha }+\gamma _{a}^{\alpha })\mu _{v}^{\alpha }}{\mu _{h}^{\alpha }}+ \frac{\beta _{va}^{\alpha }\beta _{av}^{\alpha }\varLambda _{a}^{\alpha } (\mu _{h}^{\alpha }+\gamma _{h}^{\alpha })\mu _{v}^{\alpha }}{\mu _{a}^{\alpha }} \biggr)\theta f(I_{v})I_{v} \\ &{} -\mu _{v}^{\alpha }\bigl(\mu _{a}^{\alpha }+ \gamma _{a}^{ \alpha }\bigr) \bigl(\mu _{h}^{\alpha }+ \gamma _{h}^{\alpha }\bigr) \bigl(\beta _{hv}^{ \alpha }I_{h}+ \beta _{av}^{\alpha } Ia\bigr) \bigl(1-{\mathcal{R}}^{2}_{0} \bigr). \end{aligned}$$

Since all the parameters and variables in system (6) are nonnegative, it follows that \({}^{c}_{t_{0}}D^{\alpha }_{t} {\mathcal{L}}_{0}(t)<0\) holds if \(\mathcal{R}_{0}<1\). Therefore, by the LaSalle invariance principle [49], we conclude that the DFE of system (6) is globally (uniformly) asymptotically stable whenever \({\mathcal{R}}_{0} <1\). This completes the proof. Biologically, this implies that whenever \({\mathcal{R}}_{0} <1\) then the disease dies out in the community. □

Theorem 4.5

Let\({\mathcal{E}}^{*}=(S^{*}_{i}, I^{*}_{i})\)for\(i=a, h,v\)be the endemic equilibrium point of system (6). Then, for\(\alpha \in (0,1)\)and\({\mathcal{R}}_{0} >1\), the endemic equilibrium point\({\mathcal{E}}^{*}\)is globally (uniformly) asymptotically stable.

Proof

Consider the following Lyapunov functional:

$$\begin{aligned} {\mathcal{L}}_{1}(t) =& b_{1} \biggl(S_{h}(t)-S^{*}_{h} -S^{*}_{h} \ln \frac{S_{h}(t)}{S_{h}^{*}} \biggr) +b_{2} \biggl(I_{h}(t)-I^{*}_{h} -I^{*}_{h} \ln \frac{I_{h}(t)}{I_{h}^{*}} \biggr) \\ &{}+ b_{3} \biggl(S_{a}(t)-S^{*}_{a} -S^{*}_{a} \ln \frac{S_{a}(t)}{S_{a}^{*}} \biggr)+b_{4} \biggl(I_{a}(t)-I^{*}_{a} -I^{*}_{a} \ln \frac{I_{a}(t)}{I_{a}^{*}} \biggr) \\ &{}+b5 \biggl(S_{v}(t)-S^{*}_{v} -S^{*}_{v} \ln \frac{S_{v}(t)}{S_{v}^{*}} \biggr) +b_{6} \biggl(I_{v}(t)-I^{*}_{v} -I^{*}_{v} \ln \frac{I_{v}(t)}{I_{v}^{*}} \biggr), \end{aligned}$$

where \(b_{i}=\), \(i=1,2,3,\ldots,6\), are positive constants to be determined. Applying Lemma 4.3 leads to

$$\begin{aligned} {}^{c}_{t_{0}}D^{\alpha }_{t} { \mathcal{L}}_{1}(t) \leq & b_{1} \biggl(1- \frac{S^{*}_{h}}{S_{h}} \biggr) {}^{c}_{t_{0}}D^{\alpha }_{t} S_{h} + b_{2} \biggl(1-\frac{I^{*}_{h}}{I_{h}} \biggr) {}^{c}_{t_{0}}D^{\alpha }_{t} I_{h} + b_{3} \biggl(1-\frac{S^{*}_{a}}{S_{a}} \biggr) {}^{c}_{t_{0}}D^{\alpha }_{t} S_{a} \\ &{}+ b_{4} \biggl(1-\frac{I^{*}_{a}}{I_{a}} \biggr) {}^{c}_{t_{0}}D^{ \alpha }_{t} I_{a} + b_{5} \biggl(1-\frac{S^{*}_{v}}{S_{v}} \biggr) {}^{c}_{t_{0}}D^{ \alpha }_{t} S_{v} + b_{6} \biggl(1-\frac{I^{*}_{v}}{I_{v}} \biggr) {}^{c}_{t_{0}}D^{ \alpha }_{t} I_{v}. \end{aligned}$$

Setting \(b_{i}=1\) for \(i=1,2,3,4\) and \(b_{5}=b_{6}=\frac{\beta _{vh}^{\alpha } f(I^{*}_{v})S^{*}_{h}}{\beta _{hv}^{\alpha }I^{*}_{h}S^{*}_{v}}+ \frac{\beta _{va}^{\alpha } f(I^{*}_{v})S^{*}_{a}}{\beta _{av}^{\alpha }I^{*}_{a}S^{*}_{v}}\) and utilising the following identities (which exist at the endemic point)

$$ \textstyle\begin{cases} \varLambda _{h}^{\alpha }= \beta _{vh}^{\alpha }f(I^{*}_{v})S^{*}_{h}+ \mu _{h}^{\alpha }S^{*}_{h},\qquad (\mu _{h}^{\alpha }+\gamma _{h}^{ \alpha })I^{*}_{h}= \beta _{vh}^{\alpha }f(I^{*}_{v})S^{*}_{h}, \\ \varLambda _{a}^{\alpha }= \beta _{va}^{ \alpha }f(I^{*}_{v})S^{*}_{a}+\mu _{a}^{\alpha }S^{*}_{a},\qquad (\mu _{a}^{\alpha }+\gamma _{a}^{\alpha })I^{*}_{a}= \beta _{va}^{\alpha }f(I^{*}_{v})S^{*}_{a}, \\ \sigma _{l}^{\alpha } L^{*}= (\beta _{hv}^{\alpha }I^{*}_{h}+ \beta _{av}^{\alpha }I^{*}_{a})S^{*}_{v}+\mu _{v}^{\alpha }S^{*}_{v}, \qquad \mu _{v}^{\alpha } I^{*}_{v}= (\beta _{hv}^{ \alpha }I^{*}_{h}+\beta _{av}^{\alpha }I^{*}_{a}(t))S^{*}_{v}, \end{cases} $$

one gets

$$\begin{aligned} D^{\alpha }{\mathcal{L}}_{1}(t) \leq &\mu _{h}^{\alpha }S^{*}_{h} \underbrace{ \biggl(2-\frac{S_{h}}{S^{*}_{h}}-\frac{S^{*}_{h}}{S_{h}} \biggr)} _{{({ {\mathbf{1}}})}}+ \beta _{va}^{\alpha } f\bigl(I^{*}_{v} \bigr)S^{*}_{a} \frac{\beta _{hv}^{\alpha }I^{*}_{h}}{\beta _{av}^{\alpha }I^{*}_{a}} \underbrace{ \biggl(2-\frac{S^{*}_{v}}{S_{v}}-\frac{I_{v}}{I_{v}^{*}}-\frac{S_{v}I^{*}_{v}I_{h}}{S^{*}_{v}I_{v}I^{*}_{h}}+ \frac{I_{h}}{I_{h}^{*}} \biggr)} _{{({ {\mathbf{2}}})}} \\ &{}+\beta _{vh}^{\alpha }f\bigl(I^{*}_{v} \bigr)S^{*}_{h} \underbrace{ \biggl(4- \frac{S^{*}_{h}}{S_{h}}-\frac{S_{h}I^{*}_{h}f(I_{v})}{S^{*}_{h}I_{h}f(I_{v}^{*})}-\frac{S^{*}_{v}}{S_{v}}- \frac{I_{v}}{I_{v}^{*}} -\frac{S_{v}I^{*}_{v}I_{h}}{S^{*}_{v}I_{v}I^{*}_{h}}+ \frac{f(I_{v})}{f(I_{v}^{*})} \biggr)} _{{({ {\mathbf{3}}})}} \\ &{}+\mu _{a}^{\alpha }S^{*}_{a} \underbrace{ \biggl(2-\frac{S_{a}}{S^{*}_{a}}-\frac{S^{*}_{a}}{S_{a}} \biggr)} _{{({ {\mathbf{4}}})}}+ \beta _{vh}^{\alpha } f\bigl(I^{*}_{v} \bigr)S^{*}_{h} \frac{\beta _{av}^{\alpha }I^{*}_{a}}{\beta _{hv}^{\alpha }I^{*}_{h}} \underbrace{ \biggl(2-\frac{S^{*}_{v}}{S_{v}}-\frac{I_{v}}{I_{v}^{*}}-\frac{S_{v}I^{*}_{v}I_{a}}{S^{*}_{v}I_{v}I^{*}_{a}}+ \frac{I_{a}}{I_{a}^{*}} \biggr)} _{{({ {\mathbf{5}}})}} \\ &{}+\beta _{va}^{\alpha }f\bigl(I^{*}_{v} \bigr)S^{*}_{a} \underbrace{ \biggl(4- \frac{S^{*}_{a}}{S_{a}}-\frac{S_{a}I^{*}_{a}f(I_{v})}{S^{*}_{a}I_{a}f(I_{v}^{*})}-\frac{S^{*}_{v}}{S_{v}}- \frac{I_{v}}{I_{v}^{*}} -\frac{S_{v}I^{*}_{v}I_{a}}{S^{*}_{v}I_{v}I^{*}_{a}}+ \frac{f(I_{v})}{f(I_{v}^{*})} \biggr)} _{{({ {\mathbf{6}}})}} \\ &{}+\mu _{v}^{\alpha }S^{*}_{v} \biggl( \frac{\beta _{vh}^{\alpha } f(I^{*}_{v})S^{*}_{h}}{\beta _{hv}^{\alpha }I^{*}_{h}S^{*}_{v}}+ \frac{\beta _{va}^{\alpha } f(I^{*}_{v})S^{*}_{a}}{\beta _{av}^{\alpha }I^{*}_{a}S^{*}_{v}} \biggr) \underbrace{ \biggl(2-\frac{S_{v}}{S^{*}_{v}}-\frac{S^{*}_{v}}{S_{v}} \biggr)} _{{({ {\mathbf{7}}})}}. \end{aligned}$$

Since the arithmetic mean is greater than or equal to the geometric mean, it follows that for (1), (4) and (7) the following is satisfied:

$$\begin{aligned} \biggl(2-\frac{S_{i}}{S^{*}_{i}}-\frac{S^{*}_{i}}{S_{i}} \biggr)\leq 0. \end{aligned}$$
(9)

Furthermore, let \(\varPhi (x) =1-x+\ln x\) for \(x>0\). It follows that \(\varPhi (x)\leq 0\) with equality if and only if \(x=1\). Utilising the aforementioned properties of \(\varPhi (x)\), we can demonstrate that the terms in the brackets are less or equal to zero. Let \(k=a,h\), so that from (2) and (5) we can write

$$ \begin{aligned}[b] &2-\frac{S^{*}_{v}}{S_{v}}+\frac{I_{k}}{I_{k}^{*}}- \frac{I_{v}}{I_{v}^{*}}- \frac{S_{v}I^{*}_{v}I_{k}}{S^{*}_{v}I_{v}I^{*}_{k}}, \\ & \quad =\varPhi \biggl(\frac{S^{*}_{v}}{S_{v}} \biggr)+ \varPhi \biggl( \frac{S_{v}I^{*}_{v}I_{k}}{S^{*}_{v}I_{v}I^{*}_{k}} \biggr)-\ln \biggl( \frac{I^{*}_{v}I_{k}}{I_{v}I^{*}_{k}} \biggr) + \frac{I_{k}}{I_{k}^{*}}- \frac{I_{v}}{I_{v}^{*}} \\ & \quad \leq \frac{I_{k}}{I_{k}^{*}}-\ln \biggl(\frac{I_{k}}{I_{k}^{*}} \biggr) - \frac{I_{v}}{I_{v}^{*}}+\ln \biggl(\frac{I_{v}}{I_{v}^{*}} \biggr) \\ &\quad \leq 0. \end{aligned} $$
(10)

In addition, from (3) and (6) we have

$$\begin{aligned} &4-\frac{S^{*}_{k}}{S_{k}}- \frac{S_{k}I^{*}_{k}f(I_{v})}{S^{*}_{k}I_{k}f(I_{v}^{*})}- \frac{S^{*}_{v}}{S_{v}}-\frac{I_{v}}{I_{v}^{*}} - \frac{S_{v}I^{*}_{v}I_{k}}{S^{*}_{v}I_{v}I^{*}_{k}}+ \frac{f(I_{v})}{f(I_{v}^{*})}, \\ & \quad =\varPhi \biggl(\frac{S^{*}_{k}}{S_{k}} \biggr)+\varPhi \biggl( \frac{S^{*}_{v}}{S_{v}} \biggr)+ \varPhi \biggl( \frac{S_{k}I^{*}_{k}f(I_{v})}{S^{*}_{k}I_{k}f(I_{v}^{*})} \biggr)+ \varPhi \biggl(\frac{S_{v}I^{*}_{v}I_{k}}{S^{*}_{v}I_{v}I^{*}_{k}} \biggr) \\ &\qquad {}-\frac{I_{v}}{I^{*}_{v}}+ \frac{f(I_{v})}{f(I_{v}^{*})} -\ln \biggl( \frac{f(I_{v})I^{*}_{v}}{f(I_{v}^{*})I_{v}} \biggr) \\ & \quad \leq \ln \biggl(\frac{I_{v}}{I_{v}^{*}} \biggr)- \frac{I_{v}}{I_{v}^{*}}+ \frac{f(I_{v})}{f(I_{v}^{*})}-\ln \biggl( \frac{f(I_{v})}{f(I_{v}^{*})} \biggr) \\ & \quad \leq 0. \end{aligned}$$
(11)

From (9), (10) and (11), it follows that \(D^{\alpha }{\mathcal{L}}_{1}(t)\leq 0\) whenever \({\mathcal{R}}_{0}>1\). Therefore, by the invariant principle of LaSalle [49], system (6) admits a globally (uniformly) asymptotically stable endemic equilibrium for \({\mathcal{R}}_{0}>1\). In a nutshell, the result implies that whenever \({\mathcal{R}}_{0}>1\) the disease will persist unless intervention strategies that are capable of reducing \({\mathcal{R}}_{0}\) to value less than unity are implemented. □

5 Numerical results and discussion

In this section, numerical experiments are conducted using MATLAB software in order to support analytical findings presented in the previous section. For the numerical implementation of fractional derivatives, we have utilised the Adam–Bashforth–Moulton (ABM) scheme, which has been implemented in the Matlab code fde12 by Garrappa [50]. This code implements a predictor-corrector PECE method of ABM type, as described in [51]. For aspects on convergence and accuracy of the numerical technique utilised, we refer readers to [52]. Furthermore, comprehensive details on stability of predictor-corrector algorithms for fractional differential equations are found in [53].

The baseline values for temperature dependent parameters are given in Table 1, and the remaining model parameters which are not temperature are given in Table 2. We have redefined some of the parameters as follows: \(\varLambda _{h}=\mu _{h} N_{h}\), \(\varLambda _{a}=\mu _{a} N_{a}\), implying that the host birth rate is now regarded to be equivalent to natural mortality rate. In addition, we set \(\beta _{av}= p\xi \psi \), \(\beta _{hv}=(1-p)\xi \omega \), \(\beta _{va}=p\xi u\) and \(\beta _{vh}=(1-p)\xi b\), where p is the proportion of tsetse fly bite on animals, \(\xi ^{ \alpha }\) is the fly biting rate, ψ is the probability that a susceptible fly gets infected upon contact with an infectious animals, ω is the probability that a susceptible fly gets infected upon contact with an infectious human, u and b represent the probability that an infectious fly infects an animal and a human, respectively, upon contact. In all the simulation results we set \(\omega =\psi =3.55\times 10^{-4}\) and \(b=u=8.3 \times 10^{-4}\). These baseline values were based upon consultation of several published frameworks.

Table 1 Description of temperature dependent model parameters used in system (6). All the parameter values were adopted from the work of Lord et al. [16]
Full size table
Table 2 Description of non-temperature dependent model parameters used in system (6). All the parameter values were adopted from the work of Ndondo et al. [13]
Full size table

On simulating system (6) we assumed the following initial population levels: \(L=1300\), \(N_{v}=1500\), \(S_{v}=1000\), \(I_{v}=500\), \(S_{h}=900\), \(I_{h}=100\), \(S_{a}=380\), \(I_{a}=120\) and \(\theta =0.8\). Without loss of generality, we set the values of the fractional order to be \(\alpha =0.5\), \(\alpha =0.7\), \(\alpha =0.9\), \(\alpha =1.0\). Model parameters that are considered to be independent of temperature are in Table 2. All the baseline values for these parameters were adopted from the work of Ndondo et al. [13]. Note that K will be varied in order to obtain different values of \({\mathcal{R}}_{0}\). Additional model parameters dependent on temperature are presented in Table 1, and all the baseline values were adopted from the work of Lord et al. [16].

Numerical results in Fig. 1 demonstrate the relationship between the basic reproduction number \({\mathcal{R}}_{0}\) and temperature in ∘C. We can observe that as temperature increases from the critical minimum \(T=16^{\circ }\) C, the basic reproduction number \({\mathcal{R}}_{0}\) gradually increases till the highest value is attained at optimum temperature \(T=25^{\circ }\text{C}\), thereafter \({\mathcal{R}}_{0}\) sharply declines. Furthermore, we can also note that when \(T<16^{\circ }\text{C}\) then \({\mathcal{R}}_{0} < 1\).

Figure 1
figure 1

The relationship between the basic reproduction number \({\mathcal{R}}_{0}\) and temperature T. Parameter values used are given in Tables 2 and 1. Furthermore, we set \(K_{l}=1500\), \(N_{h}=1000\), \(N_{a}=500\), \(N_{v} = 1500\) and varied the temperature from \(16\mbox{--}27 ^{\circ }\text{C}\)

Full size image

Numerical results in Fig. 2 illustrate the dynamics of the infected population when for \({\mathcal{R}}_{0} \leq 1\). As we can note, all the populations converged to the disease-free equilibrium, despite the chosen value of α. These results concur with analytical findings presented in Theorem 4.4 that whenever \({\mathcal{R}}_{0} \leq 1\) the proposed model is stable and the disease dies out in the community.

Figure 2
figure 2

Numerical results of system (6) demonstrating the convergence of infected population to the disease-free equilibrium for \({\mathcal{R}}_{0} \leq 1\). On construction of the simulations, we considered initial population levels discussed earlier, while baseline values for the model parameters are as in Tables 2 and 1. In addition, we also set \(T=16.5^{\circ }C\) and \(K=3300\), giving \({\mathcal{R}}_{0}=1.0\). As we can observe, the results concur with analytical findings presented in Theorem 4.4 that whenever \({\mathcal{R}}_{0} \leq 1\) the disease dies out in the community

Full size image

Simulation results in Fig. 3 show the solutions of model (6) at different levels of \(\alpha =(0.5,0.7,0.9,1.0)\) for \({\mathcal{R}}_{0}=3.7>1\). We set \(T=25^{\circ }C\) and \(K_{l}=3300\). As we can note, solution profiles converge to a nonzero equilibrium point, implying that whenever \({\mathcal{R}}_{0}>1\) the model is stable and admits a unique endemic equilibrium point. Biologically, this means that \({\mathcal{R}}_{0}>1\) the disease will persist in the community. These simulation results support analytical findings presented in Theorem 4.5.

Figure 3
figure 3

Numerical results of system (6) demonstrating the convergence of infected population to the endemic equilibrium for \({\mathcal{R}}_{0} > 1\). On simulating the model, we considered initial population levels discussed earlier, while baseline values for the model parameters are as in Tables 2 and 1. In addition, we also set \(T=25^{\circ }C\) and \(K=3300\), giving \({\mathcal{R}}_{0}=3.7\). As we can observe, the results concur with analytical findings presented in Theorem 4.5 that whenever \({\mathcal{R}}_{0} >1\) the system is stable and the infection persists in the community

Full size image

Figure 4 shows the numbers of infected vectors, humans and animals, at different temperature values over a period of 500 days. As we can observe, low temperature values (\(T<25^{\circ }\text{C}\)) are associated with low infection levels and as the temperature increased to the optimum value \(T=25^{\circ }\text{C}\), the number of infections increases over time. We can also observe that for \(t<100\) days the impact of different temperature values on population levels will not be extremely distinct. However, thereafter there is a significant distinction.

Figure 4
figure 4

Numerical results depicting the effects of temperature variation on the dynamics of infected hosts and vectors. We set \(\alpha =0.7\), \(K_{l}=3300\), \(N_{h}=1000\), \(N_{a}=500\), \(L= 1300\), \(N_{v} = 1500\), \(S_{v} = 1000\), \(I_{v} = 500\), \(I_{h} = 100\), \(S_{a} = 380\) and \(I_{a} = 17\). The rest of the model parameters were adopted as in Tables 2 and 1

Full size image

Next, we investigate the effects of screening infected hosts and vector control on disease dynamics. Detection and treatment of humans has been a primary control strategy for HAT. Cases detection can be carried out either periodically (usually large-scale screening) or on continuous basis (usually small scale) at health care centres [29]. In this study, we explore the potential effects of continuous detection and treatment and we follow the approach in Artzrouni and Gouteux [25]. Artzrouni and Gouteux proposed a model for HAT that had a new parameter \(C_{h}\), which was meant to account for the month percent detections of infected individuals. Furthermore, Artzrouni and Gouteux proposed that the rate of exit of infected host to the recovery stage can be presented as a composite of the intrinsic underlying disease progression (say, \(\gamma _{\mathrm{int}}\) and the removal rate by treatment (extrinsic, say \(\gamma _{\mathrm{ext}}\)) such that

$$\begin{aligned} \gamma _{h}=\gamma _{\mathrm{int}}+\gamma _{\mathrm{ext}}, \end{aligned}$$
(12)

then the monthly percent detection is given by

$$\begin{aligned} C_{h}=100\bigl[1-\exp (-30\gamma _{\mathrm{ext}})\bigr]. \end{aligned}$$
(13)

Consequently, the exit rate from the infected class for human host is given by

$$\begin{aligned} \gamma _{h}=\gamma _{\mathrm{int}}-\frac{1}{30}\ln \biggl(1- \frac{C_{h}}{100} \biggr). \end{aligned}$$
(14)

From (14) we can observe that linear detection of infected individual does not result in linear changes in \(\gamma _{h}\). Rock et al. [29] opine that this representation of the recovery rate leads to a meaningful way in which the influence of the parameter on the basic reproduction number can be extensively explored.

Despite the fact that there are several methods to control the density of the tsetse, such as aerial spraying and the deployment of natural or artificial baits, essentially altering the total population parameter \(N_{v}\), birth rate and natural mortality rate \(\mu _{v}^{\alpha }\) will alter the density of the tsetse population. Cognisant of these fundamental parameters, Artzrouni and Gouteux [25] hypothesised that tsetse controls will affect mortality rate but not the population size. Hence in an analogous approach to modelling detection and treatment of human, they model ‘natural’ mortality rate of the vectors a follows:

$$\begin{aligned} \mu _{v}=\mu _{v,\mathrm{int}}+\mu _{v,\mathrm{ext}}, \end{aligned}$$
(15)

where \(\mu _{v,\mathrm{int}}\) accounts for the mortality experienced by flies in their environment and \(\mu _{v,\mathrm{ext}}\) describes an additional death rate which occurs as result of control strategies. Furthermore, they suggested that this death rate \(\mu _{v}^{\alpha }\) is related to the daily percentage of flies killed and denoted here by \(C_{v}\):

$$\begin{aligned} C_{v}=100\bigl[1-\exp (-30\mu _{v,\mathrm{ext}})\bigr]. \end{aligned}$$
(16)

Thus, the total mortality rate of vectors due to ‘natural’ and control measures is given by

$$\begin{aligned} \mu _{v}=\mu _{v,\mathrm{int}}-\ln \biggl(1-\frac{C_{v}}{100} \biggr). \end{aligned}$$
(17)

Note that in the work of Artzrouni and Gouteux they used rates with three days as the unit of time on equation (17).

In what follows, we numerically explore the effectiveness of case detection and vector on the spread of the disease. Precisely, we will use contour plot to determine the influence of \(c_{h}\) and \(c_{v}\) on the basic reproduction number, since it an integral epidemiological metric for understanding the power of Trypanosoma brucei rhodesiense to invade the community. A contour plot in Fig. 5 illustrates the impact of human case detection and vector control on Trypanosoma brucei rhodesiense dynamics at \(T=20^{\circ }\text{C}\). As we can observe, an increase in both case detection and vector control percentages will lead to a decrease in the magnitude of \({\mathcal{R}}_{0}\). We can also note that vector control has a strong influence on minimising the magnitude of \({\mathcal{R}}_{0}\) compared to human detection. In particular, whenever \(C_{v}> 30\), then \({\mathcal{R}}_{0}< 1\) despite any value of \(C_{h}\).

Figure 5
figure 5

A contour plot illustrating the effects of human detection and vector control on Trypanosoma brucei rhodesiense dynamics. We set \(T=20^{\circ }\text{C}\), \(K_{l}=3300\), \(\beta _{hv}=\beta _{av}=3.55\times 10^{-4}\), \(\beta _{vh}=\beta _{va}=8.3\times 10^{-4}\), \(N_{h}=1000\), \(N_{a}=500\), \(\gamma _{\mathrm{int}}=0.009\) and \(\mu _{v,\mathrm{int}}=0.027\)

Full size image

A contour plot in Fig. 6 demonstrates the impact of \(C_{h}\) and \(C_{v}\) on the transmission dynamics of Trypanosoma brucei rhodesiense at \(T=25^{\circ }\text{C}\). Comparing the results in Fig. 5 and Fig. 6, we can observe that at optimum temperature \(T=25^{\circ }\text{C}\), vector control needs to be greater that 50 (\(C_{v}>50\)) in order to reduce the magnitude of the basic reproduction number to values less than unity, whereas in Fig. 5, \(C_{v}> 30\) is sufficient to obtain \({\mathcal{R}}_{0}< 1\). Therefore, we can conclude that if the average temperature in the community is very close to the optimum temperature, then intensity of vector control needs to be at least 50%.

Figure 6
figure 6

A contour plot illustrating the effects of human detection and vector control on Trypanosoma brucei rhodesiense dynamics. We set \(T=25^{\circ }\text{C}\), \(K_{l}=1500\), \(N_{h}=1000\), \(N_{a}=500\), \(\gamma _{\mathrm{int}}=0.009\) and \(\mu _{v,\mathrm{int}}=0.027\)

Full size image

In Fig. 7 we explore the relationship between temperature and \({\mathcal{R}}_{0}\) in the presence of human screening and vector control. Wet set \(C_{h}=C_{v}=50\). As we can observe, \({\mathcal{R}}_{0}>1\) for \(23< T<26^{\circ }\text{C}\). This implies that at 50% human detection and 50% killing of vectors, the disease can only persist in the community when the average temperature is between 23 and 26∘C; otherwise, the disease dies out. However, if we set \(C_{h}=50\) and \(C_{v}=55\) (Fig. 8), the disease will not persist even at optimum temperature \(T=25 ^{\circ }\text{C}\).

Figure 7
figure 7

Simulation results showing the effects of temperature on \({\mathcal{R}}_{0}\) in the presence of human screening and vector control. We set \(C_{h}=C_{v}=50\), \(K_{l}=1500\), \(N_{h}=1000\), \(N_{a}=500\), \(L= 1300\), \(N_{v} = 1500\), \(S_{v} = 1000\), \(I_{v} = 500\), \(I_{h} = 100\), \(S_{a} = 380\) and \(I_{a} = 17\). The rest of the parameter values are as in Tables 2 and 1

Full size image
Figure 8
figure 8

Simulation results showing the effects of temperature on \({\mathcal{R}}_{0}\) in the presence of human screening and vector control. We set \(C_{h}=50\), \(C_{v}=55\), \(k_{l}=1500\), \(N_{h}=1000\), \(N_{a}=500\), \(L= 1300\), \(N_{v} = 1500\), \(S_{v} = 1000\), \(I_{v} = 500\), \(I_{h} = 100\), \(S_{a} = 380\) and \(I_{a} = 17\). The rest of the parameter values are as in Tables 2 and 1

Full size image

6 Concluding remarks

In this work, a fractional-order model with long run memory has been used to explore the effects of temperature on Trypanosoma brucei rhodesiense transmission and control. The memory effects are represented by the Caputo derivative. The proposed model incorporates the interplay between the tsetse flies and two hosts, humans and animals. The model incorporates all the necessary and relevant biological information concerning transmission and control of Trypanosoma brucei rhodesiense, hence in the framework we incorporated the early stages of the vector. Key stages of the vector population that strongly depend on temperature were modelled as functions of temperature. We computed the basic reproduction number and established results on the threshold dynamics. Furthermore, we utilised the formulae proposed by Artzrouni and Gouteux [25] to explore the effects of daily human detection and vector control on long term disease dynamics. Among other several outcomes, we have established that vector control has strong influence on minimising the spread of the disease. In particular, we note that when daily averaged temperature is around \(T= 20^{\circ }C\), destruction of 30% or more vectors in three days will reduce the basic reproduction number to levels below unity despite any level of human detection. In addition, we also observed that if human detection is around 50% and vector control is 55% or more, then the disease will die out in the community even at optimum temperature \(T=25^{\circ }C\). Overall, findings from this study have demonstrated the impact of temperature and control strategies on long term dynamics of Trypanosoma brucei rhodesiense, and the outcomes enhance our understanding on effective management of the disease.

Like other modelling studies, the proposed study could be extended by validating the model using data obtained from specific countries and associated laboratory experiments conducted in those countries. Aspects of heterogeneity (high and low risk populations) can also be included. Instead of average daily temperatures, seasonal variation in temperature can also be factored into the framework.