Article contents
GROTHENDIECK GROUPS OF TRIANGULATED CATEGORIES VIA CLUSTER TILTING SUBCATEGORIES
Published online by Cambridge University Press: 11 June 2020
Abstract
Let 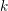 $k$ be a field, and let
$k$ be a field, and let 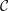 ${\mathcal{C}}$ be a
${\mathcal{C}}$ be a 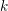 $k$-linear, Hom-finite triangulated category with split idempotents. In this paper, we show that under suitable circumstances, the Grothendieck group of
$k$-linear, Hom-finite triangulated category with split idempotents. In this paper, we show that under suitable circumstances, the Grothendieck group of 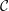 ${\mathcal{C}}$, denoted by
${\mathcal{C}}$, denoted by 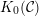 $K_{0}({\mathcal{C}})$, can be expressed as a quotient of the split Grothendieck group of a higher cluster tilting subcategory of
$K_{0}({\mathcal{C}})$, can be expressed as a quotient of the split Grothendieck group of a higher cluster tilting subcategory of 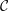 ${\mathcal{C}}$. The results we prove are higher versions of results on Grothendieck groups of triangulated categories by Xiao and Zhu and by Palu. Assume that
${\mathcal{C}}$. The results we prove are higher versions of results on Grothendieck groups of triangulated categories by Xiao and Zhu and by Palu. Assume that 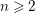 $n\geqslant 2$ is an integer;
$n\geqslant 2$ is an integer; 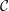 ${\mathcal{C}}$ has a Serre functor
${\mathcal{C}}$ has a Serre functor  $\mathbb{S}$ and an
$\mathbb{S}$ and an  $n$-cluster tilting subcategory
$n$-cluster tilting subcategory 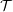 ${\mathcal{T}}$ such that
${\mathcal{T}}$ such that 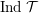 $\operatorname{Ind}{\mathcal{T}}$ is locally bounded. Then, for every indecomposable
$\operatorname{Ind}{\mathcal{T}}$ is locally bounded. Then, for every indecomposable 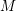 $M$ in
$M$ in 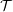 ${\mathcal{T}}$, there is an Auslander–Reiten
${\mathcal{T}}$, there is an Auslander–Reiten 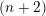 $(n+2)$-angle in
$(n+2)$-angle in 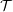 ${\mathcal{T}}$ of the form
${\mathcal{T}}$ of the form  $\mathbb{S}\unicode[STIX]{x1D6F4}^{-n}(M)\rightarrow T_{n-1}\rightarrow \cdots \rightarrow T_{0}\rightarrow M$ and
$\mathbb{S}\unicode[STIX]{x1D6F4}^{-n}(M)\rightarrow T_{n-1}\rightarrow \cdots \rightarrow T_{0}\rightarrow M$ and 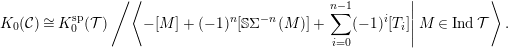 $$\begin{eqnarray}K_{0}({\mathcal{C}})\cong K_{0}^{\text{sp}}({\mathcal{T}})\left/\left\langle -[M]+(-1)^{n}[\mathbb{S}\unicode[STIX]{x1D6F4}^{-n}(M)]+\left.\mathop{\sum }_{i=0}^{n-1}(-1)^{i}[T_{i}]\right|M\in \operatorname{Ind}{\mathcal{T}}\right\rangle .\right.\end{eqnarray}$$
$$\begin{eqnarray}K_{0}({\mathcal{C}})\cong K_{0}^{\text{sp}}({\mathcal{T}})\left/\left\langle -[M]+(-1)^{n}[\mathbb{S}\unicode[STIX]{x1D6F4}^{-n}(M)]+\left.\mathop{\sum }_{i=0}^{n-1}(-1)^{i}[T_{i}]\right|M\in \operatorname{Ind}{\mathcal{T}}\right\rangle .\right.\end{eqnarray}$$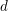 $d$ is a positive integer and
$d$ is a positive integer and 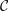 ${\mathcal{C}}$ has a
${\mathcal{C}}$ has a 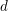 $d$-cluster tilting subcategory
$d$-cluster tilting subcategory 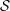 ${\mathcal{S}}$ closed under
${\mathcal{S}}$ closed under  $d$-suspension. Then,
$d$-suspension. Then, 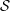 ${\mathcal{S}}$ is a so-called
${\mathcal{S}}$ is a so-called 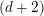 $(d+2)$-angulated category whose Grothendieck group
$(d+2)$-angulated category whose Grothendieck group 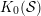 $K_{0}({\mathcal{S}})$ can be defined as a certain quotient of
$K_{0}({\mathcal{S}})$ can be defined as a certain quotient of 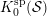 $K_{0}^{\text{sp}}({\mathcal{S}})$. We will show
$K_{0}^{\text{sp}}({\mathcal{S}})$. We will show 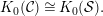 $$\begin{eqnarray}K_{0}({\mathcal{C}})\cong K_{0}({\mathcal{S}}).\end{eqnarray}$$
$$\begin{eqnarray}K_{0}({\mathcal{C}})\cong K_{0}({\mathcal{S}}).\end{eqnarray}$$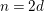 $n=2d$, that all the above assumptions hold, and that
$n=2d$, that all the above assumptions hold, and that 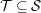 ${\mathcal{T}}\subseteq {\mathcal{S}}$. Then our results can be combined to express
${\mathcal{T}}\subseteq {\mathcal{S}}$. Then our results can be combined to express 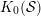 $K_{0}({\mathcal{S}})$ as a quotient of
$K_{0}({\mathcal{S}})$ as a quotient of 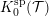 $K_{0}^{\text{sp}}({\mathcal{T}})$.
$K_{0}^{\text{sp}}({\mathcal{T}})$.
MSC classification
- Type
- Article
- Information
- Copyright
- © 2020 Foundation Nagoya Mathematical Journal
References
- 4
- Cited by





