A Multi-objective Optimization Model for Robust Skip-Stop Scheduling with Earliness and Tardiness Penalties

Abstract

Inefficient transport systems impose extra travel time for travelers, cause dissatisfaction and reduce service levels. In this study, the demand-oriented train scheduling problem is addressed using a robust skip-stop method under uncertain arrival rates during peak hours. This paper presents alternative mathematical models, including a two-stage scenario-based stochastic programming model and two robust optimization models, to minimize the total travel time of passengers and their waiting time at stations. The modeling framework accounts for the design and implementation of robust skip-stop schedules with earliness and tardiness penalties. As a case study, each of the developed models is implemented on line No. 5 of the Tehran metro, and the results are compared. To validate the skip-stop schedules, the values of the stochastic solution and the expected value of perfect information are calculated. In addition, a sensitivity analysis is conducted to test the performance of the model under different scenarios. According to the obtained results, having perfect information can reduce up to 16% of the value of the weighted objective function. The proposed skip-stop method has been shown to save about 5% in total travel time and 49% in weighted objective function, which is a summation of travel times and waiting times as against regular all-stop service. The value of stochastic solutions is about 21% of the value of the weighted objective function, which shows that the stochastic model demonstrates better performance than the deterministic model.

1 Introduction

Providing affordable and efficient transportation services to users is a vital role in rail transportation systems [1]. Rapid rail transit is recognized as one of the most efficient modes of transport in urban areas. Rail companies devote a growing amount of energy and effort to improving the efficiency and robustness of train services in daily operations [2]. A practical approach to minimizing the operational cost and, simultaneously, passenger waiting time is to optimize operational services following the spatial and temporal profiles of passenger demand [3]. The quality of rail services is directly affected by train schedules. The design and implementation of a demand-oriented train timetable is a complicated task that involves accurate estimation of the passenger demand [4]. Train timetabling is an inherently multi-objective optimization problem that studies the minimization of the train’s travel time subject to supply and demand constraints [5].

Most rapid rail transit systems face challenges, e.g., saturated demand, and look for a solution to increase service quality [6]. The service quality can be increased by adding new trains. However, this solution is costly and not economically feasible, as these extra trains may be used only at peak demand hours [7]. Principally, the satisfaction of passengers is directly affected by their travel and waiting times [8]. One of the primary sources of passenger dissatisfaction is unpredicted variations in passenger flows [9, 10]. The process of timetable adjustment supplying the passengers’ demand provides solutions with high sensitivity to the stochastic variations and requires an effective and robust solution to be applied [11]. To increase the service level for passengers, it is necessary to generate a timetable which allows passengers to arrive at their destinations on time [12]. In the railway context, robust timetables avoid unplanned delays, though to some extent such delays are caused by random disturbances [13].

Skip-stop service is one of the best-known strategies for both increasing the operational speed and decreasing the passenger waiting cost. It is commonly adopted in rapid rail transit lines, which allow trains to skip some low demand stations to reduce the train traveling time [14]. The skip-stop operation enables rail users to reduce the travel time of the trains and simultaneously increases the travel speed of some passengers. However, some passengers may experience extra waiting or access time as a result of skip-stop services [15]. The punctuality of rail services is also a primary indicator of the performance in railway systems [16], defined as the percentage of trains that arrive at their destinations with a delay below the specified threshold [17]. Train delays are unavoidable due to the random nature of the disturbance that occurs during the service [18]. Accordingly, a proper solution to train timetabling problem is to integrate the robustness and punctuality of the train services in terms of deviation between the planned and actual schedule [19].

Even though extensive literature exists on timetabling in the rail transportation system, there have not been enough studies directed toward the optimization of robust skip-stop strategies with earliness and tardiness criteria under the stochastic demand. The present research focuses on multi-objective optimization of train timetables for minimum passenger cost in terms of travel time and schedule deviation. To the best of our knowledge, a direct application of robust stop-skip scheduling has not been found in the literature; if so, it has not been addressed to theextent offered in the present study. The main contributions of the present study are as follows: first, this study presents novel mathematical formulations to obtain robust and efficient skip-stop schedules, considering uncertainty associated with an arrival rate of passengers. Second, this study develops alternative stochastic programming models for generating robust skip-stop schedules with earliness and tardiness criteria for rapid rail transit systems, with an illustration based on the Tehran metro system.

This article is organized as follows: Sect. 2 provides a literature review on the robust train timetabling problem. Section 3 presents an explanation of the mathematical optimization models. In Sect. 4, the proposed skip-stop scheduling models are evaluated, and the results are interpreted. The proposed models are implemented in real instances of the Tehran metro network. Finally, the concluding remarks are provided, and suggestions for future research are presented.

2 Literature Review

This section reviews the most significant contributions in the field of train timetabling problems. A taxonomy of the related studies is given in Table 1. Furth [20] proposed an integer programming model to solve the limited stop scheduling problem on a bus transit line. The suggested optimization model tries to minimize the deviation between the actual schedule and the initial schedule. Eberlein et al. [21] addressed the real-time skip-stop scheduling problem in the public transportation system and developed a mixed-integer nonlinear programming model. In the optimal solutions provided, dwell times, train speeds and passenger arrival rates were assumed to be deterministic and static. The researchers also proposed a heuristic algorithm to optimize skip-stop services. Vuchic [22] proposed a deterministic train scheduling model to optimize a typical pattern of the skip-stop plan. In this approach, the stations are categorized into three clusters, A, B, and AB, regarding their relative demand percentages. Sun and Hickman [23] formulated the real-time stop-skip scheduling problem as a nonlinear integer programming problem. The model accounts for the uncertainty associated with the volume of passenger boardings and alightings at stops. The large-size instances of the problem were solved using an exhaustive search method. The results indicated that the designed stop-skip scheduling model could generate a solution that outperforms the traditional all-stop service.

Table 1 A classification of the existing skip-stop scheduling models in rail rapid transit systems

Kroon et al. [24] studied the periodic train scheduling problem in the Dutch railway network under uncertainty associated with the train running time. An optimal policy for time supplement allocation was proposed, which aimed to minimize the average train delays. Kroon et al. [25] addressed the train scheduling problem by considering connections in the Dutch rail network. To ensure the desired level of schedule robustness, they developed a stochastic programming model for optimal time buffer allocation. Yang et al. [26] proposed a passenger train scheduling model for a mixed single and double-track railway. In this model, the objective function was to minimize the total passenger travel time with a penalty function. They considered the number of passengers boarding the train at each station as a random variable. A branch-and-bound (B&B) algorithm was used to solve the train timetabling problem.

Shafia et al. [46] examined the robustness and periodicity of the train schedule in a single-track railway line. They used a fuzzy programming approach to achieve a balance between the total delay of trains and the stability of the timetable. To solve large-scale instances of the problem, the simulated annealing (SA) method was utilized. Cao et al. [33] proposed a skip-stop scheduling method to find a trade-off between stopping time at stations and the waiting time for travelers. The problem was heuristically solved by an innovative Tabu search method.

Jamili and Aghaee [47] studied an operational plan for urban metro lines with a skip-stop policy under uncertainty. They proposed a robust optimization approach to design more stable skip-stop patterns. The proposed skip-stop scheduling problem was solved using a decomposition algorithm and SA. Cao et al. [35] presented a multi-objective nonlinear model to minimize waiting times for passengers using the skip-stop scheduling method. The problem was formulated as a mixed integer nonlinear programming model. The result shows that the travel time of passengers was reduced significantly by implementing the skip-stop scheduling method. Hassannayebi et al. [48] proposed robust multi-objective stochastic optimization models for train timetabling problems in transit lines. The model aims to minimize the passenger waiting times besides its variance. They evaluated the effectiveness of models through a case study in the Tehran subway system. The results show significant reductions in the passenger waiting time through the proposed robust model. Shakibayifar et al. [49] presented a train rescheduling model to minimize the total travel time of trains in Iranian rail networks. A heuristic approach was proposed to design a disposition timetable in a reasonable time. To validate the model, the re-scheduling model was tested for several disruption scenarios, each associated with random recovery time.

Recently, Qi et al. [50] proposed a robust approach to train timetabling involving train stop planning with uncertain passenger demand. The aim was to minimize unsatisfied demand while ensuring that the sum of train travel times and the total number of stops were less than the optimal deterministic solutions to some extent. Shang et al. [45] proposed a space–time-state formulation for the skip-stop scheduling problem in an urban rail transit system. The optimization model was based on the extension of a multi-commodity network flow problem. A Lagrangian heuristic was used to solve instances of the Beijing Subway system. Lee et al. [51] addressed the skip-stop scheduling problem using smartcard statistics. The aim was to reduce the overall travel time of passengers with regard to route choice behaviors. A genetic algorithm was proposed to solve instances of the Seoul urban rail system.

Despite the existing models and solution methods for the skip-stop scheduling problem, only a few papers addressed the conflicting objectives appears in a real-world setting. The present study adopts a multi-objective optimization framework for skip-stop scheduling, which leads to a more realistic solution for the studied problem. In the next section, alternative formulations for robust skip-stop scheduling are provided. The modeling framework considers multiple conflicting objectives.

3 Problem Statement and Formulation

This section gives the assumptions related to the network topology and presents the mathematical formulation of the integrated train timetabling and skip-stop scheduling problem. In this study, alternative optimization models are proposed for generating robust stop-skip schedules under stochastic passenger flows. The underlying problem in this study involves the optimal design of skip-stop schedules during peak hours in double-track rail transit lines. Unlike the regular all-stop schedule, in this method, trains stop at only a few stations instead of stopping at all stops. The proposed model minimizes the total train travel time while reducing the deviation between the planned and actual timetables. Trains can avoid stopping at some stations to shorten travel time, but at least one train should stop at each station. It is assumed that all trains have the same origins and destinations. The stopping time at the stations is determined by the number of passengers boarding or alighting at the stations. Each block can be occupied byn at most one train, and there is no possibility of train overtaking. The train timetabling model accounts for the minimum headway time and train capacity constraints. The arrival rate of passengers at the stations is an uncertain parameter, and it is given in different scenarios. Before presenting the scenario-based formulation of the skip-stop scheduling problem, the following notations for parameters and variables are given:

Sets and Subscript

$\Omega = \{ 1, \ldots ,M\}$ :

Set of trains ($i \in\Omega$)

$\Psi = \{ 1, \ldots ,N\}$ :

Set of stations ($j,k \in\Psi$)

$\xi = \{ 1, \ldots ,S\}$ :

Set of scenarios ($s \in\xi$)

Model Parameters

$C_{i}$ :

The maximum capacity of train i

$\tau_{j}$ :

The running time of the train from station j − 1 to station j

$\lambda_{jks}$ :

The arrival rate of passengers who want to travel from station j to station k under scenario s

h :

Minimum headway time

$\alpha$ :

Minimum alighting and boarding time per passenger

$t_{\text{ac}}$ :

Train acceleration time

$t_{\text{dec}}$ :

Train deceleration time

$\omega$ :

The weight coefficient for total deviations between the actual and planned timetable in the objective function $0 \le \omega \le 1$

${\text{pr}}_{s}$ :

The probability of occurrence for scenario s

w :

Penalty coefficient for tardiness

w′:

Penalty coefficient for earliness

v :

The penalty factor for passengers who have left the train at the last station

β :

The train dwell time reserved for technical operations such as the closing/opening of doors

M :

A sufficiently large positive number

Decision Variables

$d_{ijs}$ :

Dwell time of the train i at station j under scenario s

$s_{ijks}$ :

The number of passengers skipped by train i who will travel from station j to k under scenario s

$S_{ijs}$ :

Total number of passengers skipped by train i at station j under scenario s

${\text{ps}}_{ijs}$ :

Number of passengers boarded on train i at station j under scenario s

$V_{ijs}$ :

Number of passengers alighted from train i at station j under scenario s

$W_{ijks}$ :

The total number of passengers waiting for train i to travel from station j to station k under scenario s

$W_{ijks}^{{\prime }}$ :

The number of passengers boarded on train i to travel from station j to station k under scenario s

$x_{ij}$ :

If train i stops at station j, equals 1, otherwise zero

$y_{ijk}$ :

If train i stops at both station j and k equals to 1, otherwise zero

$f_{ijs}$ :

If train i has enough capacity to accommodate passengers arrives at station j, equals 1, otherwise zero

${\text{TAr}}_{ij}$ :

The arrival time of train i at station j based on the planned timetable

${\text{TDep}}_{ij}$ :

The departure time of train i from station j based on the planned timetable

${\text{Ar}}_{ijs}$ :

Arrival time of train i at station j under scenario s

${\text{Dep}}_{ijs}$ :

The departure time of train i from station j under scenario s

$a_{ijs}^{ + }$ :

The positive deviation between the actual and planned arrival time of train i at station j under scenario s (tardiness)

$a_{ijs}^{ - }$ :

The negative deviation between the actual and planned arrival time of train i at station j under scenario s (earliness)

$b_{ijs}^{ + }$ :

The positive deviation between the actual and planned departure time of train i from station j under scenario s

$b_{ijs}^{ - }$ :

The negative deviation between the actual and planned departure time of train i from station j under scenario s

$p_{ijs}$ :

The number of passengers on train i when it departs from station j under scenario s

${\text{st}}_{s}$ :

The total deviation between the actual and planned travel time under scenario s

${\text{swt}}_{s}$ :

Total waiting time of passengers under scenario s

$\theta_{s}$ :

An auxiliary variable representing the deviation between actual travel time and mean value under scenario s

$\theta_{s}^{{\prime }}$ :

An auxiliary variable representing the deviation between actual passenger waiting time and mean value under scenario s

3.1 Scenario-Based Stochastic Optimization Model

This section presents a scenario-based stochastic programming model for generating a robust stop-skip plan in an urban railway. The problem has been formulated as a multi-objective mixed-integer linear programming formulation given in Eqs. (1)–(26). Equation (1) minimizes the total travel time of trains plus absolute deviations between the actual and planned timetable under different scenarios. In the first objective function, the first term determines the travel time of each train, and the second term shows the deviations between the planned and actual arrival and departure time of trains under different scenarios. Equation (2) shows the second objective function, which accounts for the total passenger cost. The first term of this function is the average waiting time for passengers at stations under different scenarios. For passengers who have been able to board the train, the average waiting time is half the minimum headway $\left( {\frac{h}{2}} \right)$ and for those skipped by trains, it equals h. The second part of the second objective function also calculates the average number of passengers who left the last train under different scenarios, which is a kind of unsatisfied demand for passenger accommodation.

$${\text{Min}}\;Z_{1} = \underbrace {{\sum\limits_{i \in \varOmega } {({\text{TAr}}_{iM} - {\text{TAr}}_{i1} )} }}_{1} + \underbrace {{\omega \cdot \sum\limits_{i \in \varOmega } {\sum\limits_{j \in \varPsi } {\sum\limits_{s \in \xi } {{\text{pr}}_{s} \cdot (w \cdot (a_{ijs}^{ + } + b_{ijs}^{ + } )} } } + w^{{{\prime } }} (a_{ijs}^{ - } + b_{ijs}^{ - } ))}}_{2}$$

(1)

$${\text{Min}}\;Z_{2} = \underbrace {{\sum\limits_{i \in \varOmega } {\sum\limits_{j \in \varPsi } {\sum\limits_{s \in \xi } {{\text{pr}}_{s} \cdot \left( {{\text{ps}}_{ijs} \cdot \frac{h}{2} + S_{(i - 1)js} \cdot h} \right)} } } }}_{1} + \underbrace {{\upsilon \cdot \sum\limits_{i = M,j \in \varPsi } {\sum\limits_{s \in \xi } {{\text{pr}}_{s} \cdot S_{ijs} } } }}_{2}$$

(2)

Constraint (3) calculates the train dwell time under scenario s. The train dwell time is defined as a function of the number of passengers boarding/alighting the train plus a fixed time for technical operations such as the closing/opening of doors. It ensures that if train i stops at station j, this time is equal to the time taken to board passengers onto train i.

$$d_{ijs} = \beta + x_{ij} \sum\limits_{k > j} {(W_{ijks}^{{\prime }} + V_{ijs} )\alpha } \quad \forall \;i \in \varOmega ,\;j \in \varPsi ,\;s \in \xi$$

(3)

Constraint (4) states that the departure time of train i from station j under scenario s equals the arrival time of the train at the station plus the train dwell time.

$${\text{Dep}}_{ijs} = {\text{Ar}}_{ijs} + d_{ijs} \quad \forall \;i \in \varOmega ,\;j \in\Psi ,\;s \in \xi$$

(4)

Constraints (5) and (6) calculate the positive and negative deviations between the actual and planned departure and arrival times, respectively, under different scenarios.

$${\text{Ar}}_{ijs} - {\text{TAr}}_{ij} = a_{ijs}^{ + } - a_{ijs}^{ - } \quad \forall \;i \in\Omega ,\;j \in \varPsi ,\;s \in \xi$$

(5)

$${\text{Dep}}_{ijs} - {\text{TDep}}_{ij} = b_{ijs}^{ + } - b_{ijs}^{ - } \quad \forall \;i \in\Omega ,\;j \in\Psi ,\;s \in \xi$$

(6)

Equation (7) calculates the running time of train i from station j − 1 to station j under scenario s with respect to the acceleration and deceleration of trains. Likewise, the running time between two consecutive stops j − 1 and j principally comprises three terms, i.e., pure running time ($\tau_{j}$), acceleration time ($t_{\text{ac}}$), and deceleration time ($t_{\text{dec}}$).

$${\text{Ar}}_{ijs} - {\text{Dep}}_{i(j - 1)s} = \tau_{j} + t_{ac} x_{i(j - 1)} + t_{dec} x_{ij} \quad \forall \;i \in \varOmega ,\;j \in \varPsi ,\;s \in \xi$$

(7)

Constraint (8) calculates the total number of passengers skipped by train i at station j under scenario s.

$$S_{ijs} = \mathop \sum \limits_{k = j + 1}^{N} s_{ijks} \quad \forall \;i \in\Omega ,\;j \in\Psi ,\;s \in \xi$$

(8)

Constraint (9) counts the total number of passengers boarding the train i at station j under scenario s.

$${\text{ps}}_{ijs} = \mathop \sum \limits_{k = j + 1}^{N} W_{ijks}^{{\prime }} \quad \forall \;i \in\Omega ,\;j \in\Psi - \{ N\} ,\;s \in \xi$$

(9)

Constraint (10) ensures that if train i skips two stations j and k, the number of passengers boarded onto train i at station j, which are intended to alight at station k, is zero.

$$W_{ijks}^{{\prime }} \le My_{ijk} \quad \forall \;i \in\Omega ,\;j,\;k \in\Psi ,\;s \in \xi$$

(10)

Constraint (11) implies that the summation of passengers skipped and boarded on train i at station j equals the number of passengers waiting at station j. In other words, the number of passengers that could not board train i − 1 will be the number waiting for train i.

$$W_{ijks}^{{\prime }} = W_{ijks} - s_{(i - 1)jks} \quad \forall \;i \in\Omega ;\;j,\;k \in\Psi ,\;s \in \xi$$

(11)

Equation (12) defines the maximum number of passengers accommodated by train i in station j under scenario s.

$$C_{i} - p_{ijs} \le Mf_{ijs} \quad \forall \;i \in\Omega ;\;j \in\Psi ,s \in \xi$$

(12)

Constraint (13) states that if train i stops at both stations j and k, there are no left behind passengers traveling from station j to station k.

$$s_{ijks} \le M(1 - f_{ijs} ) + M(1 - y_{ijk} )\quad \forall \;i \in\Omega ;\;j,k \in\Psi ,s \in \xi$$

(13)

Constraint (14) calculates the total number of passengers traveling from station k < j to station j accommodated by train i.

$$V_{ijs} = \mathop \sum \limits_{k = 1}^{j - 1} W_{ikjs}^{{\prime }} \quad \forall \;i \in \varOmega ,\;j \in \varPsi ,\;s \in \xi$$

(14)

Constraint (15) indicates that the number of passengers waiting at station j to board train i is equal to the number of passengers who were skipped by the previous train plus the number of new passengers arriving at station j.

$$W_{ijks} = s_{i - 1,jks} + \lambda_{jks} (Ar_{ijs} - Ar_{(i - 1)js} )\quad \forall \;i \in\Omega \backslash \{ 1\} ;\;j,k \in\Psi ,k > j,\;s \in \xi$$

(15)

To ensure the quality of skip-stop services, constraint (16) ensures that all trains must stop at the first (j = 1) and last station (j = N).

$$x_{i1} + x_{iN} = 2\quad \forall \;i \in\Omega$$

(16)

Given the management regulations, constraint (17) guarantees that at least one of two successive trains must stop at each station.

$$x_{ij} + x_{(i + 1)j} \ge 1\quad \forall \;i \in \varOmega \backslash \{ M\} ;j \in\Psi$$

(17)

Likewise, constraint (18) indicates that each train must stop at at least one intermediate station.

$$\sum\limits_{{j \in \varPsi - \{ 1,N\} }} {x_{ij} \ge 1} \quad \forall \;i \in\Omega$$

(18)

Constraint (19) ensures that there must be at least one train to stop at two distinct stations j and k.

$$\sum\limits_{{i \in\Omega }} {y_{ijk} } \ge 1\quad \forall \;j,k \in\Psi$$

(19)

Constraint (20) counts the number of passengers on the train i when it departs from station j under scenario s.

$$p_{ijs} = \sum\limits_{k > j} {W_{ijks}^{{\prime }} + \sum\limits_{l < j} {\sum\limits_{m > j} {W_{ilms}^{{\prime }} } } } \quad \forall \;i \in\Omega ;\;j \in\Psi ,\;s \in \xi$$

(20)

Constraint (21) ensures that the number of passengers on the train does not exceed the maximum capacity of the train.

$$p_{ijs} \le C_{i} \quad \forall \;i \in\Omega ;\;j \in\Psi ,\;s \in \xi$$

(21)

Constraints (22) and (23) define the logical relationship between the skip-stop variables x and y. For example, constraint (23) ensures that if the train i stops at stations k and j, the value of variable y is equal to 1.

$$2y_{ijk} \le x_{ij} + x_{ik} \quad \forall \;i \in\Omega ;j,k \in\Psi$$

(22)

$$x_{ij} + x_{ik} \le 1 + y_{ijk} \quad \forall \;i \in\Omega ;\;j,k \in\Psi$$

(23)

Constraints (24) and (25) define the minimum safety headway time as a difference between the departure and arrival of two consecutive trains, respectively.

$${\text{Dep}}_{ijs} - {\text{Dep}}_{(i - 1)js} \ge h\quad \forall \;i \in\Omega \backslash \{ 1\} ;\;j \in\Psi ,s \in \xi$$

(24)

$${\text{Ar}}_{ijs} - {\text{Ar}}_{(i - 1)js} \ge h\quad \forall \;i \in\Omega ;\;j \in\Psi ,s \in \xi$$

(25)

Finally, constraint (26) defines the type and domain of the decision variables.

$$\begin{aligned} y_{ijk} ,x_{ij} \quad \in \{ 0,1\} \quad \forall \,i \in\Omega ;j,k \in\Psi \hfill \\ {\text{Ar}}_{ijs} ,{\text{Dep}}_{ijs} ,p_{ijs} ,W_{ijks}^{{\prime }} ,W_{ijks} ,V_{ijs} ,s_{ijks} ,ps_{ijs} ,S_{ijs} ,d_{ijs} \ge 0\quad \forall \;i \in \varOmega ;j,k \in\Psi ,s \in \xi \hfill \\ \end{aligned}$$

(26)

3.2 A Scenario-Based Robust Optimization Model

This section explains the robust counterpart formulation of the skip-stop scheduling problem. The method is based on the formulation of Mulvey et al. [52] as a highly successful optimization approach under uncertainty. The robust optimization model considers the scenarios and their probability of occurrence. Following the notations of Mulvey et al. [52], Eq. (27) shows the first objective function of the robust model, which comprises two parts. The first part minimizes the travel time of trains regardless of the realized scenarios. The second part minimizes the average deviation between the actual and planned timetable under different scenarios weighted by a coefficient ($\omega^{ }$). This coefficient balances the relative importance of earliness and tardiness based on user preference. Constraint (28) shows the second functional objective, which includes three terms. The first term corresponds to the minimization of the average waiting time of passengers under different scenarios. The second term minimizes the absolute deviation between the realized and expected wait time over different scenarios weighted by a coefficient ($\omega^{{\prime }}$). Finally, the third term minimizes the number of passengers who failed to board the trains (or equivalently, the unfulfilled demand) weighted by a coefficient ($\nu$). The value of the weight coefficient depends on user preference, and can be obtained by numerical experiments or sensitivity analysis.

$$\begin{aligned} {\text{Min}}\,Z_{1} = \underbrace {{\sum\limits_{{i \in\Omega }} {({\text{TAr}}_{iM} - {\text{TAr}}_{i1} )} }}_{1} + \underbrace {{\omega \cdot \sum\limits_{s \in \xi } {{\text{pr}}_{s} \cdot st_{s} } }}_{2} \hfill \\ {\text{where}}\,{\text{st}}_{s} = \sum\limits_{{i \in\Omega }} {\sum\limits_{{j \in\Psi }} {(w \cdot (a_{ijs}^{ + } + b_{ijs}^{ + } ) + w^{\prime } (a_{ijs}^{ - } + b_{ijs}^{ - } ))} } \hfill \\ \end{aligned}$$

(27)

$$\begin{aligned} {\text{Min}}\;Z_{2} = \underbrace {{\sum\limits_{s \in \xi } {pr_{s} \cdot {\text{swt}}_{s} } }}_{1} + \underbrace {{\omega^{{\prime }} \cdot \sum\limits_{s \in \xi } {pr_{s} \cdot ({\text{swt}}_{s} - \sum\limits_{{s^{{\prime }} \in \xi }} {pr_{{s^{{\prime }} }} \cdot {\text{swt}}_{{s^{{\prime }} }} } + 2\theta_{s}^{{\prime }} )} }}_{2} + \underbrace {{\upsilon \cdot \sum\limits_{{i = M,j \in\Psi }} {\sum\limits_{s \in \xi } {pr_{s} \cdot S_{ijs} } } }}_{3} \hfill \\ {\text{where}}\,{\text{swt}}_{s} = \sum\limits_{{i \in\Omega }} {\sum\limits_{{j \in\Psi }} {\left( {ps_{ijs} .\frac{h}{2} + S_{(i - 1),js} \cdot h} \right)} } \hfill \\ \end{aligned}$$

(28)

All the constraints of the stochastic optimization model are also considered in the robust optimization model. Equation (29) is added to the set of constraints for proper consideration of the deviations in the objective function.

$${\text{swt}}_{s} - \sum\limits_{{s^{{\prime }} \in \xi }} {pr_{{s^{{\prime }} }} {\text{swt}}_{{s^{{\prime }} }} } + \theta_{s}^{{\prime }} \ge 0\quad \forall s \in \xi$$

(29)

Finally, the robust skip-stop scheduling model is formulated as follows:

$${\text{Min}}\,Z_{1} = \underbrace {{\sum\limits_{i \in \varOmega } {({\text{TAr}}_{iM} - {\text{TAr}}_{i1} )} }}_{1} + \underbrace {{\sum\limits_{s \in \xi } {{\text{pr}}_{s} \cdot {\text{st}}_{s} } }}_{2}$$

(30)

$${\text{Min}}\;Z_{2} = \underbrace {{\sum\limits_{s \in \xi } {pr_{s} \cdot {\text{swt}}_{s} } }}_{1} + \underbrace {{\omega^{{\prime }} \cdot \sum\limits_{s \in \xi } {pr_{s} \cdot ({\text{swt}}_{s} } - \sum\limits_{{s^{\prime} \in \xi }} {pr_{{s^{{\prime }} }} \cdot {\text{swt}}_{{s^{{\prime }} }} } + 2\theta_{s}^{{\prime }} )}}_{2} + \underbrace {{\upsilon \cdot \sum\limits_{i = M,j \in \varPsi } {\sum\limits_{s \in \xi } {pr_{s} \cdot S_{ijs} } } }}_{3}$$

(31)

where

$$\begin{aligned} {\text{st}}_{s} = \sum\limits_{i \in \varOmega } {\sum\limits_{{j \in\Psi }} {(w \cdot (a_{ijs}^{ + } + b_{ijs}^{ + } ) + w^{{\prime }} (a_{ijs}^{ - } + b_{ijs}^{ - } ))} } \hfill \\ {\text{swt}}_{s} = \sum\limits_{i \in \varOmega } {\sum\limits_{{j \in\Psi }} {\left( {ps_{ijs} .\frac{h}{2} + S_{(i - 1)js} \cdot h} \right)} } \hfill \\ \end{aligned}$$

(32)

subject to:

$${\text{swt}}_{s} - \sum\limits_{{s^{\prime } \in \xi }} {{\text{pr}}_{{s^{\prime } }} \cdot {\text{swt}}_{{s^{\prime } }} } + \theta_{s}^{\prime } \ge 0\quad \forall s \in \xi$$

(33)

In this study, the normalized Lp-norm method is used to solve the multi-objective optimization model. In this method, the problem is solved for each objective function, and the upper and lower bounds for the objective functions are calculated. Afterward, these values are used to normalize the objective function. Constraint (34) represents the combination of two objective functions in which $\varphi \in \left[ {0,1} \right]$ is a weight factor. This weight factor indicates the relative importance of the normalized objective functions. As parameter $\varphi$ increases, the relative importance of the first objective function decreases, and the weight of the second objective function increases.

$$ {\text{Min}}\;Zt = \varphi \cdot \frac{{Z_{1} - {Z_{1}}_{min}}}{{{Z_{1}}_{max} - {Z_{1}}_{min} }} + (1 - \varphi ) \cdot \frac{{Z_{2} - {Z_{2}}_{min} } }{{{Z_{2}}_{max} - {Z_{2}}_{min} } } \hfill \quad{\text{Subject to}}: {\text{Equations}} \,(1)-(33)\\ $$

(34)

4 Numerical Results

In this section, the statistical result and the validation process are carried out using test instances of the Tehran metro system. For further verification of the optimization models, a sensitivity analysis is performed to study the effect of critical parameters on the performance of the model. The mathematical models were coded in GAMS 24.2 and run on a PC with an Intel Core i5 processor and 8 GB RAM, under the Windows 10 operating system. The proposed optimization models were solved by CPLEX 12.9 solver, which uses several state-of-the-art MILP techniques, e.g., branch and bound (B&B) and branch and cut (B&C) algorithms. The designed models are well-matched with standard optimization platforms, e.g., GAMS. It will be shown that high-quality solutions can be generated for real size instances of skip-stop scheduling problem within a reasonable time.

4.1 Case Study

In this section, the effectiveness of the proposed robust skip-stop scheduling models is verified by a real example of Tehran Metro Line No. 5. The input data are collected using a field survey and a questionnaire targeting the passengers and the Tehran Metro Organization. Suburban rail line No. 5 is about 41-kilometer long with ten stations which connect Tehran to Golshahr (Fig. 1). The underlying test example considers six trains running on a double-track rail line with ten stations. Here, five discrete scenarios represent the uncertainty associated with arrival rate. The probability of the occurrence of scenarios 1, 2, 3, 4, and 5 are considered to be 0.15, 0.2, 0.3, 0.2, and 0.15, respectively. Table 2 provides the input parameters used to solve the test problems.

Fig. 1

Route map of the Line No.5 of Tehran metro network

Table 2 Parameters values and related units used in the case study

Table 3 reports the free running time of the trains on block sections along the route.

Table 3 Train pure running time between two consecutive stations (minutes)

Arrival rates of passengers are represented by the number of travelers per second who are planning to travel between different origins and destinations (Table 4). As illustrated in Table 4, parameter $\lambda_{jk}^{{\prime }}$ corresponds to the values of the nominal arrival rate. In addition, $\rho_{s}$ is a coefficient that alters the arrival rate within the range of − 10 to 10%. For example, in the first scenario, the arrival rate is 90% of its nominal amount, while under scenario 5, the arrival rate is 10% higher than the nominal value.

Table 4 The arrival time of passengers with different origins and destinations (passengers per second)

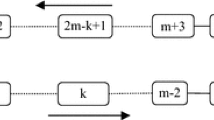
The numerical experiments are executed by setting the input parameters as $\omega = 1,\nu = 10^{3}$, and $\varphi = 0.5$. In the first step, each objective function is optimized separately, and the minimum and maximum values are obtained (Table 5). These values are entered as input parameters for the Lp-metric method, and the scenario-based skip-stop scheduling model is solved with the combined objective function. Table 6 illustrates the values of the combined objective functions and the first and second objective functions, namely as the travel time of trains and the waiting time of passengers under different scenarios. The optimal value of the normalized objective function is obtained as 0.259. According to the obtained results, the lowest and highest values of waiting time and trains’ travel time have been obtained in the first and fifth scenarios, respectively. Figure 2 shows the optimal skip-stop schedule obtained in the third scenario. As can be seen, most of the trains stop at two stations with the highest demand (stations No. 3 and 9).

Table 5 The range of the objective function values

Table 6 The objective function values ($St_{s} ,Swt_{s}$)

Fig. 2

The stop-skip pattern for trains running on Line 5

Figure 3 shows a time–space graph of the train movement obtained for the third scenario. As illustrated in this figure, trains No. 1, 3 and 5 skip stations No. 6, 7 and 8, and thus have the same arrival and departure times. As can be seen, all trains have stopped at stations No. 3 and 9 because of the high demand for travel.

Fig. 3

The time–space graph of the train movements

4.2 Stochastic Analysis of Solutions

In this section, the value of the stochastic solution for joint train timetabling and skip-stop planning problem is analyzed. Suppose z_EEV, z_WS, and z_RP are the values of the objective function corresponding to the Expected Value optimization, wait and see (in the case of having perfect information) and resource problem, respectively. It can be shown that in the case of a minimization problem, the inequities (35) are valid.

$$Z_{\text{WS}} \le Z_{\text{RP}} \le Z_{\text{EEV}}$$

(35)

Expected Value of Perfect Information (EVPI), which indicates the importance of addressing the uncertainty of information, is defined as shown in Eq. (36). EVPI measures how much imperfect information affects the value of the objective function. A low value of EVPI indicates that having complete information is not significant.

$${\text{EVPI}} = Z_{\text{RP}} - Z_{\text{WS}}$$

(36)

As another practical indicator, the Value of Stochastic Solution (VSS) is defined in Eq. (37). VSS shows how much savings can be obtained using a stochastic solution rather than a deterministic solution, such as an average value. In other words, VSS represents the cost of ignoring uncertainty during the decision-making the process. The more significant value of the VSS indicates the importance of accounting for the uncertainty of the model.

$${\text{VSS}} = Z_{\text{EEV}} - Z_{\text{RP}}$$

(37)

The calculation of z_EEV requires the values of the decision variables of the deterministic scheduling model to be entered as parameters in the stochastic optimization model. With the suggested approach, the expected value optimization model is solved and the corresponding objective value is obtained, i.e., $z_{\text{EEV}} = 0.3323$. The amount of z_ws also is equal to the average of the objective function in the case of having perfect information about the occurrence of scenarios. To obtain the wait and see value, the deterministic model is separately solved for each scenario, and the corresponding values of the objective functions are multiply by the occurrence probability of the scenarios ($z_{\text{ws}} = 0.2152$). The amount of resource function, z_RP, corresponds to the stochastic value of the objective function which is obtained, i.e., $z_{\text{RP}} = 0.25997 \,$. Finally, the values EVPI of VSS are obtained, i.e., ${\text{EVPI}} = Z_{\text{RP}} - Z_{\text{ws}} = 0.0447 \,$ and ${\text{VSS}} = Z_{\text{EEV}} - Z_{\text{RP}} = 0.07234$, respectively. It can be observed that having accurate information can reduce up to 16% the value of the combined objective function. Moreover, VSS is 21% of the value of the combined objective function, which indicates that the stochastic model outperforms the solution obtained by the deterministic optimization model.

4.3 Results of Robust Skip-Stop Scheduling Models

In this subsection, the input parameters are assumed to be $\omega = \omega^{\prime } = 1$, $\nu = 10^{3}$, and $\varphi = 0.5$. As can be seen in Table 7, the minimum and maximum values for objective functions are obtained separately. Then, the obtained payoff table is used as an input for the robust skip-stop scheduling model. Table 8 shows the values of the combined objective functions, the first and second objective functions, and the amount of earliness and tardiness under different scenarios. The optimal value of the normalized objective function is obtained, i.e., Z_t = 0.2804.

Table 7 The minimum and the maximum values of the objective functions in the robust skip-stop scheduling model

Table 8 The values of the objective functions under different scenarios

Figure 4 shows the skip-stop schedules generated in the third scenario. Likewise, compared with the result presented in previous sections, all trains stop at stations No. 3 and 9 because of the highest demand for travel. Figure 5 illustrates the corresponding time–space diagram of train movements obtained in the third scenario.

Fig. 4

The skip-stop schedule obtained for the robust optimization model

Fig. 5

The time-station graph of the train movement

4.4 Sensitivity Analysis

In this section, a sensitivity analysis is conducted to assess the effect of some key parameters on the quality of the skip-stop schedules. Table 9 shows the sensitivity analysis of the train capacity parameter. In this analysis, the train capacity rate factor is changed within a range of 50% to 110%. According to the obtained result (Table 9), with the increase in train capacity, the amount of the combined objective function is reduced. Correspondingly, the value of the second objective function, as well as the number of passengers skipped by trains and the unsatisfied demand, is reduced exponentially by increasing the capacities of the trains.

Table 9 Sensitivity analysis of train capacity parameter

Figure 6 shows the trade-off between the value of the combined objective function and the standard deviation of the passenger waiting times versus the values of weight coefficient ($\omega^{{\prime }}$). According to Fig. 6, as the value of $\omega^{{\prime }}$ increases, the combined objective function increases and the standard deviation of the passenger waiting time decreases.

Fig. 6

Sensitivity analysis for standard deviation and waiting time under different scenarios

It would also be beneficial to test the effect of relative weight coefficient on the objective values. Table 10 shows the values of the first and second objective functions against the value of φ. According to the obtained result, by increasing this coefficient, the value of the first objective function reaches its lowest cost, and in contrast, the value of the second objective function increases. Table 10 reports the total number of train stops at stations in different values of φ. As can be observed, the number of stops decreases with increasing φ, and by reducing this value, the number of stops reaches its maximum amount. Figure 7 shows the sensitivity analysis for the first and second objective functions in different values of φ. Accordingly, the decision maker can find a suitable trade-off between the values of the objective functions, i.e., Z₁ and Z₂.

Table 10 Sensitivity analysis of the φ parameter

Fig. 7

The first and second objective function value in different values of φ

Table 11 reports the values of both objective functions in the case where the number of skip-stop patterns changes. The outcomes indicate that, in case of all stop operation mode, the value of the objective function is higher than that of skip-stop service. It can be observed that by increasing the number of skip-stop patterns, the value of Z₁ decreases (Fig. 8). On the other hand, as the number of patterns increases, travel time decreases, and in contrary, passenger waiting time increases. Overall, in the underlying case study with six skip-stop patterns, the value of the combined objective function (Z_t) is reduced by 49% as compared with regular all-stop service. Furthermore, the travel time of passengers decreases by 5% compared with the regular all-stop operation. Thus, the results confirm that the proposed robust skip-stop scheduling model can significantly improve the robustness and operating efficiency of the urban rail transit system.

Table 11 Sensitivity analysis of the number of patterns

Fig. 8

The values of objective functions as against the different number of skip-stop patterns

4.5 Model Reliability Test

In this sub-section, the reliability of the optimization model is verified using test examples. Table 12 reports the results of the robust skip-stop scheduling model for a different number of trains. The results include the objective values and computational time. In this set of numerical experiments, the scale of the case study is expanded and the travel demand is increased to better highlight the performance of the robust skip-stop scheduling model. The results of computational experiments show that by increasing the number of trains, the total travel time of trains (Z₁) and total passenger waiting time (Z₂) grow almost linearly by the number of trains, while the CPU time increased exponentially. This linear behavior is expected because the total train traveling time depends on the number of trains. Also, by increasing the number of trains, the entire service time is expanded, hence the overall demand increases accordingly.

Table 12 The performance of the robust optimization model

The robust skip-stop scheduling model was able to find the optimal solution for test problems with fewer than 13 trains in a reasonable time. However, the outcomes indicate that the CPU time required to reach the optimal solution grows exponentially by increasing the number of trains as the complexity of the mathematical model increases by the size of the problem. Overall, the result confirms the applicability of the proposed robust skip-stop scheduling model to find efficient solutions in urban rail systems during peak hours. However, due to the complexity of problem size, there is a limitation of the method in real-time applications.

5 Concluding Remarks

This study addressed the joint train scheduling and train stop planning problem by considering skip-stop services during peak hours in rapid rail transit systems. We proposed robust optimization models for optimal skip-stop scheduling under uncertain arrival rates during peak hours. The objective was to minimize the total weighted travel time of passengers, wait time, and the deviation between the actual and planned timetable. The problem was formulated as a scenario-based stochastic optimization model and then modeled using a robust optimization approach. The efficiency of the proposed models was confirmed using real data from line No. 5 of the Tehran Metro in Iran. To validate the proposed robust optimization models, the EVPI and VSS indicators were calculated, and sensitivity analysis was conducted. The outcomes indicate that having complete information can reduce up to 16% the value of the combined objective function. Moreover, the value of stochastic solutions reaches 21% of the value of the deterministic solution, which indicates that the stochastic model exhibits better performance than the deterministic scheduling model. The designed skip-stop method has been shown to save about 5% in total travel time and 49% in aggregate objective function, which is a summation of travel times and passenger waiting times as against regular all-stop service. Also, the developed mathematical model could produce high-quality solutions for large size instances of the problem in a reasonable time, thus providing a practical framework for rail systems.

There are several possible extensions to this study. Future research must address the implementation of other methods such as short-turning, holding, and deadheading in combination with skip-stop schedules. It would be interesting to formulate the robust train timetabling problem as a bi-criteria optimization model, where both the operator and passenger costs are minimized. Providing multi-objective meta-heuristic optimization algorithms to find Pareto optimal solutions in the shortest possible time will be considered for future research. It would be a motivating research direction to study the effects of random disturbances, i.e., train delay, on the quality of the skip-stop services.