Introduction

Indentation tests have been used for more than a century to characterize the mechanical properties of materials. Tests involve the application of load and the measurement of the depth of penetration or the size of the residual imprint after unloading. The value of the mean contact pressure \(p_{m}\) at which there is no additional increase with indenter load is related to the hardness number H [18, 29, 48]. The mean contact pressure is equal to the hardness for indentation methods that employ the projected area of contact. Experiments have repeatedly shown that the mean contact pressure \(p_{m}\) or the hardness H is directly proportional to the yield stress \(\sigma_{y}\) of the indented material,

$$H = C\sigma_{y}$$
(1)

where C is a constraint factor, the value of which depends on the type of specimen and the geometry of the indenter [48]. For instance, \(C \approx 3\) for materials with a large ratio \(E/\sigma_{y}\), and \(C \approx 1\) for low values of \(E/\sigma_{y}\), with E = Young’s modulus of indented specimen [48]. Various models which combine the elastic and plastic responses of materials have been proposed for the determination of the hardness, and for the estimation of their mechanical properties, on the basis of indentation test results obtained with indenters of different geometries (i.e., conical, pyramidal, spherical, or flat- ended cylindrical). These models variously describe the response of indented specimens in terms of elastic deformations, radial compressions, and slip lines.

The indentation problem was also successfully approached using the finite element method of analysis in which indentations are simulated by means of elastic or rigid indenters on elastic, elastic–plastic, and viscoelastic materials, with or without adhesion or friction [5, 6, 10, 21, 22, 27, 40].

Although indentations with spherical and sharp indenters have been widely used for the characterization of material properties [15, 17, 28, 31], application of flat-ended cylindrical indenters can be also found in the literature (See, for example, [13, 40]). While the contact surface area increases with increasing load for spherical and sharp indenters, it remains constant for flat-ended cylindrical indenters; as a result, the mean contact pressure increases linearly with applied load.

A type of indentation test has also been used in Scandinavia since 1915 to estimate the consistency of clays in routine geotechnical studies. Indeed, Olsson [38] described the fall-cone test in which a cone is allowed to fall freely under its own weight from a position at rest. Olsson [38] devised a strength number proportional to the mass of a cone of 60o tip angle which would produce a penetration of 10 mm. Hansbo [23] showed that for a cone of mass m and tip angle α, the undrained shear strength is directly proportional to the square of the penetration. However, as the fall-cone test is a dynamic test in which the cone initially accelerates during its fall and then decelerates to come to rest, the constant of proportionality varies from one clay to another. As a result, the fall-cone test is mainly used as an index strength test, rather than an absolute test, like the field vane and cone penetration tests [54]. Consequently, it is more appropriate to use a static indentation test in which boundary conditions are better controlled.

In this paper a flat-ended cylindrical indentation technique is used for the characterization of the mechanical properties of a natural sensitive clay of eastern Canada. The technique involves indentation of intact specimens of clay by means of a flat-ended steel punch and allows determination of load P versus depth of penetration h curves from which elastic moduli and undrained shear strengths are deduced. These parameters are compared to data obtained from conventional geotechnical laboratory tests, such as unconfined or uniaxial compression tests, miniature vane, and Swedish fall-cone tests.

The paper also presents a brief review of the most common theories used to interpret indentation test results obtained by means of flat-ended cylindrical indenters, and as well as a numerical finite element simulation of indentation tests carried out on the clay.

Indentation theories

Elastic response

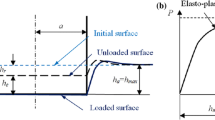
The problem of determining the stresses within an elastic half-space indented by a rigid cylindrical punch seems to have been considered first by Boussinesq [9], using the methods of potential theory. Partial numerical results based on Boussinesq’s solution were also derived in the case of the flat-ended punch [36] and a conical punch [35]. However, as Boussinesq’s method of analysis does not lend itself to practical analyses, Harding and Sneddon [24] using integral transforms obtained the general solution for the stresses and displacements generated by an axisymmetric punch on an elastic half-space. The solutions appropriate to the flat-ended cylindrical punch and the conical punch have been discussed in detail by Sneddon [45, 46], respectively. Further, Sneddon [44] gives the complete solution for the stresses and displacements resulting from the indentation of an elastic half-space by a rigid flat-ended cylindrical punch. In addition, Sneddon [43] derived the relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary shape, using a simpler method than that employed by Harding and Sneddon [24]. The results of Sneddon’s solution for the flat-ended cylindrical punch may be summarized with the help of Fig. 1 (see, also, [5, 19, 40]). The contact area is assumed to remain constant and equal to that of the indenter with radius a. The boundary conditions are:

$$\begin{aligned} & \sigma _{z} \left( {r,0} \right) = 0, \quad r > a \\ & \tau _{{rz}} \left( {r,0} \right) = 0, \quad 0 \le r \le a \\ & u_{z} \left( {r,0} \right) = h, \quad 0 \le r \le a \\ \end{aligned}$$
(2)
Fig. 1
figure 1

Punch on elastic half-space (after [19])

Full size image

The first condition indicates that the horizontal boundary outside the loaded area is free of the vertical stress. The second condition specifies that the interface between the indenter and the half-space is smooth. The third condition forces the half-space in contact with the indenter to undergo a uniform downward displacement \(u_{z}\) equal to h. In addition, the vertical stress \(\sigma_{z} \to\)\(\infty\) at \(r = a\) because of the shape of the sharp edge along the perimeter of the indenter. Although this condition causes the development of a localized plastic zone beneath the circular edge of the indenter, it does not invalidate the elastic solution, as discussed by Timoshenko and Goodier [52], Sneddon [43, 44] and Johnson [28].

The mean applied pressure \(p_{m}\), following a depth of penetration h, is given by:

$$p_{m} = \frac{P}{{\pi a^{2} }} = \frac{2Eh}{{\pi a\left( {1 - \nu^{2} } \right)}}$$
(3)

where \(P =\) applied load, and \(\nu =\) Poisson’s ratio. The distribution of the contact stress \(\sigma_{z} \left( {r \le a,\,z = 0} \right)\) is found from:

$$\sigma _{z} \left( {r,0} \right) = \frac{{p_{m} }}{{2\sqrt {1 - \left( {{r \mathord{\left/ {\vphantom {r a}} \right. \kern-\nulldelimiterspace} a}} \right)^{2} } }},\, \, r \le a$$
(4)

which shows that there is a square root singularity at \(r = a\). The vertical and horizontal displacements of the horizontal boundary, \(u_{z}\) and \(u_{r}\), are given respectively by:

$$u_{z} \left( {r,0} \right) = \frac{{2h}}{\pi }\sin ^{{ - 1}} \left( {\frac{r}{a}} \right),\quad r > a$$
(5)
$$u_{r} \left( {r,0} \right) = - \left( {\frac{{1 - 2\nu }}{{1 - \nu }}} \right)\left( {\frac{h}{\pi }} \right)\left\{ {\begin{array}{*{20}c} {\frac{{a - \left( {a^{2} - r^{2} } \right)^{{1/2}} }}{r};\quad r \le a} \\ {\frac{a}{r}\quad \quad \quad ; \quad r{{ > }}a} \\ \end{array} } \right.$$
(6)

The remaining elastic relations in terms of cylindrical coordinates \(\left( {r,\theta ,z} \right)\) are the following [17, 19, 44, 46]:

$$\begin{gathered} \sigma _{r} \left( {\rho ,\zeta } \right) = - \frac{{p_{m} }}{{2\rho }}\left[ {J_{1}^{0} \rho - \zeta \left( {\rho J_{2}^{0} - J_{1}^{1} } \right) - \left( {1 - \nu } \right)J_{0}^{1} } \right] \hfill \\ \sigma _{\theta } \left( {\rho ,\zeta } \right) = - \frac{{p_{m} }}{{2\rho }}\left[ {2\nu \rho J_{1}^{0} - \zeta J_{1}^{1} + \left( {1 - 2\nu } \right)J_{0}^{1} } \right] \hfill \\ \sigma _{z} \left( {\rho ,\zeta } \right) = - \frac{{p_{m} }}{2}\left[ {\zeta J_{2}^{0} + J_{1}^{0} } \right] \hfill \\ \tau _{{rz}} \left( {\rho ,\zeta } \right) = - \frac{{p_{m} }}{2}\zeta J_{2}^{1} \hfill \\ \end{gathered}$$
(7)

and

$$\begin{aligned} u_{r} \left( {\rho ,\zeta } \right) = \frac{{h\left[ {\zeta J_{1}^{1} - \left( {1 - 2\nu } \right)J_{0}^{1} } \right]}}{{\pi \left( {1 - \nu } \right)}} \hfill \\ u_{z} \left( {\rho ,\zeta } \right) = \frac{{h\left[ {2\left( {1 - \nu } \right)J_{0}^{0} - \zeta J_{1}^{0} } \right]}}{{\pi \left( {1 - \nu } \right)}} \hfill \\ \end{aligned}$$
(8)

with \(\rho = \frac{r}{a}\), \(\zeta = \frac{z}{a}\) and

$$\begin{gathered} J_{1}^{0} = R^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}} \sin \left( {{\phi \mathord{\left/ {\vphantom {\phi 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \hfill \\ J_{2}^{0} = r^{ * } R^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \sin \left( {\frac{{3\phi }}{2} - \theta } \right) \hfill \\ J_{1}^{1} = r^{ * } \rho ^{{ - 1}} R^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}} \sin \left( {\theta - \frac{\phi }{2}} \right) \hfill \\ J_{2}^{1} = \rho R^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \sin \left( {\frac{{3\phi }}{2}} \right) \hfill \\ J_{0}^{1} = \rho ^{{ - 1}} \left[ {1 - R^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \sin \left( {{\phi \mathord{\left/ {\vphantom {\phi 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \right] \hfill \\ J_{0}^{0} = \frac{\pi }{2} - \tan ^{{ - 1}} \left[ {\left( {\frac{{\zeta ^{2} + \rho ^{2} + R - 1}}{2}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \right] \hfill \\ \end{gathered}$$
(9)

where \(R = \left[ {\left( {\rho^{2} + \xi^{2} - 1} \right)^{2} + 4\zeta^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}\), \(r^{ * } = \left( {1 + \zeta^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}\), \(\xi \tan \theta = 1\), and \(\left( {\rho^{2} + \zeta^{2} - 1} \right)\tan \phi = 2\zeta\).

Elastic–plastic response

An indentation model which also takes into account plastic response is extremely complex to develop due to the nonlinearity of the constitutive relations (see, for instance, [55]). As a result, only approximate models have been proposed for the description of the elastic–plastic response of materials subjected to indentations by punches of different profiles, namely, the spherical cavity expansion model and the slip line theory.

For blunt indenters, including spherical and flat-ended cylindrical punches, the specimen responds in an elastic–plastic manner, and plastic flow is usually described in terms of the elastic constraint provided by the surrounding elastic material. Marsh [37], inspired by the work of Samuels and Mulhearn [41], compared the plastic deformation in the neighborhood of a blunt indenter to that which occurs during the radial expansion of a spherical cavity under internal pressure, an analysis of which was first given by Bishop et al. [7] and Hill [25]. Johnson et al. [30] replaced the expansion of the cavity with that of an incompressible hemispherical core of material subjected to internal pressure, as indicated in Fig. 2. In this model, which has been since referred to as the “expanding cavity model” or ECM, the core pressure is directly related to the mean contact pressure \(p_{m}\), that is,

$$p_{m} = \frac{2}{3}\sigma_{y} \left[ {1 + \ln \left( {\frac{E\tan \alpha }{{2\left( {1 + \nu } \right)\sigma_{y} }}} \right)} \right]$$
(10)

where \(\alpha\) is the inclination of the indenter with the specimen surface and thus leads to a value of

$$C = \frac{2}{3}\left[ {1 + \ln \left( {\frac{E\tan \alpha }{{2\left( {1 + \nu } \right)\sigma_{y} }}} \right)} \right]$$
(11)

for the constraint factor. Although the ECM cannot be directly applied to a flat-ended cylindrical punch indentation because the shape of the plastic zone evolves with the depth of penetration and tends to be similar to that around a spherical cavity only at great depth [6, 32, 55], it nonetheless represents a class of popular models that provide the capability to consider the effects of both elastic and plastic response on the evolution of the deformation fields during the indentation process [53]. For a flat-ended cylindrical punch, the relationship in Eq. (10) is usually replaced by the expression for the expansion of a spherical cavity, that is,

$$p_{m} = \frac{2}{3}\sigma_{y} \left[ {1 + \ln \left( {\frac{E}{{2\left( {1 + \nu } \right)\sigma_{y} }}} \right)} \right]$$
(12)

leading to

$$C = \frac{2}{3}\left[ {1 + \ln \left( {\frac{E}{{2\left( {1 + \nu } \right)\sigma_{y} }}} \right)} \right]$$
(13)
Fig. 2
figure 2

ECM model (from [27])

Full size image

For deeper penetrations, the plastic zone is no longer constrained by the surrounding elastic material, and the volume of the material displaced by the indenter is accommodated by the upward flow around the indenter. The same phenomenon takes place with sharp conical indenters when they first touch the specimen [48]. A cutting mechanism is involved, and new surfaces are formed beneath the indenter as the volume displaced is accommodated by the upward and lateral flow of the plastically deformed material [17]. The constraint factor in this case arises due to flow and velocity considerations [25]. In such situation, slip line theory can be applied to the modelling of the indentation because the response is similar to that which takes place with rigid plastic materials which flow at constant shear stress. Shield [42] showed that the axisymmetric flow of a rigid plastic material could be described by a slip-line field if the material obeyed the Tresca criterion, and assuming the validity of the Haar-von Karman hypothesis which states that the circumferential stress \(\sigma_{\theta }\) is equal to one of the principal stresses in the meridional plane. Shield [42] obtained the solution in the case of the rigid plastic half-space indented by a smooth flat-ended cylindrical punch. The average contact pressure \(p_{m}\) was found to be equal to \(2.845\,\sigma_{y}\) or \(5.69\,k\), where \(k\) is the maximum shear stress (or \(S_{u}\)) in the terminology used in geotechnical engineering). The vertical pressure is equal to \(5.14\,S_{u}\) beneath the perimeter of the punch and the maximum value which equals \(7.2\,S_{u}\) occurs below the axis of symmetry. It should be recalled that Lockett [34], Houlsby and Wroth [26], and Chitkara and Butt [11] also obtained \(p_{m} = 5.69\,S_{u}\) in the case of the smooth flat-ended cylindrical punch. Eason and Shield [14] considered the case of a perfectly rough punch on a rigid plastic half-space and found \(p_{m} = 6.05\,S_{u}\), indicating that the material becomes fully plastic when \(p_{m}\) reaches about \(3\,\sigma_{y}\).

Finite element analysis

As mentioned above, the indentation of an elastic-perfectly plastic material constitutes a very difficult problem to be solved analytically. However, difficulties which arise due to the unknown shape and extension of the plastic field can be minimized by means of a finite element analysis (FEA), provided: (a) an adaptive refined mesh is used to model the indented material, (b) a realistic material response is considered, and (c) the geometry and boundary conditions are properly modelled. In the present paper, an Arbitrary Lagrangian–Eulerian (ALE) based finite element analysis using Abaqus/Explicit is conducted to simulate the experimental investigations performed on natural clay specimens.

All calculations were carried out by means of an axisymmetric model; it consists of a rigid flat-ended cylindrical punch (radius of 9.975 mm and height of 9.95 mm) that penetrates a cylindrical specimen of clay (radius of 31.5 mm and height of 19.0 mm), which is encased in a steel ring (thickness of 2 mm and height of 19.0 mm). The soil specimen and the steel ring rest on a rigid horizontal platen. The analysis was carried out by means of the general-purpose code ABAQUS [1]. Because of the severe distortion that occurs mostly beneath the perimeter of the punch in contact with the clay, modelling was performed using the Arbitrary Lagrangial Eulerian (ALE) auto-adaptive remeshing technique integrated in ABAQUS/Explicit. This technique maintained a high-quality mesh throughout the indentation process.

Instead of using a finite element approach, it is also possible to perform a finite difference analysis for the study of penetration interactions. Indeed, Ghazavi and Tovaioli [20] adopted a finite difference scheme to simulate a three-dimensional model for pile driving analysis using FLAC3D. It is an explicit finite difference program for simulating the response of three-dimensional soil structures built on rock or other soil materials undergoing plastic flow. Further applications of the use of FLAC3D to other pile driving analyses are reported by Tovaioli and Ghazavi [49,50,51].

Geometry of the assembled parts

As just mentioned, the flat-ended cylindrical punch (OFGH in Fig. 3) was modelled as a rigid body. A 0.1-mm radius circular boundary was created along the perimeter of the indenter in contact with the soil, to avoid numerical singularities. The cylindrical specimen (OBCD in Fig. 3) is bounded by a rigid circular ring CM and a rigid bottom platen BC.

Fig. 3
figure 3

Undeformed geometry at the initial state

Full size image

Mechanical properties of materials

It is assumed that the clay behaves as a rate-independent isotropic linearly elastic perfectly plastic material obeying the von Mises flow rule. Values of Young’s modulus and yield stress were obtained from a series of unconfined compression tests performed on intact soil specimens. The unconfined compression tests were carried out according to ASTM [2] —Test Method for Unconfined Compressive Strength of Cohesive Soil which insures constant volume conditions, from which a value of 0.5 is deduced for Poisson’s ratio. The average value of Young’s modulus E was found equal to 15 MPa, and Poisson’s ratio \(\nu\) was assumed to be equal to 0.49 in the Finite Element Analyses to simulate constant volume conditions. The yield stress \(\sigma_{y}\) is equal to 113.4 kPa, as also found from the unconfined compression tests. Finally, the densities of the clay and of the steel indenter are considered to be: \(\rho_{clay} = 1.6 \times 10^{ - 9} \,{\text{t/mm}}^{ 3}\) and \(7.83 \times 10^{ - 9} \,{\text{t/mm}}^{ 3}\), respectively.

Interactions between assembled parts

Three surface-to-surface interactions are employed in the simulation. This type of interaction is integrated in ABAQUS/Explicit; it uses a kinematic contact method as a mechanical constraint formulation and a finite sliding formulation in which only the master surface is allowed to penetrate the slave surface. The first interaction occurs between the lateral surface (OFG in Fig. 3) of the rigid indenter which acts a master surface and the free upper horizontal surface of the specimen (OE in Fig. 3) which acts as a slave surface. The second interaction occurs on the interface represented by line BC in Fig. 3, i.e., between the horizontal bottom edge of the specimen which acts as a slave surface and the inner surface of the rigid low platen which acts as a master surface. Finally, a third interaction occurs on the interface represented by vertex CDM in Fig. 3, i.e., between the vertical cylindrical surface of the specimen (CD in Fig. 3) which acts as a slave surface and the inner vertical cylindrical surface of the container (CM in Fig. 3) which acts as a master surface. These aforementioned three interactions use the same frictionless formulation.

Experimental and numerical results

Clay

The clay tested in this study is a sensitive clay from a soil deposit in the town of Beloeil (Quebec) in eastern Canada. The site is located at a short distance from the shore of the Richelieu River, about 40 km to the south-east of Montreal. Undisturbed blocks of clay, measuring 0.3 m in width, were recovered at a depth of 3.5 m in a test excavation.

The most relevant properties of the clay are reported in Table 1, as given by Ewane et al. [16].

Table 1 Geotechnical properties of Beloeil clay
Full size table

The soil is plastic, sensitive, and lightly overconsolidated. The undrained shear strength \(S_{u}\) of the clay was determined by means of unconfined uniaxial compression (UU) tests [2], miniature vane tests (VST) [3]—Test Methods for Laboratory Miniature Vane Shear Test for Saturated Fine-Grained Clayey Soil), and Swedish fall-cone tests [47]—Determination of Undrained Shear Strength and Sensitivity of Cohesive Soils using a Fall Cone Penetrometer).

The average value of \(S_{u}\) (Tresca) equals 56.7 kPa for the UU tests, 33.5 kPa for the VSTs, and 73.4 kPa for the Swedish fall-cone tests. The lowest value of 33.5 kPa is linked to the development of cracks around the blades of the miniature vanes upon insertion of the instrument. Because the average preconsolidation pressure, \(\sigma^{\prime}_{p}\), equals 143.2 kPa, the strength ratio \(S_{u} /\sigma^{\prime}_{p}\) equals 0.396 for the UU tests, 0.233 for the miniature vane tests and 0.512 for the Swedish fall-cone tests. While the value of 0.233 is slightly low for a typical sensitive clay of eastern Canada, the remaining ratios of 0.396 and 0.512 are rather high for an average overconsolidation ratio (OCR) of 6.42. Indeed, a more realistic value would range from 0.25 to 0.30 for such case [33].

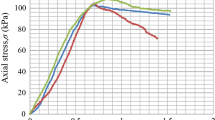
A typical undrained uniaxial (UU) compression test result is reported in Fig. 4. Values of Young’s modulus E range between 15 and 20 MPa, and the yield stress \(\sigma_{y}\) (\(\sigma_{y} = 2S_{u}\)) for Tresca criterion varies between 104 and 108 kPa.

Fig. 4
figure 4

UU tests results

Full size image

Indentation tests

Indentations were carried out using a computer-controlled universal testing machine. The 19.95 mm diameter punch was fixed to the top platen of the loading frame and was coated with graphite powder to minimize the adhesion with the clay specimen. Each clay specimen which measured 63 mm in diameter and 19 mm in height was encased in a polished Teflon coated oedometer steel ring of 2 mm in thickness and 19 mm in height to provide lateral confinement during indentation. The oedometer ring containing the clay specimen was placed on the lower platen of the loading frame. Indentation tests were performed by raising the lower platen at a constant rate of penetration of 0.5 mm/s. The preparation of the soil specimens and their installation in the oedometer rings were made following [4]—Test Method for One-Dimensional Consolidation Properties of Soils using Incremental Loading. The soil surface in contact with the cylindrical punch was trimmed flush with the plane ends of the rings. A wire saw was used for trimming the top and bottom of the specimens to minimize smearing. The load on the indenter and the depth of penetration were continuously recorded during each test. A LVDT with a precision of 0.0075 mm and a total displacement of 5 mm was used to monitor the depth of penetration of the punch. Typical results are presented in Fig. 5.

Fig. 5
figure 5

Typical indentation test results

Full size image

Examination of the experimental relationships indicates that the curves become practically linear following an initial nonlinear phase, probably caused by surface defects which induce an ill-defined initial contact with the clay surface, as also found in the indentation testing of metals [8, 56].

The slopes \(\Delta P/\Delta h\) of the linear segments of the curves shown in Fig. 5 range between 395 and 485 N/mm, with an average value of 455 N/mm. By assuming, for the moment, that the clay specimen can be considered to represent an elastic half-space, application of Eq. (3) yields \(E = 17.1\,{\text{MPa}}\) for \(P/h = \Delta P/\Delta h = 455\,{\text{N/mm}}\), \(\nu = 0.5\), and \(a = 9.975\,{\text{mm}}\). Such close agreement with the experimentally deduced values of E of 15–20 MPa as found from the uniaxial compression tests (see Fig. 4 and Table 1) is, however, purely coincidental. Indeed, results of FEA computations by Christian and Carrier [12] and Poulos [39] showed that Eq. (3) had to be modified when the thickness of the elastic medium is of limited extent. In such case, Eq. (3) should read

$$h = \frac{{P\left( {1 - \nu^{2} } \right)}}{2aE}I_{\rho }$$
(14)

where \(I_{\rho }\) is a geometrical factor that is function of the ratio of the thickness of the medium to the diameter of the punch. For \(H/2a = 19/19.95 \approx 0.95\), \(I_{\rho }\) equals 0.4 for Christian and Carrier [12], and 0.6 for Poulos [39]. Therefore, if \(I_{\rho }\) is taken equal to an average value of 0.5, the value of Young’s modulus E deduced from Eq. (14) reduces to 8.55 MPa, which is about half of the experimental results obtained from the uniaxial compression tests. Such reduced value of E is undoubtedly related to partial damage induced by penetration of the indenter, as evidenced by the progressive development of hairline radial and concentric cracks on the clay surface, around the perimeter of the indenter. Concerning the determination of the hardness H of the clay, for which there is no additional increase in the applied load during penetration, unfortunately the indentation tests were not pursued to sufficiently large depths. This notwithstanding, if the mean contact pressure of 266 kPa which corresponds to the highest applied load of \(83\,{\text{N}}\) (see Fig. 5), is considered to be equal to the hardness H, then application of Shield’s [42] solution, \(H = 2.845\,\sigma_{y}\), allows to determine the yield stress \(\sigma_{y}\) in the case of Tresca criterion. Thus, \(\sigma_{y} = 93.3\,{\text{kPa}}\) for \(H = p_{m} = 266\,{\text{kPa}}\). Such value of \(\sigma_{y}\) yields an undrained shear strength \(S_{u} = \sigma_{y} /2\) or 46.7 kPa for Tresca, and \(S_{u} = \sigma_{y} /\sqrt 3 = 53.9\,{\text{kPa}}\) for von Mises. However, according to Table 1, a value of \(S_{u} = 46.7\,{\text{kPa}}\) is about 82% of that obtained from the uniaxial compression tests.

Results of finite element analyses

FEA results were obtained for particular values (i.e. h = 0.124, 0.243, 0.349, and 0.57 mm) displacements based upon experimental test results. Figures 6 and 7 present contours of the equivalent von Mises stress \(\sigma\) which is defined as

$$\sigma = \left[ {\frac{{\left( {\sigma_{11} - \sigma_{22} } \right)^{2} + \left( {\sigma_{22} - \sigma_{33} } \right)^{2} + \left( {\sigma_{33} - \sigma_{11} } \right)^{2} + 6\sigma_{12}^{2} + 6\sigma_{23}^{2} + 6\sigma_{31}^{2} }}{2}} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$
(15a)

and in terms of principal stresses \(\sigma_{1}\), \(\sigma_{2}\), \(\sigma_{3}\), this definition can be written in a simpler form

$$\sigma = \left[ {\frac{{\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{1} } \right)^{2} }}{2}} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$
(15b)
Fig. 6
figure 6

Contours of equivalent von Mises stress for h = 0.57 mm

Full size image
Fig. 7
figure 7

Quality of distorted mesh for h = 0.57 mm

Full size image

While Fig. 8 presents contours of the total amount of equivalent plastic strain \(\bar{\varepsilon }^{pl}\) expressed by:

$$\bar{\varepsilon }^{pl} = \left. {\bar{\varepsilon }^{pl} } \right|_{0} + \int\limits_{0}^{t} {\sqrt {\frac{2}{3}\,\dot{\bar{\varepsilon }}^{pl} :\dot{\bar{\varepsilon }}^{pl} } } dt$$
(16)

where \(\left. {\bar{\varepsilon }^{pl} } \right|_{0}\) is the initial equivalent plastic strain which is zero in this present analysis; and \(\dot{\bar{\varepsilon }}^{pl}\) is the equivalent plastic strain rate.

Fig. 8
figure 8

Contours of equivalent plastic strain for h = 0.57 mm

Full size image

Although the results reported in Figs. 6, 7 and 8 indicate that most of the clay did not reach a fully plastic state for depths of indentation less than or equal to 0.57 mm, the yield stress and plastic strain contours of Figs. 7 and 8 respectively nevertheless point out that severe distortions occur immediately below the rounded perimeter of the indenter. The latter figure also shows the progression of the plastic zone toward the axis of symmetry of the clay with increasing depth of penetration.

The relationship between the computed load P versus the depth of indentation h up to a depth of penetration of 0.57 mm is presented in Fig. 9. It shows that the slope \(\Delta P/\Delta h\) is roughly constant, equal to 709.4 N/mm. Then, the adoption of Eq. (14) for the representation of an elastic response results in \(E/I_{\rho } = 26.7\,{\text{MPa}}\) for \(P/h = \Delta P/\Delta h = 709.4\,{\text{N/mm}}\), \(\nu = 0.49\), and \(a = 9.975\,{\text{mm}}\). Because the value of E used in the FEA equals 15 MPa, it follows that \(I_{\rho } = 0.56\), compared to 0.4 for Christian and Carrier [12] and 0.6 for Poulos [39], as mentioned above. In addition, the value of the constraint factor C equals 3.65 on the basis of the spherical cavity approach of Eq. (13), for \(E = 15\,{\text{MPa}}\), \(\nu = 0.49\) and \(\sigma_{y} = 113.4\,{\text{kPa}}\).

Fig. 9
figure 9

Computed load P versus depth of penetration h

Full size image

Furthermore, because the P versus h relationship shown in Fig. 9 shows that the initial “elastic” or linear phase terminates at h = 0.05 mm for P = 35.47 N, the corresponding mean contact pressure \(p_{m}\) is 113.5 kPa (Fig. 10). Thus, the value of the constraint factor \(C = p_{m} /\sigma_{y}\)\(= 1.0008\)\(= 113.5/113.4\) at the start of the non-linear response in the P versus h relationship. This observation indicates that the plastic response begins to play a role when the mean contact pressure \(p_{m} \approx \sigma_{y}\), as also found by Riccardi and Montanari [40], and as pointed out several years ago by Tabor [48] and Johnson [28] on the basis of sharp and spherical indenter test results. It should be noted that Fig. 10 also presents the central and the mean contact pressures.

Fig. 10
figure 10

Computed stresses versus depth of penetration h

Full size image

Contact pressure distribution for the characteristic depths of penetration of 0.124, 0.243, 0.349, and 0.57 mm are presented in Fig. 11. Examination of the curves reported in this figure indicates that the contact pressures which generally increase from the axis of symmetry toward the perimeter of the indenter, reach a maximum value for \(r = 8.2\) to 9.7 mm, and thereafter decrease sharply as the rounded perimeter of the indenter is approached.

Fig. 11
figure 11

Distribution of contact pressures beneath indenter

Full size image

Contact pressures computed along the bottom platen are presented in Fig. 12. All the relationships reported in this figure are characterized by a classical bell-shaped curve.

Fig. 12
figure 12

Distribution of contact pressures along lower boundary

Full size image

Finally, Fig. 13 presents the horizontal contact pressure computed along the external vertical boundary at different vertical nodal elevations. The origin of these elevations is point C in Fig. 3. Examination of all the relationships shows that the contact pressure decreases from the top to the bottom of the medium. In addition, the nodal elevations of the clay specimen along the external vertical boundary remained practically unchanged.

Fig. 13
figure 13

Distribution of horizontal pressures along lateral boundary

Full size image

Discussion

Indentation techniques and associated mathematical or numerical models used for the physical characterization of various materials require experimental validation in order to obtain accurate and precise measurements. In this study two simple mathematical models (i.e., the elastic and the elastic–plastic models) were tested in terms of their accuracy in producing values for strength parameters that could match those obtained from conventional geotechnical tests. To simplify analysis, investigators commonly assume large sample thickness and limit indentation depth to less than 10% of the sample thickness. In this study, the sample thickness being of the same order of magnitude of the diameter of the indenter, it was found necessary to take into account the limited thickness of the clay. Although such approach resulted in a better representation of the deformation mechanism involved, it nevertheless showed that the deduced values of Young’s modulus were much lower than those obtained from unconfined compression tests. The probable cause of the reduction was related to the development of concentric and radial cracks surrounding the indenter during the indentation process.

The numerical model used with the auto-adaptive remeshing technique allowed to simulate a deep penetration process. In the initial elastic phase of the simulation, the constant slope of the P versus h curve allowed to determine the value of geometrical factor \(I_{\rho }\). It was found that \(I_{\rho } = 0.56\) compared to 0.4 for Christian and Carrier [12], and 0.6 for Poulos [39]. It was also observed that while the plastic response started to become significant at a pressure \({{p_{m} } \mathord{\left/ {\vphantom {{p_{m} } {\sigma_{y} }}} \right. \kern-0pt} {\sigma_{y} }} \approx 1\), the maximum load P corresponded to \({{p_{\text{max} } } \mathord{\left/ {\vphantom {{p_{\text{max} } } {\sigma_{y} }}} \right. \kern-0pt} {\sigma_{y} }} = 3.3\). Such values which compare well with those proposed by Johnson [28] are also quite similar to the results reported by Riccardi and Montanari [40].

Conclusion

Considering the tests that employ sharp or spherical punches, the flat-ended cylindrical indentation is characterized by a constant indenter-specimen contact area; thus, elastic moduli and yield stress can be directly deduced from load or pressure-penetration curves.

Concerning the indentation tests, these were not taken to sufficiently high loads for the material to reach a full plasticity condition. This notwithstanding, the tests allowed to determine: (a) a minimum value of 266 kPa for the yield stress which permitted to obtain a Tresca shear strength of 46.7 kPa compared to the average value of 56.7 kPa obtained from the unconfined compression test; and (b) a value of 8.55 MPa for Young’s modulus, compared to an average value of 17.5 MPa, also obtained from the unconfined compression tests. The cause for the reduced value of Young’s modulus is attributed to the development of hairline concentric and radial cracks during the indentation process.

The yield stress \(\sigma_{y}\) was evidenced in the P versus h curve obtained from the finite element analysis. A value of 2.86 was derived for the constraint factor C at maximum load, based upon von Mises criterion, compared to 2.845 for Shield’s Tresca slip-line analysis.