Introduction

Optimization problems can be seen everywhere, for example, the optimization of the water distribution network [36], the optimization strategy of the resource allocation [16], the task assignment [19], and many others [1, 12, 21, 24, 39,40,41, 48, 50, 72]. As a maximum optimization problem can be transferred to a minimum one by multiplying \(-1\), in this paper, only the minimization problems are considered. The mathematical model of a minimization problem can be described in the following:

$$\begin{aligned} \min&f({\mathbf {x}}) \end{aligned}$$
(1)
$$\begin{aligned} \mathrm{s.t.}&{\mathbf {x}} \in \mathfrak {R}^{D}, \end{aligned}$$
(2)

where D is the dimension of the problem, and \(f({\mathbf {x}})\) is the objective of the optimization. Meta-heuristic optimization algorithms, including evolutionary algorithms [11, 14], and swarm optimization algorithms [15, 20, 26, 27, 31, 32, 44, 46, 56] have been paid more and more attention and applied successfully in many optimization problems [23, 27, 43, 52, 70] because of its ease of usage and independence on the characteristics of the optimization problems.

Traditional meta-heuristics have shown excellent abilities for solving lower dimensional optimization problems. However, their performances would deteriorate dramatically when the number of dimensions exceeds 100 [6], called large-scale optimization problems, because of the curse of dimensionality [34, 59]. The search process will then stagnate into a local optimum and, therefore, result in a premature convergence. Thus, it is critical to enhance the diversity of the population so as to improve the exploration capability for tackling the large-scale optimization problems. Some approaches have been proposed for solving problems with large-scale dimensions, which can be divided into two categories: cooperative coevolution (CC) methods and new learning strategies.

  1. 1.

    The cooperative coevolutionary methods adopt the divide-and-conquer strategy, which decomposes the population into a number of subpopulations and solves them independently. Many algorithms based on cooperative coevolutionary frameworks for large-scale optimization problems have been proposed, such as cooperative coevolutionary genetic algorithms [2, 3, 22, 42, 55, 69] cooperative coevolutionary PSO (CCPSO) [30], and cooperative coevolutionary DE (DECC) [29, 37, 51, 64,65,66,67], etc. The methods are efficient when the optimization problems are separable. However, the performance is not so good when the problems are nonseparable. Therefore, different decomposition strategies, such as random dynamic grouping [66], multilevel dynamic grouping [67], and differential grouping [29, 38], have been proposed. Also, it is obvious that the performance of CC algorithms is highly sensitive to the decomposition strategies for different classes of optimization problems.

  2. 2.

    In each meta-heuristic algorithm, the learning strategy plays a significant role to find an optimal solution. Therefore, researchers try to develop different learning strategies for meta-heuristic algorithms so as to enhance the exploration capability of the population, which aims to promote the chances of escaping from local optima [5,6,7,8, 17, 18, 25, 28, 47, 58]. The performance of exploration is improved by keeping the diversity of the population. However, more evaluations on the objective functions are required for the final convergence.

In recent years, the surrogate-assisted evolutionary algorithms, such as SA-COSO [54], SHPSO [68], and MGP-SLPSO [57], have been paid attention for solving computationally expensive high-dimensional problems (generally not more than 100 dimensions). However, not so many methods have been proposed for solving computationally expensive large-scale optimization problems. Ivanoe De Falco et al. [9, 10] decomposed the large-scale optimization problems into some lower-dimensional sub-problems and optimized using the surrogate-assisted optimization algorithms and parallel computing techniques. Sun et al. [53] proposed to solve large-scale optimization problems by a modified PSO algorithm assisted by the fitness estimation strategy. Generally, the number of exact fitness evaluation in the surrogate-assisted evolutionary algorithms for solving a computationally expensive problem is very limited, which will not be considered in this paper. That is, only the large-scale optimization problems with cheap fitness evaluation are considered to be solved in this paper, in which a large number of fitness evaluations are allowed.

To balance between the exploration and exploitation in solving large-scale optimization problems, in this paper, we propose a multiple strategy learning particle swarm optimization (MSL-PSO) method, in which two steps with different learning strategies are proposed to generate a new population. At the first step, the current population will be sorted from the worst to the best based on the fitness values, and each individual will probe different positions by learning from its demonstrators and the mean position of the current population. The best position probed by each individual will be kept and compose a temporary population, which will also be sorted from the worst to the best based on their fitness values. Each individual will update its position by learning demonstrators from different sub-sets of the temporary population, which is used to balance the convergence and diversity. Similar to those learning strategies that have been proposed, such as SL-PSO [6], CSO [5], and DEGLSO [63], etc., our MSL-PSO method also focuses on the learning strategy that concerns the trade-off between the convergence and diversity of the population.

The remainder of this paper is organized as follows. The section “Related work” gives a brief introduction on the canonical particle swarm optimization (PSO) algorithm and the methods for solving the large-scale optimization problems. Our proposed MSL-PSO algorithm is described in detail in the section “The proposed algorithm”. In the section “Experimental studies”, experiments are conducted to verify the effectiveness and efficiency of MSL-PSO by comparison with ten state-of-the-art algorithms. Finally, the conclusion of this paper is given in the section “Conclusion”.

Related work

Particle swarm optimization

The particle swarm optimization (PSO), which simulates the bird flocking or fish schooling, was proposed by Kennedy and Eberhart [13], is one of the swarm optimization algorithms. In PSO, each individual has its own velocity and position, which will be updated using the following equations:

$$\begin{aligned} v_{id}(t+1)= & {} \omega v_{id}(t) + c_1 r_1 (p_{id}(t)\nonumber \\&-x_{id}(t)) + c_2 r_2 (g_{d}(t)-x_{id}(t)) \end{aligned}$$
(3)
$$\begin{aligned} x_{id}(t+1)= & {} x_{id}(t)+v_{id}(t+1), \end{aligned}$$
(4)

where \({\mathbf {v}}_i(t) = (v_{i1}(t), v_{i2}(t), \ldots , v_{iD}(t))\) and \({\mathbf {x}}_i(t) = (x_{i1}(t), x_{i2}(t), \ldots , x_{iD}(t))\) represent the velocity and position of individual i at tth generation, respectively. \({\mathbf {p}}_{i}(t) = (p_{i1}(t), p_{i2}(t), \ldots , p_{iD}(t))\) and \({\mathbf {g}}(t) = (g_1(t), g_2(t), \ldots , g_D(t))\) are the best historical position of individual i and the swarm, respectively. w is called the inertia weight, \(c_1\) and \(c_2\) are two cognitive parameters, and \(r_1\) and \(r_2\) are two random number generated uniformly in the range of [0, 1]. The PSO algorithm has been shown better convergence performance; however, it is not good for solving large-scale optimization problems [6]. Therefore, different PSO variants, such as CSO [5], SL-PSO [6], LLSO [61] and DEGLSO [63], have been proposed, in which different learning strategies were utilized in the swarm optimization algorithms to improve the diversity of PSO so as to enhance the exploration capability.

Optimization of the large-scale problems

Generality, the meta-heuristic algorithms proposed for solving large-scale optimization problems can be classified into two categories. One is the cooperative coevolutionary meta-heuristic algorithms, and the other is the meta-heuristic methods with efficient learning strategies.

Cooperative coevolutionary algorithms

The cooperative coevolution (CC) mechanism divides the large-scale problem into a number of small subproblems, and then optimize them separately using the canonical meta-heuristics. Generally, there are also two categories of CC evolutionary algorithms according to the decomposition strategies: the static and dynamic decomposition strategies. The static decomposition strategy first detects the correlationship between variables and then decompose them in a fixed way before the optimization. For example, Omidvar et al. [37] proposed a differential grouping (DG) strategy, in which the problem is separated into a number of small subproblems. Mei et al. [33] extended the DG method to identify the independent subproblems to be optimized by a covariance matrix adaptation evolution strategy. Different to the static decomposition strategy, the variables are decomposed to different subproblems at different generations, which can be further classified into random-based decomposition and learning-based decomposition. Li et al. [29] proposed CCPSO2 for large-scale optimization problems, in which the random grouping was adopted to decompose the variables into subcomponents dynamically. However, the performance will be deteriorated when the problem is nonseparable. Ray and Yao [45] proposed an adaptive variable partitioning based on the correlation, which was utilized in the cooperative coevolutionary algorithms to deal with nonseparable problems.

The decomposition strategy plays significant importance in the cooperative coevolutionary algorithms. Poor decomposition will deteriorate the performance the algorithms, and also, it will be inefficient when all variances of the problem are correlated to each other.

New learning strategies for meta-heuristic algorithms

Different to the cooperative coevolutionary algorithms, some learning strategies are proposed to be put into the meta-heuristic algorithms to improve the diversity of the population, and thus enhance the exploration capability of the algorithms. In our method, we focus on studying a new learning strategy for PSO to find a global optimal solution for the large-scale optimization problems. Therefore, only PSO variants for large-scale optimization were reviewed in this section. Cheng and Jin [5] proposed a competitive swarm optimizer (CSO) algorithm, in which a random competition strategy was utilized and any individual with a better fitness value in a pair will be the winner. Instead of learning from the personal best position of the individual and of the swarm, in CSO, the loser in the pair will learn from its winner. Inspired by CSO, Yang et al. [62] proposed a segment-based predominant learning swarm optimizer (SPLSO), in which the dimension will be divided into a number of segments and variables in different segments will be evolved by learning from different exemplars. The social learning PSO [6] was also proposed by Cheng and Jin, in which the population will be sorted according to the fitness and each individual will learn from its demonstrators [4] who have better fitness values than this individual. Later, Yang et al. [61] separated the population into a number of levels based on the fitness values, and each individual will learn from particles in two higher layers.

The proposed algorithm

The trade-off between the convergence and diversity of the population is crucial for meta-heuristic algorithms to solve large-scale optimization problems, because the search space will increase exponentially when the dimension of the problem increases [62], which will put significant challenges to find the global optimal solution. PSO has been shown to be implemented easily and has quick convergence capability. However, the diversity of the population will be lost quickly after some generations because of the quick convergence of the algorithm. Therefore, the PSO algorithm is not efficient to solve large-scale optimization problems. Some PSO variants, such as CSO [5], SL-PSO [6], SPLSO [62], and LLSO [61], have put forward different learning strategies to improve the diversity of the population to solve large-scale optimization problems. In this paper, we propose a multi-strategy learning particle swarm optimization (MSL-PSO) method, in which the idea of social learning proposed in [6] is adopted to update the position of each individual in the population. However, different to the SL-PSO algorithm, two stages with different learning strategies are used to generate a new population. In the first stage, each individual will probe some positions by learning from its demonstrators who have better fitness values than this individual and the mean position of the population. The best probed position, which has the minimal fitness value among all of its probed positions, will be kept. All the best probed positions at current generation will compose a temporary population, which will be sorted from worst to best on the fitness values. Then, in the second stage, a new strategy, which is used to balance the diversity and convergence, will be used to update the velocity and position of each individual. In the following, we will give a detailed description of the proposed method.

The overall framework of MSL-PSO

Algorithm 1 gives a pseudocode of the MSL-PSO algorithm. A population Pop will be initialized, and the fitness of each individual in Pop will be evaluated. While the stopping criteria is not met, the following process will be repeated: all individuals will be sorted on the fitness values in a descending order. Each individual will probe \(K_{\max }\) positions by learning from its demonstrators and the mean position of the current population. The best probed position, which has the minimum fitness value among \(K_{\max }\) positions, will be kept for each individual (lines 6–7). All of these best probed positions will compose a temporary population NPop. Then, individuals in the NPop will also be sorted on their fitness values in a descending order. Afterwards, each individual i will find two sub-sets of NPop, one is composed of all individuals whose rank in NPop is between the rank of individual i in the sorted NPop and that of individual i in the sorted Pop, and the other is composed of all individuals whose rank is larger than that of individual i in the sorted NPop, for selecting demonstrators to update its velocity using the strategy proposed in our method (line 11). At each generation, an individual will explore \(K_{\max }+1\) different positions by the two learning criteria, and all of these \(K_{\max }+1\) positions will be evaluated using the objective function. Therefore, there will be \(K_{\max }+1\) fitness evaluations for each solution at each generation, and the total number of fitness evaluations will be \((K_{\max }+1)*\mathrm{NP}\), where NP is the size of current population.

figure a

Position probing

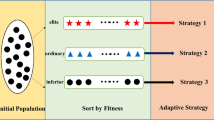
Algorithm 2 gives the detail on how an individual probes different positions by social learning technique proposed in [6]. Similar to SL-PSO [6], all individuals in the current population will be sorted in a descending order based on the fitness value, which is shown in Fig. 1. Suppose that the rank of individual i is j, and then, individuals that have larger rank than j are all demonstrators of individual i.

Fig. 1
figure 1

Population sorting

Full size image

For each individual i, \(K_{\max }\) positions will be probed using Eqs. (5) and (6) by learning from the demonstrators to improve the exploration capability of the population:

$$\begin{aligned} vv^{k}_{id}= & {} r^{k}_{1} * v_{id}(t) + r^{k}_{2} * (x_{jd}(t) - x_{id}(t)) \nonumber \\&+ \phi * r^{k}_{3} * ({\bar{x}}_d(t) - x_{id}(t)) \end{aligned}$$
(5)
$$\begin{aligned} xx^{k}_{id}= & {} x_{id}(t)+vv^{k}_{id}, \end{aligned}$$
(6)

where \(k=1,2,\ldots ,K_{\max }\); \(K_{\max }\) is the maximum number of probation for each individual. \(\mathbf {vv}^{k}_i=(vv^{k}_{i1},vv^{k}_{i2},\ldots ,vv^{k}_{iD})\) and \(\mathbf {xx}_i^{k}=(xx^{k}_{i1},xx^{k}_{i2},\ldots ,xx^{k}_{iD})\) represent the velocity and position that individual i learns from its demonstrators at kth time, respectively. \({\mathbf {v}}_i(t)=(v_{i1},v_{i2},\ldots ,v_{iD})\) and \({\mathbf {x}}_i(t)=(x_{i1},x_{i2},\ldots ,x_{iD})\) are the velocity and position of individual i at generation t, respectively. \(\bar{{\mathbf {x}}}(t)=\frac{1}{\mathrm{NP}}\sum _{i=1}^{\mathrm{NP}}{\mathbf {x}}_i\) is the mean position of the population at generation t. \(r^{k}_{1}\), \(r^{k}_2\), and \(r^{k}_3\) are random numbers uniformly generated in the range of [0, 1] at kth time. \(\phi \) is a constant called the social learning probability which is used to define the degree to learn from the mean position of the population. Note that the \(K_{\max }\) positions have little probability to be same, because the individual will choose different demonstrators to learn on each dimension. It can be easily imaged that more positions are probed by learning from demonstrators, more chances it will have to find a better solution at each generation. However, the computational resources will be quickly exhausted, because too many fitness evaluations will be consumed at each generation, which, in turn, will impede the population to explore the search space and, correspondingly, will not be able to find a good optimal solution. On the other hand, the less positions are probed, the less probability it has to find a better solution at each generation. The best probed position with the minimum fitness value among \(K_{\max }\) solutions will be kept and denoted as \(\mathbf {xc}\) (line 9 in Algorithm 2), and its corresponding velocity is denoted as \(\mathbf {vc}\).

figure b

Position updating

The convergence and diversity are two key factors in finding the global optimal solutions for large-scale optimization problems. A good performance on the diversity can improve the exploration capability, while a good performance on the convergence can speed up locating at the optimal position. Therefore, in the second stage of MSL-PSO, we propose a new strategy, in which the demonstrators of each individual are selected from two sub-sets of NPop, which is composed of all best probed positions, i.e., \(\mathrm{NPop} = \{\mathbf {xc}_1, \mathbf {xc}_2, \ldots , \mathbf {xc}_{\mathrm{NP}}\}\), to update the velocity of each individual in the population Pop. Equations (7) and (8) show how to update the velocity and position of each individual in the stage of position updating for each individual:

$$\begin{aligned} v_{id}(t+1)= & {} r_1 * vc_{id} + r_2 * (xc_{jd} - xc_{id}(t)) \nonumber \\&+\phi * r_3 * (xc_{kd} - xc_{id}(t)) \end{aligned}$$
(7)
$$\begin{aligned} x_{id}(t+1)= & {} xc_{id} + v_{id}(t+1). \end{aligned}$$
(8)

In Eqs. (7) and (8), \(\mathbf {vc}_i = (vc_{i1}, vc_{i2}, \ldots , vc_{iD})\) and \(\mathbf {xc}_i = (xc_{i1}, xc_{i2}, \ldots , xc_{iD})\) are the velocity and position, respectively, of the best probed position for individual i. j and k represent the two demonstrators in NPop for individual i to learn on dimension d. \(\phi \) is the social learning probability which has the same meaning to that in Eq. (5).

Figure 2 gives a simple example to show how to select two demonstrators in the second stage. In Fig. 2, \(\mathrm{demonstrator}\_1\) and \(\mathrm{demonstrator}\_2\) represent two sub-sets for individual i to choose demonstrators to learn, respectively. For each individual i, we have its rank in Pop and rank in NPop. When the rank of the best probed position of individual i in the NPop is worse than the rank of the individual i in the Pop, it means that it falls behind more other individuals in the NPop compared to it does in the Pop. For example in Fig. 2a, the rank of \(\mathbf {xc}_i\) in NPop is k, and the rank of \({\mathbf {x}}_i(t)\) in Pop is j, \(k<j\), then the demonstrators between k and j will be used to guide the individual to exploit a better solution. Conversely, when the rank of the best probed position of an individual i in NPop is better than that of the individual i in Pop, it means that the best probed position has a better performance among NPop than the individual i in Pop. To prevent premature convergence, we also learn from some losers of the best probe solution. Seen from Fig. 2b, we can see that \(j<k\), and the losers between j and k will be selected as one of the demonstrators. The other demonstrator is selected from the sub-set \(\mathrm{demonstrator}\_2\) which is composed of all individuals that have better fitness than the best probed position.

Fig. 2
figure 2

A simple example to show the method in the second stage

Full size image
Table 1 Summary of the CEC2008 benchmark functions
Full size table
Table 2 Summary of the CEC2010 benchmark functions
Full size table

Algorithm 3 gives the pseudocode of the position updating. Each individual i will update its velocity and position according to Eqs. ( 7) and (8), respectively. The global best position gbest will be updated if a new position is better than it.

figure c

Experimental studies

Experimental setup and benchmark functions

To verify the performance of MSL-PSO, a series of experiments are conducted on CEC2008 and CEC2010 large-scale benchmark problems. The main characteristics of these two function sets are summarized in Tables 1 and  2.

The parameter settings of MSL-PSO are given in the following: the population size NP is set to 100 if the dimension is not larger than 100, and otherwise, NP\( = M + \lfloor (D/10) \rfloor \), where \(M=100\) and D is the dimension of the problem. The social learning probability \(\phi \) is set to \(D/M*0.01\). The number of dimensionality D is set to 100, 500, and 1000 for CEC2008 test problems and 1000 for CEC2010 benchmark problems, respectively. The algorithm will be run 20 times independently on each problem. The stopping criteria are that the maximum number of function evaluation reaches \(3000 * D\). Generally, more candidate positions provided, more chances to find a better optimal solution. However, the number of fitness evaluation will be consumed much quicker if more candidate positions are considered. On the contrary, less positions are probed, less probability it has to find a better solution at each generation. To see which value is best for assisting the proposed method to obtain good optimal solutions, we compare the mean optimal solutions of the 1000-dimensional CEC2010 F9 problem obtained by the proposed method using different maximum number of candidate positions. Figure 3 gives the mean results of 20 independent runs with 1, 2, 3, and 4 positions probed by each individual at each generation, respectively. From Fig. 3, we can see that the performance of MSL-PSO is best when the maximum number of probed position is set to 3. Therefore, in our experiments, only three positions are probed for each individual by learning from its demonstrators, i.e., \(K_{\max } = 3\).

Fig. 3
figure 3

The experimental results on the 1000-dimensional CEC2010 F9 problem obtained by the proposed method with different maximum number of candidate positions

Full size image

Comparisons to the MSL-PSO variants

From the detailed description of MSL-PSO, we can see that there are two stages to generate a new position for each individual. To see the performance of our proposed method, we first compare the results obtained on F6 and F9, which are multi-model and uni-model, respectively, with two MSL-PSO variants, in which one variant uses the first stage of MSL-PSO only (denoted as mSL-PSO) and the other one replaces the strategy used in the second stage with the strategy proposed in SL-PSO (denoted as SL-PSOs). Table 3 gives the statistical results of these algorithms on CEC2010 F6 and F9 benchmark problems with 1000 dimensions. Each algorithm is run independently for 20 times on each test problem, and the Wilcoxon rank sum test with a significance level of 0.05 is applied to assess whether the performance of a solution obtained by one of the two compared algorithms is expected to be better than the other [60]. In Table 3, ‘\(+\)’,‘\(\approx \)’, and ‘−’ represent that MSL-PSO is significantly better, equivalent to, and worse than the compared algorithms, respectively, according to the Wilcoxon rank sum test on the mean fitness values. The best mean optimal solution on each benchmark problem is highlighted with an underline. From Table 3, we can see that our proposed MSL-PSO can obtain better results than mSL-PSO and SL-PSOs on both of these problems, which showed that the method using two stages is effective to solve large-scale optimization problems.

Table 3 Comparisons on the mean values and standard deviation between MSL-PSO and its variants on CEC2010 F6 and F9 test problems with 1000 dimensions (\(D=1000\))
Full size table
Table 4 Comparisons of the mean value and standard deviation between MSL-PSO and other algorithms on CEC2008 test problems with 100 dimensions (\(D=100\))
Full size table
Table 5 Comparisons of the mean value and standard deviation between MSL-PSO and other algorithms on CEC2008 test problems with 500 dimensions (\(D=500\))
Full size table
Table 6 Comparisons of the mean value and standard deviation between MSL-PSO and other algorithms on CEC2008 test problems with 1000 dimensions (\(D=1000\))
Full size table
Fig. 4
figure 4

Comparison on CEC 2008

Full size image
Fig. 5
figure 5

Comparison on CEC 2010

Full size image
Fig. 6
figure 6

Convergence tendency on F7 problem

Full size image
Fig. 7
figure 7

Convergence tendency on F8 problem

Full size image
Table 7 Comparisons of the mean value and standard deviation between MSL-PSO and other algorithms on CEC2010 test problems with 1000 dimensions (\(D=1000\))
Full size table

Comparisons to other state-of-the-art algorithms

In our experimental analysis, we further compare the results of MSL-PSO with ten state-of-the-art algorithms, which are shown in the following, to verify the performance of our proposed MSL-PSO algorithm. The best mean optimal solution on each benchmark problem is highlighted with an underline. Note that except the result of CSO, SL-PSO, and CCPSO2, all other results of the comparison algorithms are copied from their corresponding paper.

  1. 1.

    DECC-G [66]: Instead of using a static grouping, the optimization problem is randomly decomposed into k subproblems in the decision space, and then co-evolute to find the global optimal solution.

  2. 2.

    MLCC [67]: The decomposer is selected by a self-adapted mechanism based on the historic performance at the start of each cycle.

  3. 3.

    DECC-DG [29]: A differential grouping is utilized to uncover the underlying interaction structure of the decision variables, and then, a number of subproblems are formed.

  4. 4.

    CSO [5]: A new competitive learning strategy for PSO was proposed to solve the problems with large-scale dimensions, in which every two individuals will be compared on the performance, and the loser will learn from the winner and the winner be kept to next generation.

  5. 5.

    SL-PSO [6]: A new learning technique was proposed to solve large-scale optimization problems, in which the population is sorted in descending order, and each individual learns from its demonstrators who have better fitness values than this individual.

  6. 6.

    CCPSO2 [30]: It is a PSO variant based CC, in which the decision variables are randomly grouped, the size of which is also randomly generated.

  7. 7.

    sep-CMA-ES [47]: A simple covariance matrix adaptation evolution strategy variant proposed for large-scale optimization problems, in which the internal time is reduced and the space complexity is simplified from quadratic to linear.

  8. 8.

    EPUS-PSO [49]: A PSO variant is adopted to optimize the initial parameters of the Reservoir Computing. The results of EPUS-PSO are better than those obtained by an exhaustive search for global parameters generation of Reservoir Computing.

  9. 9.

    DMS-L-PSO [71]: The multi-swarm learning strategy is raised in DMS-L-PSO, and the sub-swarms will be re-grouped to exchange information among all the individuals.

  10. 10.

    MA-SW-Chains [35]: Each individual is assigned to local search intensity based on its features, and then, different local searches are chained.

Tables 4, 5, and 6 give the statistical results on CEC2008 test problems with 100, 500, and 1000 dimensions, respectively, and Fig. 4 is a bar-graph to show the number of CEC 2008 test problems with 100, 500, and 1000 dimensions that our proposed MSL-PSO obtained better, equal, and worse mean optimal results than each comparison algorithm. In Fig. 4, the region in red, red, and earth yellow represent the number of problems that MSL-PSO wins, loses, and draw with each comparison algorithm, respectively. From Tables 4, 5 and 6 and Fig. 4, we can see that MSL-PSO outperforms the other six excellent algorithms on most problems. To be specific, MSL-PSO obtains better results on 15/21 problems than SL-PSO, CCPSO2, MLCC, sep-CMA-ES, and EPUS-PSO. Specially, the mean optimal solutions found by MSL-PSO are all better than EPUS-PSO. Note that the results of DMS-L-PSO come from [71], in which the maximum number of fitness evaluation on CEC2008 is \(5000 * D\). Compared to DMS-L-PSO, we can easily find that our MSL-PSO algorithm obtained better results than DMS-L-PSO on all seven benchmark problems except F1 and F6 with 100, 500, and 1000 dimensions, respectively, even the number of fitness evaluations of DMS-L-PSO is much more than SML-PSO. From Tables 4, 5, and 6, we can see that the results of SML-PSO is not better than, but almost same to, those of DMS-L-PSO on F1 and F6, which, we think, is because a local search is utilized in the latter, so that the precise of the results can be improved. SML-PSO is better than the other compared algorithms on solving unimodal problems, i.e., F2, in CEC2008 test suite. Also, MSL-PSO gets better results on F7 than other algorithms. MSL-PSO algorithm failed to obtain better results than sep-CMA-ES and MLCC on F3 and F4, respectively; however, the result of MSL-PSO is still better than the other four compared algorithms.

Table 7 lists the results obtained by six state-of-the-art algorithms and our proposed MSL-PSO on 20 CEC2010 problems with 1000 dimensions, and Fig. 5 gives the bargraph to show the number of CEC 2010 benchmark problems with 1000 dimensions that our MSL-PSO wins, loses, and draws with each comparison algorithm. Among the 20 test instances, MSL-PSO obtained 11 best mean optimal results among all of these algorithms. Compared to CCPSO2, DECCDG, and DECC-G, which utilize the cooperative coevolutionary strategies, we can see that the proposed MSL-PSO got only four worse results than both CCPSO2 and DECCDG, and only obtain one worse mean result than DECC-G. The results compared to SL-PSO and CSO, both of which are PSO variants, show that MSL-PSO can get 18/20 and 19/20 better mean optimal solutions than both of these algorithms, which shows that our proposed learning strategy is efficient to solve the large-scale optimization problems.

For further observations, Fig. 6 and Fig. 7 plot the convergence tendency of MSL-PSO, SL-PSO, CCPSO2, CSO, and MA-SW-Chains on CEC2010 F7 and F8 problems, respectively, in which F7 is unimodal function and F8 is multimodel one. From Figs. 6 and 7, we can see that the MSL-PSO can converge much quicker than others, especially on unimodal F7. From Table 7, we can also find that MSL-PSO obtained worse results on the unimodal functions F2, F17, and F19, which, we analyze, is because all of these three problems are separable. Therefore, the cooperative coevolutionary algorithms are much suitable for solving this kind of problems.

Conclusion

A multiple-strategy learning particle swarm optimization was proposed for solving large-scale optimization problems. Some positions are probed for each individual by learning its demonstrators and the mean position of the population at first. And then, each individual updates its velocity and position by learning two demonstrators coming from different sub-sets, which is expected to balance the diversity and convergence. Experimental results show that MSL-PSO has a better performance on solving large-scale optimization problems proposed in CEC2008 and CEC2010. However, for the separable problems, its performance is not better than cooperative coevolutionary algorithms, so in the future, we will try to introduce the grouping approaches used in CC algorithms into our proposed MSL-PSO to get much better performance on solving this kind of problems.