1 Introduction

It is a common phenomenon in nature and technology that a system under noise perturbations exits a regime of its usual dynamics [1,2,3,4,5,6]. Often it is possible to define a potential function, or nonequilibrium potential [7, 8], whereby a potential well can be associated with a usual or persistent dynamics, and a saddle of the potential adjacent to the potential well is a feature through which the noise-driven exit takes place [9]. One of the two most important conditions for the possibility of defining a potential appears to be a time-scale separation in the deterministic dissipative dynamics, when the fast processes can be modeled as noise. This is a very common modeling approach in the climate sciences, known as stochastic parametrization; see [10] for a technical reference which also details many caveats. In another scenario, fast perturbations to a system may be truly exogenous. The other condition is that we are in the weak-noise limit [11], when the nonequilibrium potential turns out to be analogous with the classical mechanical action (for which reason it is also called the Freidlin-Wentzell action). The action is a solution of a Hamilton-Jacobi equation, which equation arises from a series expansion of the Fokker-Planck equation with respect to the noise strength, and is associated with the leading-order terms. The potential difference between the bottom of the potential well and the saddle is often termed a potential barrier. The expected exit time then depends on the height of this potential barrier and the (small) noise strength (as expressed by Eq. (4) in Sect. 2). Therefore, knowing the potential barrier height is often of strong interest, because then one can predict—for a given or applied noise strength—the expected escape time.

We develop an algorithm to determine the potential barrier height experimentally, provided that we have control over the noise strength. We are concerned with the situation when the experiment or numerical simulation requires large resources of time or computational power, respectively, and wish to find a protocol that provides the best estimate in a given amount of time. We encountered such a situation when wanted to determine expected transition times to the cold climate for the noisy version of a climate model; see Fig. 2 of [12].

We can envisage another application scenario as follows. Consider that there is a bistability in a deterministically parametrized version of an Earth System Model (ESM), say, a desert-forest bistability, and in a stochastically parametrized version rare transitions can occur, i.e., the system becomes transitive. The key is that one can control the noise strength associated with the stochastic parametrization of the model, and, so, one can apply stronger than realistic noise. Although it is crucial that we remain in the said weak-noise limit. Thereby one can generate transitions more frequently, such that it can become feasible even in an expensive-to-simulate ESM to determine the potential barrier height using the proposed algorithm. Subsequently, it will be just a back-on-the-envelope calculation to estimate the mean transition/exit time for realistic, much smaller, noise strengths.

When the noise strength cannot be controlled, one can apply the adaptive multilevel splitting algorithm [13] in order to determine the mean exit time. In this case there is, of course, no limitation imposed on the noise strength.

Next, in Sect. 2, we detail the derivation of the optimal noise strength for the algorithm, and also detail the iterative procedure to estimate the potential difference. Then, in Sect. 3 we provide a numerical proof-of-concept via applying the algorithm to two example systems. Finally, in Sect. 4, expanding on the above, we provide some remarks on the application and scope of the algorithm.

2 The Efficient Algorithm

First we recap the main results of the large deviation theory of noise-perturbed dynamical systems, including the exponential scaling law of mean exit times, Eq. (4), which is a key ingredient of our algorithm. A precursor to this is Kramers’ seminal work [14] on the ‘escape rate’Footnote 1 of a particle from a “deep” (1D) potential well over a barrier, a concise presentation of which can be found in Sect. 5.10.1 of [9]. We consider the rather generic situation when the dynamics is governed by the following Langevin stochastic differential equation (SDE):

$$\begin{aligned} \dot{\mathbf {x}} = \mathbf {F}(\mathbf {x}) + \sigma \mathbf {D}\varvec{\xi }(t), \end{aligned}$$
(1)

\(\mathbf {x},\mathbf {F},\varvec{\xi }\in \mathbb {R}^n\), and the diffusion matrix \(\mathbf {D}\in \mathbb {R}^{n\times n}\) is independent of \(\mathbf {x}\), i.e., the white noise \(\varvec{\xi }\) is additive. A lack of time-scale separation between resolved (\(\mathbf {x}\)) and unresolved variables in the context of stochastic parametrization leads to a memory effect, something that is not included in Eq. (1) [16]; however, this form can be recovered already by a moderate time scale separation [17]. The vector field \(\mathbf {F}(\mathbf {x})\) is such that it gives rise, under the deterministic dynamics, \(\sigma =0\), to the coexistence of multiple attractors (including the possibility of an attractor at infinity) and at least one nonattracting invariant set, often called a saddle set. The saddle set is embedded in the boundary of some basins of attraction. Based on a well-established theory due to Freidlin and Wentzell [18], and its extension [19, 20], the steady state probability distribution in the weak-noise limit, \(\sigma \ll 1\), can be written as

$$\begin{aligned} W(\mathbf {x}) \sim Z(\mathbf {x})\exp (-2\Phi (\mathbf {x})/\sigma ^2), \end{aligned}$$
(2)

in which \(\Phi (\mathbf {x})\) is called the nonequilibrium- or quasi-potential. In gradient systems where \(\mathbf {F}(\mathbf {x})=-\nabla V(\mathbf {x})\) we have that \(\Phi (\mathbf {x})=V(\mathbf {x})\), provided that \(\mathbf {D}=\mathbf {I}\). If \(\mathbf {D}\) does depend on \(\mathbf {x}\), then \(W(\mathbf {x})\) might not satisfy a large deviation law \(\lim _{\sigma \rightarrow 0}\sigma ^2\ln W(\mathbf {x})=-2\Phi (\mathbf {x})\). See e.g. [21] for an example of multiplicative noise where \(\lim _{\sigma \rightarrow 0}\sigma ^2\ln W(\mathbf {x}=x)\) does not exists for some parameter setting and W(x) has a fat tail.

The probability that a noise-perturbed trajectory does not escape the basin of attraction over a time span of \(t_t\) decays exponentially:

$$\begin{aligned} P(t_t) \sim \frac{1}{\tau }\exp (-t_t/\tau ). \end{aligned}$$
(3)

The approximation is in fact quite good already for times \(t_t\approx {{\,\mathrm{\text {E}}\,}}[t_t]=\tau \) or even smaller. The reciprocal of the expectation value \(\tau \) can be written as an integral of the probability current through the basin boundary, whose leading component as \(\sigma \rightarrow 0\) comes from a point \(\mathbf {x}_e\) where \(\Phi (\mathbf {x})\) is minimal on the boundary. It is, of course, the global minimum when multiple local minima, corresponding to multiple invariant saddle sets embedded in the basin boundary, are present. The proportionality of the probability current to \(W(\mathbf {x})\) leads [8, 11, 15, 22] to:

$$\begin{aligned} \tau \propto \exp (2\Delta \Phi /\sigma ^2), \end{aligned}$$
(4)

where

$$\begin{aligned} \Delta \Phi =\Phi (\mathbf {x}_e)-\Phi (A) \end{aligned}$$
(5)

is what we call the potential barrier height. Both the saddle and the attractor can be chaotic, in which cases \(\Phi (\mathbf {x}_e)\) and \(\Phi (A)\) have been shown [19, 20] to be constant over the saddle [19] and attractor [20], respectively.

Considering (4), the expected transition times increase “explosively” as the noise strength \(\sigma \) decreases. From the point of view of estimating \(\Delta \Phi \), say, in a setting of linear regression with \(\ln \tau \) as the dependent-and \(2\sigma ^{-2}\) as the independent variable, there seems to be a trade-off between an improving accuracy of the estimation and an increasing demand of resources as the range of the independent variable is expanded towards smaller values of \(\sigma \). Accordingly, if we fix the amount of resources that we are willing to commit, an improvement of accuracy is not guaranteed, because we can register fewer transitions with smaller values of \(\sigma \) on average. On the other hand, aiming for boosting the sample number by restricting \(\sigma \) to larger values might not improve accuracy either for the reason that Eq. (7) will illuminate below. We assume that for some \(\sigma _a\) we can estimate \(\tau =\tau _a\) arbitrarily accurately because a large number of transitions can be achieved relatively inexpensively. We also assume that in this “anchor point” (4) applies accurately:

$$\begin{aligned} \tau \approx \tau _a\exp \big (2\Delta \Phi (\sigma ^{-2} - \sigma _a^{-2})\big ), \quad \sigma <\sigma _a. \end{aligned}$$
(6)

We note in passing that in gradient systems the prefactor \(\tau _a\exp (-2\Delta \Phi \sigma _a^{-2})\) in the above is given by the Eyring-Kramers formula [23]; see a generalisation of that for irreversible diffusion processes in [24], where it is assumed, however, that the saddle is a fixed-point. Subsequently, as a departure from the regression-type estimation framework, we will identify the accuracy of estimation by

$$\begin{aligned} \delta \Delta \Phi = \frac{\sqrt{{{\,\mathrm{\text {Var}}\,}}[\ln \bar{t}_t]}}{y}, \end{aligned}$$
(7)

where we introduced \(y=\sigma ^{-2} - \sigma _a^{-2}\), and \(\bar{t}_t=\frac{1}{N}\sum _{i=1}^Nt_t\) is our finite-N estimate of \(\tau \) for a fixed \(\sigma \). Now we can see that as \(\sigma \rightarrow \sigma _a\), the inaccuracy explodes. That is, in the present specific setting of estimation there should exist an optimal value \(\sigma ^*\) of \(\sigma \). This is what we determine next.

The sum of the exponentially distributed random variables, \(N\bar{t}_t\), does in fact follow an Erlang distribution [25], and so:

$$\begin{aligned} P(\bar{t}_t) \sim \frac{1}{\tau ^N}\frac{(N\bar{t}_t)^{N-1}}{(N-1)!}\exp (-N\bar{t}_t/\tau )N. \end{aligned}$$
(8)

Note that since \({{\,\mathrm{\text {E}}\,}}[\bar{t}_t]={{\,\mathrm{\text {E}}\,}}[t_t]=\tau \), our estimator \(\bar{t}_t\) is unbiased. Furthermore, \({{\,\mathrm{\text {Var}}\,}}[\bar{t}_t]={{\,\mathrm{\text {Var}}\,}}[t_t]/N=\tau ^2/N\) in accordance with the Central Limit Theorem. It can be shown that (8) implies that

$$\begin{aligned} {{\,\mathrm{\text {Var}}\,}}[\ln \bar{t}_t] = \Psi ^{(1)}(N), \end{aligned}$$
(9)

where \(\Psi ^{(1)}(N)\) is the first derivative of the digamma function [26]. We can make the interesting observation that \({{\,\mathrm{\text {Var}}\,}}[\ln \bar{t}_t]\) does not depend on \(\tau \), only on N. Next, we make use of the approximation [26]

$$\begin{aligned} \Psi ^{(1)}(N) \sim 1/N \end{aligned}$$
(10)

and, upon substitution in (7), write that

$$\begin{aligned} \delta \Delta \Phi \sim \sqrt{\frac{\tau _a}{T}}\frac{\exp (\Delta \Phi y)}{y}, \end{aligned}$$
(11)

where, furthermore, we assumed a certain fixed commitment of resources, which can be expressed simply by \(T=N\tau \), and also made use of (6). We look for a \(\sigma =\sigma ^*\) or \(y=y^*\) that minimizes \(\delta \Delta \Phi \), for which we need to solve \({{\,\mathrm{\text {d}}\,}}\delta \Delta \Phi /{{\,\mathrm{\text {d}}\,}}y=0\). This yields our main result:

$$\begin{aligned} y^*=\Delta \Phi ^{-1}. \end{aligned}$$
(12)

We can make the interesting observation that it is independent of \(\tau _a\) and T, which we comment on shortly. Rather, \(y^*\) depends only on \(\Delta \Phi \) (in a very simple way), the unknown that we wanted to determine in the first place, and, so, the result may seem irrelevant to practice for the first sight. However, one can simply start out with an initial guess value, \(\hat{\Delta \Phi }_0\), and iteratively update the estimate as \(\hat{\Delta \Phi }_{i}\) by performing a maximum likelihood estimation (MLE) [27] each time a new value of \(t_{t,i}\) is acquired. This way, for the acquisition of \(t_{t,i+1}\), one continues the experiment/simulation with an updated noise strength \(y_{i+1}^*=\hat{\Delta \Phi }^{-1}_i\), \(i=1,\dots ,N\), according to (12). The MLE of \(\Delta \Phi \) is based on the probability distribution (3) jointly with (6). This is an analogous procedure to the well-established nonstationary extreme value statistics when one or more parameters of the Generalised Extreme Value (GEV) distribution is a function of a covariate that could depend on time (see Chapter 6 of [27]). In our case \(\tau \) and \(\sigma \) correspond to the parameter of the GEV distribution and the covariate, respectively. We recall that as \(\sigma ^*\) does not depend on T, at any time into the experiment/run (for large enough N, though, such that (10) is a good approximation) our estimate of \(\Delta \Phi \) is done most efficiently, and, so, we can revise our commitment: either stopping the experiment/run early or extending it.

3 Numerical Verification

Next, we demonstrate the use of our algorithm on two examples; in a single- as well as a multi-dimensional system.

3.1 Example 1: Overdamped Particle in a Symmetrical 1D Double-Well Potential

The governing equation of this system is the following SDE:

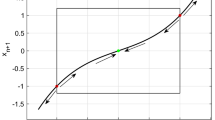
$$\begin{aligned} {{\,\mathrm{\text {d}}\,}}x = -V'{{\,\mathrm{\text {d}}\,}}t + \sigma {{\,\mathrm{\text {d}}\,}}W. \end{aligned}$$
(13)

We specify our example as: \(V=x^4/4-x^2\). The two minima are at \(x_{\pm }=\pm \sqrt{2}\), and the local maximum in between \(x_{\pm }\) is at \(x_0=0\). These are fixed points of the deterministic case (\(\sigma =0\)). A numerical solution of the SDE (13) is obtained by using an Euler-Maruyama integrator [28] with a time step size of \(h=0.02\). Examples of time series realisations are shown in Fig. 1, indicating the regime behaviour with transitions between the two regimes. The time series clearly evidence bimodal marginal distributions—corresponding to the two regimes—whose maxima, and the local minimum in between (not shown), are exactly at \(x_{\pm }=\pm \sqrt{2}\) and \(x_0=0\), respectively. With substituting these into (5) we obtain that \(\Delta V=\Delta \Phi =1\). This shows up as the slope of the curve in Fig. 2. The green coloring indicates that (4) is satisfied well even with so strong noise that the time spent in a regime is not so clear cut any more, as seen in Fig. 1 (b). The result of applying our algorithm is shown in Fig. 3, indicating that it serves its purpose, i.e., \(\Delta V=\Delta \Phi \) is correctly estimated to be about 1, and that the convergence is rather fast. Finally, Fig. 4 verifies the corner stone of the algorithm, given by Eq. (12), showing the sample standard deviation of a number of estimates. For the purpose of comparison, results with the new algorithm (horizontal red line) and, as a reference, results with different fixed sample values of \(\sigma \) (blue circle markers) are shown in one diagram, indicating that the accuracy of the estimate by our algorithm is just about the best accuracy achievable by the same amount of computation using the optimal fixed \(\sigma ^*\) (vertical gold line). Note that we chose \(N=30\) for our algorithm, resulting in some computational time T, and then we realised \(N=\lceil T/\tau (\sigma )\rceil \) transitions using the different fixed \(\sigma \)’s.

Fig. 1
figure 1

Numerical solutions of (13). a\(\sigma =1.0\), b\(\sigma =1.55\). Red and green circle markers indicate transition times defined as a first crossing to the bottom of the upper (lower) potential well since a crossing to the lower (upper) well (color figure online)

Full size image
Fig. 2
figure 2

Demonstration of the validity of (4) in (13). A straight line of slope \(\Delta V=1\) is included in the diagram for reference. The inset provides a blow-up focusing on rather strong noise strengths—the part of the curve coloured green; see also the main text. To estimate \(\tau \) we averaged \(N=200\) transition times each sample value of \(\sigma \) corresponding to a circle marker (color figure online)

Full size image
Fig. 3
figure 3

Proof of concept, I: convergence of estimates \(\hat{\Delta \Phi }_i\). The anchor \(\tau _a\) was established with \(\sigma _a=1\) using \(N=N_0=400\). Five different realizations of the experiment are shown. The initial value for each was \(\sigma _0^*=0.9<\sigma _a\). A “safeguarding” of the procedure is facilitated by overriding (12) such that \(\sigma _{i+1}^*=\sigma _a\) if \(\hat{\Delta \Phi }_i<0\) and \(\sigma _{i}^*=\sigma _{min}^*=0.6\) when (12) dictates smaller (color figure online)

Full size image
Fig. 4
figure 4

Proof of concept, II: sample standard deviation of 200 estimates \(\hat{\Delta V}_N\). For the efficient algorithm we chose \(N=30\), which implies (see the main text) the different N’s for the different fixed sample values of \(\sigma \). The vertical line marks the prediction of (12) (color figure online)

Full size image

3.2 Example 2: The Ghil-Sellers Energy Balance Climate Model (GSEBM)

One of the most striking facts about Earth’s climate is its global-scale bistability: beside the relatively warm climate that we live in, under the present astronomical conditions a very cold climate featuring a fully glaciated so-called snowball Earth is also possible, and this state might have been experienced a number of times by Earth in the past few hundred million years [29]. Different hypotheses of transitioning from the warm to the cold climate and the other way round involve external forcings, but in principle it is possible that the climate system in itself—in its autonomous form, without external effects— is transitive, at least in the warm-to-cold direction. This would be a somewhat counterintuitive scenario of no bistability in a strict sense, but the coexistence of an attractor corresponding to the cold climate and a nonattracting set [15] corresponding to the warm climate. Escape from the nonattracting set is then modeled as a noise-induced transition (when the concepts of escape rate and exit rate coalesce), where the noise models some unresolved internal, say, atmospheric and/or oceanic dynamics. Without a requirement for physical realism, we consider additive noise perturbations of the Ghil-Sellers model [30] written for the long time average surface air temperature \(T(\phi ,t)\) as a function of latitude \(\phi \in [-\pi /2,\pi /2]\) or \(x=2\phi /\pi \in [-1,1]\). The deterministic GSEBM stands in the form of a diffusive heat equation:

$$\begin{aligned} \begin{aligned} C(x)\partial _tT(t,x)&= \mu Q(x)(1-\alpha (x,T))-O(T) \\&+ M(x)\partial _{x}[(D_1(x) + D_2(x)g(T))\partial _{x}T]. \end{aligned} \end{aligned}$$
(14)

See [30, 31] for the concrete form of the equation, and [32] for a numerical implementation. The model expresses an energy budget, namely, that the tendency of internal energy in latitudinal bands on the left hand side is equal to the sum of—following the order of terms on the right—the incoming short-wave solar radiation modulated by the albedo \(\alpha \), the outgoing long-wave thermal radiation O and the rate of diffusive heat transport from neighbouring latitudinal bands. M(x) is to do with the spherical geometry, and \(D_1\) and \(D_2g(T)\) are sensible and latent heat diffusivities, respectively. A global mean albedo can be derived from the dynamics, whose temperature-dependence features a cross-over between approximately constant values for very cold and warm conditions, corresponding to a completely snow-covered ‘snowball’ and completely snow/ice-free conditions, respectively. It is this temperature dependence—giving rise also to the so-called ice-albedo positive feedback—that is responsible for the global scale bistability [31], which is a robust feature of the climate model hierarchy.

Unlike [32] that integrates the deterministic model using Matlab’s pdepe, this time we have a stochastic system at hand and, so, we take advantage of Matlab’s SDE simulation suite simulate. For this we discretize the eq. with respect to T by the ‘method of lines’, converting the PDE into an ODE, i.e., Eq. (1). The particular difference schemes that we apply, using a regular grid, are:

$$\begin{aligned} \begin{aligned} \partial _x[D_1(x)\partial _xT]\approx [(T_{j+1}-T_{j})D_{1,j+1/2} -(T_{j}-T_{j-1})D_{1,j-1/2}]/\Delta x^2, \\ \partial _x[D_2(x)g(T)\partial _xT] = \partial _x[D_2(x)\partial _xG] \approx [(G(T_{j+1})-G(T_{j}))D_{2,j+1/2}{} G(T_{j})-G(T_{j-1}))D_{2,j-1/2}]/\Delta x^2, \end{aligned} \end{aligned}$$
(15)

\(j=1,\dots ,J,\) where \(T_j\approx T(x_j)\), \(x_j=(j-1/2)\Delta x-1\), \(\Delta x=2/J\), and \(D_{1,j\pm 1/2}=D_1(x_{j\pm 1/2})\), \(x_{j\pm 1/2}=x_j\pm \Delta x/2\) (see p. 1046 of [33] regarding the x-dependent diffusivity). The boundary conditions are eliminated by the ‘method of reflection’, setting \(T_0=T_J\) and \(T_{J+1}=T_1\). Such a grid deals effectively with the singularity of M(x) at the poles, but the resulting ODE can be somewhat stiff.

Figure 5 suggests that our new algorithm works also in a multi-dimensional setting: the estimates \(\hat{\Delta \Phi }_i\) (blue markers) do convergence to the reference value (horizontal red line). It is key that the reference value is obtained by a completely independent method. In the high-dimensional setting, even in gradient systems, in general \(\Delta \Phi \) cannot be calculated analytically. To provide a reference, we calculated \(\Delta \Phi \) for the discretized system, the SDE, by an action-minimizing procedure [3], using the computer code publicly available as supplementary material of that paper. We realised the time-discretization of the instanton by breaking it down into 100 segments over a span of 2000 [Ms]. We note that for the feasibility of the minimization, already with \(J=10\), it is crucial to provide symbolically the gradient of the action with respect to the displacement of the discrete sample points of the instanton. Without this symbolic expression the minimization takes orders-of-magnitude more time (as we estimated by examining toy examples). The symbolic expression—an extremely long expression, practically impossible to keep track of manually—is generated by the code of [3], which makes use of Matlab’s symbolic algebra toolbox. For the code to be successful in this, we need to be able to obtain an explicit expression for the tendencies \(\dot{T_j}\). This could not be achieved by the sophisticated method implemented in Matlab’s pdepe, which is why we developed the discretization scheme (15) using the method of lines.

We note that an expression for the potential functional \(\Phi (T)\) of the PDE was given in [30]. However, it does not seem to be possible to evaluate this expression for the particular model at hand, not even numerically, because Eq. (7d) of [30] would need to be first integrated analytically, which does not seem feasible using symbolic algebra software. The reason for this may be that the compact expression featuring multiple applications of the absolute value function to represent the piece-wise conditional expression (arising from the cutoff values for the albedo) may be too complicated.

Fig. 5
figure 5

Sames as Fig. 3b but for the discretized GSEBM, \(J=10\), and \(\sigma _a=1.7\), \(N_0=400\), \(\sigma _0^*=1.5\), \(\sigma _{min}^*=1.0\). We considered only warm-to-cold transitions given the present day solar strength \(\mu =1\). The red horizontal line marks the potential difference \(\Delta \Phi \) between the warm climate and the saddle computed by a completely independent method; see the main text. Note that here we measure time in \(10^6\) seconds [Ms], as a departure from [31, 32] (color figure online)

Full size image

4 Closing Remarks

It is important to emphasize that we do not seek to determine an effective 1D potential, the scenario that [34] is concerned with, but the deterministic multistable part of the dynamics can be a system of any high dimensionality. In particular, an asymmetry of the potential function does not affect the proposed procedure. The condition for the existence of a quasi-potential is that the noise is weak and that, when the noise is a representation of unresolved small-scale dynamics, there is a time-scale separation between the resolved and unresolved dynamics. When the noise is weak, the probability of any escape path is exponentially small compared with the most probable exit path through the saddle where the potential over the deterministic basin boundary has a minimum. This includes the possibility of multiple saddle sets embedded in the basin boundary. An example of this may be the reduced stochastic Duffing oscillator-like system underlying the turbulent swirling flow studied in [35]. However, as in this experiment we can actually see multiple well-separated clustering of transition paths that prompt the multiplicity of local potential minima over the basin boundary, we can say that the noise is not weak in the above sense. In this case the potential barrier height should not be expected to predict the mean transition times. Nevertheless, it is not clear what errors to expect as e.g. Fig. 2 indicates that the theoretical scaling applies when the noise is rather strong.

Our algorithm relies on an anchor point in which a large number of transitions are generated so that the mean transition time can be determined highly accurately. For this to be affordable, we look to set the noise as large as possible. However, it should be weak enough such that with the variation of the noise strength the mean transition times scale according to our assumption (as in Eq. (4)), based on the existence of a quasi-potential. There seems to be no apriori indicator what noise strength is already small enough. To check that it is, perhaps the most efficient procedure is an iterative one: (1) One uses a noise strength for the anchor that is affordable by far; (2) uses our iterative algorithm to determine the optimal noise strength belonging to this anchor—alongside the estimate of the potential difference; (3) in a new secondary iterate one associates this optimal noise strength with a new anchor, and 4) determines a new estimate of the potential difference; and so on. If, as a result of the secondary iteration, two subsequent estimates of the potential difference are close, it should mean that the noise is weak enough.

The primary iteration of our algorithm, as described in Sect. 2, dictates that simulation (or experimental) runs that end up in a transition take place sequentially. If simulations are run in parallel, and a new one is started with an updated noise strength right away, then a bias arises towards shorter transition times, which implies a biased estimate of the potential difference. However, it would be a worthwhile future investigation to determine the dependence of the bias on the number of parallel simulations, as perhaps a moderate number of parallel simulations would result in a reasonably small bias, while accelerate the procedure already considerably.

A limitation of our algorithm is that it is applicable only to systems whose deterministic part is autonomous. In climate research applications—what motivated the present work—at least one periodic external forcing is always present: the seasonal cycle. There are two ways to possibly remove the issue with this external forcing. First, it might be possible to achieve dimension reduction such that the deterministic part represents the evolution of a long-term average. An example of this is the GSEBM. Second, a periodic forcing is special in that a discrete-time sampling of the dynamics by using the period of the forcing yields an autonomousdiscrete-time dynamical system, the so-called stroboscopic Poincaré return map [36, 37]. The quasi-potential can be defined also for such discrete-time maps [15, 20], and our algorithm is applicable to maps too. Then, what remains to ensure is that the noise is weak enough, as proposed above via a secondary iteration. With an aperiodic external forcing perhaps it is possible to generalise the Freidlin-Wentzell large-deviation theory of stochastic dynamical systems and define an instantaneous so-called snapshot or pullback [37] quasi-potential, as well as snapshot instantonic paths analogous to manifolds of snapshot saddles [15, 38]. However, our algorithm is based on temporal statistics and so not applicable, even in the case of quasistatically slow forcing, when snapshot objects closely trace their stationary counterparts in autonomous variants of the system. We remark that the latter setting can provide a generalised theory of stochastic resonance [39], which is relevant to approaches dealing with long paleoclimatic time series [34].