1 Introduction and motivation

This work is motivated by a meta-analysis using reported data comparing thoracoscopic, or keyhole surgery, and open surgery for treatment of asymptomatic antenatally diagnosed congenital lung malformations in young children. The mean age of the children involved in the studies is 15 months, and both surgeries have no deaths reported. Thoracoscopy has become more widely used because it requires only a small incision in the chest wall. We consider the following question: How does keyhole perform versus open w.r.t. total complications?

Adams et al. (2017) considered a meta-analysis of 12 reports comparing keyhole and open surgery as listed in Table 1. These data allow a standard meta-analysis as follows. For each study, an effect measure, here the risk ratio, is calculated associated with an estimate of its standard error. This allows a calculation of a summary measure with 95% confidence interval. We use here the package STATA15 (StataCorp. 2017) in connection with an add-on package metan (see also Palmer and Sterne 2009) for delivery of the calculation. The results are displayed in Table 2. This is an example of a standard, two-stage meta-analysis where in the first stage for each study, an effect measure is calculated and in the second stage the study-specific effect estimates are further analyzed. This approach is extensively described in the existing literature (Borenstein et al. 2009; Cooper et al. 2009; Schwarzer et al. 2015). In the application study here, there is a significant beneficial effect of keyhole surgery w.r.t. the number of complications (which includes bleeding, wound or chest infections, or tracheal injury among others) and the effect is homogeneous over the studies as the test of homogeneity is not significant. These results are also visualized in the forest plot in Fig. 1. Note that all but one of the studies show non-significant results, whereas the meta-analytic summary estimator clearly does. This demonstrates one of the benefits of a meta-analysis.

Table 1 Meta-analytic data comparing keyhole with open; given are the number of complications and the number of children enrolled for each treatment group
Full size table
Table 2 metan output and analysis comparing keyhole with open
Full size table
Fig. 1
figure 1

Forest plot based on 12 studies with complication information in open and keyhole surgery

Full size image

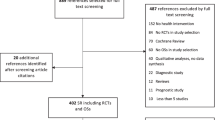
In addition to the 12 studies that have been used in Adams et al. (2017) as these included information on both treatment groups and, hence, allowing a conventional meta-analysis, there were 24 additional reports available, of which 15 had only information on keyhole and nine had only information on open surgery. So, in total there are 36 reports with 12 studies having information on both, 15 on keyhole only and nine on open only. We list these additional studies in Tables 3 and 4.

These additional 24 studies were ignored in Adams et al. (2017) as for any of these it is not possible to calculate a study-specific risk ratio estimate since a comparator treatment is missing. Hence, this does not allow a conventional two-stage meta-analysis where in the first stage a within-study effect is estimated and then this effect estimate is further analyzed in a second stage. This setting of having only one result per study available (with the comparator result missing) has not been considered in meta-analysis. To overcome this difficulty, we suggest a one-stage modelling approach which will allow to use the information from all 36 studies and which we will detail in the following section.

Table 3 Meta-analytic data comparing keyhole with open: reports from keyhole only
Full size table
Table 4 Meta-analytic data comparing keyhole with open: reports from open surgery only
Full size table

2 A count modelling approach using Poisson regression

We consider the number of complications X as a Poisson count with mean \( E(X) = \mu n\) where n is the size of the study report. Clearly, \(\mu =E(X)/n\) is the incidence risk of complications. We write for report i

$$\begin{aligned} E(X_{ij})=\mu _j n_{ij} \end{aligned}$$
(1)

for \(j=1\) (treatment=keyhole) and \(j=0\) (comparison=open), so that the risk ratio \(RR = \mu _1/\mu _0\), assumed to be independent of the study i, for the time being. Taking logarithms on both sides of (1), we yield

$$\begin{aligned} \log E(X_{ij})=\log n_{ij} + \log \mu _j = \log n_{ij} + \alpha + \beta \times j \end{aligned}$$
(2)

where \(\beta = \log (\mu _1/\mu _0)\) is the log-risk ratio, \(\alpha \) is the log-baseline risk, and \(\log n_{ij}\) enters as an offset (a covariate with a fixed, known coefficient) into the modelling. Finally, it is assumed that the count \(X_{ij}\) follows a Poisson distribution

$$\begin{aligned} X_{ij} \sim Po(x|n_{ij}\mu _j), \end{aligned}$$
(3)

where \(Po(x|\theta )= \exp (-\theta ) \theta ^x/x!\).

3 Fusion of the Poisson likelihoods

According to the available data, we have the following, three different likelihoods. The first likelihood appears for those studies where both, keyhole and open surgery, information is available:

$$\begin{aligned} L_0=\prod _{i=1}^{k_0} \left[ Po(x_{i0}|n_{i0}\exp (\alpha _i))\times Po(x_{i1}|n_{i1}\exp (\alpha _i+\beta ))\right] , \end{aligned}$$
(4)

where \(k_0\) are the reports involving both techniques.

The second likelihood occurs for those studies with only information on keyhole surgery:

$$\begin{aligned} L_1=\prod _{i=k_0+1}^{k_0+k_1} \left[ Po(x_{i1}|n_{i1}\exp (\alpha _i+\beta ))\right] , \end{aligned}$$
(5)

where \(k_1\) are the reports involving only keyhole. Finally, the third likelihood occurs for those studies with only open surgery information:

$$\begin{aligned} L_2=\prod _{i=k_0+k_1+1}^{k_0+k_1+k_2} \left[ Po(x_{i0}|n_{i0}\exp (\alpha _i)) \right] , \end{aligned}$$
(6)

where \(k_2\) are the reports involving only open surgery. This leads to the joint likelihood

$$\begin{aligned} L(\theta )=L_0(\theta ) L_1(\theta ) L_2(\theta ) \end{aligned}$$
(7)

where \(\theta \) stands for a generic parameter.

4 Poisson likelihoods with random effect for study

It appears reasonable to capture the baseline variation across studies with a random effect. Hence, let \(\alpha _i \sim N(\alpha ,\sigma ^2_{\alpha })\) be a normal random effect with mean \(\alpha \) and variance \(\sigma ^2_{\alpha }\). Then, the likelihood for studies with information on keyhole and open surgery becomes:

$$\begin{aligned} L_0 = \prod _{i=1}^{k_0} \int _{\alpha _i}[ Po(x_{i0}|n_{i0}\exp (\alpha _i))\times Po(x_{i1}|n_{i1}\exp (\alpha _i+\beta ))] \phi (\alpha _i|\alpha ,\sigma ^2_{\alpha }) \mathrm{d}\alpha _i, \end{aligned}$$
(8)

where \(\phi (\alpha _i|\alpha ,\sigma ^2_{\alpha }) \) is a normal density with mean \(\alpha \) and variance \(\sigma ^2_{\alpha }\) with similar expressions for the other likelihoods:

$$\begin{aligned} L_1=\prod _{i=k_0+1}^{k_0+k_1}\int _{\alpha _i} \left[ Po(x_{i1}|n_{i1}\exp (\alpha _i+\beta ))\right] \phi (\alpha _i|\alpha ,\sigma ^2_{\alpha })\mathrm{d}\alpha _i, \end{aligned}$$
(9)

and

$$\begin{aligned} L_2=\prod _{i=k_0+k_1+1}^{k_0+k_1+k_2} \int _{\alpha _i}\left[ Po(x_{i0}|n_{i0}\exp (\alpha _i)) \right] \phi (\alpha _i|\alpha ,\sigma ^2_{\alpha }) \mathrm{d}\alpha _i. \end{aligned}$$
(10)

Again, we can form the joint likelihood

$$\begin{aligned}L(\theta )=L_0(\theta ) L_1(\theta ) L_2(\theta ). \end{aligned}$$

In Table 5, we find the analysis for the studies with information on both groups, hence using \(L_0\), and for the studies including mixed arm information, in other words using the joint likelihood L. We note that the latter analysis shifts the borderline significance of the risk ratio to a clearly significant result. For both analysis, the baseline random effect \(\alpha _i\) for study is significant and more precisely has a positive variance, significantly different from zero.

Table 5 Some results comparing keyhole with open
Full size table

The model is easily extendible to allow heterogeneity of effect across studies

$$\begin{aligned} \beta _i \sim N(\beta ,\sigma ^2_{\beta })\end{aligned}$$

where \(\beta _i \) is now a normal random effect for study report i. For example, the likelihood for studies with only information on keyhole becomes

$$\begin{aligned} L_1=\prod _{i=k_0+1}^{k_0+k_1}\int _{\beta _i} \left[ \int _{\alpha _i} Po(x_{i1}|n_{i1}\exp (\alpha _i+\beta ))\phi (\alpha _i|\alpha ,\sigma ^2_{\alpha }) \mathrm{d}\alpha _i\right] \phi (\beta _i|\beta ,\sigma ^2_{\beta }) \mathrm{d}\beta _i, \end{aligned}$$
(11)

with similar expressions for the other likelihoods corresponding to the available study information. In Table 6, a model evaluation is provided which shows that there is no evidence for heterogeneity of effect across studies.

Table 6 Model evaluation comparing keyhole with open: log-likelihood, Akaike and Bayesian information criteria are given for the model with and without treatment random effect
Full size table

5 Simulation study

We evaluated the performance of the two Poisson regression methods: one based only on the studies with information on both arms and the other based additionally on the studies including mixed arm information, by means of simulation. We consider a Poisson model that allows a random effect for study. In the simulation study, the data were generated from two, potentially different, Poisson distributions for the treatment and comparison groups, respectively. The number of studies (k) was chosen as 20, 40, 60, and 80. Furthermore, the simulated meta-analytic data included 50% of all studies with information in two arms and 50% of all studies with information in one arm, the latter having an equal split on treatment and comparison group. The settings were set to mimic the data on comparing open and keyhole surgery. We used \(\alpha =-2, \sigma ^{2}_{\alpha }=0.7\), and \(\beta = -0.5\) and 0.5, leading to the true risk ratios of 0.61 and 1.65, respectively. For each situation, 1000 simulation replications were used.

The performance of the estimators in the Poisson model with baseline random effect was evaluated in terms of bias and root mean squared error (RMSE). As seen in Tables 7 and 8, the bias of the log-risk ratio (\(\hat{\alpha }\)) and the bias of the variance of baseline risk (\(\hat{\sigma }^{2}_{\alpha }\)) were closer to zero when using the studies with mixed arm information in comparison with the respective bias obtained from the method using the studies with information on both arms only, in almost all cases. The RMSEs of \(\hat{\beta }\) and the RMSEs of \(\hat{\sigma }^{2}_{\beta }\) computed from the method based on mixed arm information were smaller than those of the compared method in all cases. Our results emphasize that Poisson regression analysis using all available information can provide a benefit in a meta-analysis. At least in the situation studied here, it yields good performance in terms of bias and mean squared error of the estimated parameters of interest.

Table 7 The performance of estimators for meta-analysis using mixed arm information
Full size table
Table 8 The performance of estimators for meta-analysis using both arm information
Full size table

6 Diagnostics

Clearly, the approach suggested here goes beyond the conventional within-study comparison to estimate the treatment effect. Hence, we must considerate that comparing treatment across studies might lead to a different result than comparing treatment within studies. In the following, we outline a strategy to diagnose a potential discrepancy between study estimates using both arm information and study estimates using one arm information only. The strategy is as follows:

  • fit the model for all reports using \(\theta =(\alpha ,\sigma ^2_\alpha ,\beta )\)

  • fit the model for all reports but with \(\theta _1\) for the subset of reports with both surgeries and with \(\theta _2\) for the subset with only one surgery

  • evaluate

    $$\begin{aligned} 2 \log \lambda = 2 \log \left[ \frac{ L(\hat{\theta }_1) L(\hat{\theta }_2)}{L(\hat{\theta })}\right] \end{aligned}$$

    on a \(\chi ^2\)-scale with 3df

  • in the case here, \( 2 \log \lambda = 6.14\) with associated p-value = 0.1051 which is above the conventionally used threshold of 0.05, so that we do not reject the common parameter model.

A more direct (but also more limited) approach is as follows: Define the indicator variable

$$\begin{aligned}S = {\left\{ \begin{array}{ll} 1&{} \text {if report contains info on both surgeries}\\ 0&{} \text {otherwise }\end{array}\right. } \end{aligned}$$

and the effect variable

$$\begin{aligned}T = {\left\{ \begin{array}{ll} 1&{} \text { if keyhole}\\ 0&{} \text { open }\end{array}\right. } \end{aligned}$$

and assess treatment \(\times \) both/mixed information interaction \(S \times T\) by means of investigating the coefficient \(\gamma \) for significance in the model (12):

$$\begin{aligned} \log E(X_{it})=\log n_{it} + \log \mu _j = \log n_{it} + \alpha + \beta \times t + \gamma (s \times t), \end{aligned}$$
(12)

where the treatment \(t=0,1\) indicates open and keyhole surgery, respectively, and \(s=0,1\) indicates whether the study has only one type of surgery (0) or both (1).

Table 9 Assessing treatment–mixed information interaction
Full size table

We conclude from the analysis in Table 9 that there is no evidence that keyhole/open effect is differential in reports with both surgeries reported to reports with only one surgery (the treatment effect is not affected by the type of study report), so that conclusions might be based upon the total of 36 reports (Fig. 2).

Fig. 2
figure 2

Summary plot: “both” is based on all studies with complication information in open and keyhole surgery, “only one” is based on those study with reports only in one of the two groups (open or keyhole surgery), and “all” is a merger of “both” and “only one”

Full size image

7 Discussion

The paper is based on the idea of fusing several likelihoods. Here, we used mixed Poisson likelihoods. This model is often used for rates where events occur within a given person-time. If the person-time is identical for all individuals under risk, the person-time reduces to the sample size. In the latter case, the binomial model would then occur as an alternative. Also, the Poisson model is not the only possible model for offset settings, and here, an alternative could be the negative-binomial distributions. In any case, the arguments of fusing likelihoods would be identical. In addition, we argue that the mixed Poisson model that we have used here and which uses a random effect for the factor study, provides quite a flexible model.

It remains in the debate how much information can be gained from reports providing only one intervention outcome, in particular, for comparative analysis. We have indicated that gain can be reached, but it is limited. In addition, it is more appropriate from the statistical perspective to have all available information included in the analysis. Clearly, there is no doubt to use all report information if interest is in absolute risk, whether there is one-group information or two-group information per study. Of course, there is then also the question how this information could be combined, but we leave this for another discussion.