Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-19T22:56:18.648Z Has data issue: false hasContentIssue false
  • English
  • Français

RANK GENERATING FUNCTIONS FOR ODD-BALANCED UNIMODAL SEQUENCES, QUANTUM JACOBI FORMS, AND MOCK JACOBI FORMS

Part of: Basic hypergeometric functions Discontinuous groups and automorphic forms Combinatorics

Published online by Cambridge University Press:  10 January 2020

MICHAEL BARNETT ,
AMANDA FOLSOM  and
WILLIAM J. WESLEY
MICHAEL BARNETT
Affiliation:
ThoughtWorks, 15540 Spectrum Dr., Addison, TX75001, USA email michaelmbarnett@gmail.com
AMANDA FOLSOM*
Affiliation:
Department of Mathematics and Statistics,Amherst College, Seeley Mudd Building, 31 Quadrangle Dr.,Amherst, MA01002, USA email afolsom@amherst.edu
WILLIAM J. WESLEY
Affiliation:
Department of Mathematics,University of California, One Shields Ave., Davis, CA95616, USA email wjwesley@ucdavis.edu
*
✉afolsom@amherst.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 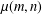$\unicode[STIX]{x1D707}(m,n)$ (respectively, 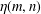$\unicode[STIX]{x1D702}(m,n)$) denote the number of odd-balanced unimodal sequences of size $2n$ and rank $m$ with even parts congruent to 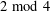$2\!\!\hspace{0.6em}{\rm mod}\hspace{0.2em}4$ (respectively, 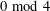$0\!\!\hspace{0.6em}{\rm mod}\hspace{0.2em}4$) and odd parts at most half the peak. We prove that two-variable generating functions for 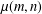$\unicode[STIX]{x1D707}(m,n)$ and 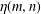$\unicode[STIX]{x1D702}(m,n)$ are simultaneously quantum Jacobi forms and mock Jacobi forms. These odd-balanced unimodal rank generating functions are also duals to partial theta functions originally studied by Ramanujan. Our results also show that there is a single 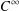$C^{\infty }$ function in 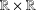$\mathbb{R}\times \mathbb{R}$ to which the errors to modularity of these two different functions extend. We also exploit the quantum Jacobi properties of these generating functions to show, when viewed as functions of the two variables 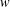$w$ and 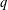$q$, how they can be expressed as the same simple Laurent polynomial when evaluated at pairs of roots of unity. Finally, we make a conjecture which fully characterizes the parity of the number of odd-balanced unimodal sequences of size $2n$ with even parts congruent to 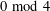$0\!\!\hspace{0.6em}{\rm mod}\hspace{0.2em}4$ and odd parts at most half the peak.

Keywords

partitionsstrongly unimodal sequencesgenerating functionsmock modular formsquantum modular formsJacobi forms

MSC classification

Primary: 05A17: Partitions of integers 11F37: Forms of half-integer weight; nonholomorphic modular forms 11F50: Jacobi forms
Secondary: 11F03: Modular and automorphic functions 11F30: Fourier coefficients of automorphic forms 33D70: Other basic hypergeometric functions and integrals in several variables
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 2 , October 2020 , pp. 157 - 175
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors are grateful for support from National Science Foundation CAREER Grant DMS-1449679 and from the Simons Foundation Fellows Program in Mathematics (awarded to the second author).

References

Andrews, G. E. and Berndt, B. C., Ramanujan’s Lost Notebook, Part II (Springer, New York, 2009).Google Scholar
Andrews, G. E., Rhoades, R. C. and Zwegers, S. P., ‘Modularity of the concave composition generating function’, Algebra Number Theory 7(9) (2013), 2103–2139.CrossRefGoogle Scholar
Atkin, A. O. L. and Swinnerton-Dyer, P., ‘Some properties of partitions’, Proc. Lond. Math. Soc. (3) 4 (1954), 84–106.CrossRefGoogle Scholar
Barnett, M., Folsom, A., Ukogu, O., Wesley, W. J. and Xu, H., ‘Quantum Jacobi forms and balanced unimodal sequences’, J. Number Theory 186 (2018), 16–34.10.1016/j.jnt.2017.10.022CrossRefGoogle Scholar
Bringmann, K. and Folsom, A., ‘Quantum Jacobi forms and finite evaluations of unimodal rank generating functions’, Arch. Math. 107 (2016), 367–378.CrossRefGoogle Scholar
Bringmann, K., Folsom, A. and Rhoades, R., ‘Unimodal sequences and ‘strange’ functions: a family of quantum modular forms’, Pacific J. Math. 274 (2015), 1–25.10.2140/pjm.2015.274.1CrossRefGoogle Scholar
Bringmann, K. and Jennings-Shaffer, C., ‘Unimodal sequence generating functions arising from partition ranks’, Res. Number Theory 5(3) (2019), Art. no. 25, 17 pp.CrossRefGoogle Scholar
Bringmann, K. and Rolen, L., ‘Radial limits of mock theta functions’, Res. Math. Sci. 2 (2015), Art. no. 17, 18 pp.10.1186/s40687-015-0035-8CrossRefGoogle Scholar
Bryson, J., Ono, K., Pitman, S. and Rhoades, R. C., ‘Unimodal sequences and quantum and mock modular forms’, Proc. Natl. Acad. Sci. USA 109 (2012), 16063–16067.10.1073/pnas.1211964109CrossRefGoogle Scholar
Eichler, M. and Zagier, D., The Theory of Jacobi Forms, Progress in Mathematics, 55 (Birkhäuser, Boston, MA, 1985).CrossRefGoogle Scholar
Folsom, A., Garthwaite, S., Kang, S.-Y., Swisher, H. and Treneer, S., ‘Quantum mock modular forms arising from eta–theta functions’, Res. Number Theory 2 (2016), Art. no. 14, 41 pp.CrossRefGoogle Scholar
Folsom, A., Ki, C., Truong Vu, Y. N. and Yang, B., ‘‘Strange’ combinatorial quantum modular forms’, J. Number Theory 170 (2017), 315–346.CrossRefGoogle Scholar
Folsom, A., Ono, K. and Rhoades, R. C., ‘Mock theta functions and quantum modular forms’, Forum Math. Pi 1 (2013), Art. no. e2, 27 pp.CrossRefGoogle Scholar
Gordon, B. and McIntosh, R. J., ‘A survey of the classical mock theta functions’, in: Partitions, q-Series, and Modular Forms, Developments in Mathematics, 23 (Springer, New York, 2012), 95–144.CrossRefGoogle Scholar
Kim, B., Lim, S. and Lovejoy, J., ‘Odd-balanced unimodal sequences and related functions: parity, mock modularity, and quantum modularity’, Proc. Amer. Math. Soc. 144 (2016), 3687–3700.CrossRefGoogle Scholar
Lovejoy, J., Private communication, September 2018.Google Scholar
Mortenson, E. T., ‘On the dual nature of partial theta functions and Appell–Lerch sums’, Adv. Math. 264 (2014), 236–260.CrossRefGoogle Scholar
Rademacher, H.,(eds. Grosswald, E. et al. ) Topics in Analytic Number Theory, Grundlehren der mathematischen Wissenschaften, 169 (Springer, New York, 1973).CrossRefGoogle Scholar
Shimura, G., ‘On modular forms of half integral weight’, Ann. of Math. (2) 97(3) (1973), 440–481.CrossRefGoogle Scholar
Zagier, D., ‘Quantum modular forms’, in: Quanta of Maths, Clay Mathematics Proceedings, 11 (American Mathematical Society, Providence, RI, 2010), 659–675.Google Scholar
Zudilin, W., ‘On three theorems of Folsom, Ono and Rhoades’, Proc. Amer. Math. Soc. 143(4) (2015), 1471–1476.CrossRefGoogle Scholar
Zwegers, S., ‘Mock theta functions’, PhD Thesis, Universiteit Utrecht, 2002.Google Scholar
Zwegers, S., ‘Multivariable Appell functions and nonholomorphic Jacobi forms’, Res. Math. Sci. 6(1) (2019), Art. no. 16, 15 pp.CrossRefGoogle Scholar