Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-15T12:06:17.758Z Has data issue: false hasContentIssue false
  • English
  • Français

Irregularities in the Distribution of Prime Numbers in a Beatty Sequence

Part of: Sequences and sets Elementary number theory

Published online by Cambridge University Press:  16 December 2019

Janyarak Tongsomporn  and
Jörn Steuding
Janyarak Tongsomporn
Affiliation:
Walailak University, School of Science, Nakhon Si Thammarat, 80 160, Thailand Email: tjanyarak@gmail.com
Jörn Steuding
Affiliation:
Department of Mathematics, Würzburg University, Am Hubland, 97 218Würzburg, Germany Email: steuding@mathematik.uni-wuerzburg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove irregularities in the distribution of prime numbers in any Beatty sequence 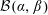${\mathcal{B}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$, where $\unicode[STIX]{x1D6FC}$ is a positive real irrational number of finite type.

Keywords

prime numbersirregularitiesMaier’s matrix methodBeatty sequence

MSC classification

Primary: 11A41: Primes
Secondary: 11B83: Special sequences and polynomials
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 738 - 743
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banks, W. D. and Shparlinski, I. E., Prime numbers with Beatty sequences. Colloq. Math. 115(2009), 147–157. https://doi.org/10.4064/cm115-2-1CrossRefGoogle Scholar
Buchstab, A. A., Asymptotic estimates of a general number-theoretic function. Mat.-Sb. (N.S.) 2(1937), 1239–1246.Google Scholar
Cramér, H., On the order of magnitude of the difference between consecutive prime numbers. Acta Arith. 2(1936), 23–46.CrossRefGoogle Scholar
Davenport, H., Multiplicative number theory, Third ed, Graduate Texts in Mathematics, 74, Springer-Verlag, New York, 2000.Google Scholar
Fraenkel, A. S., The bracket function and complementary sets of integers. Canad. J. Math. 21(1969), 6–27. https://doi.org/10.4153/CJM-1969-002-7CrossRefGoogle Scholar
Gallagher, P. X., A large sieve density estimate near 𝜎 = 1. Invent. Math. 11(1970), 329–339. https://doi.org/10.1007/BF01403187CrossRefGoogle Scholar
Granville, A., Unexpected irregularities in the distribution of prime numbers. In: Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Zürich, 1994). Birkhäuser, Basel, 1995, pp. 388–399.CrossRefGoogle Scholar
Hildebrand, A. and Maier, H., Irregularities in the distribution of primes in short intervals. J. Reine Angew. Math. 397(1989), 162–193.Google Scholar
Iwaniec, H., The sieve of Eratosthenes-Legendre. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 4(1977), 257–268.Google Scholar
Maier, H., Chains of large gaps between consecutive primes. Adv. in Math. 39(1981), 257–269. https://doi.org/10.1016/0001-8708(81)90003-7CrossRefGoogle Scholar
Maier], H., Primes in short intervals. Michigan Math. J. 32(1985), 221–225. https://doi.org/10.1307/mmj/1029003189Google Scholar
Selberg, A., On the normal density of primes in small intervalls and the difference between conscutive primes. Arch. Math. Naturvid. 47(1943), 87–105.Google Scholar
Tadee, S. and Laohakosol, V., Complementary sets and Beatty functions. Thai J. Math. 3(2005), 27–33. https://doi.org/10.1155/2005/165785Google Scholar
Thorne, F., Maier matrices beyond Z.. In: Combinatorial number theory. Walter de Gruyter, Berlin, 2009, pp. 185–192.Google Scholar
Vinogradov, I. M., The method of trigonometrical sums in the theory of numbers. Dover Publications, Mineola, NY, 2004.Google Scholar