Linear relations on LLT polynomials and their k-Schur positivity for $k=2$

Abstract

LLT polynomials are q-analogs of products of Schur functions that are known to be Schur positive by Grojnowski and Haiman. However, there is no known combinatorial formula for the coefficients in the Schur expansion. Finding such a formula also provides Schur positivity of Macdonald polynomials. On the other hand, Haiman and Haglund conjectured that LLT polynomials for skew partitions lying on k adjacent diagonals are k-Schur positive, which is much stronger than Schur positivity. In this paper, we prove the conjecture for $k=2$ by analyzing unicellular LLT polynomials. We first present a linearity theorem for unicellular LLT polynomials for $k=2$. By analyzing linear relations between LLT polynomials with known results on LLT polynomials for rectangles, we provide the 2-Schur positivity of the unicellular LLT polynomials as well as LLT polynomials appearing in Haiman–Haglund conjecture for $k=2$.

1 Introduction

LLT polynomials are certain family of symmetric functions indexed by d-tuple of skew partitions, introduced by Lascoux et al. [12] in the study of quantum affine algebras and unipotent varieties. Later, Haglund et al. [7] proved that Macdonald polynomials are positive sums of LLT polynomial indexed by d-tuple of ribbons. Grojnowski and Haiman [6] proved that LLT polynomials are Schur positive using Kazhdan–Lusztig theory. However, their proof does not provide a manifestly positive formula so finding combinatorial formulas for expansions of Macdonald polynomials and LLT polynomials remains a wide open problem. The best known result is the formula for $d=3$ due to Blasiak [3]. See [3] for more history about LLT polynomials.

In his 2006 ICM talk, Haiman announced a conjecture made by Haiman and Haglund stating that the involution image of LLT polynomials indexed by d-tuple of skew partition that lies in k-adjacent diagonals is k-Schur positive (Conjecture 2.1), which is much stronger than Schur positivity. The motivation of our paper stems from their conjecture, as our second main theorem is the proof of the conjecture for $k=2$.

The first main theorem (Theorem 4.1) shows that unicellular LLT polynomials with $k=2$ are positive sums of 2-Schur functions where the exponents of q change linearly as the index set of unicellular LLT polynomials change, providing a very nice formula. We prove this by showing that there exists a linear recurrence relation between unicellular LLT polynomials (Theorem 3.5). Note that the linear relation does not assume $k=2$, which may be useful to study LLT polynomials with any k.

The first main theorem enables us to determine all unicellular LLT polynomials with $k=2$ from LLT polynomials indexed by dominos. Then, we prove that LLT polynomials indexed by dominos are power of q times a 2-Schur function by using the fact that LLT polynomials indexed by rectangles are the same as generalized Hall–Littlewood polynomials, proved in [6]. This together with Theorem 4.1 proves Haiman–Haglund conjecture for $k=2$. See Conjecture 2.1 for the precise statement.

It is worth nothing that there is a plethysm relation between unicellular LLT polynomials and chromatic quasisymmetric functions, first found in [4] (see also [2]). Therefore, linear relations between unicellular LLT polynomials also hold for corresponding chromatic quasisymmetric functions. Chromatic quasisymmetric functions for the case of $k=2$ we considered are studied by Cho and Huh [5], and by Harada and Precup [8].

The structure of the paper is as follows: In Sect. 2, we define LLT polynomials and state Haiman–Haglund conjecture precisely. In Sects. 3 and 4, we present useful linear relations and prove the linearity theorem (Theorem 4.1). In Sect. 5, we compare LLT polynomials indexed by dominos and 2-Schur function. In Sect. 6, we prove Haiman–Haglund conjecture for $k=2$.

2 Preliminary

LLT polynomials are certain q-analogs of products of skew Schur functions defined by Lascoux et al. [12]. Below, we give an alternative definition presented in [7]. Let $\varvec{\lambda }= (\lambda ^{(0)},\lambda ^{(1)}, \ldots , \lambda ^{(d-1)})$ be a d-tuple of (skew) tableaux. Define

$$\begin{aligned} {{\,\mathrm{SSYT}\,}}_d({\varvec{\lambda }})&= \{\text {semi-standard }d\text {-tuples of tableaux of shape } \varvec{\lambda } \}.\\ {{\,\mathrm{SYT}\,}}_d({\varvec{\lambda }})&= \{\text {standard }d\text {-tuples of tableaux of shape } \varvec{\lambda } \}. \end{aligned}$$

If $\varvec{T}=(T^{(0)}, \ldots , T^{(d-1)}) \in {{\,\mathrm{SSYT}\,}}_d(\varvec{\lambda })$ has entries $1^{\pi _1},2^{\pi _2}, \ldots$, then we say that $\varvec{T}$ has shape $\varvec{\lambda }$ and weight $\pi =(\pi _1,\pi _2,\ldots )$. For a d-tuple of skew shapes $(\lambda ^{(0)},\lambda ^{(1)}, \ldots , \lambda ^{(d-1)})$, define the shifted content of a cell x by

$$\begin{aligned} {\tilde{c}}(x)= d \cdot c(x)+ i \end{aligned}$$

where x is a cell of $\lambda ^{(i)}$, where c(x) is the usual content of x regarded as a cell of $\lambda ^{(i)}$. For $\varvec{T} \in {{\,\mathrm{SSYT}\,}}_d(\varvec{\lambda })$, let $\varvec{T}(x)$ be the entry of the cell x in $\varvec{T}$. Define the set of inversions of $\varvec{T}$ by

$$\begin{aligned} {{\,\mathrm{Inv}\,}}_d(\varvec{T})= \{(x,y) \mid d> {\tilde{c}}(y)- {\tilde{c}}(x)>0 \text { and } \varvec{T}(x)>\varvec{T}(y) \}, \end{aligned}$$

and the inversion number of $\varvec{T}$ is given by $|{{\,\mathrm{Inv}\,}}_d(\varvec{T})|$, denoted by ${{\,\mathrm{inv}\,}}_d(\varvec{T})$.

By [7], the LLT polynomial ${\tilde{G}}_{{\varvec{\lambda }}}[X;q]$ is given by

$$\begin{aligned} {\tilde{G}}_{{\varvec{\lambda }}}[X;q]=\sum _{\varvec{T}\in {{\,\mathrm{SSYT}\,}}_d({\varvec{\lambda }})} q^{{{\,\mathrm{inv}\,}}_d(\varvec{T})}x^{\varvec{T}}, \end{aligned}$$

where $x^{\varvec{T}}$ is the monomial $x_1^{\pi _1}x_2^{\pi _2}\cdots$ when $\varvec{T}$ has weight $\pi$. Lascoux et al. [12] showed that ${\tilde{G}}_{\varvec{\lambda }}[X;q]$ is a symmetric function. Let $\Lambda$ be the ring of symmetric function over the coefficients ${\mathbb {Q}}[t]$, and let $\omega$ be the involution on $\Lambda$.

Define the content reading word of a d-tuple of tableaux to be the word obtained by reading entries in increasing order of shifted content. For a word $\varvec{v}=v_1v_2 \ldots v_n$, define the descent set ${{\,\mathrm{Des}\,}}(v) := \{ i \mid v_i>v_{i+1} \}$ of v, and define ${{\,\mathrm{Des}\,}}(\varvec{T})$ by the descent set of the content reading word of $\varvec{T}$. Then, Assaf [1] showed that one writes LLT polynomials in terms of Gessel’s fundamental quasisymmetric functions:

$$\begin{aligned} {\tilde{G}}_{{\varvec{\lambda }}}[X;q]= \sum _{\varvec{T}\in {{\,\mathrm{SYT}\,}}_d({\varvec{\lambda }})} q^{{{\,\mathrm{inv}\,}}_d(\varvec{T})} F_{{{\,\mathrm{Des}\,}}(\varvec{T})}. \end{aligned}$$

It is known by Grojnowski and Haiman [6] that LLT polynomials are Schur positive. Moreover, Haiman and Haglund conjectured the following stronger statement.

Conjecture 2.1

For an integer p and $k>0$ such that for any cell x in ${\varvec{\lambda }}$ the content c(x) satisfies $p\le c(x) <p+k$, then $\omega {\tilde{G}}_{{\varvec{\lambda }}}[X;q]$, the involution of the LLT polynomial for ${\varvec{\lambda }}$, is k-Schur positive.

Remark 2.2

The easiest case is $k=1$, where LLT polynomials are determined by the number n of cells in ${\varvec{\lambda }}$. In this case, $\omega {\tilde{G}}_{{\varvec{\lambda }}}[X;q]$ is equal to the Hall–Littlewood polynomial $H_{1^n}[X,q]$, which is also the 1-Schur function $s^{(1)}_{1^n}$.

There are two different ways of defining LLT polynomials that Grojnowski and Haiman [6] showed that they are essentially the same. In [6], the LLT polynomial defined above is called the new variant combinatorial LLT polynomial. Another one is called the combinatorial LLT polynomial $G'_{\mu ^{(1)}/\mu ^{(2)}}[X;u]$ defined in terms of the ribbon tableau generating function in a skew shape $\mu ^{(1)}/\mu ^{(2)}$ such that the power of u encodes the spin statistics of the ribbon tableau, defined by Lascoux et al. [12]. Grojnowski and Haiman showed in [6, Proposition 6.17] that a new variant combinatorial LLT polynomial for ${\varvec{\lambda }}$ is the same as a certain power of u times the combinatorial LLT polynomial $G'_{\mu ^{(1)}/\mu ^{(2)}}[X;u^{-1}]$ for certain skew shape $\mu ^{(1)}/\mu ^{(2)}$ where $u^2=q$. Haiman announced the conjecture in ICM 2006 talk that the combinatorial LLT polynomials are k-Schur positive, and this conjecture is equivalent to Conjecture 2.1. It seems that Haiman and Haglund contributed together to build the conjecture around 2004.

3 Unicellular LLT polynomials

In this section, we consider unicellular LLT polynomials, i.e., $\lambda ^{(i)}$ consists of one box with content $c_i$ for some $c_i \in {\mathbb {Z}}$ for all $0\le i \le d-1$. For the rest of this section, we assume that ${\varvec{\lambda }}$ satisfies the above condition unless stated otherwise. For such a ${\varvec{\lambda }}$, one can associate a permutation $w_{{\varvec{\lambda }}}$ in $S_d$ defined by

$$\begin{aligned} w_{{\varvec{\lambda }}}(i+1)= |\{j \mid {\tilde{c}}_j<{\tilde{c}}_i \}| +1, \end{aligned}$$

for $0\le i \le d-1$ where ${\tilde{c}}_i=d\cdot c_i+i$.

Let n denote the number of boxes in ${\varvec{\lambda }}$, and in this case n is equal to d. For a positive integer $i \le n$, define the number $\lambda _i$ by the cardinality of the set

$$\begin{aligned} \{j \mid {\tilde{c}}_j>{\tilde{c}}_{w_{\varvec{\lambda }}^{-1}(i)-1}+d\}. \end{aligned}$$

Note that we have $0\le \lambda _i \le i-1$. Moreover, if $i<j$, then $\lambda _i\ge \lambda _j$ since the sequence ${\tilde{c}}_{w_{\varvec{\lambda }}^{-1}(i)-1}$ is increasing. Therefore, for ${\varvec{\lambda }}$, one can associate a partition $\lambda =(\lambda _1,\ldots ,\lambda _n)$ contained in a staircase shape $(n-1,n-2,\ldots ,1)$, and one can compute the LLT polynomial ${\tilde{G}}_{{\varvec{\lambda }}}[X;q]$ in terms of $\lambda$.

For a permutation v in $S_n$ and a set D of some (i, j) satisfying $1\le i < j \le n$, define inv(v, D) by the number of inversions (p, q) of v such that $(p,q)\in D$. For a partition $\lambda \in (n-1,n-2, \ldots ,1)$, let $D_\lambda$ be the set of cells in $\lambda$ where partitions are drawn with the English convention. See Fig. 1.

Fig. 1

Unicellular ${\varvec{\lambda }}$ and corresponding $D_\lambda$ for $\lambda =(3,1)$

Proposition 3.1

If ${\varvec{\lambda }}$ lies in two adjacent diagonals, $\lambda$ is contained in $m \times (n-m)$ for some m. Conversely, if $\lambda$ is contained in $m\times (n-m)$ for some m, then there is d-tuple of cells ${\varvec{\mu }}$ lying in two adjacent diagonals such that the corresponding partition $\mu$ is equal to $\lambda$.

Proof

Let m be the number of boxes in ${\varvec{\lambda }}$ lying on the diagonal with a lower content. Then, $D_\lambda$ does not contain (i, j) with $1\le i < j \le m$. Similarly, $D_\lambda$ does not contain (i, j) with $m<i<j\le n$. Therefore, $\lambda$ is contained in $m \times (n-m)$. For the second statement, we first put m boxes at the diagonal with a content 0. Then, for each ith box with $i>m$ with respect to the shifted content order, there is a unique possible position at the diagonal with content 1 determined by $\lambda$ so ${\varvec{\mu }}$ is also determined. $\square$

One can write LLT polynomials in terms of quasisymmetric function in the following way:

Proposition 3.2

${\tilde{G}}_{{\varvec{\lambda }}}[X;q]$ is the same as

$$\begin{aligned} \sum _{v\in S_n} q^{inv(v,D_\lambda )} F_{D(v^{-1})}. \end{aligned}$$

(1)

For the rest of the paper, we denote the inverse descent set $D(v^{-1})$ by ${{\,\mathrm{ID}\,}}(v)$. If ${\varvec{\lambda }}$ is a tuple of single cells, we denote ${\tilde{G}}_{{\varvec{\lambda }}}[X;q]$ by $G_{\lambda }[X;q]$.

One can generalize Formula (1) in the following way. For a permutation w in $S_n$, let ${{\,\mathrm{Inv}\,}}(w)$ be the set of inversions of w. For a permutation w in $S_n$ and a $n \times n$ matrix $M=(m_{ij})$ with $m_{ij}=0$ unless $i<j$, define an inversion number of w with respect to M defined by

$$\begin{aligned} {{\,\mathrm{inv}\,}}(w,M):=\sum _{1\le i <j \le n} m_{ij}\cdot \chi \left( (i,j) \in {{\,\mathrm{Inv}\,}}(w)\right) . \end{aligned}$$

Here, $\chi (\text {True})=1$ and $\chi (\text {False})=0$.

It is clear that ${{\,\mathrm{inv}\,}}(w,M)$ is the usual inversion number if $m_{ij}=1$ for all $i<j$, and it is the same as the major index if $m_{i,i+1}=i$ for all i and 0 otherwise. For the rest of this paper, the matrix M satisfies the following condition:

$$\begin{aligned} \text {if }m_{ij}=0 \text { for some }i<j, \text { then } m_{kl}=0 \text { for any } k<i<j<l. \end{aligned}$$

(2)

Definition 3.3

For such a matrix M, define a function $G_M[X;q]$ defined by

$$\begin{aligned} \sum _{w \in S_n} q^{{{\,\mathrm{inv}\,}}(w,M)} F_{{{\,\mathrm{ID}\,}}(w)}. \end{aligned}$$

A relationship between $G_M[X;q]$ and unicellular LLT polynomials is as follows. If all entries of M are either 1 or 0 and satisfy condition (2), then a function $G_M[X;q]$ is the unicellular LLT polynomial $G_{\lambda }[X;q]$ by Theorem 3.2, where $\lambda _i$ is the maximum of $\text {max}\{ j \mid m_{il}=0 \text { for all } l \le j\}$ and $n+1-i$. Conversely, given $\lambda$ contained in the staircase tableau, one can define the corresponding matrix M, and we denote this matrix by $M_\lambda$.

Let $L(n,\lambda ;q)$ be $\omega G_{{\varvec{\lambda }}}[X;q]$. When n is clear, we denote $L(n,\lambda ;q)$ by $L(n,\lambda )$ in short.

Remark 3.4

It is known that $q^p \cdot L(n,\lambda ;q^{-1})=G_{{\varvec{\lambda }}}[X;q]$, where p is $\frac{n(n-1)}{2} - |\lambda |$ from [6, Lemma 6.12] and [6, Proposition 6.17].

The following theorem provides a local linear relation between unicellular LLT polynomials.

Theorem 3.5

For a partition $\lambda$ and a positive integer i such that $\lambda _i +2 \le \lambda _{i-1}$, if $i=1$, then let $\lambda _0$ be infinity. Let $\mu ^0=\lambda , \mu ^1,\mu ^2$ be partitions defined by $\mu ^a_j= \lambda _j$ if $j\ne i$ and $\mu ^a_i=\lambda _i +a$ for $a=0,1,2$. Then,

$$\begin{aligned} G_{\mu ^0}[X;q] - G_{\mu ^1}[X;q] = q (G_{\mu ^1}[X;q] - G_{\mu ^2}[X;q] ). \end{aligned}$$

when $\lambda _{n-\lambda _i-1}=\lambda _{n-\lambda _i }$. By taking the involution, we have

$$\begin{aligned} L(n,\mu ^0) - L(n,\mu ^1)= q (L(n,\mu ^1)- L(n,\mu ^2) ). \end{aligned}$$

Remark 3.6

The last condition $\lambda _{n-\lambda _i-1}=\lambda _{n-\lambda _i }$ holds if $\lambda ,\mu ^1,\mu ^2$ are contained in a rectangle $m \times (n-m)$ for some m. Indeed, since $\lambda _i+2 \le n-m$, we have $n-\lambda _i-1 \ge m+1$ so that $\lambda _{n-\lambda _i-1}=\lambda _{n-\lambda _i}=0$.

Fig. 2

$\lambda ,\mu _1,\mu _2$ for Example 3.8 and Theorem 3.5

Remark 3.7

Theorem 3.5 is equivalent to the statement that there are two symmetric functions $g_1,g_2$ satisfying

$$\begin{aligned} G_{\mu ^0}[X;q]&=g_1+g_2\\ G_{\mu ^1}[X;q]&=g_1+ q^{-1}g_2\\ G_{\mu ^2}[X;q]&=g_1+q^{-2} g_2. \end{aligned}$$

In fact, we will show that if $\mu ^a$ are contained in the rectangle $m \times (n-m)$, then the conjugates of $g_1$ and $g_2$ are both 2-Schur positive.

Proof of Theorem 3.5

We use a bijection from $S_n$ to $S_n$ described in [10].

For $1 \le x<y \le n$, let $A_{x,y}$ be the subset $\{ w \in S_n \mid (x,y) \in {{\,\mathrm{Inv}\,}}(w)\}$ of $S_n$. Consider the following bijection:

$$\begin{aligned} f_{xy} : A_{x,y} \longrightarrow A_{x,y+1} \end{aligned}$$

defined by $f_{xy}(w)=w$ if both $(x,y),(x,y+1)$ are in ${{\,\mathrm{Inv}\,}}(w)$, and $f_{xy}(w)= ws_y$ if $(x,y+1)$ is not in ${{\,\mathrm{Inv}\,}}(w)$. In the second case, (x, y) is not in ${{\,\mathrm{Inv}\,}}( ws_y)$ and $(x,y+1)$ is in ${{\,\mathrm{Inv}\,}}( ws_y)$ by the construction. A. Similarly, a slight modification of the map $f_{xy}$ and the proof of the bijectivity of $f_{xy}$ provide a bijection $f'_{xy}$ between $A^c_{x,y}$ and $A^c_{x,y+1}$, defined by $f'_{xy}(w)=w$ if $(x,y+1) \notin {{\,\mathrm{Inv}\,}}(w)$ and $f'_{xy}(w)= w s_y$ if $(x,y+1) \in {{\,\mathrm{Inv}\,}}(w)$. We denote this bijection by the same notation $f_{xy}$ so that $f_{xy}$ is a bijection from $S_n$ to $S_n$.

To prove the theorem, set $x= i$ and $y=n-1-\lambda _i$. For the example in Fig. 2, we have $x=1$ and $y=4$. It turns out that the above bijection preserves ${{\,\mathrm{inv}\,}}(w,D_{\mu ^1})$. First of all, it is obvious when $f_{xy}$ is the identity map. If $f_{xy}(w)= ws_y$, for $M=M_{\mu ^a}$ ($a=0,1,2$), we have $M_{r,y}=M_{r,y+1}$ for $r<x$ by the construction of $\mu ^a$. Moreover, $M_{y,s}=M_{y+1,s}$ for all $s>y+1$ by the condition $\lambda _{n-\lambda _i-1}=\lambda _{n-\lambda _i }$ for $M=M_{\mu ^a}$. If $\lambda$ is contained in a rectangle $m\times (n-m)$ for some m, these numbers are 0. Therefore, to show that ${{\,\mathrm{inv}\,}}(w,D_{\mu ^1})$ does not change, it is enough to show that the cardinality of the set $\{(x,y),(y,y+1)\} \cap {{\,\mathrm{inv}\,}}(w,D_{\mu ^1})$ is constant when applying the map $f_{xy}$. This condition can be checked case by case, assuming the following well-known facts: If $(x,y) \in {{\,\mathrm{inv}\,}}(w)$ and $(x,y+1) \notin {{\,\mathrm{inv}\,}}(w)$, then $(y,y+1) \notin {{\,\mathrm{inv}\,}}(w)$. Also if $(x,y) \notin {{\,\mathrm{inv}\,}}(w)$ and $(x,y+1) \in {{\,\mathrm{inv}\,}}(w)$, then $(y,y+1) \in {{\,\mathrm{inv}\,}}(w)$.

Now we are ready to prove Theorem 3.5. Let $g_1,g_2$ be the symmetric functions

$$\begin{aligned} g_1&=\omega \left( \sum _{w \in A^c_{xy}} q^{{{\,\mathrm{inv}\,}}(w,M_\lambda )}F_{{{\,\mathrm{ID}\,}}(w)}\right) \\ g_2&=\omega \left( \sum _{w \in A_{xy}} q^{{{\,\mathrm{inv}\,}}(w,M_\lambda )}F_{{{\,\mathrm{ID}\,}}(w)}\right) , \end{aligned}$$

where $\omega$ is the involution. It is clear from the definition that $G_\lambda =g_1+g_2$ and $G_{\mu ^1} = g_1 + q^{-1} g_2$. Therefore, it is enough to show that $G_{\mu ^2}=g_1 + q^{-2} g_2$. By the bijection $f_{xy}$, we have

$$\begin{aligned} g_1&=\omega \left( \sum _{w \in A^c_{x,y+1}} q^{{{\,\mathrm{inv}\,}}(w,M_{\mu ^1})}F_{{{\,\mathrm{ID}\,}}(w)}\right) \\ g_2&=\omega \left( \sum _{w \in A_{x, y+1}} q^{{{\,\mathrm{inv}\,}}(w,M_{\mu ^1})+1}F_{{{\,\mathrm{ID}\,}}(w)}\right) , \end{aligned}$$

Since $w \in A_{x,y+1}$, we have $(x,y+1) \in {{\,\mathrm{Inv}\,}}(w)$, ${{\,\mathrm{inv}\,}}(w,M_{\mu ^1})={{\,\mathrm{inv}\,}}(w,M_{\mu ^2})+1$ and

$$\begin{aligned} g_1&=\omega \left( \sum _{w \in A^c_{x,y+1}} q^{{{\,\mathrm{inv}\,}}(w,M_{\mu ^2})}F_{{{\,\mathrm{ID}\,}}(w)}\right) \\ g_2&=\omega \left( \sum _{w \in A_{x, y+1}} q^{{{\,\mathrm{inv}\,}}(w,M_{\mu ^2})+2}F_{{{\,\mathrm{ID}\,}}(w)}\right) , \end{aligned}$$

Therefore, we have

$$\begin{aligned} G_{\mu ^2}[X;q]&= \omega \left( \sum _{w \in A^c_{x+1,y}} q^{{{\,\mathrm{inv}\,}}(w,M_{\mu ^2})}F_{{{\,\mathrm{ID}\,}}(w)}\right) +\omega \left( \sum _{w \in A_{x+1, y}} q^{{{\,\mathrm{inv}\,}}(w,M_{\mu ^2})}F_{{{\,\mathrm{ID}\,}}(w)}\right) \\&= g_1+q^{-2}g_2,\\ \end{aligned}$$

we are done. $\square$

Example 3.8

For a partition $\mu$ with $\mu _1\le 2$, let $s^{(2)}_\mu$ denote the 2-Schur function indexed by $\mu$. Let $n=6$, $\lambda =(1,1)$, and $i=1$. Then, we have $\mu ^1=(2,1)$, $\mu ^2=(3,1)$, and

$$\begin{aligned} L(n,\lambda )&= s^{(2)}_{1,1,1,1,1,1}+ (q^4+2q^3)s^{(2)}_{2,1,1,1,1}+(2q^6+q^5)s^{(2)}_{2,2,1,1}+ q^7 s^{(2)}_{2,2,2}\\ L(n,\mu ^1)&= s^{(2)}_{1,1,1,1,1,1}+ 3q^3s^{(2)}_{2,1,1,1,1}+3q^5s^{(2)}_{2,2,1,1}+ q^6 s^{(2)}_{2,2,2}\\ L(n,\mu ^2)&= s^{(2)}_{1,1,1,1,1,1}+ (2q^3+q^2)s^{(2)}_{2,1,1,1,1}+(q^5+2q^4)s^{(2)}_{2,2,1,1}+ q^5 s^{(2)}_{2,2,2}. \end{aligned}$$

See Fig. 2. Therefore, one can take

$$\begin{aligned} g_1&=s^{(2)}_{1,1,1,1,1,1}+ 2q^3s^{(2)}_{2,1,1,1,1}+q^5s^{(2)}_{2,2,1,1}\\ g_2&=q^4s^{(2)}_{2,1,1,1,1}+ 2q^6s^{(2)}_{2,2,1,1}+ q^7 s^{(2)}_{2,2,2} \end{aligned}$$

so that Remark 3.7 holds.

4 Linearity theorem

In this section, we show Theorem 4.1.

Theorem 4.1

(Linearity theorem) Let $\lambda$ be the partition contained in $(n-m)^{m}$. For a subset I of $\{1,2,\ldots ,m\}$ and $i\in I$, define $e_i$ by 1 if $i\in I$ and 0 otherwise. Then, there are 2-Schur positive functions $f_{I,m}$ such that

$$\begin{aligned} L(n,\lambda )= \sum _{I \subset [m]} f_{I,m} q^{- e_I\cdot \lambda } \end{aligned}$$

(3)

where $e_I\cdot \lambda = \sum _{j=1}^m e_i \lambda _i$.

The proof of Theorem 4.1 is twofold: existence of polynomials $f_{I,m}$ satisfying the equation and 2-Schur positivity of $f_{I,m}$. Explicit formulas for $f_{I,m}$ are given in Theorems 4.8 and 4.5.

Since k-Schur functions are not easy to define but we only need 2-Schur functions, we assume the following theorem stating one important relation between LLT polynomials and 2-Schur function.

Theorem 4.2

Let $\eta _0$ be the horizontal domino (2) and $\eta _1$ be the vertical domino (1, 1). For a $0-1$ sequence $a=(a_1,\ldots ,a_m)$ and $n=2m$, define the m-tuple of tableaux $\varvec{\eta }_a=(\eta _{a_1},\ldots ,\eta _{a_m})$ such that all tableaux lie in two adjacent diagonals with contents 0 and 1. Then, we have

$$\begin{aligned} \omega ({\tilde{G}}_{\varvec{\eta }_a})=q^{M} s^{(2)}_{2^l 1^{n-2l}} \end{aligned}$$

where l is the number of 1 in a and $M=\sum _{i=1}^{\ell } (m-i)$. Similarly, for $n=2m+1$, define $\varvec{\eta }_a$ by $(\eta _{a_1},\ldots , \eta _{a_m},b)$ where b is a box with a content 0. Then, we have

$$\begin{aligned} \omega ({\tilde{G}}_{\varvec{\eta }_a})=q^{M'} s^{(2)}_{2^l 1^{n-2l}} \end{aligned}$$

where l is the number of 1 in a and $M'=\sum _{i=1}^{\ell } (m-i+1)$.

The proof of Theorem 4.2 will be given in the next section, and we prove Theorem 4.1 for $m=[n/2]$ assuming Theorem 4.2. For $m<[ n/2]$, the proof follows from the case for $m=[n/2]$.

We start by assuming $\delta _{m-1} \subset \lambda \subset \delta _m$ and writing $f_{I,m}$ in terms of $\omega ({\tilde{G}}_{\varvec{\eta }_a})$.

Theorem 4.3

Let $\delta _{m}$ be the staircase tableau $(m,m-1, \ldots , 1)$ and $m=[n/2]$. Then, Theorem 4.1 is true for $\delta _{m-1} \subset \lambda \subset \delta _m$ with

$$\begin{aligned} f_{I,m}= q^{e_I \delta _{m}} \omega ({\tilde{G}}_{\varvec{\eta }_{a_I}}) \end{aligned}$$

where $a_i$ is 1 if $i \in I$ and 0 otherwise.

Proof

Let $\lambda$ be $\delta _{m} - b_\lambda$ where $b_\lambda$ is a $0-1$ sequence of length m. Then, the theorem is equivalent to the formula

$$\begin{aligned} G_\lambda [X;q]= \sum _{I \subset \{1,2,\ldots ,m\}}q^{e_I\cdot b_\lambda } {\tilde{G}}_{\varvec{\eta }_{a_I}}[X;q]. \end{aligned}$$

(4)

which is clear by the following lemma:

Lemma 4.4

Let ${\varvec{\lambda }}$ be d-tuple of skew partitions such that $\lambda ^{(i)}$ is a single box with a content $\epsilon$ for $\epsilon =0$ or 1 and $\lambda ^{(i+1)}$ is a single box with a content $1-\epsilon$. Then,

$$\begin{aligned} {\tilde{G}}_{\varvec{\lambda }}= {\tilde{G}}_{{\varvec{\mu }}_0}+q^\epsilon {\tilde{G}}_{{\varvec{\mu }}_1} \end{aligned}$$

where ${\varvec{\mu }}_\epsilon$ is a $(d-1)$-tuple of skew partitions obtained by replacing two partitions $\lambda ^{(i)}$ and $\lambda ^{(i+1)}$ by a domino $\varvec{\eta }_\epsilon$.

The lemma is obvious by the definition of LLT polynomials and the theorem follows. $\square$

Before we prove Theorem 4.1, we list formulas for $f_{I,m}$.

Theorem 4.5

Assume that $m=[n/2]$. Let l be the size of I. If $I=\{m-l+1,m-l+2, \ldots , m \}$, then $f_{I,m}= q^{ml} s^{(2)}_{2^l 1^{n-2l}}$. For a subset I, there is a partition $\mu$ such that

$$\begin{aligned} I= \{ m-l+1-\mu _1, m-l+2-\mu _2, \ldots , m- \mu _l \} \end{aligned}$$

Then, $f_{l,m}= q^{ml+|\mu |} s^{(2)}_{2^l 1^{n-2l}}$ if n is even, and $f_{l,m}= q^{(m+1)l+|\mu |} s^{(2)}_{2^l 1^{n-2l}}$ if n is odd.

Note that for fixed l, the maximum of $ml+|\mu |$ for even n and the maximum of $(m+1)l+ |\mu |$ for odd n are the same as $l(n-l)$.

Remark 4.6

Note that the number of weak standard tableaux of length n for $k=2$ is $2^{[n/2]}$ [11] which is the same as the number of possible I for $m=[n/2]$.

The function $f_{I,m}$ when $m<[n/2]$ is the following:

Proposition 4.7

For $m\le [n/2]$, we have

$$\begin{aligned} f_{J,m}= \sum f_{I,[n/2]} \end{aligned}$$

where the sum runs over all subset $I \subset \{1,2,\ldots ,[n/2]\}$ such that $J=I \cap \{1,2,\ldots ,m\}$.

The above-mentioned formulas for $f_{I,m}$ follow from Theorems 4.2 and 4.3 assuming existence of $f_{I,m}$ satisfying Eq. (3), hence proving the existence of $f_{I,m}$ is crucial.

We need one more observation to prove the existence of $f_{I,m}$ in Theorem 4.1.

Lemma 4.8

Equation (3) in Theorem 4.1 implies Theorem 3.5 for any choice of $\lambda ,\mu ^1,\mu ^2$ satisfying the hypothesis in Theorem 3.5. Conversely, assuming the hypothesis in 3.5, if Eq. (3) holds for two of $\lambda ,\mu ^1,\mu ^2$, then Eq. (3) holds for all three partitions.

Proof

Obvious. $\square$

Now we are ready to prove Theorem 4.1.

Lemma 4.9

For $m=[n/2]$, assume that Theorem 4.1 holds for $\lambda$ satisfying $\delta _{m-1} \subset \lambda \subset \delta _m$. Then, Theorem 4.1 holds for all $\lambda \subset \delta _m$ with the same $f_{I,m}$. Moreover, Theorem 4.1 holds for all $\lambda \subset \delta _m$ for any $m\le [n/2]$.

Proof

During the proof, we will only use Theorem 3.5. Let $p=p_\lambda$ be the minimum in the set $\{ i \mid \lambda _i \ne m+1-i,m-i \}$. If the set is empty, we set $p_\lambda =m$. Note that the minimum number in the set cannot be m since $\lambda _m$ is either 0 or 1.

We use an induction on $p_\lambda$. The base case $p_\lambda =m$ follows from Theorem 4.2 and Eq. (4). Assume that Theorem 4.1 is true for all $\lambda$ with $r<p_\lambda$, and let $\nu$ be a partition with $r=p_{\nu }$. For an integer $\nu _{r+1} \le a \le m+1-r$, let $\mu ^a$ be partitions with $\mu ^a_i=\nu _i$ for $i \ne r$ and $\mu ^a_{r} = a$. Note that Theorem 4.1 is true for $\mu ^a$ with $a=m+1-r,m-r$ by the induction hypothesis. By Theorem 3.5, if we have $\mu ^{m+1-r}= g_1 + g_2$ and $\mu ^{m-r} = g_1 + q g_2$, then $\mu ^a= g_1 + q^{m+r-1-a} g_2$. By Lemma 4.8, Theorem 4.1 is true for all $\mu ^a$, including $\nu$.

To show the lemma for $m<[n/2]$ and $\lambda \subset \delta _m$, it is enough to observe $\delta _m\subset \delta _{[n/2]}$ and

$$\begin{aligned} L(n,\lambda )&= \sum _{I \subset \{1,2,\ldots ,[n/2]\}} f_{I,[n/2]} q^{- e_I\cdot \lambda } \\&= \sum _{J \subset \{1,2,\ldots ,m\}} \left( \sum _{I\cap \{1,2,\dots ,m\}=J}f_{I,[n/2]} \right) q^{- e_I\cdot \lambda } \end{aligned}$$

and hence we have

$$\begin{aligned} f_{J,m}=\sum _{I\cap \{1,2,\dots ,m\}=J} f_{I,[n/2]} \end{aligned}$$

and we are done. $\square$

Proof of Theorem 4.1

Assume that there is $\lambda$ that does not satisfy Theorem 4.1 with $f_{I,m}$ determined by Theorem 4.3 when $m=[n/2]$, and Proposition 4.7 when $m<[n/2]$. Choose $\lambda$ with minimal size. We will show that for every i, $\lambda$ satisfies the inequality $\lambda _{i}\le \lambda _{i+1}+1$. If this is true, then we have $\lambda \subset \delta _m$ and we have a contradiction by Lemma 4.9.

Assume that there is i such that $\lambda _i \ge \lambda _{i+1}+2$. For $a=1,2$, define $\mu ^a$ be the partition defined by $\mu ^a_j= \lambda _j$ for $j \ne i+1$ and $\mu ^a_{i+1}=\lambda _{i+1}+a$. Since $|\mu ^a|>|\lambda |$, $\mu ^a$ for $a=1,2$ satisfy Theorem 4.1. Therefore, by Lemma 4.8$\lambda$ also satisfies Theorem 4.1 which makes a contradiction. $\square$

5 LLT polynomials for dominos and 2-Schur functions

In this section, we prove Theorem 4.2. To prove Theorem 4.2, we introduce generalized Hall–Littlewood polynomials and 2-Schur functions. Then, we show that $\omega ({\tilde{G}}_{\varvec{\eta }_a})$ appearing in Theorem 4.3 is the same as 2-Schur functions up to a power of q.

5.1 Generalized Hall–Littlewood polynomials

For a symmetric function f, g, let $f^\perp (g)$ be the unique symmetric function satisfying $\langle g, fh \rangle = \langle f^\perp (g) , h\rangle$ for any symmetric function h. One can use this to define creation operators for the Schur functions, defined by where $h_r$ (resp. $e_r$) is the complete homogeneous symmetric function (resp. the elementary symmetric function) of degree r.

Jing [9] defined the operators for a positive integer a that generalize the creation operators for Schur functions. Define

Let $H_\lambda [X;q]$ be the Hall–Littlewood polynomials. Then, this family of operator has the property that

Shimozono and Zabrocki generalized the operators for any partition by

where

Note that if $q=0$, then and .

For tuple of partitions ${\varvec{\lambda }}= (\lambda ^{(0)},\lambda ^{(1)}, \ldots , \lambda ^{(d-1)})$, consider the generalized Hall–Littlewood polynomials defined by

Grojnowski and Haiman [6, Theorem 7.15] showed the following.

Theorem 5.1

If $\lambda ^{(i)}$ is a rectangle for all i such that contents of southwest corners of $\lambda ^{(i)}$ are weakly increasing and contents of southeast corners of $\lambda ^{(i)}$ are weakly decreasing, $K_{{\varvec{\lambda }}}[X;q]$ is equal to a power of q times $\omega ({\tilde{G}}_{{\varvec{\lambda }}'})$ where ${\varvec{\lambda }}'=(\lambda ^{(0)'},\ldots , \lambda ^{(d-1)'})$.

For our case, we set ${\varvec{\lambda }}=\varvec{\eta }_a$ with $a=(1,1,\ldots ,1,0,\ldots , 0)$ so $\lambda ^{(i)}$ are either a horizontal domino, a vertical domino or a single box. We show in Sect. 5.3 that $\omega ({\tilde{G}}_{\varvec{\eta }_a})$ only depends on the number $\ell$ of vertical dominos.

5.2 k-Schur functions

In this subsection, we show that for $a=(0^{m-\ell },1^\ell )$ and $m=[n/2]$, $K_{\varvec{\eta }_a}$ is equal to $s^{(2)}_{2^\ell 1^{n-\ell }}$. We first recall the algebraic definition of the k-Schur functions [13]. A partition $\lambda$ is called k-bounded if $\lambda _1\le k$. For a partition $\lambda$, let $h(\lambda )$ be the main hook length of $\lambda$ defined by $\lambda _1+ \ell (\lambda )-1$ where $\ell (\lambda )$ is the number of parts in $\lambda$. For a k-bounded partition $\lambda$, let $\lambda ^{\rightarrow k}$, called the k-split of $\lambda$, be $(\lambda ^{(1)},\ldots ,\lambda ^{(r)})$ where its concatenation is equal to $\lambda$, $h(\lambda ^{(i)})=k$ for all $i<r$, and $h(\lambda ^{(r)})\le k$. For example, $(3,2,2,2,1,1)^{\rightarrow 3} = \left( (3),(2,2),(2,1),(1) \right)$.

For a k-bounded partition, let $\lambda ^{\rightarrow k} =(\lambda ^{(1)},\ldots ,\lambda ^{(r)})$. The k-split polynomials are defined recursively by

with $C^{(k)}_{()}=1$. Let $T^{(k)}$ be an operator acting on the ring of symmetric functions defined by

$$\begin{aligned} T^{(k)}_i (C^{(k)}_\lambda [X;q] ) = {\left\{ \begin{array}{ll} C^{(k)}_\lambda [X;q] &{}\text {if } \lambda _1=i, \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Now we are ready to define k-Schur functions recursively.

Definition 5.2

For a k-bounded partition $\lambda$, if $\ell (\lambda )=1$ and $a\le k$, then $s^{(k)}_{a}$ is the Schur function $s_{a}$. Otherwise, for $\lambda _1 \le m \le k$, we define k-Schur functions by the following recursion:

For $k=2$, the following k-rectangular property [13, Theorem 26] of k-Schur functions is useful.

Theorem 5.3

If $\mu ,\nu ,\lambda$ are partitions where $\lambda =(\mu ,\nu )$ and $\mu _{\ell (\mu )}>\ell \ge \nu _1$, then

In particular, if $\ell \ge \lambda _1$, then

Theorem 5.3 implies that 2-Schur functions are the same as generalized Hall–Littlewood polynomials.

Theorem 5.4

Let $\lambda =(2^\ell , 1^{n-2\ell })$. Then, a 2-Schur function $s^{(2)}_{\lambda }[X;q]$ is the same as the generalized Hall–Littlewood polynomial $K_{\lambda ^{\rightarrow 2}}[X;q]$ indexed by 2-split of $\lambda$.

By Theorems 5.4 and 5.1, we know that $\omega ({\tilde{G}}_{\varvec{\eta }_a})$ for $a=(0^{m-\ell },1^\ell )$ is equal to a power of q times $s^{(2)}_{2^\ell ,1^{n-\ell }}$. To prove Theorem 4.2, we show that $\omega ({\tilde{G}}_{\varvec{\eta }_a})$ only depends on the number $\ell$ of vertical dominos and calculate the exponent of q.

5.3 Comparing different LLT polynomials

For a skew shape $\lambda$, let the content set of $\lambda$ be the set of contents of all boxes in $\lambda$. To prove that $\omega ({\tilde{G}}_{\varvec{\eta }_a})$ only depends on $\ell$, we show the following theorem.

Lemma 5.5

Let ${\varvec{\lambda }}$ be d-tuple of skew partitions such that $\lambda ^{(i)}$ is a horizontal domino with a content set $\{0,1\}$ and $\lambda ^{(i+1)}$ is a vertical domino with the content set $\{0,1\}$. Then,

$$\begin{aligned} {\tilde{G}}_{\varvec{\lambda }}={\tilde{G}}_{\varvec{\mu }}\end{aligned}$$

where ${\varvec{\mu }}$ is obtained from ${\varvec{\lambda }}$ by swapping $\lambda ^{(i)}$ and $\lambda ^{(i+1)}$.

Proof

We construct a bijection $\Psi$ between ${{\,\mathrm{SYT}\,}}({\varvec{\lambda }})$ and ${{\,\mathrm{SYT}\,}}({\varvec{\mu }})$ preserving the inversion number and entries in $\lambda ^{(j)}$ for $j\ne i,i+1$ to prove the theorem. The bijection will also preserve the set of entries at the diagonal with the content 0 so that we can assume $i=0$ and $d=2$. Indeed, we are only changing entries in ith and $(i+1)$th partitions of $\varvec{T}=(T^{(0)},\ldots , T^{(d-1)})$ so that the inversion set ${{\,\mathrm{Inv}\,}}_d(\varvec{T})$ does not change except pairs (x, y) satisfying $x,y \subset T^{(i)} \cup T^{(i+1)}$.

Assume that $i=0$ and $d=2$. For $\varvec{T} \in {{\,\mathrm{SYT}\,}}({\varvec{\lambda }})$, let

There are six possible cases for an order of a, b, c, d, and we define $\Psi$ case by case.

• (1) $a>d>c>b$: then, the number of inversions is 2 and set

  

  In this case, two pairs (a, d) and (d, b) are inversion pairs.

• (2) $a>d>b>c$: then, the number of inversion is 1 and set

  

  In this case, a pair (a, b) is an inversion pair.

• (3) $d>a>c>b$: then, the number of inversions is 2 and set

  

  In this case, two pairs (a, c) and (d, b) are inversion pairs.

• (4) $d>a>b>c$: then, the number of inversions is 1 and set

  

  In this case, a pair (d, b) is an inversion pair.

• (5) $a>b>d>c$: then, the number of inversions is 2 and set

  

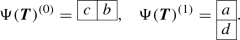
  In this case, pairs (a, b) and (b, d) are inversion pairs.

• (6) $d>c>a>b$: then, the number of inversions is 1 and set

  

  In this case, a pair (d, b) is an inversion pair.

$\square$

5.4 Proof of Theorem 4.2

Now we are ready to prove Theorem 4.2. First, note that by Theorems 5.1, 5.4 and Lemma 5.5, we know that $\omega ({\tilde{G}}_{\varvec{\eta }_a})$ is equal to $q^{p} s^{(2)}_{2^\ell 1^{n-2\ell }}$ for some integer p where $\ell$ is the number of 1 in a. To prove Theorem 4.2, we only need to show that $p=M$ for even n and $p=M'$ for odd n where $M, M'$ are defined in Theorem 4.2. Note that p is the minimum exponent of q appearing in $\omega ({\tilde{G}}_{\varvec{\eta }_a})$, since a 2-Schur function $s^{(2)}_{2^\ell 1^{n-2\ell }}$ has a term $s_{2^\ell 1^{n-2\ell }}$ with the minimum exponent 0 in its Schur expansion. We show $p=M$ for even n and leave it to readers for odd n.

By Lemma 5.5, one can assume that $a=(0^{m-\ell }1^\ell )$. First, we show that $p\ge M=\sum _{i=1}^\ell (m-i)$. For $\varvec{T}\in {{\,\mathrm{SYT}\,}}(\varvec{\eta }_a)$, $m-\ell +1\le i\le m$, and $j<i$, consider possible inversion pairs (x, y) where x is in $T^{(j)}$ and y is in $T^{(i)}$. Since $T^{(i)}$ is a vertical domino, there must be at least one inversion pair (x, y) where the cell x is in $T^{(j)}$ with a content 1 and y is a cell in $T^{(i)}$. Note that the number of (i, j) satisfying $m-\ell +1\le i\le m$, and $j<i$ is exactly M. Then, it is enough to find $\varvec{T}\in {{\,\mathrm{SYT}\,}}(\varvec{\eta }_a)$, so that there are no other inversion pairs. Indeed, one can choose $\varvec{T}$ so that for $0\le \alpha \le m-\ell -1$, numbers $\alpha +1$ and $m+\ell +\alpha +1$ appear in $T^{(\alpha )}$ and for $m-\ell \le \alpha \le m-1$, numbers $\alpha +1$ and $\alpha +\ell +1$ appear in $T^{(\alpha )}$. Then, the theorem follows. $\square$

6 Haiman–Haglund conjecture for $k=2$

In this section, we provide the 2-Schur expansion of the LLT polynomial indexed by skew shapes lying in two adjacent diagonals, confirming Conjecture 2.1 for $k=2$. Recall that for a skew shape $\lambda$, let the content set of $\lambda$ be the set of contents of all boxes in $\lambda$.

Let ${\varvec{\lambda }}=(\lambda ^{(0)},\lambda ^{(1)}, \ldots , \lambda ^{(d-1)})$ be the d-tuple of skew shapes such that $\lambda _{(i)}$ is either a vertical domino with content set $\{0,1\}$, a horizontal domino with content set $\{0,1\}$, a single cell with content 0 or a single cell with content 1. Let n be the number of boxes in ${\varvec{\lambda }}$, and let m be the number of boxes in ${\varvec{\lambda }}$ with content 0. Without loss of generality, one can assume that $m\le [n/2]$ because otherwise one can replace ${\varvec{\lambda }}$ by the conjugate of ${\varvec{\lambda }}$, defined by ${\varvec{\mu }}$ with $\mu ^{(i)}=g(\lambda ^{(d-1-i)})$ where the map $g(\mu )$ is the identity if $\mu$ is one of dominos and $g(\mu )$ is a cell with content $1-i$ if i is the content of a single cell $\mu$. One can show that LLT polynomials do not change.

For $1 \le i \le n$, let $x_i$ be the cell in ${\varvec{\lambda }}$ such that the shifted content ${\tilde{c}}_i$ of the cell $x_i$ satisfies ${\tilde{c}}_1<{\tilde{c}}_2<\cdots <{\tilde{c}}_n$. For a positive integer $i\le n$, $\lambda _i$ is the cardinality of the set

$$\begin{aligned} \{j \mid {\tilde{c}}_j \ge {\tilde{c}}_i+d\}. \end{aligned}$$

Note that $\lambda$ is a partition and $\lambda$ is contained in a rectangle $(n-m)^m$. Recall Theorem 4.1 that we have

$$\begin{aligned} L(n,\lambda )= \sum _{I \subset [m]} f_{I,m} q^{- e\cdot \lambda } \end{aligned}$$

where $e\cdot \lambda = \sum _{j=1}^m e_i \lambda _i$ and 2-Schur positive functions $f_{I,m}$. For given ${\varvec{\lambda }}$, define a subset $K \subset \{ 1,2,\ldots ,m \}$ satisfying $i \in K$ if and only if $x_{i}$ is contained in either a vertical domino and horizontal domino. Also for $i \in K$ define $\zeta _i$ by 0 if $x_{i}$ is contained in a horizontal domino, and 1 if $x_{i}$ is contained in a vertical domino. By Theorem 4.1 and Lemma 4.4, one can show that for $m\le [n/2]$, we have

$$\begin{aligned} G^{(n)}_{\varvec{\lambda }}= \sum _{\begin{array}{c} I \subset \{1, \ldots , m\} \\ e_i=\zeta _{i} \text { if } i \in I \end{array}} f_{I,m} q^{- e\cdot \lambda -z} \end{aligned}$$

where $f_{I,m}$’s are determined by Theorem 4.5 and Proposition 4.7, and z is the number of vertical dominos in ${\varvec{\lambda }}$.

By Theorem 4.5 and Proposition 4.7, we showed that $G^{(d)}_{\varvec{\lambda }}$ is 2-Schur positive, showing Conjecture 2.1 for $k=2$.

7 Concluding remarks

One of direct corollary from Theorem 4.1 is the 2-Schur expansion of product of 1-Schur functions. Note that a product of k-Schur function and $k'$-Schur function is conjecturally $(k+k')$-Schur positive.

Corollary 7.1

For $m\le n/2$ and a subset I of $\{1,2,\ldots , [n/2]\}$, let l be the size of I and $l_1$ be the size of $I \cap \{1,2,\ldots ,m\}$. Also, let $l_2$ be $\sum _{j\in I} j - { m\atopwithdelims ()2}$. Then,

$$\begin{aligned} s^{(1)}_{1^m}s^{(1)}_{1^{n-m}}= \sum _{I \subset \{1,2,\ldots , [n/2]\}} q^{-(n-m)l_1+l(n-l)- l_2} s^{(2)}_{2^l 1^{n-2l}} \end{aligned}$$

Proof

By Remark 2.2, the product $s^{(1)}_{1^m}s^{(1)}_{1^{n-m}}$ is equal to $L(n,(n-m)^m)$. Then, the corollary directly follows from Theorem 4.1 and Proposition 4.7. $\square$

Also note that Theorem 3.5 does not require the condition $k=2$, so that some of results in this paper can be generalized. Roughly speaking, Theorem 3.5 says that exponents of q are changing piecewise linearly, especially for small k. However, the identification of LLT polynomials for rectangles and generalized Hall–Littlewood polynomials does not seem to help much for $k>2$ when working with linear relations. In fact, understanding LLT polynomials indexed by ribbons is much more helpful to determine many of unicellular LLT polynomials since it is easier to use Lemma 4.8 and its obvious generalization for the case of ribbons instead of dominos. Note that finding a Schur expansion of LLT polynomials indexed by ribbons is a challenging problem as it provides a formula for Schur expansion of Macdonald polynomials as well.