Free vibration of joined cylindrical–hemispherical FGM shells

Abstract

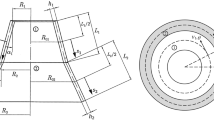
Free vibration response of a joined shell system including cylindrical and spherical shells is analyzed in this research. It is assumed that the system of joined shell is made from a functionally graded material (FGM). Properties of the shells are assumed to be graded through the thickness. Both shells are unified in thickness. To capture the effects of through-the-thickness shear deformations and rotary inertias, first-order shear deformation theory of shells is used. The Donnell type of kinematic assumptions is adopted to establish the general equations of motion and the associated boundary and continuity conditions with the aid of Hamilton’s principle. The resulting system of equations is discretized using the semi-analytical generalized differential quadrature method. Considering the clamped and free boundary conditions for the end of the cylindrical shell and intersection continuity conditions, an eigenvalue problem is established to examine the vibration frequencies of the joined shell. After proving the efficiency and validity of the present method for the case of thin isotropic homogeneous joined shells, some parametric studies are carried out for the system of combined moderately thick cylindrical–spherical shell system. Novel results are provided for the case of FGM joined shells to explore the influence of power-law index and geometric properties.

Appendix

After applying Eq. (24) to the motion equations (17) and (18), the following system of equations is extracted.

$$\begin{aligned}&A_{11}U_{,xx}^{\mathrm{c}}+\frac{A_{12}}{R}\left( -n V_{,x}^{\mathrm{c}}+ W_{,x}^{\mathrm{c}}\right) +B_{11}\Phi _{,xx}^{\mathrm{c}}-\frac{B_{12}}{R}n\Phi _{\theta ,x}^{\mathrm{c}}\nonumber \\&\quad +\,\frac{A_{66}}{R^2 } \left( -n^{2} U^{\mathrm{c}} - n RV_{,x}^{\mathrm{c}}\right) +\frac{B_{66}}{R^2}\left( -n^{2}\Phi _x^{\mathrm{c}} -n r\left( x\right) \Phi _{\theta , x}^{\mathrm{c}}\right) +\,I_1\omega ^{2}U^{\mathrm{c}}+I_2\omega ^{2}\Phi _x^{\mathrm{c}} =0\end{aligned}$$

(A.1)

$$\begin{aligned}&\frac{A_{12}n}{R }U_{,x}^{\mathrm{c}}+\frac{A_{22}}{R^2 }\left( -n^{2}V^{\mathrm{c}}+n W^{\mathrm{c}}\right) +\frac{A_{66}}{R }\left( n U_{,x}^{\mathrm{c}}+R V_{,xx}^{\mathrm{c}}\right) +\,\frac{B_{12}}{R }n\Phi _{x,x}^{\mathrm{c}}+\frac{B_{22}}{R^2}\left( -n^{2}\Phi _\theta ^{\mathrm{c}}\right) \nonumber \\&\quad +\frac{B_{66}}{R}\left( n\Phi _{x,x}^{\mathrm{c}}+R \Phi _{\theta ,xx}^{\mathrm{c}}\right) +\,\frac{\kappa A_{44} }{R^2}\left( -V^{\mathrm{c}} +R \Phi _\theta ^{\mathrm{c}} +n W^{\mathrm{c}}\right) +I_1\omega ^{2}V^{\mathrm{c}}+I_2\omega ^{2}\Phi _\theta ^{\mathrm{c}}=0\end{aligned}$$

(A.2)

$$\begin{aligned}&-\,\frac{A_{12} }{R^2}U_{,x}^{\mathrm{c}}-\frac{A_{22} }{ R^2}\left( -nV^{\mathrm{c}}+ W^{\mathrm{c}} \right) -\frac{B_{12} }{R}\Phi _{x,x}^{\mathrm{c}}+\frac{B_{22} }{R^2}n\Phi _{\theta }^{\mathrm{c}} \nonumber \\&\quad +\,\kappa A_{55}\left( \Phi _{x,x}^{\mathrm{c}}+W_{,xx}^{\mathrm{c}} \right) +\frac{\kappa A_{44}}{R^2} \left( n V^{\mathrm{c}}-n R \Phi _\theta -n^{2}W^{\mathrm{c}}\right) +I_1\omega ^{2}W^{\mathrm{c}}=0\end{aligned}$$

(A.3)

$$\begin{aligned}&B_{11}U_{,xx}^{\mathrm{c}}+\frac{B_{12}}{R }\left( -n V_{,x}^{\mathrm{c}}+ W_{,x}^{\mathrm{c}}\right) +D_{11}\Phi _{,xx}^{\mathrm{c}}-\frac{D_{12}n}{R}\Phi _{\theta ,x}^{\mathrm{c}}\nonumber \\&\quad +\,\frac{B_{66}}{R^2} \left( -n^{2} U^{\mathrm{c}} - n RV_{,x}^{\mathrm{c}}\right) +\frac{D_{66}}{R^2}\left( -n^{2}\Phi _x^{\mathrm{c}} -n R \Phi _{\theta ,x}^{\mathrm{c}}\right) \nonumber \\&\quad -\,\kappa A_{55}\left( \Phi _x^{\mathrm{c}} +W_{,x}^{\mathrm{c}}\right) +I_2\omega ^{2}U^{\mathrm{c}} +I_3\omega ^{2} \Phi _x^{\mathrm{c}} =0 \end{aligned}$$

(A.4)

$$\begin{aligned}&\frac{B_{12}}{R }nU_{,x}^{\mathrm{c}}+\frac{B_{22}}{R^2}\left( -n^{2}V^{\mathrm{c}}+n W^{\mathrm{c}}\right) +\frac{B_{66}}{R }\left( n U_{,x}^{\mathrm{c}}+RV_{,xx}^{\mathrm{c}}\right) \nonumber \\&\quad +\,\frac{D_{12}}{R}n\Phi _{x,x}^{\mathrm{c}}+\frac{D_{22}}{R^2}\left( -n^{2}\Phi _\theta ^{\mathrm{c}}\right) +\frac{D_{66}}{R}\left( n\Phi _{x,x}^{\mathrm{c}}+R \Phi _{\theta ,xx}^{\mathrm{c}}\right) \nonumber \\&\quad +\,\frac{\kappa A_{44}}{R}\left( - V^{\mathrm{c}}+R\Phi _\theta ^{\mathrm{c}} +n W^{\mathrm{c}} \right) +I_2\omega ^{2}V^{\mathrm{c}}+I_3\omega ^{2}\Phi _\theta ^{\mathrm{c}} =0\end{aligned}$$

(A.5)

$$\begin{aligned}&\frac{1}{R^2}\left\{ A_{11}U_{,\phi \phi }^{\mathrm{s}}+A_{11}\cot \left( \phi \right) U_{,\phi }^{\mathrm{s}}-\frac{A_{66}}{\sin ^2\left( \phi \right) }n^2U^{\mathrm{s}}-\left( A_{11}\cot \left( \phi \right) ^{2}+A_{12}+A_{66}\right) U^{\mathrm{s}}\right. \nonumber \\&\quad -\,\frac{\left( A_{12}+A_{66}\right) }{\sin \left( \phi \right) }nV_{,\phi }^{\mathrm{s}}+\left( A_{11}+A_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }nV^{\mathrm{s}}+\left( A_{11}+A_{12}+A_{66}\right) W_{,\phi }^{\mathrm{s}}\nonumber \\&\quad +\,B_{11}\Phi _{\phi ,\phi \phi }^{\mathrm{s}}+B_{11}\cot \left( \phi \right) \Phi _{\phi ,\phi }^{\mathrm{s}}-\frac{B_{66}}{\sin ^2\left( \phi \right) }n^2 \Phi _{\phi }^{\mathrm{s}}- \left( B_{11}\cot ^2\left( \phi \right) +B_{12}-A_{66}R\right) \Phi _{\phi }^{\mathrm{s}}\nonumber \\&\quad \left. -\,\frac{\left( B_{12}+B_{66}\right) }{\sin \left( \phi \right) }n\Phi _{\theta ,\phi }^{\mathrm{s}}+\left( B_{11}+B_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }n\Phi _{\theta }^{\mathrm{s}}\right\} +I_1{\omega }^2U^{\mathrm{s}}+I_2\omega ^{2}\Phi _{\phi }^{\mathrm{s}}=0 \end{aligned}$$

(A.6)

$$\begin{aligned}&\frac{1}{R^2}\left\{ \frac{\left( A_{12}+A_{66}\right) }{\sin \left( \phi \right) }nU_{,\phi }^{\mathrm{s}}+\left( A_{11}+A_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }nU^{\mathrm{s}}+A_{66}V_{,\phi \phi }^{\mathrm{s}}\right. \nonumber \\&\quad +\,A_{66}\cot \left( \phi \right) V_{,\phi }^{\mathrm{s}}-\frac{A_{11}}{\sin ^2\left( \phi \right) }n^2V^{\mathrm{s}}+\left( \frac{A_{66}}{\sin ^2\left( \phi \right) }-2A_{66}\cot \left( \phi \right) ^2-A_{66}\right) V^{\mathrm{s}}\nonumber \\&\quad +\,\frac{\left( A_{11}+A_{12}+A_{66}\right) }{\sin \left( \phi \right) }nW^{\mathrm{s}}+\frac{\left( B_{12}+B_{66}\right) }{\sin \left( \phi \right) }n\Phi _{\phi ,\phi }^{\mathrm{s}}+\left( B_{11}+B_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }n\Phi _{\phi }^{\mathrm{s}}\nonumber \\&\quad +\,B_{66}\Phi _{\theta ,\phi \phi }^{\mathrm{s}}+B_{66}\cot \left( \phi \right) \Phi _{\theta ,\phi }^{\mathrm{s}}-\frac{B_{11}}{\sin ^2\left( \phi \right) }n^2\Phi _{\theta }^{\mathrm{s}}\nonumber \\&\quad \left. +\,\left( \frac{B_{66}}{\sin ^2\left( \phi \right) }-2B_{66}\cot ^2\left( \phi \right) +A_{66}R\right) \Phi _{\theta }^{\mathrm{s}}\right\} +I_1{\omega }^2V^{\mathrm{s}}+I_2{\omega }^2\Phi _{\theta }^{\mathrm{s}}=0 \end{aligned}$$

(A.7)

$$\begin{aligned}&\frac{1}{R^2}\left\{ -\left( A_{11}+A_{12}+A_{66}\right) U_{,\phi }^{\mathrm{s}}-\left( A_{11}+A_{12}+A_{66}\right) \cot \left( \phi \right) U^{\mathrm{s}}\right. \nonumber \\&\quad +\,\frac{\left( A_{11}+A_{12}+A_{66}\right) }{\sin \left( \phi \right) }nV^{\mathrm{s}}+A_{66}W_{,\phi \phi }^{\mathrm{s}}-\frac{A_{66}}{\sin \left( \phi \right) ^{2}}n^2W^{\mathrm{s}}+A_{66}\cot \left( \phi \right) W_{,\phi }^{\mathrm{s}}\nonumber \\&\quad -\,2\left( A_{11}+A_{12}\right) W^{\mathrm{s}}-\left( B_{11}+B_{12}-A_{66}R\right) \Phi _{\phi .\phi }^{\mathrm{s}}\nonumber \\&\quad \left. -\,\left( B_{11}+B_{12}-A_{66}R\right) \cot \left( \phi \right) \Phi _{\phi }^{\mathrm{s}}+\frac{\left( B_{11}+B_{12}-A_{66}R\right) }{\sin \left( \phi \right) }n\Phi _{\theta }^{\mathrm{s}}\right\} +I_1{\omega }^2W^{\mathrm{s}}=0 \end{aligned}$$

(A.8)

$$\begin{aligned}&\frac{1}{R^2}\left\{ B_{11}U_{,\phi \phi }^{\mathrm{s}}+B_{11}\cot \left( \phi \right) U_{,\phi }^{\mathrm{s}}-\frac{B_{66}}{\sin ^2\left( \phi \right) }n^2U^{\mathrm{s}}-\left( B_{11}\cot ^2\left( \phi \right) +B_{12}-A_{66}R\right) U^{\mathrm{s}}\right. \nonumber \\&\quad -\,\frac{\left( B_{12}+B_{66}\right) }{\sin \left( \phi \right) }nV_{,\phi }^{\mathrm{s}}+\left( B_{11}+B_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }nV^{\mathrm{s}}+\left( B_{11}+B_{12}-A_{66}R\right) W_{,\phi }^{\mathrm{s}}\nonumber \\&\quad +\,D_{11}\Phi _{\phi ,\phi \phi }^{\mathrm{s}}+D_{11}\cot \left( \phi \right) \Phi _{\phi ,\phi }^{\mathrm{s}}-\frac{D_{66}}{\sin ^2\left( \phi \right) }n^2 \Phi _{\phi }^{\mathrm{s}}- \left( D_{11}\cot ^2\left( \phi \right) +D_{12}+A_{66}R^{2}\right) \Phi _{\phi }^{\mathrm{s}}\nonumber \\&\quad \left. -\frac{\left( D_{12}+D_{66}\right) }{\sin \left( \phi \right) }n\Phi _{\theta ,\phi }^{\mathrm{s}}+\left( D_{11}+D_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }n\Phi _{\theta }^{\mathrm{s}}\right\} +I_2{\omega }^2U^{\mathrm{s}}+I_3\omega ^{2}\Phi _{\phi }^{\mathrm{s}}=0 \end{aligned}$$

(A.9)

$$\begin{aligned}&\frac{1}{R^2}\left\{ \frac{\left( B_{12}+B_{66}\right) }{\sin \left( \phi \right) }nU_{,\phi }^{\mathrm{s}}+\left( B_{11}+B_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }nU^{\mathrm{s}}+B_{66}V_{,\phi \phi }^{\mathrm{s}}\right. \nonumber \\&\quad +\,B_{66}\cot \left( \phi \right) V_{,\phi }^{\mathrm{s}}-\frac{B_{11}}{\sin ^2\left( \phi \right) }n^2V^{\mathrm{s}}+\left( \frac{B_{66}}{\sin ^2\left( \phi \right) }-2B_{66}\cot ^2\left( \phi \right) +A_{66}R\right) V^{\mathrm{s}}\nonumber \\&\quad +\,\frac{\left( B_{11}+B_{12}-A_{66}R\right) }{\sin \left( \phi \right) }nW^{\mathrm{s}}+\frac{\left( D_{12}+D_{66}\right) }{\sin \left( \phi \right) }n\Phi _{\phi ,\phi }^{\mathrm{s}}+\left( D_{11}+D_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }n\Phi _{\phi }^{\mathrm{s}}\nonumber \\&\quad +\,D_{66}\Phi _{\theta ,\phi \phi }^{\mathrm{s}}+D_{66}\cot \left( \phi \right) \Phi _{\theta ,\phi }^{\mathrm{s}}-\frac{D_{11}}{\sin ^2\left( \phi \right) }n^2\Phi _{\theta }^{\mathrm{s}}\nonumber \\&\quad \left. +\,\left( \frac{D_{66}}{\sin ^2\left( \phi \right) }-2D_{66}\cot ^2\left( \phi \right) -A_{66}R^{2}\right) \Phi _{\theta }^{\mathrm{s}}\right\} +I_2{\omega }^2V^{\mathrm{s}}+I_3{\omega }^2\Phi _{\theta }^{\mathrm{s}}=0. \end{aligned}$$

(A.10)