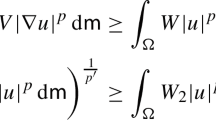Bisymmetric functionals revisited or a converse of the Fubini theorem

Abstract

We observe that bisymmetry is in fact the assertion of the Fubini theorem and we describe the form of general bisymmetric operations on some function spaces.

1 Introduction

Let us observe that the well known arithmetic mean may be treated as a functional on the space of all functions from $\mathbb Z_2$ to $\mathbb R.$ In fact, if $x:\mathbb Z_2\longrightarrow \mathbb R$ is an arbitrary function then the arithmetic mean M(x) is given by

$$\begin{aligned} M(x)= \frac{x(0)+x(1)}{2}, \, \, x:\mathbb Z_2\longrightarrow \mathbb R. \end{aligned}$$

It is rather easy to observe that M satisfies the following conditions:

• (a) M is linear,

• (b) $M(x)\le \sup x(G)$ ($\Longleftrightarrow M(x)\ge \inf x(G)$),

• (c) M is translation invariant (i.e. $M(x_a)=M(x)$ for every $a\in G$, where $x_a(t) = x (ta), \,t\in G$),

where G is an arbitrary group, in our case $G=\mathbb Z_2$. Slightly more generally, if we fix arbitrary $n\ge 2,$ then a functional M satisfying (a), (b) and (c) and defined on ${\mathcal B}(\mathbb Z_n;\mathbb R)$ (i.e. the family of all bounded functions mapping $\mathbb Z_n$ into $\mathbb R$—in fact, all the mappings from $\mathbb Z_n$ into $\mathbb R$) has to be

• (d) continuous;

• (e) reflexive, i. e.

  $$\begin{aligned} M(c{\mathbf 1}) = c \end{aligned}$$

  (1.1)

  for every $c\in \mathbb R,$ here ${\mathbf 1}:G\longrightarrow \mathbb R$ is defined by ${\mathbf 1}(t)=1, \, t\in G$;

• (f) monotonic, i. e.

  $$\begin{aligned} x\ge 0 \Longrightarrow M(x) \ge 0. \end{aligned}$$

  (1.2)

Now, from (a) we infer that

$$\begin{aligned} M(x) = \sum _{k=0}^{n-1} w_kx(k), \end{aligned}$$

(1.3)

and (1.1) implies

$$\begin{aligned} \sum _{k=0}^{n-1} w_k = 1. \end{aligned}$$

Moreover, because of (f) ((1.2), which is a consequence of (b)) we obtain

$$\begin{aligned} \bigwedge _{k\in \{0,\ldots ,n-1\}} w_k \ge 0. \end{aligned}$$

Further, because of (c) we get

$$\begin{aligned} \bigwedge _{k\in \{0,\ldots ,n-1\}} \bigwedge _{j\in \{0,\ldots ,n-1\}} w_{k+j}=w_k, \end{aligned}$$

in other words

$$\begin{aligned} \bigwedge _{k\in \{0,\ldots ,n-1\}} w_k = \frac{1}{n}. \end{aligned}$$

Hence, if M satisfies (a), (f) and (c) then it has to be the arithmetic mean.

Therefore, we have to develop some other instruments to investigate means on finite groups. It turns out that linearity is in a sense too much - it implies the form (1.3). We know several means that are not linear, but bisymmetric, i.e. satisfy the functional equation

1.1 History

In the 1940’s Aczél [1, p. 281] proved the following theorem on the form of bisymmetric means.

Theorem 1.1

The quasi-arithmetic mean

$$\begin{aligned} M(x,y) = \varphi ^{-1}\left( \frac{\varphi (x) + \varphi (y)}{2}\right) \end{aligned}$$

is the general continuous, reducible on both sides,¹ real solution of

$$\begin{aligned}&M\left[ M\left( x_{00},x_{01}\right) , M\left( x_{10},x_{11}\right) \right] \\&\qquad = M\left[ M\left( x_{00},x_{10}\right) , M\left( x_{01},x_{11}\right) \right] \end{aligned}$$

under the additional conditions $x, \, y, \, M(x,y) \in [a,b],$

$$\begin{aligned} M(x,x)= & {} x \quad \hbox {for all }x\in [a,b],\\ M(x,y)= & {} M(y,x) \quad \hbox {for all }x, \, y\in [a,b]. \end{aligned}$$

(Without symmetry M is given by

$$\begin{aligned} M(x,y) = \varphi ^{-1}\left( (1-q)\varphi (x) + q\varphi (y)\right) \end{aligned}$$

where $q\in (0,1)$.)

Remark 1.1

Without reflexivity and symmetry M is given by

$$\begin{aligned} M(x,y)= \varphi ^{-1}\left( (\alpha \varphi (x) + \beta \varphi (y) + \gamma \right) \end{aligned}$$

for some $\alpha> 0, \beta > 0$ and $\gamma \in \mathbb R$ such that

$$\begin{aligned} u,v\in [a,b] \Longrightarrow \alpha u + \beta v + \gamma \in [a,b]. \end{aligned}$$

(Volkmann [12], Maksa [9]).

Remark 1.2

It is noteworthy that the formula expressing bisymmetry is actually a form of the equality appearing in the celebrated Fubini theorem on iterated integrals.

A more general result was obtained by Münnich et al. [11] (Theorem 2).

Theorem 1.2

Let I be a real open interval, bounded or not, and let $F:I^n \rightarrow I$ ($n\ge 2$ fixed) be strictly monotone increasing in each of its arguments, continuous, and satisfy

$$\begin{aligned}&F(F(x_{00},\ldots ,x_{0n-1}),\ldots ,F(x_{n-10},\ldots ,x_{n-1n-1}))\nonumber \\&\qquad = F(F(x_{00},\ldots ,x_{n-10}),\ldots ,F(x_{0n-1},\ldots ,x_{n-1n-1})) \end{aligned}$$

(1.4)

and

$$\begin{aligned} F(x,\ldots ,x) = x, \quad x\in I. \end{aligned}$$

(1.5)

Then there are strictly monotone increasing, continuous function $\varphi :I \rightarrow \mathbb R$ and constants $\alpha _0,\ldots ,\alpha _{n-1} \in (0,1)$ such that

$$\begin{aligned} \sum _{i=0}^{n-1} \alpha _i = 1 \end{aligned}$$

and

$$\begin{aligned} F(x_0,\ldots ,x_{n-1}) = \varphi ^{-1}\left( \sum _{i=0}^{n-1} \alpha _i\varphi (x_i)\right) . \end{aligned}$$

There is also another result in this spirit. Let $A,\, B\in \mathbb {R}, \, A<B$ and denote by ${\mathcal D}(A,B)$ the family of all distribution functions $F:\mathbb {R} \longrightarrow [0,1]$ such that

• F is constant in stretches and has only a finite number of discontinuities;

• $F(x)= \frac{1}{2}\left[ F(x+) - F(x-)\right]$,²   $x\in \mathbb R$;

• $F(x)=0,\, x\le A$ and $F(x)=1, \, x\ge B$.

Note that for every $\xi \in [A,B]$ the function $E_{\xi }$ given by $E_{\xi }(x) = \frac{1}{2}(1+\mathrm{sgn}(x-\xi ))$ belongs to ${\mathcal D}(A,B)$. The following was proved by de Finetti [5] (cf. Hardy et al. [7, p. 158]).

Theorem 1.3

Suppose that $M:{\mathcal D}(A,B)\longrightarrow \mathbb {R}$ satisfies

• (a) $M\left( E_{\xi }\right) = \xi , \, \xi \in [A,B]$;

• (b) if $F_1, \, F_2 \in {\mathcal D}(A,B), \, F_1\ge F_2, \,$ and $F_1(x)>F_2(x)$ for some $x\in \mathbb {R}$, then $M(F_1)<M(F_2);$

• (c) if $F,\, F^*, \, G \in {\mathcal D}(A,B)$ and $M(F) = M(F^*),$ then

  $$\begin{aligned} M(tF+(1-t)G) = M(tF^* +(1-t)G) \end{aligned}$$

  for $t\in (0,1).$

Then there is a function $\phi$, continuous and strictly increasing in [A, B],  for which

Conversely, if M is defined by $(\sharp ),$ for a $\phi$ with the properties stated, then it satisfies (a), (b) and (c),  so that these conditions are necessary and sufficient for the representation of M in the form $(\sharp ).$

1.2 Consistent aggregation

One of the problems in which bisymmetric operations naturally arise is the so called consistent aggregation, appearing in the procedure of aggregating outputs of different producers who, with different production functions, make several goods. In this connection the following equation comes up (cf. e.g. [2])

$$\begin{aligned}&G\left( F_1\left( x_{0,0},\ldots , x_{n-1,0}\right) , \ldots , F_m\left( x_{0,m-1}, \ldots ,x_{n-1,m-1}\right) \right) \\&\qquad = F\left( G_1\left( x_{0,0},\ldots , x_{0,m-1}\right) , \ldots , G_n\left( x_{n-1,0}, \ldots ,x_{n-1,m-1}\right) \right) \end{aligned}$$

or

$$\begin{aligned}&G\left( F\left( 1,x(\cdot ,0)\right) , \ldots , F\left( m, x(\cdot ,m-1)\right) \right) \\&\qquad = F\left( G\left( 1, x(0,\cdot )\right) , \ldots , G\left( n, x(n-1,\cdot ) \right) \right) .\nonumber \end{aligned}$$

(1.6)

Equation (1.6) was solved by Maksa [9, 10].

Example 1

Put for every $y:A=\{0,\ldots ,n-1\} \longrightarrow \mathbb R$

$$\begin{aligned} F(y) = F(1,y)= F(2,y)=\cdots =F(m,y) = \sum _{s=0}^{n-1}y(s) = \int _A y(s) ds . \end{aligned}$$

Similarly, let $B=\{0,\ldots ,m-1\}.$ For every $z:B\longrightarrow \mathbb R,$ let us put

$$\begin{aligned} G(z) = G(1,z) = \cdots = G(n,z) = \sum _{t=0}^{m-1}z(t) = \int _B z(t) dt. \end{aligned}$$

Then for every $x:A\times B\longrightarrow \mathbb R,$ (1.6) becomes

$$\begin{aligned}&\sum _{t=0}^{m-1}\left( \sum _{s=0}^{n-1} x(s,t)\right) = \int _B \left( \int _A x(s,t) ds \right) dt\\&\qquad =\int _A \left( \int _B x(s,t) dt\right) ds =\sum _{s=0}^{n-1}\left( \sum _{t=0}^{m-1} x(s,t)\right) . \end{aligned}$$

Now, it is clearly seen that “consistent aggregation” is in fact the “Fubini theorem”.

Finally, let us mention the quite recent papers by Leonetti et al. [8] and Głazowska with the former authors [6] where a question of the commutativity of integral means was considered. The results are also in the spirit of the Fubini theorem. We shall use one of their theorems to prove our main result.

In the sequel we will formulate a proposition which characterizes means satisfying bisymmetry or, as we have tried to convince the reader, the assertion of the Fubini theorem. We prove Proposition 3.1 for families of finite valued functions and then extend its result to the case of some function spaces, in which finite valued functions form a dense subset (cf. Corollaries 3.1, 3.2 and 3.3). In order to do this however, we need to introduce some notations and definitions.

2 Notations and definitions

Consider $(\Omega , {\mathcal A}, \mu ),$ where $\Omega \ne \emptyset , \, \, {\mathcal A}\subset 2^{\Omega }$ is an algebra of sets, and $\mu : {\mathcal A} \rightarrow [0,\infty ]$ is an additive and nontrivial set function. Further, let ${\mathcal M}\left( \Omega \right) = \{f:\Omega \rightarrow \mathbb {R}: f \, \hbox {is }{\mathcal A}\hbox {-measurable}\}$ and ${\mathcal M}_+\left( \Omega \right) = \{f:\Omega \rightarrow \mathbb {R}_+: f \, \hbox {is }{\mathcal A}\hbox {-measurable}\}.$ Introduce a relation $\le$ in ${\mathcal M}\left( \Omega \right)$ (${\mathcal M}_+\left( \Omega \right)$) in the following way. If $f, \, g\in {\mathcal M}\left( \Omega \right) \, ( {\mathcal M}_+\left( \Omega \right) )$ then

$$\begin{aligned} f\le g \Longleftrightarrow \mu \left( \{\omega \in \Omega : f(\omega ) > g(\omega )\}\right) = 0. \end{aligned}$$

(2.1)

Actually, $\le$ is a preorder in ${\mathcal M}\left( \Omega \right)$ (${\mathcal M}_+\left( \Omega \right)$), since $f\le g$ and $g\le f$ imply that $f=g \, \, \, \mu$-almost everywhere. Also, we say that for $f,g \in {\mathcal M}\left( \Omega \right) \, ({\mathcal M}_+\left( \Omega \right) )$

$$\begin{aligned} f<g \Longleftrightarrow f\le g \wedge f\ne g \, \, \mu \hbox {-a.e.}, \end{aligned}$$

in other words

$$\begin{aligned} f< g \Longleftrightarrow f\le g \wedge \mu \left( \{\omega \in \Omega : f(\omega ) < g(\omega )\}\right) > 0. \end{aligned}$$

(2.2)

For each $n\in \mathbb N$ we call a sequence of sets $(A_0,\ldots ,A_{n-1})\subset {\mathcal A}^n$ satisfying

$$\begin{aligned} \left( \bigcup _{k=0}^{n-1} A_k = \Omega \right) \wedge \left( k\ne j \Longrightarrow A_k\cap A_j = \emptyset \right) , \end{aligned}$$

(2.3)

a partition of $\Omega .$ The family of all partitions of $\Omega$ will be denoted by ${\mathbf{P}}(\Omega )$ in the sequel. Observe that

$$\begin{aligned} \begin{aligned} {\mathbf{F}}\left( \Omega \right) =&\{ f\in {\mathcal M}\left( \Omega \right) : f(\Omega )\hbox { is finite}\} = \left\{ \sum _{k=0}^{n-1} x_k \mathbf {1}_{A_k}: n\in \mathbb N,\right. \\&(A_0,\ldots ,A_{n-1}) \in {\mathbf{P}}(\Omega ), \, x_k\in \mathbb R, k\in \{0,\ldots , n-1\} \Bigg \} \end{aligned} \end{aligned}$$

and analogously

$$\begin{aligned} \begin{aligned} {\mathbf{F}}_+\left( \Omega \right) {:}=&\{f\in {\mathcal M}_+\left( \Omega \right) : f(\Omega )\hbox { is finite}\} = \left\{ \sum _{k=0}^{n-1} x_k \mathbf {1}_{A_k}: n\in \mathbb {N},\right. \\&(A_0,\ldots ,A_{n-1}) \in {\mathbf{P}}(\Omega ) , \, x_k\ge 0, k\in \{0,\ldots , n-1\}\Bigg \} . \end{aligned} \end{aligned}$$

We will also consider the following families of functions $x:\Omega \times \Omega \longrightarrow \mathbb R:$

$$\begin{aligned} \begin{aligned}&{\mathbf{F}}\left( \Omega \times \Omega \right) {:}= \left\{ \sum _{i=0}^{n-1}\sum _{j=0}^{m-1} x_{ij} \mathbf {1}_{A_i\times B_j}: m, n\in \mathbb {N},(A_0,\ldots ,A_{n-1}),\right. \\&\left. (B_0,\ldots ,B_{m-1})\in {\mathbf{P}}(\Omega ), x_{ij}\in \mathbb R, i\in \{0,\ldots ,n-1\}, j\in \{0,\ldots , m-1\} \right\} \end{aligned} \end{aligned}$$

(2.4)

and

$$\begin{aligned} \begin{aligned}&{\mathbf{F}}_+\left( \Omega \times \Omega \right) {:}= \left\{ \sum _{i=0}^{n-1}\sum _{j=0}^{m-1} x_{ij} \mathbf {1}_{A_i\times B_j}: m, n\in \mathbb {N}, (A_0,\ldots ,A_{n-1}),\right. \\&\left. (B_0,\ldots ,B_{m-1})\in {\mathbf{P}}(\Omega ), x_{ij}\ge 0, i\in \{0,\ldots ,n-1\}, j\in \{0,\ldots , m-1\}\right\} . \end{aligned} \end{aligned}$$

(2.5)

Our aim is to study functionals defined on families of measurable functions, containing the finite valued ones. First, let us define the properties of functionals in question.

Let ${\mathcal F} \subset {\mathcal M}\left( \Omega \right) \, ({\mathcal M}_+\left( \Omega \right) )$ be such that ${\mathbf{F}}\left( \Omega \right) \subset {\mathcal F}$ (${\mathbf{F}}_+\left( \Omega \right) \subset {\mathcal F}$). We say that a functional $M: {\mathcal F} \rightarrow \mathbb R$makes no distinction between functions equal $\underline{\mu }$-a.e. iff

$$\begin{aligned} f=g \, \, \mu \hbox {-almost everywhere} \Longrightarrow M(f)=M(g). \end{aligned}$$

(2.6)

We say that M is reflexive, iff

$$\begin{aligned} M(c\mathbf {1}) = c \, \, \hbox {for every }c\in \mathbb R(\mathbb R_+). \end{aligned}$$

(2.7)

Moreover, M is $\underline{\mu }$-strictly increasing, iff

$$\begin{aligned} f< g \Longrightarrow M(f) < M(g) \end{aligned}$$

(2.8)

for every $f, g\in {\mathcal F}$ (cf. (2.2) for the definition of $f<g$).

Remark 2.1

Fix a partition $(A_0,\ldots , A_{n-1})\in {\mathbf{P}}(\Omega ).$ Take two functions from ${\mathbf{F}}\left( \Omega \right)$ (${\mathbf{F}}_+\left( \Omega \right)$) corresponding to the partition, say

$$\begin{aligned} x=\sum _{k=0}^{n-1} x_k \mathbf {1}_{A_k} \end{aligned}$$

and $y=\sum _{k=0}^{n-1} y_k \mathbf {1}_{A_k}.$ Assume that $x<y .$ In view of (2.2) we get that $x_k\le y_k,$ for each $k\in \{0,\ldots , n-1\},$ unless $\mu (A_k)=0.$ For some $k_0\in \{0,\ldots ,n-1\}$ we have to get $x_{k_0}<y_{k_0},$ and the latter has to occur together with $\mu (A_{k_0})>0 .$

Remark 2.2

As usual, we will not distinguish functions that are equal $\mu$-almost everywhere, cf. the assumption (2.6). Therefore in the definition of ${\mathbf{F}}\left( \Omega \right)$ and ${\mathbf{F}}_+\left( \Omega \right) ,$ we shall restrict ourselves to the case of such partitions $(A_0,\ldots ,A_{n-1})$ that for each $k\in \{0,\ldots ,n-1\}$ we have $\mu (A_k)>0.$ More exactly, from the equivalence class of functions equal $\mu$-a.e. we shall pick those which correspond to partitions not including nullsets. It is always possible, just by joining the nullsets to the sets of positive measure and taking the corresponding value. In the sequel we will deal also with some partitions with sets of measure zero as components, this will be the case for instance if we take a partition which results as the intersection of two partitions. More exactly, if $\Pi = (A_0,\ldots , A_{n-1})$ and $\Pi ' = (B_0,\ldots , B_{m-1})$ are two partitions of $\Omega ,$ then $\Pi \wedge \Pi ' {:}= (A_0\cap B_0,\ldots , A_i\cap B_j, \ldots , A_{n-1}\cap B_{m-1})\in {\mathbf{P}}(\Omega )$ as well but some of the sets $A_i\cap B_j$ might be $\mu$-null sets. The function $y'=\sum _{i=0}^{n-1} \sum _{j=0}^{m-1} y_{ij}\mathbf {1}_{A_i\cap B_j}$ will be replaced by an equivalent one $y= \sum _{(i,j)\in L(m,n)}y_{ij} \mathbf {1}_{C_{ij}}$ where L(m, n) denotes the set of all pairs $(i,j)\in \{0,\ldots ,m-1\}\times \{0,\ldots ,n-1\}$ such that $\mu (A_i\cap B_j)>0,$ and $C_{ij} = A_i\cap B_j$ except for one pair $(i_0,j_0)\in L(m,n)$ for which $C_{i_0j_0} = A_{i_0}\cap B_{j_0} \cup \bigcup _{(r,s)\notin L(m,n)} A_r\cap B_s.$ Then the function y corresponds to a partition containing sets with positive measure only. We will use the partition $\Pi \wedge \Pi '$ in the proof of Proposition 3.1.

Let us introduce a new definition.

Definition 2.1

Let ${\mathcal F} \subset {\mathcal M}\left( \Omega \right) \, ({\mathcal M}_+\left( \Omega \right) )$ be such that ${\mathbf{F}}\left( \Omega \right) \subset {\mathcal F}$ (${\mathbf{F}}_+\left( \Omega \right) \subset {\mathcal F}$) and let $M: {\mathcal F} \rightarrow \mathbb R.$ If $x:\Omega \times \Omega \rightarrow \mathbb R$ is such that $x(\cdot ,t)\in {\mathcal F}$ for every $t\in \Omega$ then we put

$$\begin{aligned} M_1(x) {:}= {\text {``}}\Omega \ni t \rightarrow M(x(\cdot ,t)) \in \mathbb R{\text {''}}, \end{aligned}$$

(2.9)

and if $x(s,\cdot )\in {\mathcal F}$ for every $s\in \Omega$ then we put

$$\begin{aligned} M_2(x) {:}= {\text {``}}\Omega \ni s \rightarrow M(x(s,\cdot )) \in \mathbb R{\text {''}}. \end{aligned}$$

(2.10)

We say that a function $x:\Omega \times \Omega \rightarrow \mathbb R$ is admissible if $x(\cdot ,t) \in {\mathcal F}$ for every $t\in \Omega$ and $x(s,\cdot ) \in {\mathcal F}$ for every $s\in \Omega .$ We show the following.

Lemma 2.1

Let $x\in {\mathbf{F}}\left( \Omega \times \Omega \right) ({\mathbf{F}}_+\left( \Omega \times \Omega \right) ) .$ Then x is admissible and

$$\begin{aligned} M_1(x) \in {\mathbf{F}}\left( \Omega \right) ({\mathbf{F}}_+\left( \Omega \right) ) \end{aligned}$$

and

$$\begin{aligned} M_2(x) \in {\mathbf{F}}\left( \Omega \right) ({\mathbf{F}}_+\left( \Omega \right) ). \end{aligned}$$

Proof

Suppose that

$$\begin{aligned} x(s,t)= & {} \sum _{i=0}^{n-1}\sum _{j=0}^{m-1}x_{ij}\mathbf {1}_{A_i\times B_j}(s,t)\nonumber \\= & {} \sum _{i=0}^{n-1}\sum _{j=0}^{m-1}x_{i,j}\mathbf {1}_{A_i}(s)\mathbf {1}_{ B_j}(t), \end{aligned}$$

(2.11)

for all $s,t\in \Omega ,$ where $(A_0,\ldots ,A_{n-1})$ and $(B_0,\ldots ,B_{m-1})$ are two partitions of $\Omega$ (cf. (2.3)). Then $x(\cdot , t)\in {\mathbf{F}}(\Omega ) ({\mathbf{F}}_+(\Omega ))$ for every $t\in \Omega$ and (cf. (2.9))

$$\begin{aligned} M_1(x)(t) = M\left( \sum _{i=0}^{n-1} x_{i,j}\mathbf {1}_{A_i} \right) \end{aligned}$$

for all $t\in B_j, \, j\in \{1,\ldots ,m-1\}.$ We can write it in the form

$$\begin{aligned} M_1(x) = \sum _{j=0}^{m-1} M\left( \sum _{i=0}^{n-1} x_{i,j}\mathbf {1}_{A_i} \right) \mathbf {1}_{B_j}, \end{aligned}$$

(2.12)

which proves our Lemma. Similarly we prove that (cf. (2.10))

$$\begin{aligned} M_2(x) = \sum _{i=0}^{n-1} M\left( \sum _{j=0}^{m-1} x_{i,j}\mathbf {1}_{B_j} \right) \mathbf {1}_{A_i}, \end{aligned}$$

(2.13)

and so $M_2(x)\in {\mathbf{F}}\left( \Omega \right) .$

Example 2

Suppose that $\Omega =\{\omega _1, \ldots , \omega _r\}$ for some $r\in \mathbb N,$ let ${\mathcal A}= 2^{\Omega },\, \mu ({\omega _s}) =\frac{1}{r}$ for every $s\in \{1,\ldots ,r\}$ and consider a function $x:\Omega \times \Omega \longrightarrow \mathbb R,$ defined by

$$\begin{aligned} x(s, t)= \sum _{i,j} x_{i,j} \mathbf {1}_{\{\left( \omega _i, \omega _j\right) \}}(s, t)={:} x_{s,t} \end{aligned}$$

for every $(s,t)\in \Omega \times \Omega .$ Obviously, $x\in {\mathbf{F}}\left( \Omega \times \Omega \right) .$ Let $M:{\mathbf{F}}(\Omega ) \longrightarrow \mathbb R$ be any function which is reflexive and strictly increasing, for instance suppose that

$$\begin{aligned} M(z) = M\left( \sum _{s=1}^r z_s \mathbf {1}_{\{\omega _s\}}\right) = \sum _{s=1}^r \lambda _s z_s, \end{aligned}$$

for every $z=\sum _{s=1}^r z_s\mathbf {1}_{\{\omega _s\}}$ where $\left( \lambda _1,\ldots ,\lambda _r\right)$ is a fixed vector such that $\lambda _s > 0, \, s\in \{1,\ldots ,r\}$ and $\sum _{s=1}^r \lambda _s = 1.$ Then we have

$$\begin{aligned} M_1(x)(t) = \sum _{s=1}^r \lambda _s x_{s,t}\in \mathbb R, \, t\in \{1,\ldots , r\} \end{aligned}$$

and

$$\begin{aligned} M_2(x)(s) = \sum _{t=1}^r \lambda _t x_{s,t} \in \mathbb R, \, s\in \{1,\ldots , r\}. \end{aligned}$$

Remark 2.3

Let us observe the following. Fix $m\ge 1$ and $n\ge 1,$ positive integers. Further, fix partitions $(A_0,\ldots ,A_{n-1})$ and $(B_1,\ldots ,B_{m-1})\in {\mathbf{P}}(\Omega ) .$ We assume that for every $i\in \{1,\ldots ,n-1\}$ and for every $j\in \{1,\ldots ,m-1\}$ we have

$$\begin{aligned} \mu (A_i)\mu (B_j)> 0. \end{aligned}$$

(2.14)

Let us choose arbitrary $x_{ij}\in \mathbb R, i\in \{0,\ldots ,n-1\}, \, j\in \{0,\ldots , m-1\}.$ Consider a function $x\in {\mathbf{F}}\left( \Omega \times \Omega \right) \, ({\mathbf{F}}_+\left( \Omega \times \Omega \right) ),$ defined by (2.11). We get by (2.12)) and (2.13) that $M_k(x)\in {\mathbf{F}}(\Omega )$ (${\mathbf{F}}_+(\Omega ), \, k\in \{1,2\} .$ Finally, assume that

$$\begin{aligned} M(M_1(x)) = M(M_2(x)). \end{aligned}$$

(2.15)

Define $F:\mathbb R^n\longrightarrow \mathbb R$ and $G:\mathbb R^m\longrightarrow \mathbb R\, (F:\mathbb R_+^n\longrightarrow \mathbb R, \,G:\mathbb R_+^m\longrightarrow \mathbb R)$ by

$$\begin{aligned} F(x_0,\ldots ,x_{n-1})&= M\left( \sum _{i=0}^{n-1} x_i \mathbf {1}_{A_i}\right) , \, \, (x_0,\ldots ,x_{n-1}) \in \mathbb R^n (\mathbb R_+^n);\end{aligned}$$

(2.16)

$$\begin{aligned} G(y_0,\ldots ,y_{m-1})&= M\left( \sum _{j=0}^{m-1} y_j \mathbf {1}_{B_j}\right) , \, \, (y_0,\ldots , y_{m-1}) \in \mathbb R^m (\mathbb R_+^m). \end{aligned}$$

(2.17)

In view of (2.15) we get

$$\begin{aligned}&F\left( G(x_{00},\ldots , x_{0m-1}),\ldots ,G(x_{n-10},\ldots , x_{n-1m-1})\right) \\&\qquad =F\left( M\left( \sum _{j=0}^{m-1} x_{0j}{\mathbf 1}_{B_j}\right) ,\ldots ,M\left( \sum _{j=0}^{m-1} x_{n-1j}{\mathbf 1}_{B_j}\right) \right) \\&\qquad = M\left( \sum _{i=0}^{n-1} M\left( \sum _{j=0}^{m-1} x_{ij}\mathbf {1}_{B_j}\right) {\mathbf 1}_{A_i} \right) \\&\qquad = M\left( M_2(x)\right) = M\left( M_1(x)\right) \\&\qquad =M\left( \sum _{j=0}^{m-1} M\left( \sum _{i=0}^{n-1} x_{ij}\mathbf {1}_{A_i}\right) {\mathbf 1}_{B_j} \right) \\&\qquad =G\left( M\left( \sum _{i=0}^{n-1} x_{i0}\mathbf {1}_{A_i}\right) ,\ldots , M\left( \sum _{i=0}^{n-1} x_{im-1}\mathbf {1}_{A_i}\right) \right) \\&\qquad =G\left( F(x_{00},\ldots , x_{n-10}),\ldots ,F(x_{0m-1},\ldots , x_{n-1m-1})\right) . \end{aligned}$$

Moreover, the functions $F, \, G$ are strictly increasing, which follows from the assumption (2.14) (cf. Remark 2.1). We could now use results on generalized bisymmetry from [2] or [9] but we will apply a slightly different method.

We will use in the sequel the following.

Definition 2.2

Let ${\mathcal F}\subset {\mathcal M}(\Omega ) ({\mathcal M}_+\left( \Omega \right) ).$ Suppose that a functional $M: {\mathcal F} \rightarrow \mathbb R$ satisfies (2.15) for every admissible $x:\Omega \times \Omega \rightarrow \mathbb R.$ Then we call Mbisymmetric.

Let us conclude the present section with the following remark.

Remark 2.4

We are going to give a representation of functionals M satisfying some additional conditions. We will start with determining M(y) for finite valued functions $y:\Omega \longrightarrow \mathbb R(\mathbb R_+).$ To determine M(y) we will use the Theorem 1.2. However, this theorem works “separately” in every dimension $n\in \mathbb N.$ The dimension is strictly connected with the partition generating y,  i.e. such partition $\Pi = (A_0,\ldots ,A_{n-1})\in {\mathbf{P}}(\Omega )$ that $y=\sum _{i=0}^{n-1} x_i\mathbf {1}_{A_i}$. However, any given finite function may be generated by different partitions. For instance the function $y= (x_0,x_1,x_1)$ is generated by partitions $(A_0,A_1,A_2)$ and $(A_0,\Omega \setminus A_0).$ Therefore in the sequel we have to prove that the definition of M(y) is independent of the partitions generating y,  in particular that we may use the same generating function $\varphi$ for every partition. We will do it in the proof of Proposition 3.1 below.

3 Results

3.1 Finite valued functions

First, let us prove the following.

Proposition 3.1

Let $(\Omega , {\mathcal A}, \mu )$ be a measure space and suppose that ${\mathcal F} \subset {\mathcal M}\left( \Omega \right)$$({\mathcal M}_+\left( \Omega \right) )$ is such that ${\mathbf{F}}\left( \Omega \right) \subset {\mathcal F}\, ({\mathbf{F}}_+\left( \Omega \right) \subset {\mathcal F}).$ If $M:{\mathcal F}\rightarrow \mathbb R$ makes no difference between functions equal $\mu$-a.e. (2.6), is reflexive (2.7), $\mu$-strictly increasing (2.8), continuous (in the sense that $M(f) = \lim _{n\rightarrow \infty } M(f_n)$ for every sequence $(f_n)_{n\in \mathbb N}\in {\mathcal F}^{\mathbb N}$ converging a.e. to $f\in {\mathcal F}$) and is bisymmetric (2.15) then there exist a strictly increasing and continuous function $\varphi : \mathbb R\rightarrow \mathbb R\, (\varphi : \mathbb R_+ \rightarrow \mathbb R)$ and an additive function $P:{\mathcal A}\rightarrow [0,1]$ such that

$$\begin{aligned}&P(\Omega ) = 1,\end{aligned}$$

(3.1)

$$\begin{aligned}&\bigwedge _{A\in {\mathcal A}} (P(A)>0 \Longleftrightarrow \mu (A)>0), \end{aligned}$$

(3.2)

and

$$\begin{aligned} M(y) = \varphi ^{-1}\left( \int _{\Omega } (\varphi \circ y) dP\right) \end{aligned}$$

(3.3)

for every $y\in {\mathbf{F}}(\Omega )({\mathbf{F}}_+(\Omega )).$

Proof

I. Our aim is to apply Theorem 1.2 to prove our result, with $I= \mathbb R$ ($\mathbb R_+ .$) Let us start with a partition $\Pi =(A_0,\ldots ,A_{n-1})\in {\mathbf{P}}(\Omega )$ with $\mu (A_i)> 0, \, i\in \{0,\ldots , n-1\}.$ Define $F_{\Pi }:\mathbb R^n \rightarrow \mathbb R$ ($F_{\Pi }:\mathbb R_+ ^n \rightarrow \mathbb R$) by

$$\begin{aligned} F_{\Pi }(x_0,x_1,\ldots , x_{n-1})= M\left( \sum _{i=0}^{n-1}x_i\mathbf {1}_{A_i}\right) . \end{aligned}$$

Repeating the argument from Remark 2.3 we see that $F_{\Pi }$ satisfies the bisymmetry Eq. (1.4), as well as (1.5), due to the reflexivity of M. Moreover, it is strictly increasing (cf. Remark 2.3) and continuous in the usual sense, as a function mapping $\mathbb R^n$ into $\mathbb R.$ Hence by Theorem 1.2 we get that there are a strictly increasing and continuous function $\varphi _{\Pi }: \mathbb R\longrightarrow \mathbb R$ ($\varphi _{\Pi }: \mathbb R_+ \longrightarrow \mathbb R$) and positive $\alpha _{\Pi ,i} , i\in \{0,\ldots , n-1\},$ such that $\sum _{i=0}^{n-1}\alpha _{\Pi ,i }= 1$ and

$$\begin{aligned} F_{\Pi }(x_0,x_1,\ldots ,x_{n-1})= \varphi _{\Pi }^{-1}\left( \sum _{i=0}^{n-1}\alpha _{\Pi ,i}\varphi _{\Pi }(x_i)\right) = M\left( \sum _{i=0}^{n-1}x_i\mathbf {1}_{A_i}\right) \end{aligned}$$

(3.4)

for all $(x_0,\ldots ,x_{n-1})\in \mathbb R^n (\mathbb R_+^n).$ Let us note that (3.4) holds for all functions $y\in E_{\Pi } \subset {\mathbf{F}}(\Omega )({\mathbf{F}}_+(\Omega )),$ where $E_{\Pi }$ is the linear space of functions generated by the partition $\Pi$ in the sense that

$$\begin{aligned} y=\sum _{i=0}^{n-1}x_i\mathbf {1}_{A_i} \end{aligned}$$

for some (fixed) $I\ni x_i$’s, $i\in \{0,\ldots ,n-1\}.$ In particular, if $\mu (A_0)\in (0,1)$ then formula (3.4) holds for any function $w_{(s,t)}\in E_{\Pi }$ defined as follows.

$$\begin{aligned} w_{(s,t)}(p)= & {} \left\{ \begin{array}{ll} s &{} \hbox {if }p \in A_0,\\ t &{} \hbox {if }p\in \Omega \setminus A_0. \end{array} \right. \end{aligned}$$

(3.5)

From (3.4) we infer that for every $s,t\in I$ the equality

$$\begin{aligned} M\left( w_{(s,t)}\right) = \varphi _{\Pi }^{-1}\left( \alpha _{\Pi ,0}\varphi _{\Pi }(s)+ \left( 1-\alpha _{\Pi ,0}\right) \varphi _{\Pi }(t)\right) \end{aligned}$$

(3.6)

holds.

We are going to show that in (3.4) we may consider a function $\varphi$ instead of $\varphi _{\Pi },$ in other words we are going to show that the $\varphi _{\Pi }$ in the value of M(y) is independent of the partition generating y (cf. Remark 2.4). Indeed, suppose that there is a partition $\Pi '=(B_0,\ldots , B_{m-1})\in {\mathbf{P}}(\Omega )$ such that $\mu (B_j)>0, \, j\in \{0,\ldots , m-1\}$ and

$$\begin{aligned} {\mathbf{F}}(\Omega )\ni y = \sum _{i=0}^{n-1}x_i {\mathbf 1}_{A_i} = \sum _{j=0}^{m-1} x_j^{\prime } {\mathbf 1}_{B_j}. \end{aligned}$$

Put

$$\begin{aligned} F_{\Pi '}(x_0^{\prime },\ldots ,x_{m-1}^{\prime })= M\left( \sum _{j=0}^{m-1}x_j^{\prime }{\mathbf 1}_{B_j}\right) = M(y). \end{aligned}$$

Similarly as above we can prove that there are a strictly increasing and continuous function $\varphi _{\Pi '}:\mathbb R\longrightarrow \mathbb R$ ($\varphi _{\Pi '}:\mathbb R_+ \longrightarrow \mathbb R$) and positive numbers $\beta _{\Pi ',j}, \, j\in \{0,\ldots , m-1\}$ such that

$$\begin{aligned} F_{\Pi '}(x_0^{\prime },\ldots ,x_{m-1}^{\prime }) = \varphi _{\Pi '}^{-1}\left( \sum _{j=0}^{m-1}\beta _{\Pi ',j}\varphi _{\Pi '}(x_j^{\prime })\right) \end{aligned}$$

(3.7)

for all$(x_0^{\prime },\ldots , x_{m-1}^{\prime })\in I^m,$ or for all $y\in E_{\Pi '}.$ Since

$$\begin{aligned} F_{\Pi }\left( x_0,\ldots ,x_{n-1}\right) = F_{\Pi '}(x_0^{\prime },\ldots ,x_{m-1}^{\prime }) = M(y), \end{aligned}$$

taking (3.4) and (3.7) into account we obtain

$$\begin{aligned} \varphi _{\Pi }^{-1}\left( \sum _{i=0}^{n-1}\alpha _{\Pi ,i}\varphi _{\Pi }(x_i)\right) = \varphi _{\Pi '}^{-1}\left( \sum _{j=0}^{m-1}\beta _{\Pi ',j}\varphi _{\Pi '}(x_j^{\prime })\right) = M(y), \end{aligned}$$

(3.8)

for every $y\in E_{\Pi }\cap E_{\Pi '}.$ On the other hand, one also has (let us recall that $\Pi \wedge \Pi ' =(A_0\cap B_0,\ldots , A_i\cap B_j,\ldots , A_{n-1}\cap B_{m-1})$)

$$\begin{aligned} y= \sum _{i=0}^{n-1}\sum _{j=0}^{m-1} c_{\Pi \wedge \Pi ',ij}{\mathbf 1}_{A_i\cap B_j} \end{aligned}$$

for some $c_{\Pi \wedge \Pi ',ij}, \, i\in \{0,\ldots ,n-1\}, \, j\in \{0,\ldots , m-1\}.$ Taking Remark 2.2 into account, we will replace the above by a function $y'$ equal a.e. to y and given by

$$\begin{aligned} y'= \sum _{(i,j)\in L(m,n)}c_{\Pi \wedge \Pi ',ij} \mathbf {1}_{C_{ij}}, \end{aligned}$$

(3.9)

where $\mu (C_{ij})>0, \, (i,j)\in L(m,n),$ with L(m, n) defined as in Remark 2.2. Using Theorem 1.2 together with (2.6) again we get

$$\begin{aligned} M(y)= M(y')= \varphi ^{-1}\left( \sum _{(i,j)\in L(m,n)}\gamma _{\Pi \wedge \Pi ',ij}\varphi (c_{\Pi \wedge \Pi ',ij})\right) \end{aligned}$$

for some strictly increasing $\varphi :\mathbb R\longrightarrow \mathbb R$ and some positive constants $\gamma _{\Pi \wedge \Pi ',ij}$ summing up to 1. Putting now $J{:}=\{j\in \{0,\ldots , m-1\}: (0,j) \in L(m,n)\} \ne \emptyset$ (the set J is nonempty because $\mu (A_0)>0$ and $\Pi '\in {\mathbf{P}}(\Omega )$), we see that for the function $w_{(s,t)}$ defined by (3.5) we obtain

$$\begin{aligned} M\left( w_{(s,t)}\right) = \varphi ^{-1}\left( \delta _0 \varphi (s) +\left( 1-\delta _0\right) \varphi (t) \right) , \end{aligned}$$

(3.10)

where $\delta _0{:}= \sum _{j\in J} \gamma _{\Pi \wedge \Pi ',0j}.$

Combining (3.10) with (3.6) (cf. (3.8)) and denoting $\omega = \varphi \circ \varphi _{\Pi }^{-1}$ we obtain the equation

$$\begin{aligned} \omega \left( \alpha _{\Pi ,0} \varphi _{\Pi }(s) + \left( 1-\alpha _{\Pi ,0}\right) \varphi _{\Pi }(t)\right) =\delta _0 \varphi (s) +\left( 1-\delta _0\right) \varphi (t) , \end{aligned}$$

for all $s,t\in I$ or, after substituting $u{:}=\varphi _{\Pi }(s)$ and $v{:}=\varphi _{\Pi }(t)$

$$\begin{aligned} \omega \left( \alpha _{\Pi ,0} u + \left( 1-\alpha _{\Pi ,0}\right) v\right) =\delta _0 \omega (u) +\left( 1-\delta _0\right) \omega (v), \end{aligned}$$

(3.11)

for all $u, \, v\in \varphi _{\Pi } (I)={:}K,$ where K is a real non-degenerate interval.

Applying a trick used by Daróczy and Páles [4] we see that

$$\begin{aligned} \omega \left( \frac{u+v}{2}\right) = \frac{\omega (u)+\omega (v)}{2}, \end{aligned}$$

for all $u,\, v\in K.$ This yields

$$\begin{aligned} \omega (u)= cu+d \end{aligned}$$

for some $c>0$ and $d\in \mathbb R$ and every $u\in K.$ Therefore, recalling the definition of $\omega$ we get

$$\begin{aligned} \varphi (\xi ) = c\varphi _{\Pi }(\xi ) + d, \end{aligned}$$

or

$$\begin{aligned} \varphi _{\Pi }(\xi ) = c^{-1}\varphi (\xi ) - d, \end{aligned}$$

(3.12)

for every $\xi \in \mathbb R(\mathbb R_+).$ In an analogous way we obtain

$$\begin{aligned} \varphi _{\Pi '}(\xi ) = c'^{-1}\varphi (\xi ) - d', \end{aligned}$$

(3.13)

for some constants $c'>0$ and $d'\in \mathbb R,$ and all $\xi \in \mathbb R(\mathbb R_+).$ It easily follows from (3.12) and (3.13) that (cf. (3.8))

$$\begin{aligned} M(y) = \varphi ^{-1}\left( \sum _{i=0}^{n-1}\alpha _{\Pi ,i}\varphi (x_i)\right) = \varphi ^{-1}\left( \sum _{j=0}^{m-1}\beta _{\Pi ',j}\varphi (x_j^{\prime })\right) , \end{aligned}$$

(3.14)

for every $y\in {\mathbf{F}}(\Omega ) ,$ independently of its representation. In other words, we get that the same $\varphi$ is enough to represent M(y),  for every $y\in {\mathbf{F}}(\Omega ) ( {\mathbf{F}}_+(\Omega )).$

It remains to deal with the case $\mu (A_0)=1$ but then $y=c{\mathbf 1}$ a.e. and thus $M(y)=c$ in view of (2.7), and it is a simple exercise to show that this value is independent of the partition generating y (and moreover $M(y)= \varphi ^{-1}\left( 1\cdot \varphi (c)\right)$ for any strictly increasing and continuous function $\varphi :I \rightarrow \mathbb R$).

II. Suppose now that $y, z\in {\mathbf{F}}(\Omega ) ({\mathbf{F}}_+(\Omega ))$ are two different functions. Up to now we have checked that M(y) and M(z) are generated by some monotone functions $\varphi$ and $\psi ,$ respectively. We are going to show that actually $\varphi$ and $\psi$ are conjugated. To prove it we shall use the assumed equality (2.15) to the function $x\in {\mathbf{F}}(\Omega \times \Omega ) ({\mathbf{F}}_+(\Omega \times \Omega ))$ given by

$$\begin{aligned} x(s,t)= \sum _{i=0}^{m-1}\sum _{j=0}^{n-1}y_i z_j\mathbf {1}_{A_i}(s)\mathbf {1}_{ B_j}(t)= y(s)z(t), \end{aligned}$$

for all $(s,t)\in \Omega \times \Omega ,$ where $(A_0,\ldots , A_{n-1}), \, (B_0,\ldots , B_{m-1} )\in {\mathbf{P}}(\Omega )$ are such that

$$\begin{aligned} y=\sum _{i=0}^{n-1} y_i \mathbf {1}_{A_i} \, \, \hbox {and} \, \, z=\sum _{j=0}^{m-1} z_j \mathbf {1}_{B_j}. \end{aligned}$$

In view of (2.12) and (2.13) we obtain

$$\begin{aligned} M_1(x) = \sum _{j=0}^{m-1} M\left( z_j\sum _{i=0}^{n-1} y_i \mathbf {1}_{A_i} \right) \mathbf {1}_{B_j}=\sum _{j=0}^{m-1} M\left( z_j y \right) {\mathbf 1}_{B_j}, \end{aligned}$$

and

$$\begin{aligned} M_2(x) = \sum _{i=0}^{n-1} M\left( y_i\sum _{j=0}^{m-1} z_j \mathbf {1}_{B_j} \right) \mathbf {1}_{A_i}=\sum _{i=0}^{n-1}M\left( y_i z \right) {\mathbf 1}_{ A_i}. \end{aligned}$$

Let us take $y=y_0{\mathbf 1}_{A_0} + y_1{\mathbf 1}_{\Omega \setminus A_0}$ and $z=z_0{\mathbf 1}_{B_0} + z_1{\mathbf 1}_{\Omega \setminus B_0}$ (it is rather obvious that it is enough to restrict our attention to this special case). Then (2.15) becomes

$$\begin{aligned}&\psi ^{-1}\left( \beta _0\psi \left( \varphi ^{-1}\left( \alpha _0\varphi (y_0z_0) +(1-\alpha _0)\varphi (y_1z_0)\right) \right) \right. \\&\qquad + \left. (1-\beta _0)\psi \left( \varphi ^{-1}\left( \alpha _0\varphi (y_0z_1) +(1-\alpha _0)\varphi (y_1z_1)\right) \right) \right) \\&\qquad = \varphi ^{-1}\left( \alpha _0\varphi \left( \psi ^{-1}\left( \beta _0\psi (y_0z_0) +(1-\beta _0)\psi (y_1z_0)\right) \right) \right. \\&\qquad + \left. (1-\alpha _0)\varphi \left( \psi ^{-1}\left( \beta _0\psi (y_0z_1) +(1-\beta _0)\psi (y_1z_1)\right) \right) \right) . \end{aligned}$$

Substituting $s=y_0z_0, \, t=y_1z_0, \, u=y_0z_1,$ and $v=y_1z_1$ above we get

$$\begin{aligned}&\psi ^{-1}\left( \beta _0\psi \left( \varphi ^{-1}\left( \alpha _0\varphi (s) +(1-\alpha _0)\varphi (t)\right) \right) \right. \nonumber \\&\qquad + \left. (1-\beta _0)\psi \left( \varphi ^{-1}\left( \alpha _0\varphi (u) +(1-\alpha _0)\varphi (v)\right) \right) \right) \nonumber \\&\qquad = \varphi ^{-1}\left( \alpha _0\varphi \left( \psi ^{-1}\left( \beta _0\psi (s) +(1-\beta _0)\psi (t)\right) \right) \right. \nonumber \\&\qquad + \left. (1-\alpha _0)\varphi \left( \psi ^{-1}\left( \beta _0\psi (u) +(1-\beta _0)\psi (v)\right) \right) \right) . \end{aligned}$$

However, this is an equation that was treated by Leonetti et al. [8] in a slightly more general situation (cf. also Theorem 2 in [6]). They showed (cf. Lemma 3 in [8]) that there exist real constants a, b with $a\ne 0$ such that

$$\begin{aligned} \varphi = a\psi +b. \end{aligned}$$

A straightforward calculation shows that both $\varphi$ and $\psi$ generate the same M,  more exactly we have $M(y)= \varphi ^{-1}\left( \sum _{i=0}^{n-1} \alpha _i \varphi (y_i)\right)$ and $M(z)= \varphi ^{-1}\left( \sum _{j=0}^{m-1} \beta _j \varphi (z_j)\right) .$

III. Let us pick a set $A\in {\mathcal A}$ and consider the partition $\Pi = (A,\Omega \setminus A) \in {\mathbf{P}}(\Omega ).$ If $y\in {\mathbf{F}}(\Omega ) ({\mathbf{F}}_+(\Omega ))$ is given by $y=y_0{\mathbf 1}_A + y_1{\mathbf 1}_{\Omega \setminus A}$ and $\mu (A)\cdot \mu (\Omega \setminus A) >0$ then, as we have shown above, there exist a strictly monotone and continuous function $\varphi :\mathbb R\rightarrow \mathbb R\, (\mathbb R_+\rightarrow \mathbb R)$ and a number $\alpha _{\Pi } \in (0,1)$ such that $M(y) = \varphi ^{-1}\left( \alpha _{\Pi } \varphi (y_0) + (1-\alpha _{\Pi } )\varphi (y_1)\right) .$ Now, define (cf. (3.4))

$$\begin{aligned} P(A)= & {} \left\{ \begin{array}{lll} \,\,\,0 &{} \hbox {if }\mu (A)=0,\\ \alpha _{\Pi } &{} \hbox {if }\mu (A)>0\\ \,\,\, 1 &{} \hbox {if }\mu (\Omega \setminus A)=0. \end{array} \right. \end{aligned}$$

We have to check that

• 1. P is well defined, i.e. the definition of P(A) does not depend on the partition,

• 2. P is additive,

• 3. (3.2) holds.

Ad 1. Suppose that there is another partition $\Pi '=(A,B_1,\ldots ,B_{m-1})$ and y is given by $y= y_0{\mathbf 1}_{A} +y_1{\mathbf 1}_{\Omega \setminus A} = y_0{\mathbf 1}_{A} +\sum _{j=1}^{m-1} y_j^{\prime }{\mathbf 1}_{B_j}.$ We have shown above that then y is also given by (3.9), which in the present case takes the form (put $J=\{j\in \{1,\ldots ,m-1\}: \mu (A\cap B_j)>0\}, \, J'=\{j\in \{1,\ldots ,m-1\}: \mu ((\Omega \setminus A)\cap B_j)>0\}$)

$$\begin{aligned} y= c_{\Pi \wedge \Pi ',00}{\mathbf 1}_{A} + \sum _{j\in J} c_{\Pi \wedge \Pi ',0j}{\mathbf 1}_{A\cap B_j} + \sum _{j\in J'} c_{\Pi \wedge \Pi ',1j}{\mathbf 1}_{(\Omega \setminus A)\cap B_j}. \end{aligned}$$

Put $y_0 = c_{\Pi \wedge \Pi ',0j}, j\in \{0\}\cup J$ and $y_1= c_{\Pi \wedge \Pi ',1j}, j\in J'.$ Put $\gamma _0{:}= \sum _{j\in \{0\}\cup J} \gamma _{\Pi \wedge \Pi ',0j}.$ Then we get (cf. (3.14))

$$\begin{aligned} F(y_0,y_1,\ldots ,y_1)= & {} \varphi ^{-1}\left( \alpha _{\Pi }\varphi (y_0)+(1-\alpha _{\Pi })\varphi (y_1)\right) \nonumber \\= & {} M\left( y_0{\mathbf 1}_A + y_1{\mathbf 1}_{\Omega \setminus A}\right) = \varphi ^{-1}\left( \gamma _0\varphi (y_0)+(1-\gamma _0)\varphi (y_1)\right) .\nonumber \\ \end{aligned}$$

(3.15)

It follows from (3.15) that

$$\begin{aligned} \left( \alpha _{\Pi } - \gamma _0\right) \left( \varphi (y_0) -\varphi (y_1)\right) =0 \end{aligned}$$

for every $y_0,\, y_1\in \mathbb R(\mathbb R_+ ).$ Obviously then $\alpha _{\Pi } = \gamma _0$ and the correctness of the definition of P is proved. In particular, we get (3.1).

Ad 2. As to the additivity of P, consider the following two partitions of $\Omega$:

$$\begin{aligned} (A_0,A_1, \Omega \setminus (A_0\cup A_1)) \end{aligned}$$

and

$$\begin{aligned} (A_0\cup A_1,\Omega \setminus (A_0\cup A_1)) \end{aligned}$$

for some disjoint sets $A_0, \, A_1\in {\mathcal A}.$ We may assume w.l.o.g. that $\mu (A_0)\mu (A_1)\mu (\Omega \setminus (A_0\cup A_1))>0.$ Then for every $s,t\in \mathbb R\, (\mathbb R_+)$ we have (cf. (2.16) or (2.17))

$$\begin{aligned} M\left( s{\mathbf 1}_{A_0} + s{\mathbf 1}_{A_1}+ t{\mathbf 1}_{\Omega \setminus (A_0\cup A_1)}\right) = M\left( s{\mathbf 1}_{A_0\cup A_1} + t{\mathbf 1}_{\Omega \setminus (A_0\cup A_1)}\right) , \end{aligned}$$

(3.16)

which yields (cf. (3.14) applied to the left-hand side)

$$\begin{aligned} \varphi ^{-1}\left( \alpha _0\varphi (s)+\alpha _1\varphi (s)+\alpha _2\varphi (t)\right) = \varphi ^{-1}\left( \left( \alpha _0+\alpha _1\right) \varphi (s) + \alpha _2\varphi (t)\right) , \end{aligned}$$

(3.17)

for all $s,t\in \mathbb R\, (\mathbb R_+)$. On the other hand we get

$$\begin{aligned} M\left( s{\mathbf 1}_{A_0\cup A_1} + t{\mathbf 1}_{\Omega \setminus (A_0\cup A_1)}\right) = \varphi ^{-1}\left( \beta _0 \varphi (s) + \beta _2\varphi (t)\right) \end{aligned}$$

(3.18)

for some $\beta _0, \beta _1$ and all $s,t\in \mathbb R(\mathbb R_+).$ From (3.163.17), (3.163.17) and (3.18), and the properties of $\varphi$ we get

$$\begin{aligned} \alpha _0 + \alpha _1 = \beta _0 \, \, \hbox {and }\alpha _2=\beta _2, \end{aligned}$$

which means in particular that

$$\begin{aligned} P(A_0\cup A_1) = P(A_0)+P(A_1), \end{aligned}$$

and yields the required additivity of P.

Ad 3. Now we proceed to prove the equivalence (3.2). Suppose that $A\in {\mathcal A}$ is such that $\mu (A)\mu (\Omega \setminus A)>0$. Take $s<t$ and put $x=s{\mathbf 1}_{A} + 0{\mathbf 1}_{\Omega \setminus A}$ and $y= t{\mathbf 1}_{A} + 0{\mathbf 1}_{\Omega \setminus A}.$ Since M is $\mu$-strictly increasing, we have $M(x)< M(y),$ whence (cf. (2.16)) $F(s,0)<F(t,0),$ or (cf. (3.14))

$$\begin{aligned} \varphi ^{-1}\left( P(A)\varphi (s)\right) < \varphi ^{-1}\left( P(A)\varphi (t)\right) . \end{aligned}$$

It follows that $P(A)>0.$

To see that the converse also holds, suppose that for some $A\in {\mathcal A}$ we have $P(A)> 0$ and $\mu (A)=0.$ Then $\mu (\Omega \setminus A)> 0$ and, as it follows from the first part of the present argument, $P(\Omega \setminus A)> 0.$ Let us take $s< t, \, u, v \in \mathbb R\, (\mathbb R_+)$ and define two functions $f, \, g:\Omega \longrightarrow \mathbb R$ by $f= u{\mathbf 1}_{A} + s{\mathbf 1}_{\Omega \setminus A}$ and $g= v{\mathbf 1}_{A} + t{\mathbf 1}_{\Omega \setminus A}.$ Then $f< g$ in the sense of (2.1). Thus $M(f)<M(g)$ by monotonicity which implies

$$\begin{aligned} P(A)\varphi (u) +(1-P(A))\varphi (s) < P(A)\varphi (v) +(1-P(A))\varphi (t), \end{aligned}$$

whence it follows that

$$\begin{aligned} \varphi (v)-\varphi (u) > \frac{P(\Omega \setminus A)}{P(A)}\left[ \varphi (t)-\varphi (s)\right] . \end{aligned}$$

(3.19)

Taking $v<u$ and letting $s\longrightarrow t$ in (3.19) we get

$$\begin{aligned} 0> \varphi (v)-\varphi (u)\ge 0, \end{aligned}$$

a contradiction.

IV. The formula (3.3) follows naturally. Indeed, take a $y\in {\mathbf{F}}(\Omega ) ({\mathbf{F}}_+(\Omega )),$ and suppose that there exist a partition $\Pi =(A_0,\ldots , A_{n-1})$ (with $\mu (A_i)>0, \, i\in \{0,\ldots ,n-1\}$) such that

$$\begin{aligned} y = \sum _{i=0}^{n-1} y_i{\mathbf 1}_{A_i}, \end{aligned}$$

for some $y_i\in \mathbb R(\mathbb R_+).$ Then there exist a strictly monotone function $\varphi$ and positive numbers $\alpha _i, \, i\in \{0,\ldots ,n-1\}$ such that $\sum _{i=0}^{n-1} \alpha _i =1$ and

$$\begin{aligned} M(y)= \varphi ^{-1}\left( \sum _{i=0}^{n-1}\alpha _i \varphi (y_i)\right) = \varphi ^{-1}\left( \sum _{i=0}^{n-1}P(A_i) \varphi (y_i)\right) = \varphi ^{-1}\left( \int _{\Omega } f\circ y dP\right) . \end{aligned}$$

3.2 Arbitrary case

We have proved that a continuous, bisymmetric and reflexive functional M which satisfies (2.15) is given by (3.3) for any $y\in {\mathbf{F}}(\Omega )\, ({\mathbf{F}}_+(\Omega )).$ If the set ${\mathbf{F}}(\Omega )$$({\mathbf{F}}_+(\Omega ))$ is dense in a function family ${\mathcal F}$ (or at least any element of ${\mathcal F}$ can be approximated by a sequence from ${\mathbf{F}}(\Omega )\, ({\mathbf{F}}_+(\Omega ))$) then sometimes, due to the continuity of $M, \, \varphi$ and $\varphi ^{-1}$ we may pass with $\lim$ under the sign of $\int$, and we get formula (3.3) for any $y\in X$.

Below we present two such cases: the space of bounded functions or the space of integrable functions.

Corollary 3.1

Let $\mu :2^{\Omega } \rightarrow [0,\infty ]$ be an additive, nontrivial function. Then $M: B(\Omega ,\mathbb R)\rightarrow \mathbb R$ is reflexive, $\mu$-strictly increasing, continuous and bisymmetric if, and only if, there exist a strictly increasing and continuous function $\varphi : \mathbb R\rightarrow \mathbb R$ and an additive function $P:2^{\Omega }\rightarrow [0,1]$ such that (3.1), (3.2) are satisfied and (3.3) holds for every $y\in B(\Omega ,\mathbb R).$

Proof

In the space ${\mathbf{F}}(\Omega )$ we have defined the functional M by the formula

$$\begin{aligned} M(x)= \varphi ^{-1}\left( \int _{\Omega } (\varphi \circ x) dP\right) . \end{aligned}$$

Now, this functional can be uniquely extended to a continuous functional onto the whole $B(\Omega ,\mathbb R)$ because ${\mathbf{F}}(\Omega )$ is a dense subspace of $B(\Omega ,\mathbb R).$ Indeed, for every $x\in B(\Omega ,\mathbb R)$ there exists a sequence $(x_n)_{n\in \mathbb N} \in {\mathbf{F}}(\Omega )^{\mathbb N},$ which converges uniformly to x. The sequence $(\varphi \circ x_n)_{n\in \mathbb N}$ is then uniformly convergent to $\varphi \circ x,$ due to the uniform continuity of $\varphi$ in any compact subset of $\mathbb R.$ Thus we get (considering the finiteness of $P(\Omega )$ and continuity of $\varphi ^{-1}$)

$$\begin{aligned}&\lim _{n\rightarrow \infty } M(x_n) = \lim _{n\rightarrow \infty } \varphi ^{-1}\left( \int _{\Omega } (\varphi \circ x_n) dP\right) \\&\qquad = \varphi ^{-1}\left( \lim _{n\rightarrow \infty } \int _{\Omega } (\varphi \circ x_n) dP\right) = \varphi ^{-1}\left( \int _{\Omega } \lim _{n\rightarrow \infty }(\varphi \circ x_n) dP\right) \\&\qquad = \varphi ^{-1}\left( \int _{\Omega } (\varphi \circ x) dP\right) = M(x), \end{aligned}$$

which was to be proved. It remains to show that (3.2) holds (with ${\mathcal A} = 2^{\Omega }$) but we have already proved it while showing Proposition 3.1.

Corollary 3.2

Let $(\Omega , {\mathcal A}, \mu )$ be a measure space with a finite $\mu$. Let $M{:} L^1(\Omega ,\mathbb R)\rightarrow \mathbb R$ be reflexive, $\mu$-strictly increasing, continuous and bisymmetric. Then M is given by (3.3) for every $y\in {\mathbf{F}}(\Omega )$ with some increasing and continuous $\varphi : \mathbb R\rightarrow \mathbb R$ and additive $P:{\mathcal A}\rightarrow [0,1].$ If, additionally, we assume that $\varphi$ is bounded then M is given by (3.3) for every $y\in L^1(\Omega ,\mathbb R),$ and P is a probability measure equivalent to $\mu$.

Proof

An additional assumption on $\varphi$ is needed because we want the composition $\varphi \circ y$ to be in $L^1(\Omega ,\mathbb R) .$

We know that M(y) is given by (3.3) for every $y\in {\mathbf{F}}(\Omega ):$ it follows from Proposition 3.1. But ${\mathbf{F}}(\Omega )$ is a dense subset of $L^1(\Omega , \mathbb R)$ and therefore for each $y\in L^1(\Omega , \mathbb R)$ there exists a sequence $(y_n)_{n\in \mathbb N} \in {\mathbf{F}}(\Omega ) ,$ converging to y in the norm of $L^1.$ Using the continuity of M and the fact that $\varphi$ is a homeomorphism, we get henceforth

$$\begin{aligned} M(y)= & {} M(\lim _{n\rightarrow \infty } y_n) = \lim _{n\rightarrow \infty } M(y_n)\\= & {} \lim _{n\rightarrow \infty } \varphi ^{-1}\left( \int _{\Omega } \varphi \circ y_n dP\right) = \varphi ^{-1}\left( \int _{\Omega } \varphi \circ y dP\right) . \end{aligned}$$

If $\mu$ is a measure, then we obtain the $\sigma$-additivity of P in the following way. Suppose that $A=\bigcup _{n=1}^{\infty } A_n$ where $A_n\in {\mathcal A}$ are pairwise disjoint. Fix an $N\in \mathbb N$ and consider the following finite valued function $z_N= s{\mathbf 1}_{\bigcup _{n=1}^N A_n} + t{\mathbf 1}_{\Omega \setminus \bigcup _{n=1}^N A_n}.$ Then

$$\begin{aligned} M(z_N)= & {} \varphi ^{-1}\left( P(\bigcup _{n=1}^N A_n)\varphi (s) + P(\Omega \setminus \bigcup _{n=1}^N A_n)\varphi (t)\right) \\= & {} \varphi ^{-1}\left( \sum _{n=1}^NP(A_n)\varphi (s) + \left( 1 - \sum _{n=1}^N P(A_n)\right) \varphi (t)\right) , \end{aligned}$$

and therefore

$$\begin{aligned} \varphi \left( M \left( z_N\right) \right) = \left( \sum _{n=1}^N P(A_n) \right) \varphi (s) + \left( 1 - \sum _{n=1}^N P(A_n)\right) \varphi (t). \end{aligned}$$

Since $\lim _{N\rightarrow \infty } z_N = s{\mathbf 1}_{A} + t {\mathbf 1}_{\Omega \setminus A}$ pointwise (but also in $L^1$-norm) we have by the continuity of $\varphi$ and M that

$$\begin{aligned} \lim _{N\rightarrow \infty } \varphi \left( M \left( z_N\right) \right) = P(A) \varphi (s) + \left( 1 - P(A)\right) \varphi (t) \end{aligned}$$

whence

$$\begin{aligned} \left( \lim _{N\rightarrow \infty } \sum _{n=1}^N P(A_n) - P(A)\right) \left( \varphi (s) - \varphi (t)\right) = 0 \end{aligned}$$

for every $s, t\in \mathbb R$ follows. Hence

$$\begin{aligned} \sum _{n=1}^{\infty } P(A_n) = P(A). \end{aligned}$$

Without any assumption on $\varphi$ we get the following result.

Corollary 3.3

Let $(\Omega , {\mathcal A}, \mu )$ be a measure space with a finite $\mu$. Let ${\mathcal F}$ consist of all ${\mathcal A}$-measurable, bounded and non-negative functions. Then $M: {\mathcal F}\rightarrow \mathbb R$ is reflexive, $\mu$-strictly increasing, continuous and bisymmetric if, and only if, M is given by (3.3) for every $y\in {\mathcal F}$ with some increasing and continuous $\varphi : \mathbb R\rightarrow \mathbb R$ and $P:{\mathcal A}\rightarrow [0,1]$ which is a probability measure equivalent to $\mu$.

3.3 Final remarks

At the 53rd International Symposium on Functional Equations J. Chudziak (cf. [3]) called our attention to the fact that there is a connection between the above results and utility theory. Namely, if u is an arbitrary utility function (i.e. continuous and strictly increasing), we say that $\lambda \in \mathbb R$ is a certainty equivalent of a gamble $X\in \chi _+$ iff

$$\begin{aligned} u(\lambda ) = \mathbb E(u(X)), \end{aligned}$$

whence

$$\begin{aligned} \lambda = u^{-1}[\mathbb E(u(X))]. \end{aligned}$$

(3.20)

Here the symbol $\chi _+$ denotes all the non-negative and bounded random variables. Let us note that the assumption of boundedness, which guarantees the correctness of the definition (3.20) could be replaced by the requirement of concavity for u. Indeed then the Jensen inequality is implied, and one has

$$\begin{aligned} 0\le \int _{\Omega } u\circ y dP \le u \left( \int _{\Omega } y dP \right) < \infty \end{aligned}$$

for all $y\in L^1(\Omega ,\mathbb R_+).$

The functional $M:\chi _+ \longrightarrow \mathbb R$ given by

$$\begin{aligned} M(X){:}= u^{-1}[\mathbb E(u(X))] = u^{-1}\left( \int _{\Omega }u(X)dP\right) \end{aligned}$$

(3.21)

is called equivalence functional.

Thus we can conclude our present considerations by the following.

Corollary 3.4

Let $(\Omega , {\mathcal A}, \mu )$ be a probability space. Let $\chi _+$ consist of all ${\mathcal A}$-measurable, bounded and non-negative functions. Then $M: \chi _+\rightarrow \mathbb R$ is reflexive, $\mu$-strictly increasing, continuous and bisymmetric if, and only if, M is given by (3.21) for every $X\in \chi _+ ,$ where $u:\mathbb R_+ \rightarrow \mathbb R$ is a utility function and $\mathbb E$ is the expectation taken with respect to some probability measure P,  equivalent to $\mu .$

We also have

Corollary 3.5

Let $(\Omega , {\mathcal A}, \mu )$ be a probability space. Let $M:L^1(\Omega ,\mathbb R_+)\longrightarrow \mathbb R$ be reflexive, $\mu$-strictly increasing, continuous and bisymmetric. Then, according to Proposition 3.1, there exist a probability measure P equivalent to $\mu$ and a continuous and strictly increasing function $u:\mathbb R_+ \rightarrow \mathbb R$ such that M is given by (3.21) for all $X\in {\mathbf{F}}_+(\Omega ).$ If, additionally, u is concave and non-negative then M is given by (3.21) for all $X\in L^1(\Omega ,\mathbb R_+).$