Abstract
In this paper, the generalized Love integral equation has been considered. In order to approximate the solution, a Nyström method based on a mixed quadrature rule has been proposed. Such a rule is a combination of a product and a “dilation” quadrature formula. The stability and convergence of the described numerical procedure have been discussed in suitable weighted spaces and the efficiency of the method is shown by some numerical tests.
Similar content being viewed by others
1 Introduction
In 1949, Love investigated for the first time on a mathematical model describing the capacity of a circular plane condenser consisting of two identical coaxial discs placed at a distance q and having a common radius r. In his paper [9], he proved that the capacity of each disk is given by:
where f is the solution of the following integral equations of the second kind:
with ω = q/r a real positive parameter. Then, he proved that (1.1) has a unique, continuous, real, and even solution which analytically has the following form:
where the iterated kernels are given by:
From a numerical point of view, the developed methods [7, 8, 12, 15, 17] for the undisputed most interesting case (i.e., when ω− 1 → 0) have followed the very first methods [4, 5, 16, 19, 20], and the most recent ones [11], proposed for the case when ω = 1.
If ω− 1 → 0 the kernel function is “close” to be singular on the bisector x = y. This kind of kernel belongs to the so-called nearly singular kernels class. Moreover, Phillips noted in [16] that:
Hence, for ω sufficiently large, the left-hand side of (1.1), in the case “−” is considered, becomes approximately zero which does not coincide with the right-hand side of (1.1).
In [12], the authors presented a numerical approach based on a suitable transformation to move away from the poles x = y ± ω− 1i from the real axis. The numerical method produced very accurate results in the case when ω− 1 is not so small but they are poor if ω− 1 → 0.
Then, in order to get satisfactory errors also in this latter case, in [15] the author proposed to dilate the integration interval and to decompose it into N subintervals. Hence, the equation was reduced to an equivalent system of N integral equations and a Nyström method based on a Gauss-Legendre quadrature formula was proposed for its numerical approximation. The approach produces satisfactory order of convergence even if ω− 1 is small. However, the dimension of the structured linear system that one needs to solve is very large as ω− 1 decreases.
In [7], the authors improve the results given in [15] by using the same transformation as in [8] which takes into account the behavior of the unknown function showed in (1.2). Then, they follow the approach given in [15]; i.e., they write the integral as the sum of m new integrals which are approximated by means of a n-point Gauss-Legendre quadrature rule. In this way, they get a linear system of size nm that, multiplied by suitable diagonal matrices, is equivalent to a new linear system which is solved by using a preconditioned conjugate gradient method, being the matrix of coefficients symmetric, positive definitive, and having a Toeplitz block structure.
In this paper, we consider the more general equation:
where w(x) = vα,β(x) = (1 − x)α(1 + x)β, α,β> − 1, f is the unknown function, g is a known right-hand side, μ ∈IR and 0 < ω ∈IR.
Such equation includes (1.1) (in the case when g ≡ w ≡ 1 and \(\mu =\pm \frac {1}{\pi }\)) and, at the same time, the presence of the weight w leads to the case when the unknown function has algebraic singularities at the endpoints of [− 1,1]. So, the method we propose and the theoretical results we prove can be applied not only in the special case of the Love equation but also in the general one in which the involved functions are singular at ± 1. This general case could be interesting in the future for other possible physical models.
The method we propose is a Nyström method based on a mixed quadrature formula. This is a product rule whose coefficients are computed by using a quadrature scheme. In fact, following an idea presented in [2, 15], we approximate such coefficients by using a “dilation” quadrature formula that we prove to be stable and convergent. Such an idea which consists of a preliminary dilation of the domain, that “relax” in some sense the pathological behavior of the kernel of the integral, allows us to get very accurate results when ω is large, better than those in [7, 15]. The proposed method, whose convergence and stability are proved in suitable weighted spaces, leads to a well-conditioned linear system, the dimension of which is greatly reduced w.r.t. the ones involved in [7, 15]. The size of the system we solve does not depend on the magnitude of the parameter ω and the error is of the order of the best polynomial approximation of the unknown function, independently of the value of ω. Moreover, we underline that mutatis mutandis the numerical approach could be applied to different Fredholm integral equations with other types of “nearly singular” kernels.
The outline of the paper is as follows. At first, in Section 2, we introduce the functional spaces in which we will analyze our method. In Section 3, we remind some well-known quadrature rule (Section 3.1), we study a “dilation” quadrature formula (Section 3.2), and we propose a new mixed quadrature scheme (Section 3.3) which is used in the Nyström method presented in Section 4. Section 5 shows the efficiency of the proposed procedure by means of several numerical tests, and finally, Section 6 contains the proofs of our main results.
2 Functional spaces and notations
Let us consider the following Jacobi weight function with parameters γ,δ ≥ 0
and let us define the space of weighted continuous functions defined as:
in the case when γ,δ > 0. In the case γ = 0 (respectively δ = 0), Cσ consists of all functions which are continuous on (− 1,1] (respectively [− 1,1)) and such that \(\displaystyle \lim _{x\rightarrow -1^{+}}(f \sigma )(x)=0\) \(\left (\text {respectively} \displaystyle \lim _{x\rightarrow 1^{-}}(f \sigma )(x)=0\right )\). Moreover, if γ = δ = 0 we set Cσ = C0([− 1,1]). We equip the space Cσ with the weighted uniform norm
and we remark that Cσ endowed with such a weighted norm is a Banach space.
For smoother functions, we introduce the following Sobolev-type space
where the superscript (r) denotes the r th derivative of the function f with r a positive integer and \(\varphi (x)=\sqrt {1-x^{2}}\). We equip \({\mathscr{W}}^{r}_{\sigma }\) with the norm:
Finally, for any \(p \in \mathbb {N}_{0} \cup \{ \infty \}\), we denote by Cp([− 1,1]) the set of all continuous functions having p continuous derivatives.
Throughout the whole paper, we will denote by \({\mathscr{C}}\) a positive constant which will have different meanings in different formulas. We will write \({\mathscr{C}} \neq {\mathscr{C}}(a,b,\ldots )\) in order to say that \({\mathscr{C}}\) is a positive constant independent of the parameters a,b,…, and \({\mathscr{C}} = {\mathscr{C}}(a,b,\ldots )\) to say that \({\mathscr{C}}\) depends on a,b,…. Moreover, if A,B > 0 are quantities depending on some parameters, we write \(A \sim B,\) if there exists a constant \(0<{\mathscr{C}}\neq {\mathscr{C}}(A,B)\) s.t. \(\frac {B}{{\mathscr{C}}} \leq A \leq {\mathscr{C}} B\).
3 Integration formulae
3.1 Classical quadrature formulae
In this subsection, we remind two well-known quadrature rules [10] and we mention the related convergence results which will be essential for our aims.
Let us introduce the Jacobi weight of parameters α,β> − 1, i.e.:
and let us denote by \(\left \{p_{m}\left (w\right )\right \}_{m=0}^{\infty }\) the corresponding sequence of orthonormal polynomials with positive leading coefficients, i.e.:
Then, we recall the Gauss-Jacobi quadrature rule [10]:
where \(\{{\lambda _{i}^{w}}\}_{i=1}^{m}\) denote the Christoffel numbers w.r.t. the weight function w, \(\{{\xi _{i}^{w}}\}_{i=1}^{m}\) are the zeros of pm(w,x) and \({\mathscr{R}}_{m}\) stands for the remainder term.
About the latter, it is possible to estimate it (see, for instance, [10]) in terms of the weighted error of best polynomial approximation of f ∈ Cσ, i.e.:
where \(\mathbb {P}_{m}\) denotes the set of all algebraic polynomials of degree at most m. In fact, for each f ∈ Cσ, if the parameters of the weights w and σ are such that 0 ≤ γ < α + 1 and 0 ≤ δ <β + 1, then
whereas if f ∈ C2m([− 1,1]) then
where γm(w) is the positive leading coefficient of pm(w,x) introduced in (3.2).
Now, we introduce a product rule in order to evaluate the integrals of the type
where f ∈ Cσ, h is a known kernel function and w is the weight defined in (3.1).
Such rule reads as [10]:
where \({\mathscr{E}}_{m}(f,y)\) denotes the remainder term and the coefficients \(\{A_{j}\}_{j=1}^{m}\) are defined as:
with
the j th fundamental Lagrange polynomial.
About the stability and the convergence of the above formula, it is possible to prove, by using a well-known Nevai theorem (see, for instance, [10, 13]), that if
and the weights w and σ are such that their exponents satisfy the following inequalities:
then, the rule (3.6) is stable and convergent and the following convergence estimate holds true:
Remark 3.1
Let us remark that the kernel function appearing in the Love (1.3) satisfies (3.9). Moreover, if \(\alpha , \upbeta <\frac {3}{2}\), then the parameters γ and δ can also be chosen equal to zero.
3.2 A dilation formula
In this subsection, we present a quadrature formula in order to approximate the integrals of the type:
where F is a given function, w is as in (3.1), and k(x,y,ω) is a known kernel which is close to be singular if ω− 1 → 0. This is the case of the kernel function appearing in the Love equation (1.3).
In order to construct such kind of formula, we follow the approach proposed in [2, 15] for the unweighted case.
First, in order to “relax” the “too fast” behavior of the kernel function when ω grows, we introduce in (3.13) the change of variables \(x=\frac {\eta }{\omega }, y=\frac {\theta }{\omega }\), with η,𝜃 ∈ [−ω,ω]. In this way, (3.13) is equivalent to the following integral having a dilated domain of integration [−ω,ω]:
Then, we split the new integration interval [−ω,ω] into S subintervals of size \(2 \leq d \in \mathbb {R}\) s.t. \(S= \frac {2 \omega }{d} \in \mathbb {N}\), namely \([-\omega , \omega ]= \displaystyle \bigcup _{i=1}^{S} [-\omega +(i-1)d, -\omega +id],\) getting
Now, we want to remap each integral into [− 1,1]. To this end, we introduce the invertible linear maps Ψi : [−ω + (i − 1)d,−ω + id] → [− 1,1] defined as:
and in (3.14) we make the change of variable:
In this way, we get:
where \(F_{i}(x):=F\left (\frac {{\Psi }^{-1}_{i}(x)}{\omega }\right )\), ui are the new weight functions:
and ki are the new kernel functions:
or, equivalently, in terms of the original kernel k,
Let us underline that the advantage of the change of variable we introduced in (3.13) and the splitting of the dilated interval [−ω,ω] into S parts of length d is that we reduce the computation of the integral into the computation of a sum of integrals and in each of them the kernel function ki(x,ωy,ω) has complex poles sufficiently far from the real axis. In fact, the distance from these poles to the x axis is greater than \(\frac {2}{d}\).
By approximating each integral appearing in (3.16) by means of the Gauss-Jacobi quadrature rule (3.3) with ui in place of w and kiFi instead of f, we have the following “dilation” quadrature formula:
where Λn is the remainder term.
Next results state the stability of the previous formula and give an error estimate for Λn in the case when \(F\in {\mathscr{W}}^{r}_{\sigma }\) or F ∈ C2n([− 1,1]).
Theorem 3.1
Let F ∈ Cσ be with σ as in (2.1) and let w be as in (3.1). If \(0\! \leq \! \gamma \! <\! \min \limits \{1,\alpha + 1\}\), \(0 \! \leq \! \delta <\min \limits \{1,\upbeta +1\}\) and k is s.t. \(\displaystyle \max \limits _{|y| \leq 1} \|k(\cdot ,\omega y,\omega )\|_{\infty } \! <\! +\infty \) then for the quadrature formula in (3.19) we have:
Moreover, for any \(F\in {\mathscr{W}}^{r}_{\sigma }\), if
we have
Corollary 3.1
Let F,k ∈ C2n([− 1,1]) w.r.t. the variable x. Then
with \( {\mathscr{C}} \neq {\mathscr{C}}(n,\omega ,d)\).
Remark 3.2
We outline that the quantity \(\displaystyle \frac {d}{\omega }\) appearing in both the estimates (3.22) and (3.23) is a quantity ≪ 1 if we divide the interval [−ω,ω] into a very large number of subintervals S, being \(\displaystyle \frac {d}{\omega }=\displaystyle \frac {2}{S}\). Moreover, in accordance with what proven in [14], we have experimented that an optimal choice is \(d \sim 2\). We also remark that the r-derivative of the kernel function appearing in the assumption (3.21) depends on the real parameter ω and its asymptotic behavior (with respect to such a parameter) goes like ω− 1.
3.3 A mixed quadrature formula
In this subsection, we want to propose a mixed quadrature rule which will be essential for our method. It consists in applying an m-point product rule (3.6) in order to approximate the integral:
and in approximating the coefficients Aj of such a product rule (defined in (3.7) with h(x,y) = k(x,y,ω)) by means of the n-point “dilation” quadrature formula (3.19).
Then, the mixed quadrature formula is the following:
where \({\mathscr{E}}^{n}_{m}\) is the remainder term and:
with ki and ui as in (3.18) and (3.17), respectively, and \(\ell _{j,i}^{w}\left (\xi _{\nu }^{u_{i}}\right ):={\ell _{j}^{w}}\left (\frac {{\Psi }_{i}^{-1}\left (\xi _{\nu }^{u_{i}}\right )}{\omega }\right )\) being \({\ell _{j}^{w}}\) and \({\Psi }_{i}^{-1}\) defined as in (3.8) and (3.15), respectively.
Next theorem gives an error estimate for \({\mathscr{E}}^{n}_{m}\) in the case when n = m.
Theorem 3.2
Let w and σ be defined in (3.1) and (2.1), respectively with:
If f ∈ Cσ and the kernel function k satisfies the conditions (3.9) and the assumptions given in Theorem 3.1, the following error estimate holds true:
Remark 3.3
Let us remark that if \(\alpha ,\upbeta < -\frac {1}{2}\), then the parameters of the weight σ could also be chosen equal to zero. Moreover, in Theorem 3.2, for the sake of simplicity, we considered the case m = n. Nevertheless in practice in the numerical test we can use n fixed. Indeed, according with (3.23), the error decreases exponentially and, for instance, for n = 20, d = 2, and ω = 102, the quantity before the square brackets is of the order 10− 98. Hence, the error of the mixed quadrature formula is, in practice, of the same order of the error of best approximation of f. We emphasize that the larger the ω is, the more the second term goes to zero quickly. In any case, whatever the magnitude of ω is, the first term of the estimate stated in Theorem 3.2 prevails on the second.
4 The numerical method
In this section, we propose a numerical method for the Love integral equation (1.3) which can be rewritten in operatorial form as:
where I is the identity operator and
with
The next proposition shows the mapping properties of the operator K.
Proposition 4.1
Let σ and w be defined in (2.1) and (3.1), respectively s.t. the parameters γ,δ,α and β satisfy 0 ≤ γ < 1 + α and 0 ≤ δ < 1 +β. Then \(K:C_{\sigma }\!\rightarrow \! C_{\sigma }\) is continuous, bounded and compact. Moreover, ∀f ∈ Cσ, \(K f\in {\mathscr{W}}^{r}_{\sigma }, \forall r\in \text {I\text {\hskip -1.9pt N}}\).
Remark 4.1
We remark that according to Proposition 4.1 and in virtue of the Fredholm Alternative Theorem, under the assumption Ker{I + μK} = {0}, (4.1) has a unique solution f ∈ Cσ.
The proposed numerical strategy is a Nyström method based on the mixed quadrature formula \({K_{m}^{n}}f\) introduced in (3.24). Then, we consider the functional equation:
where \({f^{n}_{m}}\) is unknown. We multiply both sides of (4.4) by the weight function σ and we collocate each equation at the points \(\{{\xi _{i}^{w}}\}_{i=1}^{m}\). In this way, we have that the quantities \(a_{i}=({f^{n}_{m}} \sigma )({\xi _{i}^{w}}) \) are the unknowns of the following m × m linear system:
where δij is the Kronecker symbol. In terms of matrices the system is \(\mathbb {A}_{m}\mathbbm {a}= \mathbbm {b},\) where \(\mathbb {A}_{m}= \mathbb {I}+ \mu \mathbb {B}_{m}\), with \(\mathbb {I}\) the identity matrix of order m and
while
Once (4.5) is solved, its solution \([\mathbbm {a}^{*}]_{i=1}^{m}=a^{*}_{i}\) allows us to construct the following weighted Nyström interpolant:
which will approximate the unknown solution f ∈ Cσ.
Next theorem states that the above described Nyström method is stable and convergent, as well as that the condition number in infinity norm of the matrix \(\mathbb {A}_{m}\); i.e., \(cond(\mathbb {A}_{m})=\|\mathbbm {A}_{m}\|_{\infty } \|\mathbbm {A}^{-1}_{m}\|_{\infty } \) is bounded by a constant which does not depend on m.
Theorem 4.1
Let w and σ be defined in (3.1) and (2.1), respectively with parameters satisfying (3.25) and (3.26), and let us assume that Ker{I + μK} = {0} in Cσ. Then, if \(g\in {\mathscr{W}}^{r}_{\sigma }\), r > 1, for m sufficiently large, the operators \(\left (I+\mu {K^{m}_{m}}\right )^{-1}\) exist and are uniformly bounded. Moreover, system (4.5) is well conditioned, since \( cond(\mathbb {A}_{m})\leq {\mathscr{C}}\) with \({\mathscr{C}}\neq {\mathscr{C}}(m)\) and the following estimate holds true:
Remark 4.2
Let us remark that the first step of our method is the natural and immediate approximation of the integral by means of the mixed quadrature formula. In doing this, we “isolate” in some sense the parameter ω in the computation of the coefficients of the rule. The collocation is independent of ω and this produces the advantage that the size of the system does not depend on it, as instead happens in other methods available in the literature [7, 15]. Moreover, as stated in estimate (4.7), the proposed global approximation method allows us to find the solution of the equation with a convergence order which is again independent of the magnitude of ω. Indeed, the error is of the order of the best polynomial approximation of f and being \(f \in {\mathscr{W}}^{r}_{\sigma }\) one has:
However, the function f naturally depends on ω, being the solution of an equation in which such a parameter appears (see also the analytical expression of the solution recalled in the “Introduction”). Consequently, the norm of the r th derivative (appearing at the right-hand side of the above estimate) depends on and becomes large for increasing values of ω. This is the only reason why for a large value of ω we need to increase the dimension of the system in order to get high precision (see Table 1).
Remark 4.3
Let us underline that the numerical method we propose leads to a not structured linear system of order m in which each element of the matrix involves S × n evaluation of a polynomial of degree m − 1. However, the fact that the matrix is not structured does not lead to any problem. In fact, as we can see in Section 5, the method produces very accurate results for small values of m and, as stated in the previous theorem, the matrix is also well-conditioned. This is also the reason why we do not propose a suitable and more performing numerical method in order to solve the linear system we get.
5 Numerical tests
In this section, we show by some numerical tests the performance of the method described in the previous section. Specifically, we first test the proposed approach on the classical Love integral equation (Example 5.1) and then we show its effectiveness on other two generalized Love’s equations (Examples 5.2 and 5.3). In all the numerical tests, the solution f is very smooth and we expect a fast convergence according to estimate (4.7).
We approximate the solutions of the test equations by means of the Nyström interpolants given by (4.6) and we compute the absolute errors:
in different points x ∈ [− 1,1]. In (5.1) \({f^{n}_{m}}\) is the solution assumed to be exact which is obtained with a fixed value m = M.
Moreover, in the tables, the CPU time average of the complete procedure (construction and solution of the linear system+construction and evaluation of the Nyström interpolant) is given. The numerical evidence is that the needed CPU time depends linearly on m and ω. Indeed, when m is doubled also is the CPU time. And if we see at the CPU time for ω = 102,103,104, it is clear that for the same value of m, if t is the time spent in the case ω = 102, then it will be about 10 ∗ t for ω = 103 and 100 ∗ t for ω = 104.
All the numerical experiments were performed in double precision arithmetic on an IntelCore i7 system (4 cores), running the Mac OS operating system and using Matlab R2018a.
Example 5.1
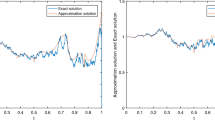
Let us consider the classical Love integral (1.3) in the space Cσ with σ ≡ 1 and \(\mu =\frac {1}{\pi }\). In Table 1 we report the results we get for different choices of ω. By comparing them with those presented in [7, Table 1, Table 3, and Table 5], we can see that, in the case when ω = 102 by solving a square system of m = 256 equations we get an error of the order of the machine precision (M.P.), instead of 10− 5 as shown in [7, Table 1]. If ω = 103, by solving a system of order 700, we get the machine precision, accuracy that in [7, Table 3] is reached with a system of 16384 equations. Similarly, the method gives accurate results also in the case when ω = 104. The first graph of Fig. 1 shows the approximated solution \(f^{20}_{700}\) with ω = 102.
Example 5.2
Let us test our method on the equation:
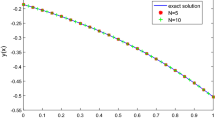
namely, a generalized Love integral equation with ω = 102 and \(\mu =\frac {1}{\pi }\). Table 2 shows the errors (5.1) that we get with \(\sigma (x)=v^{\frac {1}{2},\frac {1}{2}}(x)\), n = 20 and M = 350 for increasing value of m. As we can see by solving a linear system of order m = 256, we get the machine precision (M.P.). The second graph of Fig. 1 displays the approximate solution \(f^{20}_{512}\sigma \).
Example 5.3
Let us consider the following generalized Love’s integral equation with ω = 103:
in the space Cσ with \(\sigma (x)=v^{\frac {1}{4},\frac {1}{4}}(x)\) and where \(\mu =\frac {1}{\pi }\). Table 3 contains the accurate results we get also in this case and the last graph of Fig. 1 shows the approximated solution \(f^{20}_{512}\sigma \).
6 Proofs
Proof Proof of Theorem 3.1
First, let us prove the stability of the formula, i.e., estimate (3.20). We can write:
Then (3.20) follows taking into account the definition of ki given in (3.18), the first assumption on the kernel, and by considering that in virtue on the assumptions on the parameters of the weights, we have:
In order to prove (3.22), we can note that by (3.4), we have:
so that by using the well-known estimate [10]:
we can write:
Then, taking into account that by the assumptions \(\|k_{i}(\cdot ,\omega y,\omega )\|_{\infty }< {\mathscr{C}}\) and by applying the Favard inequality [10]:
once with the Jacobi weight v = 1, and then with v = σ, we deduce:
Now, let us note that the functions ki defined in (3.18) can be rewritten as:
where the functions Ui, defined as:
are bounded functions such that:
Hence, being for each \(i=1, \dots , S\)
by using (3.21), we get:
and therefore
□
Proof Proof of Corollary 3.1
Taking into account the error estimate (3.5), we have:
Then, by applying the Leibnitz rule, we get:
from which being [3] \(\|F^{(2n-j)}\|_{\infty } \leq {\mathscr{C}}\left [\frac {\|F\|_{\infty }}{2^{2n-j}}+2^{j} \|F^{(2n)}\|_{\infty }\right ]\), we get:
By the definitions (3.18) of the kernels ki and taking into account the form of the functions Ui given in (6.3), we can write:
and being [3]
in virtue of the assumptions on the kernel k, we have:
Thus, by replacing the above estimate in (6.4), we have:
from which we deduce
Therefore, by using the well-known Stirling formula:
and, taking into account that [10] \(\gamma _{n}(w) \sim 2^{n}\), we get the thesis. □
Proof Proof of Theorem 3.2
By (3.24), we can write:
The first term can be estimated by using (3.12) since (3.25) and (3.26) include (3.10) and (3.11). Let us now estimate the last one. By using (3.22) with r = m − 1, we can have:
and thus, by applying the weighted Bernstein inequality (see, for instance [10, p. 170]) which leads to state that \(\|{\ell ^{w}_{j}}\|_{{\mathscr{W}}^{r}_{\sigma }} \leq {\mathscr{C}} m^{m-1} \|{\ell ^{w}_{j}} \sigma \|_{\infty },\) we get:
Therefore,
being [10], in virtue of (3.10) and (3.11):
and the proof is completed. □
Proof Proof of Proposition 4.1
First, let us note that the kernel k given in (4.3) satisfies the following conditions:
By the definition (4.2), and taking into account the conditions on the parameters of the weights, we have:
from which, by using (6.6), we can deduce that the operator K is continuous and bounded. In order to prove its compactness, we remind that [18] if K satisfies the following condition:
then K is compact. We note that:
Hence, \(Kf\in {\mathscr{W}}^{r}_{\sigma }\) for each f ∈ Cσ, and by using the Favard inequality (6.2) with m instead of n, Kf in place of H and σ in place of v, we deduce (6.7). □
Proof Proof of Theorem 4.1.
The goal of the proof is to prove that
-
1.
\(\|(K-{K^{m}_{m}})f \sigma \|\) tends to zero for any f ∈ Cσ;
-
2.
The set of the operators {Km}m is collectively compact.
In fact, by condition 1, in virtue of the principle of uniform boundedness, we can deduce that \(\displaystyle \sup _{m} \|{K^{m}_{m}}\|< \infty \) and, by condition 2, we can deduct that \(\|(K-{K^{m}_{m}}){K^{m}_{m}}\|\) tends to zero [1, Lemma 4.1.2]. Consequently, under all these conditions, we can claim that for m sufficiently large, the operator \((I+\mu {K^{m}_{m}})^{-1}\) exists and it is uniformly bounded since:
i.e., the method is stable.
Condition 1 follows by Theorem 3.2. Condition 2 can be deducted by [6, Theorem 12.8] for the case γ = δ = 0. Concerning the general case, it is sufficient to prove that [18]:
To this end, let us introduce S polynomials qm,i(x,y) with i = 1,...,S of degree m in each variable, and for any f ∈ Cσ, let us define the univariate polynomial:
where we recall that \(\ell _{j,i}^{w}\left (\xi _{\nu }^{u_{i}}\right ):={\ell _{j}^{w}}\left ({\Psi }_{i}^{-1}\left (\frac {\xi _{\nu }^{u_{i}}}{\omega }\right )\right )\).
Then, in virtue of the definition (3.24), we can write:
from which by applying (6.1), (6.5), and taking into account the assumptions on the parameters of the weights, we get:
The only point remaining is to estimate the quantity \(E_{m}\left (k_{i}(x,\cdot ,\omega )\right )_{\sigma }\). To this end, taking into account the definition of ki given in (3.18) and (6.6), by using the Favard inequality (6.2), we get \(E_{m}\left (k_{i}(x,\cdot ,\omega )\right )_{\sigma }\leq \frac {{\mathscr{C}}}{m^{r}} \left (\frac {d}{\omega }\right )^{r},\) i.e., (6.8).
About the well-conditioning of the matrix \(\mathbb {A}_{m}\), it is sufficient to prove that:
To this end, we can use the same arguments in [1, p. 113] only by replacing the usual infinity norm with the weighted uniform norm of Cσ. Finally, estimate (4.7) follows taking into account that:
and by applying Theorem 3.2 to the last term. □
References
Atkinson, K.E.: The Numerical Solution of Integral Equations of the Second Kind Cambridge Monographs on Applied and Computational Mathematics, vol. 552. Cambridge University Press, Cambridge (1997)
De Bonis, M.C., Pastore, P.: A quadrature formula for integrals of highly oscillatory functions. Rend. Circ. Mat. Palermo 2, 279–303 (2010)
Ditzian, Z.: On interpolation of lp([a,b]) and weighted Sobolev spaces. Pac. J. Math. 90, 307–324 (1980)
Elliott, D.: A Cebyshev series method for the numerical solution of Fredholm integral equations. Comput. J. 6(1), 102–112 (1963)
Fox, L., Goodwin, E.T.: The numerical solution of non-singular linear integral equations. Phil. Trans. R. Soc. Lond. A 245(902), 501–534 (1953)
Kress, R.: Linear Integral Equations Applied Mathematical Sciences, vol. 82. Springer, Berlin (1989)
Lin, F.R., Shi, Y.J.: Preconditioned conjugate gradient methods for the solution of Love’s integral equation with very small parameter. J. Comput. Appl. Math. 327, 295–305 (2018)
Lin, F.-R., Lu, X., Jin, X.Q.: Sinc Nyström method for singularly perturbed Love’s integral equation. E. Asian J. Appl. Math. 3(1), 48–58 (2013)
Love, R.R.: The electrostatic field of two equal circular co-axial conducting disks. Quart. J. Mech. Appl. Math. 2(4), 428–451 (1949)
Mastroianni, G., Milovanović, G.V.: Interpolation Processes Basic Theory and Applications. Springer Monographs in Mathematics. Springer, Berlin (2008)
Milovanović, G., Joksimović, D.: Properties of Boubaker polynomials and an application to Love’s integral equation. Appl. Math. Comput. 224, 74–87 (2013)
Monegato, G., Orsi, A.P.: Product formulas for Fredholm integral equations with rational kernel functions. In: Numerical Integration III, vol. 85, pp 140–156. Springer (1988)
Nevai, P.: Mean convergence of Lagrange interpolation iii. Trans. Amer. Math. Soc. 282, 669–698 (1984)
Occorsio, D., Serafini, G.: Cubature formulae for nearly singular and highly oscillating integrals. Calcolo 55(1), Art. 4, 33 (2018)
Pastore, P.: The numerical treatment of Love’s integral equation having very small parameter. J. Comput. Appl. Math. 236(6), 1267–1281 (2011)
Phillips, J.L.: The use of collocation as a projection method for solving linear operator equations. SIAM J. Numer. Anal. 9(1), 14–28 (1972)
Sastry, S.S.: Numerical solution of non-singular Fredholm integral equations of the second kind. Indian J. Pure Appl. Math 6(7), 773–783 (1975)
Timan, A.F.: Theory of Approximation of Functions of a Real Variable. Dover, New York (1994)
Wolfe, M.A.: The numerical solution of non-singular integral and integro-differential equations by iteration with Chebyshev series. Comput. J. 12(2), 193–196 (1969)
Young, A.: The application of approximate product-integration to the numerical solution of integral equations. Proc. R. Soc. Lond. A 224(1159), 561–573 (1954)
Acknowledgments
The authors would like to thank the referees for the thorough review and the useful comments which have helped improve the contents of the paper.
Funding
Luisa Fermo is partially supported by the research project “Algorithms for Approximation with Applications [Acube], Fondazione di Sardegna - annualità 2017” and by the research project “Algorithms and Models for Imaging Science (AMIS), FSC 2014-2020 - Patto per lo Sviluppo della Regione Sardegna,” Maria Grazia Russo by INdAM-GNCS 2019 project “Discretizzazione di misure, approssimazione di operatori integrali ed applicazioni,” and Giada Serafini by Centro Universitario Cattolico (CUC).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors are members of the INdAM Research Group GNCS.This research has been accomplished within the RITA “Research ITalian network on Approximation”.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fermo, L., Russo, M.G. & Serafini, G. Numerical treatment of the generalized Love integral equation. Numer Algor 86, 1769–1789 (2021). https://doi.org/10.1007/s11075-020-00953-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-020-00953-2