From spherical to Euclidean illumination

Abstract

In this note we introduce the problem of illumination of convex bodies in spherical spaces and solve it for a large subfamily of convex bodies. We derive from it a combinatorial version of the classical illumination problem for convex bodies in Euclidean spaces as well as a solution to that for a large subfamily of convex bodies, which in dimension three leads to special Koebe polyhedra.

Appendix: Proof of Theorem 4

The following proof is a spherical analogue of the proof of the Separation Lemma in [1].

Definition 5

Let $\mathbf {K}\subset \mathbb {S}^d \subset \mathbb {E}^{d+1}$ be a convex body and F be an exposed face of $\mathbf {K}$. We define the conjugate face of F as a subset of the polar convex body ${\mathbf {K}}^*= \{ \mathbf {x}\in \mathbb {S}^d : \langle \mathbf {x}, \mathbf {y}\rangle \le 0 \hbox { for all } \mathbf {y}\in \mathbf {K}\}$ given by

$$\begin{aligned} \hat{F}:=\{\mathbf {x}\in {\mathbf {K}}^*\ |\ \langle \mathbf {x},\mathbf {y}\rangle =0\ {\text{ f }or\ all}\ \mathbf {y}\in F\}. \end{aligned}$$

(1)

One should keep in mind that $\hat{F}$ depends also on $\mathbf {K}$ and not only on F. So, if we write $\hat{\hat{F}}$, then it means $(\hat{F})^{\hat{}}$, where the right-hand circumflex refers to the spherical polar body ${\mathbf {K}}^*$. If $\mathbf {x}\in \mathbb {S}^d$, then let $\mathbf {H}_{\mathbf {x}}$ denote the open hemisphere of $\mathbb {S}^d$ with center $\mathbf {x}$.

The following statement (which one can regard as a natural spherical analogue of Theorem 2.1.4 in [11]) shows that exposed faces behave well under polarity in spherical spaces.

Proposition 1

Let $\mathbf {K}\subset \mathbb {S}^d \subset \mathbb {E}^{d+1}$ be a convex body and F be an exposed face of $\mathbf {K}$. Then $\hat{F}$ is an exposed face of ${\mathbf {K}}^*$ with $\hat{F}=\bigcap _{\mathbf {y}\in F}\left( {{\,\mathrm{bd}\,}}{\mathbf {H}_{\mathbf {y}}}\cap {\mathbf {K}}^*\right)$, where $\mathbb {S}^d{\setminus }\mathbf {H}_{\mathbf {y}}$ is a closed supporting hemisphere of ${\mathbf {K}}^*$ for every $\mathbf {y}\in F$. Moreover, $\hat{\hat{F}}=F$ and so, $F\mapsto \hat{F}$ is a bijection between the exposed faces of $\mathbf {K}$ and ${\mathbf {K}}^*$.

Proof

Without loss of generality we may assume that F is a proper exposed face of $\mathbf {K}$, i.e., there exists an open hemisphere $\mathbf {H}_{\mathbf {x}_0}$ of $\mathbb {S}^d$ such that $\emptyset \ne F=\mathbf {K}\cap {{\,\mathrm{bd}\,}}\mathbf {H}_{\mathbf {x}_o}$ and $\mathbf {K}\cap \mathbf {H}_{\mathbf {x}_0}=\emptyset$. It follows that $\mathbf {x}_0\in \hat{F}$ and so, $\hat{F}\ne \emptyset$. Now, if $\mathbf {y}\in F$, then $\mathbf {K}^*\cap \mathbf {H}_{\mathbf {y}}=\emptyset$ and $\mathbf {x}\in {{\,\mathrm{bd}\,}}\mathbf {H}_{\mathbf {y}}$ holds for all $\mathbf {x}\in \hat{F}$. Thus, $\hat{F}\subseteq \bigcap _{\mathbf {y}\in F}(\mathbf {K}^*\cap {{\,\mathrm{bd}\,}}\mathbf {H}_{\mathbf {y}})$, where $\mathbf {K}^*\cap \mathbf {H}_{\mathbf {y}}=\emptyset$ holds for all $\mathbf {y}\in F$. On the other hand, if $\mathbf {z}\in \bigcap _{\mathbf {y}\in F}(\mathbf {K}^*\cap {{\,\mathrm{bd}\,}}\mathbf {H}_{\mathbf {y}})$ with $\mathbf {K}^*\cap \mathbf {H}_{\mathbf {y}}=\emptyset$ for all $\mathbf {y}\in F$, then $\mathbf {z}\in \mathbf {K}^*$ with $\langle \mathbf {z},\mathbf {y}\rangle =0$ for all $\mathbf {y}\in F$ (and therefore $\mathbf {z}\in \hat{F}$) implying that $\bigcap _{\mathbf {y}\in F}(\mathbf {K}^*\cap {{\,\mathrm{bd}\,}}\mathbf {H}_{\mathbf {y}})\subseteq \hat{F}$. Thus, $\hat{F}=\bigcap _{\mathbf {y}\in F}(\mathbf {K}^*\cap {{\,\mathrm{bd}\,}}\mathbf {H}_{\mathbf {y}})$ with $\mathbf {K}^*\cap \mathbf {H}_{\mathbf {y}}=\emptyset$ for all $\mathbf {y}\in F$. As $\mathbf {K}^*\cap {{\,\mathrm{bd}\,}}\mathbf {H}_{\mathbf {y}}$ is a proper exposed face of $\mathbf {K}^*$ for all $\mathbf {y}\in F$ therefore $\hat{F}$ is a proper exposed face of $\mathbf {K}^*$. Applying the above argument to the exposed face $\hat{F}$ of $\mathbf {K}^*$ one obtains in a straightforward way that $\hat{\hat{F}}=F$. This completes the proof of Proposition 1.

Proposition 2

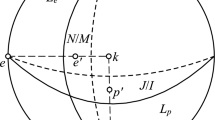
Let $\mathbf {K}\subset \mathbb {S}^d \subset \mathbb {E}^{d+1}$ be a convex body and H be a $(d-1)$-dimensional greatsphere of $\mathbb {S}^d$ with $H\cap \mathbf {K}=\emptyset$. Then $\mathbf {q}\in {{\,\mathrm{bd}\,}}\mathbf {K}$ is illuminated from $\mathbf {p}\in H$ with $\mathbf {p}\ne -\mathbf {q}$ if and only if $\hat{F}\subset \mathbf {H}_{\mathbf {p}}$, where F denotes the exposed face of $\mathbf {K}$ having smallest dimension and containing $\mathbf {q}\in {{\,\mathrm{bd}\,}}\mathbf {K}$.

Proof

Let $\mathbf {H}_{\mathbf {h}}$ be the open hemisphere with center $\mathbf {h}$ and boundary H in $\mathbb {S}^d$ such that $\mathbf {K}\subset \mathbf {H}_{\mathbf {h}}$. Clearly, $-\mathbf {h}\in {{\,\mathrm{bd}\,}}{\mathbf {H}_{\mathbf {p}}}\cap {{\,\mathrm{int}\,}}{\mathbf {K}^*}$. Proposition 1 implies that $F=\bigcap _{\mathbf {x}\in \hat{F}}\left( {{\,\mathrm{bd}\,}}{\mathbf {H}_{\mathbf {x}}}\cap {\mathbf {K}}^*\right)$, where $\mathbf {H}_{\mathbf {x}}\cap \mathbf {K}=\emptyset$ for all $\mathbf {x}\in \hat{F}$. Let $[\mathbf {p},\mathbf {q})$ denote the spherical segment of $\mathbb {S}^d$ with endpoints $\mathbf {p}$ and $\mathbf {q}$ containing $\mathbf {p}$ and not containing $\mathbf {q}$. Now, $\mathbf {q}\in {{\,\mathrm{bd}\,}}\mathbf {K}$ is illuminated from $\mathbf {p}\in H$ if and only if $[\mathbf {p},\mathbf {q})\subset \bigcap _{\mathbf {x}\in \hat{F}}\mathbf {H}_{\mathbf {x}}$, which is equivalent to $\mathbf {p}\in \bigcap _{\mathbf {x}\in \hat{F}}\mathbf {H}_{\mathbf {x}}$ (because $\pm \mathbf {q}\in \bigcap _{\mathbf {x}\in \hat{F}}{{\,\mathrm{bd}\,}}\mathbf {H}_{\mathbf {x}}$). Finally, $\mathbf {p}\in \bigcap _{\mathbf {x}\in \hat{F}}\mathbf {H}_{\mathbf {x}}$ holds if and only if $\hat{F}\subset \mathbf {H}_{\mathbf {p}}$. This finishes the proof of Proposition 2.

Now, the following statement follows from Proposition 2 and its proof in a straightforward way.

Corollary 3

Let $\mathbf {K}\subset \mathbb {S}^d \subset \mathbb {E}^{d+1}$ be a convex body and H be a $(d-1)$-dimensional greatsphere of $\mathbb {S}^d$ with $H\cap \mathbf {K}=\emptyset$. Let $\mathbf {H}_{\mathbf {h}}$ be the open hemisphere with center $\mathbf {h}$ and boundary H in $\mathbb {S}^d$ such that $\mathbf {K}\subset \mathbf {H}_{\mathbf {h}}$. Then the point set $\{\mathbf {p}_1,\dots ,\mathbf {p}_n\}\subset H$ illuminates $\mathbf {K}$ if and only if the open hemispheres $\mathbf {H}_{\mathbf {p}_1},\dots ,\mathbf {H}_{\mathbf {p}_n}$ with $-\mathbf {h}\in {{\,\mathrm{bd}\,}}{\mathbf {H}_{\mathbf {p}_i}}\cap {{\,\mathrm{int}\,}}{\mathbf {K}^*}$ for $1\le i\le n$ have the property that every (proper) exposed face of $\mathbf {K}^*$ is contained in at least one of the open hemispheres.

Finally, Corollary 3 yields Theorem 4.