An analogue of chromatic bases and p-positivity of skew Schur Q-functions

Abstract

We investigate chromatic symmetric functions in relation to the algebra $\varGamma$ of symmetric functions generated by Schur Q-functions. We construct natural bases of $\varGamma$ in terms of chromatic symmetric functions. We also consider the p-positivity of skew Schur Q-functions and find a class of p-positive ribbon Schur Q-functions, making a conjecture that they are only p-positive Schur Q-functions. We include many concrete computational results that support our conjecture.

1 Introduction

Stanley introduced chromatic symmetric functions as a symmetric function generalization of chromatic polynomials of finite simple graphs in 1995 [9]. They provided many new directions of research in relation to many different areas in mathematics, including graph theory, symmetric function theory, representation theory, and algebraic geometry. See [8] and the references therein.

It is natural to look at chromatic symmetric functions in relation to other well-known symmetric functions, and the Stanley-Stembridge conjecture on e-positivity of certain chromatic symmetric functions is one of such problems. In [2, 3], chromatic symmetric function bases of the symmetric function space $\varLambda$ were constructed and classical symmetric functions that can be realized as chromatic symmetric functions were classified.

Schur functions which correspond to the irreducible representations of the symmetric groups form an important classical basis of the algebra $\varLambda$ of symmetric functions. Schur Q-functions were introduced by Schur [7], and they generate a subalgebra $\varGamma$ of $\varLambda$. This subalgebra is particularly significant since Schur Q-functions have a deep connection to the representation theory of twisted symmetric groups ( [4, 7, 11]) and also have a well-established combinatorial theory that parallels the combinatorial theory of Schur functions due to Sagan [6] and Worley [12].

The purpose of the current paper is to investigate chromatic symmetric functions in relation to the subalgebra $\varGamma$, answering the same questions raised in [2, 3] for the algebra $\varLambda$. However, only null graphs (with isolated vertices) make symmetric functions in $\varGamma$, and we define near chromatic symmetric functions and consider the generators and bases of $\varGamma$ instead, which make natural analogues of chromatic symmetric function bases of $\varLambda$. An interesting property of a chromatic symmetric function is that its image under the well-known involution $\omega$ on $\varLambda$ is p-positive, and the classification of classical symmetric functions that are also chromatic symmetric functions was done by classifying p-positive skew Schur functions (see Proposition 6). This suggests that another interesting problem is to ask which skew Schur Q-functions are p-positive, and we work on this also. We show that only ribbon Schur Q-functions can be p-positive and found a class of p-positive ribbons. We come to make a conjecture that this class of p-positive Schur Q-functions are the only p-positive Schur Q-functions with many computational evidences. The shapes of p-positive ribbons are obtained by repeating (near) concatenation of the transpose of a shape from a basic block, and by taking their transpose or antipodal rotation. See Conjecture 1.

The rest of the current paper is organized as follows: Section 2 is to introduce background for our work, and Sect. 3 is devoted to the construction of chromatic bases of $\varGamma$. In Sect. 4, p-positivity of skew Schur Q-functions are considered, and in the final section, we make final remarks.

2 Preliminaries

In this section, we give basic definitions and setup notations and introduce known results that we will need for the development of our arguments.

A positive integer sequence $\alpha =(\alpha _1,\alpha _2,\dots ,\alpha _{\ell })$ is called a composition $\alpha$ of n, denoted $\alpha \vDash n$, if $\sum _{i}\alpha _i=n$. Given a composition $\alpha =(\alpha _1,\alpha _2,\dots ,\alpha _{\ell })$ of n, we call the $\alpha _i$ the parts of $\alpha$, $\ell =\ell (\alpha )$ the length of $\alpha$, and $n=|\alpha |$ the size of $\alpha$. We introduce a partial order on compositions which will be used. For two compositions $\alpha =(\alpha _1,\alpha _2,\dots ,\alpha _{\ell (\alpha )})$ and $\beta =(\beta _1,\beta _2,\dots ,\beta _{\ell (\beta )})$ such that $\alpha , \beta \vDash n$, we say that $\alpha$ is a coarsening of $\beta$ (or $\beta$ is a refinement of $\alpha$), denoted $\alpha \succcurlyeq \beta$, if consecutive parts of $\beta$ can be added together to yield the parts of $\alpha$. For example, $(5,2,3)\succcurlyeq (2,2,1,2,1,2)$.

A partition $\lambda =(\lambda _1, \lambda _2, \dots , \lambda _\ell )$ of n, denoted $\lambda \vdash n$, is a composition of n satisfying $\lambda _1\ge \lambda _2\ge \cdots \ge \lambda _{\ell }$ and is said to be strict if $\lambda _1>\lambda _2>\dots >\lambda _{\ell }$. We also use $\lambda =(1^{m_1}2^{m_2}\cdots )$ as an alternative notation for partitions, where $m_i=m_i(\lambda )$ is the number of appearance of the part i in the partition $\lambda$. Given two partitions $\lambda$ and $\mu$, we say that $\mu$ is contained in $\lambda$, denoted $\mu \subseteq \lambda$, if $\mu _i\le \lambda _i$ for all $i=1,2,\dots ,\ell (\mu )$. We let OP(n) be the set of all partitions of n into odd parts and SP(n) be the set of all strict partitions of n. The partition obtained by reordering the parts of a composition $\alpha$ is denoted by $\lambda (\alpha )$.

2.1 Diagrams

The (Young) diagram is a graphical interpretation of a partition $\lambda$, which is the array of left justified boxes containing $\lambda _i$ boxes in the ith row from the top. We abuse notation by denoting the diagram of a partition $\lambda$ by $\lambda$ also. For partitions $\lambda$ and $\mu$ such that $\mu \subseteq \lambda$, the skew diagram $\lambda /\mu$ is obtained from the diagram $\lambda$ by removing the boxes of the diagram $\mu$ from the top left box.

For a strict partition $\lambda$, the shifted diagram of $\lambda$, denoted $\widetilde{\lambda }$, is defined by

$$\begin{aligned} \widetilde{\lambda }=\{(i,j) \,|\, 1\le i \le \ell (\lambda ),~ i\le j \le i+\lambda _i -1 \} , \end{aligned}$$

that is obtained from the diagram $\lambda$ by shifting the ith row $(i-1)$ boxes to the right, for each $i>1$. Similarly, for strict partitions $\lambda$ and $\mu$ such that $\mu \subseteq \lambda$, the shifted skew diagram, denoted $\widetilde{\lambda / \mu }$, is obtained from $\lambda /\mu$ by shifting the ith row from the top $(i-1)$ boxes to the right for $i>1$.

We are dealing with diagrams either $\lambda /\mu$ or $\widetilde{\lambda / \mu }$ that are determined by two partitions $\mu \subseteq \lambda$, but we specify the partitions involved or the type of the diagram only when they are needed. We usually use D to denote a diagram and understand it as a set of boxes (coordinates) in the plane. For a (shifted) skew diagram, each edgewise connected part is called a component. A diagram with one component is called connected. A skew diagram D is said to be a ribbon, or a border strip, if for each box (i, j) in D the box $(i-1,j-1)$ is not contained in D. If a connected ribbon D of size n has $\alpha _i(D)$ boxes in the ith row for each $i=1, \dots , \ell$, we correspond the ribbon to the composition $\alpha (D)=(\alpha _1(D),\alpha _2(D),\dots , \alpha _\ell (D))$ of n. We abuse the notation by denoting the ribbon by $\alpha (D)$, and we call $\ell (\alpha (D))$ the length of the ribbon D.

Example 1

If $\lambda =(4,2,2)$ and $\mu =(1,1)$, then the skew diagram $\lambda /\mu$ is the ribbon $\alpha =(3,1,2)$. If $\lambda =(4,3,2)$ and $\mu =(3,2)$, then the shifted skew diagram $\widetilde{\lambda /\mu }$ is the ribbon $\beta =(1,1,2)$.

2.2 Operations on skew diagrams

We begin with recalling two classical operations on skew diagrams. For a skew diagram D, the transpose $D^t$ is obtained from D by reflecting in the main diagonal, and the antipodal rotation $D^{\circ }$ is obtained by rotating D 180 degrees in the plane.

Let $D_1$ and $D_2$ be skew diagrams. The disjoint union of $D_1$ and $D_2$, denoted $D_1 \oplus D_2$, is obtained by placing $D_1$ strictly north and east of $D_2$ such that they have no common row or column. Given $D_1\oplus D_2$, the concatenation $D_1 \cdot D_2$ (resp. near concatenation $D_1 \odot D_2$) is obtained by moving all boxes of $D_1$ exactly one cell west (resp. south). One can easily see that for ribbons $\alpha =(\alpha _1,\alpha _2,\dots ,\alpha _k)$ and $\beta =(\beta _1,\beta _2,\dots ,\beta _{\ell })$, we have $\alpha \cdot \beta =(\alpha _1,\dots ,\alpha _k,\beta _1,\dots ,\beta _{\ell })$ and $\alpha \odot \beta =(\alpha _1,\dots ,\alpha _k+\beta _1,\dots ,\beta _{\ell })$.

We note that both $\cdot$ and $\odot$ are associative, and they associate with each other. It follows that a ribbon $\alpha$ with k boxes can be uniquely written as

$$\begin{aligned} \alpha =\square \bigstar _1 \square \bigstar _2 \cdots \bigstar _{k-1} \square , \end{aligned}$$

where $\square$ denotes the diagram with one box and each $\bigstar _i$ is either $\cdot$ or $\odot$. For example, the ribbon $\alpha =(3,1,2)$ can be written as $\square \odot \square \odot \square \cdot \square \cdot \square \odot \square$.

The main operation we deal with is the composition of transposition, which was introduced in [1]. For a composition $\alpha$ and a skew diagram D, the composition of transposition of D by $\alpha$ is defined as

$$\begin{aligned} \alpha \bullet D={\left\{ \begin{array}{ll} D \bigstar _1 D^t \bigstar _2 D \bigstar _3 D^t \cdots \bigstar _{k-1} D &{} \text {if}~ |\alpha | ~\text {is odd}, \\ D \bigstar _1 D^t \bigstar _2 D \bigstar _3 D^t \cdots \bigstar _{k-1} D^t &{} \text {if}~ |\alpha | ~\text {is even}, \end{array}\right. } \end{aligned}$$

where $\alpha =\square \bigstar _1 \square \bigstar _2 \cdots \bigstar _{k-1} \square$.

Example 2

If $\alpha ^{(1)}=(1,1)$, $\alpha ^{(2)}=(2)$, and $D=(1,3)$, the composition of transposition $\alpha ^{(1)} \bullet D$ of D by $\alpha ^{(1)}$ is the ribbon (1, 3, 1, 1, 2), and $\alpha ^{(2)} \bullet \alpha ^{(1)} \bullet D$ is the ribbon (1, 3, 1, 1, 3, 4, 1, 2) as shown in the following figure, in which gray boxes represent transpose:

2.3 The algebra $\varLambda$ of symmetric functions

For a positive integer n and a partition $\lambda =(\lambda _1, \dots , \lambda _\ell )$ of n, the monomial symmetric function corresponding to $\lambda$ is defined as $m_\lambda =\sum _{(i_1,\dots , i_\ell )} x_{i_1}^{\lambda _1}\cdots x_{i_\ell }^{\lambda _\ell }\,,$ where the sum is over the $\ell$ tuples of distinct positive integers. Monomial symmetric functions are invariant under the action of permuting variables, and they form a basis of the space $\varLambda ^n$ of nth degree symmetric functions: $\varLambda ^n=\mathrm {span}_\mathbb Q \{ m_\lambda \,| \, \lambda \vdash n\}.$ The algebra $\varLambda$ of symmetric functions is the graded subalgebra of $\mathbb Q[[x_1, x_2, \dots ]]$ defined as $\varLambda =\oplus _{n\ge 0} \,\, \varLambda ^n, \text { where we set } \varLambda _0=\mathbb Q\,.$

For an integer r, the rth elementary symmetric function is $e_r=\sum _{i_1<\cdots < i_r} x_{i_1} \cdots x_{i_r}$, the rth complete homogeneous symmetric function is $h_r=\sum _{i_1\le \cdots \le i_r} x_{i_1} \cdots x_{i_r}$, and the rth power sum symmetric function is $p_r=\sum _i x_i^r$. Then, each of $\{e_\lambda \,| \, \lambda \vdash n\}$, $\{h_\lambda \,| \, \lambda \vdash n\}$ and $\{p_\lambda \,| \, \lambda \vdash n\}$ forms a nice basis of $\varLambda ^n$, where $b_\lambda =b_{\lambda _1}\cdots b_{\lambda _\ell }$ for $\lambda =(\lambda _1, \dots , \lambda _\ell )$ and $b\in \{ e, h, p\}$. Another important basis of $\varLambda ^n$ is the set $\{ s_\lambda \,|\, \lambda \vdash n\}$ of Schur functions, where $s_\lambda =\mathrm {det}( h_{\lambda _i-i+j})_{1\le i,j \le \ell (\lambda )}$.

There is a nice combinatorial model for Schur functions. For a given partition $\lambda$, a semistandard tableau T of shape $\lambda$ is a filling of the diagram of $\lambda$ with positive integers so that each row is weakly increasing and each column is strictly increasing, and the content of T is $c(T)=(c_1, c_2, \dots )$ where $c_i$ is the number of i in T. Then, $s_\lambda =\sum _T x^{c(T)}$, where the sum is over all semistandard tableaux of shape $\lambda$ and $x^{(c_1, c_2, \dots )}=\prod _i x_i^{c_i}$. We can also define a skew Schur function $s_{\lambda /\mu }$ for $\mu \subseteq \lambda$ as the generating function of semistandard tableaux of shape $\lambda /\mu$.

We say that a given symmetric function is b-positive if the function can be written as a positive linear combination of the elements of the basis $\{b_{\lambda }\}$ of $\varLambda$. We remark that in the algebra of symmetric functions $\varLambda$, there is a well-known involution $\omega$ that is defined by $\omega (p_r)=(-1)^{r-1}p_{r}$ or equivalently by $\omega (s_\lambda )=s_{\lambda ^t}$, and there is a scalar product defined by $\langle s_{\lambda },s_{\mu } \rangle =\delta _{\lambda \mu }$ or equivalently by $\langle p_{\lambda },~p_{\mu } \rangle =\delta _{\lambda \mu } z_{\lambda },$ where $z_{\lambda }=\prod _i i^{m_i}(m_i)!$ for $\lambda =(1^{m_1}2^{m_2}\cdots )$.

2.4 The subalgebra $\varGamma$ of symmetric functions

Odd power sum symmetric functions make an algebraically independent set over $\mathbb Q$ and generate the following subalgebra of $\varLambda$:

$$\begin{aligned} \varGamma =\mathbb Q [ p_1,\, p_3,\, p_5, \dots ] =\oplus _{n\ge 0} \varGamma ^n\,,\text { where } \varGamma ^n=\varGamma \cap \varLambda ^n\,. \end{aligned}$$

The subalgebra $\varGamma$ of $\varLambda$ has nice generators and basis elements that are different from the power sum symmetric functions. Skew Schur Q-functions are generating functions of marked shifted tableaux in the same way that Schur functions are generating functions of semistandard tableaux.

Let $\mathbf {P}'$ denote the set of ordered alphabet $\{1'<1<2'<2<\cdots \}$. Here, the letters $1', 2', \dots$ are said to be marked. For a letter $a \in \mathbf {P}'$, we denote the unmarked version of this letter by |a|. Let $\lambda$ and $\mu$ be strict partitions such that $\mu \subseteq \lambda$. A marked shifted tableau T of shape $\widetilde{\lambda / \mu }$ is a filling of the boxes of the shifted skew diagram $\widetilde{\lambda / \mu }$ with letters from $\mathbf {P}'$ such that

• (M1) each row and column are weakly increasing,

• (M2) each column has at most one k for each $k\ge 1$, and

• (M3) each row has at most one $k'$ for each $k\ge 1$.

The content of T is the sequence $c(T)=(c_1,c_2, \dots )$, where $c_i$ is the number of all letters a such that $|a|=i$ in T, for each $i\ge 1$.

Definition 1

For strict partitions $\lambda$ and $\mu$ with $\mu \subseteq \lambda$, the skew Schur Q-function is defined as

$$\begin{aligned} Q_{\lambda / \mu } = \sum _{T} x^{c(T)} , \end{aligned}$$

where the sum is over all marked shifted tableaux of shape $\widetilde{\lambda / \mu }$. We denote $Q_{\lambda / \emptyset }$ by $Q_{\lambda }$ and $Q_{(n)}$ by $q_n$, where we let $Q_\emptyset =q_0=1$ for convenience. For a partition $\lambda =(\lambda _1, \lambda _2, \dots , \lambda _\ell )$, we let $q_\lambda =\prod _{i=1}^\ell q_{\lambda _i}$.

Our main interest is in the algebra $\varGamma$, and we summarize some important results.

Proposition 1

[5, Chapter III] For a positive integer n,

$$\begin{aligned}&{\sum _{r=0}^n (-1)^r q_r q_{n-r} =0\,,} \end{aligned}$$

(1)

$$\begin{aligned}&q_n=\sum _{\lambda \in OP(n)}z_{\lambda }^{-1}2^{\ell (\lambda )}p_{\lambda }\,\in \varGamma \,. \end{aligned}$$

(2)

Theorem 1

[5, Chapter III]

• (a) $\varGamma =\mathbb {Q}[ q_1,\, q_3,\, q_5, \dots ]$, and $\{q_1, q_3, q_5, \dots \}$ is an algebraically independent set over $\mathbb {Q}$.

• (b) For any strict partitions $\lambda$ and $\mu$ such that $\mu \subseteq \lambda$, $Q_{\lambda /\mu }$ is a symmetric function in $\varGamma$.

• (c) For each $n\ge 1$, $\{Q_\lambda \,|\, \lambda \in SP(n)\}$ forms a basis of the space $\varGamma ^n$ of nth degree symmetric functions in $\varGamma$.

• (d) For each $n\ge 1$, both $\{p_\lambda \,|\, \lambda \in OP(n)\}$ and $\{q_\lambda \,|\, \lambda \in OP(n)\}$ are bases of $\varGamma ^n$.

For two strict partitions $\lambda$ and $\mu$ such that $\mu \subseteq \lambda$, if $\widetilde{\lambda /\mu }$ is a ribbon, then we follow the convention in [1] and use $\mathfrak r_{\alpha }$ for $Q_{\lambda /\mu }$ when $\alpha$ is the composition representing the ribbon of shape $\widetilde{\lambda /\mu }$. In this case, we also use $\alpha ^t$ and $\alpha ^\circ$ for the transpose and the antipodal rotation of $\widetilde{\lambda /\mu }$, respectively. We associate an $\ell \times \ell$ matrix $A(\alpha )$ with a composition (ribbon) $\alpha =(\alpha _1, \dots , \alpha _\ell )$, where the (i, j) entry of $A(\alpha )$ is given by

$$\begin{aligned} A(\alpha )_{i\,j}={\left\{ \begin{array}{ll} { q_{\,\alpha _i+\alpha _{i+1}+\cdots + \alpha _j}} &{} \text { if}\,\, i\le j ,\\ {q_0} &{} \text { if}\,\, j-i=1 ,\\ 0 &{} \text { otherwise}\,. \end{array}\right. } \end{aligned}$$

(3)

Proposition 2

[1, Proposition 3.3] Let $\alpha$ and $\beta$ be ribbons. Then,

$$\begin{aligned}&\mathfrak r_{\alpha }=\mathfrak r_{\alpha ^t}=\mathfrak r_{\alpha ^\circ } \end{aligned}$$

(4)

$$\begin{aligned}&\mathfrak r_{\alpha }=\det (A(\alpha )) \end{aligned}$$

(5)

$$\begin{aligned}&\mathfrak r_{\alpha }=(-1)^{\ell (\alpha )}\sum _{\gamma \succcurlyeq \alpha }(-1)^{\ell (\gamma )}q_{\lambda (\gamma )} \end{aligned}$$

(6)

$$\begin{aligned}&\mathfrak r_{\alpha } \mathfrak r_{\beta }=\mathfrak r_{\alpha \cdot \beta }+\mathfrak r_{\alpha \odot \beta } \end{aligned}$$

(7)

$$\begin{aligned}&\mathfrak r_{\alpha }^{\, 2} = 2\mathfrak r_{\alpha \cdot \alpha ^t} = 2\mathfrak r_{\alpha \odot \alpha ^t}\, . \end{aligned}$$

(8)

3 A basis of the algebra $\varGamma$ involving graphs

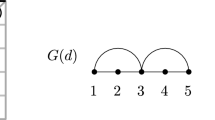
In this section, we construct new bases for the algebra $\varGamma$, whose elements are generated by the chromatic symmetric functions of the star graphs (see Fig. 1) and the triangles. These are analogues of the chromatic symmetric function bases for the algebra $\varLambda$ introduced in [2].

We begin by defining the chromatic symmetric functions.

Let $G=(V,E)$ be a simple graph with a vertex set $V=\{v_1, v_2, \dots , v_n\}$ and an edge set E. A function $\kappa : V \rightarrow \{1,2,\dots \}$ is called a proper coloring of G if $\{v_i,v_j\} \in E$ implies that $\kappa (v_i) \ne \kappa (v_j)$. The chromatic symmetric function of G is defined as

$$\begin{aligned} X_G =\sum _{\kappa } x_{\kappa (v_1)}\dots x_{\kappa (v_n)}, \end{aligned}$$

where the sum is over all proper colorings of G. It is an immediate consequence of the definition of $X_G$ that if a graph G is a disjoint union of subgraphs $G_1, G_2,\dots , G_{\ell }$, then we have $X_G=\prod _{i=1}^{\ell }X_{G_i}$. Moreover, $X_{G}$ is a symmetric function, and one can expand $X_G$ in terms of the basic bases of symmetric functions. As we consider the algebra $\varGamma =\mathbb Q [p_1, p_3, p_5, \dots ]$ in this paper, we are especially interested in the expansion of chromatic symmetric functions into power sum symmetric functions $p_{\lambda }$ among other basic bases. Stanley [9] found a nice explicit p-expansion formula of the chromatic symmetric functions.

Fig. 1

Star graphs

Theorem 2

[9, Theorem 2.5, Corollary 2.7] For a simple graph $G=(V,E)$ with n vertices, let $\lambda (S)$ be the partition of n whose parts are equal to the numbers of vertices in the connected components of the spanning subgraph of G with an edge set S. Then, the chromatic symmetric function of G can be written as

$$\begin{aligned} X_G=\sum _{S\subseteq E} (-1)^{|S|}p_{\lambda (S)}, \end{aligned}$$

and the symmetric function $\omega (X_G)$ is p-positive.

Example 3

[2, Theorem 8] We give the chromatic symmetric functions $X_G$ of two exemplary graphs G.

• (a) For the triangle $C_3$, the cycle with three vertices, we have

  $$\begin{aligned} X_{C_3}=p_1^3-3p_2p_1+2p_3\,. \end{aligned}$$

• (b) For the star graph $S_n$, the tree with one internal vertex and $n-1$ leaves, we have

  $$\begin{aligned} X_{S_n}=\sum _{r=0}^{n-1}(-1)^r \left( {\begin{array}{c}n-1\\ r\end{array}}\right) p_{r+1}p_{1}^{n-r-1}\,. \end{aligned}$$

In [2], the authors obtained numerous new bases for the algebra of symmetric functions whose generators are chromatic symmetric functions.

Theorem 3

[2, Theorem 5] Let $G_{\lambda }=G_{\lambda _1} \cup \cdots \cup G_{\lambda _{\ell }}$ denote a graph with connected components $G_{\lambda _1},\dots , G_{\lambda _{\ell }}$ such that $G_k$ has k vertices for each k. Then, the set

$$\begin{aligned} \{X_{G_{\lambda }}\,|\,\lambda \vdash n\} \end{aligned}$$

forms a $\mathbb {Q}$-basis of $\varLambda ^n$.

It is natural to ask for which graphs G, a set $\{X_{G}\}$ forms a basis of $\varGamma ^n$. However, it follows from Theorem 2 that $X_G$ does not belong to $\varGamma$ if G has an edge.

Proposition 3

Let G be a finite simple graph. Then, G has no edge if and only if $X_G \in \varGamma$.

Proof

Let G be a simple graph with n vertices. If G has no edge, then $X_G=p_1^n \in \varGamma$.

We now let G be a graph having m edges such that $X_G \in \varGamma$. By Theorem 2, we have

$$\begin{aligned} X_G=p_1^n -m\, p_2 p_1^{n-2} +\sum _{|S|\ge 2}(-1)^{|S|}p_{\lambda (S)}\,. \end{aligned}$$

Since $p_n$, $n\ge 0$, are algebraically independent and $\{p_1,p_3,p_5,\dots \}$ generates $\varGamma$, for $X_G$ to be in $\varGamma$ the second term $m\,p_2p_1^{n-2}$ must be 0, that is $m=0$. Hence, G has no edge. $\square$

A graph with no edge is called a null graph. Due to Proposition 3, the only chromatic symmetric functions contained in $\varGamma$ are $X_G=p_1^n$ for the null graphs G with n vertices and there can not be a chromatic symmetric function basis for $\varGamma$. A symmetric function f in $\varGamma$ satisfies $\omega (f)=f$, and we consider the symmetrization of the chromatic symmetric functions instead. For a simple graph G, we define a near chromatic symmetric function of G to be

$$\begin{aligned} Y_G=(X_G+\omega (X_G))/2 \,. \end{aligned}$$

Then, it is clear from the definition that $\omega (Y_G)=Y_G$. We also note that if $X_G\in \varGamma$, then $Y_{G}=X_{G}$ and it follows that $\omega (Y_G)=Y_G$ is p-positive. From Example 3, we obtain two near chromatic symmetric functions which belong to the algebra $\varGamma$.

Proposition 4

For a graph G, let $Y_{G}$ be its near chromatic symmetric function.

• (a) For the triangle $C_3$, we have

  $$\begin{aligned}Y_{C_3}=p_1^3+2p_3\,.\end{aligned}$$

• (b) For the star graph $S_n$, we have

  $$\begin{aligned} Y_{S_n}={\left\{ \begin{array}{ll} \left( {\begin{array}{c}n-1\\ 0\end{array}}\right) p_{1}^n+\left( {\begin{array}{c}n-1\\ 2\end{array}}\right) p_3p_{1}^{n-3}+\cdots + \left( {\begin{array}{c}n-1\\ n-1\end{array}}\right) p_{n} &{} \text {if}~ n ~\text {is odd},\\ \left( {\begin{array}{c}n-1\\ 0\end{array}}\right) p_1^{n}+\left( {\begin{array}{c}n-1\\ 2\end{array}}\right) p_3p_{1}^{n-3}+\cdots + \left( {\begin{array}{c}n-1\\ n-2\end{array}}\right) p_{n-1}p_1 &{} \text {if}~ n ~\text {is even}\,.\\ \end{array}\right. } \end{aligned}$$

  Moreover, {$Y_{S_n}\,|\, n \text {: odd }\}$ is algebraically independent over $\mathbb {Q}$.

As the near chromatic symmetric function $Y_G$ is obtained from the p-expansion of $X_G$ by getting rid of all terms $p_{\lambda }$ for partitions $\lambda$ with an odd number of even parts, $Y_G$ can belong to $\varGamma$ for some graphs G although $X_G$ is not an element of $\varGamma$. It turns out that there is no connected graph G such that $Y_{G}\in \varGamma$ except $C_3$ and $S_n$ for $n\ge 1$.

We say that two edges $\{v_1, v_2\}$ and $\{v_3, v_4\}$ are disjoint if $v_1, v_2, v_3$, and $v_4$ are all distinct.

Lemma 1

Let G be a simple graph such that $Y_G\in \varGamma$. Then, G has no pair of disjoint edges. Furthermore, if G is connected, then G is either $C_3$ or $S_n$ for $n\ge 1$.

Proof

We suppose that there are r different ways to select two disjoint edges of G. By Theorem 2, the coefficient of $p_2^2p_1^{n-4}$ in the p-expansion of $X_G$ is equal to r. Hence, from the definition of $Y_G$, the coefficient of $p_2^2p_1^{n-4}$ in the p-expansion of $Y_{G}$ is also r, and if $Y_G \in \varGamma$, then r must be zero so that G has no pair of disjoint edges. It is easy to see that a connected graph with no pair of disjoint edges is either $C_3$ or $S_n$ for $n\ge 1$. $\square$

From Lemma 1, we can see that $Y_G$ need not be the same as $\prod _{i}Y_{G_i}$, where $G_i$ are the connected components of G. We now classify all the graphs G such that $Y_G\in \varGamma$.

Proposition 5

Let G be a simple graph. Then, $Y_G\in \varGamma$ if and only if G is a disjoint union of a graph H and a null graph, where H is one of the graphs $C_3$ and $S_n$ for $n\ge 1$.

Proof

We first note that if G is a disjoint union of H and the null graph with d vertices, then

$$\begin{aligned} Y_{G}=p_1^{d}\,Y_{H}\in \varGamma \,. \end{aligned}$$

Now, we suppose that G is a simple graph such that $Y_G \in \varGamma$. From Lemma 1, G has no pair of disjoint edges. Hence, all edges are in the same connected component of G, say H, so that G is a disjoint union of H and a null graph. Moreover, H is either $C_3$ or $S_n$ for $n\ge 1$ since H is a connected graph with no pair of disjoint edges. $\square$

We have come to the conclusion that there are only two generator sets of near chromatic symmetric functions for the algebra $\varGamma$ which are algebraically independent:

Theorem 4

Two sets $\{Y_{S_1}, Y_{C_3}, Y_{S_5}, Y_{S_7}, \dots \}$ and $\{Y_{S_1}, Y_{S_3}, Y_{S_5}, Y_{S_7}, \dots \}$ of near chromatic symmetric functions are algebraically independent generator sets for the algebra $\varGamma$. Moreover, they are the only algebraically independent generator sets for $\varGamma$ consisting of near chromatic symmetric functions.

Proof

Since $\varGamma$ is generated by odd power sum symmetric functions and $p_k$ for odd k are algebraically independent, it is immediate from Proposition 4 that two given sets are algebraically independent and

$$\begin{aligned} \varGamma =\mathbb {Q}[Y_{S_1}, Y_{C_3}, Y_{S_5}, Y_{S_7}, \dots ] =\mathbb {Q}[Y_{S_1}, Y_{S_3}, Y_{S_5}, Y_{S_7}, \dots ]\,. \end{aligned}$$

Proposition 5 proves that there is no other algebraically independent generator set of near chromatic symmetric functions. $\square$

We close this section by giving new bases for the space $\varGamma ^n$ of nth degree symmetric functions in $\varGamma$. For a given set $\mathbf {B}=\{G_1, G_3, G_5, \dots \}$ of simple graphs where $G_k$ has k vertices for $k=1, 3, 5, \dots$, we define a set $\mathscr {Y}(\mathbf {B})\subseteq \varGamma$ of symmetric functions in $\varGamma$ as $\mathscr {Y}(\mathbf {B})=\{\prod _{i}Y_{G_{\lambda _i}}\,|\,\lambda \in OP(n)\}$.

Theorem 5

Let $S_n$ be the star graph with n vertices for $n\ge 1$ and $C_3$ be the triangle. Let $\mathbf {B}_1=\{S_1, C_3, S_5, S_7, \dots \}$ and $\mathbf {B}_2=\{S_1, S_3, S_5, S_7, \dots \}$. Then, $\mathscr {Y}(\mathbf {B}_1)$ and $\mathscr {Y}(\mathbf {B}_2)$ are bases of $\varGamma ^n$.

Proof

We know from Proposition 4 that $\mathscr {Y}(\mathbf {B}_1)$ and $\mathscr {Y}(\mathbf {B}_2)$ are linearly independent. Since both sets have |OP(n)| elements and $\mathrm {dim} \varGamma =|OP(n)|$ by Theorem 1, the proof is completed. $\square$

4 On p-positivity of skew Schur Q-functions

There are many positivity questions in the theory of symmetric functions, mainly on Schur positivity, e-positivity or h-positivity, which are raised usually in relation to the representation theory, but not so many questions on p-positivity. However, in the work related to the chromatic symmetric functions, p-positivity problems naturally appear. This is basically because $X_G$ has the interesting property that $\omega (X_G)$ is p-positive. For instance, in the work on classifying classical symmetric functions that can be realized as chromatic symmetric functions in [3], knowing the p-positivity of skew Schur functions played an important role.

Proposition 6

[3, Proposition 2.6] A skew Schur function $s_D$ is p-positive if and only if D is a horizontal strip.

As a Schur Q-analogue of Proposition 6, we work on the classification of p-positive skew Schur Q-functions. Throughout the section, any shifted skew diagram $\widetilde{\lambda /\mu }$ is regarded to be connected unless specifically noted. We recall from Theorem 1 (d) that a skew Schur Q-function can be written as a linear sum of odd power sum symmetric functions, and also recall the scalar product on $\varLambda$ satisfying $\langle s_{\lambda },s_{\mu } \rangle =\delta _{\lambda \mu }$ and $\langle p_{\lambda },p_{\mu } \rangle =\delta _{\lambda \mu } z_{\lambda }$. To begin with, we show that a skew Schur Q-function $Q_{\lambda /\mu }$ is not p-positive unless $\widetilde{\lambda /\mu }$ is a ribbon.

Proposition 7

If a shifted skew diagram $\widetilde{\lambda /\mu }$ contains three boxes $(i,j),~(i,j+1)$, and $(i+1,j+1)$ for some i and j, then the skew Schur Q-function $Q_{\lambda /\mu }$ is not p-positive.

The above proposition is immediate from the following lemma.

Lemma 2

Let $\widetilde{\lambda /\mu }$ be a shifted skew diagram of size n that contains three boxes $(i,j),~(i,j+1)$, and $(i+1,j+1)$ for some i and j. If $Q_{\lambda /\mu }=\sum _{\lambda \in OP(n)} a_{\lambda } p_{\lambda }$, then $\sum _{\lambda \in OP(n)}a_{\lambda }=0$.

Proof

We first note that there is no marked shifted tableau of shape $\widetilde{\lambda /\mu }$ with weight (n), since $\widetilde{\lambda /\mu }$ contains two diagonally consecutive boxes (i, j) and $(i+1,j+1)$. This implies that $\langle Q_{\lambda /\mu },s_{(n)}\rangle =0$ since $x_1^n$ can appear only in $s_{(n)}$ among Schur functions. Due to the Murnaghan–Nakayama rule [10, Corollary 7.17.5], the Schur function of one-row shape is expanded as a sum of power sum symmetric functions as follows:

$$\begin{aligned} s_{(n)}=\sum _{\lambda \vdash n} z_{\lambda }^{-1}p_{\lambda } \, . \end{aligned}$$

Therefore, we have

$$\begin{aligned} \left\langle \sum _{\lambda \in OP(n)}a_{\lambda }p_{\lambda },~\sum _{\lambda \vdash n}z_{\lambda }^{-1} p_{\lambda } \right\rangle =\sum _{\lambda \in OP(n)}a_{\lambda }=0 \, . \end{aligned}$$

$\square$

4.1 A class of p-positive ribbon Schur Q-functions

In Proposition 7, we showed that only ribbon Schur Q-functions can be p-positive. In this subsection, we construct an infinite family of p-positive ribbon Schur Q-functions.

For positive integers n and k such that $k \le n$, we denote by $\triangle _{n,k}$ the ribbon whose shape is $\widetilde{\lambda /\mu }$, where $\lambda =(n,n-1,\cdots , n-k+1)$ and $\mu =(n-1,n-2,\cdots ,n-k+1)$ if $k>1$, $\mu =\emptyset$ if $k=1$. For example, $\triangle _{n,1}$ is the one-row diagram of size n, and $\triangle _{n,n}$ is the one-column diagram of size n (see Fig. 2).

Lemma 3

Let n and k be positive integers such that $k \le n$. Then, we have the following:

• (a) $\displaystyle {\mathfrak {r}_{\triangle _{n,k}}=\sum _{i=0}^{k-1}(-1)^{k+i-1}q_{n-i}\,q_{i}}$.

• (b) $\mathfrak {r}_{\triangle _{n,n-k+1}}=\mathfrak {r}_{\triangle _{n,k}}$.

Proof

Since ${\triangle _{1,n}}^t = \triangle _{n,n}$, by Proposition 2 (4) we have $\mathfrak {r}_{\triangle _{n,1}} = \mathfrak {r}_{\triangle _{n,n}}$. For given n and k, we let $\alpha _{n, k}$ be the composition corresponding to the ribbon $\triangle _{n, k}$ and $A(\alpha _{n, k})$ be the $k \times k$ matrix associated to $\alpha _{n, k}$, that is defined in (3).

(a) We induct on k. For $k = 1$, by the definition of skew Schur Q-functions $\mathfrak {r}_{\triangle _{n,1}}=q_nq_0$. Suppose that the assertion is true for $k \le n-2$. By Proposition 2 (5), we have

$$\begin{aligned} \mathfrak {r}_{\triangle _{n,k+1}}= & {} \det (A(\alpha _{n, k+1}))\\= & {} (-1)\det (A(\alpha _{n,k})) + q_{n-k}\det (A(\alpha _{k,k})) \\= & {} (-1) \cdot \mathfrak {r}_{\triangle _{n,k}} \, + \, q_{n-k} \cdot \mathfrak {r}_{\triangle _{k,k}}\\= & {} \sum _{i=0}^{k-1}(-1)^{(k+1)+i-1}q_{n-i}\,q_{i} \, + \, q_{n-k}\,q_k \, = \, \sum _{i=0}^{k}(-1)^{(k+1)+i-1}q_{n-i}\,q_{i} \,. \end{aligned}$$

Here, the fourth equality follows from the induction hypothesis and the observation $\mathfrak {r}_{\triangle _{k,1}} = \mathfrak {r}_{\triangle _{k,k}}$.

(b) By using (a) and Proposition 1 (1), we have

$$\begin{aligned} \mathfrak {r}_{\triangle _{n,n-k+1}}-\mathfrak {r}_{\triangle _{n,k}}= & {} \, \sum _{i=0}^{n-k}(-1)^{n-k+i}q_{n-i}\,q_i \, - \, \sum _{i=0}^{k-1}(-1)^{k+i-1}q_{n-i}\,q_i\\= & {} \, (-1)^{n-k}\sum _{i=0}^{n}(-1)^{i}q_{n-i}q_i=0 \, . \end{aligned}$$

$\square$

We state a useful lemma that is an easy consequence of Proposition 1 (2).

Lemma 4

Let $\lambda$ be an odd partition and $\mu$ be a partition such that $|\lambda |=|\mu |$. If $\lambda$ is not a refinement of $\mu$, then

$$\begin{aligned} \langle p_{\lambda },\,q_{\mu }\rangle =0\,. \end{aligned}$$

Due to Lemma 3 and Proposition 1 (2), we can explicitly write the p-expansion of $\mathfrak {r}_{\triangle _{n,k}}$ for given integers n and k. The cases where $k = 1$ and $k = 3$ are particularly noteworthy because the ribbon Schur Q-functions corresponding to ${\triangle _{n,1}}$ and ${\triangle _{n,3}}$ are p-positive (see Proposition 8). Furthermore, we anticipate that all ribbons whose corresponding ribbon Schur Q-function is p-positive are constructible from ${\triangle _{n,1}}$ and ${\triangle _{n,3}}$ (see Theorem 7 and Conjecture 1).

Proposition 8

Let n be a positive integer.

• (a) For $n\ge 1$, $\displaystyle {\mathfrak r_{\triangle _{n,1}} = \sum _{\lambda \in OP(n)} z_{\lambda }^{-1}2^{\ell (\lambda )} \,p_{\lambda }}\,.$

• (b) For $n\ge 3$, $\displaystyle {\mathfrak r_{\triangle _{n,3}} = \sum _{\lambda \in OP(n)} c_\lambda \,p_{\lambda }\,}$, where

  $$\begin{aligned} c_\lambda = {\left\{ \begin{array}{ll} z_{\lambda }^{-1}\,2^{\ell (\lambda )} &{} \text {if} \ m_1(\lambda )=0,\\ 0 &{} \text {if} \ m_1(\lambda ) = 1 \ \text {or} \ 2 ,\\ \left( {\begin{array}{c}m_1(\lambda )-1\\ 2\end{array}}\right) \,z_{\lambda }^{-1}\,2^{\ell (\lambda )}&\text {if} \ m_1(\lambda )\ge 3\,. \end{array}\right. } \end{aligned}$$

Consequently, $\mathfrak {r}_{\triangle _{n,1}}$ and $\mathfrak {r}_{\triangle _{n,3}}$ are p-positive.

Proof

(a) Since $\mathfrak {r}_{\triangle _{n,1}} = q_n$ by Lemma 3 (a), it is immediate from Proposition 1 (2).

(b) We recall Lemma 3 (a) and Proposition 1 (2):

$$\begin{aligned} \mathfrak {r}_{\triangle _{n,k}}=\sum _{i=0}^{k-1}(-1)^{k+i-1}q_{n-i}q_{i}\qquad \text {and} \qquad q_n=\sum _{\lambda \in OP(n)}z_{\lambda }^{-1}2^{\ell (\lambda )}p_{\lambda }\,. \end{aligned}$$

Using Lemma 3 (a), for odd partitions $\lambda$, we have

$$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,\mathfrak {r}_{\triangle _{n,3}}\rangle = \langle p_{\lambda },\,q_n - q_{n-1}q_1 + q_{n-2}q_2\rangle \, \end{aligned}$$

which is determined according to the numbers $m_1(\lambda )$ and $\ell (\lambda )$ as follows:

• If $m_1(\lambda )=0$, then we have

  $$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,q_n \rangle =2^{\ell (\lambda )}\,. \end{aligned}$$

• If $m_1(\lambda )=1$, then we have

  $$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,q_n - q_{n-1}q_1 \rangle =2^{\ell (\lambda )}(1-1)=0\,. \end{aligned}$$

• If $m_1(\lambda )\ge 2$, then we have

  $$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,q_n - q_{n-1}q_1 + q_{n-2}q_2\rangle= & {} 2^{\ell (\lambda )}\{1-m_1(\lambda )+m_1(\lambda )(m_1(\lambda )-1)/2\}\,\\= & {} 2^{\ell (\lambda )}(m_1(\lambda )-1)(m_1(\lambda )-2)/2\,. \end{aligned}$$

In each case, the first equality follows from Lemma 4 and the second equality follows from Proposition 1 (2). $\square$

We classify p-positive ribbons of the form $\triangle _{n,k}$ in the following theorem.

Theorem 6

Let n and k be positive integers such that $n \ge k$.

• (a) For $n\le 2$, $\mathfrak {r}_{\triangle _{n,k}}$ is p-positive.

• (b) For odd $n\ge 3$, $\mathfrak {r}_{\triangle _{n,k}}$ is p-positive if and only if $k\in \{1,\,3,\,n-2,\,n\}$.

• (c) For even $n\ge 4$, $\mathfrak {r}_{\triangle _{n,k}}$ is p-positive if and only if $k\in \{1,\,3,\,n/2,\,n/2+1,\,n-2,\,n\}$.

Proof

By Lemma 3 (a), $\triangle _{1,1}=q_1=2p_1$ and $\triangle _{2,1}=\triangle _{2,2}=q_2=2 p_1^2$. Hence, (a) is proved.

For $n\ge 3$, due to Lemma 3 (b) and Proposition 8, it suffices to show that the assertion is true for $1<k\le \lceil n/2 \rceil$ and $k\ne 3$. To show that a ribbon Schur Q-function $\mathfrak {r}_{\triangle _{n,k}}$ is not p-positive, we show that the value $z_{\lambda }c_\lambda$ is negative for some specific $\lambda$ when we let $\mathfrak {r}_{\triangle _{n,k}} = \sum _{\lambda \in OP(n)} c_\lambda \, p_\lambda$. To calculate the value $z_{\lambda }c_{\lambda }$, we again use Lemma 3 (a), Lemma 4, and Proposition 1 (2) as in the proof of Proposition 8 (b).

(b) Let $n\ge 3$ be an odd integer. We first show that for even k, the value $z_{(n)}c_{(n)}$ is negative so that $\mathfrak {r}_{\triangle _{n,k}}$ is not p-positive:

$$\begin{aligned} z_{(n)}c_{(n)}=\langle p_{(n)},\,\mathfrak {r}_{\triangle _{n,k}}\rangle =\langle p_{(n)},\,(-1)^{k-1}q_n\rangle =\langle p_{(n)},\,(-1)^{k-1}z_{(n)}^{-1}2^1p_{(n)}\rangle =-2 \,. \end{aligned}$$

We now assume that $k\ge 5$ is odd and show that the value $z_{\lambda }c_{\lambda }$ is negative when $\lambda =\lambda ((k-2)^{2} \, (n-2k+4)^1)$.

• If $k-2>n-2k+4$, then $\lambda =((k-2)^{2} \, (n-2k+4)^1)$ and we have

  $$\begin{aligned}&z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,\mathfrak {r}_{\triangle _{n,k}} \rangle =\langle p_{\lambda },\,q_n-q_{2k-4}q_{n-2k+4}-q_{n-k+2}q_{k-2}\rangle \\&\quad =2^3(1-1-2)=-16\,. \end{aligned}$$

• If $k-2 \le n-2k+4$, then $\lambda =((n-2k+4)^1\,(k-2)^2)$ and we have

  $$\begin{aligned} z_{\lambda }c_{\lambda }= & {} \langle p_{\lambda },\,\mathfrak {r}_{\triangle _{n,k}} \rangle \\= & {} \langle p_{\lambda },\,q_n-q_{n-k+2}q_{k-2}\rangle = {\left\{ \begin{array}{ll} 2^3(1-3)=-16 &{} \text {if } k-2=n-2k+4,\\ 2^3(1-2)=-8 &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

(c) We first show that $\mathfrak {r}_{\triangle _{2k,k}}$ is p-positive. Let $\alpha =(1^k)$ be a composition of k. Since $\mathfrak {r}_{\alpha }=q_{k}$ and $\triangle _{2k,k}=\alpha \odot \alpha ^t$, it follows from Proposition 2 (8) that $\mathfrak {r}_{\triangle _{2k,k}}=q_k^2/2$ which is p-positive.

To complete the proof, we have to show that $\mathfrak {r}_{\triangle _{n,k}}$ is not p-positive for $1< k < n/2$ and $k \ne 3$.

For even k, let $\lambda =(n/2,\,n/2)$ if n/2 is odd and $\lambda =(n/2+1,\,n/2-1)$ otherwise, then the value

$$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,\mathfrak {r}_{\triangle _{n,k}} \rangle =\langle p_{\lambda },\,-q_n\rangle \end{aligned}$$

is negative in both cases. For odd k, we show that $z_{\lambda }c_{\lambda }$ is negative for $\lambda =(n-k-4,k-2,3,3)$. Note that $n-k-4 \ge k-2 \ge 3$.

• If $k=5$, then $\lambda =(n-9,3,3,3)$ and the value

  $$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,\mathfrak {r}_{\triangle _{n,k}} \rangle =\langle p_{\lambda },\,q_n-q_{n-3}q_{3}\rangle \end{aligned}$$

  is equal to $2^4(1-4)=-48$ if $n=12$ and $2^4(1-3)=-32$ otherwise.

• If $k>5$, then we have

  $$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,\mathfrak {r}_{\triangle _{n,k}} \rangle =\langle p_{\lambda },\,q_n-q_{n-3}q_{3}+q_{n-6}q_{6}-q_{n-k+2}q_{k-2}\rangle \end{aligned}$$

  is equal to $2^4(1-2+1-2)=-32$ if $n-k-4=k-2$ and $2^4(1-2+1-1)=-16$ otherwise.

$\square$

Fig. 2

The elements of the set $\mathfrak {B}_4$ of basic blocks of size 4

We classified all p-positive ribbons of the form $\triangle _{n,k}$, and Proposition 2 (4) tells us that their transpose, antipodal rotation, and antipodal rotation of transpose are all p-positive. For each $n \ge 1$, we define $\mathfrak {B}_n$, called the set of basic blocks of size n, by

$$\begin{aligned} \mathfrak {B}_n := \left\{ \triangle _{n,1}, \, {\triangle _{n,1}}^t, \, \triangle _{n,3}, \, {\triangle _{n,3}}^t, \, {\triangle _{n,3}}^\circ , \, ( {\triangle _{n,3}}^t)^\circ \right\} \, , \end{aligned}$$

and $\mathfrak {B}$ to be the union of all $\mathfrak {B}_n$. We call $\mathfrak {B}$ the set of basic blocks. See Fig. 2 for example. Note that if $n \le 3$, then $\mathfrak {B}_n = \{ \triangle _{n,1}, \, {\triangle _{n,1}}^t \}$, and all ribbons in $\mathfrak {B}$ are p-positive.

We state the main theorem of this section, in which an infinite family of p-positive ribbons is constructed from our basic blocks.

Theorem 7

Let $\mathfrak {B}$ be the set of basic blocks. If a ribbon D is of the form

$$\begin{aligned} D = \alpha ^{(k)} \bullet \cdots \bullet \alpha ^{(2)} \bullet \alpha ^{(1)} \bullet B \end{aligned}$$

for some $B \in \mathfrak {B}$ and a positive integer k with compositions $\alpha ^{(i)}\in \{ (2), (1,1)\}$ for each $1 \le i \le k$, then $\mathfrak {r}_D$ is p-positive.

Proof

We first observe that $(2)\bullet B= B \odot B^t$ and $(1,1)\bullet B= B \cdot B^t$. Hence, if we let $D_i=\alpha ^{(i)}\bullet \cdots \bullet \alpha ^{(1)}\bullet B$ for $1 \le i \le k$, then we can easily see that $\mathfrak r_{D_{i+1}}=\frac{1}{2} \mathfrak r_{D_i}^2$ for $0 \le i \le k-1$ by Proposition 2 (8). It follows that $\mathfrak r_{D}=\frac{1}{2^k} (\mathfrak r_B)^{2^k}$, and therefore $\mathfrak r_{D}$ is p-positive. $\square$

We remark that we do not include $\triangle _{n,\frac{n}{2}}$, ${\triangle _{n,\frac{n}{2}}}^t(=\triangle _{n,\frac{n}{2}+1})$, ${\triangle _{n,\frac{n}{2}}}^{\circ }$, and ${({\triangle _{n,\frac{n}{2}}}^t)}^{\circ }$ in $\mathfrak {B}$ since all of them can be obtained from basic blocks by taking a composition of transposition as in Theorem 7. For instance, $\triangle _{n,\frac{n}{2}} = (2) \bullet {\triangle _{\frac{n}{2},1}}^t$.

4.2 A conjecture on the classification of p-positive ribbons

Our conjecture is that the converse of Theorem 7 is also true. That is, for connected $\widetilde{\lambda /\mu }$, $Q_{\lambda /\mu }$ is p-positive if and only if $\widetilde{\lambda /\mu }$ is a ribbon obtained by applying finite number of compositions of transposition by either (1, 1) or (2) to a basic block. Remember that $\mathfrak {B}$ is the set of basic blocks.

Conjecture 1

For a connected D, if $\mathfrak {r}_D$ is p-positive, then either $D \in \mathfrak {B}$ or

$$\begin{aligned} D = \alpha ^{(k)} \bullet \cdots \bullet \alpha ^{(2)} \bullet \alpha ^{(1)} \bullet B \end{aligned}$$

for some $B \in \mathfrak {B}$ and a positive integer k with compositions $\alpha ^{(i)}\in \{ (2), (1,1)\}$ for $1 \le i \le k$.

We verified the conjecture for all cases up to $n = 12$ via Sage computation, and in what follows, we list some evidence to support Conjecture 1. To begin with, we recall that for each ribbon D, there are four kinds of equivalent ribbons in the sense that

$$\begin{aligned} \mathfrak {r}_D = \mathfrak {r}_{D^t} = \mathfrak {r}_{D^\circ } = \mathfrak {r}_{(D^t)^\circ } \,. \end{aligned}$$

We also recall a ribbon D corresponding to the composition $\alpha (D) = ( \alpha _1(D), \cdots , \alpha _\ell (D) )$ whose ith part is equal to the number of boxes on the ith row of D. Note that if $\alpha _1(D) >1$, then $\alpha _1((D^t)^\circ ) = 1$. Since our goal is to determine the p-positivity of $\mathfrak {r}_D$, it is enough to consider the ribbons with $\alpha _1(D) = 1$. Hence, from now on, we always assume that a ribbon has a only one box on the first row. We say that a box (i, j) in D is a corner of D if the box $(i-1, j)$ is contained in D, but $(i+1, j)$ is not in D. Let c(D) be the number of all corners in D.

We summarize some properties that the coefficients in the p-expansion of ribbon Schur functions satisfy.

Lemma 5

Let D be a connected ribbon of size n with length $\ell$. If $\mathfrak {r}_D = \sum _{\lambda \in OP(n)} c_\lambda \, p_\lambda$, then we have the following:

• (a) ${\sum _{\lambda \in OP(n)} c_\lambda = 2}$.

• (b) If n is odd, then $c_{(n)} = (-1)^{\ell +1} \, 2/n$.

• (c) If $\alpha _1(D)=1$ and $\alpha _\ell (D) > 1$, then $\sum _{\lambda \in OP(n)}m_1(\lambda )c_{\lambda } = 8 c(D).$

• (d) If $\alpha _1(D)=\alpha _\ell (D) = 1$, then $\sum _{\lambda \in OP(n)}m_1(\lambda )c_{\lambda }= 8c(D)- 4$ for $n \ge 2$.

Proof

(a) Since D is a ribbon, there are exactly two kinds of marked shifted tableaux of shape D and weight (n). Thus, we have

$$\begin{aligned} \langle \ \mathfrak {r}_{D},~ s_{(n)} \rangle = \left\langle \sum _{\lambda \in OP(n)}c_{\lambda }p_{\lambda }, ~\sum _{\lambda \vdash n}z_{\lambda }^{-1} p_{\lambda } \right\rangle = \sum _{\lambda \in OP(n)}c_{\lambda } = 2 \, . \end{aligned}$$

(b) This implication is immediate from Proposition 2 (6) and Proposition 1 (2).

(c) Let T be a marked shifted tableau of shape D and weight $(n-1,1)$. We use T(i, j) for the content filled in the box (i, j) of T. First, notice that if T(i, j) is 2 or $2'$, then the box (i, j) should be a corner of D. Hence, we can choose a box to place either 2 or $2'$ among c(D) corners. Second, if $|T(i,j)| = 2$, then $T(i-1, j)$ can be either 1 or $1'$. Lastly, since $\alpha _\ell (D) > 1$, the leftmost box on the $\ell$th row of D is not a corner and this box must be filled with either 1 or $1'$. In all, we conclude that the number of marked shifted tableaux of shape D and weight $(n-1,1)$ is 8c(D), and thus,

$$\begin{aligned} 8c(D) = \langle \mathfrak {r}_D, s_{(n)} + s_{(n-1,1)}\rangle = \langle \mathfrak {r}_D, s_{(n)} \rangle + \langle \mathfrak {r}_D, s_{(n-1,1)}\rangle \, . \end{aligned}$$

Finally, using the following Murnaghan–Nakayama rule for $s_{(n-1,1)}$,

$$\begin{aligned} s_{(n-1,1)}=\sum _{\lambda \vdash n} z_{\lambda }^{-1}(m_1(\lambda )-1)p_{\lambda } , \end{aligned}$$

we deduce that

$$\begin{aligned} 8c(D) = \sum _{\lambda \in OP(n)}c_\lambda + \sum _{\lambda \in OP(n)} (m_1(\lambda )-1)\, c_\lambda \, = \, \sum _{\lambda \in OP(n)} m_1(\lambda )\, c_\lambda \, . \end{aligned}$$

(d) This can be proved in a similar way as in (b). But, in this case, the unique box, say b, on the $\ell$th row of D is a corner. Thus, b can be filled with 2 or $2'$, and the number of such marked shifted tableaux of shape D and weight $(n-1, 1)$ is 4. This implies that

$$\begin{aligned} \langle \mathfrak {r}_D, ~s_{(n)}+s_{(n-1,1)} \rangle = 8(c(D)-1)+4 = 8c(D) - 4\,. \end{aligned}$$

$\square$

The following corollary shows that $\mathfrak {r}_D$ is not p-positive if c(D) is sufficiently large.

Corollary 1

For a connected ribbon D of size n, if $c(D) > 1/2 +n/4$, then $\mathfrak {r}_D$ is not p-positive.

Proof

By Lemma 5, we have

$$\begin{aligned} \sum _{\lambda \in OP(n)}(n-m_1(\lambda )) \, c_{\lambda }\le 2n- 8c(D) + 4 , \end{aligned}$$

which turns out to be negative if $c(D) > 1/2+n/4$. Since $m_1(\lambda )$ is at most n, the number $n-m_1(\lambda )$ is always nonnegative. Therefore, $c_{\lambda }<0$ for some $\lambda$. $\square$

Remark 1

Let D be a ribbon of the form $D = {\alpha ^{(k)} \bullet \cdots \bullet \alpha ^{(2)} \bullet \alpha ^{(1)} \bullet B}$ as in Conjecture 1. Since we assume that $\alpha _1(D) = 1$, B should be a basic block satisfying that $\alpha _{1}(B) =1$. Let $\ell$ be the length of B. If $\alpha _\ell (B) \ne 1$, then the number of corners in $\alpha ^{(i)} \bullet \alpha ^{(i-1)} \bullet \cdots \bullet \alpha ^{(1)} \bullet B$ is twice the number of corners in $\alpha ^{(i-1)} \bullet \cdots \bullet \alpha ^{(1)} \bullet B$ for $1 \le i \le k$. It follows that $c(D) = 2^k$ from $c(B) = 1$. On the other hand, if $\alpha _\ell (B) = 1$, that is, B is a one-row diagram, then $\alpha ^{(1)} \bullet B = \triangle _{2n, n}$ or $\triangle _{2n, n+1}$, and thus, $c(\alpha ^{(1)} \bullet B) = c(B) =1$. Hence, $c(D) = 2^{k-1}$. Notice that $c(D) \le 2^{k-1}$ if $2 \le |B| \le 3$ as $\alpha _\ell (B) = 1$ and $c(D) \le 2^k$ otherwise. In both cases, we can derive that $c(D) \le |D|/4 < 1/2 + |D|/4$.

According to Conjecture 1, if the number of boxes $n=|D|$ of the ribbon is odd, then $\mathfrak {r}_D$ is p-positive only when D is a basic block. We prove that $\mathfrak {r}_D$ is not p-positive if $D\not \in \mathfrak {B}$ satisfies certain conditions, when |D| is odd.

When the length of the ribbon is even, non p-positivity of $\mathfrak {r}_D$ immediately follows from Lemma 5.

Theorem 8

Let $D\not \in \mathfrak {B}$ be a ribbon with odd number of boxes. If the length of D is even, then $\mathfrak {r}_D$ is not p-positive.

For the ribbons of odd length, more work has to be done. We set up some necessary notions first. For a given ribbon D of length $\ell$, we define the head length of D by the smallest index i such that the ith row of D contains at least two boxes. We define the tail length of a ribbon according to the number of boxes in the last row: If $\alpha _{\ell }(D)=1$, then we define the tail length of D by the smallest index j such that $(\ell - j +1)$st row of D contains at least two boxes. Otherwise, we define the tail length of D by $\alpha _\ell (D)$.

Example 4

If $D_1 = (1,3,1,1,1)$, then the head length and the tail length of $D_1$ are 2 and 4, respectively. On the other hand, if $D_2 = (1,3,1,1,2)$, then the head length and the tail length of $D_2$ are 2 and 2, respectively.

Theorem 9

Let $D=(\alpha _1(D),\alpha _2(D), \dots , \alpha _{\ell }(D))\not \in \mathfrak {B}$ be a ribbon with an odd number of boxes such that $\alpha _1 (D) =1$. If the length of D is odd, then $\mathfrak {r}_D$ is not p-positive in the following cases, where k and m are the head length and the tail length of D, respectively:

• (a) $\alpha _\ell (D) >1$ and k is even.

• (b) $\alpha _\ell (D) >1$, k is odd and m is even.

• (c) $\alpha _\ell (D) =1$ and $k=m$.

Proof

We let n be the number of boxes of D, that is assumed to be odd. Without loss of generality, we may assume that $m \ge k$. Let $\mathfrak {r}_D = \sum _{\lambda \in OP(n)} c_\lambda p_\lambda$. We use Proposition 1 (2), Proposition 2 (6), and Lemma 4 in the proofs that follow.

(a) To prove the assertion, we show that the coefficient $c_\lambda$ is negative, where $\lambda = \lambda (n-k, k-1, 1)$. Note that $m=\alpha _\ell (D)>1$ in this case.

We first suppose that $k = 2$ so that $\lambda =(n-2,1,1)$. Then, we have

$$\begin{aligned} z_{\lambda }c_{\lambda }= {\left\{ \begin{array}{ll} \langle p_{\lambda },\,q_n- q_{n-1}q_1 - q_{n-2}q_2\rangle =-16 &{} \text {if}\ m=2,\\ \langle p_{\lambda },\,q_n- q_{n-1}q_1 \rangle =-8 &{} \text {if}\ m>3\,. \end{array}\right. } \end{aligned}$$

Now suppose that k is even such that $k > 2$. Note that $n-k$, $k-1$, and 1 are mutually distinct due to the assumptions we make. Then,

$$\begin{aligned} z_{\lambda }c_{\lambda }= {\left\{ \begin{array}{ll} \langle p_{\lambda },\,q_n- q_{n-1}q_1 - q_{n-k+1} q_{k-1} - q_{n-k} q_{k}\rangle =-16 &{} \text {if}\ m=k,\\ \langle p_{\lambda },\,q_n- q_{n-1}q_1 - q_{n-k+1} q_{k-1} \rangle =-8 &{} \text {if} \ m>k \,. \end{array}\right. } \end{aligned}$$

(b) Now we consider odd k and even $m=\alpha _\ell (D)>1$ and we trace the coefficient $c_\lambda$ with $\lambda = \lambda (n-m, m-1,1)$. Note that $m-1\ne 1$ since $\alpha (D)=1$ implies $k> 1$, while it is possible that $n-m=m-1$.

• If there is an index i such that $\alpha _1(D) + \cdots + \alpha _{i-1}(D) = m-1$ and $\alpha _i(D) = 1$, then

  $$\begin{aligned} z_{\lambda }c_{\lambda }= & {} \langle p_{\lambda },\,q_n- q_{n-1}q_1 - q_{n-m+1}q_{m-1} - 2 q_{n-m} q_m + 2q_{n-m} q_{m-1} q_1 \rangle \\= & {} {\left\{ \begin{array}{ll} -16 &{} \text {if} \ n-m = m-1, \\ -8 &{} \text {otherwise}\,. \end{array}\right. }\,. \end{aligned}$$

• If there is an index i such that $\alpha _1(D) + \cdots + \alpha _{i-1}(D) = m-1$ and $\alpha _i(D) > 1$, then

  $$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,q_n- q_{n-1} q_1 - q_{n-m+1} q_{m-1} - q_{n-m}q_m \rangle = {\left\{ \begin{array}{ll} -32 &{} \text {if} \ n-m = m-1, \\ -16 &{} \text {otherwise}\,. \end{array}\right. } \end{aligned}$$

• If there is an index i such that $\alpha _1(D) + \cdots + \alpha _{i}(D)= m$ and $\alpha _i(D)>1$, then

  $$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,q_n- q_{n-1}q_1 - 2q_{n-m} q_m + q_{n-m}q_{m-1} q_1\rangle = {\left\{ \begin{array}{ll} -16 &{} \text {if} \ n-m = m-1, \\ -8 &{} \text {otherwise}\,. \end{array}\right. }\,. \end{aligned}$$

• If there is no index i such that $\alpha _1(D) + \cdots + \alpha _{i}(D) = m-1$ or m, then

  $$\begin{aligned} z_{\lambda }c_{\lambda }=\langle p_{\lambda },\,q_n- q_{n-1} q_1- q_{n-m} q_m\rangle = {\left\{ \begin{array}{ll} -16 &{} \text {if} \ n-m = m-1, \\ -8 &{} \text {otherwise}\,. \end{array}\right. } \end{aligned}$$

(c) This can be proven in a similar way as in (b) by tracing the coefficient $c_\lambda$, where $\lambda = \lambda (n-m, m-1, 1)$ if $k = m$ is even and $\lambda = \lambda (n-m-1, m, 1)$ otherwise. $\square$

5 Concluding remarks

Conjecture 1 is about the p-positive connected ribbons. For a ribbon D having r connected components, say $D=D_1\cup \cdots \cup D_r$, the ribbon Schur Q-function of D is decomposed as $\mathfrak {r}_D=\prod _{i=1}^r \mathfrak {r}_{D_i}$. Since a product of p-positive symmetric functions is p-positive, we know that if D is a ribbon having p-positive ribbons as its connected components, then $\mathfrak {r}_D$ is p-positive. However, the converse is not true in general, that is, the p-positivity of $\prod _{i=1}^r \mathfrak {r}_{D_i}$ does not guarantee the p-positivity of each $\mathfrak {r}_{D_i}$, and the classification of all p-positive ribbons needs more sophisticated work. We nevertheless make a conjecture, which we checked with Sage for some specific cases.

Conjecture 2

Let $D=D_1\cup \cdots \cup D_r$ be a ribbon with connected components $D_i$, $i=1, \dots , r$. Then, $\mathfrak {r}_D$ is p-positive if and only if $\mathfrak {r}_{D_i}$ is p-positive for all i.