1 Introduction

In neural networks dynamics, inertial neural networks can be described as second-order differential equations, and the inertial term is used as a convenient tool for causing bifurcation and chaos [1, 2]. Consequently, dynamic analyses on constant delayed inertial neural networks have been extensively explored, and plentiful important results have been gained in [3–11] and the references cited therein. It should be adverted to that all research approaches involved in the above papers are on the base of the reduced order strategy, which will produce a large amount of computation and has no practical value. Therefore, the authors in [12, 13] used non-reduced order strategy to explore the synchronization and stability in inertial neural networks. As is well known, the neural networks involving time-varying parameters will have more practical issues [14–16]. In particular, taking the global Lipschitz activation functions, the authors in [12, 13] applied some novel Lyapunov functionals instead of the classical reduced order strategy and established a set of new conditions to illustrate the dynamic behaviors such as synchronization and stability in non-autonomous inertial neural networks. Yet in some applications, activation functions without Lipschitz conditions are inevitably encountered. However, there is little research on the convergence of non-autonomous inertial neural networks without taking the global Lipschitz requirements in activation functions.

For the last few years, the dynamics in proportional delayed neural networks have attracted widespread concern because of biological and physical applications (see [17–22]). Particularly, the global convergence of proportional delayed neural networks without inertial terms has been widely studied in [23–30]. Unfortunately, so far, there has been no publishing article using non-reduced order strategy to establish the global convergence analysis on inertial proportional delayed neural networks without global Lipschitz activation functions.

On account of the above considerations, in this paper, our aim is to utilize the non-reduced order strategy to deal with the global convergence of the following inertial proportional delayed neural networks:

$$\begin{aligned} z_{i}''(t) =&- \bar{a}_{i}(t)z_{i}'(t) \\ &{} -\bar{b}_{i}(t)z_{i}(t)+\sum _{j=1}^{n}\bar{c}_{ij}(t)F_{j} \bigl(z_{j}(t)\bigr) +\sum_{j=1}^{n} \bar{d}_{ij}(t)G_{j}\bigl(z_{j}( q_{ij} t )\bigr)+J_{i}(t), \end{aligned}$$
(1.1)

involving initial values

$$ z_{i}(\theta)=\varphi_{i}(\theta),\qquad z_{i}'(\theta)= \psi _{i}(\theta),\qquad \tau_{i}t_{0} \leq \theta\leq t_{0},\quad \varphi_{i}, \psi_{i}\in C\bigl([ \tau_{i}t_{0} , t_{0}], \mathbb{R}\bigr), $$
(1.2)

where \(t\geq t_{0}>0\), \(\tau_{i}= \min_{1\leq j\leq n}\{q_{ij}\}\), \(\bar{c}_{ij}, \bar{d}_{ij} :\mathbb{R}\rightarrow\mathbb{R}\), and \(\bar{a}_{i},\bar{b}_{i} :\mathbb{R}\rightarrow(0, +\infty)\) are continuous and bounded, and \(i,j\in Q= \{1,2,\ldots,n\}\), \(z_{i}''(t)\) is called an inertial term of (1.1), \(z(t)=(z_{1}(t), z_{2}(t),\ldots, z_{n}(t))\) is the state vector, proportional delay factor \(q _{ij} \) satisfies the conditions that \(0 < q _{ij} < 1\), \(J_{i}(t)\) is the continuous external input, and the continuous activation functions \(G_{j} \) and \(F_{j} \) involve two nonnegative constants \(L^{F}_{j}\) and \(L^{G}_{j}\) satisfying

$$ \bigl\vert F_{j}(\theta) \bigr\vert \leq L^{F} _{j} \vert \theta \vert ,\qquad \bigl\vert G_{j}( \theta) \bigr\vert \leq L^{G}_{j} \vert \theta \vert \quad\mbox{for all } \theta \in\mathbb{ R}, j\in Q, $$
(1.3)

which abstain the global Lipschitz conditions.

Remark 1.1

Via the step and step approach, one can prove the existence and uniqueness for every solution of initial value problem (1.1) and (1.2) on \([t_{0}, +\infty)\).

The remainder of this paper is organized as follows. We apply Barbalat’s lemma to set the main result in Sect. 2. The validity of our methods is shown by an application example in Sect. 3. Finally, Sect. 4 concludes the paper with discussion.

2 Global convergence of inertial proportional delayed neural networks

Lemma 2.1

(see [31, Barbalat’s lemma])

Let\(g (t)\)be uniformly continuous on\([t_{0}, +\infty)\)and\(\int_{t_{0}}^{+\infty}g(s)\,ds<+\infty\), then\(\lim_{t\rightarrow+\infty} g(t) =0\).

Theorem 2.1

Suppose that (1.3) holds, and the following assumptions are satisfied:

\((T_{1})\):

\(W(t)= \int_{t_{0}}^{t}w(s)\,ds\)is bounded on\([t_{0}, +\infty)\), where\(w(t)=\max_{i\in Q}|J_{i}(t)|\).

\((T_{2})\):

For\(i, j\in Q\), \(\bar{a}_{i}' (t)\), \(\bar{b}_{i} '(t)\)and\((|\bar{c}_{ij}(t)|L^{F}_{j} +|\bar{d}_{ij}(t)|L^{G}_{j})'\)are bounded and continuous on\([t_{0}, +\infty)\).

\((T_{3})\):

There are constants\(\alpha_{i}\geq0\), \(\beta_{i}>0\), and\(\gamma_{i}\geq0\)such that

$$ \sup_{t\in[t_{0}, +\infty)}A_{i} (t)< 0,\qquad \inf _{t\in [t_{0}, +\infty)} \bigl\{ 4A_{i}(t)B_{i }(t)- C_{i}^{2}(t)\bigr\} >0, \quad\forall i\in Q, $$
(2.1)

where

$$\left \{ \textstyle\begin{array}{l} A_{i}(t) = \alpha_{i}\gamma_{i}-\bar{a}_{i}(t)\alpha_{i}^{2} + \frac{1}{2}\alpha_{i}^{2}\sum_{j=1}^{n}( \vert \bar{c}_{ij}(t) \vert L^{F}_{j} + \vert \bar{d}_{ij}(t) \vert L^{G}_{j}) , \\ B_{i}(t) = -\bar{b}_{i}(t)\alpha_{i}\gamma_{i} +\frac{1}{2}\sum_{j=1}^{n}( \vert \bar{c}_{ij}(t) \vert L^{F}_{j}+ \vert \bar {d}_{ij}(t) \vert L^{G}_{j} ) \vert \alpha_{i}\gamma_{i} \vert \\ \phantom{B_{i}(t) =}{}+\frac{1}{2}\sum_{j=1}^{n}\alpha_{j}^{2}( \vert \bar{c}_{ji}(t) \vert L^{F}_{i} + \bar{d}_{ji}^{+} L^{G}_{i}\frac{1}{q _{ji} } ) +\frac{1}{2}\sum_{j=1}^{n}( \vert \bar{c}_{ji}(t) \vert L^{F}_{i} + \bar{d}_{ji}^{+} L^{G}_{i}\frac{1}{q _{ji} } ) \vert \alpha_{j}\gamma_{j} \vert , \\ C_{i}(t) = \beta_{i}+\gamma_{i}^{2} -\bar{a}_{i}(t)\alpha_{i}\gamma_{i}-\bar{b}_{i}(t)\alpha_{i}^{2}, \quad\bar {d}_{ij}^{+}=\sup_{t\in\mathbb{R}} \vert \bar{d}_{ij}(t) \vert , i,j\in Q . \end{array}\displaystyle \right . $$

Moreover, label\(z (t)=(z_{1}(t), z_{2}(t),\ldots, z_{n}(t))\)as a solution of the initial value problem of (1.1) and (1.2). Then

$$\lim_{t\rightarrow+\infty} z_{i}(t) =0, \qquad\lim _{t\rightarrow+\infty} z_{i}'(t) =0, \quad i\in Q. $$

Proof

From \((T_{1})\), \((T_{3})\), one can see that there exist constants \(\sigma,\delta\in(0, +\infty)\) satisfying

$$ \left . \textstyle\begin{array}{l} -\sigma=\max_{i\in Q}\sup_{t\in[t_{0}, +\infty)}e^{-W(t)} A_{i} (t) , \\ -\delta=\max_{i\in Q}\sup_{t\in[t_{0}, +\infty)}e^{-W(t)}(B_{i} (t)-\frac{(C _{i}(t)) ^{2}}{4A_{i} (t)}). \end{array}\displaystyle \right \} $$
(2.2)

Define

$$\begin{aligned} U(t) =&e^{-W(t)} \Biggl\{ \frac{1}{2}\sum _{i=1}^{n}\beta_{i}z_{i}^{2}(t) +\frac{1}{2}\sum_{i=1}^{n} \bigl(\alpha_{i} z _{i}'(t)+ \gamma_{i}z_{i}(t)\bigr)^{2} \\ &{}+\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha_{i}^{2} \bar{d}_{ij} ^{+}+ \vert \alpha_{i} \gamma_{i} \vert \bar{d}_{ij} ^{+}\bigr) L^{G}_{j} \int_{q _{ij}t }^{t}z_{j}^{2}(s) \frac{1}{q _{ij} } \,ds+\frac{1}{2}\sum_{i=1}^{n} \alpha_{i}^{2} \Biggr\} . \end{aligned}$$

In view of \((T_{1})\) and (1.1), we have

$$\begin{aligned} &U ' (t) \\ &\quad= -w(t)U(t)+e^{-W(t)} \Biggl\{ \sum _{i=1}^{n}\bigl(\beta_{i}+ \gamma_{i}^{2}\bigr)z_{i}(t)z '_{i}(t) +\sum_{i=1}^{n} \alpha_{i}\bigl(\alpha_{i}z '_{i}(t)+ \gamma_{i}z_{i}(t)\bigr) \\ &\qquad{}\times\Biggl[-\bar{a}_{i}(t)z '_{i}(t)- \bar{b}_{i}(t)z_{i}(t)+\sum _{j=1}^{n}\bar{c}_{ij}(t)\widetilde {F}_{j}\bigl(z_{j}(t)\bigr) +\sum _{j=1}^{n}\bar{d}_{ij}(t) \widetilde{G}_{j}\bigl(z_{j}(q_{ij}t) \bigr)+J_{i}(t)\Biggr] \\ &\qquad{}+\sum_{i=1}^{n} \alpha_{i}\gamma_{i}\bigl(z '_{i} (t)\bigr)^{2}+\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha_{i}^{2} \bar{d}_{ij} ^{+}+ \vert \alpha_{i} \gamma_{i} \vert \bar{d}_{ij} ^{+}\bigr) L^{G}_{j}\biggl[z_{j}^{2}(t) \frac{1}{q _{ij} } -z_{j}^{2}(q_{ij}t) \biggr] \Biggr\} \\ &\quad\leq e^{-W(t)} \Biggl\{ -w(t)\frac{1}{2}\sum _{i=1}^{n}\bigl[\bigl( \alpha_{i} z _{i}'(t)+ \gamma_{i}z_{i}(t)\bigr)^{2} -2 \alpha_{i} \bigl\vert \alpha_{i} z _{i}'(t)+\gamma_{i}z_{i}(t) \bigr\vert +\alpha_{i}^{2}\bigr] \\ &\qquad{}+ \Biggl[\sum_{i=1}^{n}\bigl( \beta_{i}+\gamma_{i}^{2} - \bar{a}_{i}(t)\alpha_{i}\gamma_{i}- \bar{b}_{i}(t)\alpha_{i}^{2} \bigr)z_{i}(t)z '_{i}(t) +\sum _{i=1}^{n}\bigl( \alpha_{i} \gamma_{i}-\bar{a}_{i}(t)\alpha_{i}^{2} \bigr) \bigl(z '_{i}(t)\bigr)^{2} \\ &\qquad{}-\sum_{i=1}^{n} \bar{b}_{i}(t)\alpha_{i}\gamma_{i} z_{i}^{2}(t) +\frac{1}{2}\sum _{i=1}^{n}\sum_{j=1}^{n} \bigl(\alpha_{i}^{2}\bar{d}_{ij} ^{+}+ \vert \alpha_{i}\gamma_{i} \vert \bar{d}_{ij} ^{+}\bigr)\frac{1}{q _{ij} }L^{G}_{j}z_{j}^{2}(t) \\ &\qquad{}-\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha_{i}^{2} \bar{d}_{ij} ^{+}+ \vert \alpha_{i} \gamma_{i} \vert \bar{d}_{ij} ^{+}\bigr) L^{G}_{j} z_{j}^{2} \bigl(q_{ij}(t)\bigr) \\ &\qquad{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha_{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha_{i}\gamma_{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert \bar{c}_{ij}(t) \bigr\vert \bigl\vert F_{j}\bigl(z_{j}(t)\bigr) \bigr\vert \\ &\qquad{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha_{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha_{i}\gamma_{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert \bar{d}_{ij}(t) \bigr\vert \bigl\vert G_{j}\bigl(z_{j}(q_{ij}t) \bigr) \bigr\vert \Biggr] \Biggr\} \\ &\quad\leq e^{-W(t)} \Biggl\{ \sum _{i=1}^{n}\bigl(\beta_{i}+ \gamma_{i}^{2} -\bar{a}_{i}(t) \alpha_{i}\gamma_{i}-\bar{b}_{i}(t) \alpha_{i}^{2}\bigr)z_{i}(t) z '_{i}(t) +\sum_{i=1}^{n} \bigl( \alpha_{i}\gamma_{i}-\bar{a}_{i}(t) \alpha_{i}^{2}\bigr) \bigl(z '_{i}(t) \bigr)^{2} \\ &\qquad{}+\sum_{i=1}^{n} \Biggl[-\bar{b}_{i}(t)\alpha_{i}\gamma_{i} +\frac{1}{2}\sum_{j=1}^{n} \bigl(\alpha_{j}^{2} \bar{d}_{ji} ^{+}+ \vert \alpha_{j}\gamma_{j} \vert \bar{d}_{ji} ^{+}\bigr)\frac{1}{q _{ji} } L^{G}_{i}\Biggr]z_{i}^{2}(t) \\ &\qquad{}-\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl(\alpha _{i}^{2}\bar{d}_{ij} ^{+}+ \vert \alpha_{i}\gamma_{i} \vert \bar{d}_{ij} ^{+}\bigr) L^{G}_{j} z_{j}^{2}(q_{ij}t) \\ &\qquad{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha_{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha_{i}\gamma_{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert \bar{c}_{ij}(t) \bigr\vert \bigl\vert F_{j}\bigl(z_{j}(t)\bigr) \bigr\vert \\ &\qquad{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha_{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha_{i}\gamma_{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert \bar{d}_{ij}(t) \bigr\vert \bigl\vert G_{j}\bigl(z_{j}(q_{ij}t) \bigr) \bigr\vert \Biggr\} . \end{aligned}$$
(2.3)

From (1.3) and the fact that \(uv \leq\frac{1}{2} (u^{2} + v^{2})\) (\(u, v\in\mathbb{R}\)), one gains

$$\begin{aligned} &\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha_{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha_{i}\gamma_{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert \bar{c}_{ij}(t) \bigr\vert \bigl\vert F_{j}\bigl(z_{j}(t )\bigr) \bigr\vert \\ &\quad\leq\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\alpha_{i}^{2} \bigl\vert \bar {c}_{ij}(t) \bigr\vert L^{F}_{j} \bigl( \bigl(z '_{i}(t)\bigr)^{2}+z_{j}^{2}(t) \bigr) +\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \vert \alpha_{i}\gamma_{i} \vert \bigl\vert \bar {c}_{ij}(t) \bigr\vert L^{F}_{j} \bigl(z_{i}^{2}(t)+z_{j}^{2}(t) \bigr) \\ &\quad=\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\alpha_{i}^{2} \bigl\vert \bar {c}_{ij}(t) \bigr\vert L^{F}_{j} \bigl(z '_{i}(t)\bigr)^{2} \\ &\qquad{}+\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\bigl( \vert \alpha_{i}\gamma_{i} \vert \bigl\vert \bar {c}_{ij}(t) \bigr\vert L^{F}_{j} + \alpha_{j}^{2} \bigl\vert \bar{c}_{ji}(t) \bigr\vert L^{F}_{i}+ \vert \alpha_{j} \gamma_{j} \vert \bigl\vert \bar {c}_{ji}(t) \bigr\vert L^{F}_{i}\bigr)z_{i}^{2}(t) \end{aligned}$$

and

$$\begin{aligned} &\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha_{i}^{2} \bigl\vert z '_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma_{i} \vert \bigl\vert z_{i}(t) \bigr\vert \bigr) \bigl\vert \bar{d}_{ij}(t) \bigr\vert \bigl\vert G_{j}\bigl(z_{j}(q_{ij} t )\bigr) \bigr\vert \\ &\quad\leq\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\alpha_{i}^{2} \bigl\vert \bar{d}_{ij}(t) \bigr\vert L^{G}_{j} \bigl( \bigl(z' _{i}(t)\bigr)^{2}+z_{j}^{2}(q_{ij} t)\bigr) \\ &\qquad{}+\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \vert \alpha_{i}\gamma_{i} \vert \bigl\vert \bar{d}_{ij}(t) \bigr\vert L^{G}_{j} \bigl(z_{i}^{2}(t)+z_{j}^{2}(q_{ij} t)\bigr) \\ &\quad= \frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n}\alpha_{i}^{2} \bigl\vert \bar {d}_{ij}(t) \bigr\vert L^{G}_{j} \bigl(z '_{i}(t)\bigr)^{2} + \frac{1}{2}\sum_{i=1}^{n}\sum _{j=1}^{n} \vert \alpha_{i} \gamma_{i} \vert \bigl\vert \bar {d}_{ij}(t) \bigr\vert L^{G}_{j}z_{i}^{2}(t) \\ &\qquad{}+\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \bigl( \alpha_{i}^{2} \bigl\vert \bar{d}_{ij}(t) \bigr\vert L^{G}_{j}+ \vert \alpha_{i} \gamma_{i} \vert \bigl\vert \bar {d}_{ij}(t) \bigr\vert L^{G}_{j}\bigr)z_{j}^{2}(q_{ij} t), \end{aligned}$$

which, together with \((T_{3})\), (2.2), and (2.3), yield

$$\begin{aligned} U'(t) \leq&e^{-W(t)} \Biggl\{ \sum _{i=1}^{n}\bigl(\beta_{i}+ \gamma_{i}^{2} -\bar{a}_{i}(t) \alpha_{i}\gamma_{i}-\bar{b}_{i}(t) \alpha_{i}^{2}\bigr)z_{i}(t) z '_{i}(t) \\ &{}+\sum_{i=1}^{n}\Biggl[ \alpha_{i}\gamma_{i}-\bar {a}_{i}(t) \alpha_{i}^{2} + \frac{1}{2} \alpha_{i}^{2}\sum_{j=1}^{n} \bigl( \bigl\vert \bar{c}_{ij}(t) \bigr\vert L^{F}_{j} + \bigl\vert \bar{d}_{ij}(t) \bigr\vert L^{G}_{j} \bigr)\Biggr]\bigl(z '_{i}(t)\bigr)^{2} \\ &{}+\sum_{i=1}^{n}\Biggl[- \bar{b}_{i}(t)\alpha_{i}\gamma_{i} + \frac{1}{2}\sum_{j=1}^{n}\bigl( \bigl\vert \bar{c}_{ij}(t) \bigr\vert L^{F}_{j}+ \bigl\vert \bar {d}_{ij}(t) \bigr\vert L^{G}_{j} \bigr) \vert \alpha_{i}\gamma_{i} \vert \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \alpha_{j}^{2}\biggl( \bigl\vert \bar {c}_{ji}(t) \bigr\vert L^{F}_{i} + \bar{d}_{ji}^{+} L^{G}_{i} \frac{1}{q _{ji} } \biggr) \\ &{}+\frac{1}{2}\sum_{j=1}^{n} \biggl( \bigl\vert \bar{c}_{ji}(t) \bigr\vert L^{F}_{i} + \bar{d}_{ji}^{+} L^{G}_{i} \frac{1}{q _{ji} }\biggr) \vert \alpha_{j}\gamma _{j} \vert \Biggr]z_{i}^{2}(t) \Biggr\} \\ =& e^{-W(t)} \Biggl\{ \sum_{i=1}^{n} \bigl(A _{i} (t) \bigl(z '_{i}(t) \bigr)^{2}+B _{i}(t)z_{i}^{2}(t)+C _{i}(t)z_{i}(t) z '_{i}(t) \bigr) \Biggr\} \\ =&e^{-W(t)} \Biggl\{ \sum_{i=1}^{n}A_{i} (t) \biggl( z '_{i}(t)+\frac{C_{i} (t)}{2A_{i} (t)}z_{i}(t) \biggr)^{2} +\sum_{i=1}^{n} \biggl(B_{i} (t)-\frac{(C _{i}(t)) ^{2}}{4A_{i} (t)}\biggr) z_{i}^{2}(t) \Biggr\} \\ \leq&-\sigma\sum_{i=1}^{n} \biggl( z '_{i}(t)+\frac{C_{i} (t)}{2A_{i} (t)}z_{i}(t) \biggr)^{2} -\delta\sum_{i=1}^{n} z_{i}^{2}(t) \\ \leq&0, \quad\forall t \in[t_{0}, +\infty). \end{aligned}$$
(2.4)

Consequently, \(U (t)\leq U (t_{0})\) holds on \(t \in[t_{0}, +\infty)\), and

$$\frac{1}{2}\sum_{i=1}^{n} \beta_{i}z_{i}^{2}(t) +\frac{1}{2} \sum_{i=1}^{n}\bigl(\alpha_{i} z '_{i}(t)+\gamma_{i}z_{i}(t) \bigr)^{2} \leq U (t_{0}),\quad t \in[t_{0}, + \infty). $$

Note that

$$\alpha_{i} \bigl\vert z '_{i}(t) \bigr\vert \leq \bigl\vert \alpha_{i} z'_{i}(t) +\gamma_{i}z_{i}(t) \bigr\vert + \bigl\vert \gamma_{i}z_{i}(t) \bigr\vert , $$

one can obtain the uniform boundedness of \(z '_{i}(t)\) and \(z_{i}(t)\) on \([t_{0}, +\infty)\), where \(i\in Q\). This entails the uniform boundedness of \(z ''_{i}(t)\) for all \(t\in[t_{0}, +\infty)\) and \(i\in Q\). Clearly, on \([t_{0}, +\infty)\), it follows from \((T_{2}) \) that \(\sum_{i=1}^{n} ( z '_{i}(t)+\frac{C_{i} (t)}{2A_{i} (t)}z_{i}(t))^{2}\) and \(\sum_{i=1}^{n} z_{i}^{2}(t)\) are uniformly continuous for all \(i\in Q\).

Furthermore, (2.4) leads to

$$\sum_{i=1}^{n} \biggl( z '_{i}(t)+\frac{C_{i} (t)}{2A_{i} (t)}z_{i}(t) \biggr)^{2}\leq-\frac{1}{\sigma}U'(t),\qquad \sum _{i=1}^{n} z_{i}^{2}(t) \leq-\frac{1}{\delta}U'(t),\quad \forall t\geq t_{0}, $$

and

$$\lim_{t\rightarrow+\infty} \int_{t_{0}}^{t}\sum_{i=1}^{n} \biggl( z '_{i}(s)+\frac{C_{i} (s)}{2A_{i} (s)}z_{i}(s) \biggr)^{2}\,ds\leq \frac{U(t_{0})}{\sigma},\qquad \lim_{t\rightarrow+\infty} \int _{t_{0}}^{t}\sum_{i=1}^{n} z_{i}^{2}(s)\,ds\leq\frac{U(t_{0})}{\delta}. $$

This and Lemma 2.1 suggest that

$$\lim_{t\rightarrow+\infty}z_{i} (t)=0,\qquad \lim _{t\rightarrow+\infty}\biggl( z '_{i}(t)+ \frac{C_{i} (t)}{2A_{i} (t)}z_{i}(t)\biggr)=0,\qquad \lim_{t\rightarrow+\infty}z_{i}' (t)=0,\quad i\in Q, $$

which finishes the proof of Theorem 2.1. □

Remark 2.1

Most recently, taking the global Lipschitz activation functions, the authors in [12, 13] applied the non-reduced order strategy to reveal the convergence on the state vectors of inertial constant delayed neural networks. Unfortunately, the authors in [12, 13] have not given any opinion on the convergence of the inertial proportional delayed neural networks without choosing global Lipschitz activation functions. In this present paper, without taking the global Lipschitz activation functions, the convergence for all solutions and their derivatives in inertial proportional delayed neural networks are established. Therefore, compared with the methods in references [12] and [13], our method has fewer conditions and a simpler proof.

3 An illustrative numerical example

In this section, an example is given to reveal analytical results obtained in the previous sections graphically.

Example 3.1

Consider model (1.1) with the following proportional delays and time-varying coefficients:

$$ \left \{ \textstyle\begin{array}{l} z_{1}''(t) = -4.81e^{\sin^{2}t} z_{1}'(t) -(8.21+ \sin ^{2}t)z_{1}(t)+ 1.21(\sin^{2} t) F _{1}(z_{1}(t)) \\ \phantom{z_{1}''(t) =} {} + 1.51 (\cos^{2} t) F _{2}(z_{2}(t)) -0.81 (\sin^{2} t) G _{1}(z_{1}( 0.5 t ))\\ \phantom{z_{1}''(t) =}+1.91 (\cos^{2} t) G _{2}(z_{2}( 0.5 t ))+\frac {40 t}{1+t^{4}} , \\ z_{2}''(t) = {-}5.71 e^{\cos^{2}t} z_{2}'(t) -(10.91+\sin ^{2}t)z_{2}(t)- 0.91 (\sin^{2} t) F_{1}(z_{1}(t)) \\\phantom{z_{2}''(t) =} {} - 1.71 (\cos^{2}t) F_{2}(z_{2}(t))-2.51 (\sin^{2}t) G_{1}(z_{1}( 0.5 t ))\\ \phantom{z_{2}''(t) =} {}+2.11(\cos^{2} t) G_{2}(z_{2}( 0.5t ))+\frac {60 t}{1+t^{5}} , \end{array}\displaystyle \right . $$
(3.1)

where \(t\geq t_{0}=1\), \(F_{1}(u) = G_{1}(u) = 0.25(|u + 1|-|u-1|)\), \(F_{2}(u) = G_{2}(u) = 0.5 u\sin u\).

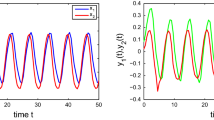
Choose \(\alpha_{i}=\gamma_{i}=1\), \(\beta_{1}=3.8\), \(\beta_{2}=5.3\), \(L^{F}_{i} = L^{G}_{i} =0.5\), \(i=1,2\), one can show that \((T_{1})\), \((T_{2})\), \((T_{3})\), and (1.3) are satisfied in system (3.1). Hence, from Theorem 2.1, we can obtain that all state vectors of (3.1) and their derivatives converge to zero vector. The simulation results are given in Fig. 1 and Fig. 2.

Figure 1
figure 1

Numerical solutions \(z(t)\) on system (3.1). Numerical solutions \(z(t)\) to example (3.1) with initial values: \((\varphi_{1}(s),\varphi_{2}(s),\psi_{1}(s),\psi_{2}(s))\equiv (2,-4,0,0), (3,-2,0,0), (-3,4,0,0)\), \(t_{0}=1\)

Full size image
Figure 2
figure 2

Numerical solutions \(z'(t)\) on system (3.1). Numerical solutions \(z'(t)\) to example (3.1) with initial values: \((\varphi_{1}(s),\varphi_{2}(s),\psi_{1}(s),\psi_{2}(s))\equiv (2,-4,0,0), (3,-2,0,0), (-3,4,0,0)\), \(t_{0}=1\)

Full size image

Remark 3.1

As far as the authors know, no one has used the non-reduced order strategy to study the global convergence of inertial proportional delay neural networks without the global Lipschitz activation functions. Moreober, the results in [35–89] have not touched on the global convergence of inertial proportional delay neural networks. It should be noted that the global Lipschitz assumption about the activation function is not applicable to system (3.1), and we can easily discover that all achievements in [3–13] and [32–89] cannot be directly used to establish the global convergence of (3.1).

4 Conclusions

In this paper, the global convergence of a class of inertial proportional delayed neural networks without the global Lipschitz activation functions is explored without involving the reduced order strategy. Some sufficient assertions have been obtained by using novel Lyapunov function and differential inequality. It is worth noting that the conditions adopted in this manuscript are easy to be checked with simple inequality strategy, which provides a possible approach for the investigation of dynamic behavior on other delayed neural networks with inertial terms and without the global Lipschitz activation functions.