Abstract
We introduce an automatic method for producing stateful ML programs together with proofs of correctness from monadic functions in HOL. Our mechanism supports references, exceptions, and I/O operations, and can generate functions manipulating local state, which can then be encapsulated for use in a pure context. We apply this approach to several non-trivial examples, including the instruction encoder and register allocator of the otherwise pure CakeML compiler, which now benefits from better runtime performance. This development has been carried out in the HOL4 theorem prover.
Similar content being viewed by others
1 Introduction
This paper is about bridging the gap between programs verified in logic and verified implementations of those programs in a programming language (and ultimately machine code). As a toy example, consider computing the nth Fibonacci number. The following is a recursion equation for a function,  , in higher-order logic (HOL) that does the job:
, in higher-order logic (HOL) that does the job:

A hand-written implementation (shown here in CakeML [10], which has similar syntax and semantics to Standard ML) would look something like this:

In moving from mathematics to a real implementation, some issues are apparent:
-
(i)
We use a tail-recursive linear-time algorithm, rather than the exponential-time recursion equation.
-
(ii)
The whole program is not a pure function: it does I/O, reading its argument from the command line and printing the answer to standard output.
-
(iii)
We use exception handling to deal with malformed inputs (if the arguments do not start with a string representing a natural number, hd or s2n may raise an exception).
The first of these issues (i) can easily be handled in the realm of logical functions. We define a tail-recursive version in logic:

then produce a correctness theorem,  , with a simple inductive proof (a 5-line tactic proof in HOL4, not shown).
, with a simple inductive proof (a 5-line tactic proof in HOL4, not shown).
Now, because  is a logical function with an obvious computational counterpart, we can use proof-producing synthesis techniques [14] to automatically synthesise code verified to compute it. We thereby produce something like the first line of the CakeML code above, along with a theorem relating the semantics of the synthesised code back to the function in logic.
is a logical function with an obvious computational counterpart, we can use proof-producing synthesis techniques [14] to automatically synthesise code verified to compute it. We thereby produce something like the first line of the CakeML code above, along with a theorem relating the semantics of the synthesised code back to the function in logic.
But when it comes to handling the other two issues, (ii) and (iii), and producing and verifying the remaining three lines of CakeML code, our options are less straightforward. The first issue was easy because we were working with a shallow embedding, where one writes the program as a function in logic and proves properties about that function directly. Shallow embeddings rely on an analogy between mathematical functions and procedures in a pure functional programming language. However, effects like state, I/O, and exceptions, can stretch this analogy too far. The alternative is a deep embedding: one writes the program as an input to a formal semantics, which can accurately model computational effects, and proves properties about its execution under those semantics.
Proofs about shallow embeddings are relatively easy since they are in the native language of the theorem prover, whereas proofs about deep embeddings are filled with tedious details because of the indirection through an explicit semantics. Still, the explicit semantics make deep embeddings more realistic. An intermediate option that is suitable for the effects we are interested in—state/references, exceptions, and I/O—is to use monadic functions: one writes (shallow) functions that represent computations, aided by a composition operator (monadic bind) for stitching together effects. The monadic approach to writing effectful code in a pure language may be familiar from the Haskell language which made it popular.
For our nth Fibonacci example, we can model the effects of the whole program with a monadic function,  , that calls the pure function
, that calls the pure function  to do the calculation. Figure 1 shows how
to do the calculation. Figure 1 shows how  can be written using
can be written using  -notation familiar from Haskell. This is as close as we can get to capturing the effectful behaviour of the desired CakeML program while remaining in a shallow embedding. Now how can we produce real code along with a proof that it has the correct semantics? If we use the proof-producing synthesis techniques mentioned above [14], we produce pure CakeML code that exposes the monadic plumbing in an explicit state-passing style. But we would prefer verified effectful code that uses native features of the target language (CakeML) to implement the monadic effects.
-notation familiar from Haskell. This is as close as we can get to capturing the effectful behaviour of the desired CakeML program while remaining in a shallow embedding. Now how can we produce real code along with a proof that it has the correct semantics? If we use the proof-producing synthesis techniques mentioned above [14], we produce pure CakeML code that exposes the monadic plumbing in an explicit state-passing style. But we would prefer verified effectful code that uses native features of the target language (CakeML) to implement the monadic effects.

In this paper, we present an automated technique for producing verified effectful code that handles I/O, exceptions, and other issues arising in the move from mathematics to real implementations. Our technique systematically establishes a connection between shallowly embedded functions in HOL with monadic effects and deeply embedded programs in the impure functional language CakeML. The synthesised code is efficient insofar as it uses the native effects of the target language and is close to what a real implementer would write. For example, given the monadic  function above, our technique produces essentially the same CakeML program as on the first page (but with a let for every monad bind), together with a proof that the synthesised program is a refinement.
function above, our technique produces essentially the same CakeML program as on the first page (but with a let for every monad bind), together with a proof that the synthesised program is a refinement.
Contributions. Our technique for producing verified effectful code from monadic functions builds on a previous limited approach [14]. The new generalised method adds support for the following features:
-
global references and exceptions (as before, but generalised),
-
mutable arrays (both fixed and variable size),
-
input/output (I/O) effects,
-
local mutable arrays and references, which can be integrated seamlessly with code synthesis for otherwise pure functions,
-
composable effects, whereby different state and exception monads can be combined using a lifting operator, and,
-
support for recursive programs where termination depends on monadic state.
As a result, we can now write whole programs as shallow embeddings and obtain real verified code via synthesis. Prior to this work, whole program verification in CakeML involved manual deep embedding proofs for (at the very least) the I/O wrapper. To exercise our toolchain, we apply it to several examples:
-
the nth Fibonacci example already seen (exceptions, I/O)
-
the Floyd Warshall algorithm for finding shortest paths (arrays)
-
an in-place quicksort algorithm (polymorphic local arrays, exceptions)
-
the instruction encoder in the CakeML compiler’s assembler (local arrays)
-
the CakeML compiler’s register allocator (local refs, arrays)
-
the Candle theorem prover’s kernel [9] (global refs, exceptions)
-
an OpenTheory [8] article checker (global refs, exceptions, I/O)
In Sect. 6, we compare runtimes with the previous non-stateful versions of CakeML’s register allocator and instruction encoder; and for the OpenTheory reader we compare the amount of code/proof required before and after using our technique.
The HOL4 development is at https://code.cakeml.org; our new synthesis tool is at https://code.cakeml.org/tree/master/translator/monadic.
Additions. This paper is an extended version of our earlier conference paper [6]. The following contributions are new to this work: a brief discussion of how polymorphic functions that use type variables in their local state can be synthesized (Sect. 4), a section on synthesis of recursive programs where termination depends on the monadic state (Sect. 5), and new case studies using our tool, e.g., quicksort with polymorphic local arrays (Sect. 4), and the CakeML compiler’s instruction encoder (Sect. 6).
2 High-Level Ideas
This paper combines the following three concepts in order to deliver the contributions listed above. The main ideas will be described briefly in this section, while subsequent sections will provide details. The three concepts are:
-
(i)
synthesis of stateful ML code as described in our previous work [14],
-
(ii)
separation logic [16] as used by characteristic formulae for CakeML [5], and
-
(iii)
a new abstract synthesis mode for the CakeML synthesis tools [14].
Our previous work on proof-producing synthesis of stateful ML (i) was severely limited by the requirement to have a hard-coded invariant on the program’s state. There was no support for I/O and all references had to be declared globally. At the time of its development, we did not have a satisfactory way of generalising the hard-coded state invariant.
In this paper we show (in Sect. 3) that the separation logic of CF (2) can be used to neatly generalise the hard-coded state invariant of our prior work (i). CF-style separation logic easily supports references and arrays, including resizable arrays, and, supports I/O too because it allows us to treat I/O components as if they are heap components. Furthermore, by carefully designing the integration of (i) and (2), we retain the frame rule from the separation logic. In the context of code synthesis, this frame rule allows us to implement a lifting feature for changing the type of the state-and-exception monads. Being able to change types in the monads allows us to develop reusable libraries—e.g. verified file I/O functions—that users can lift into the monad that is appropriate for their application.
The combination of (i) and (2) does not by itself support synthesis of code with local state due to inherited limitations of (i), wherein the generated code must be produced as a concrete list of global declarations. For example, if monadic functions, say  and
and  , refer to a common reference, say r, then r must be defined globally:
, refer to a common reference, say r, then r must be defined globally:

In this paper (in Sect. 4), we introduce a new abstract synthesis mode (3) which removes the requirement of generating code that only consists of a list of global declarations, and, as a result, we are now able to synthesise code such as the following, where the reference r is a local variable:

In the input to the synthesis tool, this declaration and initialisation of local state corresponds to applying the state-and-exception monad. Expressions that fully apply the state-and-exception monad can subsequently be used in the synthesis of pure CakeML code: the monadic synthesis tool can prove a pure specification for such expressions, thereby encapsulating the monadic features.
3 Generalised Approach to Synthesis of Stateful ML Code
This section describes how our previous approach to proof-producing synthesis of stateful ML code [14] has been generalised. In particular, we explain how the separation logic from our previous work on characteristic formulae [5] has been used for the generalisation (Sect. 3.3); and how this new approach adds support for user-defined references, fixed- and variable-length arrays, I/O functions (Sect. 3.4), and a handy feature for reusing state-and-exception monads (Sect. 3.5).
In order to make this paper as self-contained as possible, we start with a brief look at how the semantics of CakeML is defined (Sect. 3.1) and how our previous work on synthesis of pure CakeML code works (Sect. 3.2), since the new synthesis method for stateful code is an evolution of the original approach for pure code.
3.1 Preliminaries: CakeML Semantics
The semantics of the CakeML language is defined in the functional big-step style [15], which means that the semantics is an interpreter defined as a functional program in the logic of a theorem prover.
The definition of the semantics is layered. At the top-level the  function defines what the observable I/O events are for a given whole program. However, more relevant to the presentation in this paper is the next layer down: a function called
function defines what the observable I/O events are for a given whole program. However, more relevant to the presentation in this paper is the next layer down: a function called  that describes exactly how expressions evaluate. The type of the
that describes exactly how expressions evaluate. The type of the  function is shown below. This function takes as arguments a state (with a type variable for the I/O environment), a value environment, and a list of expressions to evaluate. It returns a new state and a value result.
function is shown below. This function takes as arguments a state (with a type variable for the I/O environment), a value environment, and a list of expressions to evaluate. It returns a new state and a value result.

The semantics state is defined as the record type below. The fields relevant for this presentation are:  ,
,  and
and  . The
. The  field is a list of store values that acts as a mapping from reference names (list index) to reference and array values (list element). The
field is a list of store values that acts as a mapping from reference names (list index) to reference and array values (list element). The  is a logical clock for the functional big-step style. The clock allows us to prove termination of
is a logical clock for the functional big-step style. The clock allows us to prove termination of  and is, at the same time, used for reasoning about divergence. Lastly,
and is, at the same time, used for reasoning about divergence. Lastly,  is the parametrised oracle model of the foreign function interface, i.e. I/O environment.
is the parametrised oracle model of the foreign function interface, i.e. I/O environment.

A call to the function  returns one of two results:
returns one of two results:  for successfully terminating computations, and
for successfully terminating computations, and  for stuck computations.
for stuck computations.
Successful computations,  , return a list
, return a list  of CakeML values. CakeML values are modelled in the semantics using a datatype called
of CakeML values. CakeML values are modelled in the semantics using a datatype called  . This datatype includes (among other things) constructors for (mutually recursive) closures (
. This datatype includes (among other things) constructors for (mutually recursive) closures ( and
and  ), datatype constructor values (
), datatype constructor values ( ), and literal values (
), and literal values ( ) such as integers, strings, characters etc. These will be explained when needed in the rest of the paper.
) such as integers, strings, characters etc. These will be explained when needed in the rest of the paper.
Stuck computations,  , carry an error value
, carry an error value  that is one of the following. For this paper,
that is one of the following. For this paper,  is the most relevant case.
is the most relevant case.
-
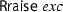 indicates that evaluation results in an uncaught exception
indicates that evaluation results in an uncaught exception  . These exceptions can be caught with a handle in CakeML.
. These exceptions can be caught with a handle in CakeML. -
 indicates that evaluation of the expression consumes all of the logical clock. Programs that hit this error for all initial values of the clock are considered diverging.
indicates that evaluation of the expression consumes all of the logical clock. Programs that hit this error for all initial values of the clock are considered diverging. -
 , for other kinds of errors, e.g. when evaluating ill-typed expressions, or attempting to access unbound variables.
, for other kinds of errors, e.g. when evaluating ill-typed expressions, or attempting to access unbound variables.
3.2 Preliminaries: Synthesis of Pure ML Code
Our previous work [14] describes a proof-producing algorithm for synthesising CakeML functions from functions in higher-order logic. Here proof-producing means that each execution proves a theorem (called a certificate theorem) guaranteeing correctness of that execution of the algorithm. In our setting, these theorems relate the CakeML semantics of the synthesised code with the given HOL function.
The whole approach is centred around a systematic way of proving theorems relating HOL functions (i.e. HOL terms) with CakeML expressions. In order for us to state relations between HOL terms and CakeML expressions, we need a way to state relations between HOL terms and CakeML values. For this we use relations ( ,
,  \(\cdot \), \(\cdot \longrightarrow \cdot \), etc.) which we call refinement invariants. The definition of the simple
\(\cdot \), \(\cdot \longrightarrow \cdot \), etc.) which we call refinement invariants. The definition of the simple  refinement invariant is shown below:
refinement invariant is shown below:  is true if CakeML value
is true if CakeML value  of type
of type  represents the HOL integer
represents the HOL integer  of type
of type  .
.

Most refinement invariants are more complicated, e.g.  states that CakeML value
states that CakeML value  represents lists of int lists
represents lists of int lists  of HOL type
of HOL type  .
.
We now turn to CakeML expressions: we define a predicate called  in order to conveniently state relationships between HOL terms and CakeML expressions. The intuition is that
in order to conveniently state relationships between HOL terms and CakeML expressions. The intuition is that  is true if
is true if  evaluates (in environment
evaluates (in environment  ) to some result
) to some result  (of HOL type
(of HOL type  ) such that
) such that  holds for
holds for  , i.e.
, i.e.  . The formal definition below is cluttered by details regarding the clock and references: there must be a large enough clock and
. The formal definition below is cluttered by details regarding the clock and references: there must be a large enough clock and  may allocate new references,
may allocate new references,  , but must not modify any existing references,
, but must not modify any existing references,  . We express this restriction on the references using list append
. We express this restriction on the references using list append  . Note that any list index that can be looked up in
. Note that any list index that can be looked up in  has the same look up in
has the same look up in  .
.

The use of  and the main idea behind the synthesis algorithm is most conveniently described using an example. The example we consider here is the following HOL function:
and the main idea behind the synthesis algorithm is most conveniently described using an example. The example we consider here is the following HOL function:

The main part of the synthesis algorithm proceeds as a syntactic bottom-up pass over the given HOL term. In this case, the bottom-up pass traverses HOL term  . The result of each stage of the pass is a theorem stated in terms of
. The result of each stage of the pass is a theorem stated in terms of  in the format shown below. Such theorems state a connection between a HOL term
in the format shown below. Such theorems state a connection between a HOL term  and some generated
and some generated  w.r.t. a refinement invariant
w.r.t. a refinement invariant  that is appropriate for the type of
that is appropriate for the type of  .
.

For our little example, the algorithm derives the following theorems for the subterms  and
and  , which are the leaves of the HOL term. Here and elsewhere in this paper, we display CakeML abstract syntax as concrete syntax inside \(\lfloor {}\cdots \rfloor {}\), i.e. \(\lfloor {}\texttt {1}\rfloor {}\) is actually the CakeML expression
, which are the leaves of the HOL term. Here and elsewhere in this paper, we display CakeML abstract syntax as concrete syntax inside \(\lfloor {}\cdots \rfloor {}\), i.e. \(\lfloor {}\texttt {1}\rfloor {}\) is actually the CakeML expression  in the theorem prover HOL4; similarly \(\lfloor {}\texttt {x}\rfloor {}\) is actually displayed as
in the theorem prover HOL4; similarly \(\lfloor {}\texttt {x}\rfloor {}\) is actually displayed as  in HOL4. Note that both theorems below are of the required general format.
in HOL4. Note that both theorems below are of the required general format.

The algorithm uses theorems (1) when proving a theorem for the compound expression  . The process is aided by an auxiliary lemma for integer addition, shown below. The synthesis algorithm is supported by several such pre-proved lemmas for various common operations.
. The process is aided by an auxiliary lemma for integer addition, shown below. The synthesis algorithm is supported by several such pre-proved lemmas for various common operations.

By choosing the right specialisations for the variables,  ,
,  ,
,  ,
,  , the algorithm derives the following theorem for the body of the running example. Here the assumption on evaluation of \(\lfloor {}\texttt {x}\rfloor {}\) was inherited from (1).
, the algorithm derives the following theorem for the body of the running example. Here the assumption on evaluation of \(\lfloor {}\texttt {x}\rfloor {}\) was inherited from (1).

Next, the algorithm needs to introduce the \(\lambda \)-binder in  . This can be done by instantiation of the following pre-proved lemma. Note that the lemma below introduces a refinement invariant for function types, \(\longrightarrow \), which combines refinement invariants for the input and output types of the function [14].
. This can be done by instantiation of the following pre-proved lemma. Note that the lemma below introduces a refinement invariant for function types, \(\longrightarrow \), which combines refinement invariants for the input and output types of the function [14].

An appropriate instantiation and combination with (2) produces the following:

which, after only minor reformulation, becomes a certificate theorem for the given HOL function  :
:

Additional notes. The main part of the synthesis algorithm is always a bottom-up traversal as described above. However, synthesis of recursive functions requires an additional post-processing phase which involves an automatic induction proof. We omit a detailed description of such induction proofs since we have described our solution previously [14]. However, we discuss our solution at a high level in Sect. 5.3 where we explain how the previously published approach has been modified to tackle monadic programs in which termination depends on the monadic state.
3.3 Synthesis of Stateful ML Code
Our algorithm for synthesis of stateful ML is very similar to the algorithm described above for synthesis of pure CakeML code. The main differences are:
-
the input HOL terms must be written in a state-and-exception monad, and
-
instead of
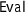 and \(\cdot \longrightarrow \cdot \), the derived theorems use
and \(\cdot \longrightarrow \cdot \), the derived theorems use  and \(\cdot \longrightarrow ^{M}\cdot \),
and \(\cdot \longrightarrow ^{M}\cdot \),
where  and \(\cdot \longrightarrow ^{M}\cdot \) relate the monad’s state to the references and foreign function interface of the underlying CakeML state (fields
and \(\cdot \longrightarrow ^{M}\cdot \) relate the monad’s state to the references and foreign function interface of the underlying CakeML state (fields  and
and  ). These concepts will be described below.
). These concepts will be described below.
Generic state-and-exception monad. The new generalised synthesis work-flow uses the following state-and-exception monad  , where
, where  is the state type,
is the state type,  is the return type, and
is the return type, and  is the exception type.
is the exception type.

We define the following interface for this monad type. Note that syntactic sugar is often used: in our case, we write  (as was done in Sect. 1) when we mean
(as was done in Sect. 1) when we mean  .
.

Functions that update the content of state can only be defined once the state type is instantiated. A function for changing a monad  to have a different state type is introduced in Sect. 3.5.
to have a different state type is introduced in Sect. 3.5.
Definitions and lemmas for synthesis. We define  as follows. A CakeML source expression
as follows. A CakeML source expression  is considered to satisfy an execution relation
is considered to satisfy an execution relation  if for any CakeML state
if for any CakeML state  , which is related by
, which is related by  to the state monad state
to the state monad state  and state assertion
and state assertion  , the CakeML expression
, the CakeML expression  evaluates to a result
evaluates to a result  such that the relation
such that the relation  accepts the transition and
accepts the transition and  holds for state assertion
holds for state assertion  . The auxiliary functions
. The auxiliary functions  and
and  will be described below. The first argument
will be described below. The first argument  can be used to restrict effects to references only, as described a few paragraphs further down.
can be used to restrict effects to references only, as described a few paragraphs further down.

In the definition above,  and
and  are used to check that the user-specified state assertion
are used to check that the user-specified state assertion  relates the CakeML states and the monad states. Furthermore,
relates the CakeML states and the monad states. Furthermore,  ensures that the separation logic frame rule is true. Both use the separation logic set-up from our previous work on characteristic formulae for CakeML [5], where we define a function
ensures that the separation logic frame rule is true. Both use the separation logic set-up from our previous work on characteristic formulae for CakeML [5], where we define a function  which, given a projection
which, given a projection  and CakeML state
and CakeML state  , turns the CakeML state into a set representation of the reference store and foreign-function interface (used for I/O).
, turns the CakeML state into a set representation of the reference store and foreign-function interface (used for I/O).
The  in the definition above is a pair
in the definition above is a pair  containing a heap assertion
containing a heap assertion  and the projection
and the projection  . We define
. We define  to state that the heap assertion produced by applying
to state that the heap assertion produced by applying  to the current monad state
to the current monad state  must be true for some subset produced by
must be true for some subset produced by  when applied to the CakeML state
when applied to the CakeML state  . Here
. Here  is the separating conjunction and
is the separating conjunction and  is true for any heap.
is true for any heap.

The relation  states: any frame
states: any frame  that is true separately from
that is true separately from  for the initial state is also true for the final state; and if the references-only
for the initial state is also true for the final state; and if the references-only  configuration is set, then the only difference in the states must be in the references and clock, i.e. no I/O operations are permitted. The
configuration is set, then the only difference in the states must be in the references and clock, i.e. no I/O operations are permitted. The  flag is instantiated to true when a pure specification (
flag is instantiated to true when a pure specification ( ) is proved for local state (Sect. 4).
) is proved for local state (Sect. 4).

We prove lemmas to aid the synthesis algorithm in construction of proofs. The lemmas shown in this paper use the following definition of  .
.

Synthesis makes use of the following two lemmas in proofs involving monadic  and
and  . For
. For  , synthesis proves an
, synthesis proves an  -theorem for
-theorem for  . For
. For  , it proves a theorem that fits the shape of the first four lines of the lemma and returns a theorem consisting of the last two lines, appropriately instantiated.
, it proves a theorem that fits the shape of the first four lines of the lemma and returns a theorem consisting of the last two lines, appropriately instantiated.

3.4 References, Arrays and I/O
The synthesis algorithm uses specialised lemmas when the generic state-and-exception monad has been instantiated. Consider the following instantiation of the monad’s state type to a record type. The programmer’s intention is that the lists are to be synthesised to arrays in CakeML and the I/O component  is a model of a file system (taken from a library).
is a model of a file system (taken from a library).

With the help of getter- and setter-functions and library functions for file I/O, users can conveniently write monadic functions that operate over this state type.
When it comes to synthesis, the automation instantiates  with an appropriate heap assertion, in this instance:
with an appropriate heap assertion, in this instance:  . The user has informed the synthesis tool that
. The user has informed the synthesis tool that  is to be a fixed-size array and
is to be a fixed-size array and  is to be a resizable-size array. A resizable-array is implemented as a reference that contains an array, since CakeML (like SML) does not directly support resizing arrays. Below,
is to be a resizable-size array. A resizable-array is implemented as a reference that contains an array, since CakeML (like SML) does not directly support resizing arrays. Below,  asserts that
asserts that  relates the value held in a reference at a fixed store location
relates the value held in a reference at a fixed store location  to the integer in
to the integer in  . Similarly,
. Similarly,  and
and  specify a connection for the array fields. Lastly,
specify a connection for the array fields. Lastly,  is a heap assertion for the file I/O taken from a library.
is a heap assertion for the file I/O taken from a library.

Automation specialises pre-proved  lemmas for each term that might be encountered in the monadic functions. As an example, a monadic function might contain an automatically defined function
lemmas for each term that might be encountered in the monadic functions. As an example, a monadic function might contain an automatically defined function  for updating array
for updating array  . Anticipating this, synthesis automation can, at set-up time, automatically derive the following lemma which it can use when it encounters
. Anticipating this, synthesis automation can, at set-up time, automatically derive the following lemma which it can use when it encounters  .
.

3.5 Combining Monad State Types
Previously developed monadic functions (e.g. from an existing library) can be used as part of a larger context, by combining state-and-exception monads with different state types. Consider the case of the file I/O in the example from above. The following  theorem has been proved in the CakeML basis library.
theorem has been proved in the CakeML basis library.

This can be used directly if the state type of the monad is the  type. However, our example above uses
type. However, our example above uses  as the state type.
as the state type.
To overcome such type mismatches, we define a function  which can bring a monadic operation defined in libraries into the required context. The type of
which can bring a monadic operation defined in libraries into the required context. The type of  is
is  , for appropriate
, for appropriate  and
and  .
.

Our  function changes the state type. A simpler lifting operation can be used to change the exception type.
function changes the state type. A simpler lifting operation can be used to change the exception type.
For our example, we define  as a function that performs
as a function that performs  on the
on the  -part of a
-part of a  . (The
. (The  example in Sect. 1 used a similar
example in Sect. 1 used a similar  .)
.)

Our synthesis mechanism automatically derives a lemma that can transfer any  result for the file I/O model to a similar
result for the file I/O model to a similar  result wrapped in the
result wrapped in the  function. Such lemmas are possible because of the separation logic frame rule that is part of
function. Such lemmas are possible because of the separation logic frame rule that is part of  . The generic lemma is the following:
. The generic lemma is the following:

And the following is the transferred lemma, which enables synthesis of HOL terms of the form  for
for  -synthesisable
-synthesisable  .
.

Changing the monad state type comes at no additional cost to the user; our tool is able to derive both the generic and transferred  lemmas, when provided with the original
lemmas, when provided with the original  result.
result.
4 Local State and the Abstract Synthesis Mode
This section explains how we have adapted the method described above to also support generation of code that uses local state and local exceptions. These features enable use of stateful code ( ) in a pure context (
) in a pure context ( ). We used these features to significantly speed up parts of the CakeML compiler (see Sect. 6).
). We used these features to significantly speed up parts of the CakeML compiler (see Sect. 6).
In the monadic functions, users indicate that they want local state to be generated by using the following  function. In the logic, the
function. In the logic, the  function essentially just applies a monadic function
function essentially just applies a monadic function  to an explicitly provided state
to an explicitly provided state  .
.

In the generated code, an application of  to a concrete monadic function, say
to a concrete monadic function, say  , results in code of the following form:
, results in code of the following form:

Synthesis of locally effectful code is made complicated in our setting for two reasons: (i) there are no fixed locations where the references and arrays are stored, e.g. we cannot define  as used in the definition of
as used in the definition of  in Sect. 3.4; and (ii) the local names of state components must be in scope for all of the function definitions that depend on local state.
in Sect. 3.4; and (ii) the local names of state components must be in scope for all of the function definitions that depend on local state.
Our solution to challenge (i) is to leave the location values as variables ( ,
,  ,
,  ) in the heap assertion when synthesising local state. To illustrate, we will adapt the
) in the heap assertion when synthesising local state. To illustrate, we will adapt the  from Sect. 3.4: we omit
from Sect. 3.4: we omit  in the state because I/O cannot be made local. The local-state enabled heap assertion is:
in the state because I/O cannot be made local. The local-state enabled heap assertion is:

The lemmas referring to local state now assume they can find the right variable locations with variable look-ups.

Challenge (ii) was caused by technical details of our previous synthesis methods. The previous version was set up to only produce top-level declarations, which is incompatible with the requirement to have local (not globally fixed) state declarations shared between several functions. The requirement to only have top-level declarations arose from our desire to keep things simple: each synthesised function is attached to the end of a concrete linear program that is being built. It is beneficial to be concrete because then each assumption on the lexical environment where the function is defined can be proved immediately on definition. We will call this old approach the concrete mode of synthesis, since it eagerly builds a concrete program.
In order to support having functions access local state, we implement a new abstract mode of synthesis. In the abstract mode, each assumption on the lexical environment is left as an unproved side condition as long as possible. This allows us to define functions in a dynamic environment.
To prove a pure specification ( ) from the
) from the  theorems, the automation first proves that the generated state-allocation and -initialisation code establishes the relevant heap assertion (e.g.
theorems, the automation first proves that the generated state-allocation and -initialisation code establishes the relevant heap assertion (e.g.  ); it then composes the abstractly synthesised code while proving the environment-related side conditions (e.g. presence of
); it then composes the abstractly synthesised code while proving the environment-related side conditions (e.g. presence of  ). The final proof of an
). The final proof of an  theorem requires instantiating the references-only
theorem requires instantiating the references-only  flag to true, in order to know that no I/O occurs (Sect. 3.3).
flag to true, in order to know that no I/O occurs (Sect. 3.3).
4.1 Type Variables in Local Monadic State
Our previous approach [14] allowed synthesis of (pure) polymorphic functions. Our new mechanism is able to support the same level of generality by permitting type variables in the type of monadic state that is used locally. As an example, consider a monadic implementation of an in-place quicksort algorithm,  , with the following type signature:
, with the following type signature:

The function  takes a list of values of type
takes a list of values of type  and an ordering on
and an ordering on  as input, producing a sorted list as output. However, internally it copies the input list into a mutable array in order to perform fast in-place random accesses.
as input, producing a sorted list as output. However, internally it copies the input list into a mutable array in order to perform fast in-place random accesses.
The heap assertion for  is called
is called  , and is defined below:
, and is defined below:

Here,  is a refinement invariant for logical values of type
is a refinement invariant for logical values of type  . This parametrisation over state type variables is similar to the way in which location values were parametrised to solve challenge (i) above.
. This parametrisation over state type variables is similar to the way in which location values were parametrised to solve challenge (i) above.
Applying  to
to  , and synthesising CakeML from the result gives the following certificate theorem which makes the stateful
, and synthesising CakeML from the result gives the following certificate theorem which makes the stateful  callable from pure translations.
callable from pure translations.

Here  is the refinement invariant for type
is the refinement invariant for type  .
.
For the quicksort example, we have manually proved that  will always return a
will always return a  value, provided the comparison function orders values of type
value, provided the comparison function orders values of type  . The result of this effort is CakeML code for
. The result of this effort is CakeML code for  that uses state internally, but can be used as if it is a completely pure function without any use of state or exceptions.
that uses state internally, but can be used as if it is a completely pure function without any use of state or exceptions.
5 Termination That Depends on Monadic State
In this section, we describe how the proof-producing synthesis method in Sect. 3 has been extended to deal with a class of recursive monadic functions whose termination depends on the state hidden in the monad. This class of functions creates new difficulties, as (i) the HOL4 function definition system is unable to prove termination of these functions; and, (ii) our synthesis method relies on induction theorems produced by the definition system to discharge preconditions during synthesis.
We address issue (i) by extending the HOL4 definition system with a set of congruence rewrites for the monadic bind operation,  (Sect. 5.2). We then explain, at a high level, how the proof-producing synthesis in Sect. 3 is extended to deal with the preconditions that arise when synthesising code from recursive monadic functions (Sect. 5.3).
(Sect. 5.2). We then explain, at a high level, how the proof-producing synthesis in Sect. 3 is extended to deal with the preconditions that arise when synthesising code from recursive monadic functions (Sect. 5.3).
We begin with a brief overview of how recursive function definitions are handled by the HOL4 function definition system (Sect. 5.1).
5.1 Preliminaries: Function Definitions in HOL4
In order to accept recursive function definitions, the HOL4 system requires a well-founded relation to be found between the arguments of the function, and those of recursive applications. The system automatically extracts conditions that this relation must satisfy, attempts to guess a well-founded relation based on these conditions, and then uses this relation to solve the termination goal.
Function definitions involving higher-order functions (e.g.  ) sometimes causes the system to derive unprovable termination conditions, if it cannot extract enough information about recursive applications. When this occurs, the user must provide a congruence theorem that specifies the context of the higher-order function. The system uses this theorem to derive correct termination conditions, by rewriting recursive applications.
) sometimes causes the system to derive unprovable termination conditions, if it cannot extract enough information about recursive applications. When this occurs, the user must provide a congruence theorem that specifies the context of the higher-order function. The system uses this theorem to derive correct termination conditions, by rewriting recursive applications.
5.2 Termination of Recursive Monadic Functions
By default, the HOL4 system is unable to automatically prove termination of recursive monadic functions involving  . To aid the system in extracting provable termination conditions, we introduce the following congruence theorem for
. To aid the system in extracting provable termination conditions, we introduce the following congruence theorem for  :
:

Theorem (3) expresses a rewrite of the term  in terms of rewrites involving its component subterms (
in terms of rewrites involving its component subterms ( ,
,  , and
, and  ), but allows for the assumption that
), but allows for the assumption that  (the rewritten effect) must execute successfully.
(the rewritten effect) must execute successfully.
However, rewriting definitions with (3) is not always sufficient: in addition to ensuring that the effect  in
in  executed successfully, the HOL4 system must also know the value and state resulting from its execution. This problem arises because the monadic state argument to
executed successfully, the HOL4 system must also know the value and state resulting from its execution. This problem arises because the monadic state argument to  is left implicit in user definitions. We address this issue by rewriting the defining equations of monadic functions using \(\eta \)-expansion before passing them to the definition system, making all partial
is left implicit in user definitions. We address this issue by rewriting the defining equations of monadic functions using \(\eta \)-expansion before passing them to the definition system, making all partial  applications syntactically fully applied. The whole process is automated so that it is opaque to the user, allowing definition of recursive monadic functions with no additional effort.
applications syntactically fully applied. The whole process is automated so that it is opaque to the user, allowing definition of recursive monadic functions with no additional effort.
5.3 Synthesising ML from Recursive Monadic Functions
The proof-producing synthesis method described in Sect. 3.2 is syntax-directed and proceeds in a bottom-up manner. For recursive functions, a tweak to this strategy is required, as bottom-up traversal would require any recursive calls to be treated before the calling function (this is clearly cyclic).
We begin with a brief explanation of how our previous (pure) synthesis tool [14] tackles recursive functions, before outlining how our new approach builds on this.
Pure recursive functions. As an example, consider the function  that computes the greatest common divisor of two positive integers:
that computes the greatest common divisor of two positive integers:

Before traversing the function body of  in a bottom-up manner, we simply assume the desired
in a bottom-up manner, we simply assume the desired  result to hold for all recursive applications in the function definition, and record their arguments during synthesis. This results in the following
result to hold for all recursive applications in the function definition, and record their arguments during synthesis. This results in the following  theorem for
theorem for  (where
(where  is defined as
is defined as  ), and is used to record arguments for recursive applications):
), and is used to record arguments for recursive applications):

and below is the desired  result for
result for  :
:

Theorems (4) and (5) match the shape of the hypothesis and conclusion (respectively) of the induction theorem for  :
:

By instantiating this induction theorem appropriately, the preconditions in (4) can be discharged (and if automatic proof fails, the goal is left for the user to prove).
Monadic recursive functions. Function definitions whose termination depends on the monad give rise to induction theorems which also depend on the monad. This creates issues, as the monad argument is left implicit in the definition. As an example, here is a function  that searches through an array for a value:
that searches through an array for a value:

When given the above definition, the HOL4 system automatically derives the following induction theorem:

The context of recursive applications ( and
and  ) has been extracted correctly by HOL4, using the congruence theorem (3) and automated \(\eta \)-expansion for
) has been extracted correctly by HOL4, using the congruence theorem (3) and automated \(\eta \)-expansion for  (see Sect. 5.2).
(see Sect. 5.2).
However, there is now a mismatch between the desired form of the  result and the conclusion of the induction theorem: the latter depends explictly on the state, but the function depends on it only implicitly. We have modified our synthesis tool to account for this, in order to correctly discharge the necessary preconditions as above. When preconditions cannot be automatically discharged, they are left as proof obligations to the user, and the partial results derived are saved in the HOL4 theorem database.
result and the conclusion of the induction theorem: the latter depends explictly on the state, but the function depends on it only implicitly. We have modified our synthesis tool to account for this, in order to correctly discharge the necessary preconditions as above. When preconditions cannot be automatically discharged, they are left as proof obligations to the user, and the partial results derived are saved in the HOL4 theorem database.
6 Case Studies and Experiments
In this section, we present the runtime and proof size results of applying our method to some case studies.
Register Allocation. The CakeML compiler’s register allocator is written with a state (and exception) monad but it was previously synthesized to pure CakeML code. We updated it to use the new synthesis tool, resulting in the automatic generation of stateful CakeML code. The allocator benefits significantly from this change because it can now make use of CakeML arrays via the synthesis tool. It was previously confined to using tree-like functional arrays for its internal state, leading to logarithmic access overheads. This is not a specific issue for the CakeML compiler; a verified register allocator for CompCert [3] also reported log-factor overheads due to (functional) array accesses.
Tests were carried out using versions of the bootstrapped CakeML compiler. We ran each test 50 times on the same input program, recording time elapsed in each compiler phase. For each test, we also compared the resulting executables 10 times, to confirm that both compilers generated code of comparable quality (i.e. runtime performance). Performance experiments were carried out on an Intel i7-2600 running at 3.4GHz with 16 GB of RAM. The results are summarized in Table 1. Full data is available at https://cakeml.org/ijcar18.zip.Footnote 1
In the largest program (Knuth–Bendix), the new register allocator ran 15 times faster (with a wide 95% CI of 11.76–20.93 due in turn to a high standard deviation on the runtimes for the old code). In the smaller pidigits benchmark, the new register allocator ran 9.01 times faster (95% CI of 9.01–9.02). Across 6 example input programs, we saw ratios of runtimes between 7.58 and 15.06. Register allocation was previously such a significant part of the compiler runtime that this improvement results in runtime improvements for the whole compiler (on these benchmark programs) of factors between 2 and 9 times.
Speeding up the CakeML compiler. The register allocator exemplifies one way the synthesis tool can be used to improve existing, verified CakeML programs and in particular, the CakeML compiler itself. Briefly, the steps are: (i) re-implement slow parts of the compiler with, e.g., an appropriate state monad, (ii) verify that this new implementation produces the same result as the existing (verified) implementation, (iii) swap in the new implementation, which synthesizes to stateful code, during the bootstrap of the CakeML compiler. (iv) The preceeding steps can be repeated as desired, relying on the automated synthesis tool for quick iteration.
As another example, we used the synthesis tool to improve the assembly phase of the compiler. A major part of time spent in this phase is running the instruction encoder, which performs several word arithmetic operations when it computes the byte-level representation of each instruction. However, duplicate instructions appear very frequently, so we implemented a cache of the byte-level representations backed by a hash table represented as a state monad (i). This caching implementation is then verified (ii), before a verified implementation is synthesized where the hash table is implemented as an array (iii). We also iterated through several candidate hash functions (iv). Overall, this change took about 1-person week to implement, verify, and integrate in the CakeML compiler. We benchmarked the cross-compile bootstrap times of the CakeML compiler after this change to measure its impact across different CakeML compilation targets. Results are summarized in Table 2. Across compilation targets, the assembly phase is between 1.25 to 1.64 times faster.
OpenTheory Article Checker. The type changing feature from Sect. 3.5 enabled us to produce an OpenTheory [8] article checker with our new synthesis approach, and reduce the amount of manual proof required in a previous version. The checker reads articles from the file system, and performs each logical inference in the OpenTheory framework using the verified Candle kernel [9]. Previously, the I/O code for the checker was implemented in stateful CakeML, and verified manually using characteristic formulae. By replacing the manually verified I/O wrapper by monadic code we removed 400 lines of tedious manual proof.
7 Related Work
Effectful code using monads. Our work on encapsulating stateful computations (Sect. 4) in pure programs is similar in purpose to that of the ST monad [12]. The main difference is how this encapsulation is performed: the ST monad relies on parametric polymorphism to prevent references from escaping their scope, whereas we utilise lexical scoping in synthesised code to achieve a similar effect.
Imperative HOL by Bulwahn et al. [4] is a framework for implementing and reasoning about effectful programs in Isabelle/HOL. Monadic functions are used to describe stateful computations which act on the heap, in a similar way as Sect. 3 but with some important differences. Instead of using a state monad, the authors introduce a polymorphic heap monad—similar in spirit to the ST monad, but without encapsulation—where polymorphism is achieved by mapping HOL types to the natural numbers. Contrary to our approach, this allows for heap elements (e.g. references) to be declared on-the-fly and used as first-class values. The drawback, however, is that only countable types can be stored on the heap; in particular, the heap monad does not admit function-typed values, which our work supports.
More recently, Lammich [11] has built a framework for the refinement of pure data structures into imperative counterparts, in Imperative HOL. The refinement process is automated, and refinements are verified using a program logic based on separation logic, which comes with proof-tools to aid the user in verification.
Both developments [4, 11] differ from ours in that they lack a verified mechanism for extracting executable code from shallow embeddings. Although stateful computations are implemented and verified within the confines of higher-order logic, Imperative HOL relies on the unverified code-generation mechanisms of Isabelle/HOL. Moreover, neither work presents a way to deal with I/O effects.
Verified Compilation. Mechanisms for synthesising programs from shallow embeddings defined in the logics of interactive theorem provers exist as components of several verified compiler projects [1, 7, 13, 14]. Although the main contribution of our work is proof-producing synthesis, comparisons are relevant as our synthesis tool plays an important part in the CakeML compiler [10]. To the best of our knowledge, ours is the first work combining effectful computations with proof-producing synthesis and fully verified compilation.
CertiCoq by Anand et al. [1] strives to be a fully verified optimising compiler for functional programs implemented in Coq. The compiler front-end supports the full syntax of the dependently typed logic Gallina, which is reified into a deep embedding and compiled to Cminor through a series of verified compilation steps [1]. Contrary to the approach we have taken [14] (see Sect. 3.2), this reification is neither verified nor proof-producing, and the resulting embedding has no formal semantics (although there are attempts to resolve this issue [2]). Moreover, as of yet, no support exists for expressing effectful computations (such as in Sect. 3.4) in the logic. Instead, effects are deferred to wrapper code from which the compiled functions can be called, and this wrapper code must be manually verified.
The Œuf compiler by Mullen et al. [13] is similar in spirit to CertiCoq in that it compiles pure Coq functions to Cminor through a verified process. Similarly, compiled functions are pure, and effects must be performed by wrapper code. Unlike CertiCoq, Œuf supports only a limited subset of Gallina, from which it synthesises deeply embedded functions in the Œuf-language. The Œuf language has both denotational and operational semantics, and the resulting syntax is automatically proven equivalent with the corresponding logical functions through a process of computational denotation [13].
Hupel and Nipkow [7] have developed a compiler from Isabelle/HOL to CakeML AST. The compiler satisfies a partial correctness guarantee: if the generated CakeML code terminates, then the result of execution is guaranteed to relate to an equality in HOL. Our approach proves termination of the code.
8 Conclusion
This paper describes a technique that makes it possible to synthesise whole programs from monadic functions in HOL, with automatic proofs relating the generated effectful code to the original functions. Using the separation logic from characteristic formulae for CakeML, the synthesis mechanism supports references, exceptions, I/O, reusable library developments, encapsulation of locally stateful computations inside pure functions, and code generation for functions where termination depends on state. To our knowledge, this is the first proof-producing synthesis technique with the aforementioned features.
We hope that the techniques developed in this paper will allow users of the CakeML tools to develop verified code using only shallow embeddings. We hope that only expert users, who develop libraries, will need to delve into manual reasoning in CF or direct reasoning about deeply embedded CakeML programs.
Notes
These tests were performed for the earlier conference version of this paper [6] comparing two earlier versions of the CakeML compiler. The compiler has changed significantly since then but we have we kept these experiments because they provide a fairer comparison of register allocation performance with/without using the synthesis tool to generate stateful code.
References
Anand, A., Appel, A., Morrisett, G., Paraskevopoulou, Z., Pollack, R., Belanger, O.S., Sozeau, M., Weaver, M.: CertiCoq: a verified compiler for Coq. In: CoqPL (2017)
Anand, A., Boulier, S., Tabareau, N., Sozeau, M.: Typed template Coq—certified meta-programming in Coq. In: CoqPL (2018)
Blazy, S., Robillard, B., Appel, A.W.: Formal verification of coalescing graph-coloring register allocation. In: ESOP, Volume 6012 of LNCS (2010)
Bulwahn, L., Krauss, A., Haftmann, F., Erkök, L., Matthews, J.: Imperative functional programming with Isabelle/HOL. In: Mohamed, O.A., Muñoz, C.A., Tahar, S. (eds.) TPHOLs, Volume 5170 of LNCS, pp. 134–149 (2008)
Guéneau, A., Myreen, M.O., Kumar, R., Norrish, M.L.: Verified characteristic formulae for CakeML. In: Yang, H. (ed.) ESOP, Volume 10201 of LNCS, pp. 584–610 (2017)
Ho, S., Abrahamsson, O., Kumar, R., Myreen, M.O., Tan, Y.K., Norrish, M.: Proof-producing synthesis of CakeML with I/O and local state from monadic HOL functions. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR, pp. 646–662 (2018)
Hupel, L., Nipkow, T.: A verified compiler from Isabelle/HOL to CakeML. In: Ahmed, A. (ed.) European Symposium on Programming (ESOP). Springer, Berlin (2018)
Hurd, J.: The OpenTheory standard theory library. In: Bobaru, M.G., Havelund, K., Holzmann, G.J., Joshi, R. (eds.) NFM, Volume 6617 of LNCS, pp. 177–191 (2011)
Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: Self-formalisation of higher-order logic-semantics, soundness, and a verified implementation. J. Autom. Reason. 56(3), 221–259 (2016)
Kumar, R., Myreen, M.O., Norrish, M., Owens, S.: CakeML: a verified implementation of ML. In: Suresh, J., Sewell, P. (eds.) POPL, pp. 179–192 (2014)
Lammich, P.: Refinement to Imperative/HOL. In: ITP, Volume 9236 of LNCS (2015)
Launchbury, J., Peyton Jones, S.L.: Lazy functional state threads. In: Sarkar, V., Ryder, B.G., Soffa, M.L. (eds.) PLDI, pp. 24–35 (1994)
Mullen, E., Pernsteiner, S., Wilcox, J.R., Tatlock, Z., Grossman, D.: Œuf: minimizing the Coq extraction TCB. In: CPP (2018)
Myreen, M.O., Owens, S.: Proof-producing translation of higher-order logic into pure and stateful ML. J. Funct. Program. 24(2–3), 284–315 (2014)
Owens, S., Myreen, M.O., Kumar, R., Tan, Y.K.: Functional big-step semantics. In: Thiemann, P. (ed.) ESOP, Volume 9632 of LNCS, pp. 589–615 (2016)
Reynolds, J.C.: Separation logic: a logic for shared mutable data structures. In: LICS, pp. 55–74 (2002)
Acknowledgements
Open access funding provided by Chalmers University of Technology. The first and fifth authors were partly supported by the Swedish Foundation for Strategic Research. The seventh author was supported by an A*STAR National Science Scholarship (Ph.D.), Singapore. The third author was supported by the UK Research Institute in Verified Trustworthy Software Systems (VeTSS).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abrahamsson, O., Ho, S., Kanabar, H. et al. Proof-Producing Synthesis of CakeML from Monadic HOL Functions. J Autom Reasoning 64, 1287–1306 (2020). https://doi.org/10.1007/s10817-020-09559-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-020-09559-8





 -notation in logic
-notation in logic indicates that evaluation results in an uncaught exception
indicates that evaluation results in an uncaught exception  . These exceptions can be caught with a
. These exceptions can be caught with a  indicates that evaluation of the expression consumes all of the logical clock. Programs that hit this error for all initial values of the clock are considered diverging.
indicates that evaluation of the expression consumes all of the logical clock. Programs that hit this error for all initial values of the clock are considered diverging. , for other kinds of errors, e.g. when evaluating ill-typed expressions, or attempting to access unbound variables.
, for other kinds of errors, e.g. when evaluating ill-typed expressions, or attempting to access unbound variables. and
and  and
and