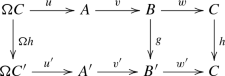$d\mathbb {Z}$-Cluster tilting subcategories of singularity categories

Abstract

For an exact category ${{\mathcal {E}}}$ with enough projectives and with a $d\mathbb {Z}$-cluster tilting subcategory, we show that the singularity category of ${{\mathcal {E}}}$ admits a $d\mathbb {Z}$-cluster tilting subcategory. To do this we introduce cluster tilting subcategories of left triangulated categories, and we show that there is a correspondence between cluster tilting subcategories of ${{\mathcal {E}}}$ and ${\underline{{{\mathcal {E}}}}}$. We also deduce that the Gorenstein projectives of ${{\mathcal {E}}}$ admit a $d\mathbb {Z}$-cluster tilting subcategory under some assumptions. Finally, we compute the $d\mathbb {Z}$-cluster tilting subcategory of the singularity category for a finite-dimensional algebra which is not Iwanaga–Gorenstein.

1 Introduction

Auslander–Reiten theory is a fundamental tool to describe the module category of finite-dimensional algebras, see [7] and [4, 44, 45]. A generalization of this theory, called higher Auslander–Reiten theory, was introduced by Iyama in [25] and further developed in [24, 27]. In this case, the objects of study are module categories equipped with a d-cluster tilting subcategory. We refer to [2, 16, 21,22,23, 29,30,31,32,33, 35, 37] for some other important papers. Also, see [26] for a survey of the theory and [36] for an introduction.

Let $\Lambda$ be a finite-dimensional algebra and let ${\text {mod}}\Lambda$ be the category of finitely generated right $\Lambda$-modules. Assume $\Lambda$ has global dimension d. If ${{\mathcal {M}}}$ is a d-cluster tilting subcategory in ${\text {mod}}\Lambda$ then the subcategory

$$\begin{aligned} {{\mathcal {U}}}= {\text {add}}\{M[di]\in D^b({\text {mod}}\Lambda ) \mid M\in {{\mathcal {M}}}\text { and }i\in \mathbb {Z}\} \end{aligned}$$

is d-cluster tilting inside the bounded derived category $D^b({\text {mod}}\Lambda )$ [27, Theorem 1.21] (this can be extended to $\tau _d$-finite algebras [27, Theorem 1.23] and cluster categories [1, Theorem 4.10] and [17, Theorem 2.2]). The subcategory ${{\mathcal {U}}}$ can be considered as a higher analogue of the derived category of a hereditary algebra. On the other hand, if $\Lambda$ does not have global dimension d, then there is no known cluster tilting subcategory inside $D^b({\text {mod}}\Lambda )$ in general. As shown in [34], the naive approach doesn’t necessarily give a cluster tilting subcategory even when ${{\mathcal {M}}}$ is $d\mathbb {Z}$-cluster tilting.

In this paper we consider instead the singularity category

$$\begin{aligned} D_{{\text {sing}}}(\Lambda ):=K^{-,b}({\text {proj}} \Lambda )/K^b({\text {proj}} \Lambda ) \end{aligned}$$

where $K^b({\text {proj}} \Lambda )$ and $K^{-,b}({\text {proj}} \Lambda )$ denote the bounded homotopy category of finitely generated projective modules and the right bounded homotopy category with bounded homology of finitely generated projective modules, respectively. The singularity category was introduced by Buchweitz in [11] as an useful invariant of the ring $\Lambda$. Via the equivalence $K^{-,b}({\text {proj}} \Lambda )\cong D^b({\text {mod}}\Lambda )$ we get an equivalence

$$\begin{aligned} K^{-,b}({\text {proj}} \Lambda )/K^b({\text {proj}} \Lambda )\cong D^b({\text {mod}}\Lambda )/{\text {perf}} \Lambda \end{aligned}$$

(1.1)

and hence $D_{{\text {sing}}}(\Lambda )$ can be realized as a quotient of $D^b({\text {mod}}\Lambda )$. We show that if ${\text {mod}}\Lambda$ has a $d\mathbb {Z}$-cluster tilting subcategory, then $D_{{\text {sing}}}(\Lambda )$ has a $d\mathbb {Z}$-cluster tilting subcategory. In fact, we show this more generally for any exact category with enough projectives.

Theorem 1.2

Let ${{\mathcal {E}}}$ be an exact category with enough projectives ${{\mathcal {P}}}$ and with a $d\mathbb {Z}$-cluster tilting subcategory ${{\mathcal {M}}}$. Then the subcategory

$$\begin{aligned} \{P^{\bullet }\in K^{-,b}({{\mathcal {P}}})/K^b({{\mathcal {P}}}) \mid Z^{di}(P^{\bullet })\in {{\mathcal {M}}}\text { for all } i\ll 0\} \end{aligned}$$

is a $d\mathbb {Z}$-cluster tilting subcategory of $K^{-,b}({{\mathcal {P}}})/K^b({{\mathcal {P}}})$.

Via the equivalence (1.1) this corresponds to the subcategory

$$\begin{aligned} \{C^{\bullet }\in D^b({\text {mod}}\Lambda )/{\text {perf}} \Lambda \mid C^{\bullet }\cong M[di] \text { for some } M\in {{\mathcal {M}}}\text { and } i\in \mathbb {Z}\} \end{aligned}$$

in $D^b({\text {mod}}\Lambda )/{\text {perf}}\Lambda$. Notice that this subcategory is closed under direct sums since any object in $D^b({\text {mod}}\Lambda )/{\text {perf}}\Lambda$ is isomorphic to a stalk complex. There are many examples of d-cluster tilting subcategories of singularity categories of Iwanaga–Gorenstein rings, see [28], but Theorem 1.2 is the first result for non-Iwanaga–Gorenstein rings. For such rings the singularity category is more difficult to control since it is not enhanced by the Gorenstein projective modules. However, it is still possible to compute the subcategory explicitly, which we do in Example 8.4.

To prove Theorem 1.2, we use the left triangulated structure of ${\underline{{{\mathcal {E}}}}}$, see Definition 3.1 and Theorem 3.2. More precisely, we introduce d-cluster tilting subcategories of left triangulated categories, and we show that there is a one-to-one correspondence between d and $d\mathbb {Z}$-cluster tilting subcategories of ${{\mathcal {E}}}$ and ${\underline{{{\mathcal {E}}}}}$, see Theorem 6.1. Furthermore, we show that if a left triangulated category has a $d\mathbb {Z}$-cluster tilting subcategory, then its stabilization has a $d\mathbb {Z}$-cluster tilting subcategory. We then conclude using the fact that the stabilization of ${\underline{{{\mathcal {E}}}}}$ is the singularity category, which was proved in [39].

We also obtain a corollary for Gorenstein projective modules, which we state below in the special case where ${{\mathcal {E}}}={\text {mod}}\Lambda$. Recall that $\Lambda$ is Iwanaga–Gorenstein if it has finite selfinjective dimension, and that in this case the Gorenstein projectives are

$$\begin{aligned} {{\mathcal {G}}}{{\mathcal {P}}}({\text {mod}}\Lambda ) := \{M\in {\text {mod}}\Lambda \mid {\text {Ext}}^{i}_{\Lambda }(M,\Lambda )=0 \text { for }i>0\}. \end{aligned}$$

Corollary 1.3

(Corollary 7.3) Assume $\Lambda$ is Iwanaga–Gorenstein, and let ${{\mathcal {M}}}$ be a $d\mathbb {Z}$-cluster tilting subcategory of ${\text {mod}}\Lambda$. Then

$$\begin{aligned} {{\mathcal {M}}}\cap {{\mathcal {G}}}{{\mathcal {P}}}({\text {mod}}\Lambda ) \end{aligned}$$

is a $d\mathbb {Z}$-cluster tilting subcategory of ${{\mathcal {G}}}{{\mathcal {P}}}({\text {mod}}\Lambda )$.

We now describe the structure of the paper. In Sects. 2, 3 and 4 we recall the essential notions and results which we need. In Sect. 5 we introduce cluster tilting subcategories for left triangulated categories. We show that for a left triangulated category ${{\mathcal {C}}}$ with a $d\mathbb {Z}$-cluster tilting subcategory, the stabilization $\mathbb {Z}{{\mathcal {C}}}$ has a $d\mathbb {Z}$-cluster tilting subcategory. We also investigate the $(d+2)$-angulated structure of this subcategory. Our main result in Sect. 6 is Theorem 6.1, which gives a correspondence between d-cluster tilting subcategories of ${{\mathcal {E}}}$ and ${\underline{{{\mathcal {E}}}}}$ when ${{\mathcal {E}}}$ is an exact category with enough projectives. In Sect. 7 we investigate the relationship with Gorenstein projectives. In Sect. 8 we compute the cluster tilting subcategory of the singularity category in two examples.

2 Exact categories

Here we define exact categories, following the conventions in [12].

Definition 2.1

An exact category ${{\mathcal {E}}}$ is an additive category equipped with a distinguished class of sequences

$$\begin{aligned} 0\rightarrow E_3\xrightarrow {f} E_2\xrightarrow {g}E_1\rightarrow 0 \end{aligned}$$

where f is the kernel of g and g is the cokernel of f. The morphisms f are called admissible monomorphisms, and the morphisms g are called admissible epimorphisms. The following axioms need to be satisfied:

(E0):

For all object E in ${{\mathcal {E}}}$ the identity morphism $1_E:E\rightarrow E$ is an admissible monomorphism;

(E0$^{\mathrm {op}}$):

For all object E in ${{\mathcal {E}}}$ the identity morphism $1_E:E\rightarrow E$ is an admissible epimorphism;

(E1):

The composite of two admissible monomorphism is an admissible monomorphism;

(E1$^{\mathrm {op}}$):

The composite of two admissible epimorphisms is an admissible epimorphism;

(E2):

The pushout of an admissible monomorphism exists and yields an admissible monomorphisms. In other words, given an admissible monomorphism $f:E_0\rightarrow E_1$ and a morphism $g:E_0\rightarrow E_2$ there exists a pushout diagram

where k is an admissible monomorphism;

(E2$^{\mathrm {op}}$):

The pullback of an admissible epimorphism exists and yields an admissible epimorphism. In other words, given an admissible epimorphism $f:E_1\rightarrow E_0$ and a morphism $g:E_2\rightarrow E_0$ there exists a pullback diagram

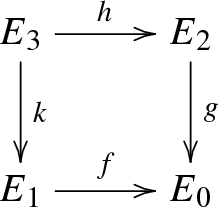
where h is an admissible epimorphism.

A sequence in ${{\mathcal {E}}}$

$$\begin{aligned} \cdots \rightarrow E_1\rightarrow E_0\rightarrow \cdots \end{aligned}$$

is called exact if there exist exact sequences $0\rightarrow K_i\rightarrow E_i\rightarrow K_{i-1}\rightarrow 0$ such that the maps $E_i\rightarrow E_{i-1}$ are equal to the composites $E_i\rightarrow K_{i-1}\rightarrow E_{i-1}$. If ${{\mathcal {E}}}$ is an exact category, then the opposite category ${{\mathcal {E}}}^{\mathrm {op}}$ becomes an exact category in a natural way. If ${{\mathcal {F}}}\subset {{\mathcal {E}}}$ is a full subcategory of ${{\mathcal {E}}}$ which is closed under extensions, then the class of sequences $0\rightarrow F_1\xrightarrow {} F_2\xrightarrow {}F_3\rightarrow 0$ in ${{\mathcal {F}}}$ which are exact in ${{\mathcal {E}}}$ makes ${{\mathcal {F}}}$ into an exact category. We say that ${{\mathcal {F}}}$ is an exact subcategory of ${{\mathcal {E}}}$.

An object P in ${{\mathcal {E}}}$ is projective if for any admissible epimorphism $E_1\rightarrow E_0$ the induced map ${{\mathcal {E}}}(P,E_1)\rightarrow {{\mathcal {E}}}(P,E_0)$ is an epimorphism. We let ${{\mathcal {P}}}$ denote the subcategory of ${{\mathcal {E}}}$ consisting of the projective objects. The exact category ${{\mathcal {E}}}$ has enough projectives if for any object E in ${{\mathcal {E}}}$ there exists an admissible epimorphism $P\rightarrow E$ with $P\in {{\mathcal {P}}}$. In this case we let ${\underline{{{\mathcal {E}}}}}={{\mathcal {E}}}/{{\mathcal {P}}}$ denote the stable category of ${{\mathcal {E}}}$ modulo projectives. For any object E or morphism f in ${{\mathcal {E}}}$ we denote the corresponding object or morphism in ${\underline{{{\mathcal {E}}}}}$ by ${\underline{E}}$ or ${\underline{f}}$. Since ${{\mathcal {E}}}$ has enough projectives, ${\underline{f}}=0$ for a morphism $f:E\rightarrow E'$ if and only if f factors through an admissible epimorphism $P\rightarrow E'$ with P projective. Using this, it follows by the same argument as in the proof of [19, Theorem 2.2] that for any two objects $E_0$ and $E_1$ in ${{\mathcal {E}}}$ there exists an isomorphism $\underline{E_1}\cong \underline{E_2}$ in ${\underline{{{\mathcal {E}}}}}$ if and only if there exist projective objects $P,Q\in {{\mathcal {E}}}$ and an isomorphism

$$\begin{aligned} E_0\oplus P\cong E_1\oplus Q \end{aligned}$$

(2.2)

in ${{\mathcal {E}}}$.

Next we define the syzygy functor:

Definition 2.3

[19] Let ${{\mathcal {E}}}$ be an exact category with enough projectives. For each object $E\in {{\mathcal {E}}}$ choose an admissible epimorphism $p_E:P_E\rightarrow E$ with $P_E$ projective. The syzygy functor $\Omega :{\underline{{{\mathcal {E}}}}}\rightarrow {\underline{{{\mathcal {E}}}}}$ is defined as follows: For an object $E\in {{\mathcal {E}}}$ we set $\Omega {\underline{E}}= \underline{{\text {Ker}}p_E}$. For a morphism $f:E_0\rightarrow E_1$ we set $\Omega ({\underline{f}})={\underline{h}}$ where $g:P_{E_0}\rightarrow P_{E_1}$ and $h:{\text {Ker}}p_{E_0}\rightarrow {\text {Ker}}p_{E_1}$ are morphisms in ${{\mathcal {E}}}$ making the diagram

commutative.

Note that $\Omega ({\underline{f}})$ is independent of the choice of morphisms g and h, and up to isomorphism the syzygy functor is independent of the choice of the admissible epimorphisms $p_E$, see Section 3 in [19] for details. By abuse of notation, for $E\in {{\mathcal {E}}}$ and $i\ge 0$ we let $\Omega ^iE$ denote a choice of an object in ${{\mathcal {E}}}$ satisfying $\underline{\Omega ^iE}\cong \Omega ^i{\underline{E}}$.

An object I in ${{\mathcal {E}}}$ is injective if it is projective in ${{\mathcal {E}}}^{\mathrm {op}}$, and ${{\mathcal {E}}}$ has enough injectives if ${{\mathcal {E}}}^{\mathrm {op}}$ has enough projectives. The exact category ${{\mathcal {E}}}$ is called Frobenius if ${{\mathcal {E}}}$ has enough projectives and enough injectives, and if the projective and injective objects coincide. In this case, the stable category ${\underline{{{\mathcal {E}}}}}$ becomes a triangulated category where the suspension functor is the quasi-inverse of $\Omega$. We refer to [18, Section I.2] for more details.

We end this section with the following lemma, which we need later.

Lemma 2.4

Let ${{\mathcal {E}}}$ be an exact category with enough projectives, and let E be an object in ${{\mathcal {E}}}$. The following statements are equivalent:

• (i) ${\text {Ext}}^1_{{{\mathcal {E}}}}(E,P)=0$ for all $P\in {{\mathcal {P}}}$;

• (ii) The map

  $$\begin{aligned} {\text {Hom}}_{{\underline{{{\mathcal {E}}}}}}({\underline{E}},\underline{E'}) \rightarrow {\text {Hom}}_{{\underline{{{\mathcal {E}}}}}}(\Omega ({\underline{E}}), \Omega (\underline{E'})) \quad {\underline{f}}\mapsto \Omega ({\underline{f}}) \end{aligned}$$

  is an isomorphism for all $E'\in {{\mathcal {E}}}$.

Proof

This is well known, see [5, Proposition 2.43]. See also [41, Lemma 9] for a direct proof which can be translated verbatim to an exact category. $\square$

3 Left triangulated categories

Here we recall the notion of a left triangulated category. This was first considered in [38, 39] (where it would be called a co-suspended category), and later in [3, 8, 9]. A higher dimensional version has also been introduced in [42].

Let ${{\mathcal {C}}}$ be a category and $\Omega :{{\mathcal {C}}}\rightarrow {{\mathcal {C}}}$ an endofunctor. A sequence of the form

$$\begin{aligned} \Omega C\rightarrow A\rightarrow B\rightarrow C \end{aligned}$$

is called an $\Omega$-sequence. A morphism of $\Omega$-sequences $\Omega C\rightarrow A\rightarrow B\rightarrow C$ and $\Omega C'\rightarrow A'\rightarrow B'\rightarrow C'$ is a commutative diagram

Composition of morphism is given in the canonical way.

Definition 3.1

A left triangulated category is an additive category ${{\mathcal {C}}}$ equipped with an additive endofunctor $\Omega :{{\mathcal {C}}}\rightarrow {{\mathcal {C}}}$ and a class of $\Omega$-sequences called triangles, which satisfy the following axioms:

• (T0) Any $\Omega$-sequence which is isomorphic to a triangle is a triangle itself;

• (T1) For each $C\in {{\mathcal {C}}}$ the $\Omega$-sequence $0\rightarrow C\xrightarrow {1}C\rightarrow 0$ is a triangle;

• (T2) For any morphism $w:B\rightarrow C$ there exists a triangle $\Omega C\rightarrow A\rightarrow B\xrightarrow {w} C$

• (T3) If $\Omega C\xrightarrow {u} A\xrightarrow {v} B\xrightarrow {w} C$ is a triangle, then $\Omega B\xrightarrow {-\Omega (w)} \Omega C\xrightarrow {u} A\xrightarrow {v} B$ is a triangle;

• (T4) Given a diagram

  

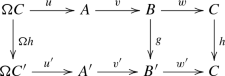
  where the rows are triangles and the square commutes, then there exists a morphism $f:A\rightarrow A'$ making the whole diagram commute;

• (T5) Given two morphisms $w:B\rightarrow C$ and $h:C\rightarrow D$, triangles $\Omega C\xrightarrow {u} A\xrightarrow {v} B\xrightarrow {w} C$ and $\Omega D\xrightarrow {f} E\xrightarrow {g} C\xrightarrow {h} D$, then there exists a commutative diagram

  

  where the middle row and the second column are also triangles.

If $\Omega C\rightarrow A\rightarrow B\xrightarrow {} C$ is a triangle and $D\in {{\mathcal {C}}}$, then applying ${\text {Hom}}_{{{\mathcal {C}}}}(D,-)$ gives a long exact sequence

$$\begin{aligned}&\cdots \rightarrow {\text {Hom}}_{{{\mathcal {C}}}}(D,\Omega ^{i+1} C)\rightarrow {\text {Hom}}_{{{\mathcal {C}}}}(D,\Omega ^i A)\rightarrow {\text {Hom}}_{{{\mathcal {C}}}}(D,\Omega ^i B)\xrightarrow {} \cdots \\&\cdots \rightarrow {\text {Hom}}_{{{\mathcal {C}}}}(D,\Omega C)\rightarrow {\text {Hom}}_{{{\mathcal {C}}}}(D, A)\rightarrow {\text {Hom}}_{{{\mathcal {C}}}}(D,B) \rightarrow {\text {Hom}}_{{{\mathcal {C}}}}(D,C) \end{aligned}$$

see [3, Corollary 1.5]. In particular, if $0\rightarrow A\xrightarrow {v}B\rightarrow 0$ is a triangle, then ${\text {Hom}}_{{{\mathcal {C}}}}(D, A)\xrightarrow {v\circ -} {\text {Hom}}_{{{\mathcal {C}}}}(D,B)$ is an isomorphism for all $D\in {{\mathcal {C}}}$, so v must be an isomorphism.

Assume ${{\mathcal {E}}}$ is an exact category with enough projectives. Any diagram of the form

induces a sequence $\Omega \underline{E_1}\xrightarrow {{\underline{u}}} \underline{E_3}\xrightarrow {{\underline{v}}}\underline{E_2}\xrightarrow {{\underline{w}}}\underline{E_1}$ in ${\underline{{{\mathcal {E}}}}}$. The following result follows from [9, Theorem 3.1].

Theorem 3.2

Let ${{\mathcal {E}}}$ be an exact category with enough projectives. Then the stable category ${\underline{{{\mathcal {E}}}}}$ together with syzygy functor $\Omega :{\underline{{{\mathcal {E}}}}}\rightarrow {\underline{{{\mathcal {E}}}}}$ and the class of all $\Omega$-sequences isomorphic to a sequence $\Omega \underline{E_1}\xrightarrow {{\underline{u}}} \underline{E_3}\xrightarrow {{\underline{v}}}\underline{E_2}\xrightarrow {{\underline{w}}}\underline{E_1}$ as above is a left triangulated category.

Now assume ${{\mathcal {C}}}$ is a category and $\Omega :{{\mathcal {C}}}\rightarrow {{\mathcal {C}}}$ is an endofunctor. Let $\mathbb {Z}{{\mathcal {C}}}$ be the stabilization of ${{\mathcal {E}}}$ [20]. Explicitly, the objects of $\mathbb {Z}{{\mathcal {C}}}$ are pairs (C, n) where C is an object in ${{\mathcal {C}}}$ and $n\in \mathbb {Z}$ is an integer. The morphism space between two objects (C, m) and $(C',n)$ is given by

$$\begin{aligned} {\text {Hom}}_{\mathbb {Z}{{\mathcal {C}}}}((C,m),(C',n)):= {\text {colim}}_{k}{\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^{m+k}(C),\Omega ^{n+k}(C')) \end{aligned}$$

where the colimit is taken over all $k\in \mathbb {Z}$ such that $m+k\ge 0$, and $n+k\ge 0$. Since this is a filtered colimit, it follows that any morphism $(C,m)\rightarrow (C',n)$ has a representative $\Omega ^{m+k}(C)\rightarrow \Omega ^{n+k}(C')$ in ${{\mathcal {C}}}$ for some k. Composition $(C,m)\rightarrow (C',n)\rightarrow (C'',p)$ in $\mathbb {Z}{{\mathcal {C}}}$ is given by composing representatives $\Omega ^{m+k}(C)\rightarrow \Omega ^{n+k}(C')\rightarrow \Omega ^{p+k}(C'')$ in ${{\mathcal {C}}}$. The category $\mathbb {Z}{{\mathcal {C}}}$ comes equipped with mutual inverse automorphisms

$$\begin{aligned} \Sigma :\mathbb {Z}{{\mathcal {C}}}\rightarrow \mathbb {Z}{{\mathcal {C}}}\quad \text {and} \quad \Omega :\mathbb {Z}{{\mathcal {C}}}\rightarrow \mathbb {Z}{{\mathcal {C}}}\end{aligned}$$

(3.3)

given by $\Sigma (C,n)=(C,n-1)$ and $\Omega (C,n)=(C,n+1)$ on objects and by the canonical identifications

$$\begin{aligned}&{\text {colim}}_{k}{\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^{m+k}C,\Omega ^{n+k}C')\cong {\text {colim}}_{k}{\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^{m-1+k}C,\Omega ^{n-1+k}C') \\&{\text {colim}}_{k}{\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^{m+k}C,\Omega ^{n+k}C')\cong {\text {colim}}_{k}{\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^{m+1+k}C,\Omega ^{n+1+k}C') \end{aligned}$$

to get maps

$$\begin{aligned}&{\text {Hom}}_{\mathbb {Z}{{\mathcal {C}}}}((C,m),(C',n))\xrightarrow {\cong } {\text {Hom}}_{\mathbb {Z}{{\mathcal {C}}}}((C,m-1),(C',n-1)) \quad f\mapsto \Sigma (f) \\&{\text {Hom}}_{\mathbb {Z}{{\mathcal {C}}}}((C,m),(C',n))\xrightarrow {\cong } {\text {Hom}}_{\mathbb {Z}{{\mathcal {C}}}}((C,m+1),(C',n+1)) \quad f\mapsto \Omega (f) \end{aligned}$$

on the morphisms spaces.

If ${{\mathcal {C}}}$ is a left triangulated category, then $\mathbb {Z}{{\mathcal {C}}}$ also comes equipped with a class of sequences

$$\begin{aligned} \Omega (C_1,n_1)\rightarrow (C_3,n_3)\rightarrow (C_2,n_2)\rightarrow (C_1,n_1) \end{aligned}$$

called standard triangles, which are induced from a sequence

$$\begin{aligned} \Omega ^{k+n_1+1}(C_1)\xrightarrow {u}\Omega ^{k+n_3}(C_3)\xrightarrow {v} \Omega ^{k+n_2}(C_2)\xrightarrow {w} \Omega ^{k+n_1}(C_1) \end{aligned}$$

in ${{\mathcal {C}}}$ for some integer $k\in \mathbb {Z}$, and where

$$\begin{aligned} \Omega ^{k+n_1+1}(C_1)\xrightarrow {(-1)^{k}u}\Omega ^{k+n_3}(C_3)\xrightarrow {(-1)^k v} \Omega ^{k+n_2}(C_2)\xrightarrow {(-1)^k w} \Omega ^{k+n_1}(C_1) \end{aligned}$$

is a triangle in ${{\mathcal {C}}}$.

Theorem 3.4

[39] The following hold:

• (i) If ${{\mathcal {C}}}$ is a left triangulated category, then $\mathbb {Z}{{\mathcal {C}}}$ becomes a triangulated category with suspension functor $\Sigma$ and with triangles being the standard triangles given above.

• (ii) Let ${{\mathcal {E}}}$ be an exact category with enough projectives ${{\mathcal {P}}}$. Then there exists an equivalence of triangulated categories

  $$\begin{aligned} \mathbb {Z}{\underline{{{\mathcal {E}}}}}\xrightarrow {\cong } K^{-,b}({{\mathcal {P}}})/K^b({{\mathcal {P}}}) \end{aligned}$$

  sending an object $({\underline{E}},n)$ to a complex $P^{\bullet }[-n]$, where $P^{\bullet }$ is a projective resolution of E concentrated in degrees $\le 0$.

Here $K^b({{\mathcal {P}}})$ and $K^{-,b}({{\mathcal {P}}})$ denote the bounded homotopy category with components in ${{\mathcal {P}}}$ and the right bounded homotopy category with bounded homology and with components in ${{\mathcal {P}}}$, respectively. The Verdier quotient

$$\begin{aligned} D_{{\text {sing}}}({{\mathcal {E}}}):=K^{-,b}({{\mathcal {P}}})/K^b({{\mathcal {P}}}) \end{aligned}$$

is the singularity category of ${{\mathcal {E}}}$. We refer to Section 4 in [40] for details on Verdier quotients and localization of triangulated categories.

4 Cluster tilting subcategories

Let ${{\mathcal {E}}}$ be an additive category and ${{\mathcal {M}}}$ a full additive subcategory of ${{\mathcal {E}}}$. We recall the following notions.

• (i) A morphism $M\rightarrow E$ in ${{\mathcal {E}}}$ with $M\in {{\mathcal {M}}}$ is called a right ${{\mathcal {M}}}$ -approximation if the induced morphism ${{\mathcal {E}}}(M',M)\rightarrow {{\mathcal {E}}}(M',E)$ is an epimorphism for all $M'\in {{\mathcal {M}}}$;

• (ii) A morphism $E\rightarrow M$ in ${{\mathcal {E}}}$ with $M\in {{\mathcal {M}}}$ is called a left ${{\mathcal {M}}}$ -approximation if the induced morphism ${{\mathcal {E}}}(M,M')\rightarrow {{\mathcal {E}}}(E,M')$ is an epimorphism for all $M'\in {{\mathcal {M}}}$;

• (iii) ${{\mathcal {M}}}$ is contravariantly finite in ${{\mathcal {E}}}$ if for all objects $E\in {{\mathcal {E}}}$ there exists a right ${{\mathcal {M}}}$-approximation $M\rightarrow E$;

• (iv) ${{\mathcal {M}}}$ is covariantly finite in ${{\mathcal {E}}}$ if for all objects $E\in {{\mathcal {E}}}$ there exists a left ${{\mathcal {M}}}$-approximation $E\rightarrow M$;

• (v) ${{\mathcal {M}}}$ is functorially finite in ${{\mathcal {E}}}$ if it is contravariantly finite and covariantly finite in ${{\mathcal {E}}}$.

We recall the definition of d and $d\mathbb {Z}$-cluster tilting subcategories in the following. If ${{\mathcal {E}}}$ is triangulated with suspension functor $\Sigma$, then by ${\text {Ext}}^i_{{{\mathcal {E}}}}(E,E')$ we mean the Hom-space ${\text {Hom}}_{{{\mathcal {E}}}}(E,\Sigma ^i(E'))$.

Definition 4.1

Let ${{\mathcal {E}}}$ be an exact or a triangulated category, let ${{\mathcal {M}}}$ be a full subcategory of ${{\mathcal {E}}}$, and let $d>0$ be a positive integer. We say that ${{\mathcal {M}}}$ is d -cluster tilting in ${{\mathcal {E}}}$ if the following hold:

• (i) ${{\mathcal {M}}}$ is functorially finite in ${{\mathcal {E}}}$;

• (ii) We have

  $$\begin{aligned} {{\mathcal {M}}}&= \{E\in {{\mathcal {E}}}\mid {\text {Ext}}^i_{{{\mathcal {E}}}}(E,{{\mathcal {M}}})=0 \text { for }1\le i\le d-1\} \\&= \{E\in {{\mathcal {E}}}\mid {\text {Ext}}^i_{{{\mathcal {E}}}}({{\mathcal {M}}},E)=0 \text { for }1\le i\le d-1\}; \end{aligned}$$

• (iii) If ${{\mathcal {E}}}$ is exact then ${{\mathcal {M}}}$ is a generating and cogenerating subcategory of ${{\mathcal {E}}}$, i.e. for any object $E\in {{\mathcal {E}}}$ there exists an admissible monomorphism $E\rightarrow M$ with $M\in {{\mathcal {M}}}$ and an admissible epimorphism $M'\rightarrow E$ with $M'\in {{\mathcal {M}}}$.

If furthermore ${\text {Ext}}^i_{{{\mathcal {E}}}}({{\mathcal {M}}},{{\mathcal {M}}})=0$ for $i\notin d\mathbb {Z}$, then we say that ${{\mathcal {M}}}$ is $d\mathbb {Z}$ -cluster tilting in ${{\mathcal {E}}}$.

Remark 4.2

We have the following:

• (i) If ${{\mathcal {E}}}$ is exact with enough projectives and injectives, then condition (iii) follows from conditions (i) and (ii). Therefore, (iii) is often not assumed.

• (ii) If ${{\mathcal {E}}}$ is an exact category with enough projectives and ${{\mathcal {M}}}$ is d-cluster tilting in ${{\mathcal {E}}}$, then ${{\mathcal {M}}}$ is $d\mathbb {Z}$-cluster tilting in ${{\mathcal {E}}}$ if and only if $\Omega ^d({\underline{{{\mathcal {M}}}}})\subset {\underline{{{\mathcal {M}}}}}$.

• (iii) If ${{\mathcal {E}}}$ is triangulated with suspension functor $\Sigma$ and ${{\mathcal {M}}}$ is d-cluster tilting in ${{\mathcal {E}}}$, then the following conditions are equivalent:

  • (a) ${{\mathcal {M}}}$ is $d\mathbb {Z}$-cluster tilting in ${{\mathcal {E}}}$;

  • (b) $\Sigma ^d({{\mathcal {M}}})\subset {{\mathcal {M}}}$;

  • (c) $\Sigma ^{-d}({{\mathcal {M}}})\subset {{\mathcal {M}}}$.

We need following result later:

Proposition 4.3

(Proposition 2.2.2 in [25]) Let ${{\mathcal {E}}}$ be an exact category and ${{\mathcal {M}}}$ a full subcategory of ${{\mathcal {E}}}$. Assume ${{\mathcal {M}}}$ is closed under direct summands and satisfies ${\text {Ext}}^i_{{{\mathcal {E}}}}({{\mathcal {M}}},{{\mathcal {M}}})=0$ for $1\le i\le d-1$. Assume furthermore that condition (i) and (iii) in Definition 4.1 holds for ${{\mathcal {M}}}$. Then the following are equivalent for each $0\le n\le d-1$:

(a):

${{\mathcal {M}}}$ is a d-cluster tilting subcategory of ${{\mathcal {E}}}$;

$(b_n)$:

If $E\in {{\mathcal {E}}}$ satisfies ${\text {Ext}}^i_{{{\mathcal {E}}}}({{\mathcal {M}}},E)=0$ for $1\le i\le n$, then there exists an exact sequence $0\rightarrow M_{d-n}\rightarrow \cdots \rightarrow M_1\rightarrow E\rightarrow 0$ with $M_j\in {{\mathcal {M}}}$ for $1\le j\le d-n$;

$(c_n)$:

If $E\in {{\mathcal {E}}}$ satisfies ${\text {Ext}}^i_{{{\mathcal {E}}}}(E,{{\mathcal {M}}})=0$ for $1\le i\le n$, then there exists an exact sequence $0\rightarrow E\rightarrow M^1\rightarrow \cdots \rightarrow M^{d-n}\rightarrow 0$ with $M^j\in {{\mathcal {M}}}$ for $1\le j\le d-n$.

Proof

For any $E\in {{\mathcal {E}}}$ choose a right ${{\mathcal {M}}}$-approximation $f:M\rightarrow E$ and an admissible epimorphism $g:M'\rightarrow E$ with $M'\in {{\mathcal {M}}}$. Then the morphism $\begin{bmatrix}f&g\end{bmatrix}:M\oplus M'\rightarrow E$ is a right ${{\mathcal {M}}}$-approximation and an admissible epimorphism. Similarly, one can construct a left ${{\mathcal {M}}}$-approximation which is an admissible monomorphism for any $E\in {{\mathcal {E}}}$. Using this, the proof of Proposition 2.2.2 in [25] goes through in exactly the same way for exact categories, so the claim holds. $\square$

The following result shows that condition $(b_0)+(c_0)$ is equivalent to d-cluster tilting without the assumption that ${{\mathcal {M}}}$ is functorially finite.

Proposition 4.4

Let ${{\mathcal {E}}}$ be an exact category and ${{\mathcal {M}}}$ a full subcategory of ${{\mathcal {E}}}$. Assume ${{\mathcal {M}}}$ is closed under direct summands and satisfies ${\text {Ext}}^i_{{{\mathcal {E}}}}({{\mathcal {M}}},{{\mathcal {M}}})=0$ for $1\le i\le d-1$. Then the following are equivalent:

• (i) ${{\mathcal {M}}}$ is a d-cluster tilting subcategory of ${{\mathcal {E}}}$;

• (ii) For each $E\in {{\mathcal {E}}}$ there exists exact sequences

  $$\begin{aligned}&0\rightarrow M_{d}\rightarrow \cdots \rightarrow M_1\rightarrow E\rightarrow 0 \\&0\rightarrow E\rightarrow M^1\rightarrow \cdots \rightarrow M^{d}\rightarrow 0 \end{aligned}$$

  with $M^i\in {{\mathcal {M}}}$ and $M_i\in {{\mathcal {M}}}$ for $1\le i\le d$.

Proof

The implication (i)$\implies$(ii) follows from the implications $(a){\implies }(b_0)$ and $(a){\implies }(c_0)$ in Proposition 4.3. For the converse, let $E\in {{\mathcal {E}}}$, and choose an exact sequence

$$\begin{aligned} 0\rightarrow E\xrightarrow {f^1}M^1\xrightarrow {f^2}\cdots \xrightarrow {f^d}M^d\rightarrow 0 \end{aligned}$$

with $M^i\in {{\mathcal {M}}}$ for $1\le i\le d$. Let $M\in {{\mathcal {M}}}$ be arbitrary. Applying ${\text {Hom}}_{{{\mathcal {E}}}}(-,M)$ to the short exact sequence

$$\begin{aligned} 0\rightarrow {\text {Coker}}f^i\rightarrow M^{i+1}\rightarrow {\text {Coker}}f^{i+1}\rightarrow 0 \end{aligned}$$

we get that

$$\begin{aligned} {\text {Ext}}^{j+1}_{{{\mathcal {E}}}}({\text {Coker}}f^{i+1},M)\cong {\text {Ext}}^{j}_{{{\mathcal {E}}}}({\text {Coker}}f^{i},M) \end{aligned}$$

for $1\le j\le d-2$. Hence, it follows that

$$\begin{aligned} 0={\text {Ext}}^{d-1}_{{{\mathcal {E}}}}(M^d,M)\cong {\text {Ext}}^{d-2}_{{{\mathcal {E}}}}({\text {Coker}}f^{d-2},M)\cong \cdots \cong {\text {Ext}}^1_{{{\mathcal {E}}}}({\text {Coker}}f^1,M). \end{aligned}$$

Therefore, the map

$$\begin{aligned} {\text {Hom}}_{{{\mathcal {E}}}}(M^1,M)\rightarrow {\text {Hom}}_{{{\mathcal {E}}}}(E,M) \end{aligned}$$

is an epimorphism. Since $M\in {{\mathcal {M}}}$ was arbitrary, we get that $f^1:E\rightarrow M^1$ is a left ${{\mathcal {M}}}$-approximation. Hence, ${{\mathcal {M}}}$ is covariantly finite. Furthermore, if we assume ${\text {Ext}}^i_{{{\mathcal {E}}}}(M',E)=0$ for $1\le i\le d-1$ and $M'\in {{\mathcal {M}}}$, then the same argument as above with M replaced by E shows that the map

$$\begin{aligned} {\text {Hom}}_{{{\mathcal {E}}}}(M^1,E)\rightarrow {\text {Hom}}_{{{\mathcal {E}}}}(E,E) \end{aligned}$$

is an epimorphism. Therefore, $f^1:E\rightarrow M^1$ is a split monomorphism. Since $f^1$ is also an admissible monomorphism, it follows that E is a summand of $M^1$. Hence, we get that $E\in {{\mathcal {M}}}$. Since ${\text {Ext}}^i_{{{\mathcal {E}}}}({{\mathcal {M}}},{{\mathcal {M}}})=0$ for $1\le i\le d-1$, this shows the equality

$$\begin{aligned} {{\mathcal {M}}}=\{E\in {{\mathcal {E}}}\mid {\text {Ext}}^i_{{{\mathcal {E}}}}({{\mathcal {M}}},E)=0 \text { for }1\le i\le d-1 \}. \end{aligned}$$

The fact that ${{\mathcal {M}}}$ is contravariantly finite and the equality

$$\begin{aligned} {{\mathcal {M}}}=\{E\in {{\mathcal {E}}}\mid {\text {Ext}}^i_{{{\mathcal {E}}}}(E,{{\mathcal {M}}})=0 \text { for }1\le i\le d-1 \} \end{aligned}$$

follows by a dual argument. Finally, ${{\mathcal {M}}}$ being generating and cogenerating follows from the existence of the exact sequences in part (ii) of the proposition. $\square$

5 Cluster tilting subcategories of left triangulated categories

In this section we define cluster tilting subcategories of left triangulated categories. We show that when the ambient category is triangulated, then this coincides with the classical definition. Finally, we show that if a left triangulated category ${{\mathcal {C}}}$ has a $d\mathbb {Z}$-cluster tilting subcategory, then so does the stabilization $\mathbb {Z}{{\mathcal {C}}}$.

Let ${{\mathcal {C}}}$ be a left triangulated category. We call a sequence in ${{\mathcal {C}}}$

$$\begin{aligned} \Omega ^d(C_1)\xrightarrow {\alpha _{d+2}}C_{d+2}\xrightarrow {\alpha _{d+1}} C_{d+1}\xrightarrow {\alpha _{d}} \cdots \xrightarrow {\alpha _{2}} C_2\xrightarrow {\alpha _{1}} C_1 \end{aligned}$$

a $(d+2)$ -angle if there exists a diagram

where an arrow denotes a morphism $C'\leftarrow \Omega (C)$ in ${{\mathcal {C}}}$, each oriented triangle is a triangle in ${{\mathcal {C}}}$, each non-oriented triangle commute, and $\alpha _{d+2}$ is equal to the composite

$$\begin{aligned} \Omega ^d(C_{1})\rightarrow \Omega ^{d-1}(C_{2.5})\rightarrow \cdots \rightarrow \Omega (C_{d.5})\rightarrow C_{d+2}. \end{aligned}$$

Note that here the symbol n.5 means $n+0.5$. This definition of $(d+2)$-angle differs slightly from [32], where they do not include the morphism $\Omega ^d(C_1)\rightarrow C_{d+2}$ in the definition.

Definition 5.1

Let ${{\mathcal {C}}}$ be a left triangulated category and $d>0$ a positive integer. A full additive subcategory ${{\mathcal {X}}}$ of ${{\mathcal {C}}}$ is d -cluster tilting if it satisfies the following:

• (i) ${{\mathcal {X}}}$ is closed under direct summands in ${{\mathcal {C}}}$;

• (ii) For all objects C in ${{\mathcal {C}}}$ there exist $(d+2)$-angles

  $$\begin{aligned} 0\rightarrow C\rightarrow X^1\rightarrow \cdots \rightarrow X^d\rightarrow 0 \end{aligned}$$

  and

  $$\begin{aligned} 0\rightarrow X_d\rightarrow \cdots \rightarrow X_1\rightarrow C\rightarrow 0 \end{aligned}$$

  with $X_i,X^i\in {{\mathcal {X}}}$ for $1\le i\le d$;

• (iii) For C in ${{\mathcal {C}}}$ and X in ${{\mathcal {X}}}$ the map

  $$\begin{aligned} {\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^{i-1}(X),C)\rightarrow {\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^{i}(X),\Omega (C)) \quad f\mapsto \Omega (f) \end{aligned}$$

  is an isomorphism for $1\le i\le d-1$;

• (iv) If X and $X'$ are in ${{\mathcal {X}}}$, then

  $$\begin{aligned} {\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^i(X'),X)=0 \end{aligned}$$

  for $1\le i\le d-1$.

If furthermore $\Omega ^d({{\mathcal {X}}})\subset {{\mathcal {X}}}$, then we say that ${{\mathcal {X}}}$ is $d\mathbb {Z}$ -cluster tilting in ${{\mathcal {C}}}$.

We use the terminology d-cluster tilting since for an exact category ${{\mathcal {E}}}$ with enough projectives we then get a correspondence between d-cluster tilting subcategories of ${{\mathcal {E}}}$ and ${\underline{{{\mathcal {E}}}}}$, see Theorem 6.1.

Remark 5.2

We see that condition (ii) in Definition 5.1 is similar to condition (ii) in Proposition 4.4, and it can be considered as a substitute of Definition 4.1 (ii) and of functorially finiteness. The fact that it behaves much better under stabilization is also a crucial property we need.

Next we show that Definitions 5.1 and 4.1 are equivalent when $\Omega$ is an automorphism, i.e. when ${{\mathcal {C}}}$ is triangulated. In the following we let $\Sigma$ denote the quasi-inverse of $\Omega$.

Proposition 5.3

A subcategory of a triangulated category ${{\mathcal {C}}}$ is d or $d\mathbb {Z}$-cluster tilting in the sense of Definition 5.1 if and only if it is d or $d\mathbb {Z}$-cluster tilting in the sense of Definition 4.1.

Proof

By Remark 4.2 (iii) the claim for $d\mathbb {Z}$-cluster tilting subcategories follows immediately from the claim for d-cluster tilting subcategories. Hence, we only prove the latter. Note that a d-cluster tilting subcategory in the sense of Definition 4.1 obviously satisfies (i), (iii) and (iv) in Definition 5.1, while axiom (ii) follows from [32, Corollary 3.3] and its dual. For the converse, assume ${{\mathcal {X}}}\subset {{\mathcal {C}}}$ is d-cluster tilting in the sense of Definition 5.1. As usual, for subcategories ${{\mathcal {Y}}}'$ and ${{\mathcal {Y}}}$ of ${{\mathcal {C}}}$, we denote by ${{\mathcal {Y}}}'*{{\mathcal {Y}}}$ the subcategory consisting of all $C\in {{\mathcal {C}}}$ admitting a triangle $Y'\rightarrow C\rightarrow Y\rightarrow \Sigma Y'$ with $Y'\in {{\mathcal {Y}}}'$ and $Y\in {{\mathcal {Y}}}$. By Definition 5.1 (ii) we have ${{\mathcal {C}}}=\Omega ^{d-1}{{\mathcal {X}}}*\cdots *\Omega {{\mathcal {X}}}*{{\mathcal {X}}}$. For each $C\in {{\mathcal {C}}}$, take a triangle

$$\begin{aligned} Y\xrightarrow {f} C\xrightarrow {g} X\rightarrow \Sigma Y \end{aligned}$$

with $Y\in \Omega ^{d-1}{{\mathcal {X}}}*\cdots *\Omega {{\mathcal {X}}}$ and $X\in {{\mathcal {X}}}$. Since ${\text {Hom}}_{{{\mathcal {C}}}}(Y,{{\mathcal {X}}})=0$ by Definition 5.1 (iv), g is a left ${{\mathcal {X}}}$-approximation and hence ${{\mathcal {X}}}$ is covariantly finite. Moreover, if ${\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^iX,C)=0$ for $1\le i\le d-1$, then $f=0$ and hence $C\in {{\mathcal {X}}}$. Since ${\text {Hom}}_{{{\mathcal {C}}}}({{\mathcal {X}}},\Sigma ^iX)=0$ for $1\le i\le d-1$ and $X\in {{\mathcal {X}}}$ by Definition 5.1(iv), this shows that

$$\begin{aligned} {{\mathcal {X}}}= \{C\in {{\mathcal {C}}}\mid {\text {Hom}}_{{{\mathcal {C}}}}({{\mathcal {X}}},\Sigma ^iC)=0 \text { for }1\le i\le d-1\}. \end{aligned}$$

The fact that ${{\mathcal {X}}}$ is contravariantly finite and the equality

$$\begin{aligned} {{\mathcal {X}}}= \{C\in {{\mathcal {C}}}\mid {\text {Hom}}_{{{\mathcal {C}}}}(C,\Sigma ^i({{\mathcal {X}}}))=0 \text { for }1\le i\le d-1\} \end{aligned}$$

is shown dually. $\square$

Recall that the stabilization $\mathbb {Z}{{\mathcal {C}}}$ of a left triangulated category ${{\mathcal {C}}}$ is a triangulated category, see Theorem 3.4.

Definition 5.4

Let ${{\mathcal {C}}}$ be a left triangulated category and ${{\mathcal {X}}}$ a $d\mathbb {Z}$-cluster tilting subcategory of ${{\mathcal {C}}}$. Define $d\mathbb {Z}{{\mathcal {X}}}$ to be the full subcategory of $\mathbb {Z}{{\mathcal {C}}}$ consisting of all objects isomorphic to objects of the form (X, dk) with $X\in {{\mathcal {X}}}$ and $k\in \mathbb {Z}$.

Our goal is to show that $d\mathbb {Z}{{\mathcal {X}}}$ is $d\mathbb {Z}$-cluster tilting in $\mathbb {Z}{{\mathcal {C}}}$.

Lemma 5.5

The subcategory $d\mathbb {Z}{{\mathcal {X}}}$ is closed under direct summands.

Proof

Two objects (C, n) and $(C',n')$ are isomorphic in $\mathbb {Z}{{\mathcal {C}}}$ if and only if there exists an integer k such that $\Omega ^{k+n}(C)$ and $\Omega ^{k+n'}(C')$ are isomorphic in ${{\mathcal {C}}}$. Hence, $d\mathbb {Z}{{\mathcal {X}}}$ consists of all objects (C, n) such that there exists an integer k with $\Omega ^{dk+n}(C)\in {{\mathcal {X}}}$. Now assume that

$$\begin{aligned} (C_1,n_1)\oplus (C_2,n_2)\in d\mathbb {Z}{{\mathcal {X}}}. \end{aligned}$$

Choose $n:=\min (n_1,n_2)$. Then $(C_1,n_1)\cong (\Omega ^{n_1-n}(C_1),n)$ and $(C_2,n_2)\cong (\Omega ^{n_2-n}(C_2),n)$, and hence

$$\begin{aligned} (C_1,n_1)\oplus (C_2,n_2)\cong (\Omega ^{n_1-n}(C_1)\oplus \Omega ^{n_2-n}(C_2),n)\in d\mathbb {Z}{{\mathcal {X}}}. \end{aligned}$$

Therefore there exists an integer k such that

$$\begin{aligned} \Omega ^{dk+n_1}(C_1)\oplus \Omega ^{dk+n_2}(C_2)\in {{\mathcal {X}}}. \end{aligned}$$

Since ${{\mathcal {X}}}$ is closed under direct summands by Definition 5.1(i), we have that

$$\begin{aligned} \Omega ^{dk+n_1}(C_1)\in {{\mathcal {X}}}\quad \text {and} \quad \Omega ^{dk+n_2}(C_2)\in {{\mathcal {X}}}\end{aligned}$$

and hence

$$\begin{aligned} (C_1,n_1)\in d\mathbb {Z}{{\mathcal {X}}}\quad \text {and} \quad (C_2,n_2)\in d\mathbb {Z}{{\mathcal {X}}}. \end{aligned}$$

This proves the claim. $\square$

Lemma 5.6

If $(X,dn)\in d\mathbb {Z}{{\mathcal {X}}}$ and $(X',dn')\in d\mathbb {Z}{{\mathcal {X}}}$, then

$$\begin{aligned} {\text {Hom}}_{\mathbb {Z}{{\mathcal {C}}}}(\Omega ^i(X,dn),(X',dn'))=0 \end{aligned}$$

for $1\le i\le d-1$

Proof

We have that

$$\begin{aligned} {\text {Hom}}_{\mathbb {Z}{{\mathcal {C}}}}(\Omega ^i(X,dn),(X',dn')) = {\text {colim}}_{k'} {\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^i(\Omega ^{k'+dn}(X)),\Omega ^{k'+dn'}(X')). \end{aligned}$$

But

$$\begin{aligned} {\text {Hom}}_{{{\mathcal {C}}}}(\Omega ^i(\Omega ^{dk+dn}(X)),\Omega ^{dk+dn'}(X'))=0 \end{aligned}$$

for all k such that $dk+dn>0$ and $dk+dn'>0$ by Definition 5.1 (iv), since $\Omega ^{dk+dn}(X)\in {{\mathcal {X}}}$ and $\Omega ^{dk'+dn}(X')\in {{\mathcal {X}}}$. Hence, the colimit must be 0, which proves the claim. $\square$

Theorem 5.7

Let ${{\mathcal {C}}}$ be a left triangulated category and ${{\mathcal {X}}}$ a $d\mathbb {Z}$-cluster tilting subcategory of ${{\mathcal {C}}}$. Then $d\mathbb {Z}{{\mathcal {X}}}$ is a $d\mathbb {Z}$-cluster tilting subcategory of the triangulated category $\mathbb {Z}{{\mathcal {C}}}$.

Proof

We show that $d\mathbb {Z}{{\mathcal {X}}}$ satisfies Definition 5.1. Note that axiom (i) and (iv) follows from Lemmas 5.5 and 5.6 respectively, and axiom (iii) is clear since $\mathbb {Z}{{\mathcal {C}}}$ is a triangulated category. It therefore only remains to show axiom (ii). Let $(C,n)\in \mathbb {Z}{{\mathcal {C}}}$ be arbitrary. Choose k such that $dk<n$. Then we have an isomorphism $(C,n)\cong (\Omega ^{n-dk}(C),dk)$. Hence, we can assume for simplicity that $n=dk$. Now choose $(d+2)$-angles

$$\begin{aligned}&0\rightarrow C\rightarrow X^1\rightarrow \cdots X^d\rightarrow 0 \\&0\rightarrow X_d\rightarrow \cdots \rightarrow X_1\rightarrow C\rightarrow 0 \end{aligned}$$

in ${{\mathcal {C}}}$ with $X_i,X^i\in {{\mathcal {X}}}$ for $1\le i\le d$. Applying Axiom (T3) in Definition 3.1 repeatedly, we obtain $(d+2)$-angles

$$\begin{aligned}&0\rightarrow \Omega ^{dk}(C)\rightarrow \Omega ^{dk}(X^1)\rightarrow \cdots \Omega ^{dk}(X^d)\rightarrow 0 \\&0\rightarrow \Omega ^{dk}(X_d)\rightarrow \cdots \rightarrow \Omega ^{dk}(X_1)\rightarrow \Omega ^{dk}(C)\rightarrow 0 \end{aligned}$$

in ${{\mathcal {C}}}$. But they give $(d+2)$-angles

$$\begin{aligned}&0\rightarrow (C,dk)\rightarrow (X^1,dk)\rightarrow \cdots (X^d,dk)\rightarrow 0 \\&0\rightarrow (X_d,dk)\rightarrow \cdots \rightarrow (X_1,dk)\rightarrow (C,dk)\rightarrow 0 \end{aligned}$$

in $\mathbb {Z}{{\mathcal {C}}}$, which prove the claim. $\square$

Remark 5.8

Note that the proof of Theorem 5.7 does not use axiom (iii) in Definition 5.1. This axiom is needed to prove Theorem 6.1 (and in particular Lemma 6.4) to get a correspondence between $d\mathbb {Z}$-cluster tilting subcategories in the exact category ${{\mathcal {E}}}$ and in the left triangulated category ${\underline{{{\mathcal {E}}}}}$

The category $d\mathbb {Z}{{\mathcal {X}}}$ is also equivalent to the stabilization of ${{\mathcal {X}}}$ with respect to the functor

$$\begin{aligned} \Omega ^d:{{\mathcal {X}}}\rightarrow {{\mathcal {X}}}. \end{aligned}$$

Hence, it can be computed without describing the categories ${{\mathcal {C}}}$ and $\mathbb {Z}{{\mathcal {C}}}$, which is more complicated to do in general.

Since $d\mathbb {Z}{{\mathcal {X}}}$ is a $d\mathbb {Z}$-cluster tilting subcategory of $\mathbb {Z}{{\mathcal {C}}}$, it has the structure of a $(d+2)$-angulated category [16, Theorem 4.1], where

$$\begin{aligned} \Sigma ^d:d\mathbb {Z}{{\mathcal {X}}}\rightarrow d\mathbb {Z}{{\mathcal {X}}}\quad \Sigma ^d(X,nd)=(X,n(d-1)) \end{aligned}$$

is the suspension functor (see (3.3)) applied d times. The $(d+2)$-angles in the sense of [16] are all $(d+2)$-angles in $\mathbb {Z}{{\mathcal {C}}}$ in our sense

$$\begin{aligned} \Omega ^d(E_1)\xrightarrow {\alpha _{d+2}} E_{d+2}\xrightarrow {\alpha _{d+1}}E_{d+1}\xrightarrow {\alpha _{d}}\cdots \xrightarrow {\alpha _{1}}E_{1} \end{aligned}$$

where $E_i\in d\mathbb {Z}{{\mathcal {X}}}$ for $1\le i\le d+2$.

Lemma 5.9

A sequence

$$\begin{aligned} \Omega ^d(X_1,dn_1)\rightarrow (X_{d+2},dn_{d+2})\xrightarrow {}(X_{d+1},dn_{d+1})\xrightarrow {} \cdots \xrightarrow {}(X_{1},dn_{1}) \end{aligned}$$

in $d\mathbb {Z}{{\mathcal {X}}}$ with $X_i\in {{\mathcal {X}}}$ for $1\le i\le d+2$ is a $(d+2)$-angle if and only if it is induced from a sequence in ${{\mathcal {C}}}$ of the form

$$\begin{aligned} \Omega ^{d(k+n_1+1)}(X_1)\xrightarrow {u_{d+2}}\Omega ^{d(k+n_{d+2})}(X_{d+2})\xrightarrow {u_{d+1}}\cdots \xrightarrow {u_1} \Omega ^{d(k+n_1)}(X_1) \end{aligned}$$

where

$$\begin{aligned} \Omega ^{d(k+n_1+1)}(X_1)\xrightarrow {(-1)^{dk}u_{d+2}}\Omega ^{d(k+n_{d+2})}(X_{d+2})\xrightarrow {(-1)^{dk}u_{d+1}}\cdots \xrightarrow {(-1)^{dk}u_1} \Omega ^{d(k+n_1)}(X_1) \end{aligned}$$

is a $(d+2)$-angle in ${{\mathcal {C}}}$.

Proof

This follows immediately from the description of the triangles in $\mathbb {Z}{{\mathcal {C}}}$ together with axiom (T3) in Definition 3.1. $\square$

6 d-cluster tilting in stable categories

Let ${{\mathcal {E}}}$ be an exact category with enough projectives. In this section we compare cluster tilting subcategories in the exact category ${{\mathcal {E}}}$ and those in the left triangulated category ${\underline{{{\mathcal {E}}}}}$. Our main goal is to prove the following theorem:

Theorem 6.1

Let ${{\mathcal {E}}}$ be an exact category with enough projectives ${{\mathcal {P}}}$, and ${{\mathcal {M}}}$ a full subcategory of ${{\mathcal {E}}}$.

• (i) ${{\mathcal {M}}}$ is a d-cluster tilting subcategory of ${{\mathcal {E}}}$ if and only if ${\underline{{{\mathcal {M}}}}}$ is a d-cluster tilting subcategory of ${\underline{{{\mathcal {E}}}}}$;

• (ii) ${{\mathcal {M}}}$ is a $d\mathbb {Z}$-cluster tilting subcategory of ${{\mathcal {E}}}$ if and only if ${\underline{{{\mathcal {M}}}}}$ is a $d\mathbb {Z}$-cluster tilting subcategory of ${\underline{{{\mathcal {E}}}}}$.

In the special case when ${{\mathcal {E}}}$ is Frobenius (and hence ${\underline{{{\mathcal {E}}}}}$ is triangulated) the theorem is easy and well-known.

We start by proving one direction of the theorem.

Proof of “only if” part of Theorem 6.1

If ${{\mathcal {M}}}$ is $d\mathbb {Z}$-cluster tilting, then for each $1\le i\le d-1$, we have ${\text {Ext}}^d_{{{\mathcal {E}}}}(\Omega ^dM',M)={\text {Ext}}^{i+d}_{{{\mathcal {E}}}}(M',M)=0$ where $M,M'\in {{\mathcal {M}}}$. Therefore $\Omega ^d({\underline{{{\mathcal {M}}}}})\subseteq {\underline{{{\mathcal {M}}}}}$. Hence the “only if” part of Theorem 6.1 (ii) follows from the “only if” part of Theorem 6.1 (i) by Remark 4.2 (ii).

Assume ${{\mathcal {M}}}$ is d-cluster tilting in ${{\mathcal {E}}}$. Since ${{\mathcal {M}}}$ is closed under direct summands, it follows using the description of the isomorphisms from (2.2) that ${\underline{{{\mathcal {M}}}}}$ is closed under direct summands. Now for $E\in {{\mathcal {E}}}$ we can choose exact sequences

$$\begin{aligned}&0\rightarrow E\xrightarrow {f^1}M^1\xrightarrow {f^2}\cdots \xrightarrow {f^d}M^d\rightarrow 0 \\&0\rightarrow M_d\xrightarrow {g_d} \cdots \xrightarrow {g_2} M_1\xrightarrow {g_1} E\rightarrow 0 \end{aligned}$$

in ${{\mathcal {E}}}$ with $M_i,M^i\in {{\mathcal {M}}}$ for $1\le i\le d$ by Proposition 4.3. By definition of the left triangulated structure of ${\underline{{{\mathcal {E}}}}}$, we get $(d+2)$-angles

and

This shows that part (ii) of Definition 5.1 holds for ${\underline{{{\mathcal {M}}}}}$. Also, by Lemma 2.4 the map

$$\begin{aligned} {\text {Hom}}_{{\underline{{{\mathcal {E}}}}}}(\Omega ^{i-1}({\underline{M}}),{\underline{E}})\rightarrow {\text {Hom}}_{{\underline{{{\mathcal {E}}}}}}(\Omega ^{i}({\underline{M}}),\Omega ({\underline{E}})) \quad {\underline{f}} \mapsto \Omega ({\underline{f}}) \end{aligned}$$

is an isomorphism for any $M\in {{\mathcal {M}}}$, $E\in {{\mathcal {E}}}$ and $1\le i\le d-1$ since

$$\begin{aligned} {\text {Ext}}^1_{{{\mathcal {E}}}}(\Omega ^{i-1}M,P)\cong {\text {Ext}}^i_{{{\mathcal {E}}}}(M,P)=0 \end{aligned}$$

for all $P\in {{\mathcal {P}}}$. Hence, part (iii) of Definition 5.1 also holds for ${\underline{{{\mathcal {M}}}}}$. Finally, to prove part (iv), we use the basic fact that if ${\text {Ext}}^1_{{{\mathcal {E}}}}(E,{{\mathcal {P}}})=0$, then

$$\begin{aligned} {\text {Hom}}_{{\underline{{{\mathcal {E}}}}}}(\Omega ({\underline{E}}),\underline{E'})\cong {\text {Ext}}^1_{{{\mathcal {E}}}}(E,E') \end{aligned}$$

for all $E'\in {{\mathcal {E}}}$. In particular, since ${\text {Ext}}^{i}_{{{\mathcal {E}}}}(M,{{\mathcal {P}}})=0$ for all $1\le i \le d-1$ and $M\in {{\mathcal {M}}}$, it follows that

$$\begin{aligned} {\text {Hom}}_{{\underline{{{\mathcal {E}}}}}}(\Omega ^{i}({\underline{M}}),\underline{M'})\cong {\text {Ext}}^1_{{{\mathcal {E}}}}(\Omega ^{i-1}M,M')\cong {\text {Ext}}^i_{{{\mathcal {E}}}}(M,M')=0 \end{aligned}$$

for $1\le i\le d-1$ and $M'\in {{\mathcal {M}}}$. This proves the claim. $\square$

Proof of Theorem 1.2

By Theorem 5.7 and the “only if” part of Theorem 6.1 we know that $d\mathbb {Z}{\underline{{{\mathcal {M}}}}}$ is $d\mathbb {Z}$-cluster tilting in $\mathbb {Z}{\underline{{{\mathcal {E}}}}}$. Furthermore, under the equivalence $\mathbb {Z}{\underline{{{\mathcal {E}}}}}\xrightarrow {\cong } K^{-,b}({{\mathcal {P}}})/K^b({{\mathcal {P}}})$ in Theorem 3.4 an object $({\underline{E}},n)$ gets sent to $P^{\bullet }[-n]$ where $P^{\bullet }$ is a projective resolution of E. Then $\underline{Z^{-di}(P^{\bullet }[-n])}=\Omega ^{di+n}({\underline{E}})$ holds for $i\gg 0$. Thus $\underline{Z^{-di}(P^{\bullet }[-n])}\in {\underline{{{\mathcal {M}}}}}$ holds for all $i\gg 0$ exactly when $({\underline{E}},n)\in d\mathbb {Z}{\underline{{{\mathcal {M}}}}}$. Hence, $d\mathbb {Z}{\underline{{{\mathcal {M}}}}}$ corresponds to the subcategory in Theorem 1.2 under the equivalence $\mathbb {Z}{\underline{{{\mathcal {E}}}}}\xrightarrow {\cong } K^{-,b}({{\mathcal {P}}})/K^b({{\mathcal {P}}})$, which proves the claim. $\square$

Remark 6.2

Combining Lemma 5.9 with the description of the triangles in ${\underline{{{\mathcal {E}}}}}$, one obtains a description of the $(d+2)$-angles in $d\mathbb {Z}{\underline{{{\mathcal {M}}}}}$. Explicitly, consider all sequences

$$\begin{aligned} \Omega ^d(\underline{M_1},dn_1)\rightarrow ({\underline{M}}_{d+2},dn_{d+2})\xrightarrow {} \cdots \xrightarrow {}({\underline{M}}_{1},dn_{1}) \end{aligned}$$

in $d\mathbb {Z}{\underline{{{\mathcal {E}}}}}$ with $\underline{M_i}\in {\underline{{{\mathcal {M}}}}}$ for all i, which arises from a sequence in ${{\mathcal {E}}}$

$$\begin{aligned} N_1'\xrightarrow {u_{d+2}} N_{d+2}\xrightarrow {u_{d+1}} \cdots \xrightarrow {u_{1}}N_1 \end{aligned}$$

under isomorphisms $\underline{N_i}\cong \Omega ^{d(k+n_{i})}\underline{M_{i}}$ and $\underline{N'_{1}}\cong \Omega ^{d(k+n_{1}+1)}\underline{M_{1}}$, and such that there exists a commutative diagram

(6.3)

with exact rows, where $P_1,\cdots , P_d$ are projective. If we call such a sequence in $d\mathbb {Z}{\underline{{{\mathcal {M}}}}}$ a standard $(d+2)$-angle, then a $(d+2)$-angle of $d\mathbb {Z}{\underline{{{\mathcal {M}}}}}$ is precisely a sequence which is isomorphic to a standard $(d+2)$-angle.

We now want to show the “if” part of Theorem 6.1. To this end, we fix a full subcategory ${{\mathcal {M}}}$ of ${{\mathcal {E}}}$ and assume ${\underline{{{\mathcal {M}}}}}$ is d-cluster tilting in the left triangulated category ${\underline{{{\mathcal {E}}}}}$. Our goal is to show that ${{\mathcal {M}}}$ is d-cluster tilting in ${{\mathcal {E}}}$.

Lemma 6.4

If $M,M'\in {{\mathcal {M}}}$, then

$$\begin{aligned} {\text {Ext}}^i_{{{\mathcal {E}}}}(M,M')=0 \end{aligned}$$

for $1\le i\le d-1$.

Proof

By Lemma 2.4 and Definition 5.1 (iii) we have that

$$\begin{aligned} {\text {Ext}}^i_{{{\mathcal {E}}}}(M,P)\cong {\text {Ext}}^1_{{{\mathcal {E}}}}(\Omega ^{i-1}M,P)=0 \end{aligned}$$

for $P\in {{\mathcal {E}}}$ projective and $1\le i\le d-1$. Next, using the fact that if ${\text {Ext}}^1_{{{\mathcal {E}}}}(E,{{\mathcal {P}}})=0$, then ${\text {Ext}}^1_{{{\mathcal {E}}}}(E,E')\cong {\text {Hom}}_{{\underline{{{\mathcal {E}}}}}}(\Omega ({\underline{E}}),\underline{E'})$ for all $E'\in {{\mathcal {E}}}$, it follows that

$$\begin{aligned} {\text {Ext}}^i_{{{\mathcal {E}}}}(M,M')\cong {\text {Ext}}^1_{{{\mathcal {E}}}}(\Omega ^{i-1}M,M')\cong {\text {Hom}}_{{\underline{{{\mathcal {E}}}}}}(\Omega ^i({\underline{M}}),\underline{M'})=0 \end{aligned}$$

for all $1\le i\le d-1$ by Definition 5.1 (iv). This proves the claim. $\square$

Lemma 6.5

For any object $E\in {{\mathcal {E}}}$ there exist exact sequences

$$\begin{aligned} 0\rightarrow E\rightarrow M^1\rightarrow \cdots \rightarrow M^d\rightarrow 0 \end{aligned}$$

and

$$\begin{aligned} 0\rightarrow M_d\rightarrow \cdots \rightarrow M_1\rightarrow E\rightarrow 0 \end{aligned}$$

where $M_i,M^i\in {{\mathcal {M}}}$ for $1\le i\le d$.

Proof

Let $E\in {{\mathcal {E}}}$ be arbitrary, and choose a $(d+2)$-angle

$$\begin{aligned} 0\rightarrow E\rightarrow X^1\rightarrow \cdots \rightarrow X^d\rightarrow 0 \end{aligned}$$

in ${\underline{{{\mathcal {E}}}}}$ with $X^i\in {\underline{{{\mathcal {M}}}}}$ for $1\le i\le d$. Hence, by definition of triangles in ${\underline{{{\mathcal {E}}}}}$ (see Sect. 3) there exist a projective object $P\in {{\mathcal {E}}}$ and an exact sequence

$$\begin{aligned} 0\rightarrow E\oplus P\xrightarrow {f^1}N^1\xrightarrow {f^2}\cdots \xrightarrow {f^d}N^d\rightarrow 0. \end{aligned}$$

in ${{\mathcal {E}}}$, with $N^i\in {{\mathcal {M}}}$ for $1\le i\le d$. Since

$$\begin{aligned} 0={\text {Ext}}^{d-1}_{{{\mathcal {E}}}}(N^d,P)\cong {\text {Ext}}^{d-2}_{{{\mathcal {E}}}}({\text {Coker}}f^{d-2},P)\cong \cdots \cong {\text {Ext}}^1_{{{\mathcal {E}}}}({\text {Coker}}f^1,P) \end{aligned}$$

it follows that the map

$$\begin{aligned} {\text {Hom}}_{{{\mathcal {E}}}}(N^1,P)\rightarrow {\text {Hom}}_{{{\mathcal {E}}}}(E\oplus P,P)\rightarrow 0 \end{aligned}$$

is an epimorphism. Hence, the inclusion

$$\begin{aligned} P\xrightarrow {\begin{bmatrix}0\\ 1\end{bmatrix}}E\oplus P\xrightarrow {f^1}N^1 \end{aligned}$$

is a split monomorphism. The inclusion is also a composite of two admissible monomorphism, and it is therefore admissible. Therefore, its cokernel exists, which we denote by $M^1$. We can therefore write the sequence as

$$\begin{aligned} 0\rightarrow E\oplus P\xrightarrow {\begin{bmatrix}g^1&{}0\\ 0&{}1\end{bmatrix}}M^1\oplus P\xrightarrow {\begin{bmatrix}g^2&0\end{bmatrix}}N^2\xrightarrow {f^3} \cdots \xrightarrow {f^d}N^d\rightarrow 0 \end{aligned}$$

for some morphisms $g^1,g^2$. It follows from [12, Corollary 2.18] that the sequence

$$\begin{aligned} 0\rightarrow E\xrightarrow {g^1}M^1\xrightarrow {g^2}N^2\xrightarrow {f^3}\cdots \xrightarrow {f^d}N^d\rightarrow 0 \end{aligned}$$

is exact. This proves one part of the lemma. The other part is proved dually. $\square$

Proof of “if” part of Theorem 6.1 Part (i) follows from Proposition 4.4,

Lemmas 6.4 and 6.5. Part (ii) follows from part (i) together with Remark 4.2 (ii). $\square$

7 Gorenstein projectives

In this section we consider the subcategory of Gorenstein projective objects in ${{\mathcal {E}}}$. These objects were first introduced in [5] for modules over a noetherian ring. We refer to [13] for a survey of the theory for Artin algebras, and to [14] for more general rings.

Let ${{\mathcal {E}}}$ be an exact category with enough projectives ${{\mathcal {P}}}$. Recall that a long exact sequence

$$\begin{aligned} P^{\bullet }=\cdots \rightarrow P^0\rightarrow P^{1}\rightarrow \cdots \end{aligned}$$

of projective objects in ${{\mathcal {E}}}$ is called totally acyclic if the complex

$$\begin{aligned} {\text {Hom}}_{{{\mathcal {E}}}}(P^{\bullet },Q)= \cdots \rightarrow {\text {Hom}}_{{{\mathcal {E}}}}(P^{1},Q)\rightarrow {\text {Hom}}_{{{\mathcal {E}}}}(P^0,Q)\rightarrow \cdots \end{aligned}$$

is acyclic for all projective objects Q in ${{\mathcal {E}}}$. An object $G\in {{\mathcal {E}}}$ is called Gorenstein projective if there exists a totally acyclic complex $P^{\bullet }$ with

$$\begin{aligned} G=Z^0(P^{\bullet }):={\text {Ker}}(P^0\rightarrow P^{1}). \end{aligned}$$

We let ${{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$ denote the subcategory of ${{\mathcal {E}}}$ consisting of all Gorenstein projective objects. The subcategory ${{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$ is closed in ${{\mathcal {E}}}$ under extensions, direct summands, and kernels of admissible epimorphisms. In fact, the proof of [13, Proposition 2.1.7] also works for exact categories. In particular, $\Omega :{\underline{{{\mathcal {E}}}}}\rightarrow {\underline{{{\mathcal {E}}}}}$ restricts to a functor

$$\begin{aligned} \Omega :\underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})\rightarrow \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}}). \end{aligned}$$

The Gorenstein projective dimension of an object $E\in {{\mathcal {E}}}$, denoted $\dim _{{{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})}E$, is the smallest integer n such that $\Omega ^n({\underline{E}})\in \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$. We write $\dim _{{{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})}E=\infty$ if no such integer exists.

Since ${{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$ is an extension closed subcategory of ${{\mathcal {E}}}$, it inherits an exact structure making the inclusion

$$\begin{aligned} {{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})\rightarrow {{\mathcal {E}}}\end{aligned}$$

into an exact functor. Under this exact structure ${{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$ becomes a Frobenius exact category with projective/injective objects being the objects in ${{\mathcal {P}}}$, see [13, Proposition 2.1.11]. Hence, $\underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$ is a triangulated category. In particular, $\Omega :\underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})\rightarrow \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$ is an autoequivalence, and the quasi-inverse of $\Omega$ is the suspension functor for the triangulated category. The triangles in $\underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$ are precisely all triangles in the left triangulated category ${\underline{{{\mathcal {E}}}}}$ with components in $\underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$. In particular, we see that the canonical functor

$$\begin{aligned} {\underline{{{\mathcal {E}}}}}\rightarrow \mathbb {Z}{\underline{{{\mathcal {E}}}}} \quad \quad {\underline{E}}\mapsto ({\underline{E}},0) \end{aligned}$$

restrict to a functor of triangulated categories

$$\begin{aligned} \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})\rightarrow \mathbb {Z}{\underline{{{\mathcal {E}}}}}. \end{aligned}$$

This functor is fully faithful since $\Omega$ is an autoequivalence on $\underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$. The result below gives necessary and sufficient condition for it to be an equivalence. It was first shown in [11] for a noetherian ring.

Proposition 7.1

The essential image of the functor $\underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})\rightarrow \mathbb {Z}{\underline{{{\mathcal {E}}}}}$ is

$$\begin{aligned} \{({\underline{E}},n)\in \mathbb {Z}{\underline{{{\mathcal {E}}}}}\mid \dim _{{{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})}E<\infty \}. \end{aligned}$$

In particular, the functor is an equivalence if and only if $\dim _{{{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})}E<\infty$ for all $E\in {{\mathcal {E}}}$.

Proof

If $({\underline{E}},n)\cong ({\underline{G}},0)$ in $\mathbb {Z}{\underline{E}}$ with $G\in {{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$, then $\Omega ^{k+n}({\underline{E}})\cong \Omega ^k({\underline{G}})$ in ${\underline{{{\mathcal {E}}}}}$ for some $k>0$. Since $\Omega ^k({\underline{G}})\in \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$ it follows that E has finite Gorenstein projective dimension. Conversely, if $\dim _{{{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})}E=k<\infty$, then for any $n\in \mathbb {Z}$ there exist isomorphisms

$$\begin{aligned} ({\underline{E}},n)\cong (\Omega ^{k}{\underline{E}},n-k)\cong (\Omega ^{n-k}(\Omega ^{k}{\underline{E}}),0) \end{aligned}$$

and since $\Omega ^k{\underline{E}}\in \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$, it follows that $\Omega ^{n-k}(\Omega ^{k}{\underline{E}})\in \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$. This proves the claim. $\square$

As a corollary of this result one can deduce [10, Theorem 3.6] in the case of Artin algebras.

Proposition 7.2

Let $\Lambda$ be an Artin algebra. Then the canonical functor

$$\begin{aligned} \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({\text {mod}}\Lambda )\rightarrow D^b({\text {mod}}\Lambda )/{\text {perf}}\Lambda \end{aligned}$$

sending M to itself considered as a stalk complex in degree 0 is an equivalence if and only if $\Lambda$ is Iwanaga–Gorenstein.

Proof

This follows from Theorem 3.4 (ii) and Proposition 7.1 applied to ${{\mathcal {E}}}={\text {mod}}\Lambda$ together with [6, Proposition 4.2]. $\square$

We now relate this to the theory of cluster tilting subcategories.

Theorem 7.3

Assume $\dim _{{{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})}E<\infty$ for all $E\in {{\mathcal {E}}}$. Let ${{\mathcal {M}}}$ be a $d\mathbb {Z}$-cluster tilting subcategory of ${{\mathcal {E}}}$. Then ${{\mathcal {M}}}\cap {{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$ is a $d\mathbb {Z}$-cluster tilting subcategory of ${{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$.

Proof

Since ${{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$ is Frobenius and ${{\mathcal {M}}}\cap {{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$ contains ${{\mathcal {P}}}$, it follows that ${{\mathcal {M}}}\cap {{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$ is a $d\mathbb {Z}$-cluster tilting subcategory of ${{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$ if and only if $\underline{{{\mathcal {M}}}\cap {{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})}$ is a $d\mathbb {Z}$-cluster tilting subcategory of the triangulated category $\underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$. This is the easy case of Theorem 6.1. Now by Lemma 7.1 we have an equivalence of triangulated categories

$$\begin{aligned} \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})\xrightarrow {\cong } \mathbb {Z}{\underline{{{\mathcal {E}}}}} \end{aligned}$$

and since $d\mathbb {Z}{\underline{{{\mathcal {M}}}}}$ is a $d\mathbb {Z}$-cluster tilting subcategory of $\mathbb {Z}{\underline{{{\mathcal {E}}}}}$ by Theorem 5.7, the preimage of $d\mathbb {Z}{\underline{{{\mathcal {M}}}}}$ is a $d\mathbb {Z}$ cluster tilting subcategory of $\underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$. Explicitly, the preimage consists of all objects ${\underline{G}}\in \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$ such that $\Omega ^{dk}({\underline{G}})\in {\underline{{{\mathcal {M}}}}}$ for some integer $k\ge 0$. To show that this is equal to $\underline{{{\mathcal {M}}}\cap {{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})}$, we only need to show that such a G is contained in ${{\mathcal {M}}}$. Note first that since $G\in {{\mathcal {G}}}{{\mathcal {P}}}({{\mathcal {E}}})$, it follows that ${\text {Ext}}^i_{{{\mathcal {E}}}}(G,P)=0$ for all $P\in {{\mathcal {P}}}$. Hence, by a dimension shifting argument we get that

$$\begin{aligned} {\text {Ext}}^i_{{{\mathcal {E}}}}(G,E)\cong {\text {Ext}}^{i+j}_{{{\mathcal {E}}}}(G,\Omega ^j E) \end{aligned}$$

for any $E\in {{\mathcal {E}}}$ and any $j\ge 0$. Now let $M\in {{\mathcal {M}}}$ be arbitrary, and choose an integer $k\ge 0$ such that $\Omega ^{dk}({\underline{G}})\in {\underline{{{\mathcal {M}}}}}$ and $\Omega ^{dk}({\underline{M}})\in \underline{{{\mathcal {G}}}{{\mathcal {P}}}}({{\mathcal {E}}})$. It follows that

$$\begin{aligned} {\text {Ext}}^i_{{{\mathcal {E}}}}(G,M)\cong {\text {Ext}}^{i+dk}_{{{\mathcal {E}}}}(G,\Omega ^{dk}M)\cong {\text {Ext}}^{i}_{{{\mathcal {E}}}}(\Omega ^{dk} G,\Omega ^{dk}M)=0 \end{aligned}$$

for $1\le i\le d-1$ where we use dimension shifting and the fact that $\Omega ^{dk}M\in {{\mathcal {M}}}$ since ${{\mathcal {M}}}$ is $d\mathbb {Z}$-cluster tilting. Since $M\in {{\mathcal {M}}}$ was arbitrary, it follows that $G\in {{\mathcal {M}}}$, which proves the claim. $\square$

8 Examples

In this section we compute the singularity category for a higher Nakayama algebras of type $\mathbb {A}^{\infty }_{\infty }$, see [35]. For higher Nakayama algebras of type ${\tilde{\mathbb {A}}}$ we refer to Section 4.3 in [43].

Example 8.1

We follow the notation in [35]. Let k be a field. Let ${\underline{l}}=(\cdots ,l_{-1},l_0,l_1,\cdots )$ be the Kupisch Series of type $\mathbb {A}^{\infty }_{\infty }$ [35, Definition 3.10] given by

$$\begin{aligned} l_i= {\left\{ \begin{array}{ll} 2, &{} \text {if}\ i \equiv 1 {\text {mod}} 4 \\ 3, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

Let $A^{(2)}_{{\underline{l}}}$ be the 2-Nakayama k-algebra with Kupisch series ${\underline{l}}$ [35, Definition 3.13]. Explicitly, $A^{(2)}_{{\underline{l}}}$ is the k-linear category given by the infinite periodic quiver

(8.2)

with period 4, and with relations making all squares commute, and such that the following composites are 0.

$$\begin{aligned}&(a,a)\rightarrow (a,a+1)\rightarrow (a+1,a+1)&\text {for all } a\in \mathbb {Z}\\&(a,a+2)\rightarrow (a+1,a+2)\rightarrow (a+1,a+3)&\text {if } a\equiv 0,1 {\text {mod}} 4 \\&(a,a+1)\rightarrow (a+1,a+1)\rightarrow (a+1,a+2)&\text {if } a\equiv 3 {\text {mod}} 4. \end{aligned}$$

By [35, Theorem 3.16] we know that the category of finitely presented modules ${\text {mod}}A^{(2)}_{{\underline{l}}}$ has a $2\mathbb {Z}$-cluster tilting subcategory ${{\mathcal {M}}}^{(2)}_{{\underline{l}}}$. Explicitly, ${{\mathcal {M}}}^{(2)}_{{\underline{l}}}$ is the k-linear additive category given by the infinite periodic quiver

(8.3)

with period 4, and with relations

$$\begin{aligned} \alpha _j({\underline{a}}+e_i)\alpha _i({\underline{a}})-\alpha _i({\underline{a}}+e_j)\alpha _j({\underline{a}}) \end{aligned}$$

for any vertex ${\underline{a}}=(a_1,a_2,a_3)$ and integers $1\le i,j\le 3$, excluding the composites

$$\begin{aligned} 012\rightarrow 112\rightarrow 113 \quad 022\rightarrow 122\rightarrow 123 \quad 123\rightarrow 223\rightarrow 224 \\ 133\rightarrow 233\rightarrow 234 \quad 344\rightarrow 444\rightarrow 445 \end{aligned}$$

modulo 4. Here $e_1=(1,0,0)$, $e_2=(0,1,0)$ and $e_3=(0,0,1)$ are the unit vectors and

$$\begin{aligned} \alpha _i({\underline{a}}):{\underline{a}} \rightarrow {\underline{a}} + e_i \end{aligned}$$

is defined to be the unique arrow if it exists, and 0 otherwise. In particular, some of the relations are zero relations, for example $000\rightarrow 001\rightarrow 011$. Also, similar as in Proposition 2.22 in [35] the projective modules in ${\text {mod}}A^{(2)}_{{\underline{l}}}$ correspond to the vertices $(\lambda _1,\lambda _2,\lambda _3)$ with $\lambda _1=\lambda _3+1-l_{\lambda _3}$, which are precisely

$$\begin{aligned} {{\mathcal {S}}}:= & {} \{(001),(011),(002),(012),(022),(113),(123), \\&(133),(224),(234),(244),(445) { \text{ mod }} 4\} \end{aligned}$$

coloured in red in diagram (8.3). Also, as obtained in the proof of Proposition 2.25 in [35], the 2-syzygy of a non-projective object corresponding to a vertex $(\lambda _1,\lambda _2,\lambda _3)$ is

$$\begin{aligned} \Omega ^2(\lambda _1,\lambda _2,\lambda _3)= (\lambda _3+1-l_{\lambda _3},\lambda _1-1,\lambda _2-1). \end{aligned}$$

A simple computation shows that

$$\begin{aligned}&\Omega ^2(444)= (233) \quad \Omega ^2(233)=(112) \quad \Omega ^2(112)=(000) \\&\Omega ^2(344)= (223) \quad \Omega ^2(223)=(111) \quad \Omega ^2(111)=(000) \\&\Omega ^2(334)= (222) \quad \Omega ^2(222)=(011)\in {{\mathcal {S}}}\\&\Omega ^2(333)= (122) \quad \Omega ^2(122)=(001)\in {{\mathcal {S}}}. \end{aligned}$$

Hence, in $2\mathbb {Z}\underline{{{\mathcal {M}}}^{(2)}_{{\underline{l}}}}$ we have that any nonzero indecomposable object is isomorphic to (000, d) for some integer $d\in \mathbb {Z}$. Also, we have that

$$\begin{aligned} {\text {Hom}}_{2\mathbb {Z}\underline{{{\mathcal {M}}}^{(2)}_{{\underline{l}}}}}((000,d),(000,d'))= {\left\{ \begin{array}{ll} 0, &{}\quad \text {if}\ d\ne d' \\ k, &{}\quad \text {if}\ d=d'. \end{array}\right. } \end{aligned}$$

This shows that as additive categories we have an equivalence

$$\begin{aligned} 2\mathbb {Z}\underline{{{\mathcal {M}}}^{(2)}_{{\underline{l}}}}\cong \bigoplus _{i\in \mathbb {Z}} {\text {mod}}k. \end{aligned}$$

Example 8.4

We continue with the notation of the previous example. Consider the canonical automorphism $\phi :A^{(2)}_{{\underline{l}}}\rightarrow A^{(2)}_{{\underline{l}}}$ sending a vertex (i, j) to $(i-4,j-4)$. Let $\phi ^*:{\text {mod}}A^{(2)}_{{\underline{l}}}\rightarrow {\text {mod}}A^{(2)}_{{\underline{l}}}$ be the induced equivalence, which sends a module M to $M\circ \phi ^{-1}$. Then $\phi ^*$ restricts to an equivalence

$$\begin{aligned} \phi ^*:{{\mathcal {M}}}^{(2)}_{{\underline{l}}}\rightarrow {{\mathcal {M}}}^{(2)}_{{\underline{l}}} \end{aligned}$$

sending a vertex $(a_1,a_2,a_3)$ to $(a_1-4,a_2-4,a_3-4)$. This follows from the definition of the embedding ${{\mathcal {M}}}^{(2)}_{{\underline{l}}}\rightarrow {\text {mod}}A^{(2)}_{{\underline{l}}}$, see [35, Proposition 1.12]. Let

$$\begin{aligned} {\widetilde{A}}_{\underline{l'}}^{(2)}=A^{(2)}_{{\underline{l}}}/\phi \end{aligned}$$

be the orbit category. This is a higher Nakayama algebra of type ${\widetilde{\mathbb {A}}}$ with Kupisch Series $\underline{l'}=(3,2,3,3)$, see [35, Definition 4.11]. The canonical functor $F:A^{(2)}_{{\underline{l}}}\rightarrow A^{(2)}_{{\underline{l}}}/\phi$ induces a restriction functor

$$\begin{aligned} F^*:{\text {Mod}}{\widetilde{A}}_{\underline{l'}}^{(2)}\rightarrow {\text {Mod}}A^{(2)}_{{\underline{l}}} \end{aligned}$$

with left adjoint (called the push down functor)

$$\begin{aligned} F_*:{\text {Mod}}A^{(2)}_{{\underline{l}}}\rightarrow {\text {Mod}}{\widetilde{A}}_{\underline{l'}}^{(2)}. \end{aligned}$$

The functor $F_*$ is exact and restricts to a well-defined functor between the categories of finitely presented modules

$$\begin{aligned} F_*:{\text {mod}}A^{(2)}_{{\underline{l}}}\rightarrow {\text {mod}}{\widetilde{A}}_{\underline{l'}}^{(2)} \end{aligned}$$

see [15, Section 14.3]. Now the subcategory ${{\mathcal {M}}}^{(2)}_{\underline{l'}}:= F_*({{\mathcal {M}}}^{(2)}_{{\underline{l}}})$ is $2\mathbb {Z}$-cluster tilting in ${\text {mod}}{\widetilde{A}}_{\underline{l'}}^{(2)}$ by [35, Theorem 4.12]. It follows from [15, Section 14.4] that there exists an equivalence ${{\mathcal {M}}}^{(2)}_{\underline{l'}}\cong {{\mathcal {M}}}^{(2)}_{{\underline{l}}}/\phi ^*$ such that the composite

$$\begin{aligned} {{\mathcal {M}}}^{(2)}_{{\underline{l}}}\xrightarrow {F_*} {{\mathcal {M}}}^{(2)}_{\underline{l'}}\xrightarrow {\cong } {{\mathcal {M}}}^{(2)}_{{\underline{l}}}/\phi ^* \end{aligned}$$

is just the natural projection functor. Now $F_*$ is exact and preserves projectives, and hence the computations of the projectives and the syzygies in Example 8.1 are also valid for ${{\mathcal {M}}}^{(2)}_{\underline{l'}}$. It follows that as additive categories we have an equivalence

$$\begin{aligned} 2\mathbb {Z}\underline{{{\mathcal {M}}}^{(2)}_{\underline{l'}}}\cong \bigoplus _{1\le i\le 4} {\text {mod}}k. \end{aligned}$$

Finally, note that the module corresponding to vertex (344) is injective in ${\text {mod}}{\widetilde{A}}_{\underline{l'}}^{(2)}$, and by the computations of the syzygy above we see that it has infinite projective dimension. This shows that algebra ${\widetilde{A}}_{\underline{l'}}^{(2)}$ is not Iwanaga–Gorenstein.