1 Introduction

1.1 General introduction

An insurance company’s credit rating indicates its ability to pay customer’s claims. A bad credit rating can affect a company’s business plan, growth potential or even survival chances if new finance is needed to fulfil the capital requirements prescribed by Solvency II. The rating process run by a credit rating agency includes quantitative and qualitative analysis, where cash flow is one of the most important factors. Particular attention is paid to dividend payments, which are commonly believed to indicate a company’s financial health.

Searching for the optimal strategy which maximises the value of expected discounted dividends under different constraints and in different setups has been a popular problem in actuarial mathematics for a long time. The papers by Shreve et al. (1984), Asmussen and Taksar (1997), Azcue and Muler (2005) are just some examples. For a detailed review we refer for instance to the survey by Albrecher and Thonhauser (2009). The papers mentioned above assume the discounting rate to remain constant up to the considered time horizon, often chosen to be infinite. Following the recent crisis with ultra low interest rates in Europe, the question arises whether the discounting of cash flows by a constant discounting rate could be considered as an admissible assumption. A stochastic discounting factor increases the dimension of the considered problem along with the complexity. Nevertheless, in recent years stochastic discounting has become a topical question in dividend maximisation problems. For instance Jiang and Pistorius (2012) model the interest rate by a positive deterministic function of the current state of a given Markov chain. If the drift of the underlying surplus process is positive in each state, they prove that it is optimal to adopt a regime-dependent barrier strategy; if the drift is small and negative in one state, the optimal strategy has a different form, which is explicitly identified for the two regimes case.

Akyildirim et al. (2014) consider two macroeconomic factors: the interest rates and the issuance costs. Both factors are assumed to be governed by an exogenous Markov chain. The optimal dividend policy is characterised by dependence on these two factors: all things being equal, firms distribute more dividends when interest rates are high and less when issuing costs are high.

Where Jiang and Pistorius (2012) use the fixed point theorem in order to obtain their results, Akyildirim et al. (2014) apply the direct approach by solving the corresponding ODEs, a method we will use in our paper.

In the present paper, we take into account the time-varying interest by introducing a discounting factor given by an exponential Cox–Ingersoll–Ross (CIR) process. A CIR process is a squared diffusion process, which can attain non-negative values and hit zero for special parameters. Here, we would like to emphasise that in contrast to the usual financial setup, we are modelling the compound interest and not the short rate. Negative interest rates have governed the markets in the last several years, keeping insurance companies under pressure. Therefore, assuming a market interest rate to be given by a non-negative CIR process would not be realistic. The case of consumption maximisation with an Ornstein–Uhlenbeck process describing the interest rates has been considered in Eisenberg (2018). The logic behind the choice of a CIR process is that we would rather look at the preferences of the insurer than at the real market-given interest. The non-negativity of CIR processes describing the compound preference implies that for the insurer money today is preferable to money tomorrow. This idea conforms to the work of the famous Austrian economist Böhm-Bawerk claiming an always positive preference interest, see Von Böhm-Bawerk (1890). On the website of the Mises Institute (The Ludwig von Mises Institute for Austrian Economics 1999), named after the most famous student of Böhm-Bawerk economist Ludwig von Mises, one finds plenty of essays defending the thesis of Böhm-Bawerk and examining counterarguments. A detailed discussion of the topic certainly goes beyond the scope of the present paper. Hence, we refer for instance to an essay by Polleit (2015) and give below a digest of the theory that serves as an economic basis for the mathematical model presented in the following chapters. The theory of positive time preference distinguishes between the market and the originary interest rate. While the first is the interest rate observed on deposit or loan markets, the originary interest rate measures consumption today compared to consumption tomorrow, i.e. the time preference. According to Böhm-Bawerk and his student von Mises the originary interest rate and consequently the (compound) time preference are always positive. Some modern economists, for instance Alchian (2018), even call a positive time preference the “principle of rationality”. However, an insurance company cannot ignore negative market interest rates governing the European markets in the recent years. With this in mind, the oscillations of a CIR process can be interpreted as the dependence of the insurer’s preferences on the movements of the market interest rate: if the compound preference goes down the market rate is supposed to be negative and vice versa, whereas the compound preference always stays positive. Usually, when modelling interest rates in financially motivated problems one assumes CIR to be mean-reverting. However, under this assumption our problem would be ill-posed on the one hand, and would contradict the thesis in Von Böhm-Bawerk (1890), that the value of goods decreases by postponing the consumption, on the other hand. Therefore, we require the CIR process to be non-mean-reverting, implying the almost sure convergence to infinity, shown in Sect. 1.2.

We assume that the underlying income process is a linear function of time without a random component. Our target is to maximise the expected discounted consumption. This structure yields a two-dimensional problem where the optimal consumption strategy depends on the parameters of the underlying CIR process. For instance, for a highly volatile discounting factor, it might be optimal to wait with the consumption until the discounting process approaches some relatively small positive level, taking into account that the waiting period could last forever. In the low volatility case, we prove that the optimal strategy will always be to spend the maximal possible amount independent of the discounting factor.

Additionally, we consider an insurance company whose surplus is described by a Brownian motion with drift independent of the CIR. Here, we again have a two-dimensional problem. However, the problem formulation puts an emphasis on the ruin time of the underlying surplus process. We are able to reduce the problem to the classical setup with a constant discounting rate for some special parameters of the CIR process.

To the best of our knowledge, this paper is the first to study an exponential CIR as a discounting factor in the context of consumption/dividend maximisation problems. Despite the fact that the value function depends on two variables—the surplus and the discounting process—we are able to find explicit expressions for the optimal strategy and the value function in the deterministic income case and (under some restrictions on the underlying CIR) in the case of Brownian risk model.

It will be of major importance for the understanding of the paper to remind the reader on some properties and results connected to CIR processes. Accordingly, we organise the paper as follows: in the next subsection we give an overview of CIR processes. For the convenience of reading, we postpone the technical proofs to the “Appendix”.

In Sect. 2, we consider the case of a deterministic, linear in time income process, which can be interpreted as the income of an individual or household. There, we will distinguish between two different cases concerning the parameters of the considered CIR process and give explicit expressions for the optimal strategy and the value function. In Sect. 2.4, we solve the problem of dividend maximisation for special parameters of the underlying CIR process. Conclusion at the end of Sect. 2 gives an overview of the possible future research directions. Some technical proofs are given in the “Appendix”, Sect. 1.

1.2 Preliminaries

For the sake of clarity of presentation, we postpone most of the proofs of this subsection to the “Appendix”, Sect. 1. In the following sections, we use the common notation: \(\mathbb {P}[\;\cdot \;|Y_0=y]=\mathbb {P}_y[\;\cdot \;]\) and \(\mathbb {E}[\;\cdot \; |Y_0=y]=\mathbb {E}_y[\;\cdot \;]\) for any stochastic process \(\{Y_t\}\). In the remainder of the paper we let \(r=\{r_t\}\) be a Cox–Ingersoll–Ross (CIR) process

$$\begin{aligned} \,\mathrm{d}r_t=(a r_t+b)\,\mathrm{d}t+\delta \sqrt{r_t}\,\mathrm{d}W_t, \end{aligned}$$
(1)

where a, b and \(\delta \) are positive constants and \(W=\{W_t\}\) is a standard Brownian motion. Due, for example, to Ethier and Kurtz (1986), CIR processes have the strong Markov property. We define

$$\begin{aligned} M(r,t):=\mathbb {E}_r[e^{-r_t}]. \end{aligned}$$

Due to Cox et al. (1985), we know that the density function of \(r_t\) with initial value r is given by

$$\begin{aligned} f(y):=c(t)e^{-u(t,r)-v(t,y)}\left( \frac{v(t,y)}{u(t,r)}\right) ^{q/2}I_q \left( 2\sqrt{u(t,r)v(t,y)}\right) , \end{aligned}$$
(2)

where \(I_q(x)=\sum \nolimits _{m=0}^\infty \frac{1}{m!\Gamma (m+q+1)}\Big (\frac{x}{2}\Big )^{2m+q}\) is the modified Bessel function of the first kind and

$$\begin{aligned}&c(t):=\frac{2a}{(e^{at}-1)\delta ^2},&q:=\frac{2b}{\delta ^2}-1,\\&u(t,r):=c(t)re^{at},&v(t,y):=c(t)y. \end{aligned}$$

Also, one has that

$$\begin{aligned}&M(r,t)=\mathbb {E}_r[e^{- r_t}]= e^{-\frac{2ab}{\delta ^2}t}\beta (t)^{\frac{2b}{\delta ^2}}\cdot e^{-r \beta (t)}, \end{aligned}$$
(3)

where \(\beta (t):=\frac{1}{\frac{\delta ^2}{2a}+\big (1-\frac{\delta ^2}{2a}\big )e^{-at}}\).

Lemma 1.1

In the case \(\frac{\delta ^2}{2}\le a\), the function M(r, t) is strictly decreasing in t and the process \(\{e^{-r_t}\}\) is a supermartingale.

Proof

Using that \(\beta '(t)=a\big (1-\frac{\delta ^2}{2a}\big )e^{-at}\beta (t)^2>0\), we obtain

$$\begin{aligned} M_t(r,t)=M(r,t)\left\{ -b \beta (t)-r ae^{-at}\left( 1-\frac{\delta ^2}{2a}\right) \beta (t)^2\right\} <0 \end{aligned}$$

for all \(r\in \mathbb {R}_+\). The supermartingale property follows immediately due to the Markov property and the structure of M. \(\square \)

Lemma 1.2

Due to Revuz and Yor (1999, p. 282), the function M(r, t) solves the partial differential equation

$$\begin{aligned} (ar+b)M_r(r,t)+\frac{\delta ^2 r}{2}M_{rr}(r,t)-M_t(r,t)=0. \end{aligned}$$

The below lemma ensures the well-posedness of the problems we are going to consider.

Lemma 1.3

If \(a>0\) then the CIR process \(\{r_t\}\) fulfils \(\lim \limits _{t\rightarrow \infty }r_t=\infty \) a.s.

For the proof refer to the “Appendix”, Sect. 1.

The usual method for proving a verification theorem is to apply Ito’s formula, and to prove the stochastic integral to be a martingale. Later, we will see that the following result provides the necessary martingale argument for the verification theorem.

Lemma 1.4

For \(2b<\delta ^2\) let q be given as in (2), then it holds that

$$\begin{aligned}&\int _0^\infty y^{-\frac{2b}{\delta ^2}} e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y<\infty ,\\&\int _0^s \mathbb {E}_r\big [r_t^{-2q-1}\big ]\,\mathrm{d}t<\infty \quad \text{ for } \text{ all } s\in \mathbb {R}_+. \end{aligned}$$

Proof

Since \(2b<\delta ^2\) it holds that \(-1<q<0\) and

$$\begin{aligned} \int _0^\infty y^{-\frac{2b}{\delta ^2}} e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y&= \int _0^\infty y^{\left( 1-\frac{2b}{\delta ^2}\right) -1} e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y =\Gamma (-q)\left( \frac{2a}{\delta ^2}\right) ^{q}<\infty . \end{aligned}$$

Further, using (2) and the bounded convergence theorem, we get:

$$\begin{aligned} \mathbb {E}_r\big [r_t^{-2q-1}\big ]&=\sum \limits _{m=0}^\infty \frac{c(t)^{q+1+2m}e^{-c(t)re^{at}}}{m!\Gamma (m+q+1)}\int _0^\infty y^{m-\frac{2b}{\delta ^2}}e^{-\frac{4a}{\delta ^2}y}e^{-c(t)y}\,\mathrm{d}y\\&=\sum \limits _{m=0}^\infty \frac{c(t)^{q+1+2m}e^{-c(t)re^{at}}}{m!\Gamma (m+q+1)}\cdot \frac{\Gamma (m-q)}{\left( \frac{4a}{\delta ^2}+c(t)\right) ^{m-q}}. \end{aligned}$$

As \(\lim \limits _{t\rightarrow 0} c(t)^{q+1+2m}e^{-c(t)re^{at}}=0\), the above power series is integrable over (0, s) for every \(s\in \mathbb {R}_+\). \(\square \)

Throughout this paper we will use the following notation: for a fixed \(r^*\in \mathbb {R}_+\), we define

$$\begin{aligned} \tau :=\inf \{t \ge 0: r_t=r^*\}. \end{aligned}$$
(4)

Further, we let

$$\begin{aligned}&\psi _1(r):=\mathbb {E}_r\left[ \int _0^{\tau }e^{-r_s}\,\mathrm{d}s\right] , \text{ for } r\le r^*,\end{aligned}$$
(5)
$$\begin{aligned}&\phi _1(r):=\mathbb {E}_r\Big [\mathbb {1}_{[\tau <\infty ]}\Big ], \text{ for } r\ge r^*,\end{aligned}$$
(6)
$$\begin{aligned}&\phi _2(r):=\mathbb {E}_r\Big [\mathbb {1}_{[\tau <\infty ]}\tau \Big ] \text{ for } r\ge r^*. \end{aligned}$$
(7)

Since \(\lim \limits _{t\rightarrow \infty } r_t=\infty \) a.s., we know \(\tau <\infty \) a.s.

Lemma 1.5

The functions \(\psi _1(r)\), \(\phi _1(r)\) and \(\phi _2(r)\) solve the differential equations

$$\begin{aligned}&e^{-r}+(ar+b)g'(r)+\frac{\delta ^2r}{2} g''(r)=0, \end{aligned}$$
(8)
$$\begin{aligned}&(ar+b)g'(r)+\frac{\delta ^2r}{2}g''(r)=0,\end{aligned}$$
(9)
$$\begin{aligned}&(ar+b)g'(r)+\frac{\delta ^2r}{2}g''(r)+\phi _1(r)=0, \end{aligned}$$
(10)

respectively with boundary conditions

$$\begin{aligned}&\psi _1(r^*)=0 \text{ and } \psi _1'(0)=-\frac{1}{b},\\&\phi _1(r^*)=1 \text{ and } \phi _1(\infty )=0,\\&\phi _2(r^*)=0 \text{ and } \phi _2(\infty )=0. \end{aligned}$$

For the proof, following the method described in Shreve et al. (1984, p. 57), refer to the “Appendix”, Sect. 1.

2 Main results

Before considering an insurance company with surplus process following a Brownian motion, we look at the problem of consumption maximisation for an individual with a deterministic income. The discounting factor is assumed to be given by an exponential CIR process, \(\{e^{-r_t}\}\). The filtration \(\{\mathcal {F}_t\}\) is generated by \(\{r_t\}\). Let the income process of the considered individual or household be given by

$$\begin{aligned} X_t=x+\mu t, \quad \mu >0. \end{aligned}$$

Let C denote the accumulated consumption process up to time t and the ex-consumption income be given by

$$\begin{aligned} X^C_t=x+\mu t-C_t. \end{aligned}$$

We call a strategy C admissible if it is adapted to the filtration \(\{\mathcal {F}_t\}\), is non-decreasing and fulfils \(C_0\ge 0\), \(X_t^C\ge 0\) for all \(t\in \mathbb {R}_+\), meaning in particular that \(C_t\le x+\mu t\). In the following, we denote the set of all admissible strategies by \(\mathfrak A\). The following notation will be used throughout this section:

$$\begin{aligned}&V^C(r,x):=\mathbb {E}_{(r,x)}\left[ \int _0^\infty e^{-r_s}\,\mathrm{d}C_s\right] ,\\&V(r,x):=\sup \limits _{C\in \mathfrak A} V^C(r,x). \end{aligned}$$

We call \(V^C(r,x)\) the performance function corresponding to the strategy C and V(r, x) the value function. Our target is to find an optimal consumption strategy, such that the expected discounted consumption

$$\begin{aligned} \mathbb {E}_{(r,x)}\left[ \int _0^\infty e^{-r_s}\,\mathrm{d}C_s\right] \end{aligned}$$

is maximised, i.e. to find the value function V(r, x) and an admissible strategy \(C^*\) such that \(V(r,x)=V^{C^*}(r,x)\). Note that the problem we are looking at is well-defined because we assume \(r_t\) to be non-mean-reverting. Indeed, because \(X_t\ge C_t\) for every admissible strategy C, using Lemmata 1.1, 1.3 and Tonelli’s theorem we have

$$\begin{aligned} V^C(r,x)&=\mathbb {E}_{(r,x)}\left[ \int _0^\infty e^{-r_s}\,\mathrm{d}C_s\right] \le \mathbb {E}_{(r,x)}\left[ \int _0^\infty e^{-r_s}C_s\,\mathrm{d}s\right] \le \mathbb {E}_{(r,x)}\left[ \int _0^\infty e^{-r_s}X_s\,\mathrm{d}s\right] \\&=\int _0^\infty M(r,s)X_s\,\mathrm{d}s\le \max \left( 1,\frac{2a}{\delta ^2}\right) \int _0^\infty e^{-\frac{2ab}{\delta ^2}s}(x+\mu s)\,\mathrm{d}s<\infty , \end{aligned}$$

as \(0<\beta (t)\le \max \Big (1,\frac{2a}{\delta ^2}\Big )\).

The Hamilton–Jacobi–Bellman (HJB) equation can be motivated using the standard methods from stochastic control theory, we therefore omit the detailed derivation and refer the reader to Schmidli (2008, pp. 98,103) and references therein. The HJB equation consists of two partial differential equations with linear coefficients:

$$\begin{aligned} \max \left\{ \mu V_x+(ar+b) V_r+\frac{\delta ^2r}{2}V_{rr},e^{-r}-V_x\right\} =0. \end{aligned}$$
(11)

Theorem 2.5 below illustrates that the HJB equation corresponds to the problem we consider.

To simplify our considerations we introduce the following notation

$$\begin{aligned} \mathcal L(f)(r,x)=\mu f_x(r,x)+(ar+b) f_r(r,x)+\frac{\delta ^2r}{2}f_{rr}(r,x) \end{aligned}$$

for any appropriate function \(f:\mathbb {R}_+^2\rightarrow \mathbb {R}\).

In order to get an idea of how the value function and the optimal strategy look, we first consider the performance function corresponding to the strategy “maximal spending”, i.e. \(C_t^{\max }=x+\mu t\). Using Fubini’s theorem, this performance function is given by

$$\begin{aligned} H(r,x):=x e^{-r}+\mu \mathbb {E}_r\left[ \int _0^\infty e^{-r_s}\,\mathrm{d}s\right] = x e^{-r}+\mu \int _0^\infty M(r,s)\,\mathrm{d}s, \end{aligned}$$
(12)

with \(M(r,t)=\mathbb {E}_r[e^{-r_t}]\). The function M fulfils \(M\in \mathcal C^{2,1}(\mathbb {R}_+^2)\) and solves the differential equation

$$\begin{aligned} (ar+b)M_r(r,t)+\frac{\delta ^2 r}{2}M_{rr}(r,t)-M_t(r,t)=0. \end{aligned}$$

refer to the “Appendix”, Sect. 1. In particular this means, that using the Leibniz integral rule, we have

$$\begin{aligned} H_r(r,x)=- x e^{-r}+\mu \int _0^\infty M_r(r,s)\,\mathrm{d}s\quad \text{ and } \quad H_{rr}(r,x)=x e^{-r}+\mu \int _0^\infty M_{rr}(r,s)\,\mathrm{d}s. \end{aligned}$$

Inserting H(r, x) into the HJB equation yields \(e^{-r}-H_x(r,x)=0\) on the one hand and on the other hand

$$\begin{aligned} \mu H_x+(ar+b) H_r+\frac{\delta ^2r}{2}H_{rr}&=\mu e^{-r}+xe^{-r}\left( -ar-b+\frac{\delta ^2r}{2}\right) +\mu \\&{}\int _0^\infty (ar+b)M_r(r,s)+\frac{\delta ^2 r}{2}M_{rr}(r,s)\,\mathrm{d}s\\&=\mu e^{-r}+xe^{-r}\left( -ar-b+\frac{\delta ^2r}{2}\right) +\mu \int _0^\infty M_s(r,s)\,\mathrm{d}s\\&=\mu e^{-r}+xe^{-r}\left( -ar-b+\frac{\delta ^2r}{2}\right) -\mu e^{-r}\\&= xe^{-r}\left( -ar-b+\frac{\delta ^2r}{2}\right) , \end{aligned}$$

using \(\int _0^\infty M_s(r,s)\,\mathrm{d}s=M(r,s)\Big |_0^\infty =-e^{-r}\) and the differential equation for M.

Note that the sign of the above expression does not depend on x and we define

$$\begin{aligned} R:=\frac{b}{\frac{\delta ^2}{2}-a}. \end{aligned}$$
(13)

for \(\frac{\delta ^2}{2}>a\).

In the following section we consider different combinations of the parameters a, b and \(\delta \), influencing the solution to the HJB equation (11).

2.1 The case \(\frac{\delta ^2}{2}\le a\)

In this case it clearly holds that

$$\begin{aligned} -ar-b+\frac{\delta ^2r}{2}<0 \end{aligned}$$

independently of b and r, which in turn means H(r, x) solves the HJB equation (11). The inequality \(\frac{\delta ^2}{2}\le a\) can be interpreted in the following way. The volatility of the CIR process compared to the speed of drifting towards infinity is relatively small, so that the probability of downward excursions becomes negligible. Therefore, it is always better to consume the maximal possible amount available right now, because the expected preference factor M(r, t) will be decreasing in t for every value of r.

We can now formulate the following verification theorem:

Theorem 2.1

The function H(r, x) is the value function and the strategy \(C^{\max }_t:=x+\mu t\) “\(\rightsquigarrow \) to always spend the maximal possible amount independent of r and x” is the optimal strategy. This means \(V(r,x)=H(r,x)=V^{C^{\max }}(r,x)\).

We skip the proof, since it is similar to the proof of the verification theorem in the next subsection.

2.2 The case \(a<\frac{\delta ^2}{2}\)

If \(a<\frac{\delta ^2}{2}\), the volatility of the CIR process is high enough to produce downwards excursions with a sufficient probability. This means that, depending on the initial value r, it may be better to abandon the immediate consumption in favour of a later consumption with a higher compound preference. In this case, H(r, x) defined in (12) does not solve the HJB equation (11) for \(r>R\).

In Schmidli (2008, p. 27) for instance, one finds that there are two methods for solving an optimisation problem: to show directly that the value function solves the HJB equation or to guess the optimal strategy and to prove that the corresponding return function solves the HJB equation. Here, we will follow the second method.

We conjecture that the optimal strategy is of a barrier type in the following sense: there is a positive constant \(\bar{r}\in \mathbb {R}_+\) such that it is optimal to wait with the consumption if \(r>\bar{r}\) and to immediately spend everything if \(r\le \bar{r}\). Since we do not know what the optimal preference barrier should look like, we let \(\bar{r}\in \mathbb {R}_+\) be arbitrary but fixed and follow the barrier strategy with the barrier \(\bar{r}\) as described above. With a slight abuse of notation, in the following we use the stopping time \(\tau \) defined in (4) with \(\bar{r}\) instead of \(r^*\). The return function corresponding to the above barrier strategy consists of two parts:

$$\begin{aligned}&F(r,x):=xe^{-r}+\mu \mathbb {E}_r\left[ \int _0^\tau e^{-r_s}\,\mathrm{d}s\right] +\tilde{F},\quad r\le \bar{r}\\&\text{ and }\\&G(r,x):=\mathbb {E}_r\Big [\big (x+\mu \tau \big )\mathbb {1}_{[\tau<\infty ]}\Big ]e^{-\bar{r}}+\tilde{F}\mathbb {E}_r\Big [\mathbb {1}_{[\tau <\infty ]}\Big ],\quad r> \bar{r}, \end{aligned}$$

where \(\tilde{F}\) is some positive constant whose value should be determined later. This means that F describes the spending if the initial value \(r_0=r\le \bar{r}\), and G describes the spending after the waiting time until \(r_t\) approaches \(\bar{r}\) or \(\infty \).

By construction, \(G(\bar{r},x)=F(\bar{r},x)\) and \(G_x(\bar{r},x)=F_x(\bar{r},x)\) for all \(x\in \mathbb {R}_+\).

The question is whether G and F given above solve the HJB equation (11) on \([\bar{r},\infty )\) and on \([0,\bar{r}]\) respectively and fulfil \(G_r(\bar{r}, x) = F_r(\bar{r}, x)\) and \(G_{rr}(\bar{r}, x) = F_{rr}(\bar{r}, x)\) for all \(x\in \mathbb {R}_+\) with bounded derivatives \(F_r\) and \(G_r\).

2.2.1 Properties of F and G

In this subsection, we investigate the properties of functions F and G. Using notation (5), we can rewrite F as follows

$$\begin{aligned} F(r,x)=xe^{-r}+\mu \psi _1(r)+\tilde{F}. \end{aligned}$$

That is, inserting the function F into the HJB equation (11) we obtain on the one hand \(e^{-r}-F_x=0\) and on the other hand, using Lemma 1.5:

$$\begin{aligned} \mathcal {L}(F)(r,x)&=\mu e^{-r}+xe^{-r} \left( -ar-b+\frac{\delta ^2r}{2}\right) +\mu (ar+b)\psi _1'+\mu \frac{\delta ^2 r}{2}\psi _1''(r)\\&=xe^{-r}\left( -ar-b+\frac{\delta ^2r}{2}\right) . \end{aligned}$$

Thus, F solves the HJB equation (11) on the set \([0,\bar{r}]\times \mathbb {R}_+\), if \(\bar{r}\le R\), for R defined in (13).

Consider now the function G. Using Definitions (6) and (7), G can be rewritten such that

$$\begin{aligned} G(r,x)=x\phi _1(r)e^{-\bar{r}}+\mu \phi _2(r)e^{-\bar{r}}+\tilde{F}\phi _1(r). \end{aligned}$$

We now find the conditions under which G solves the HJB equation (11) on the interval \([\bar{r},\infty )\). Lemma 1.5 yields

$$\begin{aligned} \mathcal L(G)(r,x)&=\mu \phi _1(r)e^{-\bar{r}}+\big (xe^{-\bar{r}}+\tilde{F}\big )\left\{ (ar+b)\phi _1'(r)+\frac{\delta ^2r}{2}\phi _1''(r)\right\} \\&\quad + \mu e^{-\bar{r}} \left\{ (ar+b)\phi _2'(r)+\frac{\delta ^2r}{2}\phi _2''(r)\right\} \\&= \mu \phi _1(r)e^{-\bar{r}}-\mu \phi _1(r)e^{-\bar{r}}=0. \end{aligned}$$

We therefore consider \(e^{-r}-G_x(r,x)\) and search for conditions satisfying the relation \(e^{-r}-G_x(r,x)\le 0\) on \([\bar{r},\infty )\times \mathbb {R}_+\). First, we prove the following auxiliary result:

Lemma 2.2

The function \(\phi _1(r)\) is decreasing, and there is a unique \(r^*\in [0,R]\) such that

$$\begin{aligned} \phi _1(r^*)=-\phi _1'( r^*)=1\quad \text{ and }\quad \phi _1(r)>-\phi _1'(r)\quad \text{ for } r>r^*. \end{aligned}$$

Proof

For the proof consult the “Appendix”, Sect. 1. \(\square \)

The following Lemma considers the expression \(e^{-r}-G_x(r,x)\) when the barrier is given by \(r^*\) defined above.

Lemma 2.3

Let \(\bar{r} = r^*\), defined in Lemma 2.2. Then, for all \(r> r^*\) the following inequality holds true:

$$\begin{aligned} G_x(r,x)=\phi _1(r)e^{-r^*}> e^{-r} . \end{aligned}$$

Proof

Deriving \(e^r\phi _1(r)\) yields \(\big (e^r\phi _1(r)\big )'=e^r\phi _1(r)\left( 1+\frac{\phi _1'(r)}{\phi _1(r)}\right) > 0\), using Lemma 2.2. Then,

$$\begin{aligned} e^{-r}-G_x(r,x)=e^{-r}e^{-r^*}\Big (e^{r^*}-e^r\phi _1(r)\Big )<e^{-r}e^{-r^*}\Big (e^{r^*}-e^{r^*}\phi _1(r^*)\Big )=0 \end{aligned}$$

for \(r>r^*\). \(\square \)

We can therefore conclude that G solves the HJB (11) on \([r^*,\infty )\) if \(\bar{r}=r^*\).

2.2.2 The optimal strategy and verification theorem

From now on we assume \(\bar{r}=r^*\), i.e. \(\frac{\phi _1'(r^*)}{\phi _1(r^*)}=-1\).

Due to Lemma 2.2, both functions F and G solve the HJB equation (11) on \([0,r^*]\) and on \([r^*,\infty )\) respectively. Next, we consider the derivatives \(G_r(r^*,x)\), \(F_r(r^*,x)\) and \(G_{rr}(r^*,x)\), \(F_{rr}(r^*,x)\) in order to guarantee a smooth value function. It holds that

$$\begin{aligned} G_r(r^*,x)&=xe^{-r^*}\phi _1'(r^*)+\mu \phi _2'(r^*)e^{-r^*}+\tilde{F}\phi _1'(r^*)\\&=-xe^{-r^*}+\mu \phi _2'(r^*)e^{-r^*}-\tilde{F},\\ F_r(r^*,x)&=-xe^{-r^*}+\mu \psi _1'(r^*) \end{aligned}$$

and

$$\begin{aligned} G_{rr}(r^*,x)&= xe^{-r^*}\phi _1''(r^*)+\mu \phi _2''(r^*)e^{-r^*}+\tilde{F}\phi _1''(r^*),\\ F_{rr}(r^*,x)&= xe^{-r^*}+\mu \psi _1''(r^*). \end{aligned}$$

Remark 2.4

Selecting

$$\begin{aligned} F(r^*,0)=\tilde{F}=\mu \phi _2'(r^*)e^{-r^*}-\mu \psi _1'(r^*) \end{aligned}$$
(14)

yields \(G_r(r^*,x)=F_r(r^*,x)\) for all \(x\in \mathbb {R}_+\). Note, it holds that \(\tilde{F}\ge 0\) due to the proof of Lemma 1.5, consult “Appendix”, Sect. 1.

Consider the differential equations (8) multiplied by \((-\mu )\); (9) multiplied by \(\tilde{F}\) and (10) multiplied by \(\mu e^{-r^*}\) at \(r^*\) such that

$$\begin{aligned}&-\mu e^{-r^*}-(ar^*+b)\mu \psi _1'(r^*)-\frac{\delta ^2r^*}{2} \mu \psi _1''(r^*)=0,\\&(ar^*+b)\tilde{F}\phi _1'(r^*)+\frac{\delta ^2r^*}{2} \tilde{F}\phi _1''(r^*)=0,\\&e^{-r^*}(ar^*+b)\mu \phi _2'(r^*)+\mu e^{-r^*}\frac{\delta ^2r^*}{2} \phi _2''(r^*)+\mu e^{-r^*}\phi _1(r^*)=0. \end{aligned}$$

Using \(\phi _1(r^*)=-\phi _1'(r^*)=1\) and summing the above equations yields

$$\begin{aligned} \begin{aligned}&(ar^*+b)\big \{\mu \phi _2'(r^*)e^{-r^*}-\mu \psi _1'(r^*)-\tilde{F}\big \}\\&=-\frac{\delta ^2r^*}{2}\big \{\mu \phi _2''(r^*)e^{-r^*}+\tilde{F}\phi _1''(r^*)-\mu \psi _1''(r^*)\big \}. \end{aligned} \end{aligned}$$

Note that by definition of \(\tilde{F}\), the lhs of the above equation equals zero, meaning \(G_{rr}(r^*,0)=F_{rr}(r^*,0)\). However, in general it does not hold that \(\phi _1''(r^*)=1\). For this reason \(G_{rr}(r^*,x)\ne F_{rr}(r^*,x)\) if \(x\ne 0\).

We formulate the following verification theorem.

Theorem 2.5

The optimal strategy \(C^*\) is to immediately spend any available amount bigger than zero if \(r\le r^*\), i.e. \(C^*_t= \big (x+\mu \lambda _{r^*}^t\big )\mathbb {1}_{[\lambda _{r^*}^t> 0]}\), where \(\lambda _{r^*}^t:=\sup \{s\in [0,t):\; r_s\le r^*\}\) with \(\sup \{\emptyset \}=0\). The value function V(r, x) solves the HJB equation (11) and fulfils \(V(r,x) =v(r,x)\) where

$$\begin{aligned} v(r,x)={\left\{ \begin{array}{ll} F(r,x) &{}\quad \text{ if } (r,x)\in [0,r^*]\times \mathbb {R}_+,\\ G(r,x)&{}\quad \text{ if } (r,x)\in [r^*,\infty )\times \mathbb {R}_+, \end{array}\right. } \end{aligned}$$

with \(F(r^*,0)=\tilde{F}\) as given in (14).

Proof

Note, it holds that

$$\begin{aligned} \{\lambda _{r^*}^t\le u\}=\left\{ \sup \{s\in [0,t):\; r_s\le r^*\}\le u\right\} =\left\{ \inf \limits _{u< s\le t}r_s> r^*\right\} . \end{aligned}$$

Since the running infimum above is \(\mathcal {F}_t\)-measurable, we can conclude that the strategy \(C^*\) is an admissible strategy.

Since \(F\in \mathcal C^{1,2}((0,r^*)\times \mathbb {R}_+)\), \(G\in \mathcal C^{1,2}((r^*,\infty )\times \mathbb {R}_+)\), \(F(r^*,x)=G(r^*,x)\), \(F_r(r^*,x)=G_r(r^*,x)\) and \({\mathbb {1}}_{[r_t=r^{*}]}=1\) a.s., by Peskir (2005) we can apply the change-of-variable formula. Let C be an arbitrary admissible strategy and \(\hat{X}\) the ex-consumption process under C. Then

$$\begin{aligned} v(r_t,\hat{X}_t)&=v(r,x)+\int _0^t \mathcal L(v)(r_s,\hat{X}_s)\,\mathrm{d}s+\int _0^t \delta \sqrt{r_s}\;v_r(r_s,\hat{X}_s)\,\mathrm{d}W_s -\int _0^t v_x(r_s,\hat{X}_s) \,\mathrm{d}C_s. \end{aligned}$$

Furthermore, we know v solves the HJB equation (11) meaning \(\mathcal L(v)(r,x)\le 0\) and \(e^{-r}-v_x(r,x)\le 0\) for all \((r,x)\in \mathbb {R}_+^2\). Therefore,

$$\begin{aligned} v(r_t,\hat{X}_t)\le v(r,x)+ \int _0^t \delta \sqrt{r_s}\;v_r(r_s,\hat{X}_s)\,\mathrm{d}W_s-\int _0^t e^{-r_s} \,\mathrm{d}C_s. \end{aligned}$$

The stochastic integral above is a martingale with expectation zero, consult the proof of Lemma 1.5 in Sect. 1. Taking expectations on both sides of the above equality, one obtains

$$\begin{aligned} \mathbb {E}_{(r,x)}\big [v(r_t,\hat{X}_t)\big ]\le v(r,x)-\mathbb {E}_{(r,x)}\left[ \int _0^t e^{-r_s} \,\mathrm{d}C_s\right] . \end{aligned}$$

As \(\lim \limits _{r\rightarrow \infty }v(r,x)=0\) and v(r, x) is bounded, by dominated convergence we can interchange limit and integration to obtain

$$\begin{aligned} v(r,x)\ge \mathbb {E}_{(r,x)}\left[ \int _0^\infty e^{-r_s} \,\mathrm{d}C_s\right] \end{aligned}$$

Taking the strategy \(C^*\) yields equality. \(\square \)

Thus, the barrier strategy with barrier given by \(r^*\), defined in Lemma 2.2, is optimal. The corresponding return function is the value function and solves the HJB equation (11).

Fig. 1
figure 1

LHS: the value function V(r, x), consisting of F(r, x) (black) and G(r, x) (grey). RHS: dependence of the barrier \(r^*\) on \(\delta ^2\)

Full size image

We can calculate the value function explicitly such that

$$\begin{aligned} \psi _1(r)&=\frac{2}{\delta ^2}\int _x^{r^*}y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\int _0^ye^{-z}z^{\frac{2b}{\delta ^2}-1}e^{\frac{2a}{\delta ^2}z}\,\mathrm{d}z\,\mathrm{d}y,\\ \phi _1(r)&=\frac{1}{\int _{r^*}^\infty y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y}\int _{r}^\infty y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y,\\ \phi _2(r)&=\frac{2}{\delta ^2}\frac{\int _{r^*}^\infty y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\int _{r^*}^y\phi _1(z)z^{\frac{2b}{\delta ^2}-1}e^{\frac{2a}{\delta ^2}z}\,\mathrm{d}z\,\mathrm{d}y}{\int _{r^*}^\infty y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y}\int _{r^*}^r y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y\\&\quad {}-\frac{2}{\delta ^2}\int _{r^*}^r y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\int _{r^*}^y\phi _1(z)z^{\frac{2b}{\delta ^2}-1}e^{\frac{2a}{\delta ^2}z}\,\mathrm{d}z\,\mathrm{d}y. \end{aligned}$$

For well-definiteness of \(\phi _1\) and \(\phi _2\) refer to the proof of Lemma 1.5 in the “Appendix”, Sect. 1.

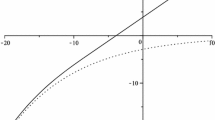
Example 2.6

Let \(a=0.001\), \(b=0.002\), \(\delta =0.07\) and \(\mu =0.5\). Both functions, F and G are illustrated in Fig. 1.

2.3 The 0-barrier strategy

In the following, we will discuss a very specific strategy for the case \(2b<\delta ^2\): “spending only if the underlying CIR hits zero”. In fact, we know from Cox et al. (1985) that if \(2b<\delta ^2\), a CIR process can attain zero with a positive probability. With growing volatility, the probability to “dive” and touch zero increases.

In Sect. 2.2, we showed that the value function solves the HJB equation (11) and that the optimal strategy is a barrier strategy with a constant barrier \(r^*\) fulfilling \(r^*\le R\), with R given in (13). By the structure of R, it holds that \(R\rightarrow 0\) as \(\delta \rightarrow \infty \). This brings up the question whether the optimal barrier could be equal to zero for some large values of \(\delta \).

Let \(\delta <\infty \) be fixed such that \(\delta ^2>2\max \{a,b\}\), meaning the probability \(\{r_t\}\) hits zero is positive. By Sect. 2.1 the function H defined in (12) is not the value function.

Consider the strategy \(C^0\) with \(C^0_t:=\big (x+\mu \lambda _0^t\big )\mathbb {1}_{[\lambda _0^t>0]}\), where \(\lambda _0^t=\sup \{s\in [0,t): r_s=0\}\) with \(\sup \{\emptyset \}=0\) “\(\rightsquigarrow \) to spend the maximal possible amount only if \(r_t=0\)”.

Letting

$$\begin{aligned} \rho _0:=\inf \{t \ge 0:\; r_t=0\}, \end{aligned}$$

we define \(\hat{\phi }_1(r):=\mathbb {E}_r[\mathbb {1}_{[\rho _0<\infty ]}]\) and \(\hat{\phi }_2(r):=\mathbb {E}_r[\rho _0\mathbb {1}_{[\rho _0<\infty ]}]\) for \(r\ge 0\).

Lemma 2.7

Functions \(\hat{\phi }_1(r)\) and \(\hat{\phi }_2(r)\) solve the differential equations (9) and (10) respectively on \((0,\infty )\). The function \(\phi _2(r)\) is finite on \((0,\infty )\) and it holds that

$$\begin{aligned} \hat{\phi }_1(r)&=\frac{1}{\int _{0}^\infty y^{-\frac{2b}{\delta ^2}} e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y}\int _r^\infty y^{-\frac{2b}{\delta ^2}} e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y\\&\text{ and }\\ \hat{\phi }_2(r)&=\frac{2}{\delta ^2}\frac{\int _{0}^\infty y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\int _{0}^y\phi _1(z)z^{\frac{2b}{\delta ^2}-1}e^{\frac{2a}{\delta ^2}z}\,\mathrm{d}z\,\mathrm{d}y}{\int _{0}^\infty y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y}\int _{0}^r y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y\\&\quad {}-\frac{2}{\delta ^2}\int _{0}^r y^{-\frac{2b}{\delta ^2}}e^{-\frac{2a}{\delta ^2}y}\int _{0}^y\phi _1(z)z^{\frac{2b}{\delta ^2}-1}e^{\frac{2a}{\delta ^2}z}\,\mathrm{d}z\,\mathrm{d}y. \end{aligned}$$

Proof

Lemma 1.4 yields \(\int _0^\infty y^{-\frac{2b}{\delta ^2}} e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y<\infty \). The functions \(\hat{\phi }_1(r)=\mathbb {E}_r[\mathbb {1}_{[\rho _0<\infty ]}]\) and \(\hat{\phi }_2(r)=\mathbb {E}_r[\rho _0\mathbb {1}_{[\rho _0<\infty ]}]\) solve the differential equations (9) and (10) respectively on \((0,\infty )\) and the function \(\hat{\phi }_2\) is finite due to Lemma 1.5. \(\square \)

Define further

$$\begin{aligned} \lambda _0 := \sup \{t \ge 0:\; r_t=0\}, \end{aligned}$$

i.e. \(\lambda _0\) is the last exit time from zero before \(\{r_t\}\) approaches \(\infty \). It is clear that under \(C^0\), when \(r_0=0\) one spends everything immediately, saves money until \(\{r_t\}\) again approaches zero and spends everything there. The game ends at time \(\lambda _0\) defined above.

Lemma 2.8

Let \(\frac{\delta ^2}{2}>b\), then

$$\begin{aligned} \lambda _0<\infty \quad \text{ a.s. } \quad \text{ and }\quad \mathbb {E}_0[\lambda _0]=\int _0^\infty t \frac{\big (e^{at}-1\big )^{-\frac{2b}{\delta ^2}}}{\int _0^\infty \big (e^{az}-1\big )^{-\frac{2b}{\delta ^2}}\,\mathrm{d}z}\,\mathrm{d}t <\infty . \end{aligned}$$

Proof

For the proof refer to the “Appendix”, Sect. 1. \(\square \)

We can now write the return function corresponding to the strategy \(C^0\):

$$\begin{aligned} V^0(r,x):=\mathbb {E}_r\big [\big (x+\mu \rho _0+\tilde{V}^0\big )\mathbb {1}_{[\rho _0<\infty ]}\big ]=(x+\tilde{V}^0)\hat{\phi }_1(r)+\mu \hat{\phi }_2(r), \end{aligned}$$

where \(\tilde{V}^0=V^0(0,0)=\mu \mathbb {E}_0[\lambda _0]\).

Proposition 2.9

The strategy \(C^0\) cannot be optimal for any \(\delta <\infty \).

Proof

Recall that the function \(\hat{\phi }_1(r)\) is given by

$$\begin{aligned} \hat{\phi }_1(r)=\frac{1}{\int _{0}^\infty y^{-\frac{2b}{\delta ^2}} e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y}\int _r^\infty y^{-\frac{2b}{\delta ^2}} e^{-\frac{2a}{\delta ^2}y}\,\mathrm{d}y. \end{aligned}$$

In particular, this means that \(\hat{\phi }_1(0)=1\) and \(\lim \limits _{r\rightarrow 0}\hat{\phi }_1'(r)=-\infty \) giving

$$\begin{aligned} e^{-r}-V^0_x(r,x)=e^{-r}-\hat{\phi }_1(r)>0 \end{aligned}$$

for \(r\in (0,\varepsilon )\) and some \(\varepsilon >0\). Therefore, \(V^0\) does not solve the HJB (11) on \((0,\varepsilon )\times \mathbb {R}_+\). Since in the previous subsection we have shown that the value function solves the HJB, we can conclude \(C^0\) will never be optimal. \(\square \)

2.4 The Brownian risk model

In this subsection, we add complexity to our model by assuming that the underlying surplus (previously called income) process is given by a Brownian motion with drift. Since it is unrealistic to assume strong random fluctuations in the income of an individual or household, we change the economic interpretation from maximising the consumption of an individual to the maximising of dividends of an insurance company. The difference to the previous case appears also in the fact that we stop our considerations when the surplus becomes negative (ruins). Taking the ruin time into consideration, destroys the linear dependence of the value function on the surplus. In general, the return function corresponding to a constant barrier strategy will have a representation as a power series with non-linear functions as summands. Therefore—using the chess terminology—in order to keep the problem in check, we assume \(\delta ^2= 2a\) for this subsection. This assumption simplifies calculations, as the exponential CIR process \(e^{-r_t}\) fulfils

$$\begin{aligned} \mathbb {E}_r[e^{-r_t}]=e^{-r}e^{-bt}, \end{aligned}$$

in this case, see (3). Thus, the dependence of \(\mathbb {E}_r[e^{-r_t}]\) on r and t can be separated, which is crucial for the optimal strategy to be a constant barrier. For \(\delta ^2\ne 2a\), the exponent of \(\mathbb {E}_r[e^{-r_t}]\) depends on the variables r and t in a highly non-linear way, suggesting that the optimal strategy in this case would depend on the CIR process.

Technically, we consider an insurance company whose surplus is given by a Brownian motion with drift \(X_t=x+\mu t+\sigma B_t\), where \(\{B_t\}\) is a standard Brownian motion and \(\mu ,\sigma >0\) are positive constants. The considered insurance company is allowed to pay out dividends, where the accumulated dividends until time t are given by \(C_t\), yielding for the ex-dividend surplus \(X^C\):

$$\begin{aligned} X_t^C=x+\mu t+\sigma B_t-C_t. \end{aligned}$$

The consideration will be stopped at the ruin time \(\tau ^C\) of \(X^C\). Let \(\{W_t\}\), the Brownian motion driving the discounting CIR process (1), be independent of \(\{B_t\}\), and the underlying filtration \(\{\mathcal {F}_t\}\) be the filtration generated by the pair \(\{W_t,B_t\}\). We call a strategy C admissible if \(C_t\) is adapted to \(\{\mathcal {F}_t\}\), \(C_0\ge 0\) and \(X_t^C\ge 0\) for all \(t\ge 0\), the set of admissible strategies will be denoted by \(\mathfrak B\).

As a risk measure we consider the value of expected discounted dividends, where the dividends are discounted by a CIR process (1).

We define the return function corresponding to some admissible strategy C to be \(V^C(r,x)=\mathbb {E}_{(r,x)}\Big [\int _0^{\tau ^C} e^{-r_s}\,\mathrm{d}C_s\Big ]\) and let

$$\begin{aligned} V(r,x)=\sup \limits _{C\in \mathfrak B}V^C(r,x). \end{aligned}$$

The HJB equation corresponding to the problem can be derived in a similar way to Schmidli (2008, pp. 98, 103):

$$\begin{aligned} \max \left\{ \mu V_x+\frac{\sigma ^2}{2}V_{xx}+(ar+b) V_r+ ar V_{rr},e^{-r}-V_x\right\} =0. \end{aligned}$$
(15)

In this setup we conjecture that the optimal strategy will be of barrier type with a constant barrier for the surplus process. This means we pay any capital larger than the barrier, independent of \(\{r_t\}\). Define now the following auxiliary quantities:

$$\begin{aligned} \begin{aligned}&\theta :=\frac{-\mu +\sqrt{\mu ^2 +2\sigma ^2 b}}{\sigma ^2},\quad \zeta :=\frac{-\mu -\sqrt{\mu ^2 +2\sigma ^2 b}}{\sigma ^2},\quad \varrho :=\frac{\ln \big (b-\mu \zeta \big )-\ln \big (b-\mu \theta \big )}{\theta -\zeta }. \end{aligned} \end{aligned}$$

Lemma 2.10

The return function \(V^\varrho (r,x)\) corresponding to the constant barrier strategy \(\varrho \) is given by

$$\begin{aligned} V^\varrho (r,x)={\left\{ \begin{array}{ll}F(r,x): &{}x\ge \varrho \\ G(r,x): &{}x\le \varrho , \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned}&F(r,x):=\big (x-\varrho +\frac{\mu }{b}\big )e^{-r},\quad \text{ if } x\ge \varrho \\&G(r,x):=e^{-r}\frac{e^{\theta x}-e^{\zeta x}}{\theta e^{\theta \varrho }-\zeta e^{\zeta \varrho }} ,\quad \text{ if } x\le \varrho . \end{aligned}$$

The functions F and G fulfil:

  • \(F(r,\varrho )=G(r,\varrho )\), \(F_r(r,\varrho )=G_r(r,\varrho )\), \(F_{rr}(r,\varrho )=G_{rr}(r,\varrho )\);

  • \(F_x(r,\varrho )=e^{-r}=G_x(r,\varrho )\) and \(F_{xx}(r,\varrho )=0=G_{xx}(r,\varrho )\) for all \(r\in \mathbb {R}_+\);

  • G(r, x) solves the partial differential equation

    $$\begin{aligned} \mu f_x+\frac{\sigma ^2}{2}f_{xx}+(ar+b) f_r+ ar f_{rr}=0 \end{aligned}$$

    and fulfils \(G_x(r,x)\ge e^{-r}\) for all \(r\in \mathbb {R}_+\) and \(x\in [0,\varrho ]\);

Proof

For the proof see Shreve et al. (1984) and Lemma 1.5.

Note, the method we are referring to in Shreve et al. (1984) is based on the application of Ito’s formula and can be used also for the two-dimensional process (r, W) and a sufficiently smooth function. Since \(\theta \), \(\zeta \) and \(\varrho \) are defined such that \(V^\varrho (r,x)\in \mathcal {C}^{(\infty ,2)}(\mathbb {R}_+^2)\), Ito’s formula can be applied and the one-dimensional result from Shreve et al. can be transferred to the problem considered in this subsection. \(\square \)

Proposition 2.11

The optimal dividend strategy \(C^*\) is to pay any capital larger than \(\varrho \), i.e.

$$\begin{aligned} C_t^*=\max \left\{ \sup \limits _{0\le s\le \tau ^*\wedge t}\left( x+\mu s+\sigma W_s\right) -\varrho ;0\right\} , \end{aligned}$$

where \(\tau ^*\) is the ruin time. The value function V(r, x) is given by F on \([\varrho ,\infty )\), by G on \([0,\varrho ]\) and solves the HJB equation (15).

Proof

Using Lemma 2.10, the proof follows the proof in Asmussen and Taksar (1997) closely, see also Schmidli (2008, p. 104). \(\square \)

Thus, if \(\delta ^2=2a\), i.e. \(e^{bt}e^{-r_t}\) is a martingale [see Lemma 1.1 and Definition (3)], the optimisation problem can be reduced to the classical dividend optimisation problem with a constant discounting rate, described in Asmussen and Taksar (1997).

2.5 Conclusion

For deterministic income we considered two different cases, differing due to the relation between parameters \(\delta ^2\) and a. In both cases, the optimal strategy is of a barrier type, i.e. it is optimal to spend all available money only if the process \(\{r_t\}\) is below a certain level, otherwise it is optimal to wait.

If the volatility coefficient \(\delta \) is relatively small, i.e. \(\delta ^2\le 2a\), the paths go “nearly deterministically” to infinity, meaning \(e^{-r_t}\) is a supermartingale. The optimal barrier therefore lies at infinity, and it is always optimal to spend the maximal possible amount.

If \(2a<\delta ^2\), the process \(\{r_t\}\), moving \(\delta ^2\) away from 2a shifts the optimal barrier from \(\infty \) to 0, see Fig. 1. This means the higher the volatility the more likely the process will hit a lower level. It makes sense to wait until the discounting process attains “small” values, and spend the saved amount there.

Finally, we showed that the strategy “spending only if \(r_t=0\)” is never optimal, i.e. the optimal barrier is always greater than zero.

Note that the above results strongly differ from the case of integrated Ornstein–Uhlenbeck (OU) discounting. There, see Eisenberg (2018), it is optimal to wait if the interest rate is below a certain level and to start consuming otherwise. The reason for the swapping of the paying behaviour in the case of a CIR discounting is rooted in the fact that in Eisenberg (2018), an OU process represents the short rate, whereas in our model the CIR process describes the compound interest/preference.

In the Brownian risk model, the case \(2a\ne \delta ^2\) has not been considered and is a subject for future research. We conjecture that the optimal strategy there will be of barrier type with a non-constant barrier depending on the underlying CIR process.