1 Introduction

The conventional dynamic theory of thermoelasticity established by Biot (1956) rests upon the hypothesis of the Fourier’s law of heat conduction in which the temperature distribution is governed by a parabolic-type partial differential equation. As a consequence, the theory predicts that a thermal signal is felt instantaneously everywhere in a body, which is not physically justifiable. To overcome this shortcoming, several theories of generalized thermoelasticity were developed in an attempt to amend the classical thermoelasticity. The first two generalized thermoelastic models are Lord–Shulman (LS) (1967) model and Green–Lindsay (GL) (1972) model. In LS model, one thermal relaxation time is introduced in the classical Fourier’s law of heat conduction, whereas in the GL model, two thermal relaxation times are inserted in the constitutive equations for force stress tensor and entropy equation. Later on, by providing sufficient basic modifications in the constitutive relations, Green and Naghdi (1991, 1992, 1993) set up three new thermoelasticity theories that permit treatment of a much wider class of heat flow problems, which are labelled as models GN-I, GN-II and GN-III. Researchers have presented a number of studies on transient response of the generalized thermoelastic problems based on these theories. For example, Othman (2004) analyzed the effect of angular velocity on the thermoelastic interactions in a homogeneous, isotropic thermally conducting elastic half-space under GL theory. Tianhu et al. (2005) presented a study on the electro-magneto-thermoelastic interactions in an infinitely long perfectly conducting solid cylinder whose surface is subjected to a thermal shock. A model of the equations of a generalized thermoelasticity theory with relaxation times for a saturated porous medium was given by Liu et al. (2011). Vu-Bac et al. (2016) presented a unified method for probabilistic sensitivity analysis for computationally expensive models with correlated inputs. Hamdia et al. (2017) performed a stochastic analysis of the fracture toughness of polymer nanoparticle composites using polynomial chaos expansion. In the frame of GL model, Kalkal et al. (2019) studied the propagation of plane waves in a fiber reinforced anisotropic thermoelastic medium with diffusion.

The linear theory of elastic materials with voids is an important generalization of the classical theory of elasticity. Mostly, this theory is useful for investigating various types of biological and geological materials for which classical theory of elasticity is inadequate. Porous materials have wide applications in the fields of materials science, drugs, petroleum industry, medical devices industry etc. Iesan (1986) proposed a theory of thermoelastic materials with voids. In this study, the constitutive equations are obtained by using the balance law of energy, the entropy production inequality and the invariance requirements under superposed rigid body motions. It is also noted that the transverse wave vibrates without affecting the temperature and porosity of the material. Cicco and Diaco (2002) established the theory of thermoelastic materials with voids in the context of GN-II model. The propagation of plane waves in a thermoelastic diffusive medium with voids was discussed by Singh (2011) in the frame of LS model of generalized thermoelasticity. Tomar et al. (2013) presented a study on the reflection phenomena of time harmonic waves in an infinite thermo-viscoelastic medium with voids. Fundamental solution to a system of differential equations in micropolar visco-thermoelastic half-space with voids was provided by Kumar et al. (2015). Abo-Dahab (2018) analyzed the influence of magnetic field on the propagation of surface waves in a rotating fiber-reinforced anisotropic viscoelastic medium in the presence of voids.

Generally, the gravitational effect in the classical theory of elasticity is neglected. Firstly, Bromwich (1898) investigated the influence of gravity field on the propagation of elastic waves in solids, particularly on an elastic globe. Biot (1965) examined the impact of gravity on surface wave propagation in an incompressible isotropic elastic medium. Under LS theory, Sarkar and Lahiri (2013) used normal mode technique together with eigen value approach to explore the effect of gravity field on the propagation of plane waves in a fiber-reinforced magneto-thermoelastic isotropic medium with two-temperature. Reflection and refraction phenomena due to an obliquely incident longitudinal wave at a plane interface between an isotropic, homogeneous, thermoelastic medium and a porous thermoelastic medium was studied by Wei et al. (2016). Recently, Abd-Alla et al. (2019) discussed the propagation of Rayleigh surface waves in an initially stressed orthotropic magneto-thermoelastic medium with rotation and gravity.

Functionally graded materials (FGMs) are non-homogeneous materials in which the composition changes gradually with a corresponding change in the properties and the volume fractions of different constituents of composite. High temperature thermal shock generates a high magnitude of thermal stresses when sudden heating and cooling happens. In this case, FGMs have thermophysical properties to permit high magnitude thermal stresses due to large temperature difference. These types of materials are massively used in important structures such as nuclear reactors, pressure vessels, pipes and chemical plants. The porosity gradient FGMs are broadly used in the biomedical application as medical implants, because they are designed to mimic the human organs, which are FGMs in nature.

The coupled thermoelastic problem of a functionally graded disk based on the classical coupled theory of thermoelasticity was considered by Bakhshi et al. (2006). The electro-magneto-thermoelastic response of an infinite functionally graded cylinder was studied by Abbas and Zenkour (2013), by employing finite element method. By using fractional order theory of thermoelasticity, Abbas (2014) scrutinized the impacts of non-homogeneity, fractional order parameter and time on functionally graded material subjected to a thermal field. The forced vibrations of a non-homogeneous, isotropic thermoelastic thin annular disk under periodic and exponential types of axi-symmetric dynamic pressures were analyzed by Mishra et al. (2017). Mehditabar et al. (2018) surveyed a three-dimensional asymmetric thermoelastic response of a rotating functionally graded truncated conical shell subjected to thermal field and inertia force.

In the current research, we consider two-dimensional disturbances in an infinite, isotropic, non-homogeneous thermoelastic half-space with voids and gravity based on LS theory. All the thermomechanical properties of the FGM under consideration are assumed to vary as an exponential power of the spatial co-ordinate. The normal mode technique is used to obtain the exact expressions of all the physical variables. The numerical results for the thermophysical fields have been obtained for a magnesium crystal-like material and have been presented graphically to estimate and highlight the effects of different parameters considered in this problem.

Although various investigations do exist to observe the disturbances in a thermoelastic medium under the effects of different parameters, the work in its present form, i.e. the disturbances in a functionally graded thermoelastic medium in the presence of voids and gravity have not been studied by any researcher till now. The present article is useful and valuable for analysis of problems involving coupled thermal shock, non-homogeneity parameter, gravitational field, voids and elastic deformation. The introduction of these parameters in the thermoelastic medium provides a more realistic model for these studies. The application of the present model can’t be ruled out in the physical word. Results carried out in this paper can be used in material science, designers of new materials, earthquake engineering, seismology, nuclear reactors and solid mechanics etc. The application of FGMs also includes the MRI scanner cryogenic tubes, the fuel tanks, the musical instruments and the X-ray tables. Considering the multifarious applications of the above problem and the non-existence of systematic investigation in the context of functionally graded thermoelastic medium with voids and gravity has inspired the authors to study the thermo-mechanical interactions in such an interesting medium.

2 Fundamental equations

According to Iesan (1986), the field equations and stress–strain-temperature relations in a generalized thermoelastic medium with voids in the presence of body forces (gravity field) are:

  1. (1)

    Kinematic relation

    $$ e_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right), $$
    (1)

    where \( \vec{u} \) is the displacement vector and \( e_{ij} \) are the components of strain.

  2. (2)

    Constitutive relations

    $$ \sigma_{ij} = 2\mu e_{ij} + \delta_{ij} \left( {\lambda e_{kk} - \beta \theta + b\phi } \right), $$
    (2)
    $$ s = - be_{kk} - \xi \phi + m\theta , $$
    (3)
    $$ h_{i} = \alpha \phi ,_{i} , $$
    (4)
    $$ h_{i,i} + s = \rho \chi \ddot{\phi }, $$
    (5)

    where \( \lambda ,\mu \) are well-known Lame’s constants, \( \beta = \left( {3\lambda + 2\mu } \right)\alpha_{t} \), \( \alpha_{t} \) is the coefficient of linear thermal expansion, \( \sigma_{ij} \) are the components of stress, \( h_{i} \) are the components of equilibrated stress vector, \( \rho \) is the reference mass density, \( \theta = T - T_{0} \), T is the absolute temperature, \( T_{0} \) is the reference temperature of the medium in its natural state assumed to be \( \left| {\theta /T_{0} } \right| < < 1 \), \( e = e_{kk} \) is the cubical dilatation, \( \phi \) is the change in volume fraction field, \( \alpha , \) b and \( \xi \) are the void material constants, \( \chi \) is the equilibrated inertia, m is thermo-void coefficient, s is the intrinsic equilibrated body force and \( \delta_{ij} \) is the Kronecker delta function.

  3. (3)

    Stress equation of motion

    $$ \sigma_{ji,j} + F_{i} = \rho \ddot{u}_{i} , $$
    (6)

    where \( F_{i} \) is the body force.

  4. (4)

    Volume fraction field equation

    $$ \alpha \nabla^{2} \phi - bu_{i,j} - \xi \phi + m\theta = \rho \chi \ddot{\phi }. $$
    (7)
  5. (5)

    Equation of heat conduction

    $$ q_{i,i} = - \rho T_{0} \dot{S}, $$
    (8)
    $$ \rho ST_{0} = \rho C_{e} \theta + \beta T_{0} e_{kk} + mT_{0} \phi , $$
    (9)

    where \( q_{i} \) are the components of heat flux vector, \( S \) is the entropy per unit volume and \( C_{e} \) is the specific heat at constant strain.

  6. (6)

    Modified Fourier’s law of heat conduction

    $$ q_{i} + \tau_{0} \dot{q}_{i} = - K\nabla \theta , $$
    (10)

    where K is the thermal conductivity and \( \tau_{0} \) is thermal relaxation time. When \( \tau_{0} = 0 \), the preceding equations governed the equations of classical theory of thermoelasticity.

With the help of Eqs. (8)–(10), one can obtain the heat conduction equation for LS model as:

$$ K\nabla^{2} \theta = \left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left( {\rho C_{e} \dot{\theta } + \beta T_{0} \dot{e} + mT_{0} \dot{\phi }} \right). $$
(11)

For a functionally graded composite, the constants \( \lambda ,\; \, \mu ,\; \, \beta ,\; \, b,\; \, \alpha,\; \, \xi ,\; \, m,\; \, \rho \) and K are no longer constant but become space-dependent. Hence we replace \( \lambda ,\; \, \mu ,\; \, \beta ,\; \, b,\; \, \alpha ,\; \, \xi ,\; \, m,\; \, \rho \) and K by \( \lambda_{0} f\left( {\vec{x}} \right) \), \( \mu_{0} f\left( {\vec{x}} \right) \), \( \beta_{0} f\left( {\vec{x}} \right) \), \( b_{0} f\left( {\vec{x}} \right) \), \( \alpha_{0} f\left( {\vec{x}} \right) \), \( \xi_{0} f\left( {\vec{x}} \right) \), \( m_{0} f\left( {\vec{x}} \right) \), \( \rho_{0} f\left( {\vec{x}} \right) \) and \( K_{0} f\left( {\vec{x}} \right) \) respectively, where \( \lambda_{0} ,\; \, \mu_{0} ,\; \, \beta_{0} ,\; \, b_{0} , \, \alpha_{0} , \, \xi_{0} , \) \( m_{0} , \, \rho_{0} \) and \( K_{0} \) are supposed to be constants and \( f\left( {\vec{x}} \right) \) is a given non-dimensional function of the spatial variable \( \vec{x} = \left( {x,\;y,\;z} \right) \). Using these values of parameters, Eqs. (2), (6), (7) and (11) take the following form (Hetnarski and Eslami 2008):

$$ \sigma_{ij} = f\left( {\vec{x}} \right)\left[ {2\mu_{0} e_{ij} + \delta_{ij} \left( {\lambda_{0} e_{kk} - \beta_{0} \theta + b_{0} \phi } \right)} \right], $$
(12)
$$ \sigma_{ji,j} + F_{i} = \rho_{0} f\left( {\vec{x}} \right)\ddot{u}_{i} , $$
(13)
$$ \left( {\alpha_{0} f\left( {\vec{x}} \right)\phi ,_{i} } \right),_{i} - b_{0} f\left( {\vec{x}} \right)u_{i,i} - \xi_{0} f\left( {\vec{x}} \right)\phi + m_{0} f\left( {\vec{x}} \right)\theta = \rho_{0} f\left( {\vec{x}} \right)\chi \ddot{\phi }, $$
(14)
$$ \left( {K_{0} f\left( {\vec{x}} \right)\theta ,_{i} } \right),_{i} = f\left( {\vec{x}} \right)\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left( {\rho_{0} C_{e} \dot{\theta } + \beta_{0} T_{0} \dot{e} + m_{0} T_{0} \dot{\phi }} \right), $$
(15)

where

$$ \beta_{0} = \left( {3\lambda_{0} + 2\mu_{0} } \right)\alpha_{t} . $$

Here, the superposed dot indicates derivative with respect to time and the comma represents derivative with respect to space variable.

3 Problem description and exponential variation of non-homogeneity

Consider a non-homogeneous, isotropic thermoelastic half-space with voids and gravity field under the purview of LS model. Choose a fixed cartesian coordinate system \( \left( {x,\;y,\;z} \right) \) having the surface of the half-space as the plane x = 0, with x-axis pointing vertically downwards into the medium. The current study is restricted to xy-plane and thus all the field quantities are independent of the spatial variable z. So, the displacement components are taken as:

$$ u_{1} = u_{1} \left( {x,y,t} \right),u_{2} = u_{2} \left( {x,y,t} \right),u_{3} = 0. $$
(16)

It is also assumed that material properties are graded only in x-direction. Hence we take \( f\left( {\vec{x}} \right) \) as \( f\left( x \right) \). In view of expression (16), the stresses arising from (12) can be expressed as follows:

$$ \sigma_{xx} = f\left( x \right)\left[ {\left( {\lambda_{0} + 2\mu_{0} } \right)\frac{{\partial u_{1} }}{\partial x} + \lambda_{0} \frac{{\partial u_{2} }}{\partial y} - \beta_{0} \theta + b_{0} \phi } \right], $$
(17)
$$ \sigma_{yy} = f\left( x \right)\left[ {\left( {\lambda_{0} + 2\mu_{0} } \right)\frac{{\partial u_{2} }}{\partial y} + \lambda_{0} \frac{{\partial u_{1} }}{\partial x} - \beta_{0} \theta + b_{0} \phi } \right], $$
(18)
$$ \sigma_{xy} = f\left( x \right)\mu_{0} \left[ {\frac{{\partial u_{1} }}{\partial y} + \frac{{\partial u_{2} }}{\partial x}} \right]. $$
(19)

For convenience, we will make use of the following non-dimensional variables to normalize the above equations:

$$ \begin{aligned} \left( {x^{\prime},y^{\prime}} \right) & = \frac{{w^{*} }}{{c_{1} }}\left( {x,y} \right), \\ \left( {u^{\prime}_{1} ,u^{\prime}_{2} } \right)& = \frac{{\rho_{0} w^{*} c_{1} }}{{\beta_{0} T_{0} }}\left( {u_{1} ,u_{2} } \right),\left( {t^{\prime},\tau^{\prime}_{0} } \right) = w^{*} \left( {t,\tau_{0} } \right),\theta^{\prime} = \frac{\theta }{{T_{0} }}, \\ \sigma^{\prime}_{ij} & = \frac{{\sigma_{ij} }}{{\beta_{0} T_{0} }},\phi^{\prime} = \frac{{w^{{*^{2} }} \chi }}{{c_{1}^{2} }}\phi ,g^{\prime} = \frac{g}{{w^{*} c_{1} }}, \\ \end{aligned} $$
(20)

where \( w^{*} = \frac{{\rho_{0} C_{e} c_{1}^{2} }}{{K_{0} }} \), \( c_{1}^{2} = \frac{{\lambda_{0} + 2\mu_{0} }}{{\rho_{0} }} \), g is the gravity field.

Now, let us consider \( f\left( x \right) = e^{ - nx} \), where n is a dimensionless non-homogeneity parameter. Hence, the thermoelastic properties of the material vary exponentially along the x-direction. Now, in terms of the dimensionless parameters defined in (20), Eqs. (13)–(15) and (17)–(19) turn to

$$ \sigma_{xx} = e^{ - nx} \left[ {\frac{{\partial u_{1} }}{\partial x} + a_{1} \frac{{\partial u_{2} }}{\partial y} - \theta + a_{2} \phi } \right], $$
(21)
$$ \sigma_{yy} = e^{ - nx} \left[ {\frac{{\partial u_{2} }}{\partial y} + a_{1} \frac{{\partial u_{1} }}{\partial x} - \theta + a_{2} \phi } \right], $$
(22)
$$ \sigma_{xy} = a_{3} e^{ - nx} \left[ {\frac{{\partial u_{1} }}{\partial y} + \frac{{\partial u_{2} }}{\partial x}} \right], $$
(23)
$$ \begin{aligned} & a_{4} \frac{{\partial^{2} u_{1} }}{{\partial x^{2} }} + a_{5} \frac{{\partial^{2} u_{2} }}{\partial x\partial y} + a_{3} \frac{{\partial^{2} u_{1} }}{{\partial y^{2} }} - \frac{\partial \theta }{\partial x} + a_{2} \frac{\partial \phi }{\partial x} - n\left[ {a_{4} \frac{{\partial u_{1} }}{\partial x} + a_{1} \frac{{\partial u_{2} }}{\partial y} - \theta + a_{2} \phi } \right] \\ & \quad + g\frac{{\partial u_{2} }}{\partial x} = \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }}, \\ \end{aligned} $$
(24)
$$ a_{4} \frac{{\partial^{2} u_{2} }}{{\partial y^{2} }} + a_{5} \frac{{\partial^{2} u_{1} }}{\partial x\partial y} + a_{3} \frac{{\partial^{2} u_{2} }}{{\partial x^{2} }} - \frac{\partial \theta }{\partial y} + a_{2} \frac{\partial \phi }{\partial y} - na_{3} \left[ {\frac{{\partial u_{1} }}{\partial y} + \frac{{\partial u_{2} }}{\partial x}} \right] - g\frac{{\partial u_{1} }}{\partial x} = \frac{{\partial^{2} u_{2} }}{{\partial t^{2} }}, $$
(25)
$$ \nabla^{2} \theta - n\frac{\partial \theta }{\partial x} = \left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left( {\frac{\partial \theta }{\partial t} + a_{6} \frac{\partial e}{\partial t} + a_{7} \frac{\partial \phi }{\partial t}} \right), $$
(26)
$$ \nabla^{2} \phi - n\frac{\partial \phi }{\partial x} - a_{8} e - a_{9} \phi + a_{10} \theta = a_{11} \frac{{\partial^{2} \phi }}{{\partial t^{2} }}, $$
(27)

where

$$ \begin{aligned} & a_{1} = \frac{{\lambda_{0} }}{{\rho_{0} c_{1}^{2} }},a_{2} = \frac{{b_{0} c_{1}^{2} }}{{w^{{*^{2} }} \chi \beta_{0} T_{0} }},a_{3} = \frac{{\mu_{0} }}{{\rho_{0} c_{1}^{2} }},a_{4} = a_{1} + 2a_{3} ,a_{5} = a_{1} + a_{3} ,a_{6} = \frac{{\beta_{0}^{2} T_{0} }}{{\rho_{0} K_{0} w^{*} }}, \\ & a_{7} = \frac{{m_{0} c_{1}^{4} }}{{w^{{*^{3} }} \chi K_{0} }},a_{8} = \frac{{\beta_{0} T_{0} b_{0} \chi }}{{\rho_{0} c_{1}^{2} \alpha_{0} }},a_{9} = \frac{{\xi_{0} c_{1}^{2} }}{{\alpha_{0} w^{{*^{2} }} }},a_{10} = \frac{{m_{0} T_{0} \chi }}{{\alpha_{0} }},a_{11} = \frac{{\rho_{0} c_{1}^{2} \chi }}{{\alpha_{0} }}. \\ \end{aligned} $$

4 Solution procedure

In the current section, normal mode technique is adopted which has the advantage of finding the exact solutions without any assumed restriction on the field variables. So, the physical variables under consideration can be decomposed in terms of normal modes in the following form:

$$ \left[ {u_{1} ,u_{2} ,\theta ,\phi ,\sigma_{ij} } \right]\left( {x,y,t} \right) = \left[ {u_{1}^{*} ,u_{2}^{*} ,\theta^{*} ,\phi^{*} ,\sigma_{ij}^{*} } \right]\left( x \right)e^{{\left( {\omega t + \iota my} \right)}} , $$
(28)

where \( u_{1}^{*} ,\; \, u_{2}^{*} ,\; \, \theta^{*} ,\; \, \phi^{*} \), and \( \sigma_{ij}^{*} \) are the corresponding amplitudes, \( \omega \) is the angular frequency, \( \iota \) is the imaginary unit and m is the wave number in y-direction.

By virtue of (28), Eqs. (24)–(27), convert to the following forms:

$$ \left( {a_{4} D^{2} + b_{1} D + b_{2} } \right)u_{1}^{*} + \left( {b_{3} D + b_{4} } \right)u_{2}^{*} - \left( {D - n} \right)\theta^{*} + \left( {a_{2} D + b_{5} } \right)\phi^{*} = 0, $$
(29)
$$ \left( {b_{6} D + b_{7} } \right)u_{1}^{*} + \left( {a_{3} D^{2} + b_{8} D + b_{9} } \right)u_{2}^{*} + b_{10} \theta^{*} + b_{11} \phi^{*} = 0, $$
(30)
$$ b_{13} Du_{1}^{*} + b_{14} u_{2}^{*} + \left( {D^{2} - nD + b_{12} } \right)\theta^{*} + b_{15} \phi^{*} = 0, $$
(31)
$$ a_{8} Du_{1}^{*} - b_{17} u_{2}^{*} - a_{10} \theta^{*} - \left( {D^{2} - nD + b_{16} } \right)\phi^{*} = 0, $$
(32)

where

\( b_{1} = - na_{4} \), \( b_{2} = - \left( {a_{3} m^{2} + \omega^{2} } \right) \), \( b_{3} = a_{5} \iota m + g \), \( b_{4} = - na_{1} \iota m \), \( b_{5} = - na_{2} \), \( b_{6} = a_{5} \iota m - g \), \( b_{7} = - na_{3} \iota m \), \( b_{8} = - na_{3} \), \( b_{9} = - \left( {m^{2} a_{4} + \omega^{2} } \right) \), \( b_{10} = - \iota m \), \( b_{11} = a_{2} \iota m \), \( b_{12} = - \left( {m^{2} + \omega \left( {1 + \tau_{0} \omega } \right)} \right) \), \( b_{13} = - a_{6} \omega \left( {1 + \tau_{0} \omega } \right) \), \( b_{14} = b_{13} \iota m \), \( b_{15} = - a_{7} \omega \left( {1 + \tau_{0} \omega } \right) \), \( b_{16} = - \left( {m^{2} + a_{9} + a_{11} \omega^{2} } \right) \), \( b_{17} = - a_{8} \iota m \).

The condition for the existence of a non-trivial solution of the system of Eqs. (29)–(32) gives

$$ \left[ {D^{8} + T_{1} D^{7} + T_{2} D^{6} + T_{3} D^{5} + T_{4} D^{4} + T_{5} D^{3} + T_{6} D^{2} + T_{7} D + T_{8} } \right]\left( {u_{1}^{*} ,u_{2}^{*} ,\theta^{*} ,\phi^{*} } \right) = 0, $$
(33)

where \( T_{i} \left( {1,2, \ldots ,8} \right) \) are listed in “Appendix”.

The solution of Eq. (33) which is bounded as \( x \to \infty \), is given by

$$ \left[ {u_{1}^{*} ,u_{2}^{*} ,\theta^{*} ,\phi^{*} } \right]\left( x \right) = \sum\limits_{i = 1}^{4} {\left[ {1,H_{1i} ,H_{2i} ,H_{3i} } \right]M_{i} \left( {m,\omega } \right)e^{{ - \lambda_{i} x}} } , $$
(34)

where \( \lambda_{i} \;\left( {i = 1,\;2,\;3,\;4} \right) \) are the roots with positive real parts of the characteristic equation of (33), \( M_{i} \left( {m,\;\omega } \right)\left( {i = 1,\;2,\;3,\;4} \right) \) are the parameters, depending upon m and \( \omega \) and

$$ H_{1i} = \frac{{E_{1} \lambda_{i}^{4} - E_{2} \lambda_{i}^{3} + E_{3} \lambda_{i}^{2} - E_{4} \lambda_{i} + E_{5} }}{{E_{6} \lambda_{i}^{5} - E_{7} \lambda_{i}^{4} + E_{8} \lambda_{i}^{3} - E_{9} \lambda_{i}^{2} + E_{10} \lambda_{i} - E_{11} }}, $$
$$ H_{2i} = \frac{{\left( {d_{11} \lambda_{i}^{2} - d_{12} \lambda_{i} + d_{13} } \right)H_{1i} + d_{10} - d_{9} \lambda_{i} }}{{d_{14} \lambda_{i} - d_{15} - b_{11} \lambda_{i}^{2} }}, $$
$$ H_{3i} = - \frac{{a_{8} \lambda_{i} + b_{17} H_{1i} + a_{10} H_{2i} }}{{\lambda_{i}^{2} + n\lambda_{i} + b_{16} }}\quad \left( {i = 1,2,3,4} \right), $$

where \( E_{1} = a_{2} d_{9} + d_{1} b_{11} \), \( E_{2} = a_{2} d_{10} + d_{6} d_{9} + d_{1} d_{14} + d_{2} b_{11} \), \( E_{3} = d_{6} d_{10} + d_{7} d_{9} + d_{1} d_{15} + d_{2} d_{14} + d_{3} b_{11} \), \( E_{4} = d_{7} d_{10} + d_{8} d_{9} + d_{2} d_{15} + d_{3} d_{14} \), \( E_{5} = d_{8} d_{10} + d_{3} d_{15} \), \( E_{6} = a_{2} d_{11} \), \( E_{7} = a_{2} d_{12} + d_{6} d_{11} \), \( E_{8} = a_{2} d_{13} + d_{6} d_{12} + d_{7} d_{11} + d_{4} b_{11} \), \( E_{9} = d_{6} d_{13} + d_{7} d_{12} + d_{8} d_{11} + d_{4} d_{14} + d_{5} b_{11} \), \( E_{10} = d_{7} d_{13} + d_{8} d_{12} + d_{4} d_{15} + d_{5} d_{14} \), \( E_{11} = d_{8} d_{13} + d_{5} d_{15} \), \( d_{1} = a_{4} b_{15} - a_{2} b_{13} \), \( d_{2} = b_{1} b_{15} - b_{5} b_{13} \), \( d_{3} = b_{2} b_{15} \), \( d_{4} = b_{3} b_{15} - a_{2} b_{14} \), \( d_{5} = b_{4} b_{15} - b_{5} b_{14} \), \( d_{6} = - na_{2} + b_{5} \), \( d_{7} = a_{2} b_{12} - nb_{5} + b_{15} \), \( d_{8} = b_{5} b_{12} - nb_{15} \), \( d_{9} = b_{11} b_{13} - b_{6} b_{15} \), \( d_{10} = - b_{7} b_{15} \), \( d_{11} = - a_{3} b_{15} \), \( d_{12} = - b_{8} b_{15} \), \( d_{13} = b_{11} b_{14} - b_{9} b_{15} \), \( d_{14} = - nb_{11} \), \( d_{15} = b_{11} b_{12} - b_{10} b_{15} \).

In view of expression (34), Eqs. (21)–(23) provide

$$ \left[ {\sigma_{xx}^{*} ,\sigma_{xy}^{*} ,\sigma_{yy}^{*} } \right]\left( x \right) = \sum\limits_{i = 1}^{4} {\left[ {H_{4i} ,H_{5i} ,H_{6i} } \right]M_{i} \left( {m,\omega } \right)e^{{ - \lambda_{i} x - nx}} } ,\text{Re} \left( {\lambda_{i} } \right) > 0, $$
(35)

where \( H_{4i} = - \lambda_{i} + \iota ma_{1} H_{1i} - H_{2i} + a_{2} H_{3i}, \, H_{5i} = a_{3} \left( {\iota m - \lambda_{i} H_{1i} } \right), \, H_{6i} = - \lambda_{i} a_{1} + \iota mH_{1i} - H_{2i} + a_{2} H_{3i}. \)

5 Application: thermal load

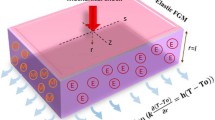
Let us consider a non-homogeneous, isotropic, generalized thermoelastic half-space with voids and gravity occupying the region \( x \ge 0 \). The thermoelastic half-space is subjected to a thermal load as shown in Fig. 1. The coefficients \( M_{i} \left( {i = 1,2,3,4} \right) \) will be determined by imposing appropriate boundary conditions, which are given by

Fig. 1
figure 1

Geometry of the problem

Full size image
  1. (1)

    Thermal boundary condition

    The bounding plane x = 0 is subjected to a thermal shock, thus the thermal boundary condition is given by

    $$ \theta \left( {0,y,t} \right) = f_{1} \left( {y,t} \right), $$
    (36)

    where \( f_{1} \left( {y,\;t} \right) \) is a given function of y and t.

  2. (2)

    Voids condition

    The change in volume fraction field is constant in x-direction, i.e.

    $$ \frac{\partial \phi }{\partial x} = 0. $$
    (37)
  3. (3)

    Mechanical boundary conditions

    The boundary plane x = 0 is taken to be traction free. So, the mechanical boundary conditions are the vanishing of normal and tangential components of stress, i.e.

    $$ \sigma_{xx} \left( {0,y,t} \right) = 0,\quad \sigma_{xy} \left( {0,y,t} \right) = 0. $$
    (38)

Taking into account the non-dimensional expressions for temperature and stresses from (34) and (35) and applying normal mode technique defined in (28), the above boundary conditions reduce to a non-homogeneous system of four equations, which can be written in matrix form as follows:

$$ \left[ {\begin{array}{*{20}c} {H_{21} } & {H_{22} } & {H_{23} } & {H_{24} } \\ { - \lambda_{1} H_{31} } & { - \lambda_{2} H_{32} } & { - \lambda_{3} H_{33} } & { - \lambda_{4} H_{34} } \\ {H_{41} } & {H_{42} } & {H_{43} } & {H_{44} } \\ {H_{51} } & {H_{52} } & {H_{53} } & {H_{54} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {M_{1} } \\ {M_{2} } \\ {M_{3} } \\ {M_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {f_{1}^{*} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right], $$
(39)

where \( f_{1}^{*} \) is the magnitude of the thermal load.

Solution of system (39) provides us the values of \( M_{i} \left( {i = 1,\;2,\;3,\;4} \right) \) as follows:

$$ M_{1} = \frac{{\Delta_{1} }}{\Delta },M_{2} = \frac{{\Delta_{2} }}{\Delta },M_{3} = \frac{{\Delta_{3} }}{\Delta },M_{4} = \frac{{\Delta_{4} }}{\Delta }, $$
(40)

where \( \Delta = H_{21} L_{1} - H_{22} L_{2} + H_{23} L_{3} - H_{24} L_{4} \), \( \Delta_{1} = f_{1}^{*} L_{1} \), \( \Delta_{2} = - f_{1}^{*} L_{2} \), \( \Delta_{3} = f_{1}^{*} L_{3} \), \( \Delta_{4} = - f_{1}^{*} L_{4} \), \( L_{1} = - \lambda_{2} H_{32} \left( {H_{43} H_{54} - H_{53} H_{44} } \right) + \lambda_{3} H_{33} \left( {H_{42} H_{54} - H_{52} H_{44} } \right) - \lambda_{4} H_{34} \left( {H_{42} H_{53} - H_{52} H_{43} } \right) \), \( L_{2} = - \lambda_{1} H_{31} \left( {H_{43} H_{54} - H_{53} H_{44} } \right) + \lambda_{3} H_{33} \left( {H_{41} H_{54} - H_{51} H_{44} } \right) - \lambda_{4} H_{34} \left( {H_{41} H_{53} - H_{51} H_{43} } \right) \), \( L_{3} = - \lambda_{1} H_{31} \left( {H_{42} H_{54} - H_{52} H_{44} } \right) + \lambda_{2} H_{32} \left( {H_{41} H_{54} - H_{51} H_{44} } \right) - \lambda_{4} H_{34} \left( {H_{41} H_{52} - H_{51} H_{42} } \right) \), \( L_{4} = - \lambda_{1} H_{31} \left( {H_{42} H_{53} - H_{52} H_{43} } \right) + \lambda_{2} H_{32} \left( {H_{41} H_{53} - H_{51} H_{43} } \right) - \lambda_{3} H_{33} \left( {H_{41} H_{52} - H_{51} H_{42} } \right) \).

Substituting (40) into expressions (34) and (35), we obtain the expressions for displacement components, force stresses, change in volume fraction field and temperature distribution for functionally graded thermoelastic medium under the influences of gravity and voids as follows:

$$ \left( {u_{1}^{*} ,u_{2}^{*} ,\theta^{*} ,\phi^{*} } \right)\left( x \right) = \frac{1}{\Delta }\sum\limits_{i = 1}^{4} {\left( {1,H_{1i} ,H_{2i} ,H_{3i} } \right)\Delta_{i} e^{{ - \lambda_{i} x}} } , $$
(41)
$$ \left( {\sigma_{xx}^{*} ,\sigma_{xy}^{*} ,\sigma_{yy}^{*} } \right)\left( x \right) = \frac{1}{\Delta }\sum\limits_{i = 1}^{4} {\left( {H_{4i} ,H_{5i} ,H_{6i} } \right)\Delta_{i} e^{{ - \lambda_{i} x - nx}} } . $$
(42)

6 Limiting cases

6.1 Ignoring voids effect

By putting \( \alpha = b = \xi = m = \chi = 0 \) into the field equations and constitutive relations, the corresponding expressions for displacements, stresses and temperature field for the functionally graded thermoelastic medium with gravity are described as:

$$ \left( {u_{1}^{*} ,u_{2}^{*} ,\theta^{*} } \right)\left( x \right) = \frac{1}{{\Delta^{*} }}\sum\limits_{i = 1}^{3} {\left( {1,H^{\prime}_{1i} ,H^{\prime}_{2i} } \right)\Delta_{i}^{*} e^{{ - \lambda_{i} x}} } , $$
(43)
$$ \left( {\sigma_{xx}^{*} ,\sigma_{xy}^{*} ,\sigma_{yy}^{*} } \right)\left( x \right) = \frac{1}{{\Delta^{*} }}\sum\limits_{i = 1}^{3} {\left( {H^{\prime}_{3i} ,H^{\prime}_{4i} ,H^{\prime}_{5i} } \right)\Delta_{i}^{*} e^{{ - \lambda_{i} x - nx}} } , $$
(44)

where

\( \Delta^{*} = H^{\prime}_{21} L^{\prime}_{1} - H^{\prime}_{22} L^{\prime}_{2} + H^{\prime}_{23} L^{\prime}_{3} \), \( \Delta_{1}^{*} = f_{1}^{*} L^{\prime}_{1} \), \( \Delta_{2}^{*} = - f_{1}^{*} L^{\prime}_{2} \), \( \Delta_{3}^{*} = f_{1}^{*} L^{\prime}_{3} \), \( L^{\prime}_{1} = H^{\prime}_{32} H^{\prime}_{43} - H^{\prime}_{42} H^{\prime}_{33} \), \( L^{\prime}_{2} = H^{\prime}_{31} H^{\prime}_{43} - H^{\prime}_{41} H^{\prime}_{33} \), \( L^{\prime}_{3} = H^{\prime}_{31} H^{\prime}_{42} - H^{\prime}_{41} H^{\prime}_{32} \), \( H^{\prime}_{1i} = \frac{{J_{1} \lambda_{i}^{2} - J_{2} \lambda_{i} + J_{3} }}{{a_{3} \lambda_{i}^{3} - J_{4} \lambda_{i}^{2} + J_{5} \lambda_{i} - J_{6} }} \), \( H^{\prime}_{2i} = \frac{{\left( {a_{3} \lambda_{i}^{2} - b_{8} \lambda_{i} + b_{9} } \right)H^{\prime}_{1i} - b_{6} \lambda_{i} + b_{7} }}{{ - b_{10} }} \), \( H^{\prime}_{3i} = - \lambda_{i} + \iota ma_{1} H^{\prime}_{1i} - H^{\prime}_{2i} \), \( H^{\prime}_{4i} = a_{2} \left( {\iota m - \lambda_{i} H^{\prime}_{1i} } \right) \), \( H^{\prime}_{5i} = \iota mH^{\prime}_{1i} - a_{1} \lambda_{i} - H^{\prime}_{2i} \), \( J_{1} = a_{4} b_{10} + b_{6} ,\;J_{2} = b_{1} b_{10} + b_{7} - nb_{6} ,\;J_{3} = b_{2} b_{10} - nb_{7} ,\;J_{4} = b_{8} - nb_{3} \), \( J_{5} = b_{3} b_{10} + b_{9} - nb_{8} ,\;J_{6} = b_{4} b_{10} - nb_{9} \).

6.2 Ignoring non-homogeneity effect

By setting n = 0 in Eqs. (21)–(27), we get required expressions for different distributions from (41) and (42). In this particular case, the results of the present problem coincide with those of Hilal and Othman (2018) with appropriate changes in loading and boundary conditions.

6.3 Ignoring gravity effect

Gravitational effect from the medium can be removed by taking g = 0 in the equation of motion. Then, we shall be dealing with the relevant problem in a functionally graded thermoelastic medium with voids. If we further neglect the influence of non-homogeneity from the medium, then our results match with those of Kumar and Rani (2005) with appropriate changes in boundary conditions and solution technique.

6.4 Ignoring relaxation time effect

To discuss the problem in a functionally graded thermoelastic medium with voids and gravity field in the context of coupled thermoelasticity (CT) model, it is sufficient to put \( \tau_{0} = 0 \) in Eq. (11). With this modification, we get the required expressions for different distributions from (41) and (42) for this limiting case.

7 Computational results and discussion

In order to illustrate the contributions of non-homogeneity parameter, voids, gravity field and relaxation time on the field variables, a numerical analysis is carried out using MATLAB. For the purpose of numerical computation, we have chosen a magnesium crystal-like material. The material constants are taken from Deswal and Hooda (2015): \( \lambda_{0} = 9.4 \times 10^{10} \,{\text{kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2} \), \( \mu_{0} = 4.0 \times 10^{10} \,{\text{kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2} \), \( \alpha_{t} = 2.36 \times 10^{ - 5} \,{\text{K}}^{ - 1} \), \( C_{e} = 9.623 \times 10^{2} \,{\text{J}}\,{\text{kg}}^{ - 1} \,{\text{K}}^{ - 1} \), \( \rho_{0} = 1.74 \times 10^{3} \,{\text{kg}}\,{\text{m}}^{ - 3} \), \( K_{0} = 2.510\,{\text{W}}\,{\text{m}}^{ - 1} \,{\text{K}}^{ - 1} \), \( T_{0} = 293\,{\text{K}} \), \( \alpha_{0} = 3.688 \times 10^{ - 5} \,{\text{N}} \), \( \xi_{0} = 1.475 \times 10^{10} {\text{N}}\,{\text{m}}^{ - 2} \), \( \tau_{0} = 0.02\,{\text{s}} \), \( \chi = 1.753 \times 10^{ - 15} \,{\text{m}}^{2} \), \( m_{0} = 7.322 \times 10^{3} \,{\text{N}}\,{\text{m}}^{ - 2} \,{\text{K}}^{ - 1} \), \( b_{0} = 1.13849 \times 10^{10} {\text{N}}\,{\text{m}}^{ - 2} \).

Since, \( \omega \) is the complex constant, we can write \( \omega = \omega_{0} + \iota \omega_{1} \) so that \( e^{\omega t} = e^{{\omega_{0} t}} \left[ {\cos \left( {\omega_{1} t} \right) + \iota \sin \left( {\omega_{1} t} \right)} \right] \). Hence for small values of time, we can take \( \omega \) as real (i.e.\( \omega = \omega_{0} \)). The other constants for numerical computation are taken as follows: \( \omega = 1,\;m = 1.2 \). Using the above numerical values of the constants, values of the non-dimensional field variables have been evaluated and results are displayed in the form of the graphs at different positions of x at t = 0.1 and y = 1.

Figures 2, 3, 4 and 5 represent the influence of non-homogeneity parameter on the distribution of field variables by considering three different values of non-homogeneity parameter as n = 0.00 (solid line), n = 0.01 (dashed line) and n = 0.02 (dotted line). Figure 2 depicts the spatial variation of normal displacement component for different values n. The figure shows that the increase in the value of n results in decrease in the numerical values of displacement field, which indicates the fact that the non-homogeneity parameter is having a notable decreasing effect on the profile of normal displacement. Figure 3 is plotted to analyze the variation of normal stress with location x for three different values of n mentioned above. As expected, normal stress is having a coincident starting point of zero magnitude for all the three values of non-homogeneity parameter, which is in quite good agreement with the boundary conditions. It can be seen from the plot that for homogeneous medium, the behaviour of normal stress \( \sigma_{xx} \) is totally opposite to that in the non-homogeneous medium. The normal stress is tensile in the homogeneous medium while it is compressive in the non-homogeneous medium. Also, the increasing value of parameter n results in increase in magnitude of normal stress, thus indicating an increasing effect on the profile. The difference in magnitudes becomes indistinct along with the passage of time. In Fig. 4, we have shown the spatial variation of change in volume fraction field \( \phi \). Presence of non-homogeneity is responsible for decreasing the numerical values of \( \phi \). It is also manifested from the plot that increasing values of n are having a decreasing effect on the magnitude of \( \phi \).The effect of non-homogeneity parameter n on temperature distribution is presented in Fig. 5. The temperature field is having a similar distribution in all the three cases. In the absence of non-homogeneity, the temperature field attains comparatively small values in the whole range. As we increase the value of non-homogeneity parameter, the numerical values of temperature field increase. The impact dies out when we move away from the boundary. It is noted that the values of temperature field are maximum for all the three cases in the vicinity of source which is physically reasonable and then diminish to zero gradually. From the physical standpoint, when the upper surface of the half-space is exposed to the thermal source, heat flux passes each infinitesimal element of the half-space sequentially. According to the energy conservation law, one portion of heat flux is absorbed by the element and makes an increase in its intrinsic energy, which is embodied as the step increase of temperature. The other portion of the heat flux continues to propagate due to the temperature gradient in the form of heat conduction. From the standpoint of mathematics, the non-Fourier thermal conduction equation is a damped wave equation, with the coefficient of \( \frac{\partial \theta }{\partial t} \) representing the amount of damping.

Fig. 2
figure 2

Effect of non-homogeneity parameter on normal displacement distribution

Full size image
Fig. 3
figure 3

Effect of non-homogeneity parameter on normal stress distribution

Full size image
Fig. 4
figure 4

Effect of non-homogeneity parameter on change in volume fraction field

Full size image
Fig. 5
figure 5

Effect of non-homogeneity parameter on temperature distribution

Full size image

The comparison of normal displacement, normal stress, change in volume fraction field and temperature field for the three different media, namely, functionally graded thermoelastic medium with voids and gravity (FGMVG), functionally graded thermoelastic medium with voids (FGMV) and functionally graded thermoelastic medium with gravity (FGMG) are displayed in Figs. 6, 7, 8 and 9. In Fig. 6, we have illustrated the normal displacement distribution with distance x to explore the effects of gravity and voids. Displacement field exhibits remarkable sensitivity towards gravity and voids. Absence of voids (FGMG) causes an increment in the magnitude of displacement and the profile is influenced to a great extent by the gravity field. The behaviour of normal stress, which is compressive in nature, is depicted in Fig. 7 for FGMVG, FGMV and FGMG media. According to the boundary conditions, normal stress starts with a value of zero magnitude in all the three cases. Presence of voids causes an increasing effect and the presence of gravity causes a decreasing effect on normal stress distribution. Figure 8 demonstrates the spatial variation of change in volume fraction field for FGMVG and FGMV media. Numerical values of \( \phi \) are large in FGMVG medium as compared to FGMV medium, which explains that presence of gravity field increases the absolute values of \( \phi \). Figure 9 displays the variation of temperature field with distance x for the three media i.e., FGMVG, FGMV and FGMG. Temperature distribution has qualitatively similar behaviour for all the media. It is also noticed that the values of temperature field decrease as we neglect the voids effect and the values increase if we neglect the effect of gravitational field from the medium.

Fig. 6
figure 6

Effects of gravity and voids on normal displacement distribution

Full size image
Fig. 7
figure 7

Effects of gravity and voids on normal stress distribution

Full size image
Fig. 8
figure 8

Effect of gravity on change in volume fraction field

Full size image
Fig. 9
figure 9

Effects of gravity and voids on temperature distribution

Full size image

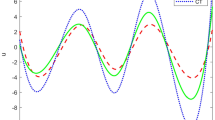
In Figs. 10, 11, 12 and 13, we have depicted the effect of relaxation time on the variations of the considered field variables. The relaxation time \( \tau_{0} = 0.02 \) corresponds to Lord–Shulman (LS) theory while \( \tau_{0} = 0.0 \) corresponds to coupled thermoelasticity (CT) theory. Figure 10 explains that the magnitude of normal displacement for LS model is less as compared to CT model, which indicates that relaxation time has a decreasing influence on the profile of normal displacement. Figure 11 demonstrates the variation of normal stress with distance x. It can be noted from the figure that the normal stress for LS theory has large numerical values in comparison to coupled thermoelasticity (CT) theory, which illuminates the fact that the relaxation time is having a significant increasing impact on normal stress distribution. Figure 12 displays the spatial variation of change in volume fraction field with distance x for two different models. Numerical values of \( \phi \) are small in LS model as compared to CT model, which explains that the presence of relaxation time decreases the absolute values of \( \phi \). Figure 13 gives the graphical description of relation between temperature field and distance x. From this figure, it is noted that the value of temperature field for LS theory is less as compared to CT theory. Thus relaxation time acts as a decreasing agent.

Fig. 10
figure 10

Effect of relaxation time on normal displacement distribution

Full size image
Fig. 11
figure 11

Effect of relaxation time on normal stress distribution

Full size image
Fig. 12
figure 12

Effect of relaxation time on change in volume fraction field

Full size image
Fig. 13
figure 13

Effect of relaxation time on temperature distribution

Full size image

The 3D plots representing normal displacement distribution, normal stress distribution, change in volume fraction field and temperature distribution are shown in Figs. 14, 15, 16 and 17 for a wide range of x (0 ≤ x ≤ 5) and for a wide range of dimensionless time t (0 ≤ t ≤ 0.5). Figure 14 illustrates the variation of normal displacement with distance x and with time t. From the figure, it is observed that displacement field shows maximum value in magnitude in the vicinity of source and the values decrease with increase in the spatial co-ordinate. The increase in the value of time results in increase in the numerical values of normal displacement. Figure 15 indicates the variation in the values of normal stress for a wide range of x and t. Numerical values of normal stress increase in the beginning and start decreasing in the neighbourhood of x = 0.61 and finally tend to zero with increasing x. The values of normal stress field increase with increasing time t. The variation of change in volume fraction field is plotted in Fig. 16 for wide ranges of x and t. Increment in the value of time has caused increment in the numerical values of \( \phi \). Figure 17 presents the distribution of temperature with distance x and time t. The temperature distribution is behaving like a decreasing function of x and an increasing function of t for the whole range.

Fig. 14
figure 14

Profile of normal displacement distribution with n = 0.01

Full size image
Fig. 15
figure 15

Profile of normal stress distribution with n = 0.01

Full size image
Fig. 16
figure 16

Profile of change in volume fraction field with n = 0.01

Full size image
Fig. 17
figure 17

Profile of temperature distribution with n = 0.01

Full size image

8 Concluding remarks

Present investigation is an effort to provide a mathematical model for determining the behaviour of normal displacement, normal stress, change in volume fraction field and temperature in a non-homogeneous, isotropic thermoelastic medium with voids and gravity under LS theory by using normal mode technique. Theoretical and numerical results demonstrate that the non-homogeneity parameter, gravity field, voids and relaxation time have prominent effects on the considered physical variables. From this work, one can infer that

  • From all the figures, it has been observed that all the physical fields have non-zero values only in the limited domain of space, which is in accordance with the notion of generalized thermoelasticity theory and support the physical facts.

  • All the considered physical quantities are strongly affected by the presence of non-homogeneity parameter. It acts to decrease the magnitudes of normal displacement and change in volume fraction field, whereas it has an increasing effect on the profile of temperature \( \theta \).

  • Significant effect of voids is observed on all the physical fields. The magnitudes of normal stress and temperature get suppressed in the absence of voids, while the magnitude of normal displacement gets increased in the absence of voids. This is due to the influences of cross effects arising from the coupling of the fields of temperature, voids and strain.

  • Presence of gravity acts to decrease the magnitudes of normal stress and temperature field. The numerical values of change in volume fraction field increase in the presence of gravitational field.

  • The time t has a noticeable increasing effect on the distributions of all the physical fields.

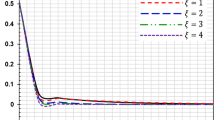
  • The comparative study of LS and CT theories suggests that relaxation time has a significant effect on the physical quantities. Relaxation time exhibits a decreasing effect on normal displacement, change in volume fraction field and temperature field, whereas it has an increasing effect on the profile of normal stress.

  • The method adopted here is applicable to a wide range of problems in thermodynamics and thermoelasticity.

The above study is of fundamental importance and finds its applications for experimental researchers/engineers working in the field of geophysics and material science. Applications of this problem are also found in the fields of seismology, geomechanics, earthquake engineering and soil dynamics etc., where the interest is about various phenomena occurring in earthquakes and measuring of displacement, stresses and temperature field due to the presence of certain sources. Problem assumes great significance in an earthquake preparation region when we think of the variation in particle motion as a possible precursor for earthquake prediction. FGMs are used in new generation spacecraft because of their multi-functional role in engineering areas. FGM coating can be used to reduce the residual and thermal stresses. This coating not only enhances the strength of the connections but can also reduce the crack driving force. In numerous applications, FGMs are found to be better substitutes for conventional homogeneous materials. Among various uses of FGMs, one such use of FGMs is in automotive brakes and clutches, where the result of frictional heat generation is the subject of concern to the engineers. FGMs are used in the defence industry for making bullet-proof vests. Some of the applications of the FGMs in the energy industry include the inner wall of nuclear reactors, the thermoelectric converter for energy conversion, the solar panel, the solar cells, the turbine blade coating etc.