Skip to main content
SpringerLink
Log in

Fourth-Order Numerical Scheme Based on Half-Step Non-Polynomial Spline Approximations for 1D Quasi-Linear Parabolic Equations

  • Published:
Numerical Analysis and Applications Aims and scope Submit manuscript

ABSTRACT

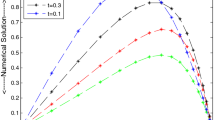
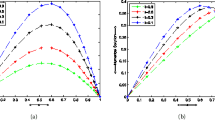
In this article, we discuss a fourth-order accurate scheme based on non-polynomial splines in tension approximations for solving quasi-linear parabolic partial differential equations (PDEs). The proposed numerical method requires only two half-step points and a central point on a uniform mesh in spatial direction. This method is derived directly from the continuity condition for the first-order derivative of the non-polynomial tension spline function. The stability of the scheme is discussed using a model linear PDE. The method is applicable for solving singular parabolic problems in polar systems. The proposed method is tested on the generalized Burgers–Huxley equation, generalized Burgers–Fisher equation, and Burgers’ equations in polar coordinates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. Bratsos, A.G., A Fourth Order Improved Numerical Scheme for the Generalized Burgers–Huxley Equation, Am. J. Comp. Math., 2011, vol. 1, pp. 152–158.

  2. Burgers, J.M., A Mathematical Model Illustrating the Theory of Turbulence, Adv. Appl. Mech., 1948, vol. 1, pp. 171–199.

  3. Celik, I., Chebyshev Wavelet Collocation Method for Solving Generalized Burgers–Huxley Equation, Math. Meth. Appl. Sci., 2016, vol. 39, no. 3, pp. 366–377.

  4. Dehghan, M., Heris, J.M., and Saadatmandi, A., Application of Semi-Analytic Methods for the Fitzhugh–Nagumo Equation, Which Models the Transmission of Nerve Impulses, Math. Meth. Appl. Sci., 2010, vol. 33, no. 11, pp. 1384–1398.

  5. Duan, Y., Kong, L., and Zhang, R., A Lattice Boltzmann Model for the Generalized Burgers–Huxley Equation, Phys. A, 2012, vol. 391, no. 3, pp. 625–632.

  6. Fisher, R.A., The Wave of Advance of Advantageous Genes,Ann. Eugenics, 1937, vol. 7, no. 4, pp. 353–369.

  7. Hageman, L.A. and Young, D.M., Applied Iterative Methods, New York: Dover, 2004.

  8. Jain, M.K., Jain, R.K., and Mohanty, R.K., High Order Difference Methods for System of 1-D Non-Linear Parabolic Partial Differential Equations, Int. J. Comp. Math., 2009, vol. 37, nos. 1/2, pp. 105–112.

  9. Kelly, C.T., Iterative Methods for Linear and Non-linear Equations, Philadelphia: SIAM Publications, 1995.

  10. Kolmogorov, A.N., Petrovskii, I.G., and Piskunov, N.S., A Study of the Equation of Diffusion with Increase in the Quantity of Matter, and Its Application to a Biological Problem, Math. Bull. Moscow Univ., 1937, vol. 1, pp. 1–26.

  11. Ksasov, B.I. and Sattayatham, P., GB-Splines of Arbitrary Order, J. Comp. Appl. Math., 1999, vol. 104, pp. 63–88.

  12. Makarov, A.A., Construction of Splines of Maximal Smoothness,J. Math. Sci., 2011, vol. 178, pp. 589–604.

  13. Mittal, R.C. and Tripathi, A., Numerical Solutions of Generalized Burgers–Fisher and Generalized Burgers–Huxley Equations Using Collocation of Cubic B-Splines, Int. J. Comp. Math., 2015, vol. 92, pp. 1053–1077.

  14. Mohammadi, R., Spline Solution of the Generalized Burgers–Fisher Equation, Appl. Analysis, 2011, vol. 91, no. 12, pp. 2189–2215.

  15. Mohammadi, R., B-Spline Collocation Algorithm for Numerical Solution of the Generalized Burgers–Huxley Equation, Num. Meth. Part. Diff. Eqs., 2013, vol. 29, no. 4, pp. 1173–1191.

  16. Mohanty, R.K., An Implicit High Accuracy Variable Mesh Scheme for 1-D Non-Linear Singular Parabolic Partial Differential Equations,Appl. Math. Comp., 2007, vol. 186, no. 1, pp. 219–229.

  17. Mohanty, R.K. and Jain, M.K., High-Accuracy Cubic Spline Alternating Group Explicit Methods for 1D Quasi-Linear Parabolic Equations, Int. J. Comp. Math., 2009, vol. 86, no. 9, pp. 1556–1571.

  18. Mohanty, R.K., A Variable Mesh C-SPLAGE Method of Accuracy for 1D Nonlinear Parabolic Equations, Appl. Math. Comp., 2009, vol. 213, no. 1, pp. 79–91.

  19. Mohanty, R.K. and Sharma, S., High Accuracy Quasi-Variable Mesh Method for the System of 1D Quasi-Linear Parabolic Partial Differential Equations Based on Off-Step Spline in Compression Approximations, Adv. Diff. Eqs., 2017, vol. 212; DOI: https://doi.org/10.1186/s13662-017-1274-3.

  20. Mohanty, R.K. and Sharma, S., A New Two-Level Implicit Scheme for the System of 1D Quasi-Linear Parabolic Partial Differential Equations Using Spline in Compression Approximations, Diff. Eqs. Dyn. Syst., 2019, vol. 27; DOI: https://doi.org/10.1007/s12591-018-0427-5.

  21. Mohanty, R.K., Sharma, S., and Singh, S., A New Two-Level Implicit Scheme of Order Two in Time and Four in Space Based on Half-Step Spline in Compression Approximations for Unsteady 1D Quasi-Linear Biharmonic Equations, Adv. Diff. Eqs., 2018, vol. 378; DOI: https://doi.org/10.1186/s13662-018-1841-2.

  22. Rashidinia, J. and Mohammadi, R., Non-Polynomial Cubic Spline Methods for the Solution of Parabolic Equations, Int. J. Comp. Math., 2008, vol. 85, no. 5, pp. 843–850.

  23. Satsuma, J., Exact Solutions of Burgers Equation with Reaction Terms, in Topics in Soliton Theory and Exactly Solvable Nonlinear Equations, Singapore: World Scientific, 1986, pp. 255–262.

  24. Topics in Soliton Theory and Exactly Solvable Nonlinear Equations, Ablowitz, M., Fuchssteiner, B., and Kruskal, M., Eds., Singapore: World Scientific, 1987.

  25. Schweikert, D.G., An Interpolating Curve Using a Spline in Tension, J. Math. Phys., 1966, vol. 45, nos. 1–4, pp. 312–317.

  26. Scott, A.C., Neurophysics, New York: Wiley, 1977.

  27. Talwar, J., Mohanty, R.K., and Singh, S., A New Spline in Compression Approximation for One Space Dimensional Quasilinear Parabolic Equations on a Variable Mesh, Appl. Math. Comp., 2015, vol. 260, iss. C, pp. 82–96.

  28. Talwar, J., Mohanty, R.K., and Singh, S., A New Algorithm Based on Spline in Tension Approximation for 1D Quasilinear Parabolic Equations on a Variable Mesh, Int. J. Comp. Math., 2016, vol. 93, no. 10, pp. 1771–1786.

  29. Wang, X.Y., Zhu, Z.S., and Lu, Y.K., Solitary Wave Solutions of the Generalized Burgers–Huxley Equation, J. Phys. A: Math. Gen., 1990, vol. 23, no. 3, pp. 271–274.

  30. Wang, X., Nerve Propagation and Wall in Liquid Crystals,Phys. Lett., 1995, vol. 112A, no. 8, pp. 402–406.

  31. Whiteman, G.B., Linear and Nonlinear Waves, New York: Wiley, 1974.

  32. Zhang, R., Yu, X., and Zhao, G., The Local Discontinuous Galerkin Method for Burgers–Huxley and Burgers–Fisher Equations,Appl. Math. Comp., 2012, vol. 218, pp. 8773–8778.

  33. Zhu, C.-G. and Kang, W.-S., Numerical Solution of Burgers–Fisher Equation by Cubic B-Spline Quasi-Interpolation,Appl. Math. Comp., 2010, vol. 216, pp. 2679–2686.

Download references

ACKNOWLEDGEMENTS

The authors would like to thank the reviewers for their valuable comments and remarks, which helped to improve the quality of the paper.

Funding

This work was supported by CSIR-SRF, grant no. 09/045(1161)/2012-EMR-I.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Faculty of Mathematics and Computer Science, South Asian University, 110021, New Delhi, India

    R. K. Mohanty

  2. Department of Mathematics, Faculty of Mathematical Sciences, University of Delhi, 110007, Delhi, India

    S. Sharma

Authors
  1. R. K. Mohanty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to R. K. Mohanty or S. Sharma.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mohanty, R.K., Sharma, S. Fourth-Order Numerical Scheme Based on Half-Step Non-Polynomial Spline Approximations for 1D Quasi-Linear Parabolic Equations. Numer. Analys. Appl. 13, 68–81 (2020). https://doi.org/10.1134/S1995423920010061

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1995423920010061

Keywords

Search

Navigation