1 Introduction

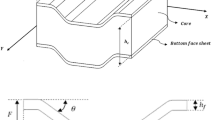
There is constant need to study new materials and structural configurations for thin-walled structures. Weight reduction and strength increase enable lighter and often more sustainable structural solutions that can be used in civil, naval and aeronautical applications. Structural efficiency in terms of strength-to-weight and stiffness-to-weight is obtained by positioning of the material according to the load-carrying mechanism of the structure. In bending dominated applications, this often results in plates with periodic microstructure, for example, single-sided stiffened plates and sandwich panels with visibly discrete core; see Fig. 1. The periodic structure allows integration of functions to the panel(e.g. air-conditioning and cable tracks). Thus, unidirectional stiffening system with coarse spacing becomes attractive structural alternative; Refs. [1,2,3,4,5,6,7,8,9,10,11,12,13]. These unidirectional plates, especially in the form of steel sandwich plates, have been found to have excellent mechanical properties for buckling, bending and impact loads [14,15,16,17,18,19,20,21]. These structures are, however, challenging in terms of structural analysis. The direct inclusion of the microstructure to computational models of the entire structure leads to expensive pre-processing, analysis and post-processing times (i.e., computationally intensive). The problem compounds if the geometry changes and analysis is needed to be repeated several times(e.g., during structural optimization or reliability analysis [18, 20]). Further complications are caused by the fact that often the failure of these panels occurs first locally in the microstructural level in the face and web-plates or at the welds by yielding or buckling, see Fig. 1. This means that certain level of accuracy is needed in the analysis of structural details.

Fig. 1
figure 1

Examples of periodic sandwich panels structural failures under different extreme loads. (Figures from: explosions Valdevit et al. [18]; full-scale ship collisions Ehlers et al. [37] and quasi-static plate punch experiments Körgesaar et al. [38])

Full size image

Homogenization is the alternative method for a direct modeling of both micro- and macrostructure. In terms of plates, it has been discussed by several authors(see, e.g., Refs. [1, 3, 4, 11,12,13,14, 20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]). In plates, the main idea is to reduce the mathematical description to Equivalent Single Layer (ESL) representation in which the deformations and stress resultants (forces and moments) are computed for known load and boundary conditions. In periodic sandwich panels, the closed unit cells, including the interacting face and web plates, form a structure that warps in bending due to the out-of-plane shear. With this phenomenon included, Libove and Hubka [1] presented an ESL-theory for corrugated-core sandwich plates which follows First order Shear Deformation Theory (FSDT). They derived the equivalent shear stiffness and provided series solutions to prevailing differential equations for bending. After this work, several papers have been written for other microstructures [26,27,28,29,30, 33, 37, 38] where the stiffness parameters change, but the differential equations remain the same. The approach has been also validated to geometrically moderate non-linear global deformations [26,27,28]. However, the problem arises in the assessment of stresses. As the local, microstructural length-scale can be close to that of macro-structural, the local oscillations of stresses within microstructure can have significant contribution to the overall stress state caused by macroscopic plate behavior. It has been experimentally shown that the out-of-plane shear damages the periodic structures from plate edges or close to point loads, thus the secondary stresses induced by shear need to be carefully assessed [20,21,22], see also Fig. 1. These findings are based on bending of plates. This situation can also occur during in-plane compression after buckling when the initially membrane-dominated responses are complemented with out-of-plane responses [39].

The objective of this study is to present the phenomena related to post-buckling response of web-core sandwich plates and thereby extending the work presented in Ref. [39]. Primary focus is on the bending responses due to the von Kármán strains. The ESL formulation based on the FSDT is utilized in order to show the connection between in- and out-of-plane deformations. In post-buckling regime, bending occurs, which activates secondary normal stresses of the microstructure. As the unit cell to plate length ratio, lmicro/lmacro, is not infinitesimal, the micro-fluctuations of stress at unit cell level contribute significantly to the total normal stress response of the face and web plates.

In order to show these aspects, we first formulate the geometrically non-linear differential equations of the problem at hand. We assume that the microstructure is linearly-elastic. Thus, at micro-scale, analytical, stiffness and strength formulations are possible and the prevailing physics can be explained in parametric form. Then we show how to eliminate the microstructural elements from the plate model. This elimination allows solution of the macro-scale problem with the classical ESL-FSDT formulations that can be found from numerous textbooks and the finite element implementations from several commercial codes. Then, at the post-processing stage we focus on assessment of stress concentrations at faces, webs and welds and reconsider the finite size of the microstructure. This shows the limitations of this paper and also the commercial FSDT-ESL FE-codes on capturing the prevailing post-buckling behavior. It also motivates extensions to the non-classical continuum mechanics formulations.

2 Theory

2.1 Notations

The plate is assumed to consist of structural elements with small thickness representing the face and web plate(s). This justifies the use of Kirchhoff hypothesis locally at the face and web-plates. The thicknesses of the top and bottom face plates are denoted by tt and tb, respectively, and these are positioned in the xy-plane. The web plates are in the xz-plane and have thickness tw, spacing s, and height hc. The plate has two coordinate systems, namely: global xyz and local xlylzl (see Fig. 2). The origin of the global coordinate system is located at the geometrical mid-plane of the plate and the origin of the local coordinate is located at the geometrical mid-planes of face or the web plates under consideration.

Fig. 2
figure 2

Web-core sandwich plate, notations and the kinematics of the First order Shear Deformation Theory (FSDT) in Equivalent Single Layer (ESL) formulation

Full size image

2.2 Classical, homogenized FSDT for periodic plates

The deformation of the periodic plate is composed of global bending deflection of the mid-surface and local deflection due to warping of face and web plates. Thus, the total deflections along the three coordinate directions of the faceplate can be represented as

$$u\left( {x,y,z,x_{l} ,y_{l} ,z_{l} } \right) = u_{0} \left( {x,y} \right) + z\phi_{g,x} \left( {x,y} \right) + z_{l} \phi_{x,l} \left( {x,y,x_{l} ,y_{l} } \right)$$
(1)
$$v\left( {x,y,z,x_{l} ,y_{l} ,z_{l} } \right) = v_{0} \left( {x,y} \right) + z\phi_{g,y} \left( {x,y} \right) + z_{l} \phi_{y,l} \left( {x,y,x_{l} ,y_{l} } \right)$$
(2)
$$w\left( {x,y,z,x_{l} ,y_{l} ,z_{l} } \right) = w_{g} \left( {x,y} \right) + w_{l} \left( {x,y,x_{l} ,y_{l} } \right).$$
(3)

where subscript 0 denotes the in-plane membrane displacements at the geometrical mid-plane, as shown in Fig. 2. The subscripts g and l denote bending actions at the geometrical mid-plane of the entire sandwich plate and face plate respectively. The global deflection of webs is defined completely by the face plate deflection at their intersection, wweb = wg. In addition, due to perfect connection with the faces, the webs bend in the y-direction due to the local deflection of the faces, wl. This deflection of the webs is defined completely by the face plate rotations at the web-to-face-interface. Thus, additional kinematical variables are not needed for the web deformations. The rotation of the mid-plane of the entire plate is denoted by ϕg, the in-plane displacements by u0 and v0 and deflection by wg. The global and local rotations are

$$\phi_{x,g} = \gamma_{xz} - \frac{{dw_{g} }}{dx} = \frac{du}{dz},\phi_{y,g} = \gamma_{yz} - \frac{{dw_{g} }}{dy} = \frac{dv}{dz}$$
(4)
$$\phi_{x,l} = - \frac{{dw_{l} }}{dx},\phi_{y,l} = - \frac{{dw_{l} }}{dy}$$
(5)

which means the sandwich plate behaves according to the FSDT. The relative strains, expressed in column vector, are

$$\left\{ \varepsilon \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx,0} } \\ {\varepsilon_{yy,0} } \\ {\gamma_{xy,0} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx,g} } \\ {\varepsilon_{yy,g} } \\ {\gamma_{xy,g} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx,l} } \\ {\varepsilon_{yy,l} } \\ {\gamma_{xy,l} } \\ \end{array} } \right\}$$
(6)

with strains defined as

$$\varepsilon_{xx,0} = \frac{{du_{0} }}{dx} + \underline{{\frac{1}{2}\left( {\frac{{dw_{g} }}{dx}} \right)^{2} }} , \varepsilon_{xx,g} = z_{g} \frac{{d\phi_{x,g} }}{dx},\varepsilon_{xx,l} = - z_{l} \frac{{d^{2} w_{l} }}{{dx^{2} }}$$
(7)
$$\varepsilon_{yy,0} = \frac{{dv_{0} }}{dy} + \underline{{\frac{1}{2}\left( {\frac{{dw_{g} }}{dy}} \right)^{2} }} ,\varepsilon_{yy,g} = z_{g} \frac{{d\phi_{y,g} }}{dy},\varepsilon_{yy,l} = - z_{l} \frac{{d^{2} w_{l} }}{{dy^{2} }}$$
(8)
$$\gamma_{xy,0} = \frac{{du_{0} }}{dy} + \frac{{dv_{0} }}{dx} + \underline{{\frac{{dw_{g} }}{dx}\frac{{dw_{g} }}{dy}}} ,\gamma_{xy,g} = z_{g} \left( {\frac{{d\phi_{x,g} }}{dy} + \frac{{d\phi_{y,g} }}{dx}} \right),\gamma_{xy,l} = - z_{l} \frac{{d^{2} w_{l} }}{dxdy}$$
(9)

where the underlined terms denote the von Kármán strains, which are accounted at the macroscale. The plates are assumed to be made of isotropic material and follow Hooke’s law. Thus, the elasticity matrices of the different layers (subscripts: t = top face, b = bottom face, w = web) of the sandwich plate are

$$\left[ {Q_{t} } \right] = \left[ {Q_{b} } \right] = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right]_{t,b} = \left[ {\begin{array}{*{20}c} {\frac{E}{{1 - \upsilon^{2} }}} & {\frac{\upsilon E}{{1 - \upsilon^{2} }}} & 0 \\ {\frac{\upsilon E}{{1 - \upsilon^{2} }}} & {\frac{E}{{1 - \upsilon^{2} }}} & 0 \\ 0 & 0 & G \\ \end{array} } \right]_{t,b}$$
(10)
$$\left[ {Q_{w} } \right] = \left[ {\begin{array}{*{20}c} {E_{w} \frac{t}{s}} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]$$
(11)

where the web properties are smeared equally over the unit cell width by the rule-of- mixtures. The stresses per layer are:

$$\left\{ {\sigma_{i} } \right\} = \left[ {E_{i} } \right]\left\{ {\varepsilon_{i} } \right\}, \;i = t,w,b$$
(12)

The stress resultants are obtained by through-thickness integration and are

$$\left\{ N \right\} = \left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} } \right\} = \mathop \smallint \limits_{ - h/2}^{h/2} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right\}dz, \;\left\{ M \right\} = \mathop \smallint \limits_{ - h/2}^{h/2} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right\}zdz,$$
(13)

Due to the periodic microstructure, smearing the shear modulus of the core by an integrating over the thickness of the sandwich does not result in correct stiffness values. In the x-direction this is due to the shear flow of the thin-walled section. In the y-direction this is due to the higher order warping deformations of the unit cells. Instead, we incorporate the shear stiffness that accounts directly these two effects and write:

$$\left\{ Q \right\} = \left\{ {\begin{array}{*{20}c} {Q_{xx} } \\ {Q_{yy} } \\ \end{array} } \right\} = \left[ {D_{Q} } \right]\left\{ {\gamma_{z} } \right\} = \left[ {\begin{array}{*{20}c} {D_{Q1} } & 0 \\ 0 & {D_{Q2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\}$$
(14)

The equilibrium of a plate element is governed by the following equations:

$$\frac{{dN_{xx} }}{dx} + \frac{{dN_{xy} }}{dy} = 0$$
(15)
$$\frac{{dN_{yy} }}{dy} + \frac{{dN_{xy} }}{dx} = 0$$
(16)
$$\frac{{dQ_{xx} }}{dx} + \frac{{dQ_{yy} }}{dy} + N^{*} w_{g} + q = 0$$
(17)
$$\frac{{dM_{xx} }}{dx} + \frac{{dM_{xy} }}{dy} - Q_{xx} + \underbrace {{\frac{{dM_{xx,l} }}{{dx_{l} }} + \frac{{dM_{xy,l} }}{{dy_{l} }}}}_{local} = 0$$
(18)
$$\frac{{dM_{yy} }}{dy} + \frac{{dM_{xy} }}{dx} - Q_{yy} + \underbrace {{\frac{{dM_{yy,l} }}{{dy_{l} }} + \frac{{dM_{xy,l} }}{{dx_{l} }}}}_{local} = 0$$
(19)
$$N^{*} w_{g} = \frac{d}{dx}\left( {N_{xx} \frac{{dw_{g} }}{dx} + N_{xy} \frac{{dw_{g} }}{dy}} \right) + \frac{d}{dy}\left( {N_{xy} \frac{{dw_{g} }}{dx} + N_{yy} \frac{{dw_{g} }}{dx}} \right)$$
(20)

where the underlined terms are associated with local shear-induced warping response. It should be also noticed that due to the von Kármán strains, the in-plane membrane and out-of-plane shear forces are coupled, by Eq. (20). The differential equations in terms of displacements are then:

$$A_{11} \left( {\frac{{d^{2} u_{0} }}{{dx^{2} }} + \frac{{dw_{g} }}{dx}\frac{{d^{2} w_{g} }}{{dx^{2} }}} \right) + A_{12} \left( {\frac{{d^{2} v_{0} }}{dxdy} + \frac{{dw_{g} }}{dy}\frac{{d^{2} w_{g} }}{dxdy}} \right) + B_{11} \frac{{d^{2} \phi_{x,g} }}{{dx^{2} }} + B_{12} \frac{{d^{2} \phi_{y,g} }}{dxdy} + B_{66} \left( {\frac{{d^{2} \phi_{x,g} }}{{dy^{2} }} + \frac{{d^{2} \phi_{y,g} }}{dxdy}} \right) + A_{66} \left( {\frac{{d^{2} u_{0} }}{{dy^{2} }} + \frac{{d^{2} v_{0} }}{dxdy} + \frac{{d^{2} w_{g} }}{dxdy}\frac{{dw_{g} }}{dy} + \frac{{dw_{g} }}{dx}\frac{{d^{2} w_{g} }}{{dy^{2} }}} \right) = 0$$
(21)
$$A_{22} \left( {\frac{{d^{2} v_{0} }}{{dy^{2} }} + \frac{{dw_{g} }}{dy}\frac{{d^{2} w_{g} }}{{dy^{2} }}} \right) + A_{12} \left( {\frac{{d^{2} u_{0} }}{dxdy} + \frac{{dw_{g} }}{dx}\frac{{d^{2} w_{g} }}{dxdy}} \right) + B_{22} \frac{{d^{2} \phi_{y,g} }}{{dy^{2} }} + B_{12} \frac{{d^{2} \phi_{x,g} }}{dxdy} + B_{66} \left( {\frac{{d^{2} \phi_{y,g} }}{{dx^{2} }} + \frac{{d^{2} \phi_{x,g} }}{dxdy}} \right) + A_{66} \left( {\frac{{d^{2} v_{0} }}{{dx^{2} }} + \frac{{d^{2} u_{0} }}{dxdy} + \frac{{d^{2} w_{g} }}{dxdy}\frac{{dw_{g} }}{dx} + \frac{{dw_{g} }}{dy}\frac{{d^{2} w_{g} }}{{dx^{2} }}} \right) = 0$$
(22)
$$D_{Qx} \left( {\frac{{d^{2} w_{g} }}{{dx^{2} }} + \frac{{d\phi_{x,g} }}{dx}} \right) + D_{Qy} \left( {\frac{{d^{2} w_{g} }}{{dy^{2} }} + \frac{{d\phi_{y,g} }}{dy}} \right) + N^{*} w_{g} + q = 0$$
(23)
$$B_{11} \left( {\frac{{d^{2} u_{0} }}{{dx^{2} }} + \frac{{dw_{g} }}{dx}\frac{{d^{2} w_{g} }}{{dx^{2} }}} \right) + B_{12} \left( {\frac{{d^{2} v_{0} }}{dxdy} + \frac{{dw_{g} }}{dy}\frac{{d^{2} w_{g} }}{dxdy}} \right) + D_{11} \frac{{d^{2} \phi_{x,g} }}{{dx^{2} }} + D_{12} \frac{{d^{2} \phi_{y,g} }}{dxdy} + D_{66} \left( {\frac{{d^{2} \phi_{x,g} }}{{dy^{2} }} + \frac{{d^{2} \phi_{y,g} }}{dxdy}} \right) + B_{66} \left( {\frac{{d^{2} u_{0} }}{{dy^{2} }} + \frac{{d^{2} v_{0} }}{dxdy} + \frac{{d^{2} w_{g} }}{dxdy}\frac{{dw_{g} }}{dy} + \frac{{dw_{g} }}{dx}\frac{{d^{2} w_{g} }}{{dy^{2} }}} \right) - D_{Q1} \left( {\frac{{dw_{g} }}{dx} + \phi_{x,g} } \right) - \underbrace {{\frac{{dM_{x,l} }}{{dx_{l} }} - \frac{{dM_{xy,l} }}{{dy_{l} }}}}_{local} = 0$$
(24)
$$B_{22} \left( {\frac{{d^{2} v_{0} }}{{dy^{2} }} + \frac{{dw_{g} }}{dy}\frac{{d^{2} w_{g} }}{{dy^{2} }}} \right) + B_{12} \left( {\frac{{d^{2} u_{0} }}{dxdy} + \frac{{dw_{g} }}{dx}\frac{{d^{2} w_{g} }}{dxdy}} \right) + D_{22} \frac{{d^{2} \phi_{y,g} }}{{dy^{2} }} + D_{12} \frac{{d^{2} \phi_{x,g} }}{dxdy} + D_{66} \left( {\frac{{d^{2} \phi_{y,g} }}{{dx^{2} }} + \frac{{d^{2} \phi_{x,g} }}{dxdy}} \right) + B_{66} \left( {\frac{{d^{2} v_{0} }}{{dx^{2} }} + \frac{{d^{2} u_{0} }}{dxdy} + \frac{{d^{2} w_{g} }}{dxdy}\frac{{dw_{g} }}{dx} + \frac{{dw_{g} }}{dy}\frac{{d^{2} w_{g} }}{{dx^{2} }}} \right) - D_{Q2} \left( {\frac{{dw_{g} }}{dy} + \phi_{y,g} } \right) - \underbrace {{\frac{{dM_{y,l} }}{{dy_{l} }} - \frac{{dM_{xy,l} }}{{dx_{l} }}}}_{local} = 0$$
(25)

The membrane, membrane-bending coupling and bending stiffnesses are

$$\left[ {A,B,D} \right] = \mathop \smallint \limits_{ - h/2}^{h/2} \left[ {Q_{i} } \right]\left( {1,z,z^{2} } \right)dz, i = t,w,b$$
(26)

The shear stiffness is obtained by unit cell analysis of the periodic structure. In x-direction (see Ref. [21]) this is:

$$D_{Q1} = k_{11}^{2} \left( {G_{t} t_{t} + G_{b} t_{b} + \frac{{t_{w} }}{s}G_{w} h_{c} } \right)$$
(27)
$$k_{11} = \sqrt {\frac{1}{{A\left( {\mathop \sum \nolimits_{i} \smallint \left( {\frac{{\tau_{i} }}{{Q_{Q,x} s}}} \right)^{2} t_{i} ds_{i} } \right)}}} ,i = t,w,b$$
(28)

where the shear correction factor is obtained by integration of shear flow through top, web and bottom faces; for details see Ref. [21]. In the y-direction the shear stiffness is computed by unit frame analysis (see Ref. [21] and Fig. 3b) and is given by

$$D_{Q2} = \frac{{12D_{w} }}{{s^{2} \left( {k_{Q} \left( {\frac{{D_{w} }}{{D_{b} }} + 6\frac{d}{s}} \right) + 12\frac{{D_{w} }}{{k_{\theta }^{b} s}} - 2\frac{d}{s}} \right)}}$$
(29)
$$k_{\theta }^{i} = \frac{{Q_{y} s}}{{\theta_{c}^{i} }},k_{1}^{t} = 1 - k_{Q} ,k_{1}^{b} = k_{Q} ,k_{2}^{t} = 2 - 3k_{Q} ,k_{2}^{b} = 3k_{Q} - 1,$$
(30)
$$k_{Q} = \frac{{1 + 12\frac{{D_{t} }}{s}\left( {\frac{1}{{k_{\theta }^{t} }} - \frac{1}{{k_{\theta }^{b} }}} \right) + 6\frac{{D_{t} }}{{D_{w} }}\frac{d}{s}}}{{1 + 12\frac{{D_{t} }}{{D_{w} }}\frac{d}{s} + \frac{{D_{t} }}{{D_{b} }}}}$$
(31)

where kθ is the rotation stiffness of the laser-stake weld and k-parameters model the relative stiffness of faces and webs. For symmetric sandwich panels the parameter kQ = 1/2 indicating that equal amount of shear is carried out by top and bottom face plates.

Fig. 3
figure 3

a Web-core sandwich under shear deformation in weak direction. b Reduction of the deformation from 3rd order polynomial to 1st order polynomial in y-direction. c The shear-induced bending stresses in the unit cell and d variation of the shear induced bending moment between the unit cells (periodic behavior is shown by dashed lines, and average behavior by points)

Full size image

2.3 Unit cell analysis for out-of-plane shear

The local response, opposite to stiffener direction, is assumed to have the same values as the global response at the unit cell edges in terms of displacement, wl(x,y) = wg(x,y), wl(x,y + s) = wg(x,y + s), as shown in Fig. 3a and b. However, along the unit cell the local displacement field in the y-direction can differ from global due to shear-induced warping (see Fig. 3b). Due to the classical continuum assumptions the average shear strain of horizontal and vertical sliding, γyz= (γyz,h+ γyz,v)/2, is utilized.

The local warping deflection due to shear force Qyy is given as (see Ref. [21]):

$$w_{i} = \frac{{Q_{Qy} sd}}{{12D_{i} }}k_{1}^{i} \left( { - \frac{{sy_{l}^{{}} }}{d} + 3\frac{{y_{l}^{2} }}{d} - 3\frac{{y_{l}^{3} }}{ds}} \right),\;i = t,b$$
(32)

with the k-factors defined in Eq. (30). The curvature is

$$\frac{{d^{2} w_{i} }}{{dx_{l}^{2} }} = \frac{{d^{2} w_{i} }}{dxdy} = 0,\frac{{d^{2} w_{i} }}{{dy_{l}^{2} }} = \frac{{Q_{Qy} s}}{{2D_{i} }}k_{1}^{i} \left( {1 - 2\frac{{y_{l}^{{}} }}{s}} \right)$$
(33)

The local bending moments and shear forces are

$$M_{x,l} = \upsilon M_{y,l} ,M_{y,l} = - \frac{{Q_{Qy} s}}{2}k_{1}^{i} \left( {1 - 2\frac{{y_{l}^{{}} }}{s}} \right),M_{xy,l} = 0$$
(34)
$$Q_{x,l} = 0,Q_{y,l} = Q_{Qy} k_{1}^{i}$$
(35)

The volume averages are

$$M_{x,l}^{*} = \mathop \smallint \nolimits_{0}^{s} \frac{{M_{x,l}^{{}} }}{V}dV = 0,M_{y,l}^{*} = 0,M_{xy,l}^{*} = 0,$$
(36)
$$Q_{x,l}^{*} = 0,Q_{y,l}^{*} = Q_{yy}^{{}} = Q_{Qy} k_{1}^{t} + Q_{Qy} k_{1}^{b}$$
(37)

Thus, with these average values the underlined terms in equilibrium Eqs. (18) and (19) and differential Eqs. (24) and (25) based on displacements become zero. The shear force Qyy is produced by the unit cell warping, see Fig. 3b. This gives us the homogenized differential equations that are derived based on the classical continuum mechanics assumption, that lmicro/lmacro = 0. These equations can be found from numerous text books of composite materials(see, e.g., Ref. [40]). In these books the corresponding analytical solutions and finite element formulations are also presented. The corresponding finite element implementations can be found from most of the commercial FE codes.

2.4 Calculation of envelope of periodic stresses from homogenized response

The periodic shear-induced bending moments and normal stresses (see Fig. 3c) are important as the with these included the total stress always exceeds the averaged, homogenized solution values. The characteristic length, lmicro, of these normal stresses is equal to web plate spacing, s, lmicro = s. These shear-induced bending moments and normal stresses have zero mean as shown in Fig. 3d and Eq. (36). Next we assume that, as the homogenized structure is in equilibrium, the periodic structure must be in equilibrium too. Then, the periodic strains and stresses are (see Ref. [21]):

$$\left\{ {\begin{array}{*{20}c} {\left\{ {\varepsilon_{0} } \right\}} \\ {\left\{ \kappa \right\}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\left[ A \right]} & {\left[ B \right]} \\ {\left[ B \right]} & {\left[ D \right]} \\ \end{array} } \right]^{ - 1} \left( {\left\{ {\begin{array}{*{20}c} {\left\{ N \right\}} \\ {\left\{ M \right\}} \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\left\{ 0 \right\}} \\ {\left\{ {M_{Q} } \right\}} \\ \end{array} } \right\}} \right)$$
(38)
$$\left\{ \varepsilon \right\} = \left\{ {\varepsilon_{0} } \right\} - z\left\{ \kappa \right\}$$
(39)
$$\left\{ \sigma \right\} = \left[ E \right]\left\{ \varepsilon \right\} + \left\{ {\sigma_{Q} } \right\}$$
(40)

where Eqs. (34) and (38) together create periodic strain field from homogenized, smooth, strain field. From strength viewpoint shape of this micro-fluctuation is not important, but the maximum value is. Thus, for linear distribution within unit cell, (see Eq. (34) and Fig. 3c and d), the maxima and minima are simply

$$M_{Q,x,i}^{max} = \pm \nu_{i} k_{1}^{i} \frac{{Q_{yy} s}}{2},M_{Q,y,i}^{max} = \pm k_{1}^{i} \frac{{Q_{yy} s}}{2},M_{Q,xy,i}^{max} = 0$$
(41)

It should be noted that when lmicro = s=0, these bending moments and resulting shear induced stresses become zero and result is the same as produced by the homogenized solution without any additional post-processing.

3 Example

3.1 General

The example presented here is taken from Ref. [39]; it is extended here in order to explain the main post-buckling phenomena. A square plate with length and width of L = B=3.60 m is considered. Thickness of the face and web plates are tt= 2.5 mm and tw= 4.0 mm, respectively. Core height is hc= 40 mm and the web plate spacing is s = 120 mm giving lmicro/lmacro= s/L = 1/30. The interface between web and face plate is assumed to be rigid in order to simplify the analysis. It has been shown in Refs. [21, 36] that non-local plate formulations are needed in the cases were the laser-stake weld is assumed to be flexible or if lmicro/lmacro-ratio would be significantly larger. In cases where the lmicro/lmacro-ratio would be significantly smaller, the shear-induced stress fluctuations would be less important. Material is assumed to be linear-elastic with Young´s modulus 206 GPa and Poisson ratio 0.3.

The FSDT-ESL problem is solved numerically by using Finite Element Method. The non-linear analysis is carried out in two steps. The first eigenmode is first computed. It is used as the shape of the initial out-of-plane imperfection and is given the magnitude of 0.01% of the plate length, L. Then, the geometrically non-linear analysis is carried out to trace the post-buckling path. Abaqus software, version 6.9, is used. A subspace iteration solver is used for the eigenvalue analysis and the modified Riks procedure for the post-buckling path. In order to secure converged results in FSDT-ESL, a mesh of 50 × 50 S4R shell elements are used. Simply supported boundary conditions are considered, with the loaded edges kept straight and the unloaded edges free to pull in.

3.2 3D Finite Shell Element Analyses for Validation

In order to validate the FSDT-ESL approach, a 3D model of the actual periodic plate is used; see Fig. 4 for details. The 3D-plate is modelled using shell elements (S4) that follow the Kirchhoff hypothesis (assumption in FSDT-ESL model). Concentrated nodal forces act at web plates in the nodes in the geometrical mid-plane. Six shell elements per web plate height and between webs are used as this has been shown to produce converged results in buckling and bending problems [20, 41]. Simply supported boundary conditions are considered, with the loaded edges kept straight by constraint equations and the unloaded edges free to move in-plane. The transverse deflection is zero only at the nodes at the geometric mid-plane. This allows the rotation of the plate around the mid-plane edge.

Fig. 4
figure 4

Description of the constrains implementation of 3D-FEA. Reproduced from Ref. [39]

Full size image

3.3 Results

The load-end-shortening, load–deflection and load-out of plane shear behavior is presented in Fig. 5, where also the comparison of the FSDT-ESL with respect to full 3D-FE model is presented. The main idea is to show the influence of the von Kármán term, Eq. (20), into the out-of-plane shear Qyy. Three load levels are selected from the curves to show the different stages of the structure undergoing non-linear deformations. Point A corresponds to linear regime, point B corresponds to the intermediate stage of transition from linear to non-linear post-buckling regime, and point C is the point of local buckling of the face plates where the assumption of linear microstructure becomes violated. Comparison of the predicted shear force Qyy-distribution from mid-span of the panel, at x = L/2, is presented in Fig. 6 for load points A and C. Figure 7 present the corresponding normal stresses with shear-induced stresses included and excluded.

Fig. 5
figure 5

Comparison of FSDT-ESL (dashed line) and 3D-FEA (solid line) in load-end-shortening, load–deflection and load-shear responses. Shear force-load marked with crosses

Full size image
Fig. 6
figure 6

Comparison of FSDT-ESL and 3D-FEA in terms of shear force Qyy at x = L/2 for Top: load-Level A, and Bottom: Load level C

Full size image
Fig. 7
figure 7

Comparison of FSDT-ESL (points, crosses) and 3D-FEA (solid line) at x = L/2. Top: x-normal stresses due to membrane action for load-levels A; Center at load-level C and Bottom: at load-level C with envelopes of the shear induced secondary normal stress

Full size image

From Fig. 5 it is clear that the non-linear response is predicted very accurately with the FSDT-ESL in comparison to the 3D-model of the actual geometry (3D-FEA). Both load-end-shortening and load–deflection curves overlap until local buckling occurs at the unit cells at point C. It is also clear that this point is well beyond the panel level buckling, around point B. After this point B, the out-of-plane shear, Qyy, increases rapidly due to the von Kármán non-linearity, see Eq. (20). Figure 6 shows that the spatial distribution of out-of-plane shear is accurately predicted with the FSDT-ESL. Even at the point of local buckling, the FSDT-ESL and 3D-FEA results overlap each other in average sense. Figure 7 shows that the membrane stresses of the face plates, predicted by both FSDT-ESL and 3D-FE methods, overlap at the load point A. In post-buckling, due to global bending, they start to differ significantly from each other. It is also seen that the membrane stress in the faces is significantly lower than the total stress at the surface of the face plates which is magnified by the secondary bending. It is seen that the stresses from 3D-FEA are within the maximum stress envelope curves defined by Eq. (41). This highlights the importance of taking the finite size, lmicro/lmacro, of the microstructure into account when computing the stress response. The stress jumps at the location of webs close to plate edges indicate significant bending in the webs and welds due to shear-induced warping of the unit cells.

4 Discussion

The investigation presented above indicates that when sandwich structures, with visible periodic core, are homogenized, special attention must be paid on the stress assessment, even in the case of buckling assessment where loading is of membrane type. In linear regime this loading is carried out mostly by pure membrane actions of face and web plates as Fig. 7 at point A indicates. As the post-buckling takes place, the membrane actions start to interact with the out-of-plane deformation, due to the von Kármán non-linearity. As the core is visibly discrete, lmicro/lmacro = 1/30, and the unit cells warp in shear, the magnitude of shear-induced secondary normal stresses at the faces and webs becomes significant. When these are added to the membrane stresses, the total stress can be significantly higher than the membrane stress only. This effect becomes larger when the role of out-of-plane shear γyz or Qyz increases and when the unit cell size increases. So, this phenomenon can be considered as type of size effect. Usually in homogenization theories we assume that these are infinitely far apart, i.e. lmicro/lmacro = 0. When departing from this assumption, very soon we end up dealing with another type of size effect, the assumptions of non-classical continuum mechanics.

This issue is seen through following example. Post-buckling analysis requires two stage analysis with initial analysis to define the initial deformation shape which is then followed by geometrically non-linear analysis. In present formulation, the bifurcation buckling load for simply supported rectangular plate is given as [40]:

$$\begin{aligned} & N_{0} = \frac{1}{{\alpha^{2} + k\beta^{2} }}\frac{{c_{55} + \frac{{c_{11} }}{{D_{Qy} }}\left( {\alpha^{2} + \beta^{2} \frac{{D_{Q2} }}{{D_{Q1} }}} \right)}}{{1 + \frac{{c_{11} }}{{D_{Q2} }}\left( {\frac{1}{{D_{Q1} }} + \frac{{c_{22} }}{{c_{11} }}\frac{{D_{Q2} }}{{D_{Q1} }} + \frac{{c_{33} }}{{c_{11} }}} \right)}} \\ & \alpha = \frac{m\pi }{a},\beta = \frac{n\pi }{b},c_{11} = c_{22} c_{33} - c_{44}^{2} ,c_{22} = D_{11} \alpha^{2} + D_{12} \beta^{2} , \\ & c_{33} = D_{66} \alpha^{2} + D_{22} \beta^{2} \;c_{44} = \left( {D_{12} + D_{66} } \right)\alpha \beta , \\ & c_{55} = D_{11} \alpha^{4} + 2\left( {D_{12} + 2D_{66} } \right)\alpha^{2} \beta^{2} + D_{22} \beta^{4} , \\ & k = \frac{{N_{yy} }}{{N_{xx} }},N_{xx} = - N_{0} ,N_{yy} = - kN_{0} , \\ \end{aligned}$$
(42)

where m and n are used to denote the number of half-waves in directions x and y respectively. In present case, the loading is assumed to be uniaxial, thus the load ratio factor k = 0, orthotropy ratio for shear, DQ1/DQ2-ratio, is very high (e.g. 100-1000). Thus, the buckling load minimum is obtained when m = n = 1. Problems with this equation occur when the load is turned to be along y-axis or biaxial compression is considered. In this case, the high orthotropy in shear causes a situation where minimum does not converge for m = n = 1, but decreases as function of n, while m = 1. In this case the buckling load in finite element solution becomes mesh size dependent; the smaller is the mesh size, the smaller is the buckling load. This is another type of size effect which results from classical continuum mechanics assumptions. The decrease is unphysical and can be corrected by incorporation non-classical continuum mechanics assumptions into our FSDT-ESL model. As shown by Romanoff and Varsta [21], Jelovica and Romanoff [42] by thick-face plates sandwich theory and by Karttunen et al. [36] by micropolar theory, the shear deformations of sandwich panels can have only finite wave-lengths, that is, finite n-values. When using thick-faces effect or micropolar solution, physically correct behavior is obtained. This is a result of the fact that we can split the out-of-plane shear strain to symmetric and antisymmetric parts [36]. Therefore, the present investigation should be extended in future to compression in transverse direction and investigations based on non-classical continuum formulations. This calls for micropolar plate elements, and recently such study has been reported by Nampally et al. [43].

In order to assess the strength of real welded structures following issue must be handled. The stress values seen in point C of the case study are very close to the material yield point. Typically, the steel used for these panels has a yield point at 355 MPa for the faces and 235 MPa or 355 MPa for the web plates. Thus, as Fig. 7, shows it is crucial to recover the microstructural stress if first fiber yield is to be assessed. The assessment of laser-stake welds is a bit more challenging. Jutila [44] carried out experiments with Digital Image correlation system of pull-out strength of laser-stake welds. Strength values up to 1000 MPa for tension for steel faces and webs of 355 MPa and 235 MPa, respectively are reported. The difference is also seen in the hardness of the welds, see Fig. 8. Due to rapid changes in the hardness, the weld deforms only moderately in softer faces and webs and microrotation is seen between these two, in the heat affected zone. This is indicating that non-classical continuum mechanics are needed in the weld modelling. However, there is another effect that requires careful investigation. This is the contact between the faces and webs at the laser-stake welds when being bended. Due to the contact, the stresses are redistributed and significant variations are seen in the moment carrying capacity of the welds due to small variations in weld geometrical properties. Measured strength values are Mcr= 1400Nm/m (see Ref. [45] for details), which corresponds Qyz = 21.5kN/m in shear. Thus, the strength of welds would not be reached yet in present context for individual stress components. Proper modelling of these phenomenon in 3D FEA is therefore a significant challenge which we cannot solve in the present context. Also, an experimental study is needed to gain more understanding of prevailing failure modes in real structures.

Fig. 8
figure 8

Strength of welds by stress resultants. Observed geometrical and material gradients in the welds. Failure mode for stress resultants Nz with microrotation at HAZ and My in the bending of welds with impact of contact to the initial stiffness and strength. See for details Refs. [43, 44]

Full size image

In the present case it is indicated that the microstructure can buckle during the deformation, which is known to reduce the stiffness globally. As the local and global deformations interact, there is a need for coupled models where the geometrical non-linearity in one length-scale can be mapped correctly to the another one. Such example in context of classical continuum mechanics has been presented in Reinaldo Goncalves et al. [46] with one way coupling and in for example Geers et al. [21] and Rabzcuk et al. [30] for two-way coupling. However, this work should be extended to the non-classical continuum mechanics due to the reasons mentioned above.

5 Conclusions

The paper presented, a phenomena related to post-buckling of web-core sandwich plates. Equivalent Single Layer (ESL) formulation with First order Shear Deformation Theory (FSDT) was used to identify the problem parameters in closed form. During the axial load increase, these plates have multiple load-carrying mechanisms that change due to von Kármán non-linearity. During the membrane-dominated loading stages, the effect of finite size of the periodic microstructure is barely present, while at higher loads when bending is activated, the finite size of the unit cells activates secondary shear-induced bending moments. Due to this effect, the normal stress levels become significantly higher than the homogenized plate theory would predict. A method to capture the envelope of the maximum values of these stresses is presented and validated with 3D-Finite Element -models of the actual geometry. It is also discussed that classical continuum mechanics has its limits when failure of welded web-core sandwich structures is concerned. The welds experience micro-rotation close to failure point. Due to this also the antisymmetric out-of-plane shear strain activates at the plate level which calls for non-classical continuum mechanics. These extensions are left for future work.