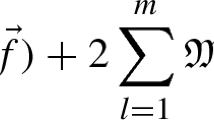Abstract
We introduce and study the bilinear fractional maximal operator
where \(O=(0,0,\ldots ,0)\in {\mathbb {R}}^n\) and \(0\le \alpha <n\), which recovers the classical bilinear maximal operator \({\mathfrak {M}}\), corresponding to the case \(\alpha =0\). When \(\alpha =0\), we demonstrate that \({\mathfrak {M}}\) is bounded and continuous from the product Triebel–Lizorkin spaces \(F_s^{p_1,q}({\mathbb {R}}^n)\times F_s^{p_2,q}({\mathbb {R}}^n)\) to \(F_s^{p,q}({\mathbb {R}}^n)\), from the product fractional Sobolev spaces \(W^{s,p_1}({\mathbb {R}}^n)\times W^{s,p_2}({\mathbb {R}}^n)\) to \(W^{s,p}({\mathbb {R}}^n)\) and from the product Besov spaces \(B_s^{p_1,q}({\mathbb {R}}^n)\times B_s^{p_2,q} ({\mathbb {R}}^n)\) to \(B_s^{p,q}({\mathbb {R}}^n)\), provided that \(0<s<1\), \(1<p_1,p_2,p,q<\infty \) and \(1/p=1/p_1+1/p_2\). When \(0<\alpha <n\), we show that \({\mathfrak {M}}_\alpha \) is bounded and continuous from \(W^{1,p_1}({\mathbb {R}}^n)\times W^{1,p_2}({\mathbb {R}}^n)\) to \(W^{1,q}({\mathbb {R}}^n)\), provided that \(1<p_1,p_2<\infty \), \(1\le {p_1p_2}/{(p_1+p_2)}<\infty \), \(0\le \alpha <n({1}/{p_1}+{1}/{p_2})\) and \({1}/{q}={1}/{p_1}+{1}/{p_2}-{\alpha }/{n}\). As an application, we obtain a weak type inequality for the Sobolev capacity, which can be used to establish the q-quasicontinuity of \({\mathfrak {M}}_\alpha (f,g)\).
Similar content being viewed by others
References
Aldaz, J.M., Pérez Lázaro, J.: Functions of bounded variation, the derivative of the one dimensional maximal function, and applications to inequalities. Trans. Am. Math. Soc. 359(5), 2443–2461 (2007)
Benedek, A., Calderón, A.P., Panzone, R.: Convolution operators on Banach space valued functions. Proc. Nat. Acad. Sci. 48, 356–365 (1962)
Bojarski, B., Hajłasz, P.: Pointwise inequalities for Sobolev functions and some applications. Studia Math. 106, 77–92 (1993)
Carneiro, E., Mardid, J.: Derivative bounds for fractional maximal functions. Trans. Am. Math. Soc. 369(6), 4063–4092 (2017)
Carneiro, E., Mardid, J., Pierce, L.B.: Endpoint Sobolev and BV continuity for maximal operators. J. Funct. Anal. 273(10), 3262–3294 (2017)
Carneiro, E., Moreira, D.: On the regularity of maximal operators. Proc. Am. Math. Soc. 136(12), 4395–4404 (2008)
Carneiro, E., Svaiter, B.F.: On the variation of maximal operators of convolution type. J. Funct. Anal. 265, 837–865 (2013)
Federer, H., Ziemer, W.: The Lebesgue set of a function whose distribution derivatives are \(p\)-th power summable. Indiana Univ. Math. J. 22, 139–158 (1972)
Frazier, M., Jawerth, B., Weiss, G.: Littlewood–Paley Theory and the Study of Function Spaces. CBMS Reg Conf Ser, vol. 79. Amer Math Soc, Providence, RI (1991)
Grafakos, L.: Classical and Modern Fourier Analysis. Prentice Hall, Upper Saddle River, NJ (2003)
Hajłasz, P., Malý, J.: On approximate differentiability of the maximal function. Proc. Am. Math. Soc. 138(1), 165–174 (2010)
Hajłasz, P., Onninen, J.: On boundedness of maximal functions in Sobolev spaces. Ann. Acad. Sci. Fenn. Math. 29(1), 167–176 (2004)
Heikkinen, T., Kinnunen, J., Korvenpää, J., Tuominen, H.: Regularity of the local fractional maximal function. Bull. Lond. Math. Soc. 53(1), 127–154 (2015)
Kinnunen, J.: The Hardy–Littlewood maximal function of a Sobolev function. Israel J. Math. 100, 117–124 (1997)
Kinnunen, J., Lindqvist, P.: The derivative of the maximal function. J. Reine. Angew. Math. 503, 161–167 (1998)
Kinnunen, J., Saksman, E.: Regularity of the fractional maximal function. Bull. Lond. Math. Soc. 35(4), 529–535 (2003)
Korry, S.: Boundedness of Hardy–Littlewood maximal operator in the framework of Lizorkin–Triebel spaces. Rev. Mat. Complut. 15(2), 401–416 (2002)
Korry, S.: A class of bounded operators on Sobolev spaces. Arch. Math. 82(1), 40–50 (2004)
Lacey, M.: The bilinear maximal function map into \(L^p\) for \(2/3<p\le 1\). Ann. Math. 151, 35–57 (2000)
Lerner, A.K., Ombrosi, S., Pérez, C., Torres, R.H., Trujillo-González, R.: New maximal functions and multiple weighted for the multilinear Calderón-Zygmund theory. Adv. Math. 220, 1222–1264 (2009)
Lewis, J.L.: On very weak solutions of certain elliptic systems. Commun. Partial Differ. Equ. 18, 1515–1537 (1993)
Liu, F.: Continuity and approximate differentiability of multisublinear fractional maximal functions. Math. Inequal. Appl. 21(1), 25–40 (2018)
Liu, F., Mao, S.: On the regularity of the one-sided Hardy–Littlewood maximal functions. Czech. Math. J. 67(1), 219–234 (2017)
Liu, F., Wu, H.: On the regularity of the multisublinear maximal functions. Can. Math. Bull. 58(4), 808–817 (2015)
Liu, F., Wu, H.: On the regularity of maximal operators supported by submanifolds. J. Math. Anal. Appl. 453, 144–158 (2017)
Luiro, H.: Continuity of the maixmal operator in Sobolev spaces. Proc. Am. Math. Soc. 135(1), 243–251 (2007)
Luiro, H.: On the regularity of the Hardy-Littlewood maximal operator on subdomains of \({\mathbb{R}}^n\). Proc. Edinb. Math. Soc. 53(1), 211–237 (2010)
Triebel, H.: Theory of Function Spaces, Monogr Math, vol. 78. Birkhäser Verlag, Basel (1983)
Yabuta, K.: Triebel–Lizorkin space boundedness of Marcinkiewicz integrals associated to surfaces. Appl. Math. J. Chin. Univ. Ser. B 30(4), 418–446 (2015)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author was partially supported by the NNSF of China (Grant No. 11701333). The second author was partially supported by NNSF of China (Grant No. 11701453) and Fundamental Research Funds for the Central Universities (Grant No.31020180QD05).
Rights and permissions
About this article
Cite this article
Liu, F., Liu, S. & Zhang, X. Regularity Properties of Bilinear Maximal Function and Its Fractional Variant. Results Math 75, 88 (2020). https://doi.org/10.1007/s00025-020-01215-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-020-01215-2