1 Introduction

In recent years, the Northern Sea Route (NSR) has received increased attention as a potential shortcut for connecting Europe and East Asia due to the reduction of ice cover and the increasing activities related to maritime transport and natural resources exploitation in the Arctic regions [1]. The NSR is a shipping lane along the Russian coast which covers several Arctic Seas: the Barents Sea, the Pechora Sea, the Kara Sea, the Laptev Sea, the East Siberian Sea and the Chukchi Sea. A good understanding of the ice environment along the NSR would promote the development of structural design and operational safety of Arctic ships and structures along the route.

For design of vessels sailing in ice-covered regions, ice loads caused by the ship–ice interaction represent the dominant source of loading. Therefore, ice actions which depend on the ice conditions, ice properties, ice failure modes and the shape and size of the structure, should be considered for design purposes [2]. It is challenging to define the ice conditions (or ice environment) that the ship is expected to encounter, since many parameters are required for such a description. The required parameters mainly include: level ice thickness, ice concentration, ice types (level ice, ice ridge, rubble field, iceberg) and ice age (first-year ice, multi-year ice) [3]. For ice properties, both physical and mechanical properties of the sea ice should be considered. Physical properties generally comprise the temperature, density, salinity, porosity and grain size of the ice features. While, ice flexural strength, compressive strength, shear strength and elastic modulus are mechanical properties that could be required for calculation of ice actions on Arctic ships and structures [4]. There are mainly five failure modes that may exist in connection with the ice and structure interaction process, i.e., the bending failure, crushing failure, creep, buckling and splitting. These failure modes generally depend on the relative velocity between the ice feature and the structure, the shape of structure, ice stress distribution and the ice strength. Details of these failure modes can be found in references [4, 5].

In this work, first-year level ice along the NSR is selected for the study considering the fact that the ice conditions along the commercial Arctic shipping routes, such as the NSR, are mostly first year and ice rarely appear during the summer seasons [6]. Furthermore, the physical and mechanical properties of first-year level ice have been studied extensively in many decades and reliable relationships have been established between the physical characteristics and the mechanical properties. The ship and level ice interaction process is initiated by a localized crushing of the ice edge, and then the crushing force and the contact area between the ship and level ice sheet increase as the ship advances and penetrates the ice features. The ice sheet eventually deflects and the bending stresses promote a flexural failure at a certain breaking distance from the crushing region [7]. Therefore, the physical parameter, ice thickness and the mechanical parameters, flexural strength and compressive strength of the ice sheet are considered to be the most important parameters for determining the ice actions on ice-going vessels.

Two methods are often used to obtain ice thickness and ice property data: by measurements (e.g., in situ measurements, remote sensing) or by theoretical estimation. It is well known that the values of ice thickness and ice properties depend on the climatic conditions, i.e., the seasonal effects. It is difficult and expensive to obtain the data at a given site along the NSR by continuous observations or measurements, especially the ice strength. Nevertheless, theoretical estimation based on well-established empirical models is a reliable and efficient way. The ice thickness can be estimated by applying the Stefan equation model [4, 8] when the air temperature records at a given site are available. Subsequently, a theoretical scheme based on the air temperature as input is applied to estimate the corresponding ice flexural strength and compressive strength. It should be mentioned that although global warming is a general trend, we did not consider this effect when dealing with the historical data of air temperature.

In addition to the estimation of ice thickness and ice strength, the covariation between these parameters is also of key importance. Former research in Refs [9, 10] showed that the correlation between the thickness and strength of the ice feature has a significant influence on extreme ice load levels acting on structures. However, estimation of the covariation between random variables without available joint samples of values will usually be a difficult task [11]. In this work, a novel probabilistic model is introduced to describe the distribution of ice flexural strength (as a function of the porosity). The correlation between ice thickness and ice flexural strength can be quantified. However, regarding the compressive strength, such a probabilistic model is not available due to the insufficient experimental data. The correlation coefficients between ice thickness and ice compressive strength as well as between ice compressive strength and ice flexural strength should accordingly be considered as the upper limits.

The present work is organized as follows. Sections 2 and 3 describe the theoretical methods and empirical formulas used for the estimation of the ice thickness and ice strength, respectively. The procedure is summarized at the end of Sect. 3. The estimation of the ice thickness and ice strength at four representative sites along the NSR are given in Sect. 4 based on the air temperature records and the proposed theoretical scheme. In Sect. 5, a probabilistic model is introduced to describe the distribution of the ice flexural strength, and the correlation between the ice parameters is also addressed.

2 Ice thickness

Ice thickness is considered as the most representative parameter for characterization of the severity of ice conditions. The thickness of first-year ice is directly related to the ambient air temperature, the freezing time, balance between ocean heat fluxes from the sea to the ice, and surface radiation that are from the ice to the atmosphere. There are several methods to measure the ice thickness, such as remote sensing by satellite technology, electromagnetic (EM) measurements, upward looking sonar (ULS) techniques and in situ drilling. Among these methods, in situ drilling is the most accurate method to obtain the level ice thickness. However, ice thickness can vary significantly between different locations and seasons. Therefore, application of this method for long-term measurement of ice thickness in different areas along the NSR would be inefficient and expensive.

Alternatively, ice thickness can also be estimated by the freezing degree method if the historical data of daily average air temperature are given. Based on the Stefan equation [8], the ice thickness, h, is given as:

$$h = ({{2k_{\text{i}} } \mathord{\left/ {\vphantom {{2k_{\text{i}} } {\rho_{\text{i}} L}}} \right. \kern-0pt} {\rho_{\text{i}} L}})^{0.5} \left[ {(T_{\text{b}} - T_{\text{a}} )t} \right]{\kern 1pt}^{0.5} ,$$
(1)

where ki is the thermal conductivity of ice, ρi denotes the ice density, L represents the latent heat of fusion of ice, and t is the time. Ta and Tb are the daily average air temperature and the temperature at the bottom of the ice sheet, respectively. h is given in meters, and t is 86,400 s/day. Approximate values of ki = 2.1 W/m °C, and L = 290,000 J/kg are given in Ref. [12].

The bottom temperature of the ice sheet, Tb, is assumed to be the same as the freezing point of sea water, Tf, which is about − 2 °C. Moreover, the surface temperature of the ice sheet, Ts, is related to Ta by the following relationship [13]:

$$\left\{ {\begin{array}{*{20}c} {T_{{\text{s}}} = T_{a} } & {{\text{for}} - 10{\kern 1pt} {\kern 1pt} ^{{\text{o}}} {\text{C}} \le T_{{\text{a}}} \le - 2^{{\text{o}}} {\text{C}}} \\ {{\text{T}}_{s} = 0.6T_{{\text{a}}} } & {{\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} T_{{\text{a}}} < - 10{\kern 1pt} {\kern 1pt} ^{{\text{o}}} {\text{C}}} \\ \end{array} } \right..$$
(2)

It should be noted that direct application of the Stefan equation will generally overestimate the ice thickness, because the effect of snow cover is neglected. The snow cover has an important insulating effect and may reduce the ice growth substantially compared to the prediction from Eq. (1). To consider this effect, an empirical factor, α, is introduced in the Stefan equation. Based on the records of daily average air temperature and the relationship given by Eq. 2, sea ice thickness in the ice growth season becomes:

$$h = \alpha ({{2k_{\text{i}} } \mathord{\left/ {\vphantom {{2k_{\text{i}} } {\rho_{\text{i}} L}}} \right. \kern-0pt} {\rho_{\text{i}} L}})^{0.5} \left[ {\varSigma (T_{\text{b}} - T_{\text{a}} )t} \right]{\kern 1pt}^{0.5} ,$$
(3)

where the factor α is assumed to be 0.75 in the Canadian Beaufort Sea [4].

In addition to the Stefan equation, there are also two empirical models to describe the thickness growth of sea ice thickness with consideration of the snow cover effects. These two models are the Zubov model [14] and the Lebedev model [15], which are expressed by equations related to the freezing degree days (FDD) for a winter season (or ice growth season). The accumulated FDD is given as:

$${\text{FDD}} = \sum\limits_{\text{days}} {(T_{\text{f}} - T_{\text{a}} )} .$$
(4)

In fact, the Stefan equation model given by Eq. 3 can be regarded as a specific example of the FDD method.

3 Ice properties

Sea ice is a complex material and consists of pure ice, brine (water with dissolved salts), air and solid salts (depends on temperature). Therefore, the mechanical properties of sea ice depend on its physical characteristics of sea ice, such as ice temperature, salinity, density and ice porosity. This section describes the established empirical relationships between the ice parameters for further analysis.

3.1 Physical properties

3.1.1 Ice temperature

As mentioned in Sect. 2, the temperature at the top of the ice sheet, Ts, is governed by the air temperature Ta and the temperature at the bottom of the ice, Tb. The latter is assumed to be equal to the freezing point of sea water, Tf. Throughout the ice growth season, one can usually assume that there is a linear temperature gradient through the ice sheet [13]. The temperature of the ice sheet, T varies with the ice thickness, h. The temperature profile through the ice sheet is shown in Fig. 1. Moreover, it is shown in Ref. [16] that once the decay process begins, the temperature profile changes from a linear one to a C-shape profile.

Fig. 1
figure 1

Illustration of the temperature gradient through the ice sheet, horizontal axis: temperature, vertical axis: ice thickness

Full size image

3.1.2 Sea ice salinity

When the ice grows, it traps some of the salt which is present in the sea water. Most of the brine is pushed down into the underlying water, but some is blocked in the brine pockets and gives rise to the sea ice salinity. For the first-year level ice, the salinity, S, is usually expressed as the fraction by mass of the salts contained in a unit mass [5]. For the qualification of sea ice salinity, a salinity meter is used to measure the electrical conductivity of the meltwater obtained by taking a core of sea ice. Based on the conductivity of the meltwater, the ice salinity value is estimated. In the ice growth season, the average salinity of an ice sheet, expressed as parts per thousand (ppt), can be related to the thickness of the ice, h, by the following relationship [13, 17]:

$$S = \left\{ \begin{aligned} 13.4 - 17.4\;h{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} h \le 0.34{\kern 1pt} {\kern 1pt} {\kern 1pt} m \hfill \\ 8.0 - 1.62\;h{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} h > 0.34{\kern 1pt} {\kern 1pt} {\kern 1pt} m \hfill \\ \end{aligned} \right.,$$
(5)

where h is expressed in meters. It is noted that Eq. 5 is only valid for growing sea ice and cannot be used for the ice melt season, since the salt in the ice begins to drain from the ice sheet.

3.1.3 Brine volume and total porosity

Within the sea ice, the brine, the pure ice, the air and the solid salts are assumed to exist in a thermal equilibrium [18]. The brine volume represents the amount of liquid brine within the ice and it is usually expressed in terms of volume in parts per thousand or expressed as a volume fraction [5]. In some cases, such as when brine drainage has occurred, the air volume can be significant and it is accordingly useful to know the amount of air volume in the ice. The total porosity, vT, of the ice is expressed as:

$$v_{\text{T}} = v_{\text{b}} + v_{\text{a}} ,$$
(6)

where vb and va are the relative brine volume (or brine volume fraction) and relative air volume, respectively.

Porosity of the sea ice during the growth season can be estimated from the values of ice temperature and ice salinity. It is shown in Cox and Weeks [19] that the relative brine volume can be expressed in terms of the sea ice density ρi, ice salinity S, and the temperature of the ice sheet, T, by:

$$v_{\text{b}} = {{\rho_{\text{i}} S} \mathord{\left/ {\vphantom {{\rho_{\text{i}} S} {F_{1} }}} \right. \kern-0pt} {F_{1} }}(T),$$
(7)

where the function, F1(T) is given as:

$$F_{1} (T) = \left\{ \begin{aligned} - 4.732 - 22.45T - 0.6397T^{2} - 0.01074T^{3} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 2 \ge {\kern 1pt} T \ge {\kern 1pt} - 22.9 \hfill \\ 9899 + 1309T + 55.27T^{2} + 0.716T^{3} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 2{\kern 1pt} {\kern 1pt} 2.9 \ge {\kern 1pt} {\kern 1pt} T \ge {\kern 1pt} - 30 \hfill \\ \end{aligned} \right.$$
(8)

with the variable T being given in  °C.

The relative air volume can be expressed as:

$$v_{\text{a}} = 1 - {{\rho_{\text{i}} } \mathord{\left/ {\vphantom {{\rho_{\text{i}} } {\rho_{\text{p}} (T_{\text{av}} ) + }}} \right. \kern-0pt} {\rho_{\text{p}} (T_{\text{av}} ) + }}\rho_{i} S \times {{F_{2} (T_{\text{av}} )} \mathord{\left/ {\vphantom {{F_{2} (T_{\text{av}} )} {F_{1} (T_{\text{av}} )}}} \right. \kern-0pt} {F_{1} (T_{\text{av}} )}},$$
(9)

where ρp represents the pure ice density (in Mg/m3) and it is described as:

$$\rho_{\text{p}} (T) = 0.917 - 1.403 \times 10^{ - 4} T,$$
(10)

and the function, F2(T) is given as:

$$F_{2} (T) = \left\{ \begin{aligned} 8.903 \cdot 10^{ - 2} - 1.763 \times 10^{ - 2} T - 5.33 \times 10^{ - 2} T^{2} - 8.801 \times 10^{ - 6} T^{3} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 2 \ge {\kern 1pt} T \ge {\kern 1pt} - 22.9 \hfill \\ 8.547 + 1.089T + 4.518 \times 10^{ - 2} T^{2} + 5.819 \times 10^{ - 4} T^{3} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 2{\kern 1pt} {\kern 1pt} 2.9 \ge {\kern 1pt} {\kern 1pt} T \ge {\kern 1pt} - 30. \hfill \\ \end{aligned} \right.$$
(11)

Therefore, the total porosity of the ice can be estimated by Eq. 12 given as follows:

$$v_{\text{T}} (T) = 1 - {{\rho_{\text{i}} } \mathord{\left/ {\vphantom {{\rho_{\text{i}} } {\rho_{\text{p}} (T)}}} \right. \kern-0pt} {\rho_{\text{p}} (T)}} + \left[ {{{\rho_{\text{i}} S} \mathord{\left/ {\vphantom {{\rho_{\text{i}} S} {F_{1} (T)}}} \right. \kern-0pt} {F_{1} (T)}}} \right] \times \left[ {1 + F_{2} (T)} \right].$$
(12)

Moreover, in the above-proposed model, an average density ρi = 0.907 Mg/m3 is used for the ice growth season according to Timco and Frederking [13]. In the ice decay season, Ref. [20] shows that the ice has a wide range of density and the above ice density value cannot be used for ice that is decaying.

3.2 Mechanical properties

3.2.1 Flexural strength

The flexural strength of ice samples can be measured by the simple beam or cantilever beam approach. Based on the former studies, it is found that the flexural strength of ice may depend on the porosity, salinity, grain structure and grain size, the beam size of the ice samples as well as on the test method and loading direction and loading rate [4]. It is well known that the flexural strength generally decreases for increasing brine volume, since the brine pockets reduce the strength of sea ice compared with freshwater ice. Based on a large number of tests with both large beams and small beams, Timco and O’Brien [21] showed that the average flexural strength, σf, of the first-year sea ice during the ice growth season can be expressed by the following relationship:

$$\sigma_{\text{f}} = 1.76\exp \left( { - 5.88\sqrt {v_{\text{b}} } } \right),$$
(13)

where σf is given in MPa and the average ice temperature Tav= (Ts+ Tb)/2 is applied in Eqs. (7) and (8) to estimate the average salinity and brine volume of the ice sheet.

3.2.2 Compressive strength

Similar to the ice flexural strength, the compressive strength of sea ice depends on the porosity, grain size, temperature of the ice samples, ice type (columnar or granular), strain rate, loading directions, etc. For the compressive strength of level ice during the growth season, measurements of horizontally loaded columnar ice samples have shown that the uni-axial compressive strength, σc, can be determined by Eq. (14), which is given as [13]:

$$\sigma_{\text{c}} = 37(\dot{\varepsilon })^{0.22} \left[ {1 - \sqrt {\frac{{v_{\text{T}} }}{0.27}} } \right],$$
(14)

where σc is expressed in MPa. The validity range for the strain rates \(\dot{\varepsilon }\) is from 10−7/s to 10−3/s and the compressive strength reaches its maximum when the strain rate is between 10−4/s and 10−3/s, where the ice fails at the transition between ductile and brittle deformation.

To consider the effect of temperature variation through the ice sheet (see Fig. 1) on the compressive strength, Timco and Frederking [13] developed a model to predict the full thickness compressive strength. In this model, the ice sheet is divided into nine separate layers. The top layer is selected as granular sea ice and the rest of the layers are columnar ice. The equation to calculate the compressive strength of the horizontally loaded granular ice layer can be found in Ref. [13] and the compressive strength of the other layers can be estimated by applying Eq. 14 with the information of average ice temperature, salinity and density of each layer. The average of these calculated compressive strength values can be used to estimate the large-scale compressive strength for the full ice sheet.

Finally, based on the equations described in Sect. 3, a theoretical scheme is proposed to estimate the ice thickness and ice properties, as illustrated in Fig. 2. By applying the algorithms and formula given above, the ice thickness, ice salinity, ice temperature, ice porosity and ice strength during the growth season can be estimated when the records of daily average air temperature are available.

Fig. 2
figure 2

Illustration of the scheme used to estimate the ice thickness and ice strength

Full size image

4 Ice thickness and ice properties along the NSR

4.1 Locations and air temperature data

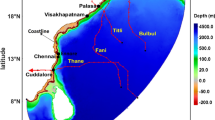
In this work, records of air temperature were obtained from the Carbon Dioxide Information Analysis Center where temperature datasets from 518 Russian weather stations are available [22]. Four representative sites along the NSR are selected and the locations are illustrated in Fig. 3. The names, locations and recording periods for the weather stations which are selected as the representative sites are given in Table 1. Furthermore, the ice growth season is selected as the period between Oct 1st and May 31st of the next year for the following studies.

Fig. 3
figure 3

The NSR (dashed line) and four representative sites (A, B, C and D) along the NSR

Full size image
Table 1 Locations of the weather station and period of air temperature records
Full size table

As mentioned above, Ta represents the daily average air temperature, i.e., the average value during one day and one night. The mean daily average temperature (MDAT) represents the statistical mean average temperature for a specific calendar day, based on a number of years of observation. Therefore, the MDAT value at a given site during a N-year period is defined as [23]:

$${\text{MDA}}T_{k} = \frac{1}{N}\sum\limits_{j = 1,N} {T_{a,jk} } ,$$
(15)

where Ta,jk represents the daily average air temperature for the kth day in the year with index number j.

As an example, the daily average air temperature collected at site A for the specific period 1959–2008 is plotted as blue dots in Fig. 4a and the corresponding MDAT during this period is plotted as a black line. Similarly, the MDAT values at the four representative sites for the corresponding record periods (see Table 1), are presented in Fig. 4b. For a given site, the lowest MDAT values are observed from the beginning of January to the end of February. For the four representative sites, it is seen in Fig. 4b that the MDAT values gradually decrease from October to February and increase from March to June, which is assumed to be the end of the ice growth season in this work. Among these sites, site A has the highest values for the MDAT; while, the lowest values of the MDAT are observed at site C.

Fig. 4
figure 4

a daily average air temperature (blue dots) and the MDAT (black line) at site A; b the MDAT values at the four representative sites

Full size image

4.2 Estimation of ice thickness and ice strength

Based on the records of daily average air temperature, empirical models, such as the Stefan equation model, the Zubov model and the Lebedev model, can be applied to estimate the (daily) ice thickness during the ice growth season. Similar to the method for calculating the MDAT values given in Eq. 15, the mean ice thickness for a day with index k is calculated as the mean value of the samples, which is a collection of ice thickness for the specific kth calendar day during the specific recording period. Moreover, estimation of the ice thickness requires the complete records of air temperature during the whole ice growth season. Therefore, lack of air temperature data for several weeks or months would result in the absence of ice thickness for the ice growth season.

From the studies in Ref. [24], the Stefan equation model, the Zubov model and the Lebedev model provide close values of the mean (daily) ice thickness at the four representative sites. In the Stefan equation model, α is selected as 0.75; therefore, it can be confirmed that this value is applicable for these locations. The mean (daily) ice thickness at the four selected sites, estimated by the Stefan equation model for the specific recording periods given in Table 1, is plotted in Fig. 5. It is seen that the mean ice thickness reaches its maximum value at the end of May and the maximum values are in the range from 1.25 m to 1.85 m. Moreover, it is observed in Figs. 4 and 5 that the warmest climatic condition corresponds to the minimum values of the mean ice thickness during the ice growth season and the mean ice thickness at sites B and C is very close due to the similar climatic conditions at these two sites.

Fig. 5
figure 5

Mean (daily) ice thickness estimated by the Stefan equation model at four representative sites

Full size image

Based on the MDAT values at the four selected sites and the original scheme proposed in Sect. 2, the flexural strength and compressive strength of the sea ice at these sites are obtained. The method used to calculate the mean (daily) ice thickness is applied to estimate the mean (daily) values of the ice flexural strength and the compressive strength at the four representative sites. These values are shown in Figs. 6 and 7, respectively. For calculation of the ice compressive strength, the strain rate \(\dot{\varepsilon }\) is set equal to 10−3/s for conservative considerations.

Fig. 6
figure 6

Mean (daily) ice flexural strength in the growth season at different sites

Full size image
Fig. 7
figure 7

Mean (daily) ice compressive strength in the growth season at different sites

Full size image

For the mean (daily) ice flexural strength, shown in Fig. 6, the peaks of the mean (daily) values can be observed in February and range from 0.5 to 0.65 MPa. Similarly, it is observed in Fig. 7 that the maxima of the mean (daily) values for the ice compressive strength range from 4.0 to 4.5 MPa in February. More importantly, it is notable that the climatic condition has a strong influence on the ice strength. For one thing, the lowest strength of the sea ice is observed at site A, which corresponds to the highest values of the MDAT and also the lowest values of the mean ice thickness among the four selected sites during the ice growth season. Furthermore, it is seen in Figs. 4b, 6 and 7 that for a given site and from October to February, the ice strength increases as the MDAT values increase, and subsequently the ice strength decreases with the increment of the MDAT values from March to May. For the purpose of engineering applications, the monthly mean values, and standard deviations of the ice thickness, ice flexural strength, ice compressive strength and the (monthly) ratios between the ice compressive strength (for different strain rates) and ice flexural strength for the four representative sites are presented as figures in the Appendix.

Furthermore, it should be noted the theoretical scheme presented in Fig. 2 is valid only for the ice growth season. Once the ice decay process begins, equations used for determining strength properties are no longer valid. It is seen in Fig. 4 that the air temperature reaches a minimum in February at all four sites, and technically, ice tends to decay when the temperature begins to rise. However, it is still unknown at which definite point the decay process begins. In this work, the theoretical scheme is assumed to be valid from October to May, which would overestimate the correct ice growth season to some extent.

5 Correlation studies

5.1 Probabilistic model for the ice flexural strength

Although the relationship between the ice flexural strength and the relative brine volume has been given by Eq. (13) as a deterministic model, it is seen in Fig. 8 that for a given value of the relative brine volume, the flexural strength of the ice samples obtained by Timco and O’Brien is scattered. Therefore, a probabilistic model as a function of the free variables (i.e., the square root of the relative brine volume, \(\sqrt {v_{\text{b}} }\)) for estimation of the ice flexural strength would be more reasonable. Similar to the probabilistic models for wind and wave statistics in Ref. [25], it is found that for a given value of \(\sqrt {v_{\text{b}} }\), the (conditional) distribution of the ice flexural strength can be described by a Gaussian distribution. Specifically, the sample data shown in Fig. 8 are divided into different classes according to the values of \(\sqrt {v_{\text{b}} }\). Based on the Gaussian probability papers, shown in Fig. 9, it is found that the Gaussian distribution is suitable for characterization of the ice flexural strength within different classes corresponding to different intervals of the square root of the relative brine volume.

Fig. 8
figure 8

Ice flexural strength σf versus the square root of the relative brine volume (the raw data are obtained from Timco and O’Brien [21])

Full size image
Fig. 9
figure 9

Gaussian probability papers for the ice flexural strength within different classes of the square root of the relative brine volume

Full size image

The conditional distribution of the ice flexural strength σf for a given value of \(\sqrt {v_{\text{b}} }\) is written as:

$$f_{{\sigma_{\text{f}} \left| {\sqrt {v_{\text{b}} } } \right.}} \left( {\sigma_{\text{f}} \left| {\sqrt {v_{\text{b}} } } \right.} \right) = \frac{1}{{\sqrt {2\pi \sigma (\sqrt {v_{\text{b}} } )} }}\exp \left\{ { - \frac{{\left( {\sigma_{\text{f}} - \mu \left( {\sqrt {v_{\text{b}} } } \right)} \right)^{2} }}{{\sigma^{2} \left( {\sqrt {v_{\text{b}} } } \right)}}} \right\},$$
(16)

in which the mean value μ and the standard deviation σ for the conditional Gaussian distribution are assumed to be dependent on \(\sqrt {v_{\text{b}} }\) in the following manner (by applying the least square error method), see also Figs. 10 and 11:

Fig. 10
figure 10

Fitted mean value of the ice flexural strength as a function of \(\sqrt {v_{\text{b}} }\)

Full size image
Fig. 11
figure 11

Fitted standard deviation of the ice flexural strength as a function of \(\sqrt {v_{\text{b}} }\)

Full size image
$$\mu \left( {\sqrt {v_{\text{b}} } } \right) = 1.76 \times \exp \left( { - 5.88\sqrt {v_{\text{b}} } } \right),$$
(17)
$$\sigma \left( {\sqrt {v_{\text{b}} } } \right) = 0.696 \cdot \exp \left( { - 1.156\sqrt {v_{\text{b}} } } \right) - 0.356.$$
(18)

After having established the probabilistic model of the flexural strength, given by Eqs. 16–18, ice strength for a single day can be simulated as a random Gaussian variable when the value of \(\sqrt {v_{\text{b}} }\) at the same day is determined by applying the algorithms described in Sect. 2. Moreover, a lower bound of 0.01 MPa is set for the simulated samples which follow the Gaussian distribution model since the value of flexural strength could not be negative as a physical parameter. As an example, the (daily) flexural strength for the ice at site A during the growth season in the period from years 1959 to 2008 are simulated according to the proposed probabilistic model and the simulated flexural strength samples are plotted in Fig. 12.

Fig. 12
figure 12

Simulated ice flexural strength samples at site A and the flexural strength for the large beam samples in Timco and O’Brien [21]

Full size image

As a verification of the simulated samples shown in Fig. 12, the flexural strength versus for large beam samples in Ref. [21] are plotted in this figure. It should be noted that the flexural strength of small beam samples is measured in laboratories at relatively low temperatures and relatively small brine volumes; while, the flexural strength of large beam samples is usually tested in situ with relatively high (air and ice) temperatures and relatively large brine volumes. Therefore, it is believed that the flexural strength of large beam samples is closer to the simulated ice flexural strength at a given site than the corresponding values from the small beam samples. It is seen in Fig. 12 that the simulated flexural strength has the same range and a similar distribution tendency as the flexural strength obtained from the large beam sample collected in Ref. [21].

Assume that X and Y are two random variables and the correlation coefficient, ρXY, for these two variables is then defined as:

$$\rho_{XY} = \frac{{{\text{Cov}}\left[ {X,Y} \right]}}{{({\text{Var}}(X) \times {\text{Var}}(Y))^{0.5} }},$$
(19)

where Var(∙) denotes variance and Cov[X, Y] is the covariance between the two variables.

The correlation coefficient between σf and \(\sqrt {v_{\text{b}} }\) estimated from all the sample points (both the small beam samples and the large beam samples) shown in Fig. 8 is − 0.7. For the large beam samples shown in Fig. 12, it is − 0.60. For the simulated samples at sites A, B, C and D, the correlation coefficients between σf and \(\sqrt {v_{\text{b}} }\) are − 0.60, − 0.56, − 0.54 and − 0.57, respectively. Therefore, it is believed that the simulated flexural strength has a similar behavior as the flexural strength obtained from the collected samples shown in Fig. 8.

5.2 Correlations between ice thickness and ice strength

In this section, the correlation between ice thickness and ice flexural strength is first studied. Based on the scheme illustrated in Fig. 2 and the probabilistic model for ice flexural strength proposed in Sect. 5.1, the corresponding (daily) ice thickness and (daily) ice flexural strength can be obtained, provided that the history of daily air temperature at a given site is available. As an illustration, the full simulated joint samples for ice thickness and ice flexural strength at site A are shown in Fig. 13.

Fig. 13
figure 13

Simulated ice flexural strength versus ice thickness at site A for different months

Full size image

Since the climatic conditions have a very strong influence on the ice condition and ice strength, the joint samples of ice thickness and flexural strength are plotted in Fig. 13 for each separate month during the ice growth season. Moreover, the correlation coefficients between these two variables for all the four sites are estimated by generating joint samples for each month and the results are summarized in Table 2. The overall correlation coefficients between ice thickness and ice flexural strength during the whole ice growth season for the selected sites A, B, C and D are 0.35, 0.29, 0.28 and 0.30, respectively.

Table 2 Correlation coefficients between ice thickness and flexural strength at different sites
Full size table

It is seen in Fig. 13 and Table 2 that a decreasing trend of the correlation coefficient with time is generally observed. From October to the end of January, one can find in Fig. 4a that the air temperature has a decreasing trend which corresponds to a reduction of ice temperature and an increment of ice thickness. Generally, colder ice corresponds to higher ice strength. Therefore, clear positive correlations between ice thickness and ice flexural strength can be observed in Fig. 13 and Table 2 for these months. On the other hand, from February to the end of the ice growth season, the air temperature gradually increases. In this period, the ice flexural strength generally exhibits a decreasing trend but the ice thickness continues to grow since the air temperature is still below the freezing point of sea water. As a result, very weak positive or even negative correlations for these two parameters have been observed during these months.

Unlike sufficient experimental data for the joint samples of ice flexural strength given in Fig. 8, the number of joint samples of ice compressive strength and total porosity vT obtained by experiments is not large enough to support the identification of a suitable conditional probabilistic model for the distribution of ice compressive strength. Therefore, correction relationships for ice compressive strength and ice thickness as well as for ice compressive strength and ice flexural strength are given as upper limit correlation coefficients during the whole ice growth season. Joint samples of ice compressive strength and ice thickness as well as joint samples of ice compressive strength and ice flexural strength are generated according to the scheme illustrated in Fig. 2. The abovementioned joint samples generated for site A are plotted in Figs. 14 and 15, respectively.

Fig. 14
figure 14

Simulated ice compressive strength versus ice thickness at site A

Full size image
Fig. 15
figure 15

Simulated ice flexural strength versus ice compressive strength at site A

Full size image

It is seen in Fig. 14 that for different ranges of ice thickness, the relationships between thickness and compressive strength are different. When the ice thickness is in the range from 0 to around 0.3 m, there is a clear positive correlation between these two parameters. For ice thickness values between 0.3 m and (around) 1.1 m, the correlation is positive but becomes weaker as the ice thickness increases. Similar to Fig. 13, when the ice thickness is higher than 1.1 m (air temperature gradually increases during this period), the distribution of the joint samples is rather scattered. The (upper limit) correlation coefficients between the ice thickness and the ice compressive strength at the selected sites A, B, C and D during the whole ice growth season are 0.48, 0.59, 0.51 and 0.54, respectively.

In Fig. 15, it is observed that the simulated ice compressive strength has a very close relationship with ice flexural strength. At site A, the (upper limit) correlation coefficient between these two parameters is 0.62. It is also observed that for increasing values of the ice compressive strength, the ice flexural strength has a wider scatter interval. This phenomenon has also been observed for the simulated joint samples of ice compressive strength and flexural strength at sites B, C and D and the correlation coefficients for these two parameters at the three sites are 0.49, 0.53 and 0.57, respectively.

6 Conclusions

This paper studies the statistics of thickness, flexural strength and compressive strength for first-year level ice along the NSR. A scheme based on empirical formulas is proposed to investigate the correlation between different parameters of ice physical and mechanical properties at four representative sites along the NSR. It is found that the climatic condition has a strong influence on the ice thickness and ice strength. The highest values of the MDAT were observed at site A, which are reflected by the minimum values of daily mean ice thickness and lowest ice strength for the four selected sites.

A novel probabilistic model is introduced to describe the distribution of ice flexural strength. The correlation between ice thickness and ice strength is studied by generating joint synthetic samples of the two parameters. It is found that from October to the end of January, there is a positive correlation between ice thickness and ice flexural strength, and then from February to the end of May, a very weak positive or even a weakly negative correlation is observed. The correlation coefficient between these two parameters during the whole ice growth season ranges from 0.28 to 0.35.

Due to the absence of a probabilistic model for description of the compressive strength, the values of the correlation coefficients for ice thickness and compressive strength as well as for compressive strength and flexural strength for the whole ice growth season should be considered as upper limits. For the four selected sites, the correlation coefficient between h and σc is in the range from 0.48 to 0.59, and the correlation coefficient between σc and σf ranges from 0.49 to 0.62. To present a more reasonable and realistic relationship for ice compressive strength related to other ice parameters, more experimental data or test data are required.