1 Introduction

Black holes, predicted by the general relativity (GR), play a crucial role for getting deep insight into our Universe, fundamental physics, and even spacetime singularities. In the last few years, one of the most important leaps in astrophysics and astrometry is to probe black holes directly by observing gravitational waves from a binary black hole merger [1,2,3,4,5,6] and by imaging the supermassive black hole shadow with the Event Horizon Telescope [7,8,9,10,11,12]. Meanwhile, these observations also open a new era for testing modified gravitational theories in the strong gravitational field. It is interesting to note that some effects of these gravitational theories on the strong gravitational field could be well investigated by using a test particle’s orbits around black holes.

In the detection of gravitational waves, for example, an extreme mass ratio inspiral is formed from one stellar mass black hole whirling closely around a supermassive one. This kind of binary black hole could be treated as a timelike particle orbiting around a black hole. For the test particle, the innermost stable circular orbits (ISCO) and the marginally bound orbits (MBO) are two critical regions. In the adiabatic inspiral regime of the gravitational wave radiation, the timelike particle’s trajectory should lie between MBO and ISCO around the black hole. These bound orbits for the particles around black holes have been considered in the geodesic study of regular Hayward black hole [13], the area and entropy spectra of black holes [14], the ringdown stage of a binary black hole coalescence [15, 16], the energy level diagrams for the Kerr black hole orbits [17], and the evolution of black holes [18,19,20].

It is well known that periodic orbits are an extremely powerful tool to describe planetary and lunar motions, long-term dynamical evolution and stability of the Solar System, and galactic dynamics. During the adiabatic inspiral regime, a series of periodic orbits serves as a continuing transitional orbit and play a significance role in the research of the gravitational wave radiation [19]. Given this fact, a taxonomy of periodic orbits for a timelike particle around black holes has been recently proposed in Ref. [21]. This taxonomy describes periodic orbits through three integers \((z,w,\nu )\), which represent zoom, whirl and vertex numbers respectively. Moreover, three integers correspond to a rational number q, which characterizes a closed periodic orbit with a given energy and angular momentum. The taxonomy of periodic orbits has been extensively studied in Kerr and Schwarzschild black holes [17, 21, 22], Reissner–Nordström black holes [23] and some others [24,25,26,27,28,29]. By using the taxonomy proposed in Ref. [21], differences and characters among various black holes show up ultimately.

Although GR is consistent with some experiments both in the weak gravitational fields and in the strong gravitational fields, some phenomena in current astrophysical observations and theoretical physics still leave the window for some modified gravity theories open. Especially, modified gravity theories are a viable and fascinating alternative to a self-consistent quantum gravity in addressing the problem for unifying gravitation within a quantum framework. Motivated by the quest for a unified theory, the five-dimensional (5D) Kaluza–Klein gravity [30, 31] and some higher-dimensional gravitational theories [32,33,34] were proposed. Among them, brane-world scenario has attracted considerable interest. For instance, one brane-world black hole was investigated in which matter is confined to the brane through the action of a confining potential without using any junction conditions [35,36,37]. This brane-world black hole could offer a geometrical explanations for the accelerated expansion of the universe and the flatness of rotation curves of galaxies. In this solution [35,36,37], there exists an m-dimensional bulk space without imposing the \(Z_{2}\) symmetry. And the vacuum field equations on the brane are modified by the \(Q_{\mu \nu }\) term which is a geometrical quantity. By using a delta function rather than a confining potential in the energy-momentum tensor, Dadhich, Maartens, Papadopoulos and Rezania (DMPR) [38] predicted exact solutions for static black holes localized on a three-brane in five-dimensional gravity in the Randall-Sundrum scenario. This DMPR brane-world black hole solution of the effective Einstein equation on the brane is under the condition that the bulk has nonzero Weyl curvature and the brane spacetime satisfies the null energy condition. Especially, the DMPR brane-world black holes have Reissner–Nordström-like solutions, where a tidal charge parameter Q is arising from the projection onto the brane of free gravitational field effects in the bulk. It is worth mentioning that the tidal charge parameter may be negative or positive. Some properties in the DMPR brane-world black holes have been attentively investigated in thermodynamics [39, 40], strong and weak gravitational lensing [41,42,43,44,45], Horizon structure [46], circular geodesic and orbital dynamics [37, 47,48,49,50], and Solar System tests [51,52,53,54,55,56], whereas the taxonomy of periodic orbits in the DMPR brane-world black holes is still missing in the literature.

In view of the unique feature of the taxonomy, in this work, periodic orbits of a timelike particle around the DMPR brane-world black holes will be investigated. The relationship between periodic orbits and rational numbers in the black holes will be studied and analyzed. In what follows, \(G=c=1\) and the metric signature is \((-,+,+,+)\). The layout of this paper is as follows. Section 2 gives the metric and geodesics in the DMPR brane-world spacetime. Section 3 describes ISCO and MBO for the particle around the DMPR brane-world black holes. By using the taxonomy [21], Sect. 4 exhibits rational numbers and periodic orbits in the black holes. Finally, conclusions and discussion are outlined in Sect. 5.

2 Metric and Geodesics in the DMPR brane-world

By considering a 5D spacetime (the bulk) with a single 4D brane, the action of the system is [52, 57]

$$\begin{aligned} S=S_{\mathrm {bulk}}+S_{\mathrm {brane}}, \end{aligned}$$
(1)

where

$$\begin{aligned} S_{\mathrm {bulk}}= & {} \int _{{}^{(5)}M}\sqrt{-{}^{(5)}g} \bigg [\frac{1}{2k^{2}_{5}}{}^{(5)}R+{}^{(5)}L_{m} +\varLambda _{5}\bigg ]\mathrm {d}^{5}X, \end{aligned}$$
(2)
$$\begin{aligned} S_{\mathrm {brane}}= & {} \int _{{}^{(4)}M}\sqrt{-{}^{(5)}g} \bigg [\frac{1}{k^{2}_{5}}K^{\pm }+L_{\mathrm {brane}}(g_{\mu \nu },\varPsi ) +\lambda _{b}\bigg ]\mathrm {d}^{4}x.\nonumber \\ \end{aligned}$$
(3)

In the above action, \(k^{2}_{5}\) is the gravitational constant in the five-dimensional spacetime, \({}^{(5)}R\) and \({}^{(5)}L_{m}\) are respectively the 5D scalar curvature and the matter Lagrangian in the bulk, \(L_{\mathrm {brane}}(g_{\mu \nu },\varPsi )\) is the Lagrangian for a generic functional of the brane metric and of the matter fields, \(K^{\pm }\) is the trace of the extrinsic curvature on either side of the brane, \(\varLambda _{5}\) is the negative vacuum energy density in the bulk, and \(\lambda _{b}\) is the brane tension and the negative vacuum energy density on the brane.

The corresponding energy–momentum tensors of bulk and brane matter fields are respectively defined by [52, 57]

$$\begin{aligned} {}^{(5)}T_{IJ}\equiv & {} -2\frac{\delta {}^{(5)}L_{m}}{\delta {}^{(5)}g^{IJ}} +{}^{(5)}g_{IJ}{}^{(5)}L_{m}, \end{aligned}$$
(4)
$$\begin{aligned} T_{\mu \nu }\equiv & {} -2\frac{\delta L_{\mathrm {brane}}}{\delta g^{\mu \nu }}+g_{\mu \nu }L_{\mathrm {brane}}. \end{aligned}$$
(5)

Variation of the action with respect to \({}^{(5)}g^{IJ}\) and \(g^{\mu \nu }\), the 5D Einstein field equation in the bulk and the 4D field equations on the brane are respectively given by [52, 57]

$$\begin{aligned} {}^{(5)}G_{IJ}= & {} -k^{2}_{5}\varLambda _{5}{}^{(5)}g_{IJ} +k^{2}_{5}\delta (Y)[-\lambda _{b}{}^{(5)}g_{IJ}+T_{IJ}], \end{aligned}$$
(6)
$$\begin{aligned} G_{\mu \nu }= & {} -\varLambda g_{\mu \nu }+k^{2}_{4}T_{\mu \nu }+k^{2}_{5}S_{\mu \nu }-E_{\mu \nu }, \end{aligned}$$
(7)

where \(S_{\mu \nu }\) is the local quadratic energy–momentum correction, \(E_{\mu \nu }\) is the projection of the 5D Weyl tensor \(C_{IAJB}\), \(\varLambda =k^{2}_{5}(\varLambda _{5}+k^{2}_{5}\lambda ^{2}_{b})/2\), and \(k^{2}_{4}=k^{4}_{5}\lambda _{b}/6\).

By considering the case of vacuum with \(\varLambda =0\), the 4D field equation on the brane (7) yields

$$\begin{aligned} R_{\mu \nu }=-E_{\mu \nu }, \end{aligned}$$
(8)

with

$$\begin{aligned} E_{\mu \nu }=-\frac{Q}{r^{4}}(2u_{\mu }u_{\nu }-2r_{\mu }r_{\nu }+g_{\mu \nu }), \end{aligned}$$
(9)

in which Q comes from the fifth dimensional space and is called as the tidal charge parameter [38]. For another interesting brane-world solution [35,36,37], by using a confining potential rather than a delta function in the energy–momentum tensor, the vacuum field equation on the brane is given by

$$\begin{aligned} R_{\mu \nu }=Q_{\mu \nu }, \end{aligned}$$
(10)

where \(Q_{\mu \nu }\) is a geometrical quantity and introduces the cosmological and dark matter parameters into the metric of the brane-world black hole (see [35,36,37] for details).

Based on the above equations, the vacuum, static and spherically symmetric metric in a brane-world spacetime predicted by Dadhich, Maartens, Papadopoulos and Rezania (DMPR) [38] is

$$\begin{aligned} \mathrm {d}s^{2}= & {} -g(r)\mathrm {d}t^{2}+\frac{1}{g(r)}\mathrm {d}r^{2} +r^{2}(\mathrm {d}\theta ^{2}+\sin ^{2}\theta \mathrm {d}\phi ^{2}), \end{aligned}$$
(11)

where

$$\begin{aligned} g(r)=1-\frac{2M}{r}+\frac{Q}{r^{2}}, \end{aligned}$$
(12)

and for the brane-world metric in Refs. [35,36,37], we have

$$\begin{aligned} g(r)=1-\frac{2M}{r}-\alpha ^{2}r^{2}-2\alpha \beta r-\beta ^{2}, \end{aligned}$$
(13)

where \(\alpha \) and \(\beta \) are respectively constants related to the cosmological and dark matter parameters. Some orbital characters around the brane-wold spactime [35,36,37] will be considered in our next step.

For the DMPR brane-world, if \(Q\sim q_{e}^{2}>0\), where \(q_{e}\) is the electric charge, Eq. (11) returns to the Reissner–Nordström (RN) solution. While the DMPR metric has an RN-like solution, it is quite different from RN one. In the DMPR brane-world, no electric field exists at all and it leads to a neutral Q. Especially, the tidal charge parameter may be negative or positive. When \(Q<0\), the DMPR metric maintains the space-like nature of the singularity (see Ref. [34] for reviews).

There exist two horizons in the DMPR brane-world, given by

$$\begin{aligned} r_{\pm }=M\pm \sqrt{M^{2}-Q}. \end{aligned}$$
(14)

When \(0\le Q\le M^{2}\), we have \(0<r_{-}\le r_{+}\le r_{s}\), where \(r_{s}\) is the Schwarzschild horizon. When \(Q<0\), only one horizon \(r_{+}=M+\sqrt{M^{2}-Q}\) lies outside \(r_{s}\). These characters are depicted in Fig. 1. From Fig. 1, it is clearly showed that two horizons get closer to each other with the increase of Q.

Fig. 1
figure 1

Horizons of the DMPR brane-world spacetime with a fixed Q

Full size image

The Lagrangian of a test particle’s geodesic motion governed by Eq. (11) is

$$\begin{aligned} 2{\mathscr {L}}=-g(r){\dot{t}}^{2}+\frac{1}{g(r)}{\dot{r}}^{2} +r^{2}({\dot{\theta }}^{2}+\sin ^{2}\theta {\dot{\phi }}^{2}), \end{aligned}$$
(15)

where a dot denotes differentiation with respect to an affine parameter. Due to the isotropic gravitational field, the motion of the particle could be confined to the plane \(\theta =\pi /2\). Then, by using \(P_{\alpha }\equiv \partial {\mathscr {L}}/\partial {\dot{q}}^{\alpha }\), we have

$$\begin{aligned} P_{t}= & {} \frac{\partial {\mathscr {L}}}{\partial {\dot{t}}}=-g(r){\dot{t}}=-E, \end{aligned}$$
(16)
$$\begin{aligned} P_{r}= & {} \frac{\partial {\mathscr {L}}}{\partial {\dot{r}}} =\frac{1}{g(r)}{\dot{r}}, \end{aligned}$$
(17)
$$\begin{aligned} P_{\phi }= & {} \frac{\partial {\mathscr {L}}}{\partial {\dot{\phi }}}=r^{2}{\dot{\phi }}=l, \end{aligned}$$
(18)

where E is the particle’s conserved energy and l is its conserved angular momentum per unit mass. The corresponding Hamiltonian is defined as

$$\begin{aligned} {\mathscr {H}}\equiv p_{\beta }{\dot{q}}^{\beta }=P_{t}{\dot{t}}+P_{r}{\dot{r}} +P_{\phi }{\dot{\phi }}-{\mathscr {L}}, \end{aligned}$$
(19)

it yields

$$\begin{aligned} 2{\mathscr {H}}=-E{\dot{t}}+\frac{1}{g(r)}{\dot{r}}^{2}+l{\dot{\phi }}=\delta , \end{aligned}$$
(20)

where

$$\begin{aligned} \delta =\left\{ \begin{array}{l} -1~~~\mathrm {for~the~timelike~particle},\\ ~~0~~~\mathrm {for~the~lightlike~particle}. \end{array} \right. \end{aligned}$$
(21)

Substituting Eqs. (16)–(18) into Eq. (20), they give

$$\begin{aligned} {\dot{r}}^{2}=g(r)\left( \frac{E^{2}}{g(r)}-\frac{l^{2}}{r^{2}}+\delta \right) . \end{aligned}$$
(22)

3 Effective potential and bound orbits for a timelike particle

The effective potential \(V_{\mathrm {eff}}\) is defined as [58]

$$\begin{aligned} V_{\mathrm {eff}}+{\dot{r}}^{2}=E^{2}. \end{aligned}$$
(23)

For a timelike particle, based on Eq. (22) and the above definition, \(V_{\mathrm {eff}}\) takes the form

$$\begin{aligned} V_{\mathrm {eff}}=g(r)\bigg (1+\frac{l^{2}}{r^{2}}\bigg ) =\bigg (1-\frac{2M}{r}+\frac{Q}{r^{2}}\bigg )\bigg (1+\frac{l^{2}}{r^{2}}\bigg ). \end{aligned}$$
(24)

The above expression shows that the effective potential is a function of the radius with l and Q as parameters. In what follows, we will consider the timelike particle between the marginally bound orbits (MBO) and the innermost stable circular orbits (ISCO) around the DMPR brane-world black holes. This will be related to the adiabatic inspiral regime in the gravitational wave radiation.

Fig. 2
figure 2

\(r_{\mathrm {MBO}}\) (red line) and \(l_{\mathrm {MBO}}\) (blue line) of the timelike particle around the DMPR brane-world black holes with respect to Q for MBO

Full size image

For MBO, the timelike particle’s orbit around the DMPR brane-world black holes satisfies the following conditions

$$\begin{aligned} V_{\mathrm {eff}}=1,\quad \partial _{r}V_{\mathrm {eff}}=0, \end{aligned}$$
(25)

which lead to

$$\begin{aligned} 2Mr^{3}-Qr^{2}-l^{2}r^{2}+2Ml^{2}r-Ql^{2}= & {} 0, \end{aligned}$$
(26)
$$\begin{aligned} Mr^{3}-Qr^{2}-l^{2}r^{2}+3Ml^{2}r-2Ql^{2}= & {} 0. \end{aligned}$$
(27)

From Eqs. (26) and (27), \(r_{\mathrm {MBO}}\) and \(l_{\mathrm {MBO}}\) can be solved numerically with a given Q. Figure 2 shows that the timelike particle’s radius and its angular momentum decrease with Q. When \(0\le Q\le M^{2}\), \(r_{\mathrm {MBO}}\le l_{\mathrm {MBO}}\). However, a negative \(Q<0\) leads to \(r_{\mathrm {MBO}}>l_{\mathrm {MBO}}\). In contrast to the Schwarzschild black holes (\(Q=0\)), the values of \(r_{\mathrm {MBO}}\) and \(l_{\mathrm {MBO}}\) with \(Q<0\) in the DMPR brane-world black holes are more large.

Fig. 3
figure 3

\(E_{\mathrm {ISCO}}\), \(l_{\mathrm {ISCO}}\) and \(r_{\mathrm {ISCO}}\) of the timelike particle around the DMPR brane-world black holes against Q for ISCO

Full size image

For ISCO, the timelike particle’s motion is described as follows

$$\begin{aligned} V_{\mathrm {eff}}=E^{2},\quad \partial _{r}V_{\mathrm {eff}}=0,\quad \partial _{r}\partial _{r}V_{\mathrm {eff}}=0. \end{aligned}$$
(28)

We derive that

$$\begin{aligned} E_{\mathrm {ISCO}}= & {} \frac{g(r_{\mathrm {ISCO}})}{\sqrt{g(r_{\mathrm {ISCO}}) -r_{\mathrm {ISCO}}g'(r_{\mathrm {ISCO}})/2}}, \end{aligned}$$
(29)
$$\begin{aligned} l_{\mathrm {ISCO}}= & {} r^{3/2}_{\mathrm {ISCO}} \sqrt{\frac{g'(r_{\mathrm {ISCO}})}{2g(r_{\mathrm {ISCO}}) -r_{\mathrm {ISCO}}g'(r_{\mathrm {ISCO}})}}, \end{aligned}$$
(30)
$$\begin{aligned} r_{\mathrm {ISCO}}= & {} \frac{3g(r_{\mathrm {ISCO}})g'(r_{\mathrm {ISCO}})}{2g'^{2}(r_{\mathrm {ISCO}})-g(r_{\mathrm {ISCO}})g''(r_{\mathrm {ISCO}})}. \end{aligned}$$
(31)

From these expressions, Fig.3 suggests that \(E_{\mathrm {ISCO}}\), \(l_{\mathrm {ISCO}}\) and \(r_{\mathrm {ISCO}}\) decrease with the increase of Q. Also, with a negative Q in the DMPR brane-world black holes for this case, the values of \(E_{\mathrm {ISCO}}\), \(l_{\mathrm {ISCO}}\) and \(r_{\mathrm {ISCO}}\) are larger than the ones in the Schwarzschild black holes.

Fig. 4
figure 4

The effective potential \(V_{\mathrm {eff}}\) as a function of r/M with a fixed Q. The angular momentum varies from \(l_{\mathrm {ISCO}}\) to \(l_{\mathrm {MBO}}\) from bottom to top. The dashed line represents the extremal points of the effective potential

Full size image
Fig. 5
figure 5

\({\dot{r}}^{2}\) as a function of r/M with \(l=(l_{\mathrm {MBO}}+l_{\mathrm {ISCO}})/2\) and a fixed Q, where E varies from 0.955 to 0.975 from bottom to top

Full size image

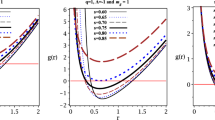
When the particle’s orbits lie between ISCO and MBO, we plot \(V_{\mathrm {eff}}\) with the tidal charge parameter Q (see Fig. 4). In Fig. 4, the bottom and the top curves represent \(V_{\mathrm {eff}}\) in \(l_{\mathrm {ISCO}}\) and \(l_{\mathrm {MBO}}\). It is shown that these curves have a sharp increase firstly, then decrease and slowly increase with r. The extremal points of \(V_{\mathrm {eff}}\) are the dashed lines in Fig. 4. From the figure, we can also see that the curves in ISCO have one extremal points and the other curves have two extremal points. These dashed lines decrease before increase with r.

Fig. 6
figure 6

Parameter regions \(\varDelta S\) for the bound orbits (in shadow) with a fixed Q

Full size image
Fig. 7
figure 7

Parameter regions \(\varDelta S\) vs Q for the bound orbits

Full size image

By taking \(l\equiv (l_{\mathrm {MBO}}+l_{\mathrm {ISCO}})/2\) and the domain of E as (0.955, 0.975), one-dimensional motion \({\dot{r}}^{2}\) in the effective potential is depicted in Fig. 5. The effects of Q on \({\dot{r}}^{2}\) clearly display. In each of the graphs of Fig. 5, it is shown that these curves have a sharp decrease firstly, then increase and slowly decrease with r later. Each curve in Fig. 5 has two extremal points. The bound orbits between ISCO and MBO we take into account only belong to these curves in which two extremal points have the opposite signs. For instance, the blue line meets this condition when \(Q=-0.5M^{2}\), where one extremal point is negative while the other is positive. After further analysis, the bound orbits in that blue line when \(Q=-0.5M^{2}\) have the energy bound (0.9588, 0.9714) for \(l=3.958M\). It fully indicates that the bound orbits around the DMPR brane-world black holes has a range of energy for a given angular momentum. This allows one to plot (l, E) regions for the bound orbits around the DMPR brane-world black holes (see Fig. 6). The shadow regions \(\varDelta S\) in Fig. 6 are l and E of the bound orbits. Furthermore, we plot parameter regions \(\varDelta S\) with respect to Q in Fig. 7. It suggest that parameter regions \(\varDelta S\) around the DMPR brane-world black holes increase with Q for the bound orbits. It also means that the shadow regions with \(Q<0\) are smaller than the ones with \(Q>0\).

4 Periodic orbits and rational numbers

Fig. 8
figure 8

Four leaves orbits around the DMPR brane-world black holes with \(\epsilon =0.5\)

Full size image
Fig. 9
figure 9

The rational number q versus E by taking Q as \(-1.5M^{2}\), \(-M^{2}\), \(-0.5M^{2}\), 0, \(0.5M^{2}\), and \(M^{2}\) with four cases: \(\epsilon =0.3\), 0.5, 0.7 and 0.9

Full size image

During the adiabatic inspiral regime, a series of periodic orbits serves as a continuing transitional orbit and play a significance role in the research of the gravitational wave radiation [19]. Given this fact, a taxonomy of periodic orbits for a timelike particle around black holes has been recently proposed in Ref. [21]. When a timelike particle lies between MBO and ISCO around a black hole, based on the taxonomy in Ref. [21], there exists an interesting topological relationship between a triplet of integers \((z,w,\nu )\) and the periodic orbits, which defines a rational number q as follows [21]

$$\begin{aligned} q=w+\frac{\nu }{z}=\frac{\varDelta \phi }{2\pi }-1, \end{aligned}$$
(32)

where

$$\begin{aligned} \varDelta \phi =\oint \mathrm {d}\phi , \end{aligned}$$
(33)

is the equatorial angle accumulated in one radial cycle from one apastron to periastron to the next apastron.

The integers \((z,w,\nu )\) have the corresponding geometric interpretations in the structure of periodic orbit [21]: z is the number of leaves for “zoom” , w is the “whirls” number around the center, and \(\nu \) is the “vertices” number formed by joining the successive apastra of the periodic orbit. In addition, \(1\le \nu \le z-1\) if \(z>1\) and \(\nu =0\) if \(z=1\) (see Ref. [21] for details). In order to show the geometric structure for \((z,w,\nu )\), for example, we consider \(q=1+1/4\) and \(q=1+3/4\) for periodic orbits around the DMPR brane-world black holes with \(Q=0.5M^{2}\) and \(Q=-0.5M^{2}\) (see Fig. 8). There are four leaves (the blue dash lines) in this figure, which means the zoom number z is 4. The number around the center (a small red line in the center) in Fig. 8 is the whirls number (namely, \(w=1\)). At the same time, we chose two cases in Fig. 8, which are \(\nu =1\) and \(\nu =3\) respectively, to display the behavior of the vertices number (the red lines).

Based on Eqs. (16)–(20), the equatorial angle Eq. (33) for the timelike particle around the DMPR brane-world black holes can be found as

$$\begin{aligned} \varDelta \phi= & {} 2\int ^{\phi _{2}}_{\phi _{1}}\mathrm {d}\phi \nonumber \\= & {} 2\int ^{\phi _{2}}_{\phi _{1}}\frac{{\dot{\phi }}}{{\dot{r}}}\mathrm {d}r\nonumber \\= & {} 2\int ^{r_{2}}_{r_{1}}\frac{l}{r^{2}\sqrt{E^{2} -\bigg [1-\frac{2M}{r}+\frac{Q}{r^{2}}\bigg ]\bigg (1+\frac{l^{2}}{r^{2}}\bigg )}} \mathrm {d}r. \end{aligned}$$
(34)

where \(\phi _{2}\) and \(\phi _{1}\) denote apastron and periastron. \(r_{1}\) and \(r_{2}\) are two turning points of the bound orbits between ISCO and MBO. From the above equation, we can see that \(\varDelta \phi \) in the DMPR brane-world black holes depends on the tidal charge parameter Q. This leads to significant differences of the timelike particle between the DMPR brane-world black holes and the RN/Schwarzschild black holes.

Fig. 10
figure 10

Periodic orbits with rational numbers (rows 1 and 3) and nearby aperiodic orbits with approximate rational numbers (rows 2 and 4) with \(\epsilon =0.9\)

Full size image
Fig. 11
figure 11

Zoom-whirl periodic orbits \((z,w,\nu )\) around the DMPR brane-world black holes with \(Q=-M^{2}\) and \(\epsilon =0.3\)

Full size image
Fig. 12
figure 12

Zoom-whirl periodic orbits \((z,w,\nu )\) around the DMPR brane-world black holes with \(Q=M^{2}\) with \(\epsilon =0.3\)

Full size image

From Eqs. (32) to (34), the rational number q and the corresponding \(\varDelta \phi \) can be obtained by numerical integration with fixed Q, E and l. Therefore, for the periodic orbits around the DMPR brane-world black holes, the rational number q versus E could be depicted, see Fig. 9. Since the value of the angular momentum in the bound orbits only varies from \(l_{\mathrm {ISCO}}\) to \(l_{\mathrm {MBO}}\), a new angular momentum is given by

$$\begin{aligned} l=l_{\mathrm {ISCO}}+\epsilon (l_{\mathrm {MBO}}-l_{\mathrm {ISCO}}), \end{aligned}$$
(35)

where \(\epsilon =0\) and \(\epsilon =1\) denote the angular momentums of ISCO and MBO respectively and we have \(0\le \epsilon \le 1\) for the bound orbits. By taking Q as \(-1.5M^{2}\), \(-M^{2}\), \(-0.5M^{2}\), 0, \(0.5M^{2}\), and \(M^{2}\) with four cases: \(\epsilon =0.3\), \(\epsilon =0.5\), \(\epsilon =0.7\) and \(\epsilon =0.9\), the rational number with the energy is plotted in Fig. 9. From the figure, the rational number q gradually increase with E firstly and then have a sharp increase especially when E becomes the maximum value. Besides, the case for \(Q<0\) are different from the cases for \(Q=0\) and \(Q>0\).

From the view of Ref. [21], a generic orbit is an accumulated angel per radial cycle. The orbit is not quite closed. On the contrary, it belongs to precession of the periodic orbit. We always treat a generic orbit as a approximate rational number. The corresponding closed periodic orbit with the rational number is a main problem which we need to deal with. For example, a rational number \(q=w+\nu /z\) gives a closed periodic orbit, whereas a approximate number \(q=w+\nu /z+\varsigma \) corresponds to nearby aperiodic orbits, where the irrational \(\varsigma \ll 1\). Figure 10 clearly shows this point. For the particle around the DMPR brane-world black holes for \(Q=M^{2}\) and \(Q=-M^{2}\) with \(\epsilon =0.9\), rows 1 and 3 are closed periodic orbits with rational numbers \(q=1/2\), 2/3 and 3/4. In Fig. 10, rows 2 and 4 are nearby aperiodic orbits with approximate rational numbers, where \(\varsigma \approx 1/100\), \(\approx 1/300\) and \(\approx 1/400\) respectively. From the above, we only need to focus on closed periodic orbits around the DMPR brane-world black holes. Any generic orbit between MBO and ISCO around the DMPR brane-world black holes could be approximated arbitrarily closely by some rational.

In Figs. 11 and 12, closed periodic orbits around the brane-world black holes have been plotted with different \((z,w,\nu )\) for a given \(\epsilon =0.3\) and Q. Here we take \(Q=-M^{2}\) and \(Q=M^{2}\) for examples. These figures show the characters of the “zoom” number z and the “whirls” number w clearly. It is worth noting that the geometric structure of periodic orbit gets more complicated with the increase of the zoom number. The energy with a fixed Q increases with the whirls number. And the energy with \(Q<0\) is larger than the one with \(Q<0\). Due to the closed periodic orbits in Figs. 11 and 12, the behavior of the vertices number does not show up. However, Fig. 8 display the behavior.

When we take \(\epsilon \) as 0.5 and 0.7 respectively, Tables 1 and 2 outline the energy of periodic orbits with a fixed q [or \((z,w,\nu )\)] and different Q. From Tables 1 and 2, it is shown that periodic orbits with \(Q<0\) in the DMPR brane-world black holes have higher energy in comparison to the ones with \(Q>0\). Especially, periodic orbits with a negative \(Q<0\) have higher energy in comparison to the Schwarzschild ones (\(Q=0\)). In addition, the energy of periodic orbits increases with \(\epsilon \) when we fix the values of Q and q. This unique signal included the energy of periodic orbits and the parameter Q might be identified and constrained through testing the bound orbits of the timelike particle and the corresponding taxonomy about periodic orbits around the DMPR brane-world black holes in the future.

Table 1 The energy \(E_{(z,w,\nu )}\) for periodic orbits \((z,w,\nu )\) [\(q=w+\nu /z\)] around the DMPR brane-world black holes for different values of Q with \(\epsilon =0.5\)
Full size table
Table 2 The energy \(E_{(z,w,\nu )}\) for periodic orbits \((z,w,\nu )\) [\(q=w+\nu /z\)] around the DMPR brane-world black holes for different values of Q with \(\epsilon =0.7\)
Full size table

5 Conclusion

In this paper, we mainly focus on the period orbits of a timelike particle around the DMPR brane-world black holes. By considering the particle orbital between the innermost stable circular orbits (ISCO) and the marginally bound orbits (MBO) around the brane-world black hole, it clearly shows that the particle’s angular momentum and its radial distance decrease with the increase of Q, where Q is a tidal charge parameter and may be negative and positive in the brane-world black holes. Furthermore, the allowed parameter regions \(\varDelta S\) of the (l, E) plane are analyzed detailedly. It suggest that parameter regions \(\varDelta S\) around the DMPR brane-world black holes increase with Q for the bound orbits.

From these results, the corresponding periodic orbits with different energy levels are analyzed numerically by employing a taxonomy [21], which is related to the adiabatic inspiral regime in the gravitational wave radiation. It clearly shows that a rational number defined by the taxonomy increases with the particle’s energy. In addition, periodic orbits with \(Q<0\) in the DMPR brane-world black holes have higher energy in comparison to the ones with \(Q>0\). Especially, periodic orbits with a negative \(Q<0\) have higher energy in comparison to the Schwarzschild ones (\(Q=0\)). Our results might provide hints for distinguishing the DMPR brane-world black holes from other black holes by the timelike particle’s periodic orbits in the future.

In the future, the detection of gravitational waves in the adiabatic inspiral regime might provide us with an unambiguity signal of Q through the corresponding taxonomy about periodic orbits around the brane-world black hole. It is worth mentioning that the motion below ISCO is in the transition regime [18]. In this regime, the trajectory for a compact body (e.g., extreme mass ratio black hole binaries) changes from inspiral to plunge gradually. We will leave the detailed investigation on this issue for future works. In addition, another open issue for the brane-world black hole is the thermodynamic characters, which will be also done in our next move. It is worth mentioning that another brane-world black hole in Refs. [35,36,37] can generate interesting cosmological consequences and is an attractive alternative to the accelerated expansion of the universe and the flatness of rotation curves of galaxies. Periodic orbits around this brane-world black hole and the corresponding thermodynamic characters will be considered in our future works.