Quasi-isotropic Biot’s Tensor for Anisotropic Porous Rocks: Experiments and Micromechanical Modelling

Abstract

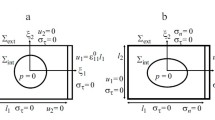
Several experimental studies, carried out on anisotropic rocks, have evidenced that even though strains, due to isotropic loading and/or internal fluid pressure, are strongly anisotropic, the resulting Biot’s tensor is almost isotropic. Those results were found on two different rocks: a clay rock (France—Bure argillite) and a sandstone from the Vosges region (France). Such (a priori) surprising results led us to develop micromechanical modelling in which anisotropy comes either from an anisotropic solid matrix (and isotropic pore space) or from an anisotropic pore space (and isotropic solid matrix). The obtained results have shown that for both cases the Biot’s tensor is virtually isotropic or presents a very weak anisotropy. This unambiguously supports the fact that a strongly anisotropic porous material is compatible with experimental measurements of isotropic (or quasi isotropic) Biot’s tensor.

Appendix: Hill Tensor of an Ellipsoid

Consider an ellipsoid defined by the equation:

$$\begin{aligned} {\varvec{z}}\cdot {\varvec{S}}\cdot {\varvec{z}}=1, \end{aligned}$$

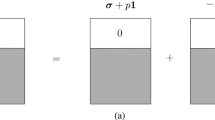
where ${\varvec{S}}$ is a positive definite symmetric second-rank tensor. This ellipsoid is embedded in an infinite linear elastic medium with elastic stiffness tensor $\mathbb {C}$. Let ${\varvec{\xi }}$ denote some vector on the unit sphere: $|{\varvec{\xi }}|=1$. The associated acoustic tensor is ${\varvec{K}}={\varvec{\xi }}\cdot \mathbb {C}\cdot {\varvec{\xi }}$. The coefficient $P_{ijkl}$ of the Hill tensor reads:

$$\begin{aligned} P_{ijkl}=\dfrac{\sqrt{\mathrm{det}\,{\varvec{S}}}}{4\pi }\int _{|{\varvec{\xi }}|=1}\dfrac{\left( \xi _j\xi _k\left( K^{-1}({\varvec{\xi }})\right) _{i\ell }\right) _{(ij),(k\ell )}}{\left( {\varvec{\xi }}\cdot {\varvec{S}}\cdot {\varvec{\xi }}\right) ^{3/2}}\,{\text {d}}S_\xi . \end{aligned}$$

(11)

In the above expression, the integral is taken with respect to ${\varvec{\xi }}$ over the unit sphere. The subscript $(ij),(k\ell )$ means that the expression is symmetrized w.r.t. the subscripts i and j, and w.r.t. the subscripts k and $\ell$:

$$\begin{aligned} (A_{ijk\ell })_{(ij),(k\ell )}=\dfrac{1}{4}\left( A_{ijk\ell }+A_{jik\ell }+A_{ij\ell k}+A_{ji\ell k} \right) . \end{aligned}$$

In Sect. 3.1.2, the Hill tensor $\mathbb {P}^m(\theta ,\phi ,X)$ refers to a spheroid with aspect ratio X, and a symmetry axis along the radial unit vector ${\varvec{e}}_r(\theta ,\phi )$:

$$\begin{aligned} {\varvec{e}}_r(\theta ,\phi )=\sin \theta \left( \cos \phi {\varvec{e}}_1+\sin \phi {\varvec{e}}_2\right) +\cos \theta {\varvec{e}}_3. \end{aligned}$$

It is recalled that the matrix is transversely isotropic (symmetry axis along ${\varvec{e}}_3$). In the spherical basis $({\varvec{e}}_r,{\varvec{e}}_\theta ,{\varvec{e}}_\phi )$, the tensor ${\varvec{S}}(\theta ,\phi ,X)$ of this spheroid reads:

$$\begin{aligned} {\varvec{S}}={\varvec{e}}_\theta \otimes {\varvec{e}}_\theta +{\varvec{e}}_\phi \otimes {\varvec{e}}_\phi +X^2{\varvec{e}}_r\otimes {\varvec{e}}_r. \end{aligned}$$

The integration variables in (11) are the two angles x and y that define the unit vector ${\varvec{\xi }}$:

$$\begin{aligned} {\varvec{\xi }}=\sin x\left( \cos y\,{\varvec{e}}_1+\sin y\,{\varvec{e}}_2\right) +\cos x\,{\varvec{e}}_3, \end{aligned}$$

where ${\text {d}}S_\xi =\sin x\,{\text {d}}x{\text {d}}y$.