Simulation of the Jiuzhaigou, China, earthquake by stochastic finite-fault method based on variable stress drop

Abstract

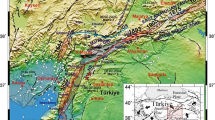
An improved stochastic finite-fault method was used to simulate the M_w 6.6 earthquake that occurred on August 8, 2017, in Jiuzhaigou, Sichuan, China. A variation of the stochastic finite-fault method, considering the dynamic corner frequency, was used to overcome the corner frequency. It explains the effect of a given slip distribution on the corner frequency of each subfault. A comparison of the response spectra (damping ratio 5%), spectral ratio (simulated values/observed values), and model deviation demonstrated that the improved corner frequency performs well for the whole periods, especially in short periods from 0.2 to 1 s. Similarly, the revised duration model and the site-amplification factor were applied to simulate the ground motion during the Jiuzhaigou earthquake, and then the response spectra were obtained. The duration of the nine near-field station recordings matched well with the simulated ground motions, and the peak ground acceleration (PGA) of most of the stations matched well with the observed PGA. In the short periods (T < 1 s), a small difference is observed between the simulated response spectra and the observed spectra for most of the stations. However, the response spectra were overestimated within the period range (0.05–10 s). Generally, the simulated ground motions obtained by using the improved model matched well with the observed ground motions, which could be considered the basis for earthquake-resistant design during the postdisaster recovery and the structural dynamic analysis of the Jiuzhaigou region.

Appendix

1.1 Derivation of the improved corner frequency

1.1.1 Derivation of the improved stress drop

The stress drop constitutes the most significant quantity in the scaling relation of the earthquake. The static stress drop Δσ_s represents the difference in the state of stress on the fault plane before and after the earthquake. The stress drop is Δσ = $\Delta \sigma_{0} { - }\Delta \sigma_{1}$, where Δσ₀ is the initial stress and $\Delta \sigma_{1}$ is the final stress.

The stress drop $\Delta \sigma$ is given by

$$\Delta \sigma_{s} = C_{s} \mu \frac{{\tilde{D}}}{{\tilde{L}}},$$

(17)

where $\tilde{D}$ represents the average (final) slip, $\tilde{L}$ represents a characteristic rupture dimension, μ denotes shear modulus, which is generally equal to 3.0 × 10¹¹ dyne/cm², C_s is a nondimensional shape factor dependent on the geometry of the order unity (Kanamori 1994). For circular faults, $C_{s} = {{7\pi } \mathord{\left/ {\vphantom {{7\pi } {16}}} \right. \kern-0pt} {16}}$ (Eshelby 1957; Keilis Borok 1959). For each subfault, we get:

$$\Delta \sigma_{ij} = C_{s} \mu \frac{{D_{ij} }}{{L_{ij} }} = \frac{7\pi }{16}\mu \frac{{D_{ij} }}{{L_{ij} }},$$

(18)

Assuming that all subfaults are identical, we can obtain the result from the sum of the two sides of Eq. (18):

$$\sum\limits_{l = 1}^{nl} {\sum\limits_{j = 1}^{nw} {\Delta \sigma_{ij} } } = \sum\limits_{i = 1}^{nl} {\sum\limits_{j = 1}^{nw} {\frac{1}{c}\mu \frac{{D_{ij} }}{{L_{ij} }}} } = \frac{7\pi }{16}\mu \frac{1}{{L_{ij} }}\sum\limits_{i = 1}^{nl} {\sum\limits_{j = 1}^{nw} {D_{ij} } } ,$$

(19)

then, we get:

$${{\left( {D_{ij} \cdot \sum\limits_{l = 1}^{nl} {\sum\limits_{j = 1}^{nw} {\Delta \sigma_{ij} } } } \right)} \mathord{\left/ {\vphantom {{\left( {D_{ij} \cdot \sum\limits_{l = 1}^{nl} {\sum\limits_{j = 1}^{nw} {\Delta \sigma_{ij} } } } \right)} {\sum\limits_{i = 1}^{nl} {\sum\limits_{j = 1}^{nw} {D_{ij} } } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{nl} {\sum\limits_{j = 1}^{nw} {D_{ij} } } }} = \frac{7\pi }{16}\mu \frac{{D_{ij} }}{{L_{ij} }},$$

(20)

Combining Eq. (18), we get:

$$\Delta \sigma_{ij} = \sum\limits_{i = 1}^{nl} {\sum\limits_{j = 1}^{mw} {\Delta \sigma_{ij} } } \cdot \frac{{D_{ij} }}{{\sum\nolimits_{i = 1}^{nl} {\sum\nolimits_{j = 1}^{mw} {D_{ij} } } }},$$

(21)

As for the stochastic finite-fault method, the physical meaning of stress drop is close to equating to the static stress drop proposed by Kanamori and Anderson (1975), and the final value of stress drop is the mean value of all subfaults.

$$\Delta \sigma { = }\frac{1}{N}\sum\limits_{i = 1}^{nl} {\sum\limits_{j = 1}^{nw} {\Delta \sigma_{ij} } } ,$$

(22)

In the equation, N stands for the subfault number. nl denotes the subfault number along the length of major fault, and nw denotes the same along the width of a major fault, respectively (nl × nw = N). Combining Eqs. (21) and (22), we obtain:

$$\Delta \sigma_{ij} = N \cdot \Delta \sigma \cdot \frac{{D_{ij} }}{{\sum\nolimits_{i = 1}^{nl} {\sum\nolimits_{j = 1}^{nw} {\Delta D_{ij} } } }},$$

(23)

Bringing Eq. (23) into the static corner frequency, f₀ = 4.9E + 6β(Δσ/M₀)^1/3, the corner frequency exhibited by each subfault can be expressed as follows:

$$f_{0ij} = 4.9 \times 10^{6} \beta \left( {\frac{{N \cdot \Delta \sigma_{ij} }}{{M_{0} }}} \right) = 4.9 \times 10^{6} \beta \left( {\frac{{\Delta \sigma_{ij} }}{{M_{0aver} }}} \right),$$

(24)

1.1.2 Derivation of the corner frequency

Combined with the definition displacement from a point shear dislocation in a homogeneous flexible space (Aki and Richards 1980, Eq. 4.32), and the seismic moment,$M\left( t \right) \equiv \mu \bar{u}\left( t \right)A$, the far-field shear wave is defined as:

$$u\left( {x,t} \right) = \frac{{R^{\theta \gamma } }}{{4\pi \rho \beta^{3} R}}\mu A\bar{u}^{'} \left( {t - {R \mathord{\left/ {\vphantom {R \beta }} \right. \kern-0pt} \beta }} \right),$$

(25)

where $u\left( {x,t} \right)$ represents the displacement at the spatial point x, ρ and μ are the density and shear modulus, respectively, $R^{\theta \gamma }$ stands for angular radiation pattern, $\bar{u}^{'} \left( t \right)$ denotes the time derivative of mean displacement throughout the dislocation plane, and A is the area of the dislocation.

The modulus of the Fourier transform of (25) is (see Beresnev and Atkinson 1997, for detail)

$$\left| {u_{n} \left( {x,f} \right)} \right| = \frac{{R^{\theta \gamma } M_{0} }}{{4\pi \rho \beta^{3} R}}\left[ {1 + \left( {{\raise0.7ex\hbox{$f$} \!\mathord{\left/ {\vphantom {f {f_{c} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${f_{c} }$}}} \right)^{2} } \right]^{{ - {{\left( {n + 1} \right)} \mathord{\left/ {\vphantom {{\left( {n + 1} \right)} 2}} \right. \kern-0pt} 2}}} ,\quad n = 1,2,$$

(26)

where we introduce the notation $\omega_{c} = {1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0pt} \tau } = 2\pi f_{c}$, and f_c is the corner frequency of the spectrum. An “omega-squared” spectrum, under the less formal development of Brune (1970, 1971), is obtained based on n = 1.

It is possible to define the rising time as the time needed by the average slip to reach a specific fraction x of the final slip, $\bar{u}\left( \infty \right)$. The most common way regarding the rising time definition is to let x = 0.5. When x = 0.5, we could define ${T \mathord{\left/ {\vphantom {T \tau }} \right. \kern-0pt} \tau } \equiv z,$ then the ω² model (Beresnev and Atkinson 1997, Eq. 6) could be expressed as follows:

$$\left( {1 + z} \right)e^{ - z} = 0.5,$$

(27)

we could get z = 1.68 by Eq. (27) and then

$$f_{c} \equiv {{\omega_{c} } \mathord{\left/ {\vphantom {{\omega_{c} } {2\pi }}} \right. \kern-0pt} {2\pi }} = {{0.27} \mathord{\left/ {\vphantom {{0.27} T}} \right. \kern-0pt} T},$$

(28)

Usually, we suppose the rise time as the time when the average slip reaches half of the final slip,$\bar{u}\left( \infty \right)$. For disk rupture, the rise time can be expressed in the form of

$$T = \frac{0.5r}{{V_{r} }},$$

(29)

r and V_r are the radius of circular crack and the rupture velocity, respectively.

Substituting Eq. (28) into (29) yields

$$f_{c} = \frac{{0.54V_{r} }}{r},$$

(30)

For a circular fault, the seismic moment can be expressed as

$$M_{0} = \mu \pi r^{2} u\left( \infty \right),$$

(31)

In the circular crack rupture model, the relationship between stress drop and radius of circular crack (Kanamori and Anderson 1975) is as follows:

$$\Delta \sigma = \frac{7\pi }{16}\mu \frac{u\left( \infty \right)}{r},$$

(32)

By substituting Eq. (32) into (31), we obtain

$$M_{0} = \frac{16\Delta \sigma }{7}r^{3} ,$$

(33)

and then the radius of the fault can be expressed as

$$r = \sqrt[3]{{\frac{{7M_{0} }}{16\Delta \sigma }}},$$

(34)

Substituting Eq. (34) into (30) yields

$$f_{c} = 7.12 \times 10^{6} V_{r} \left( {\frac{\Delta \sigma }{{M_{0} }}} \right)^{1/3} ,$$

(35)

By substituting Eq. (23) into (35), we obtain

$$f_{c} = 7.12 \times 10^{6} V_{r} \left( {\frac{{\Delta \sigma_{ij} }}{{M_{oaver} }}} \right)^{1/3} ,$$

(36)

where β denotes the shear-wave velocity in kilometers per second, Δσ denotes the stress drop in bars, and M_oaver stands for the average seismic moment in dyne-cm.