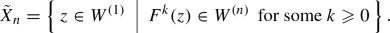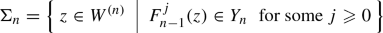Abstract
We show that the Julia set of the Feigenbaum polynomial has Hausdorff dimension less than 2 (and consequently it has zero Lebesgue measure). This solves a long-standing open question.
Similar content being viewed by others
1 Introduction
In [1, 2], Avila and Lyubich developed a new method for studying Lebesgue area and Hausdorff dimension of Julia sets of Feigenbaum maps. They constructed examples of Feigenbaum maps with Julia sets of Hausdorff dimension less than 2 and examples of Feigenbaum maps with Julia sets of positive area. Their approach can be used to determine whether for a given periodic point of renormalization the Julia set has positive area, zero area and Hausdorff dimension two, or Hausdorff dimension less than 2. However, even for the most studied examples of Feigenbaum maps (the Feigenbaum polynomial \(f_{\mathrm {Feig}}\) and the period doubling renormalization fixed point F), the calculations involved in verification are extremely computationally complex.
In this paper we present a new sufficient condition for the Julia set \(J_F\) of F to have Hausdorff dimension \(\mathrm {dim_H}(J_F)\) less than 2. Using computer-assisted means with explicit bounds on errors, we show that this condition is satisfied. Thus, we solve a long-standing open question.
Main Theorem
The Hausdorff dimension of the Julia set \(J_F\) of the Feigenbaum map F is less than 2. In particular, the Lebesgue measure of \(J_F\) is equal to zero.
The structure of the paper is as follows. In Sect. 2, we briefly recall the definition of quadratic-like renormalization, describe the relevant results of Avila and Lyubich, and introduce the Feigenbaum map F. We also define the sets \({\tilde{X}}_n\) of points whose orbits intersect certain small neighborhoods of the origin, and denote by \({\tilde{\eta }}_n\) the relative measures of \({\tilde{X}}_n\). Using the Avila-Lyubich results, we conclude that in order to prove \(\mathrm {dim_H}(J_F)<2\) it is sufficient to show that \({\tilde{\eta }}_n\) converges to 0 exponentially fast in n.
In Sect. 3, we describe the structure of the map F. Section 4 gives us distortion bounds for certain branches of inverse iterates of F. In Sect. 5, we state and prove the main result of the present paper (Theorem 5.1), which gives recursive inequalities for \(\tilde{\eta }_n\). As a result of Theorem 5.1, we obtain a sufficient condition to show \(\mathrm {dim_H}(J_F)<2\) (Corollary 5.1). This condition is one that can be checked by rigorous computer estimates, which we discuss in Sect. 6.
The authors would like to acknowledge the invaluable assistance of Misha Lyubich, who suggested the problem (as well as the collaboration) and participated in many fruitful discussions, providing constant encouragement and attention. This paper was also significantly improved by discussions with Michael Yampolsky, Sebastian van Strien and Davoud Cheraghi, to whom we are quite appreciative.
2 Preliminaries
Recall that a quadratic-like map is a ramified covering \(f:U\rightarrow V\) of degree 2, where \(U\Subset V\) are topological disks in \({{\mathbb {C}}}\). We refer the reader to [6, 22], or [24] for a more detailed treatment. For a quadratic-like map f, its filled Julia set \(K_f\) and Julia set \(J_f\) are given by

Let \(f:U\rightarrow V\) be quadratic-like. The map f is renormalizable of period \({{\varvec{n}}}\) if there there is an \(n>1\) and \(U'\subset U\) for which \(f^n:U'\rightarrow V'=f^n(U')\) is a quadratic-like map with connected Julia set \(J'\), and such that the sets \(f^i(J')\) are either disjoint from \(J'\) or intersect it only at the \(\beta \)-fixed point. In this case, \(f^n|_{U'}\) is called a pre-renormalization of\({{\varvec{f}}}\); the map \({{\mathcal {R}}}_n f:=\Lambda \circ f^n|_{U'}\circ \Lambda ^{-1}\), where \(\Lambda \) is an appropriate rescaling of \(U'\), is the renormalization of\({{\varvec{f}}}\).
An infinitely renormalizable quadratic-like map f is called a Feigenbaum map if it has bounded combinatorics (that is, there is a uniform bound on the periods n of renormalization) and of bounded type (the moduli of \(V{\smallsetminus } U\) are uniformly bounded).
The present paper is concerned with the Hausdorff dimension of the Julia set of the quadratic Feigenbaum polynomial \(f_{\mathrm {Feig}}(z)=z^2+c_{\mathrm {Feig}}\), where \(c_{\mathrm {Feig}} \approx -1.4011551890\) is the limit of the sequence of real period doubling parameters. Discovery of universality properties in the period doubling case during the 1970s by Coulet, Tresser and Feigenbaum [5, 11, 12] gave rise to the development of renormalization theory in dynamics. This development is well documented; for a brief overview, see [23, §1.5] and the references therein, for example.
The Julia set of \(f_{\mathrm {Feig}}\) has been shown to be locally connected (see [16, 18], also [4]), although the Julia set is “hairy” in the sense that it converges to the entire plane when magnified about the critical point (see [24, Thm. 8.7]). In contrast to the quadratic case, the Hausdorff dimension of the Julia set of a period-doubling Feigenbaum map tends to 2 as the order of the critical point tends to infinity [20], while the corresponding Lebesgue measure tends to zero [21].
2.1 The Avila–Lyubich trichotomy
Let f be a Feigenbaum map. Let \(f_n\) denote the n-th pre-renormalization of f, let \(J_n\) be its Julia set, and let \({{\mathcal {O}}}(f)\) be the critical orbit.
Avila and Lyubich showed the existence of domains \(U^n\subset V^n\) (called “nice domains”) for which
\(f_n(U^n)=V^n\);
\(U^n \,\supset \, J_n\cap {{\mathcal {O}}}(f)\);
\(V^{n+1}\subset U^n\);
\(f^k(\partial V^n)\cap V^n=\varnothing \) for all n, k;
\(A^n=V^n{\smallsetminus } U^n\) is “far” from \({{\mathcal {O}}}(f)\);
\({{\,\mathrm{area}\,}}(A^n)\asymp {{\,\mathrm{area}\,}}(U^n)\asymp {{\,\mathrm{diam}\,}}(U^n)^2\asymp {{\,\mathrm{diam}\,}}(V^n)^2\).
The construction of \(U^n\) and \(V^n\) involves cutting neighborhoods of zero by equipotentials and external rays of pre-renormalizations \(f_n\) of f and taking preimages under long iterates of \(f_n\).
For each \(n\in {{\mathbb {N}}}\), let \(X_n\) be the set of points in \(U^0\) that land in \(V^n\) under some iterate of f, and let \(Y_{n}\) be the set of points in \(A^n\) that never return to \(V^n\) under iterates of f. Introduce the quantities
Theorem 2.1
(Avila–Lyubich [2]) Let f be a periodic point of renormalization, i.e. there is a p so that \({{\mathcal {R}}}^p f=f\). Then exactly one of the following is true:
Lean case\(\eta _n\) converges to 0 exponentially fast, \(\inf \xi _n>0\), and \(\mathrm {dim_H}(J_f)<2\);
Balanced case\(\eta _n\asymp \xi _n\asymp \frac{1}{n}\) and \(\mathrm {dim_H}(J_f)=2\) with \({{\,\mathrm{area}\,}}(J_f)=0\);
Black Hole case\(\inf \eta _n>0\), \(\xi _n\) converges to 0 exponentially fast, and \({{\,\mathrm{area}\,}}(J_f)>0\).
Specific bounds determining the behavior of \(\eta _n\) and \(\xi _n\) depend on the geometry of \(A^n\) and \({{\mathcal {O}}}(f)\).
The proof of Theorem 2.1 relies on recursive estimates involving \(\eta _n\), \(\xi _n\), and the Poincaré series for \(f_n\). In the Lean case (relevant for this paper), Avila and Lyubich showed existence of a constant \(C>0\) which only depends on geometric bounds for \(U^n\subset V^n\) and \({{\mathcal {O}}}(f)\), such that if there exists m divisible by p with \(\eta _m<\xi _m/C\), then \(\eta _n\rightarrow 0\) exponentially fast.
Thus, to show that for the period doubling renormalization fixed point F one has \(\mathrm {dim_H}(J_F)<2\), it would be sufficient to compute this constant C and find large enough m so that \(\eta _m<\xi _m/C\). However, this task turns out to be extremely computationally complex for several reasons, including:
constructing the sets \(U^n\) and \(V^n\) is very technical, and it is difficult to obtain rigorous approximations of these sets computationally;
the geometry of \(U^n\) and \(V^n\) is complicated and \(U^n\) is not compactly contained in \(V^n\), making the corresponding geometric bounds very rough;
the constant C is given implicitly; estimates show it can be very large (on the order of \(10^{10}\)).
In our new sufficient condition for showing \(\mathrm {dim_H}(J_F)<2\), we overcome these difficulties by using the tiling of the plane by preimages of the upper and the lower half-planes as introduced in [4]. In particular, we replace the nice domains of Avila/Lyubich by the Buff tiles containing zero on the boundary. These tiles can be approximated quite efficiently and have good geometric bounds. Moreover, the scale-invariant structure of the tiling allows us to construct explicit recursive estimates for quantities which are an analogue to \(\eta _n\) directly, without using the Poincaré series. While our approach allows showing \({{\,\mathrm{area}\,}}(J_F)=0\) without appealing to Theorem 2.1, the results of [2] give the stronger result that \(\mathrm {dim_H}(J_F)<2\).
2.2 The fixed point of period-doubling renormalization
Recall (see [9]) that the fixed point F of period-doubling renormalization is a solution of Cvitanović–Feigenbaum equation:
where \(\tfrac{1}{\lambda }=2.5029\ldots \) is one of the Feigenbaum constants.
From (2.1) we immediately obtain
whenever both sides of the equation are defined.
Results of Epstein [9, 10] imply that there exists a domain  containing 0 such that
containing 0 such that  is a quadratic-like map
is a quadratic-like map

The \({{\varvec{n}}}\)th pre-renormalization\({{\varvec{F}}}_n\) of F is the restriction of \(F^{2^n}\) onto  .
.
For each \(n\in {{\mathbb {N}}}\), let \({\tilde{X}}_n\) denote the set of points \(z\in W^{(1)}\) such that \(F^k(z)\in W^{(n)}\) for some \(k\geqslant 0\). Set
Thus, \({\tilde{\eta }}_n\) is the probability that the orbit of a point randomly chosen from \(W^{(1)}\) with respect to Lebesgue measure will intersect \(W^{(n)}\). By construction, \({{\tilde{X}}}_{n+1}\subset {{\tilde{X}}}_n\) for any n. Therefore, \({\tilde{\eta }}_n\) is non-increasing in n.
Lemma 2.1
If \({\tilde{\eta }}_n\) converges to 0 exponentially fast then \(\eta _n\) also does.
Proof
The properties of nice domains imply that there exists \(n_0\) such that \(V^{n+n_0}\subset W^{(n)}\) for every n. Then \(X_{n+n_0}\subset \lambda ^{-1}{\tilde{X}}_{n+n_0+1}\) for every n, from which the lemma follows. \(\square \)
3 Structure of the Feigenbaum map F
For the proof of the following we refer the reader to [9]:
Proposition 3.1
Let \(x_0\) be the first positive preimage of 0 under F. Then
and \(\tfrac{x_0}{\lambda }\) is the first positive critical point of F.
A map \(g:U_g\rightarrow {\mathbb {C}}\) is called an analytic extension of a map \(f:U_f\rightarrow {\mathbb {C}}\) if f and g are equal on some open set. An extension \({\hat{f}}:S\supset U_f\rightarrow {\mathbb {C}}\) of f is called the maximal analytic extension if every analytic extension of f is a restriction of \({\hat{f}}\). The following crucial observation is also due to H. Epstein (cf. [9, 10]; see also [24, §7.3]):
Theorem 3.1
The map F has a maximal analytic extension \({\widehat{F}}:{\widehat{W}}\rightarrow {\mathbb {C}},\) where \({\widehat{W}}\supset {\mathbb {R}}\) is an open simply connected set which is dense in \({\mathbb {C}}\).
An approximation of the domain \({\widehat{W}}\) on which \({\widehat{F}}\) is defined. The red regions are preimages of the upper half plane \({\mathbb {H}}_+\), and the blue are preimages of \({\mathbb {H}}_-\). Recall that \({\widehat{W}}\) is open and dense in \({{\mathbb {C}}}\). Shown in shades of gray (including black and white) are points that lie in both \({\widehat{W}}\) and its complement; the shading should help give some idea of its structure (color figure online)
Let  be the upper half-plane, and let
be the upper half-plane, and let  denote the lower half-plane.
denote the lower half-plane.
For a proof of the following, see [9] or [4]:
Theorem 3.2
All critical points of \({\widehat{F}}\) are simple. The critical values of \({\widehat{F}}\) are contained in the real axis. Moreover, for any \(z\in {\widehat{W}}\) such that \({\widehat{F}}(z)\notin {\mathbb {R}}\), there exists a bounded open set \(U(z)\ni z\) such that \({\widehat{F}}\) is one-to-one on U(z) and \({\widehat{F}}(U(z))\) coincides with \({\mathbb {H}}_+\) or \({\mathbb {H}}_-\).
Following [4], we now introduce a combinatorial partition of \({\widehat{W}}\).
Definition 3.1
Denote by \({{\mathcal {P}}}\) the set of all connected components of \({\widehat{F}}^{-1}({{\mathbb {C}}}{\smallsetminus } {{\mathbb {R}}})\). For each non-negative integer n, let

Using the Cvitanović-Feigenbaum equation (2.1), we obtain that for any non-negative integer m, the partition \({\mathcal {P}}^{(m)}\) coincides with the set of connected components of the preimage of \({\mathbb {C}}{\smallsetminus }{\mathbb {R}}\) under \({\widehat{F}}^{2^m}\).
Definition 3.2
For \(k\geqslant 0\) we will refer to connected components of \({{\widehat{F}}}^{-k}({\mathbb {C}}{\smallsetminus }{\mathbb {R}})\) as tiles.
In particular, an element of \({\mathcal {P}}^{(n)}\) is a tile for any \(n\geqslant 0\), as are the half-planes \({\mathbb {H}}_+\) and \({\mathbb {H}}_-\).
Hence for any tile P, there is a \(k\geqslant 0\) so that the map \({\widehat{F}}^k\) sends P bijectively onto \({\mathbb {H}}_+\) or \({\mathbb {H}}_-\). Using Theorem 3.2 we obtain the following (Fig. 2):
Lemma 3.1
(Nesting Property) Any pair of tiles are either disjoint or one is a subset of the other.
Let us describe the structure of \({\widehat{F}}\) on the real line near the origin. Since \({\widehat{F}}\) maps \([1,\tfrac{x_0}{\lambda }]\) homeomorphically onto \([-\tfrac{1}{\lambda },-\lambda ]\), there exists a unique \(a\in (1,\tfrac{x_0}{\lambda })\) such that \({\widehat{F}}(a)=-\tfrac{x_0}{\lambda }.\)
A proof of the following can be found in [7].
Lemma 3.2
The map \({\widehat{F}}\) has exactly 3 critical points the interval (0, 6), ordered as \(0< \tfrac{x_0}{\lambda }< \tfrac{a}{\lambda } < \tfrac{x_0}{\lambda ^2}\) (Fig. 3).
Furthermore,
Tiles from \({\mathcal {P}}^{(1)}\) (blue), \({\mathcal {P}}^{(2)}\) (red), and \({\mathcal {P}}^{(3)}\) (green) in the first quadrant that intersect the Julia set \(J_F\). Compare to Fig. 1 (color figure online)
Applying Theorem 3.2 and Lemma 3.2, we see that for each of the segments \([0,\tfrac{x_0}{\lambda }]\), \([\tfrac{x_0}{\lambda },\tfrac{a}{\lambda }]\), and \([\tfrac{a}{\lambda },\tfrac{x_0}{\lambda ^2}]\) there is exactly one tile \(P\in {{\mathcal {P}}}\) in the first quadrant which contains this segment in its boundary. Notice that \({{\mathcal {P}}}\) has four-fold symmetry: it is invariant under multiplication by \(-1\) and under complex conjugation.
Definition 3.3
Let \(c_j\) be the non-negative real critical points of \({\widehat{F}}\), with \(0=c_0< c_1< c_2 <\ldots \), and for each j, let \(P_{j,\mathrm {I}}\) denote the tile of \({{\mathcal {P}}}\) in the first quadrant with \([c_j,c_{j+1}]\) in its boundary.
For each  , let \(P_{j,K}\) denote the tile in quadrant K symmetric to \(P_{j,\mathrm {I}}\) with respect to the imaginary axis, the origin, or the real axis, respectively. See Fig. 4. We will sometimes omit the second index (e.g. \(P_{2}\)); in this case we will mean any of the four symmetric tiles \(P_{j,\mathrm {I}}, P_{j,\mathrm {II}}, P_{j,\mathrm {III}},\) or \(P_{j,\mathrm {IV}}\) (or the appropriate one, depending on context).
, let \(P_{j,K}\) denote the tile in quadrant K symmetric to \(P_{j,\mathrm {I}}\) with respect to the imaginary axis, the origin, or the real axis, respectively. See Fig. 4. We will sometimes omit the second index (e.g. \(P_{2}\)); in this case we will mean any of the four symmetric tiles \(P_{j,\mathrm {I}}, P_{j,\mathrm {II}}, P_{j,\mathrm {III}},\) or \(P_{j,\mathrm {IV}}\) (or the appropriate one, depending on context).
Consistent with our earlier usage for \({{\mathcal {P}}}\), for any set P and any integer \(n\geqslant 0\), we let \({P^{(n)}} = \lambda ^n P\).
Proposition 3.2
The map \({\widehat{F}}\) satisfies the following:
- (i)
\({\widehat{F}}(P_{0,\mathrm {I}}^{(2)}) \,\subset \, P_{1,\mathrm {IV}}^{(1)}\) ;
- (ii)
\(P_{1,\mathrm {IV}}^{(2)} \cup P_{2,\mathrm {IV}}^{(2)} \,\subset \, {\widehat{F}}(P_{1,\mathrm {I}}^{(2)}) \,\subset \, P_{0,\mathrm {IV}}^{(1)} {\smallsetminus } P_{0,\mathrm {IV}}^{(2)}\) ;
- (iii)
\({\widehat{F}}(P_{2,\mathrm {I}}^{(2)})\,\subset \, P_{0,\mathrm {IV}}^{(1)}\) ;
- (iv)
\({\widehat{F}}(P_{0,\mathrm {I}}^{(1)})=P_{0,\mathrm {IV}}\), \({\widehat{F}}(P_{1,\mathrm {I}}^{(1)})=P_{0,\mathrm {III}}\).
See Fig. 4. We refer the reader to [7] for the proof of Proposition 3.2. Using part (iv) of Proposition 3.2 we obtain
Lemma 3.3
Let \(y_0\) be such that  . Then
. Then
For the reader’s convenience we list approximate values of some of the important constants.
Let \({{\,\mathrm{Int\,}\,}}S\) denote the interior of the set S. The set \({W}\) introduced in Subsection 2.2 can be written

Definition 3.4
Define each of the following quantities:
For each
 , set
, set 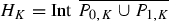 . Let
. Let 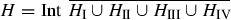 .
.For \(n\geqslant 0\), we write \(W^{(n)} = \lambda ^n\,{W}\) and \(H^{(n)}=\lambda ^n H\).
Remark 3.1
The restriction \({\widehat{F}}:{W}\rightarrow {\mathbb {C}}{\smallsetminus }((-\infty ,-\tfrac{1}{\lambda }]\cup [\tfrac{1}{\lambda ^2},\infty ))\) is a quadratic-like map.
Definition 3.5
Henceforth, we define F to be the restriction of \({\widehat{F}}\) to \({W}\). For \(n\in {{\mathbb {Z}}}_+\), let \(F_n\) denote the restriction of \(F^{2^n}\) to \(W^{(n)}\), that is, the n-th pre-renormalization of F.
Remark 3.2
The following observations are immediate from the properties of F described above.
- (i)
If n is odd then \(F^n(0)\geqslant F^3(0)=F(\lambda )\approx 0.758923\).
- (ii)
If \(F^{k}(0)\in [-\lambda ^m x_0,\lambda ^m x_0]\) (that is, if
 ), then k is divisible by \(2^m\).
), then k is divisible by \(2^m\). - (iii)
For all \(n\in {{\mathbb {N}}}\) and \(1\leqslant k< 2^{n-1}\) one has \(F^k(W^{(n)})\cap W^{(n)}=\varnothing .\)
Remark 3.3
For any finite piece of orbit \(x=x_0,x_1={\widehat{F}}(x),\ldots ,x_k={\widehat{F}}^k(x)\) such that \(x_k\) belongs to the closure of some tile T and \(D{\widehat{F}}^k(x_0)\ne 0\), one can univalently pull back T along \(x_0,\ldots ,x_k\) in a unique way. In particular, this is true under the condition that \(x_i\in W\) and \(x_i\ne 0\) for \(1\leqslant i \leqslant k-1\).
4 Distortion bounds
4.1 Copies of tiles
Definition 4.1
We will say that a tile Q is a copy of the tile\({{\varvec{P}}}\)under\({{\varvec{F}}}^k\) if there is a non-negative integer k such that \(F^k(Q)=P\).
A copy P of \(P_{0}^{(m)}\) under \(F^k\) is primitive if \(F^j(P)\cap W^{(m)}=\varnothing \) for all \(0\leqslant j<k\).
A copy P of \(P_{0}^{(m)}\) under \(F^k\) is separated if there exists \(0\leqslant j<k\) with \(F^j(P)\subset W^{(m)}\) and \(F^j(P)\cap J_F^{(m-1)}=\varnothing \) for the maximal such j.
As we shall see, separated copies of \(P_{0}^{(m)}\) are called this because they stay away from relevant parts of the postcritical set. Separated copies play an important role for us, in that they allow us to have control on the distortion of tiles under iteration of f.
Remark 4.1
We make the following useful observations.
- (i)
If Q is a copy of P under \(F^k\) then \(F^k:Q\rightarrow P\) is a bijection.
- (ii)
If Q is a copy of a separated copy T then Q is separated.
- (iii)
Let T be a separated copy of \(P_{0}^{(m)}\) with \(F^k(T)=P_{0}^{(m)}\). Then for each \(j\leqslant k\), \(F^j(T)\) is either a primitive or a separated copy of \(P_{0}^{(m)}\). In particular, the set \(P_{0}^{(m)}\) is a primitive copy of itself.
- (iv)
Copies of primitive copies need not be primitive or separated. For example, let \(T =F(P_{0,\mathrm {I}}^{(2)})\), so \(F^2(T)=P_{0,\mathrm {II}}^{(1)}\) and \(T \subset P_{1,\mathrm {IV}}^{(1)} \not \subset W^{(1)}\); see Fig. 4. Hence T is a primitive copy of \(P_{0,\mathrm {II}}^{(1)}\).
But \(P_{0,\mathrm {I}}^{(2)} \subset W^{(1)}\) and intersects \(J_F\), so \(P_{0,\mathrm {I}}^{(2)}\) is neither a primitive nor a separated copy of \(P_{0,\mathrm {II}}^{(1)}\).
Lemma 4.1
Let T be a copy of \(P_{0}^{(m)}\) under \(F^k\) with \(T\subset W^{(n-1)}\) for some \(n\leqslant m\in {{\mathbb {N}}}\). If \(T\cap J_F^{(n-1)} \ne \varnothing \), then k is divisible by \(2^{n-1}\). Moreover, \(F_{n-1}^\ell \) is defined on T for \(\ell =k/2^{n-1}\) and thus \(F_{n-1}^\ell (T)=P_{0}^{(m)}\).
Proof
Let T be as in the conditions of the lemma. Assume that k is not divisible by \(2^{n-1}\). Let r be the remainder of k modulo \(2^{n-1}\) and let \(j=2^{n-1}-r\). Then \(F^{j}(P_{0}^{(m)})=F^{2^{n-1}s}(T)\) for some integer s, therefore,
By the nesting property (Lemma 3.1), we see that \(F^{j}(P_{0}^{(m)})\subset W^{(n-1)}\) and hence \(F^j(0)\in W^{(n-1)}\). Remark 3.2 implies that \(j=2^{n-2}\). But \(F^{2^{n-2}}(0)=(-\lambda )^{n-2}\) does not belong to \(W^{(n-1)}\). This contradiction proves the first statement of the lemma.
To prove the second statement we show by induction that for all \(0\leqslant j<\ell \) one has \(F_{n-1}^j(T)\subset W^{(n-1)}\) and \(F_{n-1}^j(T)\cap J_F^{(n-1)}\ne \varnothing \). The base case of the induction \(j=0\) is given by the conditions of the lemma. The induction step follows from the nesting property and the fact that \(J_F^{(n-1)}\) is \(F_{n-1}\)-invariant. \(\square \)
Lemma 4.2
Let T be a separated copy of \(P_{0}^{(m)}\). Then \(\displaystyle T\cap J_F^{(m-1)}=\varnothing .\)
Proof
Assume that there exists a separated copy T of \(P_{0}^{(m)}\) such that \(\displaystyle T\cap J_F^{(m-1)}\ne \varnothing .\) Let k be such that \(F^k(T)=P_{0}^{(m)}\). Set \(\ell =\lfloor \tfrac{k-1}{2^{m-1}} \rfloor \), where \(\lfloor \cdot \rfloor \) denotes the integer part of a number, and set \(T_r=F^{2^{m-1}r}(T)\) for \(0\leqslant r \leqslant \ell .\) Then \(T_r\cap J_F^{(m-1)}\ne \varnothing \), and thus by the nesting property, \(T_r\subset H^{(m)}\) for all \(r\leqslant \ell \) (recall the definition of H in Definition 3.4) (Fig. 5).
Lemma 4.2 shows the above situation does not occur, that is, a separated copy T of \(P_{0}^{(m)}\) cannot intersect \(J^{(m-1)}_F\). (This illustrates the case \(r=0\) of the proof)
Since T is separated there exists \(0\leqslant r\leqslant \ell \) and \(1\leqslant j < 2^{m-1}\) such that \(F^j(T_r)\subset W^{(m)}\) and \(F^j(T_r)\cap J_F^{(m-1)}=\varnothing \). Taking into account that
from Remark 3.2(iii) we obtain that \(j\geqslant 2^{m-2}\). Similarly, since
we know that \(2^{m-1}-j\geqslant 2^{m-2}\) by again using Remark 3.2(iii) It follows that \(j=2^{m-2}\). But
(see Proposition 3.2). This contradiction finishes the proof. \(\square \)
4.2 Koebe space
In what follows, we use \({{\,\mathrm{sign}\,}}(P)\) to represent the sign of the real part of the points in P, that is, \({{\,\mathrm{sign}\,}}(P)=-1\) if P is in the left half-plane, \(+1\) otherwise.
Proposition 4.1
Let T be a primitive or a separated copy of \(P_{0}^{(m)}\) under \(F^k\) with \(m\geqslant 2\). Then the inverse branch \(\phi :P_{0}^{(m)}\rightarrow T\) of \(F^k\) analytically continues to a univalent map on \({{\,\mathrm{sign}\,}}(P_{0}^{(m)})\,\lambda ^m{{\mathbb {C}}}_\lambda \) where (Fig. 6)Footnote 1
Illustration of the statement of Proposition 4.1, which says (roughly) that primitive and separated copies of \(P_{0}^{(m)}\) have a definite Koebe space around them
Proof
Assume that the statement of Proposition 4.1 is false. Let \(m\geqslant 2\) and T be either a primitive or a separated copy of \(P_{0}^{(m)}\) such that the inverse branch of \(F^{-k}:P_{0}^{(m)}\rightarrow T\) does not have a univalent continuation on \({{\,\mathrm{sign}\,}}(P_{0}^{(m)})\,\lambda ^m{{\mathbb {C}}}_\lambda \). Take k to be the minimal integer such that there is no such continuation.
Since F is real analytic, without loss of generality we may also assume that \(P_{0}^{(m)}\subset {\mathbb {H}}_+\), that is, it is \(P_{0,\mathrm {I}}^{(m)}\) or \(P_{0,\mathrm {II}}^{(m)}\). By Remark 3.3, \(F^{-k}\) has a univalent analytic continuation \(\phi \) on \({\mathbb {H}}_+\) which can be extended to a continuous function on  . Since k is defined to be the minimal value such that \(F^{-k}\) does not extend, the unique critical point 0 must be in
. Since k is defined to be the minimal value such that \(F^{-k}\) does not extend, the unique critical point 0 must be in  ; moreover,
; moreover,
Suppose that \(\phi (0)\notin {\mathbb {R}}\). Let \(\ell \) be the minimal integer such that \(F^{\ell +1}(\phi (0))\in {{\mathbb {R}}}\), so \(F^\ell (\phi (0))\in \mathrm {i}{{\mathbb {R}}}\) and  is a non-empty segment. Since T is primitive or separated,
is a non-empty segment. Since T is primitive or separated,  cannot contain 0. Therefore,
cannot contain 0. Therefore,  is disjoint from \({{\mathbb {R}}}\). Let [x, y] denote the segment
is disjoint from \({{\mathbb {R}}}\). Let [x, y] denote the segment  where \(|x|<|y|\). See Fig. 7.
where \(|x|<|y|\). See Fig. 7.
Illustration of formula (4.2): if \(\phi (0)\not \in {{\mathbb {R}}}\), then \(F^{k-\ell }(0)\) lies between 0 and \(F^k(0)\)
Clearly, \(F^{k-\ell }(x)\) is real and  . It follows that
. It follows that  and \(F^{k-\ell }\) is one-to-one on \((x,0]\cup [0,F^\ell (0))\). Thus if \(\ell \) is nonzero, we will have
and \(F^{k-\ell }\) is one-to-one on \((x,0]\cup [0,F^\ell (0))\). Thus if \(\ell \) is nonzero, we will have
since the segment \((F^{k-\ell }(x),F^{k}(0))\) is disjoint from  . By the definition of k, we obtain that \(\ell =0\). Consequently, \(\phi (0)\in \mathrm {i}{\mathbb {R}}\cup {\mathbb {R}}\).
. By the definition of k, we obtain that \(\ell =0\). Consequently, \(\phi (0)\in \mathrm {i}{\mathbb {R}}\cup {\mathbb {R}}\).
By Remark 3.2 and (4.1), k is divisible by \(2^{m-2}\). If \(k\geqslant 2^{m+1}\), then since  the nesting property tells us that we must have \(T\subset \phi ({\mathbb {H}}_+)\subset W^{(m+1)}\). In particular, T is not primitive and so must be separated. Since \(\phi (0)\) must be either real or purely imaginary, and since
the nesting property tells us that we must have \(T\subset \phi ({\mathbb {H}}_+)\subset W^{(m+1)}\). In particular, T is not primitive and so must be separated. Since \(\phi (0)\) must be either real or purely imaginary, and since
we obtain that \(T\cap J_F^{(m-1)}\ne \varnothing \), contradicting the hypothesis of T being separated. Hence, we must have \(k<2^{m+1}\).
This leaves us with four possibilities, each of which we rule out now.
- Case\(\mathbf {k=2^m}\):
In this case, \(T\subset \phi ({\mathbb {H}}_+)=P_{0,K}^{(m)}\) for some K (see Fig. 8). In particular, T is not primitive. Since \(F^{2^m}\!\left( {{\,\mathrm{sign}\,}}(P_{0,K}^{(m)})\lambda ^m x_0\right) =0\) and \({{\,\mathrm{sign}\,}}(P_{0,K}^{(m)})\lambda ^m x_0\in \partial \phi ({\mathbb {H}}_+)\), we have \({{\,\mathrm{sign}\,}}(P_{0,K}^{(m)})\lambda ^m x_0=\phi (0)\in \partial T\) and therefore \(T\cap J_F^{(m-1)}\ne \varnothing \). From Lemma 4.2, this means T is not separated, giving a contradiction.
- Case\(\mathbf {k=2^{m-1}}\):
Then \(\phi ({\mathbb {H}}_+)=P_{0}^{(m-1)}\) (see Fig. 9). Since by (2.2) we have \(F^{2^m}(z)=(-\lambda )^mF(z/\lambda ^m)\), we can apply Proposition 3.2 to see that \(T=\pm \lambda ^{m-1} F(P_{i,K}^{(2)})\) with \(i=0\) or \(i=1\) and \(K=\mathrm {I}\) or \(K=\mathrm {IV}\). Since T is either primitive or separated, \(i\ne 1\). Again using (2.2) we obtain
$$\begin{aligned} P_{0}^{(m)}=F^{2^{m-1}}(T)=(-\lambda )^{m-1}F^2(P_{0,K}^{(2)}) =(-\lambda )^{m}F(P_{0,K}^{(1)}) \end{aligned}$$and thus \({{\,\mathrm{sign}\,}}(P_{0}^{(m)})=(-1)^m\). This contradicts (4.1), since \(F^{2^{m-1}}(0)=(-\lambda )^{m-1}\).
- Case \(\mathbf {k{=}3\cdot 2^{m-1}}\):
Here we have \(P_{0,K}^{(m)}\supset \phi ({\mathbb {H}}_+)\supset P_{0,K}^{(m+1)}\) for some K (see Fig. 10). In particular, T is not primitive. Moreover, by definition of \(y_0\) (see Lemma 3.3),
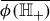 will contain either \(y=\lambda ^my_0\) or \(y=-\lambda ^my_0\) which are points of \(J_F^{(m-1)}\). Since \( F^{3\cdot 2^{m-1}}(y)=(-\lambda )^{m-1}F^3(\lambda y_0)=0\), we obtain that
will contain either \(y=\lambda ^my_0\) or \(y=-\lambda ^my_0\) which are points of \(J_F^{(m-1)}\). Since \( F^{3\cdot 2^{m-1}}(y)=(-\lambda )^{m-1}F^3(\lambda y_0)=0\), we obtain that  , and hence T intersects \(J_F^{(m-1)}\), contradicting the hypothesis that T is separated.
, and hence T intersects \(J_F^{(m-1)}\), contradicting the hypothesis that T is separated.- Case\(\mathbf {k=2^{m-2}j}\) where \({\mathbf {j}}\) is odd:
Remark 3.2 gives \(|F^k(0)|=\lambda ^{m-2}|F^j(0)|\geqslant \lambda ^{m-2}F(\lambda )\), contradicting (4.1).
A case where \(k=2^m\) in the proof of Proposition 4.1
In the proof of Proposition 4.1, the case where \(k=2^{m-1}\)
The case \(k=3\cdot 2^{m-1}\) from the proof of Proposition 4.1
Since all the possibilities for k lead to a contradition, we have established the proposition. \(\square \)
Informally speaking, Proposition 4.1 tells us that the inverse branch of the iterate of F corresponding to a separated copy T admits an analytic continuation to a region with a definite Koebe space around T.
4.3 Distortion of measurable sets
The Koebe Distortion Theorem (see [8], e.g.) implies that there exists a constant \(C>0\) such that for any univalent function \(\phi \) on \({{\mathbb {C}}}_\lambda ={{\mathbb {C}}}{\smallsetminus }\left( (-\infty ,-\tfrac{1}{\lambda }]\cup [\tfrac{F(\lambda )}{\lambda ^2},\infty ) \right) \) one has:
Recall that \(P_{0}\) is used to denote any of the tiles \(P_{0,\mathrm {I}}\), \(P_{0,\mathrm {II}}\), \(P_{0,\mathrm {III}}\), or \(P_{0,\mathrm {IV}}\) (see Definition 3.3). As a consequence of Proposition 4.1, one can show the following.
Corollary 4.1
Let A and B be two measurable subsets of \(P_{0}\) of positive measure and let T be a primitive or a separated copy of \(P_{0}^{(m)}\) under \(F^k\) for some \(k\geqslant 0\) and \(m\geqslant 2\). Then
However, we will need a slightly sharper version of this result, where the constant depends more explicitly on the set A. We devote the remainder of this section to establishing it.
Consider the slit plane \({{\mathbb {C}}}_\lambda \). From the Koebe Distortion Theorem, the function

is nonzero and finite for all z and w.
Fix a univalent map \(\phi \) on \({{\mathbb {C}}}_\lambda \). For every \(w\in {{\mathbb {C}}}_\lambda \), there is a conformal isomorphism \(H_w:{{\mathbb {C}}}_\lambda \rightarrow {{\mathbb {D}}}\) such that \(H_w(w)=0\) and \(H'_w(w)\) is a positive real number. Thus, we can write \(\phi \) as a composition \(\phi =\varphi \circ H_w\), where \(\varphi \) is a univalent map on the unit disk \({{\mathbb {D}}}\).
Applying the Koebe Distortion Theorem, we have
In particular,
The latter gives us a way to estimate C(z, w) from above.
Fix two measurable subsets A and B of \(P_{0}\) of positive measure. For any \(z\in B\) we have
For notation, set \(g_A(z)=\int \limits _{A}|{\text {d}}w|^2/C^2(z,w)\). Then we obtain
where

Observe that for two measurable sets \(A\subset A'\subset P_{0}\), we have \(M(A)\geqslant M(A')\), since for all z we have \(g_A(z)\leqslant g_{A'}(z)\).
As a consequence of Proposition 4.1 and the previous discussion, we obtain the following.
Corollary 4.2
Let A, B be two measurable subsets of \(P_{0}\) of positive measure and let T be a primitive or a separated copy of \(P_{0}^{(m)}\) under \(F^k\) for some \(k\geqslant 0\) and \(m\geqslant 2\). Then
Moreover, if \(A_1\subset A_2\) then \(M(A_1)\geqslant M(A_2)\).
Remark 4.2
While we could write the quantity \(M(A){{\,\mathrm{area}\,}}(B)\) more conventionally as \(K_A\frac{{{\,\mathrm{area}\,}}(B)}{{{\,\mathrm{area}\,}}(A)}\), it is more convenient to use M(A) since \(A_1\subset A_2\) does not imply \(K_{A_1} \geqslant K_{A_2}\).
5 Recursive estimates
Recall that F is a quadratic-like map \(F:{W}\rightarrow {\mathbb {C}}{\smallsetminus }((-\infty ,-\tfrac{1}{\lambda }]\cup [\tfrac{1}{\lambda ^2},\infty )), \) and for a point \(z\in {W}\), by the forward orbit of\({{\varvec{z}}}\) we mean the set  . Recall from Definition 3.5 that \(F_n\) denotes the n-th pre-renormalization of F, that is, the restriction of \(F^{2^n}\) to \(W^{(n)}\).
. Recall from Definition 3.5 that \(F_n\) denotes the n-th pre-renormalization of F, that is, the restriction of \(F^{2^n}\) to \(W^{(n)}\).
Definition 5.1
Define the following (some of which we have referred to in Sect. 2).
Let \({\tilde{X}}_n\) be the set of points in \(W^{(1)}\) that eventually land in \(W^{(n)}\):
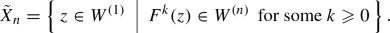
Denote by \({\tilde{\eta }}_n\) the relative measure of \({\tilde{X}}_n\) in \(W^{(1)}: {\tilde{\eta }}_{n}=\displaystyle \frac{{{\,\mathrm{area}\,}}({\tilde{X}}_{n})}{{{\,\mathrm{area}\,}}(W^{(1)})}\).
Let \(X_{n,m}\) be the set of points in \(W^{(n)}\) whose forward orbits under \(F_{n-1}\) intersect \(W^{(n+m)}\):

Let \(Y_n\) denote the set of points in \(W^{(n)}\) whose forward orbits never return to \(W^{(n)}\):

\(\Sigma _n\) is the set of points in \(W^{(n)}\) whose forward orbits under \(F_{n-1}\) intersect \(Y_n\):
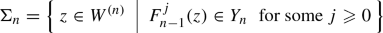
\(\Sigma _{n,m}\) is the subset of \(\Sigma _n\) with orbits that avoid \(W^{(n+m)}\):

For measurable sets A, let M(A) be as in Corollary 4.2. Then define
$$\begin{aligned} M_{n,m}=M\bigl ( (\lambda ^{-n}\Sigma _{n,m}) \cap P_{0,\mathrm {I}} \bigr ) \quad \text {and}\quad M_n = M\bigl ( (\lambda ^{-n}\Sigma _{n}) \cap P_{0,\mathrm {I}} \bigr ). \end{aligned}$$
Remark 5.1
The following observations are immediate:
- (i)
\({\tilde{X}}_{n}\) is the union of all primitive copies of \(P_{0}^{(n)}\) that lie inside \(W^{(1)}\), together with a countable collection of analytic curves (which form parts of the boundaries of these copies).
- (ii)
The relative measure of \(X_{n,m}\) in \(W^{(n)}\) is equal to \(\tilde{\eta }_{m+1}\): \(\displaystyle \frac{{{\,\mathrm{area}\,}}(X_{n,m})}{{{\,\mathrm{area}\,}}(W^{(n)})}={\tilde{\eta }}_{m+1} \).
- (iii)
By construction, \(X_{n,m}\cap \Sigma _{n,m}=\varnothing \) for all n, m.
- (iv)
\(\displaystyle \Sigma _n = \bigcup _{m\in {{\mathbb {N}}}} \Sigma _{n,m}\).
Theorem 5.1
For every \(n\geqslant 2\) and \(m\geqslant 1\), one has
Before proving Theorem 5.1, let us formulate its main corollary.
Corollary 5.1
If for some \(n\geqslant 2\) one has \({\tilde{\eta }}_n M_n{{\,\mathrm{area}\,}}(P_{0,\mathrm {I}})<1\), then the Hausdorff dimension of \(J_F\) is less than 2.
Proof
Let n be such that \({\tilde{\eta }}_nM_n{{\,\mathrm{area}\,}}(P_{0,\mathrm {I}})<1\). Then there is an m for which \({\tilde{\eta }}_n M_{n,m}{{\,\mathrm{area}\,}}(P_{0,\mathrm {I}})<1\); let \(\gamma = {\tilde{\eta }}_n M_{n,m}{{\,\mathrm{area}\,}}(P_{0,\mathrm {I}})\) for this value of n and m.
By construction \(\Sigma _{n,k}\subset \Sigma _{n,\ell }\) whenever \(k<\ell \), so Corollary 4.2 tells us that
Using Theorem 5.1 and writing \(rn+m\) as \(n+((r-1)n+m)\), we deduce that
As a result, \({\tilde{\eta }}_k\) converges to zero exponentially fast. Consequently, Lemma 2.1 tells us that the parameter \(\eta _k\) of the Avila-Lyubich Trichotomy (Theorem 2.1) also converges to zero exponentially fast. Thus, F is in the lean case and the Hausdorff dimension of \(J_F\) is less than 2. \(\square \)
5.1 The proof of Theorem 5.1
First, let us prove some auxiliary lemmas.
Lemma 5.1
Let T be a copy of \(P_{0}^{(m+n)}\) with \(T\subset W^{(1)}{\smallsetminus } X_{n,m}\). Then there is a \(k\geqslant 0\) and a primitive or separated copy Q of \(P_{0}^{(n)}\) under \(F^k\) so that \(T \subset Q \subset W^{(1)}\), with \(F^k(T)\subset X_{n,m}\) but \(Q\not \subset {\tilde{X}}_{n+m}\).
Proof
Let \(F^r(T)=P_{0}^{(m+n)}\). Let j be the minimal number for which \(F^j(T)\) intersects \(X_{n,m}\) with \(F^j(T)\subset W^{(n)}\). We now show that we must have \(F^j(T)\subset X_{n,m}\). Since \(X_{n,m}\) consists of copies of \(W^{(n+m)}\), the nesting property tells us that either \(F^{j}(T)\subset X_{n,m}\) or it contains a copy of \(P_{0}^{(m+n)}\) under \(F_{n-1}^s\) for some s; in this case \(F^j(T)\cap J_F^{(n-1)}\ne \varnothing \). By Lemma 4.1, \(r-j\) is divisible by \(2^{n-1}\). Moreover, \(F_{n-1}^p(F^j(T))=P_{0}^{(m+n)}\) for \(p=(r-j)/2^{n-1}\) and so we must have \(F^j(T)\subset X_{n,m}\).
Let Q be the unique copy of \(P_{0}^{(n)}\) under \(F^j\) containing T. Let us show that Q is either primitive or separated and \(Q{\smallsetminus }{\tilde{X}}_{n+m}\ne \varnothing \). Observe that if \(Q\subset {\tilde{X}}_{n+m}\), the nesting property and Lemma 4.1 would imply that either \(F^d(Q)\subset P_{0}^{(n+m)}\) or \(F^d(Q)\supset P_{0}^{(n+m)}\) for some \(d<j\). If Q is primitive this is clearly impossible.
Assume that Q is not primitive. Then there exists \(0\leqslant \ell <j\) such that \(F^\ell (Q)\subset W^{(n)}\). Assume that \(\ell \) is the maximal such number. If \(F^\ell (Q)\) intersects \(J_F^{(n-1)}\) then from Lemma 4.1 we obtain that \(c=(j-\ell )/2^{n-1}\) is an integer and \(F_{n-1}^c(F^\ell (Q))=P_{0}^{(n)}\). In this case \(F_{n-1}^c(F^\ell (T))=F^j(T)\subset X_{n,m}\) and so \(F^\ell (T)\subset X_{n,m}\). This contradicts the definitions of j and \(\ell \). Thus, \(F^\ell (Q)\cap J_F^{(n-1)}=\varnothing \) and so Q is separated.
Now, \(F^d(Q)\supset P_{0}^{(n+m)}\) is impossible for \(d<j\) by Lemma 4.2 and the fact that \(F^d(Q)\) is either a primitive or a separated copy of \(P_0^{(n)}\) (see Remark 4.1(iii)). On the other hand, if \(F^d(Q)\subset P_{0}^{(n+m)}\) for \(d<j\) then \(F^d(T)\subset W^{(n+m)}\subset X_{n,m}\), contradicting the definition of j. This shows that \(Q{\smallsetminus }{\tilde{X}}_{n+m}\) is nonempty, finishing the proof. \(\square \)
Lemma 5.2
For every primitive or separated copy Q of \(P_{0}^{(n)}\) for which \(Q{\smallsetminus } {\tilde{X}}_{n+m}\ne \varnothing \), one has
Proof
Assume that \(Q\cap X_{n,m}\ne \varnothing \). Then by the nesting property, Q either contains or is contained in a copy T of \(P_{0}^{(n+m)}\) under \(F_{n-1}^{\ell }\) for some \(\ell \). If \(T\subset Q\) then Q intersects \(J_F^{n-1}\), which is impossible since Q is separated. If, on the other hand, \(Q \subset T\), then by the definition of \({\tilde{X}}_{n+m}\) we have \(Q\subset {\tilde{X}}_{n+m}\), contradicting a hypothesis of the lemma. Thus, we must have \(Q\cap X_{n,m}=\varnothing \).
Now suppose that \(Q\cap \Sigma _{n,m}\) is nonempty. Let k be such that \(F^k(Q)= P_{0}^{(n)}\), and let \(\ell \) be the minimal number such that \(Q\cap F^{-\ell }_{n-1}(Y_n) \ne \varnothing \). Then
and therefore \(k\leqslant 2^{n-1}\ell \). By the nesting property,
for some quadrant L. Since \(Q\cap F_{n-1}^{-\ell }(P_{0,L}^{(n)})\) is nonempty, Q must contain a copy T of \(P_{0,L}^{(n)}\) with \(F_{n-1}^\ell (T) = P_{0,L}^{(n)}\). Therefore Q intersects \(J_F^{(n-1)}\), contradicting Lemma 4.2 and finishing the proof. \(\square \)
Let \({\mathcal {S}}{\mathcal {P}}\) be the set of all primitive or separated copies Q of \(P_{0}^{(n)}\) which lie in \(W^{(1)}\) and are such that \(Q{\smallsetminus }{\tilde{X}}_{n+m}\ne \varnothing \). For \(Q\in {\mathcal {S}}{\mathcal {P}}\) let k be such that \(F^k(Q)=P_{0}^{(n)}\). Set
Recall that \(\Sigma _{n,m}\) and \(X_{n,m}\) are symmetric with respect to the axes. Observe that \(F^k\) sends \(X_Q\) and \(\Sigma _Q\) bijectively onto the intersections of \(X_{n,m}\) and \(Z_{n,m}\), respectively, with one of the four quadrants.
Corollary 5.2
The sets from the collection  are pairwise disjoint.
are pairwise disjoint.
Proof
Since \(\Sigma _{n,m}\cap X_{n,m}=\varnothing \), we obtain immediately that \(\Sigma _Q\cap X_Q=\varnothing \) for every \(Q\in {\mathcal {S}}{\mathcal {P}}\). Let \(Q_1, Q_2\in {\mathcal {S}}{\mathcal {P}}\) be distinct copies of \(T_1=P_{0,K}^{(n)}\) and \(T_2=P_{0,L}^{(n)}\), respectively, and let \(k_1,k_2\) be such that \(F^{k_1}(Q_1)=T_1\) and \(F^{k_2}(Q_2)=T_2\).
If \(k_1=k_2\) then since \(Q_1\) and \(Q_2\) are distinct, they must be disjoint. Assume that \(k_1<k_2\) and that one of two sets \(\Sigma _{Q_1}\), \(X_{Q_1}\) intersects one of two sets \(\Sigma _{Q_2}\), \(X_{Q_2}\). By the nesting property (Lemma 3.1), \(Q_2\subset Q_1\). Since \(F^{k_1}(Q_2)\in {\mathcal {S}}{\mathcal {P}}\), we can apply Lemma 5.2 to see that
Therefore, \(Q_2\cap (\Sigma _{Q_1}\cup X_{Q_1})=\varnothing \). This contradiction finishes the proof. \(\square \)
Proof of Theorem 5.1
By Lemma 5.1, \({\tilde{X}}_{n+m}\) is the union of all sets of the form \(X_Q\), \(Q\in {\mathcal {S}}{\mathcal {P}}\), together with a countable set of analytic curves. Using the fact that \(X_{n,m}\) and \(\Sigma _{n,m}\) are symmetric with respect to the axes, Corollary 4.2, the definition of \(M_{n,m}\) (Definition 5.1), and Remark 5.1(ii), we obtain
We have
Since \(\displaystyle \big (\!\bigsqcup _{Q\in {\mathcal {S}}{\mathcal {P}}} X_Q\big ) \sqcup \big (\!\bigsqcup _{Q\in {\mathcal {S}}{\mathcal {P}}} \Sigma _Q\big ) \subset {\tilde{X}}_n\), we obtain \(\displaystyle {{\,\mathrm{area}\,}}({\tilde{X}}_{n+m}) \leqslant M_{n,m}{\tilde{\eta }}_{m+1}{{\,\mathrm{area}\,}}(P_{0,\mathrm {I}}){{\,\mathrm{area}\,}}({\tilde{X}}_n)\). \(\square \)
5.2 Estimating \({\tilde{X}}_n\) and \(\Sigma _n\)
Let \({\mathcal {P}}^{(n)}_{\!\!J}\) denote the elements of \({\mathcal {P}}^{(n)}\) that intersect \(J_F\). That is, \({\mathcal {P}}^{(n)}_{\!\!J}= \{P\in {\mathcal {P}}^{(n)} \,|\, P\cap J_F \ne \varnothing \}\). Then, for each \(n\in {{\mathbb {N}}}\), let \(V_n\) be the interior of the closure of the union of all tiles \(P\in {\mathcal {P}}^{(n)}_{\!\!J}\). Observe that the sets \(V_n\) form a collection of nested neighborhoods of \(J_F\). Figure 2 shows the tiles that make up \(V_1\), \(V_2\), and \(V_3\) in the first quadrant; \(V_2\) is also shown in Fig. 12.
Remark 5.2
In what follows, \(V_2\) shall be particularly useful. Observe that \(V_2=F^{-3}({W}).\)
Also, let \(V_{2}^{*}=(-\infty ,-\tfrac{1}{\lambda }]\cup V_2 \cup [\tfrac{1}{\lambda ^2},\infty )\).
Definition 5.2
For \(n\geqslant 3\), let \({{\widetilde{W}}_{n}}\) denote the interior of the closure of the union of the copies P of \({\mathbb {H}}_\pm \) under \(F^{2^n-6}\) with  . Notice that for each \(n\geqslant 3\) there are exactly four such copies; denote by \({{\widetilde{P}}_{n,K}}\) the copy in quadrant K (if the quadrant is omitted, we mean the appropriate copy).
. Notice that for each \(n\geqslant 3\) there are exactly four such copies; denote by \({{\widetilde{P}}_{n,K}}\) the copy in quadrant K (if the quadrant is omitted, we mean the appropriate copy).
Remark 5.3
The following observations are immediate from the definitions. See Fig. 11.
- (i)
for all \(n\geqslant 3\), \(F^{2^n-6}(\partial {{\widetilde{W}}_{n}}) = {{\mathbb {R}}}\),
- (ii)
for all \(n\geqslant 3\), \({{\widetilde{W}}_{n+1}} \,\subset \, \lambda {{\widetilde{W}}_{n}}\),
- (iii)
for all \(n\geqslant 4\), \( W^{(n)} \,\subset \, {{\widetilde{W}}_{n}} \,\subset \, W^{(n-1)}\),
- (iv)
\({{\widetilde{W}}_{3}}=W^{(1)}\),
- (v)
For \(n\geqslant k\geqslant 3\), \(F^{2^n-2^k}({{\widetilde{P}}_{n}})={{\widetilde{P}}_{k}}\).
For a point \(z_0 \not \in J_F\), the next lemma gives us explicit criteria for determining a disk of points around \(z_0\) whose orbits behave comparably. See Fig. 12.
Lemma 5.3
Let D be a disk in the complement of \(V_{2}^{*}\) and let \(D_0\) be a connected component of \(F^{-k}(D)\) for any \(k\geqslant 0\). Then for \(n\geqslant 3\), either \(D_0 \cap W^{(n)}=\varnothing \) or \(D_0 \subset {{\widetilde{W}}_{n}}\).
Illustration of Lemma 5.3: on the left is shown \(V_2\) (blue curve) and a large disk D which lies outside of \(V_{2}^{*}\). Also shown are \(W^{(2)}\), \(W^{(3)}\), \(W^{(4)}\) and \(W^{(5)}\) (in green), as well as \({{\widetilde{W}}_{4}}\) and \({{\widetilde{W}}_{5}}\) (shaded blue) and \(J_F\). Several preimages of D are drawn in light red, with the corresponding preimage of the center of D indicated by a red dot. On the right is a blow-up of the left figure. While the preimage labeled \(D_{16}\) partially intersects \(W^{(3)}\), it lies completely inside \({{\widetilde{W}}_{3}}=W^{(1)}\) (dotted line) (color figure online)
Proof
If we assume the lemma does not hold, \(D_0\) must contain points from \(\partial W^{(n)}\) and \(\partial {{\widetilde{W}}_{n}}\).
First, since \(V_2\) is a neighborhood of \(J_F\), the definition of D means it can contain no points of \(J_F\). Using \(D_j\) to denote \(F^j(D_0)\), we have \(D_j\cap J_F=\varnothing \) for \(0\leqslant j\leqslant k\).
Observe also that \(W^{(n)}\subset F^{-(2^n-4)}(V_2)\), and hence \(k\geqslant 2^n-3\). Applying Remark 5.3(i) gives
so we must have \(D_k \cap {{\mathbb {R}}}\ne \varnothing \).
Further, if for some \(j<k\) we have \(D_j\) intersecting both \({{\mathbb {R}}}\) and \(\mathrm {i}{{\mathbb {R}}}\), it can be shown by induction that \(D=D_k\) must contain both positive and negative real values, which is impossible.
If \(D_j\cap \mathrm {i}{{\mathbb {R}}}=\varnothing \) for all \(j<k\), then since \(D_j\) can contain no points of \(J_F\), we must have
This contradicts our initial hypothesis that \(D_0\) intersects \(W^{(n)}\); so for some \(j<k\), we must have \(D_j\cap \mathrm {i}{{\mathbb {R}}}\ne \varnothing \). Let s be the maximal index for which \(D_s\) intersects the imaginary axis, and let x be a point in \(D_s\cap \mathrm {i}{{\mathbb {R}}}\). Without loss of generality, we may take \({\text {Im}}(x)>0\).
As noted earlier, \(D_s\) cannot intersect both \({{\mathbb {R}}}\) and \(i{{\mathbb {R}}}\). Hence \(D_s\cap {{\mathbb {R}}}=\varnothing \). Because \(D_s\) contains a boundary point of \(F^{s}({{\widetilde{W}}_{n}})\), by Remark 5.3(i) we must have \(s\leqslant 2^n-7\). Combining this with the fact that \(k\geqslant 2^n-3\) yields \(s\leqslant k-4\).
Let \(V_{2,{{\mathbb {R}}}}\) be the union of closures of tiles from \({\mathcal {P}}^{(2)}\) which intersect \(J_F\cap {{\mathbb {R}}}\). Lemma 3.3 implies that \(V_{2,{{\mathbb {R}}}}\cap \mathrm {i}{{\mathbb {R}}}=[-\lambda y_0,\lambda y_0]\subset J_F\). Thus \(D_s\) intersects \(\mathrm {i}{{\mathbb {R}}}\) outside \(V_{2,{{\mathbb {R}}}}\), so \(\pm \lambda y_0 \not \in D_s\). Since \(D_s\) intersects \(F^{s}(W^{(n)})\) and hence also intersects \(V_{2,{{\mathbb {R}}}}\), we conclude that \(D_s\) contains a boundary point of \(V_{2,{{\mathbb {R}}}}\).
But since \(k-s\geqslant 4\) and \(F^4(\partial V_{2,{{\mathbb {R}}}}\cup [\lambda y_0,x])\subset {{\mathbb {R}}}\), it follows that \(D_k\cap {{\mathbb {R}}}\) consists of at least two connected components; this is impossible. The contradiction finishes the proof. \(\square \)
Use \({{\mathbb {D}}}_{R}(z)\) to denote the open disk of radius R centered at z, and recall the definition of \(H^{(1)}\) from Definition 3.4. From Definition 5.1, recall that \({\tilde{X}}_n\) is the set of points of \(W^{(1)}\) that eventually land in \(W^{(n)}\) under iterates of F, \(Y_n\) are points of \(W^{(n)}\) which never return to \(W^{(n)}\) under non-trivial iterates of F and \(\Sigma _n\) is the set of points in \(W^{(n)}\) that eventually land in \(Y_n\) under iterates of \(F_{n-1}\).
Applying the Koebe One-Quarter Theorem together with Lemma 5.3 yields the following two useful corollaries, which enable us to estimate the size of disks which lie outside \({\tilde{X}}_n\) or inside \(\Sigma _n\).
Corollary 5.3
Fix \(n\geqslant 3\). Let \(z\in H^{(1)}{\smallsetminus } J_F\) and let k be such that \(F^k(z)\notin V_{2}^{*}\). Suppose also that \(F^j(z)\notin {{\widetilde{W}}_{n}}\) for \(0\leqslant j\leqslant k\). Let \(D_0\) be the connected component of \(F^{-k}\bigl ({{\mathbb {D}}}_{R}(F^k(z))\bigr )\) containing z, with \(R={{\,\mathrm{dist}\,}}(F^k(z), V_{2}^{*})\). Then \(D_0\cap {\tilde{X}}_n=\varnothing \). In particular,
Corollary 5.4
Fix \(n\geqslant 3\). Let \(z\in W^{(n)}\) be such that \(w=F_{n-1}^s(z)\in Y_n\) for some s; let \(\ell \) be such that \(F^\ell (w)\notin V_{2}^{*}\). Suppose also that \(F^j(w)\notin {{\widetilde{W}}_{n}}\) for all \(0\leqslant j\leqslant \ell \).
Set \(R={{\,\mathrm{dist}\,}}(F^\ell (w), V_{2}^{*})\) and let \(D_0\) be the connected component of \(F_{n-1}^{-s}\Bigl (F^{-\ell }\left( {{\mathbb {D}}}_{R}(F^\ell (w))\right) \Bigr )\) that contains z. Then \(D_0\subset \Sigma _n\). In particular,
With Corollary 5.3 and Corollary 5.4 in hand, we have explicit, computable criteria for verifying that the hypotheses of Corollary 5.1 hold, showing that the Hausdorff dimension of \(J_F\) is less than 2.
Specifically, for some n we need to establish upper bounds on the quantities \({\tilde{\eta }}_n\) and \(M_n\). We now give algorithms to do this. These are presented assuming that F(z), \(F'(z)\), \({{\widetilde{W}}_{n}}\), \(P_{0}\), etc. can be calculated exactly. In Sect. 6, we discuss how to account for finite precision.
To bound \({\tilde{\eta }}_n\), we need an upper bound on \({{\,\mathrm{area}\,}}({\tilde{X}}_n)\), since, \({\tilde{\eta }}_n = {{\,\mathrm{area}\,}}({\tilde{X}}_n)/{{\,\mathrm{area}\,}}(W^{(1)})\) by definition. Exploiting the symmetry with respect to the axes allows us to work in first quadrant only.
Algorithm 5.1
Fix \(n\geqslant 3\) and r small. To compute an upper bound for \({{\,\mathrm{area}\,}}({\tilde{X}}_n)\), we find a collection \({{\mathcal {D}}}_{n,r}\) of disks with radius r which cover \({\tilde{X}}_n\) in the first quadrant. First, select a grid of points z so that \(\bigcup _z {{\mathbb {D}}}_{r}(z)\) covers \(P_{0}^{(1)}\). Also, choose some upper bound K on the maximum number of iterations. For each point z in the grid run the following routine.
- (i)
For \(0< j<K\), calculate \(F^j(z)\) and \(DF^j(z)\).
- (ii)
If \(F^j(z)\in {{\widetilde{W}}_{n}}\) for some j, or if \(F^j(z)\in H^{(1)}\) for all \(j<K\), add \({{\mathbb {D}}}_{r}(z)\) to \({{\mathcal {D}}}_{n,r}\), and exit the routine.
- (iii)
Let \(\ell \) be such that \(F^\ell (z)\not \in H^{(1)}\). If \({{\,\mathrm{dist}\,}}(F^\ell (z),V_{2}^{*})>4r\,|DF^\ell (z)|\), then by Corollary 5.3, the entire disk \({{\mathbb {D}}}_{r}(z)\) does not intersect \({\tilde{X}}_n\). Otherwise, add \({{\mathbb {D}}}_{r}(z)\) to \({{\mathcal {D}}}_{n,r}\).
Remark 5.4
The cover \({{\mathcal {D}}}_{n,r}\) can be calculated from \({{\mathcal {D}}}_{n,s}\) for \(r<s\) by replacing the grid covering \(P_{0}^{(1)}\) by one covering \({{\mathcal {D}}}_{n,s}\).
In order to bound \(M_n = M(\Sigma _n)\) from above, we need to construct a lower bound on \(\Sigma _n\) (i.e. a subset of \(\Sigma _n\)). As before, we can exploit symmetry and work only in the first quadrant.
Algorithm 5.2
Fix \(n\geqslant 3\) and r small. To get a lower bound for \(\Sigma _n\), we find a collection \({{\mathcal {E}}}_{n,r}\) of disks \({{\mathbb {D}}}_{r}(z) \subset \lambda ^{-n}\Sigma _n\). As in Algorithm 5.1, select a grid of points z so that \(P_{0} \subset \bigcup _z {{\mathbb {D}}}_{r}(z)\), and fix a positive integer K. For each point z from the grid run the following routine.
- (i)
For \(0< j<K\) calculate \(F^j(z)\) and \(DF^j(z)\).
- (ii)
If \(F^j(z)\in H^{(1)}\) for all \(j<K\), discard z and exit the routine.
- (iii)
Let \(0\leqslant k<K\) be the smallest number such that \(F^k(z)\not \in H^{(1)}\). Set \(w=\lambda ^nF^k(z).\)
- (iv)
For \(0< j< K\), compute \(F^{j}(w)\) and \(DF^{j}(w)\).
- (v)
If \(F^j(w)\in {{\widetilde{W}}_{n}}\) for some j, or if \(F^j(w)\in H^{(1)}\) for all j, discard z and exit the routine.
- (vi)
Let \(\ell \) be such that \(F^\ell (w)\not \in H^{(1)}\). If \({{\,\mathrm{dist}\,}}(F^\ell (w),V_{2}^{*})>4r\,|DF^\ell (w)|\cdot |DF^k(z)|\), then by Corollary 5.4, the entire disk \({{\mathbb {D}}}_{r\lambda ^n}(z)\) is contained in \(\Sigma _n\); add the disk to \({{\mathcal {E}}}_{n,r}\).
Remark 5.5
In step (i) of Algorithm 5.1 and steps (i) and (iv) of Algorithm 5.2, we need not (and should not) compute \(F^j(z)\) for all \(j<K\). Instead, we restrict our attention to iterates \(z_k=F^{j_k}(z)\) defined inductively as follows. Let \(j_0=0\). Assuming \(z_k\ne 0\), there is a maximal number \(m_k\) such that \(z_k\in W^{(m_k)}\); let \(i_k=\max \{0,m_k-1\}\). Set \(j_{k+1}=j_k+2^{i_k}\), and calculate \(z_{k+1}=F^{2^{i_k}}(z_k)\) and \(|DF^{j_{k+1}}(z)|=|DF^{j_k}(z)|\cdot |DF^{2^{i_k}}(z_k)|\) via (2.2):
Observe that \(F^{2^{i_k}}\) is the first return map from \(W^{(m_k)}\) to \(W^{(m_k-1)}\) (see Remark 3.2(iii)). Given \(n\geqslant 3\) we have \({{\widetilde{W}}_{n}}\subset W^{(n-2)}\). Hence, for \(z_k\notin {{\widetilde{W}}_{n}}\), since \(m_k\leqslant n-1\), it is not possible to have \(F^l(z_k)\in {{\widetilde{W}}_{n}}\) for any \(0<l<2^{i_k}\). Also, it can be shown that if \(z_k\in H^{(1)}\), we must have \(F^l(z_k)\in H^{(1)}\) for \(0<l<2^{i_k}\).
Also, we should consider all \(k<K\) rather than \(j<K\), bounding the number of evaluations of \(F^{2^{i_k}}\) rather than the length of the orbit of z.
Using these algorithms, we complete the proof of our main theorem, computing that
We obtain \({\tilde{\eta }}_6 M_6{{\,\mathrm{area}\,}}(P_{0})< 0.846<1\), so \(J_F\) has Hausdorff dimension less than 2.
6 Computational considerations
In this section, we discuss how we can be certain that the computation of the bounds on \({\tilde{\eta }}_{6}\), \(M(\Sigma _6)\), and \(|P_{0}|\) (which give us our main theorem) are sufficiently accurate, even though the bounds are necessarily computed with finite precision. We have two potential sources of error: we can not know the map F exactly (and consequently we must also approximate \(\lambda \) and the domains \(W^{(n)}\), \({H}\), etc.), and there will be some errors introduced by the approximation of exact quantities z by those representable on a computer.
The calculations for this paper were done primarily in Python with double-precision floating-point arithmetic satisfying the IEEE 754-2008 standard [17]. In this context, only numbers of the form \(\alpha \times 2^e\) are representable, where \(\alpha \) is a 53-bit signed (binary) integer, and the exponent e satisfies \(-1021 \leqslant e \leqslant 1024\). In particular, the only real numbers which can be represented exactly are certain dyadic rationals within a (large) range. Any real number x in the representable range can be approximated by a floating-point number \(\check{x}\) so that \(|x-\check{x}|< {\mathfrak {u}}|x|\). This number \({\mathfrak {u}}\) is called the unit roundoff; for IEEE double-precision
For more details, the reader is referred to [15] or [13], for example.
While the standard guarantees that the result of a single arithmetic operation (\(+\), −, \(*\), /) carried out on two (real) floating-point numbers will be correctly rounded with a relative error of at most \({\mathfrak {u}}\), we need to ensure that these small errors do not accumulate such that we lose control of the calculation. We primarily need to work with double-precision complex numbers; in [3], it is shown that the relative error for complex arithmetic is bounded by \(\sqrt{5}\,{\mathfrak {u}}\).
Throughout this section, we shall use the notation \(\check{x}\) to denote the approximation of the exact quantity x by one that is representable as a floating point number.
6.1 Approximating the map F and the value of \(\lambda \)
In the 1980s, Lanford [19] calculated a high-precision approximation of F as an even polynomial of degree 80. Such approximations can be computed to precision \(10^{-n}\) in a number of arithmetic operations polynomial in n [14], although the approximation given by Lanford is sufficient for our purposes.
Lanford gives strict error bounds on his approximation (which he calls \(g_n^{(0)}\) but we refer to as \(\check{F}\) for notational consistency). Specifically, we have the following.
Proposition 6.1
Let \(\check{F}\) be the degree 80 polynomial approximation of F from [19]. The following upper bounds on the error apply.
\(|F(z)-\check{F}(z)|\) | \(|F'(z)-\check{F'}(z)|\) | \(|F''(z)-\check{F''}(z)|\) | |||
|---|---|---|---|---|---|
\(1.5 \times 10^{-23}\) | for \(|z|<1.224\) | \(1.5 \times 10^{-22}\) | for \(|z|<1.12\) | \(1.5 \times 10^{-21}\) | for \(|z|<1.02\) |
\(5.5 \times 10^{-13}\) | for \(|z|<1.414\) | \(5.5 \times 10^{-12}\) | for \(|z|<1.31\) | \(5.5 \times 10^{-11}\) | for \(|z|<1.21\) |
\(5.0 \times 10^{-7}\) | for \(|z|<2.449\) | \(5.0 \times 10^{-6}\) | for \(|z|<2.34\) | \(5.0 \times 10^{-5}\) | for \(|z|<2.24\) |
\(1.7 \times 10^{-2}\) | for \(|z|<2.828\) | \(1.7 \times 10^{-1}\) | for \(|z|<2.72\) | 1.7 | for \(|z|<2.62\) |
Proof
The bounds for \(|F(z)-\check{F}(z)|\) are taken from [19]. Those for the first and second derivatives follow Lanford’s bounds via an application of Cauchy’s derivative inequalites. \(\square \)
Corollary 6.1
All of the digits in the approximations
are correct (the next two digits of \(\lambda \) are between 65 and 96).
If \(\check{F}\) is evaluated at some \(\check{z}\) using Horner’s method, we have the following bound on the accumulated arithmetic error in evaluating the polynomial:
where \(a_i\) are the coefficients of \(\check{F}\) (see [15, ch. 5] which presents the argument from [25]); a similar bound applies to the derivative. Putting this observation together with Proposition 6.1 gives us the following.
Corollary 6.2
If \(\check{z}\) is a double-precision approximation of z and \(\check{F}\) is Lanford’s polynomial approximation of F evaluated in double-precision, then we have the following upper bounds on the error.
\(|F(z)-\check{F}(\check{z})|\) | \(|F'(z)-\check{F'}(\check{z})|\) | ||
|---|---|---|---|
\(5.2884 \times 10^{-14}\) | for \(|z|<1\) | \(7.2771 \times 10^{-14}\) | for \(|z|<1\) |
\(6.4430 \times 10^{-13}\) | for \(|z|<1.414\) | \(5.5875 \times 10^{-12}\) | for \(|z|<1.31\) |
\(5.0001 \times 10^{-7}\) | for \(|z|<2.449\) | \(5.0001 \times 10^{-5}\) | for \(|z|<2.34\) |
\(1.7001 \times 10^{-2}\) | for \(|z|<2.828\) | \(1.7001 \times 10^{-1}\) | for \(|z|<2.72\) |
Observe that for \(|z|<1\), the error in using \(\check{F}(\check{z})\) is dominated by the accumulated round-offs (since F is approximated by \(\check{F}\) to better than machine precision for \(|z|<\sqrt{6}\)); for \(|z|>\sqrt{2}\), the error is dominated by the approximation of F by \(\check{F}\).
Remark 6.1
As noted in Remark 5.5, we will often want to evaluate \(F^{2^n}\!(z)\) as \((-\lambda )^n F(z/\lambda ^n)\). Since Corollary 6.1 gives \(\lambda \) and \(1/\lambda \) with greater precision than can be represented as a floating-point number, we can calculate floating-point approximations of \(\lambda ^n\) and \(\lambda ^{-n}\) with a relative error of no more than \(\frac{n{\mathfrak {u}}}{1-n{\mathfrak {u}}}<1.0102n{\mathfrak {u}}< 1.13n\times 10^{-16}\).
Remark 6.2
By the Koebe Distortion Theorem, if \(g:{{\mathbb {D}}}_{|z|}(0) \rightarrow {{\mathbb {C}}}\) is univalent and \(|\epsilon |<|z|\), then
This observation will be useful in calculating accumulated error bounds for compositions.
6.2 Approximating the sets W, \(H^{(1)}\), \(V_{2}\), and \({\widetilde{W}}_{6}\)
Definition 6.1
For complex numbers a and b, let

that is, the open rectangle in \({{\mathbb {C}}}\) with a on its lower left corner and b on its upper right.
Also, for a set A in the first quadrant, let \({{\,\mathrm{ICU}\,}}(A)\) be the interior of the closure of the union of the four symmetric copies of A, that is

where \(A^*\) is the set of complex conjugates of points of A, and \(-A\) is the negation of all points in A.
Definition 6.2
Define the following sets of floating-point numbers.
Then let
Let \(\check{V}_\mathrm {out}\) be the filled polygon with vertices at 0, 4.075i, \({9.33+.85i}\), and 9.33; set
Finally, set (Fig. 13)
As in Definition 6.2, the sets \(\check{H}_\mathrm {out}\) (in red), \(\check{H}_\mathrm {in}\) (green), and \(\check{V}_\mathrm {out}\) (blue) are shown in the first quadrant, along with \({H}\) (shaded gray) and \(V_2\) scaled by a factor of \(\lambda ^2\) (also shaded). On the right are \({{\widetilde{P}}_{6}}\) (shaded blue), \(P_{0}^{(6)}\) (outlined in green) and \(\check{\widetilde{P}}_6\) (outlined in red) (color figure online)
Remark 6.3
As should be apparent from the figures, it is possible to obtain much better approximations of the relevant sets than given in Definition 6.2. To do so, one can exploit the fact that the set \({P_{0,\mathrm {I}}}\) is fixed under the map \(F_{\lambda }(z)=\overline{F(\lambda z)}\) (see [4]). \(F_{\lambda }\) has an attracting fixed point on \(\partial {P_{0,\mathrm {I}}}\) at \(x_0\), and a repelling fixed point at \(x_1\approx 1.831+2.683i\). This point \(x_1\) is the unique point in \(\partial {P_{0,\mathrm {I}}}\cap \partial {\widehat{W}}\). Taking repeated preimages of the segment \([0,\lambda y_0]\) by the map \(\check{F}_\lambda \) yields a good approximation of \(P_{0,\mathrm {I}}\); other pieces of \({{\mathcal {P}}}\) can then be approximated via preimages of \(P_{0}\). However, the polygonal sets of Definition 6.2 are much easier to obtain sharp error bounds on, and are sufficent for our purposes.
Lemma 6.1
One has \(\check{W}_\mathrm {in}\subset {W}\subset \check{W}_\mathrm {out}\), \(\check{H}^{(1)}_\mathrm {in}\subset H^{(1)} \subset \check{H}^{(1)}_\mathrm {out}\), \(V_2 \subset \check{V}_2\), and \({{\widetilde{W}}_{6}} \subset \check{\widetilde{W}}_6\).
Proof
To see that \(\check{W}_\mathrm {in}\subset {W}\), compute the approximation of \(F(\partial \check{W}_\mathrm {in})\). For \(z\in \partial \check{W}_\mathrm {in}\) with \(|z|<\sqrt{6}\) we use \(\check{F}(\check{z})\). For \(|z|\geqslant \sqrt{6}\), we instead approximate F(z) by \((-1/\lambda )\check{F}^2(\lambda \check{z})\) (since we don’t have a bound on \(|F(z)-\check{F}(\check{z})|\) for \(|z|\geqslant \sqrt{8}\)). Observe that all points of the approximation of \(F(\partial \check{W}_\mathrm {in})\) avoid the slits \((-\infty , -1/\lambda ]\) and \([1/\lambda ^2,\infty )\) by at least \(5.4\times 10^{-4}\) for \(|\check{z}|<\sqrt{6}\) and more than 2.8 for \(|\check{z}|\geqslant \sqrt{6}\), significantly more than the error bounds given in Corollary 6.2. Since \(F({W}) = {{\mathbb {C}}}{\smallsetminus }\bigl ( (-\infty ,-1/\lambda ]\cup [1/\lambda ^2,\infty )\bigr )\), we have \(\check{W}_\mathrm {in}\subset {W}\).
A similar calculation shows that \(\check{H}^{(1)}_\mathrm {in} \subset H^{(1)}\): \(\check{F}\big (\check{Q}^{(1)}_\mathrm {in}\big )\subset \check{W}_\mathrm {in}\) with a margin of more than .004, which by Corollary 6.2 is much greater than the necessary space since \(|z|<1.75\) for \(z\in \check{Q}^{(1)}_\mathrm {in}\). Since \(\check{H}_\mathrm {in}=\check{P}_\mathrm {in}\cup \check{Q}_\mathrm {in}\), we know \(F(\check{H}^{(1)}_\mathrm {in})\subset {W}\) and thus \(\check{H}^{(1)}_\mathrm {in}\subset H^{(1)}\).
To see that \(V_2 \subset \check{V}_2\), recall from Remark 5.2 that \(V_2=F^{-3}({W}).\) We need only check that \(\check{F}^3(\partial \check{V}_2)\) stays away from \(\check{W}_\mathrm {out}\) with a sufficient margin: the distance between the boundaries of these two sets is greater than \(1.5\times 10^{-3}\) (with the closest point of \(\check{F}^3(\partial \check{V}_2)\) being the image of \(9.33\lambda ^2\)).
We calculate that \(|\check{F}^3(\check{z}) - F^3(z)| < 4\times 10^{-5}\) on \(\check{V}_2\) by observing that for \(\check{z}\in \check{V}_2\), we have \(|\check{z}|<1.50\), \(|\check{F}(\check{z})| <1.71\) and \(|\check{F}^2(\check{z})|<2.35\), with \(|\check{F}'(\check{z})| < 2.81\), \(|\check{F}'(\check{F}(\check{z}))| < 3.88\) and \(|\check{F}'(\check{F}^2(\check{z}))|<19.27\). Applying the Koebe Distortion Theorem (see Remark 6.2) twice gives an upper bound on the error of \(3.8\times 10^{-5}\). Once we establish that \({W}\subset \check{W}_\mathrm {out}\), the desired result follows.
Since \(\check{W}_\mathrm {out}\) contains points outside the domain of definition of F, we cannot verify directly that \({W}\subset \check{W}_\mathrm {out}\). Instead, to do this we use the properties of the map \(F_\lambda (z)=\overline{F(\lambda z)}\) mentioned in Remark 6.3. Notice that \(F_\lambda (z)\) can be approximated on \(\check{W}_\mathrm {out}\) with an error less than \(5.1\times 10^{-7}\) since \(|\lambda z|<1.502\) on \(\check{W}_\mathrm {out}\) (see Corollary 6.2).
Approximating \(F_\lambda (z)\) by \(\check{F}_\lambda (\check{z})=\overline{\check{F}(\lambda \check{z})}\) we observe that \(\check{F}_\lambda (\partial \check{P}_\mathrm {out})\) almost avoids \(\check{P}_\mathrm {out}\), intersecting it in two curves lying inside the triangles \(T_1 = \triangle (2.08i,\, 2.81i,\, .31+2.81i)\) and \(T_2= \triangle (2.495,\, 2.05+2.81i,\, 2.495+2.81i)\). Although the triangles \(T_1\) and \(T_2\) lie inside \(\check{P}_\mathrm {out}\), we have \({{\,\mathrm{dist}\,}}(\check{F}_\lambda ^2(T_1),\,\check{P}_\mathrm {out}) > .01\) and \({{\,\mathrm{dist}\,}}(\check{F}_\lambda ^2(T_2),\,\check{P}_\mathrm {out}) > .22\). A straightforward computation shows that for the relevant points we have \(|F^2_\lambda (z) - \check{F}_\lambda ^2(\check{z})| < 1.7\times 10^{-6}\), so \(F^2(T_1)\) and \(F^2(T_2)\) lie outside of \(\check{P}_\mathrm {out}\). This implies that \(P_{0,\mathrm {I}}\subset \check{P}_\mathrm {out}\) (and so \({W}\subset \check{W}_\mathrm {out}\) and \(V_2\subset \check{V}_2\)). See Fig. 14.
Showing that \({W}\subset \check{W}_\mathrm {out}\) and \(\check{H}^{(1)}_\mathrm {in}\subset H^{(1)}\). \(F_\lambda (\check{P}_\mathrm {out}\cup \check{Q}_\mathrm {out})\) is shaded in blue, with \(\check{P}_\mathrm {out}\) and \(\check{Q}_\mathrm {out}\) outlined in red. The image on the right is a zoom of the one on the left (color figure online)
Indeed, assume that \(P_{0,\mathrm {I}}\not \subset \check{P}_\mathrm {out}\), and let \(\Gamma \) be the closure of the part of \(\partial \check{P}_\mathrm {out}\) in the first quadrant (\(\Gamma =[2.81i,\ 2.495+2.81i]\cup [2.495+2.81i,\ 2.495]\)). Then \(\partial P_{0,\mathrm {I}}\) must intersect \(\Gamma \). Recall that \(\partial P_{0,\mathrm {I}}\) is \(F_\lambda \)-invariant with two fixed points \(x_0\) (attracting) and \(x_1\) (repelling); the two components of  are interchanged by \(F_\lambda \). Parameterize the two components of
are interchanged by \(F_\lambda \). Parameterize the two components of  so that the parameterizations are the two inverse branches of a function \(p:\partial P_{0,\mathrm {I}}{\smallsetminus }\{x_1\}\rightarrow [0,\infty )\) satisfyingFootnote 2\(p(F_\lambda (z))=\tfrac{1}{2}p(z)\) for every z and \(p(x_0)=0\). Consider the closed set \(\partial P_{0,\mathrm {I}}\cap \Gamma \); let \(z_1\) be the point where \(p(z_1)\) attains the minimum on this set. As a consequence of the previous argument, either \(F_\lambda (z_1)\) or \(F_\lambda ^3(z_1)\) lies outside \(\check{P}_\mathrm {out}\) (see Fig. 14). Therefore, there exists a point \(z_2\in P_{0,\mathrm {I}}\cap \Gamma \) with \(p(z_2)\leqslant \tfrac{1}{2}p(z_1)\). This contradicts the definition of \(z_1\), and hence \(P_{0,\mathrm {I}}\subset \check{P}_\mathrm {out}\).
so that the parameterizations are the two inverse branches of a function \(p:\partial P_{0,\mathrm {I}}{\smallsetminus }\{x_1\}\rightarrow [0,\infty )\) satisfyingFootnote 2\(p(F_\lambda (z))=\tfrac{1}{2}p(z)\) for every z and \(p(x_0)=0\). Consider the closed set \(\partial P_{0,\mathrm {I}}\cap \Gamma \); let \(z_1\) be the point where \(p(z_1)\) attains the minimum on this set. As a consequence of the previous argument, either \(F_\lambda (z_1)\) or \(F_\lambda ^3(z_1)\) lies outside \(\check{P}_\mathrm {out}\) (see Fig. 14). Therefore, there exists a point \(z_2\in P_{0,\mathrm {I}}\cap \Gamma \) with \(p(z_2)\leqslant \tfrac{1}{2}p(z_1)\). This contradicts the definition of \(z_1\), and hence \(P_{0,\mathrm {I}}\subset \check{P}_\mathrm {out}\).
To show that \(H^{(1)} \subset \check{H}^{(1)}_\mathrm {out}\) it is sufficient to confirm that \(F_\lambda (\partial \check{H}_\mathrm {out})\cap ({W}\cap {\mathbb {H}}_+)=\varnothing \). Observe that \(F_\lambda (\partial \check{H}_\mathrm {out})\cap (\check{W}_\mathrm {out}\cap {\mathbb {H}}_+)\) consists of two curves, one of which belongs to \(T_2\) and so is outside of \({W}\). The other curve \(\gamma \) joins the leftmost boundary of \(\check{W}_\mathrm {out}\) and the real axis. See Fig. 14. This curve \(\gamma \) must lie outside of \({W}\), since \({\text {Re}}\check{F}_\lambda (\check{z})<- 0.024\) for all \(z\in \gamma \) and \({\text {Re}}(z)>0\) for \(z\in F_\lambda ({W})\). The error in computing \(\check{F}_\lambda ^2\) on all of \(\check{H}_\mathrm {out}\) is less than \(2.3\times 10^{-6}\), giving a sufficient margin of error.
In order to prove that \({{\widetilde{W}}_{6}} \subset \check{\widetilde{W}}_6\), recall from Remark 5.3 (v) that \(F^{2^n - 2^k}({{\widetilde{P}}_{n}}) = {{\widetilde{P}}_{k}}\) for all \(n\geqslant k\geqslant 3\). Hence \(F^{54}({{\widetilde{P}}_{6}}) = F^{6}({{\widetilde{P}}_{4}})=P_{0}^{(2)}\). Observe that the curve \(\check{F}^{54}(\partial \check{\widetilde{P}}_6)\) avoids \(-\check{P}^{(2)}_\mathrm {out}\) except for a portion contained in the triangle \(T_3=\triangle (-\lambda x_0,\,-2.5\lambda ^2 -.1i,\,-2.5\lambda ^2)\). See Fig. 15. The image of \(\check{\widetilde{P}}_6 \cap ({{\mathbb {R}}}\cup \mathrm {i}{{\mathbb {R}}})\) is contained within the segment \((-0.30996, -0.30970)\); the remainder of the image exits through \({\mathbb {H}}_+\) before intersecting the real axis at two points, one inside \(T_3\) (more than \(3.2\times 10^{-4}\) from the vertex of \(T_3\)) and the other beyond \(+0.0085\); the remaining part of the image curve gets no closer to \(-\check{P}^{(2)}_\mathrm {out}\) than this. To see that \(T_3\) lies outside \(P_{0,\mathrm {III}}^{(2)}\), observe that \(F^2(P_{0,\mathrm {III}}^{(2)})=P_{0,\mathrm {II}}^{(1)}\), but all points of \(F^2(T_3)\) have positive real parts. We obtain that \({{\,\mathrm{dist}\,}}(\check{F}^{54}(\partial \check{\widetilde{P}}_6)\cap {\mathbb {H}}_-,\ P_{0,\mathrm {III}}^{(2)})>3.2\times 10^{-4}\).
To verify that the above calculations are sufficiently accurate we write \(\check{F}^{54} = \check{F}^{2}\circ \check{F}^{4}\circ \check{F}^{16}\circ \check{F}^{32}\) and (as noted in Remark 6.1) compute \(\check{F}^{2^n}(\check{z})\) as \((-\lambda )^n \check{F}(\check{z}/\lambda ^n)\); then we have \(|F^{54}(z) - \check{F}^{54}(\check{z})|\) no greater than \(1.3\times 10^{-10}\) for all \(z\in \check{\widetilde{W}}_6\), establishing that \({{\widetilde{W}}_{6}}\subset \check{\widetilde{W}}_6\) and completing the proof. \(\square \)
Remark 6.4
To approximate \({{\widetilde{W}}_{n}}\) for \(n>6\), the set \(\check{\widetilde{W}}_6^{(n-6)}\) may be used, since by Remark 5.3(ii) and Lemma 6.1 we have \({{\widetilde{W}}_{n}} \subset \lambda ^{n-6}\,\check{\widetilde{W}}_6\). One can use \(\check{\widetilde{W}}_4=\big \lfloor {-.09-.15i},\,{.09+.15i}\,\big \rceil \) and \(\check{\widetilde{W}}_5=(\check{P}_\mathrm {out}\cup \big \lfloor {1.2+1.79i},\,{3.0+3.65i}\,\big \rceil )^{(5)}\); \({{\widetilde{W}}_{9}}\subset \check{P}^{(9)}_\mathrm {out}\). However, we do not need to use these.
Using Lemma 6.1, we can calculate better approximations of H and W from below and from above. For instance, to find a more accurate approximation of \(P_{0,\mathrm {I}}\) from above we use the following.
Algorithm 6.1
Fix \(m\geqslant 1\) and \(t>0\) small. To compute an upper bound for \(P_{0,\mathrm {I}}\), we find a collection \({{\mathcal {S}}}_{m,t}\) of disks with radius t which cover \(P_{0,\mathrm {I}}\). First, select a grid of points z so that \(\bigcup _z {{\mathbb {D}}}_{t}(z)\) covers \(\check{P}_\mathrm {out}\). Include in \({{\mathcal {S}}}_{m,t}\) all the disks \({{\mathbb {D}}}_{t}(z)\) which intersect \(\check{P}_\mathrm {in}\). For each remaining point z in the grid, set \(w=\lambda ^n z\), \(q=\lambda ^n(0.1+0.1i)\), \(t_0=\lambda ^m t\) and run the following routine.
- (i)
For \(0< j<2^m\), calculate \(\check{w}_j=\check{F}^j(w)\). Using the Koebe Theorem and Corollary 6.2, find \(t_j\) such that \(\check{F}^j({{\mathbb {D}}}_{t_0}(w))\subset {{\mathbb {D}}}_{t_j}(\check{w}_j)\).
- (ii)
If \({{\mathbb {D}}}_{t_j}(\check{w}_j)\) contains zero, add \({{\mathbb {D}}}_{t}(z)\) to \({{\mathcal {S}}}_{m,t}\) and exit the routine.
- (iii)
If \({{\mathbb {D}}}_{t_j}(\check{w}_j)\) does not intersect \(\check{W}_\mathrm {out}\) or the quadrant to which \(\check{F}^j(q)\) belongs, discard z and exit the routine.
- (iv)
If for all \(0<j<2^m\) neither of the conditions (ii) or (iii) are satisfied, then add \({{\mathbb {D}}}_{t}(z)\) to \({{\mathcal {S}}}_{m,t}\).
6.3 Implementing Algorithms 5.1 and 5.2
We only need to make a few straightforward substitutions in order to implement the algorithms for approximating \({\tilde{X}}_6\) and \(\Sigma _6\).
We make the obvious substitution of \(F^j\) by \(\check{F}^j\) and \(DF^j\) by \(D\check{F}^j\). When calculating \(\check{F}^j\), we instead compute compositions of \(\check{F}^{2^k}\) as described in Remark 5.5, replacing the set \(W^{(n)}\) by \(\check{W}^{(n)}_\mathrm {in}\). Whenever practical, we scale \(\check{z}\) so that \(z/\lambda ^m\) lies in \(\check{W}^{(1)}_\mathrm {in}\), ensuring that we have \(|\check{z}/\lambda ^m|<1.17\). This implies by Corollary 6.2 that \(\check{F}\) and \(\check{F}'\) agree with F and \(F'\) to within \(6.5\times 10^{-13}\) and \(5.6\times 10^{-12}\), respectively. We take \(K=20\).
Further, we replace \(P_{0,\mathrm {I}}^{(1)}\) by \(\check{P}^{(1)}_\mathrm {out}\), \(V_2\) by \(\check{V}_2\), and \({{\widetilde{W}}_{6}}\) by \(\check{\widetilde{W}}_6\). When checking whether \(\check{F}^j(\check{z}) \in H^{(1)}\) for all j [step (ii) of both algorithms, as well as Algorithm 5.2(v)], we use \(\check{H}^{(1)}_\mathrm {in}\), but otherwise we use \(\check{H}^{(1)}_\mathrm {out}\) for \(H^{(1)}\).
In calculating the orbit of a point z we keep a running bound on the accumulated total difference between the true orbit \(F^j(z)\) and the aproximation \(\check{F}^j(\check{z})\), as well as the corresponding derivatives. More specifically, when calculating the iterates \(\check{z}_{k+1} = \check{F}^{j_k}(\check{z}_k)\), we use Corollary 6.2 and Remark 6.2 to compute upper bounds \(\delta _k > |DF^{j_k}(\check{z})-D\check{F}^{j_k}(\check{z})|\) and \(\epsilon _k > |F^{j_k}(\check{z})-\check{F}^{j_k}(\check{z})|\).
When calculating r in Algorithm 5.1(iii), \({{\,\mathrm{dist}\,}}(\check{F}^\ell (\check{z}),\check{V}_2^*)\) should be reduced by \(\epsilon _k\) and \(D\check{F}^\ell (\check{z}_k)\) should be increased by \(\delta _k\); similar changes should be made in Algorithm 5.2(vi).
As long as the points \(\check{z}_k\) remain in \(\check{W}^{(1)}_\mathrm {in}\) for all k, we can compute compositions of \(\check{F}^{2^n}\) with reasonably high precision.Footnote 3 In particular, if \(\check{g}_k\) is a k-fold composition of such approximations and \(g_k\) is the same composition of Feigenbaum maps \(F^{2^n}\), we have the following worst-case bounds on \(\epsilon _k\) and \(\delta _k\) for \(\check{z}_k\in \check{W}^{(1)}_\mathrm {in}\).
k | \(|g_k(z)-\check{g}_k(\check{z})|\) | \(|g_k'(z)-\check{g}_k'(\check{z})|\) |
|---|---|---|
1 | \(6.45 \times 10^{-13}\) | \(5.59 \times 10^{-12}\) |
5 | \(2.15 \times 10^{-10}\) | \(4.45 \times 10^{-9 }\) |
10 | \(2.14 \times 10^{-7}\) | \(1.43 \times 10^{-5}\) |
15 | \(2.13 \times 10^{-4}\) | \(4.57 \times 10^{-2}\) |
18 | \(1.20 \times 10^{-2}\) | 15.14 |
The above bounds are the worst case; actual calculated orbits have significantly better bounds as long as they remain within \(\check{W}^{(1)}_\mathrm {in}\). As noted earlier, we compute sharper bounds on the specific function values and derivatives for each point \(\check{z}_k\), and incorporate these into our calculations in the implementation of the algorithms. This ensures that all calculated orbits are shadowed by true orbits under F.
To estimate an upper bound on \(M_n = M\bigl (A)\) (see Corollary 4.1) with \(A=(\lambda ^{-n}\Sigma _{n}) \cap P_{0,\mathrm {I}}\), we replace the integral in the definition of \(g_A(z)\) by the Riemann sum taken over the centers of the subset \({{\mathcal {E}}}_{n,r}\) of A from Algorithm 5.2, that is
We then approximate \(M(A)\leqslant M({{\mathcal {E}}}_{n,r}) \approx \max ( 1/g_{{{\mathcal {E}}}_{n,r}}(z_{j}))\), where \(z_{j}\) ranges over centers of the disks from the covering \({{\mathcal {S}}}_{m,t}\) of \(P_{0,\mathrm {I}}\) from Algorithm 6.1 (we take \(m=2,t=2^{-6}\sqrt{2}\)). The relative error in this approximation of M(A) can be bounded by noticing that
for points \(w\in {{\mathbb {D}}}_{r}(w_k)\), the Koebe Theorem gives
Recall from Proposition 4.1 that \({{\mathbb {C}}}_\lambda ={{\mathbb {C}}}{\smallsetminus }\left( (-\infty ,-\tfrac{1}{\lambda }]\cup [\tfrac{F(\lambda )}{\lambda ^2},\infty ) \right) \).
In implementing Algorithm 5.1 to obtain \({{\mathcal {D}}}_{n,r} \supset X_n\) and Algorithm 5.2 for \({{\mathcal {E}}}_{n,r} \subset \Sigma _n\), we take \(n=6\) in both cases. For \({{\mathcal {D}}}_{n,r}\) we use \(r=2^{-17}\sqrt{2}\); for \({{\mathcal {E}}}_{n,r}\), taking \(r=2^{-11}\sqrt{2}\) is sufficient.
Notes
The set \({{\mathbb {C}}}_\lambda \) should not be confused with the slightly larger set \(F({W})={{\mathbb {C}}}{\smallsetminus }\left( (-\infty ,-\tfrac{1}{\lambda }] \cup [\tfrac{1}{\lambda ^2},\infty )\right) \) .
One way to construct such a function p is to set \(p(x_0)=0\), and for \(z\in [0,F(\lambda )]\) let \(p(z)=4-3z/F(\lambda )\). Then propagate p(z) to the rest of \(P_{0,\mathrm {I}}{\smallsetminus }\{x_1\}\) via \(p(F_\lambda (z))=\tfrac{1}{2}p(z)\).
If \(\check{z}_k\in \check{H}^{(1)}_\mathrm {out}{\smallsetminus }\check{W}^{(1)}_\mathrm {in}\) for some k, we can either use \(\check{z}_{k+2}=\check{F}(\check{z}_k)=(-1/\lambda )\check{F}^2(\lambda \check{z}_k)\) with \(\lambda \check{z}_k\) and \(F(\lambda \check{z}_k)\) in \(\check{W}^{(1)}_\mathrm {in}\), or use the bounds from Corollary 6.2 together with Remark 6.2 to calculate \(\epsilon \) and \(\delta \) for the remainder of the orbit.
References
Avila, A., Lyubich, M.: Lebesgue measure of Feigenbaum Julia sets. arXiv:1504.02986
Avila, A., Lyubich, M.: Hausdorff dimension and conformal measures of Feigenbaum Julia sets. J. Am. Math. Soc. 21, 305–383 (2008). https://doi.org/10.1090/S0894-0347-07-00583-8
Brent, R., Percival, C., Zimmermann, P.: Error bounds on complex floating-point multiplication. Math. Comput. 76(259), 1469–1481 (2007). https://doi.org/10.1090/S0025-5718-07-01931-X
Buff, X.: Geometry of the Feigenbaum map. Conform. Geom. Dyn. 3, 79–101 (1999). https://doi.org/10.1090/S1088-4173-99-00031-4
Coullet, P., Tresser, C.: Itération d’endomorphismes et groupe de renormalisation. J. Phys. Colloque 39(C5), 25–28 (1978). https://doi.org/10.1051/jphyscol:1978513
Douady, A., Hubbard, J.: On the dynamics of polynomial-like maps. Ann. Sci. Éc. Norm. Sup 18, 287–344 (1985). https://doi.org/10.24033/asens.1491
Dudko, A., Yampolsky, M.: Poly-time computability of the Feigenbaum Julia set. Ergod. Theory Dyn. Syst. 36(8), 2441–2462 (2016). https://doi.org/10.1017/etds.2015.24
Duren, P.L.: Univalent Functions. Springer, New York (1983)
Epstein, H.: Fixed points of the period-doubling operator. Lecture notes, Lausanne (1992)
Epstein, H.: Fixed points of composition operators II. Nonlinearity 2(2), 305–310 (1989). https://doi.org/10.1088/0951-7715/2/2/006
Feigenbaum, M.: Quantitative universality for a class of class of non-linear transformations. J. Stat. Phys. 19, 25–52 (1978). https://doi.org/10.1007/BF01020332
Feigenbaum, M.: The universal metric properties of non-linear transformations. J. Stat. Phys. 21, 669–706 (1979). https://doi.org/10.1007/BF01107909
Goldberg, D.: What every computer scientist should know about floating-point arithmetic. ACM Comput. Surv. 23(1), 5–48 (1991). https://doi.org/10.1145/103162.103163
Hertling, P., Spandl, C.: Computing a solution of Feigenbaum’s functional equation in polynomial time. Log. Methods Comput. Sci. 10(4), 1–9 (2014). https://doi.org/10.2168/LMCS-10(4:7)2014
Higham, N.: Accuracy and Stability of Numerical Algorithms, 2nd edn. SIAM, Philadelphia (2002)
Hu, J., Jiang, Y.: The Julia set of Feigenbaum quadratic polynomial is locally connected. Preprint (1993)
IEEE Standard for Floating-Point Arithmetic: IEEE Standard 754-2008, pp. 1–58 (2008). https://doi.org/10.1109/IEEESTD.2008.4610935
Jiang, Y.: Infinitely renormalizable quadratic polynomials. Trans. Am. Math. Soc 352(11), 5077–5091 (2000). https://doi.org/10.1090/S0002-9947-00-02514-9
Lanford III, O.: A computer-assisted proof of the Feigenbaum conjectures. Bull. Am. Math. Soc. (N.S.) 6(3), 427–434 (1982). https://doi.org/10.1090/S0273-0979-1982-15008-X
Levin, G., Świątek, G.: Hausdorff dimension of Julia sets of Feigenbaum polynomials with high criticality. Commun. Math. Phys. 258(1), 135–148 (2005). https://doi.org/10.1007/s00220-005-1332-7
Levin, G., Świątek, G.: Measure of the Julia set of the Feigenbaum map with infinite criticality. Ergod. Theory Dyn. Syst. 30(3), 855–875 (2010). https://doi.org/10.1017/S0143385709000340
Lyubich, M.: Dynamics of quadratic polynomials I–II. Acta Math. 178(2), 185–297 (1997). https://doi.org/10.1007/BF02392694
Lyubich, M.: Feigenbaum–Coullet–Tresser universality and Milnor’s hairiness conjecture. Ann. Math. 149(2), 319–420 (1999). https://doi.org/10.2307/120968
McMullen, C.: Renormalization and 3-Manifolds Which Fiber over the Circle. Annals of Mathematics Studies, vol. 142. Princeton University Press, Princeton (1996)
Wilkinson, J.H.: Rounding Errors in Algebraic Processes. Prentice-Hall, Upper Saddle River (1963)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Artem Dudko acknowledges the support by the National Science Centre, Poland, Grant 2016/23/P/ST1/04088 under POLONEZ programme which has received funding from the EU

Horizon 2020 research and innovation programme under the MSCA Grant Agreement No. 665778.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dudko, A., Sutherland, S. On the Lebesgue measure of the Feigenbaum Julia set. Invent. math. 221, 167–202 (2020). https://doi.org/10.1007/s00222-020-00949-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-020-00949-8







 , set
, set 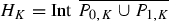 . Let
. Let 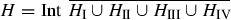 .
. ), then k is divisible by
), then k is divisible by 


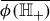 will contain either
will contain either  , and hence T intersects
, and hence T intersects