Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-23T13:26:06.968Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for additive functionals of continuous time random walks

Part of: Stochastic processes Markov processes Limit theorems

Published online by Cambridge University Press:  28 May 2020

Yuri Kondratiev ,
Yuliya Mishura Open the ORCID record for Yuliya Mishura [Opens in a new window]  and
Georgiy Shevchenko Open the ORCID record for Georgiy Shevchenko [Opens in a new window]
Yuri Kondratiev
Affiliation:
Bielefeld University, Germany (kondrat@math.uni-bielefeld.de)
Yuliya Mishura
Affiliation:
Taras Shevchenko National University of Kyiv, Ukraine (myus@univ.kiev.ua; zhora@univ.kiev.ua)
Georgiy Shevchenko
Affiliation:
Taras Shevchenko National University of Kyiv, Ukraine (myus@univ.kiev.ua; zhora@univ.kiev.ua)
Get access Rights & Permissions [Opens in a new window]

Abstract

For a continuous-time random walk X = {Xt, t ⩾ 0} (in general non-Markov), we study the asymptotic behaviour, as t → ∞, of the normalized additive functional 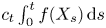$c_t\int _0^{t} f(X_s)\,{\rm d}s$, t⩾ 0. Similarly to the Markov situation, assuming that the distribution of jumps of X belongs to the domain of attraction to α-stable law with α > 1, we establish the convergence to the local time at zero of an α-stable Lévy motion. We further study a situation where X is delayed by a random environment given by the Poisson shot-noise potential: 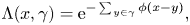$\Lambda (x,\gamma )= {\rm e}^{-\sum _{y\in \gamma } \phi (x-y)},$ where 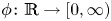$\phi \colon \mathbb R\to [0,\infty )$ is a bounded function decaying sufficiently fast, and γ is a homogeneous Poisson point process, independent of X. We find that in this case the weak limit has both ‘quenched’ component depending on Λ, and a component, where Λ is ‘averaged’.

Keywords

Continuous-time random walkAdditive functionalDomain of attraction of stable lawα-stable Lévy motionLocal timeRandom environmentPoisson shot-noise potential

MSC classification

Primary: 60G50: Sums of independent random variables; random walks
Secondary: 60J55: Local time and additive functionals 60F17: Functional limit theorems; invariance principles
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 2 , April 2021 , pp. 799 - 820
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Banis, I. I.. Convergence of densities in the L 1 metric with a stable limit law in the two-dimensional case. Litovsk. Mat. Sb. 17 (1977), 13–18. (Russian).Google Scholar
2Basu, S. K., Maejima, M. and Patra, N. K.. A nonuniform rate of convergence in a local limit theorem concerning variables in the domain of normal attraction of a stable law. Yokohama Math. J. 27 (1979), 63–72.Google Scholar
3Billingsley, P.. Convergence of probability measures. 2nd edn. Wiley Series in Probability and Statistics: Probability and Statistics, pp. x+277 (New York: John Wiley & Sons, Inc., 1999).CrossRefGoogle Scholar
4Borodin, A. N. and Ibragimov, I. A.. Limit theorems for functionals of random walks. Proceedings of the Steklov Institute of Mathematics, vol. 195, pp. viii+259 (Providence, RI: American Mathematical Society (AMS), 1995).Google Scholar
5Carmona, R. A. and Molchanov, S. A.. Stationary parabolic Anderson model and intermittency. Probab. Theory Relat. Fields 102 (1995), 433–453.CrossRefGoogle Scholar
6Eberle, A.. Markov processes. (2017) https://wt.iam.uni-bonn.de/fileadmin/WT/Inhalt/people/Andreas_Eberle/Markov_Processes_1617/MPSkript1617.pdf.Google Scholar
7Feller, W.. An introduction to probability theory and its applications. Vol. II, 2nd edn, pp. xxiv+669 (New York-London-Sydney: John Wiley & Sons, Inc., 1971).Google Scholar
8Gikhman, I. I. and Skorokhod, A. V.. Introduction to the theory of random processes. pp. xiii+516 (Philadelphia: Saunders, 1969).Google Scholar
9Ivanov, A. V. and Leonenko, N. N.. Statistical analysis of random fields. With a preface by A. V. Skorokhod. Mathematics and its Applications (Soviet Series), vol. 28, pp. x+244 (Dordrecht: Kluwer Academic Publishers Group, 1989).CrossRefGoogle Scholar
10Jacod, J.. Rates of convergence to the local time of a diffusion. Ann. Inst. H. Poincaré Probab. Stat. 34 (1998), 505–544.CrossRefGoogle Scholar
11Jeganathan, P.. Convergence of functionals of sums of r.v.s to local times of fractional stable motions. Ann. Probab. 32 (2004), 1771–1795.CrossRefGoogle Scholar
12Kartashov, Y. N. and Kulik, A. M.. Weak convergence of additive functionals of a sequence of Markov chains. Theory Stochastic Process. 15 (2009), 15–32.Google Scholar
13Kolokoltsov, V. N. and Veretennikova, M. A.. A fractional Hamilton Jacobi Bellman equation for scaled limits of controlled continuous time random walks. Commun. Appl. Ind. Math. 6 (2014), 1–18. ISSN 2038-0909, e-484.Google Scholar
14Kulik, A. M.. Markov approximation of stable processes by random walks. Theory Stochastic Process. 12 (2006), 87–93.Google Scholar
15Leonenko, N. N., Papić, I., Sikorskii, A. and Šuvak, N.. Correlated continuous time random walks and fractional Pearson diffusions. Bernoulli 24 (2018), 3603–3627.CrossRefGoogle Scholar
16Maejima, M.. A non-uniform estimate in the local limit theorem for densities. II. Yokohama Math. J. 26 (1978), 119–135.Google Scholar
17Mijatovic, A. and Uribe Bravo, G., Invariance principles for local times in regenerative settings. Preprint, 2019. arXiv:1910.09501.Google Scholar
18Resnick, S. I.. Point processes, regular variation and weak convergence. Adv. Appl. Probab. 18 (1986), 66–138.CrossRefGoogle Scholar
19Zolotarev, V. M.. One-dimensional stable distributions. Translations of Mathematical Monographs, vol. 65, pp. x+284 (Providence, RI: American Mathematical Society: 1986).CrossRefGoogle Scholar