1 Introduction

Black holes have always been very exciting and interesting objects both for their amazing gravitational and the geometrical properties, but they have now taken the center-stage after the discovery of gravitational waves produced by the merger of two stellar mass black holes in the LIGO-VIRGO detection experiment [1, 2]. In the near future it is envisaged that gravitational wave observations may uncover some of the hidden properties of the black holes which were otherwise not accessible. One of the most fundamental questions in general relativity (GR) is of course testing of the cosmic censorship conjecture (CCC) which has so far remained unproven [3]. The physical possibility of its violation in the weak form (WCCC) has of late been a very active area of research.Footnote 1

A gedanken experiment was envisaged in which over-charged/rotating test particles were bombarded into a black hole to see whether an extremal black hole could be turned into an extremal black hole [5]. The answer turned out to be negative and it was shown that particles with over-extremal parameters cannot reach the horizon of extremal black hole and thereby the horizon cannot be destroyed. Thus an extremal black hole obeys WCCC under linear test particle accretion. On the other hand it was also shown that a non-extremal black hole can never turn extremal [6] because, as extremality is approached, the allowed window of the parameter space of particles with appropriate parameters to reach the horizon pinches off. Thus extremality or the zero black hole temperature can never be attained. However, the interest in this question got revived when it was argued that a non-extremal black hole cannot be converted into an extremal one and subsequently extremal to over-extremal but extremality could be jumped over to create an over-extremal state. That is, a black hole could be overcharged [7] or overspun [8] by a discrete discontinuous accretion process. Thus a naked singularity could be created defying WCCC. On the other hand, a naked singularity was also addressed with a different prospective that whether it could be created as an end state of gravitational collapse [9,10,11,12,13,14].

This led to a spurt in activity where various authors studied overcharging/spinning of the black holes in different settings violating WCCC; [see, e.g. 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27]. In all this work, it was assumed that a test particle follows a geodesic (or the Lorentz force when charged) motion and back and radiation reaction; self-force effects were not included. It is expected, though, that when these effects will be taken into account, there would be no overcharging/spinning and destruction of the black hole horizon [28,29,30,31,32,33]. Recently, charged scalar and test fields have also been considered for testing WCCC [34, 35]. What happens is that particles/fields that could cause an over-extremal state would not be able to reach the black hole horizon. This was precisely how extremality was not destroyed or attained [5, 6]. Note that in test particle accretion the black hole is perturbed linearly, while a realistic accretion process like fluid flow would involve non-linear perturbations, which could alter the situation completely. This is what has recently been done.

An extensive analysis of non-linear accretion/perturbations has been carried out in a breakthrough work [36] leading to the expected result that the black hole horizon indeed cannot be destroyed, thereby reestablishing the validation of WCCC. The same conclusion was also obtained for Kerr–AdS black holes [37]. Following [36], a variety of work has been done as regards non-linear perturbations [38,39,40,41,42] reinforcing the result that a black hole cannot be over-charged/spun and the horizon cannot be destroyed. Furthermore, the same analysis has been done in higher dimension [43] as well, showing that a five-dimensional Myers–Perry rotating black hole [44] though could be overspun at linear order but when second order perturbations are taken into account the situation reverses—no overspinning is allowed and WCCC is restored. In this case there is yet another subtler case of a black hole with single rotation that cannot be overspun even at linear order, however, like all other cases it could be overspun when both rotations are present [45]. However, the six-dimensional rotating black hole with two rotations cannot be overspun under a linear order perturbation [46]. A charged black hole in higher dimensions could always be overcharged at linear order [47].

In this paper we would like to examine this question of linear and non-linear accretion for a charged rotating black hole in five dimensions. In four dimensions, it was straight-forward to add a charge parameter in the \(\Delta \) function of the rotating solution; i.e. \(\Delta = r^2 - 2Mr +a^2 +Q^2\). Unfortunately this does not work in five dimensions, and in fact an analogue of a Kerr–Newman black hole has not yet been found. There exists a solution in the slow rotation limit [48,49,50], and some solutions in supergravity and string theory [51,52,53,54,55,56,57]. Closest to the Kerr–Newman black hole is the one described by a minimally gauged supergravity black hole [58]. Black hole energetics in terms of ergosphere and energy extraction of this solution has been investigated [59]. We shall take this solution (by setting \(\Lambda = 0\)) of the minimally gauged supergravity black hole for a charged and rotating black hole in five dimensions and study linear and non-linear accretion for testing WCCC.

In particular it would be interesting to examine the case of single rotation for linear accretion where a black hole cannot be overspun [45] but could be overcharged [47]. It turns out that the ultimate behavior would be determined by the relative dominance of angular momentum and charge of the accreting particle. If the former is dominant, the black hole cannot be over-extremalized, while if it is the latter, it could be.

The paper is organized as follows: in Sects. 2 and 3, we describe the black hole metric and its properties and build up the background for studying linear and non-linear accretion for an over-extremalizing black hole in Sect. 4. Finally we conclude with a discussion in Sect. 5. We shall use the natural units, \(G=c=1\), throughout.

2 The black hole metric and its properties

The metric of a five-dimensional charged and rotating black hole in minimally gauged supergravity black hole models [58] is given in the Boyer–Lindquist coordinates \((t,r,\theta ,\phi ,\psi )\) by

$$\begin{aligned} ds^2= & {} -\left( \mathrm{{d}}t-a\sin ^2\theta \mathrm{{d}}\phi -b\cos ^2\theta \mathrm{{d}}\psi \right) \nonumber \\&\times \left[ f\left( \mathrm{{d}}t-a\sin ^2\theta \mathrm{{d}}\phi -b\cos ^2\theta \mathrm{{d}}\psi \right) \right. \nonumber \\&+\left. \frac{2q}{\Sigma }(b\sin ^2\theta \mathrm{{d}}\phi +a\cos ^2\theta \mathrm{{d}}\psi )\right] \nonumber \\&+\Sigma \left( \frac{r^2\mathrm{{d}}r^2}{\Delta }+\mathrm{{d}}\theta ^2\right) +\frac{\sin ^2\theta }{\Sigma } \left[ a\mathrm{{d}}t-(r^2+a^2)\mathrm{{d}}\phi \right] ^2\nonumber \\&+\frac{\cos ^2\theta }{\Sigma }\left[ b\mathrm{{d}}t-(r^2+b^2)\mathrm{{d}}\psi \right] ^2\nonumber \\&+\frac{1}{r^2\Sigma }\left[ a b \mathrm{{d}}t-b(r^2+a^2)\sin ^2\theta \mathrm{{d}}\phi \right. \nonumber \\&-\left. a(r^2+b^2)\cos ^2\theta \mathrm{{d}}\psi \right] ^2\,, \end{aligned}$$
(1)

where we have set \(\Lambda = 0\) and the metric coefficients are given by

$$\begin{aligned} f(r,\theta )= & {} \frac{(r^2+a^2)(r^2+b^2)}{r^2\Sigma }-\frac{\mu \Sigma -q^2}{\Sigma ^2},\nonumber \\ \Sigma (r,\theta )= & {} r^2+a^2\cos ^2\theta +b^2\sin ^2\theta ,\nonumber \\ \Delta (r)= & {} (r^2+a^2)(r^2+b^2)+2abq+q^2-\mu r^2\ . \end{aligned}$$
(2)

Here a and b are specific angular momenta parameters relative to two axes and they are related to the angular momenta, \(J_\phi , J_\psi \) as follows:

$$\begin{aligned} a+b=\frac{4}{\pi }\frac{J_{\phi }+J_{\psi }}{\mu +q}, \end{aligned}$$
(3)

with mass parameter \(\mu =\frac{8M}{3\pi }\) and charge parameter \(q=\frac{4Q}{\sqrt{3}\pi }\) of the black hole. The electromagnetic potential is given by

$$\begin{aligned} \mathbf{A} =\frac{-\sqrt{3}q}{2\Sigma }(\mathrm{{d}}t-a\sin ^2\theta \mathrm{{d}}\phi -b\cos ^2\theta \mathrm{{d}}\psi ). \end{aligned}$$
(4)

The horizon of the black hole follows from the relation \(\Delta =0\), i.e.

$$\begin{aligned} r_{\pm }= & {} \pm \frac{\sqrt{\mu -2q-(a+b)^2}\pm \sqrt{\mu +2q-(a-b)^2}}{2}. \end{aligned}$$
(5)

From the above expression it is evident that a horizon does not exist unless the following inequalities are satisfied: \( a^{2}+b^{2} +2|a||b|\le \mu -2q\) and \( a^{2}+b^{2} - 2|a||b|\le \mu +2q\). Let us rewrite the horizon given in the above equation in terms of the black hole mass, charge and angular momenta as

$$\begin{aligned} r_{+}= & {} \frac{1}{4\sqrt{3\pi }\left( M+\frac{\sqrt{3} Q}{2}\right) }\left[ \alpha \right. \nonumber \\&+\left. \sqrt{\alpha ^2+108 \pi J_{\phi } J_{\psi }+64 \sqrt{3}Q \left( M+\frac{\sqrt{3} Q}{2}\right) ^2 }\right] ,\nonumber \\ \end{aligned}$$
(6)

where

$$\begin{aligned} \alpha= & {} \left( 32M^3-27\pi \left( J_{\phi }+J_{\psi }\right) ^2\right. \nonumber \\&-\left. 72MQ^2-24\sqrt{3}~Q^3\right) ^{1/2}. \end{aligned}$$
(7)

Note that the black hole horizon exists if and only if \(\alpha ^2>0\), else it would be a naked singularity. Meanwhile, \(\alpha =0\) corresponds to the extremal charged rotating black hole. The area of the event horizon can be evaluated by setting \(\mathrm{{d}}r=\mathrm{{d}}t=0\) and \(r=r_{+}\) in the metric (1). The horizon metric reads

$$\begin{aligned} g_{\alpha \beta }= \left( \begin{array}{ccc} \Sigma &{} 0 &{} 0 \\ \\ 0 &{} \left( r^2+a^2+\frac{a\left[ a\left( \mu \Sigma -q^2\right) +2bq\Sigma \right] }{\Sigma }\sin ^2\theta \right) \sin ^2\theta &{} \frac{\left[ a b\left( \mu \Sigma -q^2\right) +\left( a^2+b^2\right) q\Sigma \right] }{2\Sigma }\sin ^2 2\theta \\ \\ 0 &{} \frac{\left[ a b\left( \mu \Sigma -q^2\right) +\left( a^2+b^2\right) q\Sigma \right] }{2\Sigma }\sin ^2 2\theta &{} \left( r^2+b^2+\frac{b\left[ b\left( \mu \Sigma -q^2\right) +2aq\Sigma \right] }{\Sigma }\cos ^2\theta \right) \cos ^2\theta \\ \\ \end{array}\right) . \end{aligned}$$
(8)

The horizon area is computed as

$$\begin{aligned} A=\int _{\Xi _{3}}\sqrt{\mathrm{{det}}|g_{\alpha \beta }|}\mathrm{{d}}\theta \mathrm{{d}}\phi \mathrm{{d}}\psi = \frac{2\pi ^2}{r_{+}}\left( \mu r_{+}^2-abq -q^2\right) ,\nonumber \\ \end{aligned}$$
(9)

which must not decrease in any physical process according to the famous area non-decrease theorem [60].

The angular velocities along the \(\phi \) and \(\psi \) directions at the horizon \(r=r_{+}\) are given by

$$\begin{aligned} \Omega _{+}^{(\phi )}= & {} \frac{a(r_+^2+b^2)+bq}{(r_+^2+a^2)(r_+^2+b^2)+abq}, \end{aligned}$$
(10)
$$\begin{aligned} \Omega _{+}^{(\psi )}= & {} \frac{b(r_+^2+a^2)+aq}{(r_+^2+a^2)(r_+^2+b^2)+abq}, \end{aligned}$$
(11)

for which the Killing field, \(\chi =\chi ^\alpha \partial _\alpha \), takes the form

$$\begin{aligned} \chi =\chi _{(t)}+\Omega _{+}^{(\phi )}\chi _{(\phi )} +\Omega _{+}^{(\psi )}\chi _{(\psi )}. \end{aligned}$$
(12)

Then surface gravity is defined by

$$\begin{aligned} 2k\chi _{\alpha }=\nabla _{\alpha }\left( -\chi _{\beta }\chi ^{\beta }\right) |_{r=r_+}\, , \end{aligned}$$
(13)

or by

$$\begin{aligned} k^2=-\frac{1}{2}\left( \nabla _{\alpha }\chi _{\beta }\right) \left( \nabla ^{\alpha } \chi ^{\beta }\right) |_{r=r_+}\,. \end{aligned}$$
(14)

The surface gravity and electromagnetic potential at the horizon are, respectively, given by

$$\begin{aligned} k=\frac{\left( 2r_{+}^2+a^2+b^2-\mu \right) r_{+}}{\mu r_{+}^2-abq-q^2} \end{aligned}$$
(15)

and

$$\begin{aligned} \Phi =-\chi ^{\alpha }{} \mathbf{A} _{\alpha }\vert _{r=r_{+}}=\frac{\sqrt{3}q r_{+}^2}{\mu r_{+}^2-abq-q^2}. \end{aligned}$$
(16)

3 Varitional identities and perturbation inequalities

It is well known that the Lagrangian L for a diffeomorphism covariant theory in n-dimensional manifold \(\mathcal M\) can be described by a metric \(g_{\alpha \beta }\) with symmetrized covariant derivative and curvature tensor and other physical fields \(\psi \) [61]. The variation of Lagrangian is then written as

$$\begin{aligned} \delta L=E \delta \phi +\mathrm{{d}}{\Theta }(\phi ,\delta \phi ), \end{aligned}$$
(17)

where we define all dynamical fields through \(\phi =(g_{\alpha \beta },\psi )\) and E as a parameter of Lagrangian, which consists of the fields \(\phi \). Then the equation of motion is given by \({E}=0\), while \({\Theta }\) represents the symplectic potential \((n-1)\)-form and is written as

$$\begin{aligned} {\omega }(\phi ,\delta _1\phi ,\delta _2\phi )=\delta _1{\Theta }(\phi ,\delta _2\phi ) -\delta _2{\Theta }(\phi ,\delta _1\phi )\,, \end{aligned}$$
(18)

where \(\delta _{1,2}\) refers to the variations. The Noether current 5-form relative a vector field \(\zeta ^{\alpha }\) is defined by

$$\begin{aligned} {J}_\zeta ={\Theta }(\phi ,{L}_\zeta \phi )-\zeta \cdot {L}, \end{aligned}$$
(19)

for which \(d{J}_\zeta =0\) is the equation of motion. According to [62], one can define the Noether current in the following form:

$$\begin{aligned} { J}_\zeta =d{Q}_\zeta + {C}_\zeta , \end{aligned}$$
(20)

where \({Q}_\zeta \) is referred to as the Noether charge, while \({C}_\zeta =\zeta ^{\alpha }{C}_{\alpha }\) is the constraint of the theory; \({C}_\zeta =0\) corresponds to the case when the equations of motion are satisfied.

From Eqs. (19) and (20) for fixed \(\zeta ^{\alpha }\), we write the linear variational identity on a Cauchy surface \(\Xi \)

$$\begin{aligned} \int _{\partial \Xi }\delta {Q}_\zeta -\zeta \cdot {\Theta }(\phi ,\delta \phi )= & {} \int _{\Xi }{\omega }(\phi ,\delta \phi ,\mathcal {L}_\zeta \phi )\nonumber \\&-\int _{\Xi }\zeta \cdot {E}\delta \phi -\int _{\Xi }\delta \mathbf {C}_\zeta , \end{aligned}$$
(21)

where the first term on the right is defined by

$$\begin{aligned} \delta H_{\zeta }=\int _{\Xi }{\omega }(\phi ,\delta \phi ,\mathcal {L}_\zeta \phi )\, , \end{aligned}$$
(22)

which represents the variation of the Hamiltonian associated with the vector field \(\zeta ^{\alpha }\). This reduces to \(\delta H_{\zeta }=0\) if and only if \(\zeta ^{\alpha }\) is a Killing vector and a symmetry of \(\phi \), thus satisfying both the equation of motion \({E}=0\) and \(\mathcal {L}_\zeta \phi =0\). On the basis of a linear variational identity, the non-linear one on the same surface is then defined by

$$\begin{aligned} \int _{\partial \Xi }\delta ^2 {Q}_\zeta -\zeta \cdot \delta {\Theta }(\phi ,\delta \phi )]= & {} \int _{\Xi }{\omega } (\phi ,\delta \phi ,\mathcal {L}_\zeta \delta \phi )\nonumber \\&-\int _{\Xi }\zeta \cdot \delta {E}\delta \phi -\int _{\Xi }\delta ^2 {C}_\zeta .\nonumber \\ \end{aligned}$$
(23)

Since \(\zeta ^{\alpha }\) is assumed to be a Killing field, Eq. (21) for the linear variation reduces to

$$\begin{aligned} \int _{\partial \Xi }\delta {Q}_\chi -\chi \cdot {\Theta }(\phi ,\delta \phi )= & {} -\int _{\Xi }\delta \mathbf {C}_\chi , \end{aligned}$$
(24)

where \(\chi ^{\alpha }=\chi _{(t)}^{\alpha }+\Omega _{+}^{(\phi )}\chi _{(\phi )}^{\alpha } +\Omega _{+}^{(\psi )}\chi _{(\psi )}^{\alpha }\) is the Killing vector with the horizon angular velocity \(\Omega _{+}^{(\phi ,\psi )}\). The Cauchy surface \(\Xi \) defines the bifurcation surface B at one end and spatial infinity at the other. Let us then rewrite the left-hand side of Eq. (24) on the Cauchy surface \(\Xi \) thus:

$$\begin{aligned} \int _{\partial \Xi }\delta {Q}_\chi -\chi \cdot {\Theta }(\phi ,\delta \phi )= & {} \int _{\infty }\delta {Q}_\chi -\chi \cdot {\Theta }(\phi ,\delta \phi )\nonumber \\&-\int _{B}\delta {Q}_\chi -\chi \cdot {\Theta }(\phi ,\delta \phi ). \end{aligned}$$
(25)

The contribution to boundary integral at infinity then yields

$$\begin{aligned} \int _{\infty }\delta {Q}_\chi -\chi \cdot {\Theta }(\phi ,\delta \phi )= & {} \delta M-\Omega _{+}^{(\phi )}\delta J_{\phi }-\Omega _{+}^{(\psi )}\delta J_{\psi }\, \nonumber \\ \end{aligned}$$
(26)

with ADM mass M and angular momenta \(J_{\phi ,\psi }\). From Eqs. (24)–(26), one can define the linear order variational identity (21) as

$$\begin{aligned} \delta M-\Omega _{+}^{(\phi )}\delta J_{\phi }-\Omega _{+}^{(\psi )}\delta J_{\psi }= & {} \int _B[\delta {Q}_\chi -\chi \cdot {\Theta }(\phi ,\delta \phi )]\nonumber \\&-\int _\Xi \delta {C}_\chi , \end{aligned}$$
(27)

for given Cauchy surface \(\Xi \) with a bifurcation surface B on which the equation of motion is satisfied.

On the other hand the non-linear variational identity (23) then reads

$$\begin{aligned} \delta ^2 M- & {} \Omega _{+}^{(\phi )}\delta ^2 J_{\phi }-\Omega _{+}^{(\psi )}\delta ^2 J_{\psi }\nonumber \\&= \int _B[\delta ^2 {Q}_\chi -\chi \cdot \delta {\Theta }(\phi ,\delta \phi )]\nonumber \\- & {} \int _\Xi \chi \cdot \delta {E}\delta \phi -\int _\Xi \delta ^2 {C}_\chi +\mathcal {E}_\Xi (\phi ,\delta \phi ), \end{aligned}$$
(28)

where \(\mathcal {E}_\Xi (\phi ,\delta \phi )\) is the canonical energy on the Cauchy surface \(\Xi \) as a non-linear correction to \(\delta \phi \).

For Eqs. (27) and (28), the symplectic potential 4-form is defined by

$$\begin{aligned} \Theta _{ijkh}\left( \phi ,\delta \phi \right)= & {} \frac{1}{16\pi } \epsilon _{ijkh\alpha }g^{\alpha \beta } g^{\gamma \eta }(\triangledown _{\eta } \delta g_{\beta \gamma }-\triangledown _{\beta }\delta g_{\gamma \eta })\nonumber \\&-\frac{1}{4\pi }\epsilon _{ijkh\alpha }F^{\alpha \beta }\delta \mathbf{A} _{\beta }, \end{aligned}$$
(29)

where the first term on the right is responsible for the GR part, while the second is for the electromagnetic part where the Lagrangian is

$$\begin{aligned} L=\frac{\epsilon }{16\pi }\left( R-F^{\alpha \beta }F_{\alpha \beta }\right) . \end{aligned}$$
(30)

Hence we have

$$\begin{aligned} E(\phi )\delta \phi =-{\epsilon }\left( \frac{1}{2} T^{\alpha \beta } \delta g_{\alpha \beta }+j^\alpha \delta \mathbf{A} _{\alpha }\right) , \end{aligned}$$
(31)

where \(j^a=\frac{1}{4\pi } \triangledown _{b} F^{ab}\). Equation (29) yields the corresponding symplectic current

$$\begin{aligned} \omega _{ijkh}= & {} \frac{1}{4\pi }\left[ \delta _{2}(\epsilon _{ijkh\alpha } F^{\alpha \beta }) \delta _{1} \mathbf{A} _{\beta }-\delta _{1}(\epsilon _{ijkh\alpha } F^{\alpha \beta }) \delta _{2} \mathbf{A} _{\beta }\right] \nonumber \\&+\frac{1}{16\pi }\epsilon _{ijkh\alpha } w^{\alpha }, \end{aligned}$$
(32)

with

$$\begin{aligned} w^{i}= & {} P^{ijkh\alpha \beta }\left( \delta _{2} g_{jk} \triangledown _{h}\delta _{1}g_{\alpha \beta }-\delta _{1} g_{jk} \triangledown _{h}\delta _{2}g_{\alpha \beta }\right) ,\nonumber \\ P^{ijkh\alpha \beta }= & {} g^{i\alpha } g^{\beta j} g^{k h}-\frac{1}{2}g^{ih} g^{j\alpha } g^{\beta k} - \frac{1}{2}g^{i j} g^{k h} g^{\alpha \beta }\nonumber \\&- \frac{1}{2}g^{j k} g^{i\alpha } g^{\beta h} + \frac{1}{2}g^{jk} g^{i h} g^{\alpha \beta }. \end{aligned}$$
(33)

Taking into account \(\mathcal {L}_{\zeta } g_{\alpha \beta } = \triangledown _{\alpha }\zeta _{\beta } +\triangledown _{\beta }\zeta _{\alpha }\) and \(\triangledown _{\alpha }{} \mathbf{A} _{\beta }=F_{\alpha \beta }+\triangledown _{\beta }{} \mathbf{A} _{\alpha }\), the Noether current 4-form is given by

$$\begin{aligned} (J_{\zeta })_{ijkh}= & {} \frac{1}{8\pi }\epsilon _{ijkh\alpha } \triangledown _{\beta }(\triangledown ^{[\beta } \chi ^{\alpha ]}) + \epsilon _{ijkh\alpha } T_{\beta }^{\alpha } \zeta ^{\beta }\nonumber \\&+\frac{1}{4\pi }\epsilon _{ijkh \alpha }\triangledown _{\gamma }(F^{\gamma \alpha } \mathbf{A} _{\beta } \zeta ^{\beta }) + \epsilon _{ijkh\alpha } \mathbf{A} _{\beta } j^{\alpha } \chi ^{\beta };\nonumber \\ \end{aligned}$$
(34)

the Noether charge \(Q_{\zeta }\) and the constraint \(C_{\zeta }\) read

$$\begin{aligned} (Q_{\zeta })_{ijk}= & {} -\frac{1}{16\pi }\epsilon _{ijk \alpha \beta }\triangledown ^{\alpha }\zeta ^{\beta }-\frac{1}{8\pi }\epsilon _{ijk \alpha \beta } F^{\alpha \beta } \mathbf{A} _{\gamma } \zeta ^{\gamma }\,, \nonumber \\ (C_{\gamma })_{ijkh}= & {} \epsilon _{ijkh \alpha }(T_{\gamma }^{\alpha } + \mathbf{A} _{\gamma } j^{\alpha }). \end{aligned}$$
(35)

4 Over-extremalizing black hole via gedanken experiments

4.1 Extremal case

Here we consider a particle absorption by an extremal black hole of mass M, angular momenta \(J_{\psi }\) and \(J_{\phi }\) and electric charge Q. From Eq. (7), the extremality condition reads

$$\begin{aligned} 32M^3=27\pi \left( J_{\phi }+J_{\psi }\right) ^2+72MQ^2+24\sqrt{3}~Q^3. \end{aligned}$$
(36)

A particle of energy \(\delta M\) and angular momenta \(\delta J_{\psi }\) and \(\delta J_{\phi }\) and charge \(\delta Q\) is thrown into the black hole horizon. This leads to an increase in the corresponding parameters of the black hole, and a perturbed stationary state would be attained with the parameters \(M + \delta M\), \(J + \delta J_{\phi }\), \(J + \delta J_{\psi }\), and \(Q+\delta Q\). The condition for over-extremalization or WCCC violation would require the following inequality:

$$\begin{aligned} 96M^2\delta M< & {} 54\pi \left( J_{\phi }+J_{\psi }\right) \left( \delta J_{\phi }+\delta J_{\psi }\right) +72Q^2\delta M\nonumber \\&+144MQ\delta Q +72\sqrt{3}~Q^2\delta Q, \end{aligned}$$
(37)

for first order linear accretion. An extremal black hole will be pushed to an over-extremal state if and only if

$$\begin{aligned} \delta M- & {} \frac{9\pi \left( J_{\phi }+J_{\psi }\right) }{4(4M^2-3Q^2)}\left( \delta J_{\phi }+\delta J_{\psi }\right) \nonumber \\- & {} \frac{3\left( 2MQ-\sqrt{3}Q^2\right) }{\left( 4M^2-3Q^2\right) }\delta Q<0. \end{aligned}$$
(38)

We should then examine whether an over-extremal state satisfying Eq. (38) does or does not occur. Let us suppose that a black hole with an initial given state is bombarded by test particles of appropriate parameters described by the stress-energy tensor \(T_{\alpha \beta }\). Consequently, the black hole parameters are increased by the following amounts [36]:

$$\begin{aligned} \delta M= & {} \int _{H}\epsilon _{ijkh \alpha }\chi _{(t)}^{\gamma }\left( \delta T_{\gamma }^{\alpha } + \mathbf{A} _{\gamma } \delta j^{\alpha }\right) \,, \end{aligned}$$
(39)
$$\begin{aligned} \delta J_{\phi }= & {} -\int _{H}\epsilon _{ijkh \alpha }\chi _{(\phi )}^{\gamma }\left( \delta T_{\gamma }^{\alpha } + \mathbf{A} _{\gamma } \delta j^{\alpha }\right) , \end{aligned}$$
(40)
$$\begin{aligned} \delta J_{\psi }= & {} -\int _{H}\epsilon _{ijkh \alpha }\chi _{(\psi )}^{\gamma }\left( \delta T_{\gamma }^{\alpha } + \mathbf{A} _{\gamma } \delta j^{\alpha }\right) \, , \end{aligned}$$
(41)

where the integration is over a surface element on the event horizon \(r_{+}\). We assume that at the end of the process, the black hole attains another stationary state. Since the term \(\int _B[\delta {Q}_\chi -\chi \cdot {\Theta }(\phi ,\delta \phi )]\) vanishes because of no perturbation at the bifurcation surface [36], Eq. (27) then yields

$$\begin{aligned}&\delta M-\Omega _{+}^{(\phi )}\delta J_{\phi }-\Omega _{+}^{(\psi )}\delta J_{\psi }=-\int _\Xi \delta {C}_\gamma \nonumber \\&\quad =-\int _{H}\epsilon _{ijkh \alpha }\left( \chi _{(t)}^{\gamma }+\Omega _{+}^{(\phi )}\chi _{(\phi )}^{\gamma } +\Omega _{+}^{(\psi )}\chi _{(\psi )}^{\gamma }\right) \nonumber \\&\qquad \times \left( \delta T_{\gamma }^{\alpha } + \mathbf{A} _{\gamma } \delta j^{\alpha }\right) , \end{aligned}$$
(42)

where \(\chi ^{\gamma }\) is the null generator of the horizon \(r_+\). Equation (42) ensures that a particle crossed the horizon eventually. Bearing in mind \(\Phi =-\chi ^{\gamma }{} \mathbf{A} _{\gamma }\vert _{r=r_{+}}\) and using \(\int _{H}\delta (\epsilon _{ijkh \alpha }j^{\alpha })=\delta Q\) for the perturbed charge fallen into the horizon \(r_{+}\), we rewrite Eq. (42) as

$$\begin{aligned} \delta M- & {} \Omega _{+}^{(\phi )}\delta J_{\phi }-\Omega _{+}^{(\psi )}\delta J_{\psi }-\Phi _{+}\delta Q\nonumber \\&= - \int _{H}\epsilon _{ijkh \alpha } \chi _{\gamma } \delta T^{\gamma \alpha }, \end{aligned}$$
(43)

where the volume element on the horizon is written as \(\epsilon _{ijkh \alpha }=-5\tilde{\epsilon }_{[ijkh} k_{\alpha ]}\) We then write

$$\begin{aligned} - \int _{H}\epsilon _{ijkh \alpha } \chi _{\gamma } \delta T^{\gamma \alpha }=\int _{H}\tilde{\epsilon }_{ijkh} \chi _{\gamma }k_{\alpha } \delta T^{\gamma \alpha }. \end{aligned}$$
(44)

This clearly shows that the right-hand side is only positive when the null energy condition is satisfied, i.e. \(\delta T_{\alpha \beta }k^{\alpha }k^{\beta }\ge 0\). This leads to the inequality

$$\begin{aligned} \delta M- & {} \Omega _{+}\left( \delta J_{\phi }+\delta J_{\psi }\right) -\Phi _{+}\delta Q\ge 0. \end{aligned}$$
(45)

For the extremal black hole we have

$$\begin{aligned} \Omega _{+}= & {} \frac{9\pi \left( J_{\phi }+J_{\psi }\right) }{4(4M^2-3Q^2)}, \end{aligned}$$
(46)
$$\begin{aligned} \Phi _{+}= & {} \frac{3\left( 2MQ-\sqrt{3}Q^2\right) }{\left( 4M^2-3Q^2\right) }\,, \end{aligned}$$
(47)

and the inequality (45) becomes

$$\begin{aligned} \delta M- & {} \frac{9\pi \left( J_{\phi }+J_{\psi }\right) }{4(4M^2-3Q^2)}\left( \delta J_{\phi }+\delta J_{\psi }\right) \nonumber \\- & {} \frac{3\left( 2MQ-\sqrt{3}Q^2\right) }{\left( 4M^2-3Q^2\right) }\delta Q\ge 0. \end{aligned}$$
(48)

This inequality clearly contradicts the inequality (38). Thus an extremal black hole cannot be overspun and WCCC holds.

Furthermore, we must show that the new perturbed state is also indeed extremal. We need to ensure that it is indeed not possible to over-extremalize an extremal black hole. From the first law of black hole dynamics we write

$$\begin{aligned} \delta M= \frac{k}{8\pi }\delta A+\Omega ^{(\phi )}\delta J_{\phi }+\Omega ^{(\psi )}\delta J_{\psi }+\Phi \delta Q, \end{aligned}$$
(49)

where \(M=M(A,J_{\phi },J_{\psi },Q)\) and the horizon area, \(A=A(J_{\phi },J_{\psi },Q)\). For the extremal black hole, we will consider a variation in the mass,

$$\begin{aligned} \delta M_\mathrm{{ext}}= & {} \left( \frac{\partial M}{\partial A}\frac{\partial A_\mathrm{{ext}}}{\partial J_{\phi }}+\frac{\partial M}{\partial J_{\phi }}\right) \delta J_{\phi }\nonumber \\&+\left( \frac{\partial M}{\partial A}\frac{\partial A_\mathrm{{ext}}}{\partial J_{\psi }}+\frac{\partial M}{\partial J_{\psi }}\right) \delta J_{\psi }\nonumber \\&+\left( \frac{\partial M}{\partial A}\frac{\partial A_\mathrm{{ext}}}{\partial Q}+\frac{\partial M}{\partial Q}\right) \delta Q\nonumber \\= & {} \frac{k}{8\pi }\delta A + \Omega _{+}^{(\phi )}\delta J_{\phi }+\Omega _{+}^{(\psi )}\delta J_{\psi }+\Phi _{+}\delta Q, \end{aligned}$$
(50)

where

$$\begin{aligned} k= & {} \frac{\partial M}{\partial A}, \end{aligned}$$
(51)
$$\begin{aligned} \delta A= & {} \frac{\partial A_\mathrm{{ext}}}{\partial J_{\phi }}\delta J_{\phi }+\frac{\partial A_\mathrm{{ext}}}{\partial J_{\psi }}\delta J_{\psi }+\frac{\partial A_\mathrm{{ext}}}{\partial Q}\delta Q. \end{aligned}$$
(52)

The surface gravity goes to zero \(k\rightarrow 0\) for an extremal black hole. As a result, Eq. (50) yields

$$\begin{aligned} \delta M_\mathrm{{ext}}=\Omega _{+}\left( \delta J_{\phi }+\delta J_{\psi }\right) +\Phi _{+}\delta Q, \end{aligned}$$
(53)

which characterizes an extremal black hole \(M=M_\mathrm{{ext}}(J_{\phi },J_{\psi },Q)\). The black hole exists provided \(M \ge M_\mathrm{{ext}}(J_{\phi },J_{\psi },Q)\), and if the opposite is the case, \(M < M_\mathrm{{ext}}(J_{\phi },J_{\psi },Q)\), an over-extremal state occurs. If a particle with angular momenta and charge crosses the horizon of an extremal black hole this results in a black hole’s angular momenta and charge being enhanced to \(J_{\phi }+\delta J_{\phi }\), \(J_{\psi }+\delta J_{\psi }\) and \(Q+\delta Q\). In view of Eqs. (45) and (53), we then write for the final mass

$$\begin{aligned} M+\delta M\ge & {} M+\Omega _{+}\left( \delta J_{\phi }+\delta J_{\psi }\right) +\Phi _{+}\delta Q\nonumber \\= & {} M_\mathrm{{ext}}(J_{\phi },J_{\psi },Q)+\delta M_\mathrm{{ext}}\nonumber \\= & {} M_\mathrm{{ext}}(J_{\phi }+\delta J_{\phi },J_{\psi }+\delta J_{\psi },Q+\delta Q). \end{aligned}$$
(54)

As is clear from the above equation, the final black hole mass is not less than the initial extremal mass and hence it has not been over-extremalized. All this is in agreement with the third law of black hole thermodynamics [5, 6, 63, 64]. Thus an extremal black hole cannot be converted into an over-extremal state, and there occurs no violation of WCCC.

Next, we investigate the over-extremal state for a near-extremal black hole for linear and non-linear perturbations through gedanken experiments.

4.2 Near-extremal case

In this subsection we apply new gedanken experiment developed by Sorce and Wald [36] to an over-extremalized near-extremal black hole. According to the gedanken experiment one should take into account a one-parameter family of fields \(\phi (\lambda )\) and the background spacetime is characterized by \(T_{\alpha \beta }=0\) and \(j^{\alpha }=0\). For this we have already considered a hypersurface as \(\Xi =\Xi _{1}\cup H\) endowed with specific properties. So this hypersurface contains such a region from which a bifurcation surface B starts and continues up the horizon portion H of \(\Xi \) till it becomes spacelike \(\Xi _{1}\). After that it reaches spatial infinity to become asymptotically flat. Based on the particular characteristics of the \(\Xi \), we work on the second order variational identity for a near-extremal black hole. Let us recall Eq. (28),

$$\begin{aligned}&\delta ^2 M-\Omega _{+}^{(\phi )}\delta ^2 J_{\phi }-\Omega _{+}^{(\psi )}\delta ^2 J_{\psi }\nonumber \\&\quad =\int _B[\delta ^2 {Q}_\chi -\chi \cdot \delta {\Theta }(\phi ,\delta \phi )]\nonumber \\&\qquad -\int _\Xi \chi \cdot \delta {E}\delta \phi -\int _\Xi \delta ^2 {C}_\chi +\mathcal {E}_\Xi (\phi ,\delta \phi )\nonumber \\&\quad = \int _B[\delta ^2 {Q}_\chi -\chi \cdot \delta {\Theta }(\phi ,\delta \phi )]+\mathcal {E}_H(\phi ,\delta \phi )\nonumber \\&\qquad -\int _H\chi \cdot \delta {E}\delta \phi \nonumber \\&\qquad -\int _{H}\epsilon _{ijkh \alpha }\left( \chi _{(t)}^{\gamma }+\Omega _{+}^{(\phi )}\chi _{(\phi )}^{\gamma } +\Omega _{+}^{(\psi )}\chi _{(\psi )}^{\gamma }\right) \nonumber \\&\qquad \times \left( \delta ^2 T_{\gamma }^{\alpha } + \mathbf{A} _{\gamma } \delta ^2 j^{\alpha }\right) \nonumber \\&\quad = \int _B[\delta ^2 {Q}_\chi -\chi \cdot \delta {\Theta }(\phi ,\delta \phi )]+\mathcal {E}_H(\phi ,\delta \phi )\nonumber \\&\qquad + \int _{H}\tilde{\epsilon }_{ijkh} \chi _{\gamma }k_{\alpha } \delta ^2 T^{\gamma \alpha }+\Phi _{+}\delta ^2 Q, \end{aligned}$$
(55)

where \(\chi ^{\alpha }\) is tangent to H and we applied the gauge condition \(\chi ^{\alpha }\delta \mathbf{A} _{\alpha }=0\) on H. In the last step, we impose the null energy condition \(\delta ^2 T_{\alpha \beta }k^{\alpha }k^{\beta }\ge 0\) to rewrite the above equation

$$\begin{aligned} \delta ^2 M- & {} \Omega _{+}^{(\phi )}\delta ^2 J_{\phi }-\Omega _{+}^{(\psi )}\delta ^2 J_{\psi }-\Phi _{+}\delta ^2 Q\nonumber \\&= \int _B[\delta ^2 {Q}_\chi -\chi \cdot \delta {\Theta }(\phi ,\delta \phi )]+\mathcal {E}_H(\phi ,\delta \phi )\, . \end{aligned}$$
(56)

Let us then evaluate the first and second terms on the right-hand side of Eq. (56) and rewrite these terms for a one-parameter field \(\phi ^{MGS}(\lambda )\),

$$\begin{aligned} \int _B[\delta ^2 {Q}_\chi -\chi \cdot \delta {\Theta }(\phi ,\delta \phi ^{MGS})] ~~\text{ and }~~\mathcal {E}_{H}(\phi ,\delta \phi ^{MGS}) ,\nonumber \\ \end{aligned}$$
(57)

where \(\delta \phi ^{MGS}\) is the perturbation caused by matter falling into the minimally gauged supergravity black hole with the following parameters:

$$\begin{aligned} M(\lambda )= & {} M+\lambda \delta M,\nonumber \\ J_{\phi }(\lambda )= & {} J_{\phi }+\lambda \delta J_{\phi }, \nonumber \\ J_{\psi }(\lambda )= & {} J_{\psi }+\lambda \delta J_{\psi }, \nonumber \\ Q(\lambda )= & {} Q+\lambda \delta Q. \end{aligned}$$
(58)

Note here that we choose \(\delta M\), \(\delta Q\), and \(\delta J_{\phi ,\psi }\) in such a way that they are consistent with the linear order perturbation, Eq. (45). However, \(\delta ^2 M=\delta ^2 J_{\phi ,\psi }=\delta ^2 Q_{B}=\delta E=\mathcal {E}_{H}(\phi ,\delta \phi ^{MGS})=0\) is satisfied for this one-parameter family of fields. Thus, by imposing the condition \(\chi ^{\alpha }=0\) at the bifurcation surface B we have

$$\begin{aligned} \delta ^2 M- & {} \Omega _{+}^{(\phi )}\delta ^2 J_{\phi }-\Omega _{+}^{(\psi )}\delta ^2 J_{\psi }-\Phi _{+}\delta ^2 Q\nonumber \\&=\int _B[\delta ^2 {Q}_\chi -\chi \cdot \delta {\Theta }(\phi ,\delta \phi ^{MGS})]\nonumber \\&\ge -\frac{k}{8\pi }\delta ^2 A^{MGS}. \end{aligned}$$
(59)

This is the non-linear variational identity for the one-parameter family of perturbation.

Following the above procedure we apply this new version of gedanken experiment to probe over-extremalization of a near-extremal black hole. Let us recall the extremality condition Eq. (36),

$$\begin{aligned} 32M^3-27\pi \left( J_{\phi }+J_{\psi }\right) ^2-72MQ^2-24\sqrt{3}~Q^3=0. \end{aligned}$$

Thus a near-extremal state is characterized as

$$\begin{aligned} f(\lambda )= & {} 32M(\lambda )^3-27\pi \left[ J_{\phi }(\lambda )+J_{\psi }(\lambda )\right] ^2\nonumber \\&-72M(\lambda )Q(\lambda )^2-24\sqrt{3}~Q(\lambda )^3\,, \end{aligned}$$
(60)

where \(f(0)=\alpha ^2\), a bit larger than zero, and \(M(\lambda )\), \(J_{\phi }(\lambda )\), \(J_{\psi }(\lambda )\) and \( Q(\lambda )\) are defined by Eq. (58). To jump from a sub-extremal to an over-extremal state we must obtain \(f(\lambda )<0\), and for that we now expand \(f(\lambda )\) up to second order in \(\alpha \) and \(\lambda \) as

$$\begin{aligned} f(\lambda )=\alpha ^2+f_1\lambda +f_2\lambda ^2+O(\lambda ^3, \lambda ^2\alpha , \lambda \alpha ^2,\alpha ^3), \end{aligned}$$
(61)

where

$$\begin{aligned} f_1= & {} 24\left( 4M^2-3Q^2\right) \left[ \delta M- \frac{9\pi \left( J_{\phi }+J_{\psi }\right) }{4(4M^2-3Q^2)}\right. \nonumber \\&\quad \left( \delta J_{\phi }+\delta J_{\psi }\right) \nonumber \\&\left. -\frac{3\left( 2MQ-\sqrt{3}Q^2\right) }{\left( 4M^2-3Q^2\right) }~\delta Q \right] , \end{aligned}$$
(62)
$$\begin{aligned} f_2= & {} \left\{ 12\left( 4M^2-3Q^2\right) \left[ \delta ^2 M\right. \right. \nonumber \\&\quad -\frac{9\pi \left( J_{\phi }+J_{\psi }\right) }{4(4M^2-3Q^2)}\left( \delta ^2 J_{\phi }+\delta ^2 J_{\psi }\right) \nonumber \\&\left. -\frac{3\left( 2MQ-\sqrt{3}Q^2\right) }{\left( 4M^2-3Q^2\right) }~\delta ^2 Q\right] \nonumber \\&+ 96M(\delta M)^2-27\pi \left( \delta J_{\phi }+\delta J_{\psi }\right) ^2\nonumber \\&\left. +72\left( M(\delta Q)^2+2Q\delta M\delta Q +\sqrt{3}Q(\delta Q)^2\right) \right\} . \end{aligned}$$
(63)

In Eq. (62), the expression in brackets is written for an optimal choice of the linear order correction

$$\begin{aligned}&\delta M -\frac{9\pi \left( J_{\phi }+J_{\psi }\right) }{4(4M^2-3Q^2)}\left( \delta J_{\phi }+\delta J_{\psi }\right) +\frac{3\left( 2MQ-\sqrt{3}Q^2\right) }{\left( 4M^2-3Q^2\right) }~\delta Q =\nonumber \\&\quad -\frac{\sqrt{27 \pi J_{\phi } J_{\psi }+4 \sqrt{3} Q \left( 2 M+\sqrt{3} Q\right) ^2}}{\left( 27 \pi J_{\phi } J_{\psi }+4 \sqrt{3} Q \left( 2 M+\sqrt{3} Q\right) ^2\right) ^2 \left( 9\pi (J_{\phi }+J_{\psi })^2+\frac{4\sqrt{3}}{3}Q\left( 2 M+\sqrt{3} Q\right) ^2\right) ^2}\nonumber \\&\quad \times \left[ 6 \pi \left( M+\frac{\sqrt{3} Q}{2}\right) \left( 144 \sqrt{3} \pi Q \left( M+\frac{\sqrt{3} Q}{2}\right) ^2 \right. \right. [\delta J_{\psi } J_{\phi }^3+2 J_{\psi } J_{\phi }^2 (\delta J_{\phi }+2 \delta J_{\psi })+2 J_{\phi } J_{\psi }^2\nonumber \\&(\delta J_{\psi }+2 \delta J_{\phi })+\delta J_{\phi } J_{\psi }^3] + 243 \pi ^2 {J_{\phi }} {J_{\psi }} ({J_{\phi }}+{J_{\psi }})^2 (\delta J_{\psi } {J_{\phi }}+\delta J_{\phi } {J_{\psi }})+16 Q^2 \left( 2 M+\sqrt{3} Q\right) ^4 \big [{J_{\phi }} (\delta J_{\phi }+2 \delta J_{\psi })\nonumber \\&\left. +{J_{\psi }} (\delta J_{\psi }+2 \delta J_{\phi })\big ]\right) + 256 Q^2 \left( M+\frac{\sqrt{3} Q}{2}\right) ^4 \left. \left( 9 \sqrt{3} \pi {J_{\phi }} {J_{\psi }}+4 Q \left( 2 M+\sqrt{3} Q\right) ^2\right) \delta Q \right] {\alpha }. \end{aligned}$$
(64)

4.3 With two rotations

4.3.1 Linear order accretion

In view of Eq. (64), we rewrite \(f(\lambda )\) for a linear order correction as

$$\begin{aligned} f(\lambda )= & {} \alpha ^2-\frac{6\left( 2 M+\sqrt{3} Q\right) ^{-1}}{\left( 27 \pi J_{\phi } J_{\psi }+4 \sqrt{3} Q \left( 2 M+\sqrt{3} Q\right) ^2\right) ^{1/2} \left( 9\pi (J_{\phi }+J_{\psi })^2+\frac{4\sqrt{3}}{3}Q\left( 2 M+\sqrt{3} Q\right) ^2\right) ^2}\nonumber \\&\times \left[ 6 \pi \left( M+\frac{\sqrt{3} Q}{2}\right) \left( 144 \sqrt{3} \pi Q \left( M+\frac{\sqrt{3} Q}{2}\right) ^2\right. \right. [\delta J_{\psi } J_{\phi }^3+2 J_{\psi } J_{\phi }^2 (\delta J_{\phi }+2 \delta J_{\psi })+2 J_{\phi } J_{\psi }^2\nonumber \\&(\delta J_{\psi }+2 \delta J_{\phi })+\delta J_{\phi } J_{\psi }^3] + 243 \pi ^2 {J_{\phi }} {J_{\psi }} ({J_{\phi }}+{J_{\psi }})^2 (\delta J_{\psi } {J_{\phi }}+\delta J_{\phi } {J_{\psi }})+16 Q^2 \left( 2 M+\sqrt{3} Q\right) ^4 \big [{J_{\phi }} (\delta J_{\phi }+2 \delta J_{\psi })\nonumber \\&\left. +{J_{\psi }}(\delta J_{\psi }+2 \delta J_{\phi })\big ]\right) + 256 Q^2 \left( M+\frac{\sqrt{3} Q}{2}\right) ^4 \left( 9 \sqrt{3} \pi {J_{\phi }} {J_{\psi }}\right. \left. \left. +4 Q \left( 2 M+\sqrt{3} Q\right) ^2\right) \delta Q \right] ~{\alpha }~{\lambda } +\mathcal {O}(\lambda ^2), \end{aligned}$$
(65)

from which it is evident that it is always possible to obtain \(f(\lambda )<0\) for suitable values of given parameters. Thus a black hole could be over-extremalized. To ensure this, we try to explore \(f(\lambda )\) numerically. From Eq. (5), the extremal condition \(\mu -2q=(a+b)^2\) yields

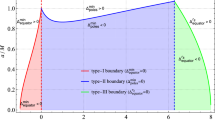
$$\begin{aligned} \sqrt{\frac{32}{27\pi }\left( M-\sqrt{3}Q\right) }=\frac{J_{\phi }+J_{\psi }}{M+\frac{\sqrt{3}}{2}Q}\, . \end{aligned}$$
(66)

From Eq. (66) it is clear that near-extremality requires \(Q^2 < M^2/3 \), which in turn allows us to choose \(Q=0.5M\). For given \(Q=0.5 M\), \(f(0)=\alpha ^2\) corresponding to the near extremality defines the angular momenta numerically, \(J_{\phi }+J_{\psi }=0.322011\) for the given value \(\alpha =0.01\). For this thought experiment one can take different values of the black hole parameters and even smaller values of \(\alpha \). Setting \(M=1\), let us choose \(\delta J_{\phi }=0.001\ll J_{\phi } \), \(\delta J_{\psi }=0.001\ll J_{\psi } \) and \(\delta Q=0.003 \ll Q\) in order for the test particle approximation to remain valid. Let us now evaluate Eq. (65) numerically, whereby \(f(0.1)=-0.00045<0\). That is, it could be over-extremalized under linear order accretion. It thus indicates violation of WCCC at the linear order. The obtained numerical results are shown in Fig. 1.

Fig. 1
figure 1

\(f(\lambda )\) against \(\lambda \) for the given values of the test particle and black hole parameters

Full size image

4.3.2 Non-linear order accretion

We here consider the second order particle accretion \(O(\lambda ^2)\) so as to understand what might happen in the non-linear regime. Let us start from Eq. (63), where the non-linear terms are given by

$$\begin{aligned}&\delta ^2 M-\frac{9\pi \left( J_{\phi }+J_{\psi }\right) }{4(4M^2-3Q^2)}\left( \delta ^2 J_{\phi }+\delta ^2 J_{\psi }\right) \nonumber \\&\quad -\frac{3\left( 2MQ-\sqrt{3}Q^2\right) }{\left( 4M^2-3Q^2\right) }~\delta ^2 Q \nonumber \\&\quad \ge -\frac{k}{8\pi }\delta ^2 A= \frac{1}{12\left( 4M^2-3Q^2\right) \alpha ^2}\nonumber \\&\quad \times \Bigg (N_{1}\left( M,Q,J_{\phi },J_{\psi }\right) \delta M^2\nonumber \\&\quad +N_{2}\left( M,Q,J_{\phi },J_{\psi },\delta J_{\phi },\delta J_{\psi }\right) \delta M\nonumber \\&\quad +N_{3}\left( M,Q,J_{\phi }\right) \delta J_{\psi }^2\nonumber \\&\quad +N_{4}\left( M,Q,J_{\phi },J_{\psi }\right) \delta J_{\phi }\delta J_{\psi }\nonumber \\&\quad +N_{5}\left( M,Q,J_{\phi },J_{\psi },\delta J_{\phi },\delta J_{\psi }\right) \delta M\delta Q+N_{6}\left( M,Q,J_{\psi }\right) \nonumber \\&\quad \times \delta J_{\phi }^2+N_{7}\left( M,Q,J_{\phi },J_{\psi },\delta J_{\phi },\delta J_{\psi }\right) \delta Q\nonumber \\&\quad +N_{8}\left( M,Q,J_{\phi },J_{\psi }\right) \delta Q^2\Bigg ). \end{aligned}$$
(67)

Here the function \(N_{i}\) is related to the black hole parameters in a complicated way. When we take into account a non-linear term \(O(\lambda ^2)\) by using Eq. (67) and optimal choice of linear order correction, the function \(f(\lambda )\) takes the form

$$\begin{aligned} f(\lambda )> & {} \left( \alpha -\frac{3\left( 2 M+\sqrt{3} Q\right) ^{-1}~\lambda }{\left( 27 \pi J_{\phi } J_{\psi }+4 \sqrt{3} Q \left( 2 M+\sqrt{3} Q\right) ^2\right) ^{1/2} \left( 9\pi (J_{\phi }+J_{\psi })^2+\frac{4\sqrt{3}}{3}Q\left( 2 M+\sqrt{3} Q\right) ^2\right) ^2}\right. \nonumber \\&\times \left[ 6 \pi \left( M+\frac{\sqrt{3} Q}{2}\right) \left( 144 \sqrt{3} \pi Q \left( M+\frac{\sqrt{3} Q}{2}\right) ^2 \right. \right. \Big [\delta J_{\psi } J_{\phi }^3+2 J_{\psi } J_{\phi }^2 (\delta J_{\phi }+2 \delta J_{\psi })+2 J_{\phi } J_{\psi }^2(\delta J_{\psi }\nonumber \\&\quad +2 \delta J_{\phi })+\delta J_{\phi } J_{\psi }^3\Big ] + 243 \pi ^2 {J_{\phi }} {J_{\psi }} ({J_{\phi }}+{J_{\psi }})^2 (\delta J_{\psi } {J_{\phi }}+\delta J_{\phi } {J_{\psi }})+16 Q^2 \left( 2 M+\sqrt{3} Q\right) ^4 \big [{J_{\phi }} (\delta J_{\phi }+2 \delta J_{\psi })\nonumber \\&\left. +{J_{\psi }}(\delta J_{\psi }+2 \delta J_{\phi })\big ]\right) + 256 Q^2 \left( M+\frac{\sqrt{3} Q}{2}\right) ^4 \left. \left. \left( 9 \sqrt{3} \pi {J_{\phi }} {J_{\psi }}+4 Q \left( 2 M+\sqrt{3} Q\right) ^2\right) \delta Q \right] \right) ^2\nonumber \\&+\mathcal {O}(\alpha ^3,\alpha ^2\lambda ,\alpha \lambda ^2,\lambda ^{3}). \end{aligned}$$
(68)

This clearly shows that always \(f(\lambda ) > 0\). Thus, it verifies the expected result that a five-dimensional charged rotating black hole in minimally gauged supergravity cannot be over-extremalized for non-linear order accretion, while the opposite is true for linear order accretion. Under non-linear accretion WCCC is therefore always obeyed.

4.4 With single rotation

4.4.1 Linear order accretion

Let us consider a particular case of single rotation, for which Eq. (65) takes the following form:

$$\begin{aligned} f(\lambda )= & {} \alpha ^2-\frac{48\times 3^{3/4}Q^{3/2}\left( 2 M+\sqrt{3} Q\right) ^3}{\left( 9\sqrt{3}\pi J_{\psi }^2+4Q\left( 2 M+\sqrt{3} Q\right) ^2\right) ^2}\nonumber \\&\times \bigg (3\pi J_{\psi }\delta J_{\psi }+4Q\left( 2M+\sqrt{3}Q\right) \delta Q\bigg )\alpha \lambda \nonumber \\&+\mathcal {O}(\lambda ^2). \end{aligned}$$
(69)

It is clear from the above equation that overspinning/charging is quite possible in general. However, let us consider the various cases separately.

  • \(\delta Q=0\). Note that in the limit \(Q \rightarrow 0 \) one can reach \(f(\lambda )>0\), for which the black hole could not be overspun, thereby verifying the validity of the WCCC for a black hole having a single rotation. This verifies the recently obtained result Ref. [45] that WCCC is obeyed for single rotation even at linear order accretion. Consider the numerical example: for \(Q=0.5\), \(J_{\psi }=0.322011\), \(\delta J_{\psi }=0.001\), and \(\alpha =0.01\) with \(\lambda =0.1\) we get \(f(\lambda )=0.000041 >0\). Thus WCCC would always hold good for a neutral particle.

  • \(\delta J_{\psi }=0\). It is well known that a four-dimensional charged black hole could be overcharged [47]. To be a bit more quantitative let us reconsider Eq. (69), for \(Q=0.5\), \(J_{\psi }=0.322011\), \(\delta Q=0.003\), and \(\alpha =0.01\) with \(\lambda =0.1\): we get \(f(\lambda )=-0.00048 <0\). With this we again verify the result of Ref. [47] that WCCC could as in four dimensions be violated.

Thus a five-dimensional black hole with single rotation could be overcharged but not overspun. The natural question then arises what happens to five-dimensional charged black hole with a single rotation—could it be overcharged or overspun under bombardment of over-charged particles?

Fig. 2
figure 2

From left: \(f(\lambda )\) for \(\delta J_{\psi } \ll \delta Q\) and \(\delta J_{\psi }\gg \delta Q \) against \(\lambda \) for the given values of the test particle and black hole parameters

Full size image

  • We know that a black hole cannot be overspun but it could be over-charged. When both charge and rotation are present, the outcome should depend on which one is the greater. The question is: does this dominance refer to black hole rotation and charge parameters or that of the impinging particles? It turns out that it refers to the parameters of the impinging particles. We will show this by numerical examples. Let us begin with \(\delta J_{\psi } < \delta Q\). The question is, what might happen in this case? To answer this question we must approach, as in previous cases, the problem quantitatively. For given \(Q=0.5\), \(J_{\psi }=0.322011\), \(\delta Q=0.003\), \(\delta J_{\psi }=0.0001\), and \(\alpha =0.01\) with \(\lambda =0.1\) leads to \(f(\lambda )=-0.0002445\), and so the black hole could be over-extremalized violating the CCC. Let us now interchange the black hole parameters and keep the rest of the parameters unchanged. That is, \(Q=0.353553\), \(J_{\psi }=0.499394\), \(\delta Q=0.003\), \(\delta J_{\psi }=0.0001\), and \(\alpha =0.01\) with \(\lambda =0.1\) will give \(f(\lambda )=-0.00001495 <0\), implying over-extremalization.

  • \(\delta J_{\psi } > \delta Q\). Let us again consider the numerical exercise: Take a) \(Q=0.5\), \(J_{\psi }=0.322011\) and b) \(Q=0.353553\), \(J_{\psi }=0.499394\) for given \(\delta Q=0.0003\), \(\delta J_{\psi }=0.001\), and \(\alpha =0.01\) with \(\lambda =0.1\). That leads to a) \(f(\lambda )=6.3832\times 10^{-6}>0\) and b) \(f(\lambda )=50.1196\times 10^{-6}>0\). It cannot be over-extremalized, and WCCC continues to hold ground.

  • \(\delta J_{\psi } = \delta Q\). Let us consider the values of the parameters to be as follows: a) \(Q=0.5\), \(J_{\psi }=0.322011\) and b) \(Q=0.353553\), \(J_{\psi }=0.499394\) for given \(\delta Q=0.003\), \(\delta J_{\psi }=0.003\), and \(\alpha =0.01\) with \(\lambda =0.1\), we get a) \(f(\lambda )=-0.000417867 <0\) and b) \(f(\lambda )=-0.000116191 <0\). This shows that the black hole could reach an over-extremal state when impinging particles have angular momentum equal to charge.

What emerges from this analysis is that a black hole with single rotation for linear accretion obeys WCCC so long as \(\delta Q < \delta J{\psi }\), and the opposite is true for \(\delta Q \ge \delta J{\psi }\) irrespective of the relative dominance of the black hole rotation and charge parameters. In Fig. 2 we verify the above numerical analysis for \(\delta Q > \delta J{\psi }\) and \(\delta Q < \delta J{\psi }\), respectively. Interestingly, in the case of equality of angular momentum and charge of impinging particles it is the charge’s interaction that plays a dominant role for the over-extremalizing process.

4.4.2 Non-linear order accretion

Let us rewrite Eq. (68) in the case of a single rotation,

$$\begin{aligned} f(\lambda )= & {} \left( \alpha -\frac{48\times 3^{3/4}Q^{3/2}\left( 2 M+\sqrt{3} Q\right) ^3\bigg (3\pi J_{\psi }\delta J_{\psi }+4Q\left( 2M+\sqrt{3}Q\right) \delta Q\bigg )}{\left( 9\sqrt{3}\pi J_{\psi }^2+4Q\left( 2 M+\sqrt{3} Q\right) ^2\right) ^2} \lambda \right) ^2 +\mathcal {O}(\alpha ^3,\alpha ^2\lambda ,\alpha \lambda ^2,\lambda ^{3}). \end{aligned}$$
(70)

From this, it is clear that the black hole cannot be over-extremalized when second order perturbations, \(\mathcal {O}(\lambda ^2)\), are taken in account. For non-linear accretion, WCCC thus always holds good.

5 Conclusions

It is well known that there does not exist a true analogue of the four-dimensional Kerr–Newman rotating charged black hole in five dimensions. On the other hand there exists an analogue of a Kerr rotating black hole in five or more dimensions [44]. Strangely, electric charge cannot be injected onto a rotating black hole. However, there exists a very close cousin of the Kerr–Newman black hole in a minimally gauged supergravity solution of rotating and charged black hole [58]. To this black hole we have in this paper extended the analysis of over-extremalization under a linear and non-linear accretion process [43].

In general it turns out that, as for all other cases, over-extremalizing is possible for linear order, while it gets miraculously reversed when non-linear perturbations are included. The five-dimensional black hole in question thus falls in line with all other black holes: WCCC could be violated at linear order but it is always restored at non-linear order accretion. However, there is a subtle exception for a rotating black hole in five dimensions, which has two rotation axes permitting two rotation parameters.

Very recently, some of us [45] have demonstrated a remarkable property of a black hole with single rotation. Unlike a four-dimensional black hole, it cannot be overspun even at the linear order accretion while it could be overspun when both rotations are present. This property is, however, carried through for the five-dimensional rotating charged black hole under study. A charged black hole could always be overcharged under linear accretion. In this case there are both rotations and charge present. Hence the question: when would it be over-extremalized and when not? As expected it turns out that when the rotation parameter of the impinging particle is greater than its charge, over-extremalizing is prohibited while the opposite is the case when charge is greater than or equal to the rotation parameter. It is interesting that in the case of equality of rotation and charge parameters, it is the latter’s contribution that dominates. In all this, the relative dominance of charge or rotation of the black hole is, however, irrelevant.

As pointed out in [45], a black hole with single rotation in five dimensions is a different entity, like extremal black hole. The latter can never be over-extremalized and, interestingly, so is the case for the former. It seems that when a black hole has the maximum number of rotations that are permitted in a given spacetime dimension, it can be overspun under linear order accretion, while if it has less than the maximum allowed, it cannot be overspun. In four dimensions, the maximum allowed number of parameters is one and that is why it can be overspun, while in five dimensions the maximum number allowed is two. That is why it can perhaps only violate WCCC when both rotations are present, but not for single rotation.

It may be noted that for non-linear accretion we have a neat analytical expression showing \(f(\lambda ) > 0\), indicating the absence of over-extremalization. However, for linear order perturbations we had to resort to a numerical evaluation because calculations were too involved and complicated. For over-extremalization, any specific example is good enough to show that it occurs, while for its absence one has to show that that it is never possible. We do, however, consider an optimal choice of parameters which would indicate that the result would hold good in general for any other choice of parameters. Most importantly it is the non-linear regime that has the final and determining say, which has been established rigorously and analytically.