Abstract
We study, using mean curvature flow methods, \(2+1\) dimensional cosmologies with a positive cosmological constant and matter satisfying the dominant and the strong energy conditions. If the spatial slices are compact with non-positive Euler characteristic and are initially expanding everywhere, then we prove that the spatial slices reach infinite volume, asymptotically converge on average to de Sitter and they become, almost everywhere, physically indistinguishable from de Sitter. This holds true notwithstanding the presence of initial arbitrarily-large density fluctuations and the formation of black holes.



Similar content being viewed by others
Notes
This indeed confirms what was expected in [2]: once the initial conditions are taken from a general enough class, since the system is very non-linear and even forms singularities, it explores the whole class of non-linear solutions after a Hubble time.
In this paper the inflaton potential is replaced by a cosmological constant. Therefore we do not address issues like how likely it is for the inflaton to start sufficiently far away from the minimum of the potential. In numerical studies [2, 5, 6] it was observed that once the initial conditions of the inflaton field are entirely contained within the inflationary part of the potential, it behaves effectively like a cosmological constant. This justifies and motivates our approximation.
Technically, however, we need to assume, as we will do in this paper, the absence of finite-volume singularities, i.e. that the expanding spacetime simply comes to an end on some spacelike surface that is not a zero-volume crunch (see [3]). Such finite-volume singularities seem to us highly artificial and unphysical on general grounds, and can probably be forbidden with appropriate conditions on the stress-energy tensor, see [16].
For SEC indeed
$$\begin{aligned} T_{\mu \nu } = \partial _\mu \phi \partial _\nu \phi - \frac{1}{2} g_{\mu \nu } (\partial \phi )^2 \quad \Rightarrow \quad \left( T_{\mu \nu }- \frac{g_{\mu \nu }}{n-1} T\right) k^\mu k^\nu = (\partial \phi \cdot k)^2 \ge 0. \end{aligned}$$(5)For example in a Schwarzschild-de Sitter spacetime in the standard coordinates, one could take \({\tilde{t}}\) to be a function of r for r close to 0, so the level sets \(S_c\) would be \(r=\mathrm{const}\).
One can get this equation similarly to the derivation of the Raychauduri equation, bearing in mind that we are not following geodesics orthogonal to the surface.
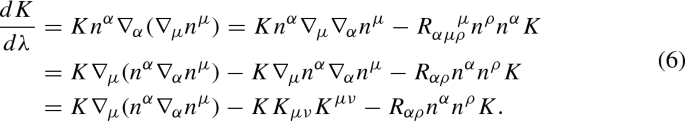
Imposing that \(n^\mu \) remain perpendicular to the surface one gets

Therefore
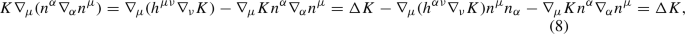
where in the last step, to obtain the Laplacian on the surface, we separated the covariant derivative in the components parallel and orthogonal to the surface. Plugging this expression in Eq. (6) one obtains Eq. (9) after separating the contribution of the cosmological constant and the traceless part of \(K_{\mu \nu }\).
This formula can be easily derived. Consider the gradient of the height function projected on the surface
$$\begin{aligned} \nabla _\parallel {}^\mu {\tilde{u}} = \nabla _\parallel {}^\mu {\tilde{t}} = (g^{\mu \nu } +n^\mu n^\nu ) \partial _\nu {\tilde{t}} = \partial ^\mu {\tilde{t}} + {\tilde{v}} {\tilde{N}}^{-1} n^\mu . \end{aligned}$$(22)We can now take a second derivative and trace it on the surface
$$\begin{aligned} \Delta {\tilde{u}} = \nabla _{\parallel }{}_{\mu } \nabla _\parallel {}^\mu {\tilde{u}}= h^\nu _\mu {{\bar{\nabla }}}_\nu \nabla _\parallel {}^\mu {\tilde{u}} =h^\nu _\mu {{\bar{\nabla }}}_\nu \partial ^\mu {\tilde{t}} + h^\nu _\mu {{\bar{\nabla }}}_\nu ({\tilde{v}} {\tilde{N}}^{-1} n^\mu ) = {\mathrm{div}}{\bar{\nabla }} {\tilde{t}} + {\tilde{v}} {\tilde{N}}^{-1} K , \end{aligned}$$(23)where
$$\begin{aligned} {\mathrm{div}}{\bar{\nabla }} {\tilde{t}} \equiv h^\nu _\mu {{\bar{\nabla }}}_\nu \partial ^\mu {\tilde{t}} . \end{aligned}$$(24)In fact, one can write Eq. (9) as
$$\begin{aligned} \frac{d K}{d \lambda } -\Delta K + \frac{1}{n} K\left( K^2-K_{\Lambda _2}^2\right) + \sigma ^2 K + {{\bar{R}}}^{(m)}_{\mu \nu } n^\mu n^\nu K =0 , \end{aligned}$$with
$$\begin{aligned} {\bar{R}}^{(m)}_{\mu \nu } \equiv 8\pi G \left( T_{\mu \nu }-\frac{g_{\mu \nu }}{n-1} T\right) +\frac{16\pi G}{n-1} g_{\mu \nu }\left( V(\phi )-\Lambda _2\right) \ , \end{aligned}$$where \(T_{\mu \nu }\) is the part of the stress tensor that satisfies SEC. Given the upper bound on \(V(\phi )\), \({\bar{R}}^{(m)}_{\mu \nu } n^\mu n^\nu \ge 0\), and Theorem 2 follows.
In the case of the torus one can have \({^{(2)}\!R} = 0\) everywhere, which allows \(K \le K_\Lambda \) everywhere. Still, all our conclusions hold, as can be seen from the sentence below the formulation of Theorem 2. Notice, however, that this is a particularly simple case: Eq. (28) would imply \(K = K_\Lambda \) and \(\sigma _{\mu \nu } =0\). Also \(T_{\mu \nu }n^\nu n^\mu =0\) and this would imply \(T_{\mu \nu } =0\) because of the DEC (see the discussion below). Therefore, one has the flat slicing of de Sitter space.
Notice that in this case one could have \(K_m(\lambda )\le K_\Lambda \) everywhere, but all our conclusions still apply in light of the sentence below the formulation of Theorem 2.
Static black holes do not really exist in \(2+1\) dimensions, but generically crunching singularities will form. We loosely refer to these as black holes.
It is tempting to say that the regions that converge to de Sitter (up to corrections of vanishing physical volume) will be screened by an event horizon from the other regions that do not converge to de Sitter. However this seems hard to prove. One could imagine that, instead of localised spaceships, the regions of no-convergence with vanishing physical volume are filamentary structures that connect each Hubble patch to far-away regions of finite physical volume that do not converge to de Sitter. Since one does not have pointwise convergence to de Sitter along these structures, one could imagine that these filaments are enough to allow the regions that do not converge to de Sitter to wander around and sooner or later visit any Hubble patch.
Perhaps more simply, one can conclude that since the energy of each region goes to zero, these regions cannot have asymptotically-vanishing physical volume because of quantum mechanics, and so cannot densely populate the whole volume, against the hypothesis.
References
Ijjas, A., Steinhardt, P.J.: Implications of Planck 2015 for inflationary, ekpyrotic and anamorphic bouncing cosmologies. Class. Quantum Gravit. 33, 044001 (2016). arXiv:1512.09010
East, W.E., Kleban, M., Linde, A., Senatore, L.: Beginning inflation in an inhomogeneous universe. JCAP 1609, 010 (2016). arXiv:1511.05143
Kleban, M., Senatore, L.: Inhomogeneous anisotropic cosmology. JCAP 1610, 022 (2016). arXiv:1602.03520
Barrow, J.D., Tipler, F.J.: Closed universes: their future evolution and final state. Mon. Not. R. Astron. Soc. 216, 395–402 (1985)
Clough, K., Lim, E.A., DiNunno, B.S., Fischler, W., Flauger, R., Paban, S.: Robustness of inflation to inhomogeneous initial conditions. JCAP 1709, 025 (2017). arXiv:1608.04408
Clough, K., Flauger, R., Lim, E.A.: Robustness of inflation to large tensor perturbations. JCAP 1805, 065 (2018). arXiv:1712.07352
Pretorius, F.: Evolution of binary black hole spacetimes. Phys. Rev. Lett. 95, 121101 (2005). arXiv:gr-qc/0507014
Besse, A.: Einstein Manifolds. Classics in Mathematics. World Publishing Company, Cleveland (1987)
Thurston, W., Levy, S.: Three-Dimensional Geometry and Topology. No. v. 1 in Luis A. Caffarelli. Princeton University Press, Cambridge (1997)
Perelman, G.: Manifolds of positive Ricci curvature with almost maximal volume. J. Am. Math. Soc. 7, 299–305 (1994)
Gerhardt, C.: Curvature Problems. International Press, Boston (2006)
Creminelli, P., Kleban, M., Mirbabayi, M., Senatore, L., Vasy, A.: In progress
Geroch, R.: Domain of dependence. J. Math. Phys. 11, 437–449 (1970)
Ecker, K., Huisken, G.: Parabolic methods for the construction of spacelike slices of prescribed mean curvature in cosmological spacetimes. Commun. Math. Phys. 135, 595 (1991)
Eardley, D.M., Smarr, L.: Time functions in numerical relativity: marginally bound dust collapse. Phys. Rev. D 19, 2239–2259 (1979)
Barrow, J.D., Galloway, G.J., Tipler, F.J.: The closed-universe recollapse conjecture. Mon. Not. R. Astron. Soc. 223, 835–844 (1986)
Ecker, K.: On mean curvature flow of spacelike hypersurfaces in asymptotically at space-times. J. Austr. Mat. Soc. 55, 41 (1993)
Mirbabayi, M.: Topology of cosmological black holes. arXiv:1810.01431
Bartnik, R.: Existence of maximal surfaces in asymptotically flat spacetimes. Commun. Math. Phys. 94, 155–175 (1984)
Wald, R.M.: General Relativity. The University of Chicago Press, Chicago (1984)
Wald, R.M.: Asymptotic behavior of homogeneous cosmological models in the presence of a positive cosmological constant. Phys. Rev. D 28, 2118–2120 (1983)
Acknowledgements
It is a pleasure to thank Or Hershkovits for collaboration in the earlier stages of this work and for patient mathematical consultancy. We also thank Klaus Ecker, Alan Guth, Larry Guth, Matt Kleban, Rafe Mazzeo, Mehrdad Mirbabayi, Richard Schoen, and Vicharit Yingcharoenrat for useful conversations. LS is partially supported by Simons Foundation Origins of the Universe program (Modern Inflationary Cosmology collaboration) and by NSF award 1720397. AV is partially supported by NSF award DMS-1664683.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Chrusciel
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Creminelli, P., Senatore, L. & Vasy, A. Asymptotic Behavior of Cosmologies with \(\Lambda >0\) in \(2+1\) Dimensions. Commun. Math. Phys. 376, 1155–1170 (2020). https://doi.org/10.1007/s00220-020-03706-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-020-03706-3