Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-18T22:30:09.403Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximizing Bernoulli measures and dimension gaps for countable branched systems

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Smooth dynamical systems: general theory

Published online by Cambridge University Press:  26 May 2020

SIMON BAKER  and
NATALIA JURGA
SIMON BAKER
Affiliation:
School of Mathematics, University of Birmingham, Birmingham, B15 2TT, UK email simonbaker412@gmail.com
NATALIA JURGA
Affiliation:
Mathematical Institute, University of St Andrews, KY16 9SS, UK email natalia-j@live.co.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Kifer, Peres, and Weiss proved in [A dimension gap for continued fractions with independent digits. Israel J. Math.124 (2001), 61–76] that there exists 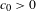$c_{0}>0$, such that 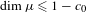$\dim \unicode[STIX]{x1D707}\leq 1-c_{0}$ for any probability measure $\unicode[STIX]{x1D707}$, which makes the digits of the continued fraction expansion independent and identically distributed random variables. In this paper we prove that amongst this class of measures, there exists one whose dimension is maximal. Our results also apply in the more general setting of countable branched systems.

Keywords

continued fractionsBernoulli measuresdimensions of measures

MSC classification

Primary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension 37C45: Dimension theory of dynamical systems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 7 , July 2021 , pp. 1921 - 1939
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Fan, A. H., Liao, L. and Ma, J. H.. On the frequency of partial quotients of regular continued fractions. Math. Proc. Cambridge Philos. Soc. 148(1) (2010), 179–192.Google Scholar
Jurga, N.. A new proof of the dimension gap for the Gauss map. Preprint, arXiv:1806.00841 [math.DS].Google Scholar
Kifer, Y., Peres, Y. and Weiss, B.. A dimension gap for continued fractions with independent digits. Israel J. Math. 124 (2001), 61–76.10.1007/BF02772607CrossRefGoogle Scholar
Kinney, J. and Pitcher, T.. The dimension of some sets defined in terms of f-expansions. Z. Wahrsch. Verw. Gebiete 4 (1965/1966), 293–315.CrossRefGoogle Scholar
Mauldin, D. and Urbanski, M.. Graph Directed Markov Systems: Geometry and Dynamics of Limit Sets (Cambridge Tracts in Mathematics, 148) . Cambridge University Press, Cambridge, 2003.Google Scholar
Rapaport, A.. A dimension gap for continued fractions with independent digits – the non stationary case. Israel J. Math. 227(2) (2018), 911–930.CrossRefGoogle Scholar
Walters, P.. Invariant measures and equilibrium states for some mappings which expand distances. Trans. Amer. Math. Soc. 236 (1978), 121–153.CrossRefGoogle Scholar