On the tuning of static pull-in instability and nonlinear vibrations of functionally graded micro-resonators with three different configurations

Abstract

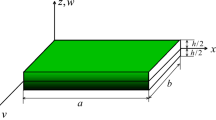
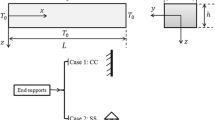
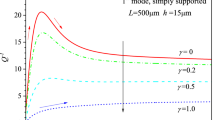
In this paper, the vibrational behavior of a functionally graded (FG) micro-resonator is investigated for three different configurations based on the Euler–Bernoulli beam model and the Von Karman nonlinear strain assumption. The three configurations include: (1) an FG micro-resonator with a fixed foundation, (2) piezoelectric layers added to the first model, and (3) a second fixed foundation added to the first model. These investigations are performed under the effect of electrostatic forces, the forces caused by the deformations of piezoelectric layers due to the applied voltage, Casimir forces, and uniform temperature changes. The equations governing the vibrational behaviors are obtained using the Hamilton’s principle and the modified couple stress theory. Static deformations and the fundamental vibrational mode are calculated using the differential quadrature method in the spatial domain for all three configurations. Furthermore, the dynamic equations are obtained from the Galerkin discretization and solved with multiple time scales technique. The results show that the frequency behavior of a micro-resonator can be adjusted using the three models.

Appendix

In differential quadrature method, the domain is discretized in N grid points along the x-direction. At a given grid point $x_{i}$, derivatives of a function can be approximated as [51]:

$$\begin{aligned} \left. {\frac{{\partial f\left( {x,t} \right)}}{\partial x}} \right|_{{x = x_{i} }} & = \mathop \sum \limits_{j = 1}^{N} A_{ij} f\left( {x_{j} ,t} \right) = \mathop \sum \limits_{j = 1}^{N} A_{ij} f_{j} \left( t \right),\left. {\frac{{\partial^{2} f\left( {x,t} \right)}}{{\partial x^{2} }}} \right|_{{x = x_{i} }} = \mathop \sum \limits_{j = 1}^{N} B_{ij} f_{j} \left( t \right), \\ \left. {\frac{{\partial^{3} f\left( {x,t} \right)}}{{\partial x^{3} }}} \right|_{{x = x_{i} }} & = \mathop \sum \limits_{j = 1}^{N} C_{ij} f_{j} \left( t \right),\left. {\frac{{\partial^{4} f\left( {x,t} \right)}}{{\partial x^{4} }}} \right|_{{x = x_{i} }} = \mathop \sum \limits_{j = 1}^{N} D_{ij} f_{j} \left( t \right). \\ \end{aligned}$$

$A_{ij} ,B_{ij} ,C_{ij}$ and $D_{ij}$ denote the weighting coefficients, which are used in the first-, second-, third- and fourth-order derivatives, respectively. $A_{ij}$ is determined as follows:

$$A_{ij} = \left\{ {\begin{array}{*{20}l} {\frac{1}{L}\frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}}} \hfill & {{\text{for}}\quad i \ne j} \hfill \\ {\mathop{\mathop{\sum}\limits_{i = 1}}\limits_{i \ne j}}^{N} A_{ij} \hfill & {{\text{for}}\quad i = j} \hfill \\ \end{array} } \right.\quad i,j = 1,2, \ldots ,N,$$

where $M\left( {x_{i} } \right) = \mathop \prod \nolimits_{j = 1}^{N} \left( {x_{i} - x_{j} } \right)$. Other weighting coefficients are calculated based on $A_{ij}$ as:

$$B_{ij} = \left[ { A_{ij} } \right]^{2} ,\quad C_{ij} = \left[ { A_{ij} } \right]^{3} ,\quad D_{ij} = \left[ { A_{ij} } \right]^{4} .$$

and

$$\bar{D}_{ij} = \mathop \sum \limits_{m = 2}^{N - 1} B_{im} B_{mj}\quad \kappa = \frac{{\partial^{2} w}}{{\partial x^{2} }}$$

The weighting coefficients of the IQM can be written in the following form [52]:

$$\left\{ R \right\} = \left[ X \right]^{ - 1} \left\{ I \right\}$$