Introduction

The first quantum key distribution (QKD) protocol has been proposed by Bennett and Brassard in 1984; the protocol was based on the fundamentals of quantum mechanics1. Since then, the security of QKD has always been the central issue in the quantum cryptographic field2. Trace distance is a very important security criterion3,4. It provides the universal composable security5,6, which can guarantee the security of key regardless of its application such as one-time pad (OTP). This is why many studies choose trace distance for the security criterion3,4,7,8.

In a classical practical cryptosystem, the impact of guessing probability on security is very important9,10. Specifically, the key generated by the QKD protocol is not based on the presumed hardness of mathematical problems; thus, the eavesdropper Eve can only guess the final key via the measurement result of her probe. The guessing probability intuitively describes the probability that Eve can correctly guess the final key, which can reflect the number of guesses that Eve requires to obtain the final key.

There are few studies on the guessing probability of QKD. Because there are more rigorous security criterions, such as the trace distance5,6, which gives the composable security. This makes the theoretical foundation for security of QKD crucially important. However, in the real application of QKD projects, customers often ask the question of guessing probability. The existing prior art results cannot give them a satisfactory upper bound11. Consequently, some people questioned the security of QKD by relying on the prior art results of guessing probability12. For example, according to the existing result11, the guessing probability of the ε-secure key is approximately 10−9 if ε is approximately 10−9. From the perspective of guessing probability, the security of the value 10−9 is equivalent to that of a 30 perfect bits. The existing classical computer systems can easily crack such key. In practice, it is not unusual to request a much smaller guessing probability such as 10−100 or 10−1000. Therefore, it is beneficial to find a more tightened upper bound of guessing probability.

As an important criterion in cryptography, guessing probability alone cannot guarantee the security of the final key. However, the large value of the loose upper bound of the guessing probability does not indicate the insecurity of the final key12 because the value is not achievable by Eve, and one can find a more tightened value for the upper bound of the guessing probability. Here, by applying the trace distance criterion2, we find such tightened bound. We show that the guessing probability is actually smaller than the existing bound values by many orders of magnitude if one takes the privacy amplification by Toeplitz matrix. This shows that the trace distance criterion2 can actually produce a much better result than what was assumed previously in the viewpoint of guessing probability.

Results

We consider the security definitions of a practical QKD protocol with finite size under the framework of composable security3,4,13,14. Suppose that Alice and Bob get two N-bit sifted key strings, s and \({\bf{s}}^{\prime}\). By performing an error correction and private amplification scheme, Alice gets an n1-bit key k, and Bob gets an estimate key \(\hat{{\bf{k}}}\) of k from s and \({\bf{s}}^{\prime}\). The protocol is εcor-correct if \(P[{\bf{k}}\,\ne\, \hat{{\bf{k}}}]\le {\varepsilon }_{{\rm{cor}}}\). In general, the key k of Alice can be correlated with an eavesdropper system, and the density matrix of Alice and Eve is ρAE. The protocol outputs an ε-secure key7, if

$$\frac{1}{2}\parallel {\rho }_{{\rm{AE}}}-{\rho }_{{\rm{U}}}\otimes {\rho }_{{\rm{E}}}{\parallel }_{1}\le \varepsilon ,$$
(1)

where ∥ ⋅ ∥1 denotes the trace norm, ρU is the fully mixed state of Alice’s system. The protocol is εtol-secure if εcor and ε satisfy εcor + ε ≤ εtol, which means that it is εtol-indistinguishable from a perfect protocol (which is correct and secret). Without any loss of generality, we consider the case of εcor = ε in this article.

We define the security level:

Definition 1

If key k is ε-secure, the security level of key k is ε

For symbol clarity, we will use notation εk for the security level of key k. With this definition, we can say that the key k is εk-secure or that its security level is εk

We define the guessing probability:

Definition 2

Let the final key generated by the QKD protocol be k; the guessing probability of k is defined as the success probability of the attacker Eve guessing the final key via her measurement result and is denoted as p(k).

Lemma 1

The guessing probability of εk-secure key k with length n1 is not larger than \(\frac{1}{{2}^{{n}_{1}}}+{\varepsilon }_{{\bf{k}}}\)

This is a conclusion from ref. 11. The proof has been already given in ref. 11; for the convenience of readers, we write the proof again in the “Methods” section

According to Lemma 1, the guessing probability of key k can be divided into two parts; one part \({2}^{-{n}_{1}}\) is related to the length of the key, the other part εk(n1) is related to the security level. Under the framework of universally composable security, when calculating the final key length, we often make the security level to be between 10−9 and 10−24, which is much bigger than \({2}^{-{n}_{1}}\) because n1 is often 103, 104, or larger. Therefore, \({2}^{-{n}_{1}}\) can be ignored and \(p({\bf{k}})\le \bar{p}({\bf{k}}) \sim {\mathcal{O}}(\varepsilon ({\bf{k}}))\). However, the guessing probability of a secure key with a length of tens of bits can also reach this magnitude. Therefore, when the secure requirements are very high, it is clearly not enough for a key with a length of thousands of bits or even longer if the upper bound of guessing probability only stops at this magnitude. Therefore, we cannot simply use this formula alone to obtain the upper bound of the guessing probability. Fortunately, we have a much better way for tightening the bound. The approach will be presented below.

Lemma 2

If key k can be mapped to string \({\bf{k}}^{\prime}\) by a map M that is known to Eve, then the guessing probability of k cannot be larger than the guessing probability of string \({\bf{k}}^{\prime}\), i.e.,

$$p({\bf{k}})\le p({\bf{k}}^{\prime} ).$$
(2)

Here \(p({\bf{k}}),p({\bf{k}}^{\prime} )\) are the guessing probabilities of k and \({\bf{k}}^{\prime}\), respectively

Proof. This lemma is clear because when Eve can correctly guess k, Eve can obtain \({\bf{k}}^{\prime}\) by knowing the map M. Otherwise, Eve can still correctly guess the \({\bf{k}}^{\prime}\) with a probability not less than 0, i.e., \(p({\bf{k}}^{\prime} )=p({\bf{k}})+\delta ,\delta \ge 0\).

Theorem 1

If the εk-secure key k with a length n1 can be mapped to the \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure key \({\bf{k}}^{\prime}\) with length n2, the guessing probability of k cannot be larger than \({\bf{k}}^{\prime}\), i.e.,

$$p({\bf{k}})\le \bar{p}({\bf{k}}^{\prime} )=\frac{1}{{2}^{{n}_{2}}}+{\varepsilon }_{{\bf{k}}^{\prime} }.$$
(3)

Proof. This theorem actually requires two conditions:

  1. (i)

    the final key k can be mapped to the string \({\bf{k}}^{\prime}\),

  2. (ii)

    the string \({\bf{k}}^{\prime}\) can be regarded as a \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure key.

Using the above-mentioned conditions, the proof is very simple. Given the condition (i), we can apply Lemma 2 to obtain

$$p({\bf{k}})\le p({\bf{k}}^{\prime} ).$$
(4)

Given the condition (ii), we can apply Lemma 1 to obtain

$$p({\bf{k}}^{\prime} )\le \bar{p}({\bf{k}}^{\prime} )=\frac{1}{{2}^{{n}_{2}}}+{\varepsilon }_{{\bf{k}}^{\prime} },$$
(5)

where \(\bar{p}({\bf{k}}^{\prime} )\) is the upper bound of \(p({\bf{k}}^{\prime} )\). According to Eqs. (4) and (5), we can obtain

$$p({\bf{k}})\le \bar{p}({\bf{k}}^{\prime} )=\frac{1}{{2}^{{n}_{2}}}+{\varepsilon }_{{\bf{k}}^{\prime} }.$$
(6)

This ends our proof of Theorem 1

As discussed above, if the length of the final key k and the string \({\bf{k}}^{\prime}\) are very large, then \({2}^{-{n}_{1}}\) and \({2}^{-{n}_{2}}\) can be ignored. Meanwhile, if n2 < n1 and \({\varepsilon }_{{\bf{k}}^{\prime} }\,<\,{\varepsilon }_{{\bf{k}}}\), then \({2}^{-{n}_{2}}+{\varepsilon }_{{\bf{k}}^{\prime} } \sim {\varepsilon }_{{\bf{k}}^{\prime} }\le {\varepsilon }_{{\bf{k}}} \sim {2}^{-{n}_{1}}+{\varepsilon }_{{\bf{k}}}\). Thus, Theorem 1 can provide a tighter upper bound of guessing probability.

Using Theorem 1, it is now possible for us to obtain the upper bound of the guessing probability of the εk-secure key k more tightly. Instead of directly applying Lemma 1, we choose to first map k to an n2-bit string \({\bf{k}}^{\prime} =M({\bf{k}})\). If the string \({\bf{k}}^{\prime}\) itself can be regarded as an \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure final key, we can apply Theorem 1 by calculating \(\bar{p}({\bf{k}}^{\prime} )\). In addition, we can obtain a much smaller upper bound of the guessing probability of k if \({\varepsilon }_{{\bf{k}}^{\prime} }\) is very small and n2 is not too small. Now, the remaining problems are to determine the map M, to make sure that \({\bf{k}}^{\prime} =M({\bf{k}})\) is another key that is \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure, and to calculate \({\varepsilon }_{{\bf{k}}^{\prime} }\). We start our method with the hashing function in the key distillation.

Our hashing function

We use the key distillation with the random matrix. Denote RnN as the n × N random matrix with each element being randomly chosen to be either 0 or 1. In addition, we represent the N-bit sifted string s by a column vector, which contains N elements. To obtain the n-bit final key, we use the calculation RnNs. It can be easily confirmed that our random matrix belongs to the class of two-universal hashing function family2.

Suppose we have distilled out the n1-bit key k from the N-bit sifted key s through hashing by our random matrix \({R}_{{n}_{1}N}\). We can map the n1-bit key k into the n2-bit string \({\bf{k}}^{\prime} =M({\bf{k}})\) by deleting the last n1 − n2 bits from the key string k. Clearly, this string \({\bf{k}}^{\prime}\) mapped from k can be also regarded as another final key distilled from the sift key s by the n2 × N random hashing matrix \({R}_{{n}_{2}N}\), which is a submatrix of \({R}_{{n}_{1}N}\). In summary, we have

$${\bf{k}}^{\prime} =M({\bf{k}})={R}_{{n}_{2}N}{\bf{s}}.$$
(7)

This means that \({\bf{k}}^{\prime}\) is a string mapped from key k. Moreover, \({\bf{k}}^{\prime}\) can be regarded as another final key of length n2 distilled from the sifted key s. Because the two conditions in Theorem 1 are satisfied, according to Theorem 1, we can obtain a tightened upper bound of p(k) with Eq. (3) if we know the security level of key \({\bf{k}}^{\prime}\), i.e., the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\). Because our random matrix is a class of two-universal hashing function, the value \({\varepsilon }_{{\bf{k}}^{\prime} }\) depends on n24. The details are shown in the “Methods” section and explain the calculation of \({\varepsilon }_{{\bf{k}}^{\prime} }\) for n2. Hence, in the QKD protocol that uses a random hashing matrix presented here, to obtain the upper bound of the guessing probability of the n1-bit final key k, we can summarize the procedure above by the following scheme:

Scheme (1) Given the n1-bit final key k, we delete its last n1 − n2 bits and obtain a string \({\bf{k}}^{\prime}\). (2) We regard \({\bf{k}}^{\prime}\) as another possible final key that is \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure. Compute the \({\varepsilon }_{{\bf{k}}^{\prime} }\) value of \({\bf{k}}^{\prime}\) with the input parameters N and n2. (3) Calculate \(\bar{p}({\bf{k}})\) by Theorem 1 through Eq. (3).

Because on our scheme the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\) is dependent on n2, as shown in the “Methods” section, we can now replace \({\varepsilon }_{{\bf{k}}^{\prime} }\) by a functional form, \({\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\). To obtain the tightened upper bound value of the guessing probability in scheme 1, we need to choose an appropriate n2 value. In our calculation, we set the condition

$${2}^{-{n}_{2}}={\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2}),$$
(8)

for the appropriate n2.

For any n > n2, we have \({\varepsilon }_{{\bf{k}}}(n)\,>\,{\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})={2}^{-{n}_{2}}\); however, for any n < n2, we have \({2}^{-n}\,>\,{2}^{-{n}_{2}}\). In conclusion, if n ≠ n2, \({2}^{-n}+{\varepsilon }_{{\bf{k}}}(n)\,>\,{2}^{-{n}_{2}}\). Therefore, in this study, we set \({2}^{-{n}_{2}}={\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\), and obtain a tightened guessing probability \({2}^{-{n}_{2}+1}\).

Once we determine the value n2 and the corresponding \({\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\), we calculate \(\bar{p}({\bf{k}}^{\prime} )\) by Eq. (3). Clearly, this is the upper bound of the guessing probability of the final key k of length n1 provided that

$${n}_{1}\,>\,{n}_{2}.$$
(9)

Thus, we can actually use a more efficient scheme to obtain the upper bound of the guessing probability of key k, as the following Theorem 2:

As shown in Fig. 1, the arrow between s and k indicates that the εk-secure n1-bit final key k can be distilled from the N-bit sifted key s using a random matrix \({R}_{{n}_{1}N}\), i.e. \({\bf{k}}={R}_{{n}_{1}N}{\bf{s}}\). The arrow between k and \({\bf{k}}^{\prime}\) indicates that there exists a map M that can map the key k into \({\bf{k}}^{\prime}\), i.e., \({\bf{k}}^{\prime} =M({\bf{k}})\). The arrow between the sifted key s and \({\bf{k}}^{\prime}\) indicates that if a random hashing matrix \({R}_{{n}_{2}N}\) is used to distill the final key, we have \({\bf{k}}^{\prime} ={R}_{{n}_{2}N}{\bf{s}}\). Then if n2 satisfies the condition in Theorem 2, a tightened guessing probability of k can be obtained.

Fig. 1: Flow chart of our method of bounding the guessing probability.
figure 1

The arrow between s and k indicates that the εk-secure n1-bit final key k can be distilled from the N-bit sifted key s using a random matrix \({R}_{{n}_{1}N}\), i.e., \({\bf{k}}={R}_{{n}_{1}N}{\bf{s}}\). The arrow between k and \({\bf{k}}^{\prime}\) indicates that there exists a map M that can map the key k into \({\bf{k}}^{\prime}\), i.e. \({\bf{k}}^{\prime} =M({\bf{k}})\). The arrow between the sifted key S and \({\bf{k}}^{\prime}\) indicates that if a random hashing matrix \({R}_{{n}_{2}N}\) is used to distill the final key, we have \({\bf{k}}^{\prime} ={R}_{{n}_{2}N}{\bf{s}}\). Then, if n2 satisfies the condition in Theorem 2, a tightened guessing probability of k can be obtained.

Full size image

There are two important points need to be noticed. First, when applying our theorem to obtain the nontrivial upper bound of the guessing probability for the final key k, we do not really need to transform k to another string \({\bf{k}}^{\prime}\), and we only need the existence of a map that can map k to \({\bf{k}}^{\prime}\) mathematically. That is to say, we use the final key k, but its guessing probability is calculated from the shorter key \({\bf{k}}^{\prime}\). As shown above, the existence has been proven. Second, in this study, we use the random matrix RnN as a family of two-universal hash functions to distill the key to illustrate our conclusion more intuitively. Of course, we can also use the modified Toeplitz matrix8 instead of the random matrix RnN. Thus, the final key k can be also mapped to the string \({\bf{k}}^{\prime}\), and the string \({\bf{k}}^{\prime}\) can also be regarded as the \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure key. This means that the proposed theorem in this study still holds.

Theorem 2

In the QKD protocol, if the n1-bit final key k is distilled from the sifted key s using a random matrix \({R}_{{n}_{1}N}\), the guessing probability of k can be upper bounded by

$$p({\bf{k}})\le \bar{p}({\bf{k}}^{\prime} )={2}^{-({n}_{2}-1)},$$
(10)

where \({\bf{k}}^{\prime} =M({\bf{k}})={R}_{{n}_{2}N}{\bf{s}}\) and n2 satisfies \({2}^{-{n}_{2}}={\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2}),{n}_{2}\,<\,{n}_{1}.\)

Discussion

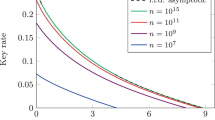
Table 1 describes the upper bounds of the guessing probability calculated by different Ntol, where Ntol is the length of the total string that includes the sifted keys for key generation and the string used to do parameter estimation. In Table 1, Ntol = 104, 105, and 106. Table 1 shows that when Ntol = 106, n = 4.90 × 105 and the guessing probabilities obtained using the methods of ref. 12 and ref. 11 are approximately 10−6 and 10−9, respectively. However, using our method, the guessing probability can be reduced to 2 × 10−3277, which is more tightened by thousands of orders of magnitude than prior art methods. With an increase in the length of Ntol, the length of the final key also increases; however, the guessing probabilities in ref. 12 and ref. 11 almost remain unchanged. Compared with ref. 12 and ref. 11, the guessing probability obtained by our method is considerably reduced, which is more realistic and tighter. It should be noted that we calculate the case without the known-plaintext attack (KPA) in Table 1. Now, we consider the case of KPA in QKD using our method. Suppose that Eve knows the t bits of the final n2-bit key \({\bf{k}}^{\prime}\); then, the guessing probability of the \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure key \({\bf{k}}^{\prime}\) is \({p}_{{\rm{KPA}}}({\bf{k}}^{\prime} )\le {2}^{-({n}_{2}-t-1)}\). Now, the upper bound of the guessing probability of key \({\bf{k}}^{\prime}\) is equal to that of an ideal (n2 − t − 1)-bit key.

Table 1 Comparison of the guessing probability, where Qtol = 2.14% is the channel error tolerance, Nz = 0.22Ntol is the length of the string used to do parameter estimation, Ntol is the total length of the sifted key, N = 0.78Ntol is the length of the string for key generation, ε = 10−9 is the security level, n is the length of the 10−9-secure key, and pg is the probability of correctly guessing the final key. Specifically, \({p}_{{\rm{g}}}^{{\rm{Thm.2}}}\) is the result of Theorem 2 of this work.
Full size table

Table 2 compares the length of the ε-secure key n and the length of \(\varepsilon ^{\prime}\)-secure key \(n^{\prime}\) when the total length of the sifted key is 104, 105, and 106. This table shows that if only using Lemma 1 to obtain a smaller guessing probability, ε needs to be reduced. Accordingly, the length of the final key and the key rate will be considerably reduced. For example, from Table 2, when Ntol = 106, if the customer wants to reduce the guessing probability from 10−9 to 2 × 10−3277, the length of the key will become \(n^{\prime} =1.1\times 1{0}^{4}\), and the key rate will become \(r^{\prime} =0.01\). This result is much lower than the original key length n = 4.9 × 105 and the key rate r = 0.49. Using our result, there is actually no bit cost for a much smaller bound value of guessing probability. For example, when Ntol = 106, we can upper bound the guessing probability by 2 × 10−3277 by setting ε = 10−9. Thus, without reducing the value of ε, we can obtain a tightened upper bound of guessing probability \({p}_{{\rm{g}}}^{{\rm{Thm.2}}}\) of k, as can be seen from Table 1.

Table 2 Comparison of the rate r = n/Ntol and \(r^{\prime} =n^{\prime} /{N}_{{\rm{tol}}}\) under the same parameters shows in Table 1. ε and \(\varepsilon ^{\prime}\) are the security levels, n and \(n^{\prime}\) are the length of ε-secure key and the length of \(\varepsilon ^{\prime}\)-secure key, respectively.
Full size table

Our result shows that in terms of guessing probability, the performance of the existing trace distance security is much better than what has been assumed in the past. Incidentally, in ref. 11, a looser upper bound, 10−6 for Eve’s guessing probability, was presented12. We emphasize that this looser upper bound does not in any sense challenge the validity of the existing security proof of QKD11. Although the large value of lower bound of Eve’s guessing probability can show insecurity, the large value of upper bound cannot show insecurity. If one does not make any effort, one can also obtain a large-value upper bound of 100% for Eve’s guessing probability. Such value is correct for the upper bound but not meaningful. If any new upper bound is larger than that in the prior art result, it means that the “new upper bound” is trivial and meaningless rather than the prior art result is invalid. Thus, the looser upper bound presented by ref. 12 only shows that Eve’s guessing probability of the key is smaller than 10−6. It does not conflict with more tightened results presented elsewhere.

In this study, our goal is to obtain a tightened guessing probability. On the basis of the existing secure criterion (Trace distance) and the general property of guessing probability, we propose a simple and efficient method to tighten the upper bound of the guessing probability. We find that the guessing probability p(k) of k can be upper bounded by \({2}^{-({n}_{2}-1)}\), where n2 satisfies \({2}^{-{n}_{2}}={\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\) and n2 < n1. Specifically, a simple random matrix RnN can be used to distill the final key. Compared with the prior art results, of which the upper bound of the guessing probability of the ε-secure key is approximately ε, our method provides a more tightened upper bound. Therefore, the loose upper bound for the guessing probability obtained in ref. 12 cannot be regarded as evidence to question the validity of existing the security proof of QKD.

Methods

Proof of Lemma 1

Lemma 1

The guessing probability of the εk-secure key k with length n1 is not larger than \(\frac{1}{{2}^{{n}_{1}}}+{\varepsilon }_{{\bf{k}}}\).

This is a conclusion obtained from ref. 11. The proof has been already presented in ref. 11. Here, for the convenience of the reader, we write the proof again.

Proof. Let the n-bit string x be the εx-secure key in \({\mathcal{X}}\). The density matrix of Alice and Eve is ρXE and satisfies

$${\rho }_{{\rm{XE}}}=\sum _{{\bf{x}}\in {\mathcal{X}}}\left|{\bf{x}}\right\rangle \left\langle {\bf{x}}\right|\otimes {\rho }_{E}^{{\bf{x}}},$$
(11)
$$\frac{1}{2}\parallel {\rho }_{{\rm{XE}}}-{\rho }_{{{\rm{U}}}_{{\bf{x}}}}\otimes {\rho }_{{\rm{E}}}{\parallel }_{1}\le {\varepsilon }_{{\bf{x}}},$$

where \({\rho }_{{{\rm{U}}}_{{\bf{x}}}}\) is the fully mixed state in \({\mathcal{X}}\). Then we have

$$\frac{1}{2}\parallel {\rho }_{{\rm{XE}}}-{\rho }_{{{\rm{U}}}_{{\bf{x}}}}\otimes {\rho }_{{\rm{E}}}{\parallel }_{1}$$
$$\ge \frac{1}{2}{\left\Vert {\sum \limits_{{\bf{x}}\in {\mathcal{X}}}}q({\bf{x}})\left|{\bf{x}}\right\rangle \left\langle {\bf{x}}\right|-\sum _{{\bf{x}}\in {\mathcal{X}}}\frac{1}{{2}^{n}}\left|{\bf{x}}\right\rangle \left\langle {\bf{x}}\right|\right\Vert }_{1}$$
(12)
$$=\frac{1}{2}{\sum \limits_{{\bf{x}}\in {\mathcal{X}}}}\left\vert q({\bf{x}})-\frac{1}{{2}^{n}}\right\vert .$$

Eve’s guessing probability of string x is q(x), and the maximum guessing probability is \({p}_{{\rm{g}}}={\max }_{{\bf{x}}\in {\mathcal{X}}}\{q({\bf{x}})\}\). Without any loss of generality, it is possible to assume that the maximum guessing probability is \(q({\bf{x}}^{\prime} )\). Note that \({\sum }_{{\bf{x}}\in {\mathcal{X}}}q({\bf{x}})=1\), then the following holds

$$\frac{1}{2}{\sum }_{{\bf{x}}\in {\mathcal{X}}}\left\vert q({\bf{x}})-\frac{1}{{2}^{n}}\right\vert$$
(13)
$$=\frac{1}{2}\left\vert q({\bf{x}}^{\prime} )-\frac{1}{{2}^{n}}\right\vert +\frac{1}{2}{\sum \limits_{{\bf{x}}\in {\mathcal{X}},{\bf{x}}\ne {\bf{x}}^{\prime}}}\left\vert q({\bf{x}})-\frac{1}{{2}^{n}}\right\vert$$
$$\ge \frac{1}{2}\left\vert q({\bf{x}}^{\prime} )-\frac{1}{{2}^{n}}\right\vert +\frac{1}{2}\left\vert {\sum \limits_{{\bf{x}}\in {\mathcal{X}},{\bf{x}}\ne {\bf{x}}^{\prime}}}[q({\bf{x}})-\frac{1}{{2}^{n}}]\right\vert$$
$$=\left\vert q({\bf{x}}^{\prime} )-\frac{1}{{2}^{n}}\right\vert .$$

From Eqs. (11) to (13), we have \({p}_{{\rm{g}}}\le {2}^{-{n}_{1}}+{\varepsilon }_{{\bf{x}}}\); thus, for the n1-bit εk-secure key k, the guessing probability satisfies

$$p({\bf{k}})\le \bar{p}({\bf{k}})=\frac{1}{{2}^{{n}_{1}}}+{\varepsilon }_{{\bf{k}}},$$
(14)

where \(\bar{p}({\bf{k}})\) is the upper bound of p(k). This ends our proof of Lemma 1.

Calculation of \({\varepsilon }_{{\bf{k}}}^{\prime}\)

We consider the security definitions of a practical QKD protocol with a finite size under the framework of composable security4,13,14. Suppose that Alice and Bob get two N-bit sifted key strings. By performing an error correction and private amplification scheme, Alice get an n-bit final key k and Bob get an estimate \(\hat{{\bf{k}}}\) of k. The protocol is εcor-correct if \(P[{\bf{k}}\,\ne\, \hat{{\bf{k}}}]\le {\varepsilon }_{{\rm{cor}}}\). In general, the key k of Alice can be correlated with an eavesdropper system, and the density matrix of Alice and Eve is ρAE.

The protocol outputs an εk-secure key13, if

$$\frac{1}{2}\parallel {\rho }_{{\rm{AE}}}-{\rho }_{{\rm{U}}}\otimes {\rho }_{{\rm{E}}}{\parallel }_{1}\le {\varepsilon }_{{\bf{k}}},$$
(15)

where ∥ ⋅ ∥1 denotes the trace norm, ρU is the fully mixed state of Alice's system. The protocol is εtol-secure if εcor and εk satisfies εcor + εk ≤ εtol, which means that it is εtol-indistinguishable from an ideal protocol. Without any loss of generality, we consider the case of εcor = εk.

From Lemma 1, we can calculate \(\bar{p}({\bf{k}})\) given the n-bit εk-secure key k. In this situation, \(\bar{p}({\bf{k}})={2}^{-n}+{\varepsilon }_{{\bf{k}}}\). However, in our method, we only know N and n2, which are the length of the sifted key and \({\bf{k}}^{\prime}\). (The string \({\bf{k}}^{\prime}\) itself can be also regarded as another final key distilled from the sifted key.) To get a tightened upper bound of the guessing probability of k, we need to obtain the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\). According to ref. 4, with N and n2, the final key is \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure if \({\varepsilon }_{{\bf{k}}^{\prime} }\) satisfies the following equation:

$${n}_{2}\le N[1-h({Q}_{{\rm{tol}}}+\mu )]-fNh({Q}_{{\rm{tol}}})-\mathrm{log}\,\frac{2}{{\varepsilon }_{{\bf{k}}^{\prime} }^{3}},$$
(16)

where \(\mu =\sqrt{\frac{N+{N}_{z}}{N{N}_{z}}\frac{{N}_{z}+1}{{N}_{z}}\mathrm{ln}\,\frac{2}{{\varepsilon }_{{\bf{k}}^{\prime} }}}\), Nz is the length of string used for parameter estimation, f = 1.1, h denotes the binary Shannon entropy function, \(h(x)=-x\,{\log}\,x-(1-x){\log}\,(1-x)\) and Qtol represents the channel error tolerance. To obtain nontrivial results, we use equality in Eq. (16) to calculate the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\), given the input n2. Since \({\varepsilon }_{{\bf{k}}^{\prime} }\) is dependent on n2, we use notation \({\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\) for \({\varepsilon }_{{\bf{k}}^{\prime} }\). Here, \({\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\), if n2 is given and we numerically find the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\) by Eq. (16).

In our calculation, we choose a specific n2-value that satisfies

$${2}^{-{n}_{2}}={\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2}).$$
(17)

In combination with Eq. (16), we obtain the following equation for the tightened \({\varepsilon }_{{\bf{k}}^{\prime} }\) value:

$$-{\log}\,{\varepsilon }_{{\bf{k}}^{\prime} }=N[1-h({Q}_{{\rm{tol}}}+\mu )]-fNh({Q}_{{\rm{tol}}})-{\log}\,\frac{2}{{\varepsilon }_{{\bf{k}}^{\prime} }^{3}},$$
(18)

and we can calculate the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\) and then calculate the guessing probability by Eq. (8) in our main body text.