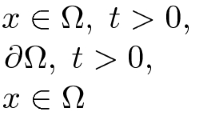The main aim of the present paper is to investigate the conditions under which the nonnegative solutions blow-up for the parabolic problem \( \frac{\partial u}{\partial t}=-{\left(-\Delta \right)}^{\frac{\alpha }{2}}u+\frac{c}{{\left|x\right|}^{\alpha }}u\kern1em \mathrm{in}\kern1em {\mathrm{\mathbb{R}}}^{\mathrm{d}}\times \left(0,T\right), \) where 0 < α < min(2, d), \( {\left(-\Delta \right)}^{\frac{\alpha }{2}} \)is the fractional Laplacian on ℝd and the initial condition u0 is in L2(ℝd).
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. B. Ben Amor and T. Kenzizi, “The heat equation for the Dirichlet fractional Laplacian with negative potentials: existence and blow-up of nonnegative solutions,” Acta Math. Sinica (Engl. Ser.) (2017).
K. Bogdan and T. Byczkowski, “Potential theory for the ↵-stable Schr¨odinger operator on bounded Lipschitz domains,” Stud. Math., 133, No. 1, 53–92 (1999).
K. Bogdan, T. Byczkowski, T. Kulczycki, M. Ryznar, R. Song, and Z. Vondraˇcek, “Potential analysis of stable processes and its extensions,” Lect. Notes Math., 1980 (2009).
P. Baras and J. A. Goldstein, “The heat equation with a singular potential,” Trans. Amer. Math. Soc., 284, No. 1, 121–139 (1984).
P. Baras and J. A. Goldstein, “Remarks on the inverse square potential in quantum mechanics,” North-Holland Math. Stud., 92, 31–35 (1984).
R. Blumenthal and R. Getoor, “The asymptotic distribution of the eigenvalues for a class of Markov operators,” Pacific J. Math., 9, 399–408 (1959).
C. Berg and G. Forst, Potential Theory on Locally Compact Abelian Groups, Springer-Verlag, New York (1975).
R. Bannuelos and T. Kulczycki, “Trace estimates for stable processes,” Probab. Theory Related Fields, 142, 313–338 (2008).
Z. Q. Chen, P. Kim, and R. Song, “Heat kernel estimates for the Dirichlet fractional Laplacian,” J. Europ. Math. Soc., 12, 1307–1329 (2010).
X. Cabré and Y. Martel, “Existence versus explosion instantanée pour des équations de la chaleur linéaires avec potentiel singulier,” C. R. Math. Acad. Sci. Paris, 329, No. 11, 973–978 (1999).
Z. Q. Chen and T. Kumagai, “Heat kernel estimates for stable-like processes on d-sets,” Stochastic Process. Appl., 108, 27–62 (2003).
E. B. Davies, Spectral Theory and Differential Operators, Cambridge Univ. Press, Cambridge (1995).
E. B. Davies, Heat Kernels and Spectral Theory, Cambridge Univ. Press, Cambridge (1989).
J. L. Doob, Classical Potential Theory and Its Probabilistic Counterpart, Springer, New York (1983).
M. Fukushima, Y. Oshima, and M. Takeda, “Dirichlet forms and symmetric Markov processes,” De Gruyter Stud. Math., 19, 489 (2011).
J. A. Goldstein and Q. S. Zhang, “On a degenerate heat equation with a singular potential,” J. Funct. Anal., 186, 342–359 (2001).
T. Kenzizi, “Existence of nonnegative solutions for a fractional parabolic equation in the whole space,” Ukr. Math. J., 71, No. 8, 1064–1072 (2019).
M. Kwa´snicki, “Ten equivalent definitions of the fractional Laplace operator,” arXiv: 1507.07356v2[math.AP], 14 September (2015).
K. Kaleta and T. Kulczycki, “Intrinsic ultracontractivity for Schr¨odinger operators based on fractional Laplacians,” Potential Anal., 33, No. 4, 313–339 (2010).
M. Bonforte, G. Grillo, and J. L. Vazquez, “Quantitative local bounds for subcritical semilinear elliptic equations,” Milan J. Math., 80, 65–118 (2012).
H. Park and R. Song, “Trace estimates for relativistic stable processes,” Potential Anal., 41, 1273–1291 (2014).
G. F. Roach, Green’s Functions: Introductory Theory with Applications, Van Nostrand (1970).
L. Silvestre, “Regularity of the obstacle problem for a fractional power of the Laplace operator,” Comm. Pure Appl. Math., 60, No. 1, 67–112 (2007).
K. Yosida, “Functional analysis,” Classics in Mathematics, Springer-Verlag, Berlin; Heidelberg (1995).
V. M. Zolotarev, One-Dimensional Stable Distributions, Nauka, Moscow (1983).
H. Weyl, “U¨ ber beschra¨nkte quadratische Formen, deren differenz vollstetig ist,” Rend. Circ. Mat. Palermo (2), 27, 373–392 (1909).
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Ukrains’kyi Matematychnyi Zhurnal, Vol. 71, No. 11, pp. 1502–1518, November, 2019.
Rights and permissions
About this article
Cite this article
Kenzizi, T. A Parabolic Equation for the Fractional Laplacian in the Entire Space: Blow-Up of Nonnegative Solutions. Ukr Math J 71, 1719–1738 (2020). https://doi.org/10.1007/s11253-020-01743-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-020-01743-8