A study on the response of PLGA 85/15 under compression and heat-treatment testing cycles

Abstract

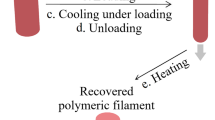
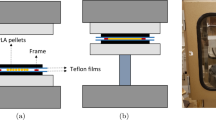
Poly(lactic-co-glycolic acid) (PLGA) is one of the most prominent bioresorbable materials, currently used in several medical applications (screws, craniofacial plates etc.). Looking to extend the knowledge about the thermomechanical behavior of bioresorbable medical materials, this research presents a series of experiments and results based on nonhomogeneous compression tests for the polymer PLGA 85/15. Instead of focusing on tensile and bending conditions for compression-molded products, such as usually presented in the literature, attention is given to compression tests and samples machined from injection-molded parts. Additionally, PLGA strain rate sensitivity, which is an issue less discussed in the literature, is analyzed. In the current study, this material is tested by observing the main features related to resorbable medical materials. The effects of a material heat treatment that are associated with PLGA shape-memory properties are investigated. Differential scanning calorimetry (DSC) was also employed in the thermal characterization. A finite element analysis of the compression testing provides a complementary overview of the mechanical behavior of PLGA 85/15. Results indicate that PLGA has a linear rate-insensitive response for small strains but presents a strong rate dependence for strains beyond the material yielding. PLGA shows a remarkable post-yielding strain-softening behavior, with a steep descent slope. Samples present significant mechanical changes after heat treatment at temperatures above $T_{g}$, with reduction of 35% in the material elastic modulus and 30% in the upper-yielding stress and no significant changes for further heat-treatment procedures. DSC analysis confirmed the existence of significant residual stress in PLGA specimens. Mechanical deformation and manly heat treatment seem to reduce this residual stress caused by molecular orientation and rapid solidification. Finally, finite element simulations show that the limit of the homogeneity hypothesis is associated with the yield strain, after which highly non-uniform stresses develop.

Appendix A: Constitutive model

The constitutive updates framework, in which the model used in the present work was formulated, is set down by a minimization procedure involving the incremental potentials $\mathscr{W}({\mathscr{E}}_{n+1})$, $\mathscr{\bar{W}}({\mathscr{E}}_{n+1})$ and the set of state variables ${\mathscr{E}}_{n+1}=\{\mathbf{C}_{n+1},\mathbf{Z}_{n+1}\}$, where $\mathbf{C}_{n+1}$ is the right Cauchy-Green deformation tensor, $\mathbf{Z}_{n+1}$ is the set of dissipative variables. Thus, the mechanical problem is defined by

$$\begin{aligned} &\mathscr{\bar{W}}({\mathscr{E}}_{n+1})=\min _{\mathbf{Z}_{n+1}} \mathscr{W}({\mathscr{E}}_{n+1}), \quad \mathscr{W}({\mathscr{E}}_{n+1})= \left [ W({\mathscr{E}}_{n+1})-W({\mathscr{E}}_{n})\right ] +\Delta t \phi ^{\ast }\text{,} \end{aligned}$$

(1)

$$\begin{aligned} &\mathbf{S}_{n+1}\equiv 2 \frac{\partial \mathscr{\bar{W}}}{\partial \mathbf{C}_{n+1}}, \quad \boldsymbol{\sigma }_{n+1}={J}^{-1}\mathbf{F}_{n+1}\mathbf{S}_{n+1}\mathbf{F}_{n+1}^{T}, \end{aligned}$$

(2)

where $W$ is the Helmholtz free energy, $\phi ^{\ast }$ is the incremental dissipative function, $\mathbf{S}_{n+1}$ is the second Piola-Kirchhoff, $\boldsymbol{\sigma }_{n+1}$ is the Cauchy stress tensor, and $J=\left ( \det \mathbf{C}\right )^{\frac{1}{2}}$. In the current model, the Helmholtz free energy is decomposed as $W=W^{e}+U+W^{p}$ and the following functional forms were chosen:

$$\begin{aligned} &W^{e}=\mu \hat{\varepsilon }_{n+1}^{e},\qquad U=\frac{1}{2}K\left ( \ln {J}\right ) ^{2},\qquad W^{p}=H\left [ \frac{\left ( e^{n\ \alpha }-1\right ) }{n}-\alpha \right ], \end{aligned}$$

(3)

$$\begin{aligned} &\phi ^{\ast }=\sigma _{Y}\dot{\alpha }+ \frac{\mathtt{c}f_{A}(\alpha _{n+1})}{\eta +1}\left ( \frac{\dot{\alpha }}{\mathtt{c}}\right ) ^{\eta +1}, \end{aligned}$$

(4)

$$\begin{aligned} &f_{A}(\alpha _{n+1})=s_{\infty }+e^{-s_{z}\alpha _{n+1}}\left [ (s_{0}-s_{ \infty })\cosh \left ( s_{b}\alpha _{n+1}\right ) +s_{g}\sinh \left ( s_{b} \alpha _{n+1}\right ) \right ], \end{aligned}$$

(5)

where $W^{e}$, $U$, $W^{p}$ are, respectively, the isochoric-elastic, volumetric-elastic and plastic contributions of the free energy potential, $\hat{\varepsilon }_{n+1}^{e}$ is the elastic logarithmic strain, $\alpha$ is the internal variable associated with the isotropic hardening. Furthermore, the following approach is employed: $\dot{\alpha }=\frac{\Delta \alpha }{\Delta t}$, where $\Delta ()=()_{n+1}-()_{n}$, and an important parametrization is adopted for the evolution of the plastic velocity gradient $\mathbf{D}^{p}=\dot{\alpha }\mathbf{M}$, where $\dot{\alpha }$ and $\mathbf{M}$ are, respectively, the amplitude and the direction tensor related to $\mathbf{D}^{p}$. In Eq. (4), the first two expressions are related to the viscoplastic response of the model. By following Farias et al. (2019), the function $f_{A}(\alpha _{n+1})$ is associated with the plastic flow resistance of the material, allowing for the effect of initial hardening and post-yielding softening.

Considering Eqs. (3), (4) and (5), one will find a total of 12 constitutive parameters. The parameters $\mu$ and $K$ are the shear and bulk elasticity modulus, $\sigma _{Y}$ is the initial yield stress, $H$ and $n$ are the modulus and exponential parameters of the hardening model, $\eta$ and $\mathtt{c}$ are related to viscoplastic parameters associated with Perzyna function, $s_{\infty }$, $s_{0}$, $s_{g}$, $s_{z}$ and $s_{b}$ are related to the plastic flow resistance. These variables should be then characterized by experimental and identification procedures.

The solution of the constitutive problem can be obtained by finding initially the values of ${\Delta \alpha }$, $\mathbf{M}$. The direction tensor $\mathbf{M}$ is obtained analytically, resulting in $\mathbf{M}=\sqrt{\frac{3}{2}} \frac{\ln \hat{\mathbf{C}}_{n+1}^{pr}}{\left \Vert \ln \hat{\mathbf{C}}_{n+1}^{pr}\right \Vert }$, where $\hat{\mathbf{C}}_{n+1}^{pr}$ is a predictor for the isochoric right Cauchy-Green deformation tensor. The variables ${\Delta \alpha }$, are obtained by solving the residuals $r_{1}=\frac{\partial \mathscr{W}}{\partial \Delta \alpha }$. Thus, it is possible to compute the stress update $\mathbf{S}_{n+1}$, as well as the Cauchy stress tensor $\boldsymbol{\sigma }_{n+1}$.

In order to proceed with the simulations, the set of parameters shown in Table 4 were considered.

Table 4 Constitutive parameters

The process of parameter identification was performed by using optimization techniques to minimize a norm of the difference between experimental and numerical curves. The objective function takes into account the error of curves at three deformation rates simultaneously.