Skip to main content
SpringerLink
Log in

Effects of velocity second slip model and induced magnetic field on peristaltic transport of non-Newtonian fluid in the presence of double-diffusivity convection in nanofluids

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

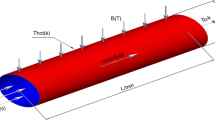
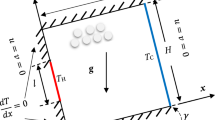
The significance of velocity second slip model of non-Newtonian fluid on peristaltic pumping in existence of double-diffusivity convection in nanofluids and induced magnetic field is deliberated. Mathematical modelling of current problem is defined in fixed frame of reference and then abridges under well- known conjecture of long wavelength and low but finite Reynolds number approximation. Precise results of coupled nonlinear partial differential equations are presented. Graphical results exhibit the performance of various supportive parameters. The phenomenon of stream functions with different wave forms is also discussed in detail. The effects of thermal energy, solute concentration, and nanoparticle fraction are also described using graphical representation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

Abbreviations

U, V :

Velocities in x and y directions in fixed frame

p :

Pressure

g :

Acceleration due to gravity

\(\varTheta \) :

Nanoparticle volume fraction

\(a_{1} \) and \(b_{1} \) :

Amplitudes of waves

\(\sigma \) :

Electrical conductivity

\(\mu _\mathrm{e}\) :

Magnetic permeability

\(\lambda _{{1}} \) :

Ratio of relaxation to retardation times

\(\rho _{\mathrm{f}_{0} } \) :

Fluid density at \(T_{0} \)

Re:

Reynolds number

\(D_\mathrm{B} \) :

Brownian diffusion coefficient

\(D_\mathrm{s} \) :

Solutal diffusivity

\(D_\mathrm{CT} \) :

Soret diffusivity

\(\left( {\rho c} \right) _\mathrm{f} \) :

Heat capacity of fluid

Q :

Volume flow rate

\(\gamma \) :

Dimensionless solutal (species) concentration

\(\theta \) :

Temperature of fluid in dimensionless form

\(G_\mathrm{rF} \) :

Nanoparticle Grashof number

C :

Solutal concentration

\(N_\mathrm{t}\) :

Thermophoretic parameter

\(N_\mathrm{CT}\) :

Soret parameter

Ln:

Nanofluid Lewis number

\(\mu \) :

Fluid viscosity

\(\lambda \) :

Wave length

T :

Denotes temperature

k :

Thermal conductivity

\(d_{{1} } +d_{{2} }\) :

Width of channel

\(\dot{{\gamma }}\) :

Shear rate

\(\in \) :

Magnetic diffusivity

\(\lambda _{{2} }\) :

Retardation time

\(\rho _\mathrm{f} \) :

Fluid density

\(\rho _{p} \) :

Nanoparticle mass density

\(D_\mathrm{T} \) :

Thermophoretic diffusion coefficient

\(D_\mathrm{TC} \) :

Dufour diffusivity

\(\delta \) :

Dimensionless wave number

\(\left( {\rho c} \right) _{p} \) :

Effective heat capacity of nanoparticle,

\(\varPsi \) :

Stream function

\(\varOmega \) :

Nanoparticle volume fraction

\(G_\mathrm{rT} \) :

Thermal Grashof number

\(G_\mathrm{rc} \) :

Solutal Grashof number

Pr:

Prandtl number

\(R_\mathrm{m}\) :

Magnetic Reynolds number

\(N_\mathrm{b}\) :

Brownian motion parameter

\(N_\mathrm{TC}\) :

Dufour parameter

Le:

Regular Lewis number

References

  1. Latham, T. W.: Fluid motion in a peristaltic pump, M.Sc. Thesis, MIT, Cambridge (1966)

  2. Shapiro, A.H., Jaffrin, M.Y., Weinberg, S.L.: Peristaltic pumping with long wavelengths at low Reynolds number 37, 799–825 (1969)

  3. Ellahi, R., Rahman, S.U., Nadeem, S., Vafai, K.: A mathematical study of non-Newtonian micropolar fluid in arterial blood flow through composite stenosis. J. Appl. Math. Inf. Sci. 8, 1–7 (2014)

    Google Scholar 

  4. Ellahi, R., Riaz, A., Sohail, S., Mushtaq, M.: Series solutions of magnetohydrodynamic peristaltic flow of a jeffrey fluid in eccentric cylinders. J. Appl. Math. Inf. Sci. 7, 1441–1449 (2013)

    Google Scholar 

  5. Akram, Safia, Mekheimer, KhS, elmaboud, Y.Abd: Particulate suspension slip flow induced by peristaltic waves in a rectangular duct: effect of lateral walls. Alex. Eng. J. 57, 407–414 (2018)

    Google Scholar 

  6. Akram, Safia, Nadeem, S.: Influence of induced magnetic field and partial slip on the peristaltic flow of a couple stress fluid in an asymmetric channel. Iran. J. Chem. Chem. Eng. 33, 43–52 (2014)

    Google Scholar 

  7. Ellahi, R., Hussain, F., Ishtiaq, F., Hussain, A.: Peristaltic transport of Jeffrey fluid in a rectangular duct through a porous medium under the effect of partial slip: an application to upgrade industrial sieves/filters. Pramana 93(3), 34 (2019)

    Google Scholar 

  8. Riaz, Arshad, Ellahi, R., Nadeem, S.: Peristaltic transport of a Carreau fluid in a compliant rectangular duct. Alex. Eng. J. 53, 475–484 (2014)

    Google Scholar 

  9. Eldabe, N.T., El-Sayed, M.F., Ghaly, A.Y., Sayed, H.M.: Peristaltically induced transport of a MHD biviscosity fluid in a non-uniform tube. Physica A 383, 253–266 (2007)

    Google Scholar 

  10. Mishra, M., Rao, A Ramachandra: Peristaltic transport of a Newtonian fluid in an asymmetric channel. Z. Angew. Math. Phys. 54, 532–550 (2003)

    MathSciNet  MATH  Google Scholar 

  11. Ellahi, R., Hassan, M., Zeeshan, A., Khan, Ambreen A: The shape effects of nanoparticles suspended in HFE-7100 over wedge with entropy generation and mixed convection. Appl. Nanosci. 6, 641–651 (2016)

    Google Scholar 

  12. Ellahi, R., Zeeshan, A., Hassan, Mohsan: Particle shape effects on marangoni convection boundary layer flow of a nanofluid. Int. J. Numer. Methods Heat Fluid Flow 26, 2160–2174 (2016)

    Google Scholar 

  13. Akram, Safia: Nanofluid effects on peristaltic transport of a fourth grade fluid in the occurrence of inclined magnetic field. Sci. Iran. 23, 1502–1516 (2016)

    Google Scholar 

  14. Ellahi, R., Zeeshan, A., Hussain, Farooq, Asadollahi, A.: Peristaltic blood flow of couple stress fluid suspended with nanoparticles under the influence of chemical reaction and activation energy. Symmetry 11(2), 276 (2019)

    MATH  Google Scholar 

  15. Choi, S.U.S.: Enhancing thermal conductivity of fluid with nanoparticles. In: Developments and Applications of non-Newtonian Flow, ASME FED, vol. 66(231), pp. 99–105

  16. Mekheimer, K.S., elmaboud, Y.Abd: The influence of heat transfer and magnetic field on peristaltic transport of a Newtonian fluid in a vertical annulus: application of an endoscope. Phys. Lett. A 372, 1657–1665 (2008)

    MATH  Google Scholar 

  17. Pankhurst, Q.A., Connolly, J., Jones, S.K., Dobson, J.: Applications of magnetic nanoparticles in biomedicine. J. Phys. D 36, R167–R181 (2003)

    Google Scholar 

  18. Habibi, M.R., Ghassemi, M., Hamedi, M.H.: Analysis of high gradient magnetic field effects on distribution of nanoparticles injected into pulsatile blood stream. J. Magn. Magn. Mater. 324, 1473–1482 (2012)

    Google Scholar 

  19. Nield, D.A., Kuznetsov, A.V.: The onset of double diffusivity convection in a nanofluid layer. Int. J. Heat Fluid Flow 32, 771–776 (2011)

    Google Scholar 

  20. Kuznetsov, A.V., Nield, D.A.: Double-diffusivity natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 50, 712–717 (2011)

    Google Scholar 

  21. Bég, O.A., Tripathi, D.: Mathematica simulation of peristaltic pumping with double-diffusivity convection in nanofluids a bio-nanoengineering model. Proc. Inst. Mech. Eng. Part N J. Nanoeng. Nanosyst. 225, 99–114 (2011). https://doi.org/10.1177/1740349912437087

    Google Scholar 

  22. Waqar, A., Khan, A.Waqar, Uddin, Md Jashim, Ismail, A.I.Md: Hydrodynamic and thermal slip effect on double-diffusivity free convective boundary layer flow of a nanofluid past a flat vertical plate in the moving free stream. PLoS ONE 8, e54024 (2013)

    Google Scholar 

  23. Akram, Safia, Zafar, M., Nadeem, S.: Peristaltic transport of a Jeffrey fluid with double-diffusivity convection in nanofluids in the presence of inclined magnetic field. Int. J. Geom. Methods in Mod. Phys. 15, 1850181 (2018)

    MATH  Google Scholar 

  24. Akram, Safia, Afzal, Farkhanda, Imran, Muhammad: Influence of metachronal wave on hyperbolic tangent fluid model with inclined magnetic field. Int. J. Geom. Methods Mod. Phys. 15, 1950139 (2019)

    MathSciNet  Google Scholar 

  25. Bhatti, M.M., Zeeshan, A., Ellahi, R.: Electromagnetohydrodynamic (EMHD) peristaltic flow of solid particles in a third-grade fluid with heat transfer. Mech. Ind. 18(3), 314 (2017)

    Google Scholar 

  26. Ellahi, R., Bhatti, M.Mubashir, Riaz, A., Sheikholeslami, M.: Effects of magneto hydrodynamics on peristaltic flow of Jeffery fluid in a rectangular duct through a porous medium. J. Porous Med. 17, 143–157 (2014)

    Google Scholar 

  27. Akram, Safia, Aly, Emad H., Afzal, Farkhanda, Nadeem, S.: Effect of the variable viscosity on the peristaltic flow of newtonian fluid coated with magnetic field: application of adomian decomposition method for endoscope. Coatings 9, 524 (2019)

    Google Scholar 

  28. Navier, C.L.M.H.: Sur les lois du movement des fluids. Mem. Acad. R. Sci. Inst. Fr. 6, 389–440 (1827)

    Google Scholar 

  29. Mandviwalla, X., Archer, R.: The influence of slip boundary conditions on peristaltic pumping in a rectangular channel. J. Fluids Eng. 130, 124501–124502 (2008)

    Google Scholar 

  30. Akram, S., Nadeem, S.: Significance of nanofluid and partial slip on the peristaltic transport of a non-Newtonian fluid with different waveforms. IEEE Trans. Nanotechnol. 13, 375–385 (2014)

    Google Scholar 

  31. Akbar, N.S., Nadeem, S., Hayat, T.: Simulation of thermal and velocity slip on the peristaltic flow of a Johnson-Segalman fluid in an inclined asymmetric channel. Int. J. Heat Mass Transf. 55, 5495–5502 (2012)

    Google Scholar 

  32. Ebaid, A.: Effects of magnetic field and wall slip conditions on the peristaltic transport of a Newtonian fluid in an asymmetric channel. Phys. Lett. A 372, 4493–4499 (2008)

    MATH  Google Scholar 

  33. Roşca, A.V., Pop, I.: Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Transf. 60, 355–364 (2013)

    Google Scholar 

  34. Aly, E.H.: Effect of the velocity slip boundary condition on the flow and heat transfer of nanofluids over a stretching sheet. J. Comput. Theor. Nanosci. 12, 2428–2436 (2015)

    Google Scholar 

  35. Aly, E.H., Vajravelu, K.: Exact and numerical solutions of MHD nano boundary-layer flows over stretching surfaces in porous medium. Appl. Math. Comput. 232, 191–204 (2014)

    MathSciNet  MATH  Google Scholar 

  36. Aly, E. H., Ebaid, A.: Effect of the velocity second slip boundary condition on the peristaltic flow of nanofluids in an asymmetric channel: exact solution. Abstract and Applied Analysis, in the special issue: Analytical and Numerical Approaches for Complicated Nonlinear Equations, vol. 2014, Article ID 191876 (2014). https://doi.org/10.1155/2014/191876.

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. MCS, National University of Sciences and Technology, Islamabad, Pakistan

    Safia Akram, Alia Razia & Farkhanda Afzal

Authors
  1. Safia Akram
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alia Razia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Farkhanda Afzal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Safia Akram.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

$$\begin{aligned} \xi _{0}= & {} G_{\mathrm{rF}} \left( {-\frac{e^{-h_{1} m_{2} }N_\mathrm{t} }{N_\mathrm{b} \left( {e^{-h_{2} m_{2} }-e^{-h_{1} m_{2} }} \right) }+\frac{h_{1} N_\mathrm{t} }{\left( {h_{2} -h_{1} } \right) \,N_\mathrm{b} }+\frac{h_{1} }{h_{2} -h_{1} }} \right) \\&+\,G_{\mathrm{rc}} \left( {\frac{N_{\mathrm{CT}} e^{-h_{1} m_{2} }}{e^{-h_{2} m_{2} }-e^{-h_{1} m_{2} }}-\frac{h_{1} N_{\mathrm{CT}} }{h_{2} -h_{1} }-\frac{h_{1} }{h_{2} -h_{1} }} \right) -\frac{G_{\mathrm{rt}} e^{-h_{1} m_{2} }}{e^{-h_{2} m_{2} }-e^{-h_{1} m_{2} }}, \\ \xi _{1}= & {} \frac{e^{\left( {h_{1} +h_{2} } \right) \,m_{2} }\left( {N_\mathrm{b} \left( {G_{\mathrm{rt}} -N_{\mathrm{CT}} G_{\mathrm{rc}} } \right) +G_{\mathrm{rF}} N_\mathrm{t} } \right) }{N_\mathrm{b} \left( {e^{h_{1} m_{2} }-e^{h_{2} m_{2} }} \right) },\\ \xi _{2}= & {} \frac{G_{\mathrm{rF}} \left( {N_\mathrm{b} +N_\mathrm{t} } \right) -N_\mathrm{b} \left( {N_{\mathrm{CT}} +1} \right) \,G_{\mathrm{rc}} }{\left( {h_{1} -h_{2} } \right) \,N_\mathrm{b} }, \\ \xi _{3}= & {} \frac{m_{2}^{2} }{m_{1}^{2} \left( {m_{1}^{2} -m_{2}^{2} } \right) }-\frac{1}{m_{1}^{2} -m_{2}^{2} },_{{}} \xi _{4} =E+\frac{\xi _{0} }{m_{1}^{2} },\\ K_{0}= & {} \frac{e^{h_{1} m_{1} }\left( {\lambda _{1} +m_{1} \left( {\eta _{1} +\eta _{2} m_{1} } \right) +1} \right) }{\lambda _{1} +1}, \\ K_{1}= & {} \frac{e^{h_{2} m_{1} }\left( {\lambda _{1} -m_{1} \left( {\eta _{1} +\eta _{2} m_{1} } \right) +1} \right) }{\lambda _{1} +1}, \\ K_{2}= & {} \frac{e^{-h_{1} m_{1} }\left( {\lambda _{1} +\eta _{2} m_{1}^{2} -\eta _{1} m_{1} +1} \right) }{\lambda _{1} +1}, \\ K_{3}= & {} \frac{e^{-h_{2} m_{1} }\left( {\lambda _{1} +m_{1} \left( {\eta _{1} -\eta _{2} m_{1} } \right) +1} \right) }{\lambda _{1} +1}, \\ K_{4}= & {} \frac{\xi _{1} e^{-h_{2} m_{2} }\left( {-\lambda _{1} +\eta _{2} m_{2}^{2} -\eta _{1} m_{2} -1} \right) }{\left( {\lambda _{1} +1} \right) \,\left( {m_{2}^{2} -m_{1}^{2} } \right) }, \\ K_{5}= & {} -\frac{\xi _{1} e^{-h_{1} m_{2} }\left( {\lambda _{1} +\eta _{2} m_{2}^{2} -\eta _{1} m_{2} +1} \right) }{\left( {\lambda _{1} +1} \right) \,\left( {m_{2}^{2} -m_{1}^{2} } \right) }, \\ K_{6}= & {} \xi _{3} \left( {K_{1} -K_{0} } \right) \,\left( {\xi _{3} \left( {\frac{e^{-h_{1} m_{1} }}{m_{1} }-\frac{e^{-h_{2} m_{1} }}{m_{1} }} \right) -K_{2} \left( {h_{2} \xi _{3} -h_{1} \xi _{3} } \right) } \right) , \\ K_{7}= & {} \xi _{3} \left( {K_{3} -K_{2} } \right) \,\left( {\xi _{3} \left( {\frac{e^{h_{2} m_{1} }}{m_{1} }-\frac{e^{h_{1} m_{1} }}{m_{1} }} \right) -K_{0} \left( {h_{2} \xi _{3} -h_{1} \xi _{3} } \right) } \right) , \\ K_{8}= & {} \frac{\xi _{1} \left( {e^{-h_{1} m_{2} }-e^{-h_{2} m_{2} }} \right) }{m_{2} \left( {m_{1}^{2} -m_{2}^{2} } \right) }+\frac{\xi _{2} \left( {h_{2}^{2} -h_{1}^{2} } \right) }{2m_{1}^{2} }+(h_{2} -h_{1} )\xi _{4}, \\ K_{9}= & {} \frac{\xi _{3} \left( {e^{h_{2} m_{1} }-e^{h_{1} m_{1} }} \right) }{m_{1} }-K_{0} \xi _{3} \left( {h_{2} -h_{1} } \right) , \\ K_{10}= & {} -\frac{\eta _{1} \xi _{2} }{m_{1}^{2} \left( {\lambda _{1} +1} \right) }+\frac{h_{2} \xi _{2} }{m_{1}^{2} }+K_{4} +\xi _{4} +1, \\ K_{11}= & {} \frac{\xi _{2} \eta _{1} }{m_{1}^{2} \left( {\lambda _{1} +1} \right) }+\frac{h_{1} \xi _{2} }{m_{1}^{2} }+K_{5} +\xi _{4} +1, \\ K_{12}= & {} \xi _{3} \left( {K_{1} -K_{0} } \right) \,\left( {\xi _{3} \left( {F+K_{8} } \right) -K_{11} \left( {h_{2} -h_{1} } \right) \,\xi _{3} } \right) ,\\ K_{13}= & {} e^{h_{1} m_{1} }\xi _{3} \left( {K_{10} -K_{11} } \right) \,\left( {h_{1} m_{1} \left( {\lambda _{1} +m_{1} \left( {\eta _{1} +\eta _{2} m_{1} } \right) +1} \right) -\lambda _{1} -1} \right) ,\\ K_{14}= & {} e^{-h_{1} m_{1} }\left( {h_{1} m_{1} (1+\lambda _{1} -\eta _{1} m_{1} +\eta _{2} m_{1}^{2} )+\lambda _{1} +1} \right) ,\\ K_{15}= & {} \frac{K_{13} \left( {K_{3} -K_{2} } \right) \,\xi _{3} }{\left( {\lambda _{1} +1} \right) \,m_{1} \left( {K_{1} -K_{0} } \right) \,\xi _{3} },\\ K_{16}= & {} e^{2h_{2} m_{1} }\left( {-\lambda _{1} +m_{1} \left( {\eta _{1} +\eta _{2} m_{1} } \right) -1} \right) \,\left( {\lambda _{1} +\eta _{2} m_{1}^{2} -\eta _{1} m_{1} +1} \right) \\&-\,e^{2h_{1} m_{1} }\left( {-\lambda _{1} +\eta _{2} m_{1}^{2} -\eta _{1} m_{1} -1} \right) \,\left( {\lambda _{1} +m_{1} \left( {\eta _{1} +\eta _{2} m_{1} } \right) +1} \right) , \\ K_{17}= & {} e^{h_{2} m_{1} }\left( {-\lambda _{1} +m_{1} \left( {\eta _{1} +\eta _{2} m_{1} } \right) -1} \right) +e^{h_{1} m_{1} }\left( {\lambda _{1} +m_{1} \left( {\eta _{1} +\eta _{2} m_{1} } \right) +1} \right) ,\\ K_{18}= & {} \xi _{3} \left( {K_{1} -K_{0} } \right) \,\left( {\xi _{3} \left( {F+K_{8} } \right) -K_{11} \left( {h_{2} -h_{1} } \right) \,\xi _{3} } \right) -K_{9} \xi _{3} \left( {K_{10} -K_{11} } \right) , \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Akram, S., Razia, A. & Afzal, F. Effects of velocity second slip model and induced magnetic field on peristaltic transport of non-Newtonian fluid in the presence of double-diffusivity convection in nanofluids. Arch Appl Mech 90, 1583–1603 (2020). https://doi.org/10.1007/s00419-020-01685-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-020-01685-4

Keywords

Search

Navigation