Introduction

By a mechanical cleavage method1, the number of layers in graphite is decreased from a huge number to unity, and graphene can be simply defined as a single layer of graphite. But, above how many layers of graphene can we regard it as if “graphite”? This is a natural question for many readers. We answer the question by calculating the optical properties of an N-layer graphene as a function of the number of layers N. In the process of solving this problem, we noticed that various interesting aspects lie behind it. They include not only scientific problems but also important problems related to applications. For example, what is the optimum N for absorbing light most efficiently? Interestingly, the answer is related to a fundamental physics constant, namely the fine-structure constant α ≃ 1/137.

The exfoliation of a single-layer graphene from graphite provided a great opportunity to explore the behavior of massless Dirac fermions2,3. It is widely recognized that because of the conical band structure unique to massless Dirac fermions, graphene absorbs light in accordance with the fine-structure constant2,4,5. Considering the fact that graphite generally possesses massive Dirac fermions6, there should be interesting physics relevant to a change in N from ∞ to 1. Furthermore, the “mass” is closely related to stacking order and interlayer distance which are changed by thermal expansion caused by absorption of light. Therefore, it is meaningful to investigate the optical properties of an N-layer graphene as a function of N.

In this paper, we show the universal layer number in graphite to be 2/πα. By employing the transfer matrix method, we show simultaneously that for light in the infrared to visible range, an N-layer graphene with N above 1500 may be regarded as graphite, on the basis of a convergence criterion. This also enables us to obtain the simplest expression for the optical constants of graphite, which is written in terms of α and interlayer distance only5. The validity of the method is proved by the fact that the calculated reflectance reproduces experimentally observed reflectivity of graphite7. When similar considerations are applied to the general van der Waals heterostructures, many insights besides those into graphite will be obtained.

Results

Universal layer number and optical definition of graphite

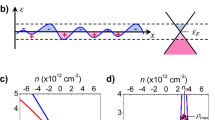
Figure 1a shows the N-dependence of the absorptance AN. The solid curves are obtained by the transfer matrix method for different wavelengths, while the dashed curve at the top is from a simpler model that neglects the reflection. There are three noticeable points in this figure. First, for a small N value below 20, it is hard to distinguish between the results of the two models. This means that the reflection is suppressed and negligible for such N values, which are the systems that were studied extensively after the discovery of graphene. The simplified model is justified for a small N although it fails to explain the fact that graphite gleams. Second, there is a lump-like structure at around 90 that is almost independent of the wavelength. This suggests the presence of a universal number of layers. Figure 1b, which shows the N-dependence of the reflectance RN and transmittance TN for a wavelength at 1550 nm, reveals that the lump-like structure corresponds to the layer number at which RN and TN cross each other. In other words, because RN increases and TN decreases with increasing N, RN + TN takes an extremal value at the crossing point where the condition RN = TN is satisfied. To confirm that the crossing point is exactly given by a universal layer number N =  2/πα, we take the ω → 0 limit in Eq. (4) which immediately gives \({R}_{N}={(\frac{\pi \alpha N}{2+\pi \alpha N})}^{2}\) and \({T}_{N}={(\frac{2}{2+\pi \alpha N})}^{2}\). The emergence of the universal layer number in light absorption is intriguing, because the lump-like structure exhibits a maximum efficiency of 50% for a wide range of wavelengths (>1500 nm) at this universal layer number (2/πα ≈ 87). Physically, maximum efficiency is achieved by the fact that the electric field is not decaying and almost constant (due to boundary reflection). As a result, each layer absorbs an almost equal amount of light most efficiently. Third, AN is almost saturated above about 500 and 670 for 532 and 1550 nm, respectively. The critical layer number, defined more precisely by the tolerance ∣AN − A∞∣ ≤ 10−3, increases with decreasing photon energy, as shown in Fig. 1c. The critical layer number is closely related to the light frequency of interest, and the energy dependence must be relevant to that of the field localization, because the convergence of AN means that TN approaches 0. For light in a wide range of frequencies from infrared to visible, Fig. 1c clearly shows that for N > 1500, AN meets the convergence criterion. Therefore, the condition N > 1500 serves as the definition of “graphite” or more exactly, the lower limit of the number of layers that can be considered graphite from the optics point of view.

Fig. 1: Calculated results.
figure 1

a The light absorptance AN is plotted as a function of the number of graphene layers N for different wavelengths. The arrows indicate the N values above which satisfy the convergence criterion ∣AN − A∞∣ ≤ 10−3. The dashed curve is the result of the simplified model which neglects the reflection. b The N-dependence of the reflectance RN and transmittance TN for 1550 nm. The intersection of RN and TN appears at N = 2/πα. c A contour plot of ∣AN − A∞∣ is shown with the curve of the more stricter convergence criterion ∣AN − A∞∣ ≤ 10−4. The dashed curve is 2δ(ω)/d. The kinks in the 10−3 and 10−4 curves arise because ∣AN − A∞∣ approaches zero as increasing N like a damped oscillation in a manner dependent on photon energy. d The theoretical results reproduce satisfactory the experimental reflectivity of graphite (dashed curve). The correction to πα improves.

Full size image

The results in Fig. 1a, b, c can be qualitatively understood with the basic knowledge about the absorption of light in thin films8. For a very thin film, absorption indeed scales linearly with the real part of the dynamical conductivity and thus also with the number of layers, shown by the simplified model. If the dynamical conductivity does not depend on the frequency, then also the absorption is necessarily dispersionless. Above a certain thickness, this linear approximation fails, while the wave nature of light starts to play a role (thickness is still small, but no longer fully negligible as compared with the wavelength). The absorption then becomes dispersive and it does not go linearly (not even monotonically) with the thickness anymore. Such behavior is well described in classical works on the optical properties of solids8. The only difference here is the non-dispersive conductivity of graphene due to interband transitions.

Simple formula for optical constant of graphite

We now derive a simple formula for the refractive index n and extinction coefficient κ of graphite. The proof consists of two logical steps. First, the optical constants are determined by the dynamical conductivity of graphite σgraphite as (n + iκ)2 = 1 + iσgraphite/ϵ0ω. As a result, we can obtain a theoretical Rgraphite by the standard formula; Rgraphite = [(n − 1)2 + κ2]/[(n + 1)2 + κ2], if σgraphite is known. Second, by the ansatz σgraphite = σgraphene/d5,9, it can be shown that the resultant Rgraphite exactly reproduces the infinitely large N of the transfer matrix model (A∞ = 1 − Rgraphite). Therefore, with the transfer matrix model we establish the following simple analytical expression of the optical constants of graphite,

$$n(\omega )=\sqrt{\frac{1+\sqrt{1+{\left(\frac{\pi \alpha c}{\omega d}\right)}^{2}}}{2}},\kappa (\omega )=\frac{1}{2n(\omega )}\frac{\pi \alpha c}{\omega d}.$$
(1)

These can be used to capture the changes in d caused, for example, by a high pressure10, temperature increase (thermal expansion) due to light absorption, and the propagation of a strain pulse11, through the reflectivity of graphite. We note that the frequency dependence of the critical layer number shown in Fig. 1c is explained by the field localization characterized by the skin-depth δ(ω) ≡ c/ωκ(ω) = (2/πα)n(ω)d, since n(ω) increases as ω decreases. Note also that it contains 2/πα as the characteristic layer number.

We note that the α value cannot change with pressure, so any pressure-induced change to the linear-band structure results in a change of the reflectance. But it is not due to a pressure-induced changes of α but due to a breakdown of the simple description of the reflectance in terms of α and d only.

Discussion

Here, we compare the calculation with an experiment for graphite (highly oriented pyrolithic graphite)7. By using the above-mentioned formula with the optical constants measured for an ordinary ray, we plot the reflectivity as a function of photon energy in Fig. 1d (dashed curve). We compare it with the result calculated with N = 1500, for which there is little discrepancy between theory and experiment at least for photon energy below 0.5 eV. The difference seen from 0.5 to 1.5 eV means extra absorption, which may be the effects of thermal expansion and diffusion12. This speculation is consistent with the fact that Rgraphite decreases with increasing d. The discrepancy between theory and experiment seen at high energy above 1.5 eV is suppressed by the inclusion of the correction πα(1 + 0.05(ℏω/t)2), where t = 3 eV is the hopping integral. The need to correct the conductivity arises partly because of the breakdown of the Dirac cone approximation at high energy13. Our model of graphite, based on the assumption that electrons at different layers interact only through electromagnetic fields14, satisfactory reproduces the experimental result for the reflectance of graphite, despite its simplicity. Our aim was to describe the optical properties of an N-layer graphene in a simplified situation, namely, in the absence of a substrate. In particular, for a small N with non-negligible transmittance, there is a possibility that the transmittance (and therefore the absorptance) is modified by a special substrate. The transfer matrix method can be modified to incorporate the effect of a substrate, which might be necessary if we are to understand the results for a complicated situation.

Finally, we show the correction to AN caused by an electronic coupling between layers that is expected to exist for natural graphite with AB stacking dominance10,15. The energy dispersion relation changes from massless Dirac fermions to massive Dirac fermions with the “mass” \({m}_{r}={\gamma }_{1}\cos \left(\frac{r\pi }{N+1}\right)\), where r (=1, ⋯ , N) is the wavenumber of the standing wave formed along the c-axis by an interlayer hopping of γ1 (= 0.4 eV)6,16. We calculated interband dynamical conductivity of an N-layer graphene with AB stacking and found that it is expressed in terms of the mass variables as

$${\sigma }_{N}(\omega ) =\frac{\pi \alpha }{d}\frac{{\epsilon }_{0}c}{N} \, \mathop{\sum }\limits_{r = 1}^{N}\Bigg\{\left(1-\frac{2{m}_{r}}{\hslash \omega -2{m}_{r}}\right)\Theta (\hslash \omega -2({m}_{r}+| {m}_{r}| )) \\ \,\,\,\,+ {\left(\frac{2{m}_{r}}{\hslash \omega }\right)}^{2}\Theta (\hslash \omega -2| {m}_{r}| )\Bigg\},$$
(2)

where Θ(x) denotes the step function satisfying Θ(x) = 1 for x ≥ 0 and 0 otherwise. This formula reproduces the results obtained previously for small N values17,18,19 and infinite N20. By defining the relative permittivity as \({\varepsilon }_{N}(\omega )\equiv 1+i\frac{{\sigma }_{N}(\omega )}{{\epsilon }_{0}\omega }\), we can obtain the reflection amplitude as \({c}_{0}^{r}=\frac{i \big(\sqrt{{\varepsilon }_{N}}-\frac{1}{\sqrt{{\varepsilon }_{N}}}\big)\sin \left(\sqrt{{\varepsilon }_{N}}\frac{\omega ({z}_{N}-{z}_{1})}{c}\right)}{2\cos \left(\sqrt{{\varepsilon }_{N}}\frac{\omega ({z}_{N}-{z}_{1})}{c}\right)-i\big(\sqrt{{\varepsilon }_{N}}+\frac{1}{\sqrt{{\varepsilon }_{N}}}\big)\sin \left(\sqrt{{\varepsilon }_{N}}\frac{\omega ({z}_{N}-{z}_{1})}{c}\right)}\). Figure 2 shows the resultant AN for three photon energies ℏω = 0.8, 0.4, and 0.2 eV. The correction to the lump-like structure is seen. Interestingly, the correction is most pronounced when photon energy is near 2γ1 and is suppressed by decreasing photon energy. The former originates from the fact that σN(ω) is enhanced by direct interband transitions at ℏω = 2γ110,15. The latter is relevant to the fact that the effect of the γ1 is removed from σN(ω) in the ω → 0 limit: indeed, \({\mathrm{lim}\,}_{\omega \to 0}{\sigma }_{N}(\omega )=\pi \alpha {\epsilon }_{0}c/d\) provided that the system is undoped. Our analysis presented here is limited to AB stacking, and there is a possibility that σN(ω) undergoes further correction because the low-energy band structure is perturbed by an interlayer interaction in a stacking dependent manner6,21.

Fig. 2: Correction to universal layer number by interlayer electronic coupling.
figure 2

The N-dependence on the absorptance AN is shown for several photon energies \(\hbar\omega\) = 0.8, 0.4, and 0.2 eV. The solid (dashed dotted) curves are the results calculated with (without) the interlayer electronic coupling. The correction appears as a slight change in the lump-like structure.

Full size image

In summary, we have proposed the concept of a universal number of layers 2/πα ≈ 87. When the optical properties of an N-layer graphene are viewed as a function of N, 2/πα is much larger than the layer numbers that have been studying extensively after the discovery of the graphene monolayer. Our approaches based on the simple approximation of separated, electrically uncoupled graphene N layers is applicable to other graphene-like materials, multilayer epitaxial graphene and turbostratic graphite22, besides highly oriented pyrolithic graphite. We extended the study to natural graphite, by including interlayer electronic coupling, and found that the N-dependence of absorptance would exhibit a correction to the universal layer number for specific photon energy. When similar considerations are applied to the general van der Waals heterostructures, many insights besides those into graphite will be obtained.

Methods

The transfer matrix method is useful for determining the propagation of waves such as electrons, light, and phonons23 in a superlattice and has also been used for a superlattice containing graphene24,25,26. Our superlattice is shown in Fig. 3, where the previously unreported key idea relates to the interlayer space between adjacent graphene layers as a constituent of the superlattice. In other words, graphite is a superlattice consisting of a vacuum and an atomic layer. The arrows along the z-axis indicate the propagation direction of light; the first graphene layer transmits and reflects the incident light in the forward and backward directions with the amplitudes \({c}_{1}^{t}\) and \({c}_{0}^{r}\), which are to be determined. Such transmission and reflection are repeated at each layer. The absolute square of \({c}_{N}^{t}\) and \({c}_{0}^{r}\) corresponds to the transmittance TN and reflectance RN, respectively. The total absorptance is given by AN = 1 − RN − TN, which is equivalent to the sum of the energies absorbed by each graphene layer.

Fig. 3: N-layer graphene with light.
figure 3

Light propagation in an N-layer graphene superlattice is shown schematically. A linearly polarized light expressed by Ex and By, is assumed in the transfer matrix method. The electromagnetic fields at the i-th interlayer space (zi ≤ z ≤ zi+1) are written in terms of the amplitudes \({c}_{i}^{t}\) and \({c}_{i}^{r}\) as \({E}_{i}(z)={c}_{i}^{t}{e}^{i\omega z/c}+{c}_{i}^{r}{e}^{-i\omega z/c}\) and \(c{B}_{i}(z)={c}_{i}^{t}{e}^{i\omega z/c}-{c}_{i}^{r}{e}^{-i\omega z/c}\). The interlayer distance d is 0.335 nm.

Full size image

The electromagnetic fields of adjacent layers are related by the transfer matrix T given by

$$\left(\begin{array}{l}{E}_{i+1}\\ {B}_{i+1}\end{array}\right)=\left(\begin{array}{ll}\cos \left(\frac{\omega d}{c}\right)&ic\sin \left(\frac{\omega d}{c}\right)\\ \frac{i}{c}\sin \left(\frac{\omega d}{c}\right)&\cos \left(\frac{\omega d}{c}\right)\end{array}\right)\left(\begin{array}{ll}1&0\\ -\frac{\pi \alpha }{c}&1\end{array}\right)\left(\begin{array}{l}{E}_{i}\\ {B}_{i}\end{array}\right).$$
(3)

The T matrix is obtained from Maxwell’s equations and is actually the product of two matrices. The first matrix expresses the propagation of electromagnetic fields in the interlayer vacuum space, which is fixed by the interlayer distance d, angular frequency of light ω, and speed of light c. The second matrix represents the boundary condition of graphene; the electric field is continuous (\({E}_{i+1}^{\prime}={E}_{i}\)), while the magnetic field is discontinuous (\({B}_{i+1}^{\prime}={B}_{i}-(\pi \alpha /c){E}_{i}\)). The discontinuity is given by the current in graphene, Ji = σgrapheneEi, where σgraphene = παϵ0c is the graphene’s dynamical conductivity, divided by −ϵ0c2 according to Ampére’s circuital law. By multiplying the transfer matrix with the field at an infinitesimal distance above the top layer N − 1 times, we can determine the field at an infinitesimal distance below the N-th layer,

$$\left(\begin{array}{l}{E}_{N}^{\prime}({z}_{N})\\ {B}_{N}^{\prime}({z}_{N})\end{array}\right)=\left(\begin{array}{ll}1&0\\ -\frac{\pi \alpha }{c}&1\end{array}\right){T}^{N-1}\left(\begin{array}{l}{E}_{0}({z}_{1})\\ {B}_{0}({z}_{1})\end{array}\right).$$
(4)

Because \({E}_{0}({z}_{1})={e}^{i\omega {z}_{1}/c}+{c}_{0}^{r}{e}^{-i\omega {z}_{1}/c}\) and \(c{B}_{0}({z}_{1})={e}^{i\omega {z}_{1}/c}-{c}_{0}^{r}{e}^{-i\omega {z}_{1}/c}\) for the light at the entrance, and \({E}_{N}^{\prime}({z}_{N})={c}_{N}^{t}{e}^{i\omega {z}_{N}/c}\) and \(c{B}_{N}^{\prime}({z}_{N})={c}_{N}^{t}{e}^{i\omega {z}_{N}/c}\) for the field at the exit, Eq. (4) provides two equations for determining the amplitudes \({c}_{0}^{r}\) and \({c}_{N}^{t}\). Once \({c}_{0}^{r}\) is known, \({c}_{i}^{t}\) and \({c}_{i}^{r}\) can be calculated by using Eq. (3), and the field configuration is locally determined. Please note that in the ω → 0 limit in Eq. (4), we obtain

$$\left(\begin{array}{l}{E}_{N}^{\prime}({z}_{N})\\ {B}_{N}^{\prime}({z}_{N})\end{array}\right)=\left(\begin{array}{ll}1&0\\ -\frac{\pi \alpha N}{c}&1\end{array}\right)\left(\begin{array}{l}{E}_{0}({z}_{1})\\ {B}_{0}({z}_{1})\end{array}\right)$$
(5)

which immediately gives \({R}_{N}={\left(\frac{\pi \alpha N}{2+\pi \alpha N}\right)}^{2}\) and \({T}_{N}={\left(\frac{2}{2+\pi \alpha N}\right)}^{2}\).

For comparison with the transfer matrix model, we use a simpler model that neglects the reflection. The first layer absorbs πα of the incident light and transmits the remaining 1 − πα. Because the second layer absorbs πα of the transmitted light, the amount of transmitted light after the second layer becomes (1 − πα)2. By repeating the calculation, we find that the transmittance after N layers is given by (1 − πα)N and that the absorptance becomes 1 −  (1 − πα)N. This result is independent of ω in contrast to AN.