1 Introduction

With the increasing requirements for the complicated [1] and strict quality required work-piece [2] with sculptured or free-form surfaces [3, 4], five-axis machine tools are indispensable in the modern manufacturing industry [5]. Two additional rotary axes are applied for controlling orientation of the cutting tool [6, 7], and continuously adjusted the cutter’s effective curvature [8]. Compared with three-axis machine tools, there are more advantages in five-axis machine tools, such as higher machining efficiency [9], lower cutting time [10], less work-piece set-up time [11], and higher productivity [5]. However, 80% of total error sources are introduced for the additional rotary axes [12], and bring about flaws and defects in finished work-piece. Hence, researching on geometric errors of rotary axes is significant to improve machining accuracy of five-axis machine tools [13].

Over the past few decades, the error measurement researches have been refined into the error parameters of the movement axis, which makes it possible to calculate the volumetric error of any position and orientation among the workspace of machine tools [14]. DBB is a mature measuring instrument [15] and preferred to be utilized to test volumetric errors of rotary axes [16,17,18] in order to identify the error parameters. Zhang et al. [19] designed two DBB-measuring paths which are in different horizontal planes for decoupling geometric errors of five-axis machine tools’ rotary table. Lee et al. [6] simplified the measurement procedures of DBB by using a single controlled axis during the measurement. Xiang et al. [15] adopted three measuring patterns to obtain a circular trajectory which is generated by the linkage of two rotary axes for identifying the linkage errors of a five-axis machine tool. Lei et al. [12] developed a general ball bar test method for inspecting dynamic errors of rotary axes in five-axis machine tools. Jiang et al. [11] presented a new DBB measurement procedure which avoids coupling among axes and is universal to all types of five-axis machine tools. Chen et al. [20] proposed a circular fitting method to identify the five-axis machine tool’s linkage errors by DBB, measured the integrated errors of a tilt table’s sensitive direction. Jiang et al. [21] presented a comprehensive geometric model which could depict universal kinematic errors of universal machine tools without Abbe errors [22]. Fu et al. [23] developed a systematic accuracy enhancement approach of five-axis machine tools based on differential motion matrix. Lu et al. [24] presented a new two-dimensional method which could analyze spindle radial error motion measurement. In order to improve machining accuracy of non-orthogonal five-axis machine tools, Wu et al. [25] established an integrated geometric error modeling method based on the relative motion constraint equations, and developed an effective iterative compensation method. Liu et al. [18] proposed a volumetric accuracy enhancement method of rotary axes based on screw theory, and established the geometric error model via constructing equivalent rotary axis.

As can be observed in the abovementioned researches, the present work about rotary axis is aiming at geometric errors modeling, identification, and compensation; the aspect in predicting geometric errors of rotary axes is ignored. Geometric errors, which provide guidance for the accuracy design of new machine tools during the design process [26], are one of the most important parameters of accuracy design. In the initial design stage of machine tools, only the information of tolerances of rotary axes are known, while geometric errors are unknown, since geometric errors are parameters generated after assembly of machine tools [7, 25, 27, 28]. Nowadays, the way that designers and engineers obtain geometric errors is just by making use of design experiences [26] without quantify, which cause some inherent and unavoidable defects of the machine tools. Therefore, an effective approach to the prediction and calibration of geometric errors during the design stage of machine tools is significant in practice.

There are several researches have predicted geometric errors of translational axes. Wu et al. [27] proposed a prediction and compensation method of integrated geometric errors for translational axes in one type five-axis machine tools to enhance positioning accuracy. Ekinci et al. [29] considered machine errors at more fundamental levels and presented a method of expressing the geometric profile errors of guideways by Fourier series. Based on Ekinci’s theory, Fan et al. [26] have worked out the mapping relationship between geometric profile errors of machine tools’ guideways and the tolerances, demonstrated that in design stage geometric errors are possible to be known parameters. However, unlike linear axes, the motion of rotary axes is cyclic [1]; there exist fundamental differences in internal structure between rotary axes and translational axes; the theoretical models of two kinds of axes are diverse. So the proposed method of predicting geometric errors to multi-axis machine tools’ linear axes is rarely available for rotary axes. To sum up, it is necessary to develop a predicting method which is aiming at geometric errors of five-axis machine tools’ rotary axes.

In this study, a systematic approach to predict geometric errors of rotary axes in five-axis machine tools based on tolerances is developed. The ties between geometric errors and tolerances are geometric profile errors. Truncated Fourier series is utilized to represent rotary axis error motion, which is cyclic in nature over 360-degree repeating travel. After that, to verify the effectiveness of presented theory, a geometric error identification model of rotary axes based on DBB is established; the transformation of rotary axis is represented by HTM. And lastly, a measuring experiment according to the established identification model is conducted on rotary axes of a five-axis gantry-type milling machine tool. The rest of this paper is arranged as follows: In Section 2, mapping relationships among kinematic errors, geometric profile errors, and tolerances of rotary axes are determined, and kinematic error prediction models are established based on it. In Section 3, identification models of kinematic errors for one type five-axis machine tools’ rotary axes based on DBB are established. In Section 4, a verification experiment is presented. And finally, some conclusions are drawn in Section 5.

2 Positioning error modeling

2.1 Error components definition

Figure 1 shows the five-axis machine tool studied in this paper, which consists of machine bed (body 1) where work-piece placed on, X-axis slide carriage (body 2), Y-axis slide carriage (body 3), Z-axis slide carriage (body 4), C-axis (body 5), and B-axis (body 6). According to the notation of an axis movement standardized in [30], there are 3 linear axes, X-, Y-, and Z-axis that could be notated in X, Y, and Z, respectively, and 2 rotary axes B- and C-axis simplified in B and C which rotate around Y and Z separately. All of the abovementioned components are seen as rigid bodies in this research. The chosen machine tool is in serial kinematic structure, and could be described in WFXYZCBT from work-piece to tool based on the notation of Schwerd [31]. W denotes work-piece, T denotes tool, and F denotes machine bed. The characteristic of serial structures is that all axes can be moved independently [7]. In this study, the rotary axes are extracted for further research; the specific is shown in Fig. 2.

Fig. 1
figure 1

Structure of gantry-type milling machine tool

Full size image
Fig. 2
figure 2

Rotary axes of gantry-type milling machine tool

Full size image

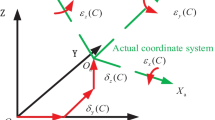
According to ISO 230-7 [32], geometric errors are categorized as position independent geometric errors (PIGEs) and position dependent geometric errors (PDGEs), where “position” refers to the command for a controlled axis [11]. PIGEs are introduced in the assembly process and constant regardless of the position of the axis, while PDGEs change with motion and mainly result from the imperfections in components [6]; therefore, they are also mentioned as location errors and kinematic errors [31]. Taking C rotary axis as an instance, its schematic diagram of PIGEs in the C-axis reference coordinate is shown in Fig. 3, where εxC, εyC represent the verticality error of between X, Y-axis, and C rotary axis separately. Based on rigid body motion theory, there are six inherent component error parameters of a rotary axis [14]; thus, each moving axis of machine tool has six PDGEs. Figure 4 shows six PDGEs of C-axis, where δi(C) and εi(C) (i = x, y, z) represent the linear errors and the angular errors of C-axis along the i direction separately. For a five-axis machine tool, classifying into 3 linear errors, 2 angular errors, and 1 angular positioning error. All geometric error parameters of B- and C-axis are listed in Table 1.

Fig. 3
figure 3

Squareness errors of C-axis

Full size image
Fig. 4
figure 4

The six basic error components of C-axis

Full size image
Table 1 Geometric error parameters
Full size table

2.2 Kinematic error prediction model of rotary axis based on tolerance

Rotary axes’ kinematic errors are resulted from manufacturing deviation of their geometric profile errors. Specifically, according to [33], error motions of rotary axes are physically caused by 2 factors: non-round bearing surfaces and interaction between supporting structure/bearings and internal or external excitations. Figure 5 shows the internal structure of rotary axis, and Fig. 6 shows the rotary motion considering errors. In conjunction with the abovementioned, there are some relationships between the kinematic errors of rotary axes and their geometric profile errors. In the design stage, geometric profile errors of key components are expressed as tolerances, whose values are known. Consequently, the mapping relationship between kinematic error and tolerance is able to be established via rotary axes’ geometric profile errors as a tie, and geometric errors would be predicted based on tolerances.

Fig. 5
figure 5

Internal structure diagram of rotary axis

Full size image
Fig. 6
figure 6

Error motion diagram of rotary axis

Full size image

2.2.1 Mapping relationship between tolerance and geometric error

According to [33], a typical case of error motion is shown as Fig. 7, Fourier series is suitable to express the error motion of rotary axes as Eq. (1) shown, where T denotes the tolerance of rotary motion error, θdenotes the rotary angle, and λ denotes the period of revolution. With the increase of the term of Fourier series, the amplitude of each harmonic constituent gradually decreases; therefore, the influence of geometric profile errors on kinematic errors of rotary axis will decrease as well. This paper aimed at a type of mill high precision milling machine tool whose first term of Fourier series with the largest wavelength has a significant influence on the error motion of rotary axis as well as could express the error motion generally as Fig. 8 shown [33]. Thus, the fundamental error motion, which is the sinusoidal portion of the total error motion that occurs at the rotation frequency, is selected to replace the whole complexed error motion. In addition, it could be observed that the essence of rotary axes’ motion is a cyclic motion with period 2π [2]; the error motion of rotary axis in Cartesian coordinate system could be illustrated as Fig. 9; f(θ) denotes the error motion of rotary axis. Overall, a general mapping model of tolerance and error motion profile of rotary axes could be gotten as Eq. (2) shown.

$$ f\left(\theta \right)=T\sum \limits_{n=1,3,5\dots}^{\infty}\frac{1}{n}\sin \left(\frac{2\pi n\theta}{\lambda}\right) $$
(1)
$$ f\left(\theta \right)=T\sin \left(\theta \right) $$
(2)
Fig. 7
figure 7

Total error motion polar plot

Full size image
Fig. 8
figure 8

First order of error motion polar plot

Full size image
Fig. 9
figure 9

Rectilinear plot of error motion

Full size image

2.2.2 Mapping relationship between geometric profile error and geometric error

This part, it takes C-axis, which is installed in two borings of the stator, as an instance. Figure 10 shows error motion of C-axis, fh1(C) and fh2(C) denotes error appearance between up-boring and down-boring to match surface of C-axis, respectively; LC denotes the length of C-axis, and R denotes the radius of C-axis lower end face.

Fig. 10
figure 10

Schematic diagram of C-axis error motion

Full size image

According to the geometric relationship between error appearance and geometric errors which is shown in Fig. 10, the mapping relationships between geometric profile errors and geometric errors of rotary axes are as following:

$$ {\delta}_x(C)={f}_{h2}(C)-{f}_{h1}(C) $$
(3)
$$ {\varepsilon}_y(C)=\frac{\delta_x(C)}{L_C}=\frac{f_{h2}(C)-{f}_{h1}(C)}{L_C} $$
(4)
$$ {\delta}_y(C)={f}_{h2}(C)-{f}_{h1}(C) $$
(5)
$$ {\varepsilon}_x(C)=\frac{\delta_y(C)}{L_C}=\frac{f_{h2}(C)-{f}_{h1}(C)}{L_C} $$
(6)
$$ {\delta}_z(C)=R\times {\varepsilon}_y(C)=\frac{R\left({f}_{h2}(C)-{f}_{h1}(C)\right)}{L_C} $$
(7)

2.2.3 Mapping relationship between tolerance and geometric error

For translational axes, the position errors are represented by cumulative-lead error of screw which could be divided into lead deviation and the cumulative representative lead error. [26]. While as Fig. 11 shown, when it comes to rotary axis, the position error is commonly seen as a whole. Commanding C-axis rotate θc, the actual location is deviated from the ideal location, and the value of deviation is represented as Tθc. The specific condition of error motion is depicted as Fig. 12, sinusoidal curve is utilized to fit the various deviation as variable fz(C), and the rotary error motion could be expressed as Eq. (8).

$$ {\varepsilon}_z(C)={f}_z(C) $$
(8)
Fig. 11
figure 11

Schematic diagram of rotary error motion of C-axis

Full size image
Fig. 12
figure 12

Unfolding schematic diagram of rotary error motion

Full size image

By Eq. (2) to Eq. (8), the mapping mathematical model between tolerance and geometric errors of rotary axis could be gotten as Eq. (9) to Eq. (14). Th1 denotes the tolerance of error profile of fh1(C), Th2 denotes the tolerance of error profile of fh2(C), Th denotes the tolerance of radial error, and Tθc denotes the tolerance of rotary error.

$$ {\delta}_x(C)=\left({T}_{h2}-{T}_{h1}\right)\sin {\theta}_c={T}_h\sin {\theta}_c $$
(9)
$$ {\delta}_y(C)=\left({T}_{h2}-{T}_{h1}\right)\sin {\theta}_c={T}_h\sin {\theta}_c $$
(10)
$$ {\delta}_z(C)=\frac{R\left({T}_{h2}-{T}_{h1}\right)}{L_C}\sin {\theta}_c=\frac{R{T}_h}{L_C}\sin {\theta}_c $$
(11)
$$ {\varepsilon}_x(C)=\frac{\left({T}_{h2}-{T}_{h1}\right)}{L_C}\sin {\theta}_c=\frac{T_h}{L_C}\sin {\theta}_c $$
(12)
$$ {\varepsilon}_y(C)=\frac{\left({T}_{h2}-{T}_{h1}\right)}{L_C}\sin {\theta}_c=\frac{T_h}{L_C}\sin {\theta}_c $$
(13)
$$ {\varepsilon}_Z(C)={T}_{\theta c}\sin {\theta}_c $$
(14)

3 The measurement and identification of geometric error of rotary axes

3.1 The measurement principle based on DBB

DBB measurement system, as shown in Fig. 13, is a precise instrument which is utilized to investigate geometric errors of rotary axes in this study. There are 2 sockets within a DBB measurement system. Socket 1 is clamped by the tool holder on the spindle, another one, Socket 2, is set on the workbench. Two balls of the DBB, Ball 1 and Ball 2, are installed in ball bowls of two sockets, respectively. The measurement of the rotary axes is realized by the high-precision sensor of DBB measurement system that is able to test the displacement deviation between two balls’ center positions (Fig. 14).

Fig. 13
figure 13

Structure of double ball-bar

Full size image
Fig. 14
figure 14

Mechanism of error generation of C-X detection mode

Full size image

According to Section 2, there are 12 kinematic error parameters that are needed to be identified, including 6 linear errors (δx(b), δy(b), δz(b), δx(c), δy(c), δz(c)), 4 angular errors (εx(b), εz(b), εx(c), εy(c)), and 2 angular positioning errors (εy(b), εz(c)). Two angular positioning errors (εy(b), εz(c)) could be directly tested by the calibration device Renishaw XR20-W without identification. Thus, there are 10 geometric errors of rotary axis that are required to be indirectly identified by DBB. In this paper, C-axis is taken as an example to illustrate the DBB identification.

3.2 Kinematic error identification model based on HTM

When it comes to identify geometric errors of C-axis, follow steps below: test errors in X-Z, Y-Z, and X-Y plane, respectively, which are also called C-X mode, C-Y mode, and C-Z mode separately. The transformations of C-axis are represented by 4 × 4 HTMs.

3.2.1 C-X mode

Under this test mode, adjust the rotary angle of C-axis and B-axis to 0°, parallel the double ball-bar and the X axis of the machine tool, then rotate C-axis and test the variation in X direction. The projection of X-Z plane is shown in Fig. 13, while Pc and Pc’ denote ideal and real coordinate origin of C-axis in X-Z plane, respectively, △x denotes the positioning error of C-axis in X direction, △β denotes angular error of C-axis in X-Z plane, Dcx1 and D’cx1 denote the ideal and the real position of ball 1 in C-axis coordinate, and Hcx1 denotes the theoretical distance between Pc to Dcx1 which is under the mode C-X-1 as shown in Fig. 15a. As far as Dcx2, D’cx2, and Hcx2, they denotes the ideal position, actual position, and theoretical distance between Dcx2 and Hcx2 separately under C-X-2 mode as shown in Fig. 15b.

Fig. 15
figure 15

Schematic diagram of error detection method of C-X mode

Full size image

Dc is ball 1’s ideal position in C-axis coordinate system during the process of C-axis rotating, c denotes the rotary angle of C-axis, Hc denotes the distance between Dc to Pc in general, and Hcx1 and Hcx2 are given value of Hc in C-X-1 mode and C-X-2 mode, respectively. Dc could be expressed by Eq. (15). The expansion form is as Eq. (16). D’c, the practical position of the ball 1, would be calculated by Eq. (17), and could be arranged as Eq. (19). The variation of bar in X direction could be computed via Eq. (16) and Eq. (18), and the computed results are as Eq. (19) and Eq. (20).

$$ {\boldsymbol{D}}_c=\left[\begin{array}{ccc}\cos (c)& -\sin (c)& 0\kern0.5em 0\\ {}\sin (c)& \cos (c)& 0\kern0.5em 0\\ {}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}\begin{array}{cc}1& 0\end{array}\\ {}\begin{array}{cc}0& 1\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}-{H}_c\\ {}1\end{array}\end{array}\right] $$
(15)
$$ {\boldsymbol{D}}_c=\left[\begin{array}{c}0\\ {}0\\ {}-{H}_c\end{array}\right] $$
(16)
$$ {\displaystyle \begin{array}{c}{\boldsymbol{D}}_c^{\prime }=\left[\begin{array}{ccc}1& 0& {\varepsilon}_{\mathrm{x}c}\kern0.5em 0\\ {}1& 1& \begin{array}{cc}-{\varepsilon}_{\mathrm{y}c}& 0\end{array}\\ {}\begin{array}{c}-{\varepsilon}_{\mathrm{x}c}\\ {}0\end{array}& \begin{array}{c}{\varepsilon}_{\mathrm{x}c}\\ {}0\end{array}& \begin{array}{c}\begin{array}{cc}1& 0\end{array}\\ {}\begin{array}{cc}0& 1\end{array}\end{array}\end{array}\right]\left[\begin{array}{ccc}\cos (c)& -\sin (c)& \begin{array}{cc}0& 0\end{array}\\ {}\sin (c)& \cos (c)& \begin{array}{cc}0& 0\end{array}\\ {}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}\begin{array}{cc}1& 0\end{array}\\ {}\begin{array}{cc}0& 1\end{array}\end{array}\end{array}\right]\\ {}\left[\begin{array}{ccc}1& -{\varepsilon}_z(C)& \begin{array}{cc}{\varepsilon}_{\mathrm{y}}(C)& {\delta}_{\mathrm{x}}(c)\end{array}\\ {}{\varepsilon}_{\mathrm{z}}(C)& 1& \begin{array}{cc}-{\varepsilon}_{\mathrm{x}}(C)& {\delta}_y(c)\end{array}\\ {}\begin{array}{c}-{\varepsilon}_{\mathrm{y}}(C)\\ {}0\end{array}& \begin{array}{c}-{\varepsilon}_{\mathrm{x}}(C)\\ {}0\end{array}& \begin{array}{c}\begin{array}{cc}1& {\delta}_z(c)\end{array}\\ {}\begin{array}{cc}0& 1\end{array}\end{array}\end{array}\right]\left[\begin{array}{ccc}1& -{\varepsilon}_{b\mathrm{z}}& \begin{array}{cc}0& 0\end{array}\\ {}{\varepsilon}_{bz}& 1& \begin{array}{cc}-{\varepsilon}_{\mathrm{x}\mathrm{b}}& 0\end{array}\\ {}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}{\varepsilon}_{\mathrm{x}b}\\ {}0\end{array}& \begin{array}{c}\begin{array}{cc}1& 0\end{array}\\ {}\begin{array}{cc}0& 1\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}-{H}_c\\ {}1\end{array}\end{array}\right]\end{array}} $$
(17)
$$ {\displaystyle \begin{array}{c}{D}_{\mathrm{cx}}^{\prime }=\cos (c){\delta}_{\mathrm{x}}(c)-\sin (c){\delta}_{\mathrm{y}}(c)-{H}_c\cos (c){\varepsilon}_{\mathrm{y}}(c)\\ {}-{H}_c\sin (c){\varepsilon}_{\mathrm{x}}(c)-{H}_c{\varepsilon}_{\mathrm{x}\mathrm{c}}-{H}_c\sin (c){\varepsilon}_{\mathrm{bz}}\\ {}\begin{array}{c}{D}_{c\mathrm{y}}^{\prime }=\cos (c){\delta}_{\mathrm{x}}(c)+\sin (c){\delta}_{\mathrm{x}}(c)+{H}_c\cos (c){\varepsilon}_{\mathrm{x}}(c)\\ {}\begin{array}{c}-{H}_c\sin (c){\varepsilon}_{\mathrm{y}}(c)+{H}_c{\varepsilon}_{\mathrm{y}c}+{H}_c\cos (c){\varepsilon}_{bz}\\ {}{D}_{\mathrm{cz}}^{\prime }={\delta}_{\mathrm{z}}(c)-{H}_c\end{array}\end{array}\end{array}} $$
(18)
$$ {\displaystyle \begin{array}{c}\Delta {L}_{c\mathrm{x}}={D}_{c\mathrm{x}}^{\prime }-{D}_{c\mathrm{x}}\\ {}\begin{array}{c}=\cos (c){\delta}_{\mathrm{x}}(c)-\sin (c){\delta}_{\mathrm{y}}(c)-{H}_c\cos (c){\varepsilon}_{\mathrm{y}}(c)\\ {}-{H}_c\sin (c){\varepsilon}_{\mathrm{x}}(c)-{H}_c{\varepsilon}_{\mathrm{x}\mathrm{c}}-{H}_c\sin (c){\varepsilon}_{\mathrm{bz}}\end{array}\end{array}} $$
(19)
$$ {\displaystyle \begin{array}{c}\cos (c){\delta}_{\mathrm{x}}(c)-\sin (c){\delta}_{\mathrm{y}}(c)-{H}_c\cos (c){\varepsilon}_{\mathrm{y}}(c)-{H}_c\sin (c){\varepsilon}_{\mathrm{x}}(c)\\ {}=\Delta {L}_{c\mathrm{x}}+{H}_c{\varepsilon}_{\mathrm{x}\mathrm{c}}+{H}_c\sin (c){\varepsilon}_{bz}\end{array}} $$
(20)

Obviously, acoording to Eq. (20), different values of the variation of bar, △Lcx1 and △Lcx2, would get through changing the distance between ball 1 and the origin coordinate system of C-axis. There are 4 terms without solution as seen in Eq. (21); however, the rand of the coefficient matrix is 2 merely, other terms still need to be solved.

$$ {\displaystyle \begin{array}{c}\left[\begin{array}{ccc}\cos (c)& -\sin (c)& -{H}_{\mathrm{c}1}\cos (c)\kern0.5em {H}_{c1}\sin (c)\\ {}\cos (c)& -\sin (c)& \begin{array}{cc}-{H}_{\mathrm{c}2}\cos (c)& {H}_{c2}\sin (c)\end{array}\end{array}\right]\left\lceil \begin{array}{c}{\delta}_{\mathrm{x}}(c)\\ {}{\delta}_{\mathrm{y}}(c)\\ {}\begin{array}{c}{\varepsilon}_{\mathrm{y}}(c)\\ {}{\varepsilon}_{\mathrm{x}}(c)\end{array}\end{array}\right\rceil \\ {}=\left[\begin{array}{c}\Delta {L}_{c\mathrm{x}1}+{H}_{\mathrm{c}1}{\varepsilon}_{xc}+{H}_{c1}\sin (c){\varepsilon}_{bz}\\ {}\Delta {L}_{c\mathrm{x}2}+{H}_{\mathrm{c}2}{\varepsilon}_{\mathrm{x}\mathrm{c}}+{H}_{c2}\sin (c){\varepsilon}_{bz}\end{array}\right]\end{array}} $$
(21)

3.2.2 C-Y mode

There are two sub-mode in mode C-Y as shown in Fig. 16. Under this mode, based on the similar principle as C-X mode, keep the angle of B-axis and C-axis in 0°, paralell the Y-axis and machine tool, then rotate C-axis and test the variation of the bar’s length in Y direction. In the sub-mode 1, C-Y-1 mode, Dcy1 denotes the ideal position of ball 1, and Hcy1 denotes the theoretical distance between Pc and Dcy1, while D’cy1 denotes the actual situation. Under the C-Y-2 mode, Dcy2 denotes the ideal position of ball 1 in another angle, Hcy2 denotes the theoretical distance between Pc and Hc2, and D’cy2 denotes the real situation.

Fig. 16
figure 16

Schematic diagram of error detection method of C-Y mode

Full size image

The variation of bar’s length in Y direction could be calculated via Eq. (16) and Eq. (18), as Eq. (22) expressed. In this Equation, the parameters εyc, εbz are given; therefore, the variation of the length of bar 1 could be simplified as Eq. (23). Similar to C-X mode’s process, combining Eq. (21) and Eq. (23) to get Eq. (24). It is obvious that the matrix is non-singular; thus, the 4 geometric error parameters of C-axis could be figured out as Eq. (25) to Eq. (28).

$$ {\displaystyle \begin{array}{c}\Delta {L}_{c\mathrm{y}}={D}_{c\mathrm{y}}^{\prime }-{D}_{c\mathrm{y}}\\ {}\begin{array}{c}=\cos (c){\delta}_{\mathrm{y}}(c)+\sin (c){\delta}_{\mathrm{x}}(c)+{H}_c\cos (c){\varepsilon}_{\mathrm{x}}(c)\\ {}-{H}_c\sin (c){\varepsilon}_{\mathrm{y}}(c)+{H}_c{\varepsilon}_{\mathrm{y}c}+{H}_c\cos (c){\varepsilon}_{b\mathrm{z}}\end{array}\end{array}} $$
(22)
$$ {\displaystyle \begin{array}{c}\cos (c){\delta}_{\mathrm{y}}(c)+\sin (c){\delta}_{\mathrm{x}}(c)+{H}_c\cos (c){\varepsilon}_{\mathrm{x}}(c)-{H}_c\sin (c){\varepsilon}_{\mathrm{y}}(c)\\ {}={\Delta L}_{c\mathrm{y}}-{H}_c{\varepsilon}_{\mathrm{y}c}-{H}_c\cos (c){\varepsilon}_{\mathrm{bz}}\end{array}} $$
(23)
$$ {\displaystyle \begin{array}{c}\left[\begin{array}{c}\begin{array}{ccc}\cos (c)& -\sin (c)& -{H}_{\mathrm{c}\mathrm{y}1}\cos (c)\kern0.5em {H}_{\mathrm{c}\mathrm{y}1}\sin (c)\\ {}\cos (c)& -\sin (c)& \begin{array}{cc}-{H}_{c\mathrm{y}2}\cos (c)& {H}_{\mathrm{c}\mathrm{y}2}\sin (c)\end{array}\end{array}\\ {}\begin{array}{c}\begin{array}{ccc}\sin (c)& \cos (c)& \begin{array}{cc}-{H}_{\mathrm{c}y1}\sin (c)& {H}_{\mathrm{c}y1}\cos (c)\end{array}\end{array}\\ {}\begin{array}{ccc}\sin (c)& \cos (c)& \begin{array}{cc}-{H}_{\mathrm{c}\mathrm{y}2}\sin (c)& {H}_{\mathrm{c}y2}\cos (c)\end{array}\end{array}\end{array}\end{array}\right]\left\lceil \begin{array}{c}{\delta}_{\mathrm{x}}(c)\\ {}{\delta}_{\mathrm{y}}(c)\\ {}\begin{array}{c}{\varepsilon}_{\mathrm{y}}(c)\\ {}{\varepsilon}_{\mathrm{x}}(c)\end{array}\end{array}\right\rceil \\ {}=\left[\begin{array}{c}\begin{array}{c}\Delta {L}_{c\mathrm{x}1}+{H}_{cy1}{\varepsilon}_{\mathrm{x}c}+{H}_{\mathrm{c}\mathrm{y}1}\sin (c){\varepsilon}_{bz}\\ {}\Delta {L}_{c\mathrm{x}2}+{H}_{c\mathrm{y}2}{\varepsilon}_{\mathrm{x}c}+{H}_{\mathrm{c}\mathrm{y}2}\sin (c){\varepsilon}_{bz}\end{array}\\ {}\Delta {L}_{c\mathrm{y}1}+{H}_{c\mathrm{y}1}{\varepsilon}_{\mathrm{y}c}+{H}_{cy1}\cos (c){\varepsilon}_{bz}\\ {}\Delta {L}_{\mathrm{c}\mathrm{y}2}+{H}_{\mathrm{c}\mathrm{y}2}{\varepsilon}_{yc}+{H}_{\mathrm{c}\mathrm{y}2}\cos (c){\varepsilon}_{b\mathrm{z}}\end{array}\right]\end{array}} $$
(24)
$$ {\displaystyle \begin{array}{c}{\varepsilon}_{\mathrm{x}}(c)=\frac{\cos (c)\left(\Delta {L}_{c\mathrm{y}1}-\Delta {L}_{\mathrm{c}y2}\right)+\sin (c)\left(\Delta {L}_{\mathrm{c}\mathrm{x}2}-\Delta {L}_{\mathrm{c}\mathrm{x}1}\right)}{H_{cy1}-{H}_{cy2}}\\ {}-\cos (c){\varepsilon}_{\mathrm{y}c}-\sin (c){\varepsilon}_{xc}-{\varepsilon}_{bz}\end{array}} $$
(25)
$$ {\displaystyle \begin{array}{c}{\varepsilon}_{\mathrm{x}}(c)=\frac{\cos (c)\left(\Delta {L}_{cx2}-\Delta {L}_{cx1}\right)+\sin (c)\left(\Delta {L}_{cy2}-\Delta {L}_{cy1}\right)}{H_{cy1}-{H}_{cy2}}\\ {}-\cos (c){\varepsilon}_{yc}-\sin (c){\varepsilon}_{yc}\end{array}} $$
(26)
$$ {\delta}_{\mathrm{y}}(c)=\frac{\sin (c)\left({H}_{c2}\Delta {L}_{cx1}-{H}_{c1}\Delta {L}_{cx2}\right)+\cos (c)\left({H}_{c1}\Delta {L}_{cy2}-{H}_{c2}\Delta {L}_{cy1}\right)}{H_{\mathrm{cy}1}-{H}_{\mathrm{cy}2}} $$
(27)
$$ {\delta}_{\mathrm{x}}(c)=\frac{\sin (c)\left({H}_{c1}\Delta {L}_{cx2}-{H}_{c2}\Delta {L}_{c\mathrm{x}1}\right)+\sin (c)\left({H}_{c1}\Delta {L}_{cy2}-{H}_{c2}\Delta {L}_{\mathrm{cy}1}\right)}{H_{c\mathrm{y}1}-{H}_{c\mathrm{y}2}} $$
(28)

3.2.3 C-Z mode

Lastly, to distinguish the axial aligning errors of C-axis, C-Z mode is proposed as shown in Fig. 17. Adjust B- and C-axis to 0°, paralell the bar and Z-axis, then rotate Z-axis to test the variation of bar in Z direction. Till now, there is only one error parameter that is unknown, thus only one identifying equation is needed to establish in this mode. Dcz denotes the ideal situation of ball 1, and the distance between Pc and Dcz is indicated as Hcz, the actual situation of ball 1 is indicated as D’cz.

Fig. 17
figure 17

Schematic diagram of error detection method of C-Z mode

Full size image

The variation of bar, calculated by Eq. (16) to Eq. (18), is expressed by Eq. (29).

$$ \Delta {L}_{\mathrm{cz}}={D}_{\mathrm{cz}}^{\prime }-{D}_{cz}={\delta}_z(c) $$
(29)

So far, 5 geometric errors of C-axis have been identified totally.

4 Experimental verification

In order to validate the feasibility, accuracy, and effectiveness of the proposed approach of predicting rotary axes’ kinematic, experiments are conducted on a gantry-type milling machine tools. A DBB system, QC20-W provided by Renishaw, is utilized in this experiment, and the main parameters are shown in Table 1. The installation of DBB is shown in Fig. 15. Before measuring, the machine tool is warmed up for 20 min according to the standard procedure [34], and in order to minimize the impact of thermal error, the ambient temperature is controlled within 20 ± 2 °C [18]. What is more, for eliminating the influence of three translational axes, geometric errors of linear axes are measured and compensated to be significantly small and can be neglected [35]. Moreover, the test was repeated until the repeatability was within the tolerance to guarantee the measurement stability, averages, and standard deviations of all testing results that are calculated based on the repeatability tests Fig. 18.

Fig. 18
figure 18

Initial installation of DBB measurement system

Full size image

Kinematic errors of rotary axes are tested based on the identification method which is presented in Section 3. Take C-axis as an instance, the relative parameters of the test experiment is listed in Tables 2 and 3. The error measurement curve in C-X, Y, and Z mode, which indicate the relationship between rotary angle and variation of DBB, is shown in Fig. 19.

Table 2 QC20-W DBB system performance indicators
Full size table
Table 3 C-axis measurement parameters
Full size table
Fig. 19
figure 19

Direct measurement results of DBB

Full size image

Finally, bring the measurement values of bar’s length into identification model to obtain identification points based on the proposed identification method in Section 3, at the same time, bring the factory and tolerance parameters of the machine tool provided by the manufacturer into Eq. (9) to Eq. (14), then analyze the fitting of identification points and prediction model curves, the mathematical expressions of geometric error prediction model of C-axis are listed in the second column of Table 5. The comparison results of prediction model and measurement result is shown in Fig. 20.

Fig. 20
figure 20

Comparisons between identification result and prediction model of C-axis geometric errors

Full size image

From Fig. 20, it can be seen that the minimum and maximum identified position error value of C-axis are − 13.6 μm and 32.7 μm, respectively, which means the range of the identified position error δx(c)i is 46.3 μm; and the minimum and maximum predicted position error value of C-axis are − 11.7 μm and − 31.9 μm, respectively, which means the range of the predicted position error δx(c)p is 43.6 μm. The difference value between the range of measured result and predicted result is 2.7 μm. Similarly, the range of the measured and predicted results, and difference values of other kinematic errors can be obtained, as shown in Table 4.

Table 4 The range of predicted and measured values of kinematic errors
Full size table

Different values may be caused by two primary causes, (1) the existence of non-geometric error sources, such as control errors, dynamitic errors, assembly inaccuracy, and thermal errors; and (2) some assumptions were utilized for predicting kinematic errors.

Obviously, most of the measurement points are within the confidence interval of prediction model. After further quantification, the evaluation indexes of C-axis prediction model is shown in the third and fourth column of Table 5, where SSE denotes residual sum of squares between estimated value and identified point, R2 denotes fitting equation’s coefficient of determination. The quantitative analysis result shows that, the presented predicting model is able to reflect the motion laws of C-axis kinematic errors. The proposed geometric error prediction method of rotary axes makes it possible for further guiding early accuracy design of multi-axis machine tools.

Table 5 Geometric error prediction models of C-axis and the assessment
Full size table

5 Conclusion

This paper proposes a novel geometric errors predicting method of five-axis machine tools’ rotary axes, based on tolerance. The key in this method is that it takes geometric profile error as a bridge to link geometric error and tolerance. Compared with previous researches, there are some following advantages of this new approach:

  1. (1)

    Consider geometric errors in more fundamental level and take into account the basic factors, geometric profile errors, and tolerances of key components. Therefore, the established kinematic error model is satisfied with the structural feature of rotary axis.

  2. (2)

    According to the structural feature, the periodic variation regulation of rotary axis kinematic errors is calculated by Fourier series function and expressed by tolerances. It realizes that predict kinematic errors of rotary axes in design stage.

  3. (3)

    In consideration of the dynamic characteristic of rotary axes’, kinematic errors establish a more practical identifying model of rotary axes based on DBB.

To verify the effectiveness of the presented method, a measuring experiment is conducted. The SEE and R2 could be calculated according to experimental identifying results and predicting model, the SSE of εz(c), δx(c), εy(c),δz(c), εx(c), and δy(c) are 7.7716 × 10−11, 1.2064 × 10−4, 2.7838 × 10−10, 2.9639 × 10−7, 1.8966 × 10−10, and 2.7838 × 10−10, respectively; and the R2 are 0.8978, 0.9876, 0.9978, 0.9453, 0.9985, and 0.9978, respectively. The experimental results show that the predicted models of rotary axes’ kinematic errors are in coincidence with the measured results basically, little residual errors are able to be neglect. Hence, there is no doubt that the approach is reliable and effective for predicting geometric errors of rotary axes in a five-axis machine tool. Furthermore, this method is universal, and could be extended to other configurations of five-axis machine tools as well.

Despite the progress made in this work, only the first order of Fourier series is selected to be used; consequently, there is a space to shrink the error remainder. In further researches, there would be more orders taken into account to improve the accuracy of prediction. In addition, the prediction effect of C-axis vertical positioning error, δz(c) whose R2 is 0.9453, is not accuracy enough compared with another 5 items of the geometric error parameters, therefore needed to be further improved in the future as well.