Coupled channel analysis of ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$, ${\pi ^0\eta \eta }$ and ${K^+K^-\pi ^0}$ at 900 MeV/c and of ${\pi \pi }$-scattering data

Abstract

A partial wave analysis of antiproton–proton annihilation data in flight at 900 $\mathrm {MeV/}c$ into ${\pi ^0\pi ^0\eta }$, ${\pi ^0\eta \eta }$ and ${K^+K^-\pi ^0}$ is presented. The data were taken at LEAR by the Crystal Barrel experiment in 1996. The three channels have been coupled together with $\pi \pi$-scattering isospin I = 0 S- and D-wave as well as I = 1 P-wave data utilizing the K-matrix approach. Analyticity is treated using Chew–Mandelstam functions. In the fit all ingredients of the K-matrix, including resonance masses and widths, were treated as free parameters. In spite of the large number of parameters, the fit results are in the ballpark of the values published by the Particle Data Group. In the channel ${\pi ^0\pi ^0\eta }$ a significant contribution of the spin exotic $I^G=1^-$ $J^{PC}=1^{-+}$ $\pi _1$-wave with a coupling to $\pi ^0 \eta$ is observed. Furthermore the contributions of $\phi (1020) \pi ^0$ and $K^*(892)^\pm K^\mp$ in the channel ${K^+K^-\pi ^0}$ have been studied in detail. The differential production cross section for the two reactions and the spin-density-matrix elements for the $\phi (1020)$ and $K^*(892)^\pm$ have been extracted. No spin-alignment is observed for both vector mesons. The spin density matrix elements have been also determined for the spin exotic wave.

1 Introduction

Two decades ago ${\bar{p}p}$ annihilation data in flight from the Crystal Barrel experiment have already been analyzed by combining different channels [1, 2]. Such an approach provides good means to face the challenges related to the large number of possible initial ${\bar{p}p}$ states and of overlapping resonances with the same quantum numbers in the light meson sector. The most important advantages compared to single channel fits are the ability to provide additional constraints by sharing common production amplitudes over different channels and to describe the dynamical parts in a more sophisticated way so that the conservation of unitarity and analyticity is better fulfilled. During the last years lots of efforts have been put into a better understanding of the $\pi \pi$-scattering waves. By considering dispersion relations and crossing symmetries the phase shifts and inelasticities for energies below $\sqrt{s} \; < \; 1.425\;$ $\mathrm {GeV/}c^2$ can be now described very precisely [3] and have been taken into account in this analysis. In addition over the last two decades the computing power has improved dramatically so that nowadays more extensive coupled channel analyses can be performed on a reasonable time scale. The reanalysis of the Crystal Barrel data in combination with $\pi \pi$-scattering data therefore helps to better understand the production mechanism of light meson states in the ${\bar{p}p}$ annihilation process.

The ${\bar{p}p}$ data presented here have been measured by the Crystal Barrel experiment at LEAR (Low Energy Antiproton Ring) in the year 1996. The analysis has been performed with PAWIAN (PArtial Wave Interactive ANalysis), a powerful, user-friendly and highly modular partial wave analysis software package with the ability to support single and coupled channel fits with data obtained from different hadron spectroscopy experiments [4]. The analysis of the channels ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$, ${\pi ^0\eta \eta }$ and ${K^+K^-\pi ^0}$ at a beam momentum of 900 $\mathrm {MeV/}c$ coupled together with $\pi \pi$ scattering data could be considerably improved compared to previous analyses [1, 2, 5, 6] with emphasis on the following aspects:

• The three channels are dominated by $f_0$ and $f_2$ resonances decaying to $\pi ^0\pi ^0$, $\eta \eta$ and $K^+ K^-$, respectively. The goal therefore is to determine the pole positions properly and to some extent the partial widths of these resonances utilizing the K-matrix technique with P-vector approach. The fundamental requirements of unitarity and analyticity are realized by making use of Chew–Mandelstam functions proposed by [7, 8]. The advantage of this description is that the search for resonances and the determination of their properties is not limited to the real axis of the complex energy plane where the data are located. Instead, it is possible to investigate the analytic structure over the full complex energy plane.

• The channel ${K^+K^-\pi ^0}$ is of special interest. Only by coupling it to the other two channels it is feasible to disentangle the $f_{J}$ and $a_{J}$ resonance contributions decaying to $K^+K^-$. This is possible because the ${\pi ^0\pi ^0\eta }$ channel contains only the production amplitudes for the reactions ${\bar{p}p}$ $\,\rightarrow \,$ $a_{J}\pi ^0$ and the ${\pi ^0\eta \eta }$ channel only the amplitudes for ${\bar{p}p}$ $\,\rightarrow \,$ $f_{J}\pi ^0$. By sharing these production amplitudes and by constraining in addition the $\rho \pi ^0$ contribution with I = 1 P-wave ${\pi \pi }$-scattering data the decays proceeding via $\phi (1020) \pi ^0$ and $K^*(892)^\pm K^\mp$ can be well extracted. Based on the fitted amplitudes the spin density matrix (SDM) elements for the two vector mesons $\phi (1020)$ and $K^*(892)^\pm$ can be determined which provide the full information on the underlying production process. The comparison with the $\omega$ production in the channel ${\bar{p}p}\,\rightarrow \,\omega \pi ^0$[9] delivers new information about the ${\bar{p}p}$ production process of light mesons with strange-quark content. The reaction ${\bar{p}p}\,\rightarrow \,K^+K^-\pi ^0$ has already been studied in detail for beam momenta between 1.0 and 2.5 $\mathrm {GeV/}c$[10]. Due to the limited number of events only SDM elements averaged over the production angle have been determined. With the data and the refined analysis presented here it is even possible to extract the production angle dependence of the SDM elements with good accuracy.

• In ${\bar{p}p}$ and $\bar{p} n$ annihilations the spin exotic wave $\pi _1$ was so far only visible in annihilations at rest [11, 12]. It was the aim of this refined analysis to trace it also in ${\bar{p}p}$ experiments in flight. Also here the extraction of the SDM elements might help to better understand the annihilation process for this kind of reaction.

• The outcome of this analysis provides also new and very helpful insights for high quality and high statistics experiments like PANDA [13]. One major physics topic of PANDA is the spectroscopy of exotic and non-exotic states in the charmonium and open charm mass regions in ${\bar{p}p}$ production and formation processes. In particular similarities between the ${\bar{p}p}$ annihilation processes into the channels $\phi (1020) \pi ^0$, $K^*(892)^\pm K^\mp$ and the channels $J/\psi \pi ^0$, $D^* \bar{D}$ consisting of charm quarks can be expected.

2 Crystal Barrel experiment

The Crystal Barrel detector has been designed with a cylindrical geometry along the beam axis. A liquid hydrogen target cell with a length of 4.4 cm and a diameter of 1.6 cm was located in the center of the detector where the ${\bar{p}p}$ annihilation took place. Antiprotons that passed the target without annihilation were vetoed by a downstream scintillation detector. The target was surrounded by a silicon vertex detector, followed by a jet drift chamber which covered 90% and 64% of the full solid angle for the inner and outer layer, respectively. These devices together with a solenoid magnet providing a homogeneous 1.5 T magnetic field parallel to the incident beam guaranteed a good vertex reconstruction, tracking and identification for charged particles. For the accurate measurement of the energy and flight direction of photons the detector was equipped with a barrel-shaped calorimeter consisting of 1380 CsI(Tl) crystals covering the full azimuth range of 360$^\circ$ and polar angles from 12$^\circ$ to 168$^\circ$. With this electromagnetic calorimeter, located between the jet drift chamber and the solenoid magnet, an energy resolution of $\sigma _E/E \approx$ 2.5 % and an angular resolution of 1.2$^\circ$ in $\theta$ and $\phi$ each have been achieved for photons with an energy of 1 GeV. A detailed description of the full detector can be found elsewhere [14].

3 Data selection

The basic reconstruction and event selection was performed in analogy to older publications by the Crystal Barrel Collaboration (see e.g. [1, 2, 5, 6]). In addition, neural networks were used to detect electromagnetic [15] and hadronic [16] split-offs, that could be falsely registered as photon candidates in the electromagnetic calorimeter. For all three reactions considered here an exclusive reconstruction was performed. Thus, events are only accepted and subjected to further analysis if all final state particles have been detected.

3.1 Selection criteria

$\pi ^0\pi ^0\eta$: This reaction results in a final state of six photons, thus the number of tracks is required to be zero. Furthermore, the number of photon candidates after application of the split-off detection must be exactly six. Since the final state photons can be combined in multiple ways to form the required $\pi ^0$ and $\eta$ resonances, kinematic fits under the hypotheses $6\gamma$, $\pi ^0\pi ^0 \gamma \gamma$, $\pi ^0\pi ^0\eta$, $\pi ^0\eta \eta$, $3\pi ^0$, $\omega \omega$ and $3\eta$ are performed. For all hypotheses energy and momentum conservation are required, as well as additional constraints of the invariant two-photon mass to match the respective intermediate resonances $\pi ^0$ or $\eta$. For the signal channel the fit must converge with a confidence level (CL) greater than 10%, corresponding to a probability of $p>0.1$, while $p<0.001$ is required for most background hypotheses. For the $\omega \omega$ hypothesis a requirement of $p<0.01$ is used. A previous analysis of the $\pi ^0\pi ^0\eta$ final state based on the same data set has shown [2], that after the application of kinematic fits events originating from the reaction ${\bar{p}}p \,\rightarrow \,\omega (\,\rightarrow \,\gamma \pi ^0) \pi ^0\pi ^0 \,\rightarrow \,7\gamma$ represent the main source of remaining background. For these events in most cases one of the seven final state photons escapes the detection. To effectively suppress this type of background events, we make use of a sophisticated event-based method, which is described in Sect. 3.2.

$\pi ^0\eta \eta :$ Since also this reaction results in a six photon final state, the basic selection criteria are very similar to the ones applied in the $\pi ^0\pi ^0\eta$ case. Also here, multiple kinematic fits are performed to improve the quality of the selected data sample. All kinematic fits require conservation of energy and momentum and additional constraints to the $\pi ^0$ or $\eta$ mass, where applicable. Again, the fit is required to converge for the signal channel with $p>0.1$. More stringent requirements are set to reduce background from the reactions ${\bar{p}}p \,\rightarrow \,\omega \omega$ ($p<0.01$) and ${\bar{p}}p \,\rightarrow \,3\eta$ ($p<0.1$). Similar to the $\pi ^0\pi ^0\eta$ channel, it is expected that prominent background due to the reaction ${\bar{p}}p \,\rightarrow \,\omega \pi ^0\pi ^0 \,\rightarrow \,7\gamma$ remains after the selection. This type of background can appear below both $\eta$ signals and is treated with the event-based background suppression described in Sect. 3.2.

$K^+ K^- \pi ^0:$ For this reaction, exactly two oppositely charged kaons are required, which must originate from a common vertex within the target cell. Furthermore, the number of accepted photon candidates after application of the split-off detection is required to be two. Since pions and kaons can not be separated easily by using the information on the differential energy loss from the drift chamber for momenta above 500 $\mathrm {MeV/}c$  the main background for the reaction under study is expected to be ${\bar{p}}p \,\rightarrow \,\pi ^+\pi ^- \pi ^0$. To suppress background and to improve the quality of the data the events are subjected to kinematic fits under the hypotheses ${\bar{p}}p \,\rightarrow \,K^+ K^- \pi ^0$, $K^+K^- \gamma \gamma$, $\pi ^+\pi ^-\pi ^0$, $\pi ^+\pi ^-\eta$, $K^+K^-\eta$, $\pi ^+\pi ^-\eta '$ and $K^+ K^- \eta '$. For each hypothesis the conservation of momentum and energy are required (four constraint fit) as well as an additional constraint to the invariant two-photon mass, which must match the mass of $\pi ^0$, $\eta$ or $\eta '$, where applicable. To accept an event, it is required that the kinematic fit converges for the signal hypothesis with $p>0,1$, while for background suppression $p<0.01$ for the $\pi ^+\pi ^-\pi ^0$-hypothesis and $p<10^{-5}$ for all other hypotheses is required. For the signal hypothesis, the distribution of the CL is found to be almost flat for $p>10\%$, while all pull distributions exhibit a Gaussian shape centered at $\mu =0$ with a width of $\sigma \approx 1$. This indicates a high quality of the data and a properly adjusted error matrix. The CL distribution along with some pull distributions are exemplarily shown for this channel in Fig. 1. After application of these selection criteria the remaining background estimated from the sidebands of the $\pi ^0$ signal in the distribution of the invariant two-photon mass is negligibly small. Thus, no further steps are taken to reduce remaining background and the finally selected 17529 events are used for the partial wave analysis.

Fig. 1

Confidence level and exemplary pull distributions obtained from the kinematic fit for the hypothesis ${\bar{p}}p\,\rightarrow \,K^+K^-\pi ^0$. The confidence level a shows a flat distribution towards large p values and an enhancement for low values, which is caused by background or misreconstructed events. The pull distributions for the angles $\phi$, $\theta$ (b, c) and the square root of the energy (d) for reconstructed photons show a Gaussian shape centered at zero with a width of approximately one. The mean values $\mu$ are extracted from the fit (red). All four distributions show the good quality of the selected data and indicate a well understood error matrix

3.2 Additional signal-background separation

The remaining background contribution for the reactions resulting in a final state consisting of six photons can in principle stem from various sources and is mostly irreducible using simple one-dimensional selection criteria. To identify and suppress this type of background, a signal weight factor Q is assigned to each event. In contrast to other methods, as e.g. the side-band subtraction method for binned data, the procedure employed here is an event based method. No details about the sources of all non-interfering background contributions must be known a priory. This method is described in detail in [17] and was successfully applied in earlier analyses by the CLAS collaboration [18, 19] as well as in a recent re-analysis of Crystal Barrel data [9]. In principle the method relies on the fact, that background events cannot reproduce the narrow mass shape of resonances as e.g. $\pi ^0$ or $\eta$ in the corresponding invariant mass spectrum. To apply the method the nearest neighbors in the phase space for each event must be identified. Therefore, a metric containing relevant kinematic variables must be defined. As described above, the main background for the reaction ${\bar{p}}p \,\rightarrow \,\pi ^0\pi ^0\eta$ stems from processes resulting into a $7\gamma$ final state, where no $\eta$ meson is involved in the decay. Therefore, the method is applied to the invariant two-photon mass in the $\eta$ signal region. The metric was chosen to consist of four kinematic variables, namely the polar production angle of the $\eta$ meson in the center-of-mass frame, the polar and azimuthal decay angles of one of the $\pi ^0$’s in the $\pi ^0\pi ^0$ helicity frame as well as the polar decay angle of the $\eta$ meson in the $\pi ^0\eta$ helicity frame. Figure 2a shows the distribution of the invariant two-photon mass for the 100 nearest neighbors of a selected event identified with the metric described above. The Q-factor for the event under consideration is then defined as the signal-to-background fraction at the position of the event, obtained from an unbinned fit to this distribution containing a description of the signal (described by a Gaussian function) and a linear background, as visualized in Fig. 2a. The same event weight method has been applied for the reaction ${\bar{p}}p \,\rightarrow \,\pi ^0\eta \eta$. Also here, the dominant background contribution stems from reactions, which do not involve an $\eta$ meson. In contrast to the reaction described above, the Q-factor method now has to be applied to the two-dimensional invariant two-photon distribution to simultaneously consider background below both $\eta$ resonances. The metric again consists of four variables, namely the polar production angle of the $\pi ^0$ in the center-of-mass frame, the polar and azimuthal decay angles of one of the two $\eta$ mesons in the $\eta \eta$ helicity frame and the polar decay angle of that $\eta$ meson in the $\pi ^0\eta$ helicity frame. In this case a number of 200 nearest neighbors is identified for each event and the signal is described by a two-dimensional Gaussian function, while the background is parameterized with a linear function independently for both invariant two-photon masses. The Q-factor is then calculated in the same way as for the one dimensional case.

The performance of the Q-factor method is evaluated using dedicated Monte Carlo samples which are generated using proper amplitude models for signal and background contributions. The background can be clearly identified and after application of the Q-factor method we obtain clean data samples which are used as input for the partial wave analysis.

Fig. 2

Performance of the Q-factor method for background below the $\eta$ signal appearing in the reaction ${\bar{p}}p \,\rightarrow \,\pi ^0\pi ^0\eta$. a Shows the invariant two-photon mass for 100 nearest neighbors of a selected $\pi ^0\pi ^0\eta$ event. The green curve shows the total fit result. The blue and red shapes represent the signal and background contributions, respectively. The vertical line denotes the position of the actual event. b Shows the invariant two-photon mass for all events after application of the Q-factor method for the identified signal (blue) and background (red) components

3.3 Overview of the selected ${\bar{p}}p$ data samples

After application of the Q-factor method, a sample of 90408 signal events for the $\pi ^0\pi ^0\eta$ channel is obtained. Figure 3 shows the Dalitz plot of the selected and Q-weighted $\pi ^0\pi ^0\eta$ events. Prominent structures possibly originating from contributions of the $a_2(1320)$ as well as the $f_2(1270)$ meson are clearly visible. Furthermore, possible structures around 1 GeV$/c^2$ can be seen, which may originate from contributions of the $a_0(980)$ and $f_0(980)$ states.

Fig. 3

Dalitz plot for the $\pi ^0 \pi ^0 \eta$ data after application of the background suppression, not corrected for acceptance. Some resonance masses of interest are marked with thin black lines and gray labels (two entries per event)

Fig. 4

Dalitz plot for the $\pi ^0 \eta \eta$ data after application of the background suppression, not corrected for acceptance. Some resonance masses of interest are marked with thin black lines and gray labels (two entries per event)

Fig. 5

Dalitz plot for the $K^+ K^- \pi ^0$ data after application of the background suppression, not corrected for acceptance. Some resonance masses of interest are marked with thin black lines and gray labels

Figure 4 shows the corresponding plot for the $\pi ^0\eta \eta$ channel, for which in total 10533 weighted events were retained. Also here, a strong structure at the mass of the $a_2(1320)$ meson is observed, as well as a rather strong signal of the $a_0(980)$ in comparison with the $\pi ^0\pi ^0\eta$ channel. A strong contribution around 1.5 $\mathrm {GeV/}c^2$ is obvious, originating from an $f_2^{'}(1525)$, an $f_0(1500)$ or both. Figure 5 shows the Dalitz-plot for all 17529 selected events for the $K^+K^-\pi ^0$ channel. It is dominated by bands corresponding to contributions of the $K^*(892)^\pm$ meson decaying into $K^\pm \pi ^0$. At the edge of the phase space a structure corresponding to the $\phi (1020)$ meson is visible, as well as structures around 1.3, 1.5 and 1.7 $\mathrm {GeV/}c^2$. The respective invariant mass plots and the efficiency corrected decay angular distributions are shown in Figs. 7, 8 and 9. Table 1 summarizes the size of the selected samples and the corresponding number of signal events.

3.4 Overview of the scattering data

Most of the $f_0$, $f_2$ and $\rho$ resonances in the light meson sector are characterized by the coupling to several decay channels. Therefore different sets of scattering data are included which results in an adequate consideration of unitarity. The individual sets of scattering data used in the coupled channel fit are as follows: For the reaction $\pi \pi \rightarrow \pi \pi$, $I=0$ S- and D-wave (S0- and D0-wave, associated with $f_0$ and $f_2$ resonances) and $I=1$ P-wave (P1-wave, associated with $\rho$ resonances) are taken into account from [3] for the energy region from the $\pi \pi$ threshold up to $\sqrt{s}\;=\;1.425\,$ $\mathrm {GeV/}c^2$. These model independent descriptions for the phase shift and the inelasticity are based on dispersion relations and crossing symmetries. Since the errors provided in [3] are very small and only based on the uncertainties of the underlying theory, systematic errors of 0.001 for the inelasticity and of $0.01^\circ$ for the phase motion have been added for the combined fit with the ${\bar{p}p}$ data. The remaining energy range between $\sqrt{s} \; > \; 1.425\,$ $\mathrm {GeV/}c^2$ and $\sqrt{s} \; <\;1.9\,$ $\mathrm {GeV/}c^2$ is covered by the CERN-Munich data [20] where the solutions have been chosen which are labeled with ($-\;-\;-$) and ($-\;+\;-$) in [21] and [22], respectively. The modulo squares of the T-matrix for the S0- and D0-wave of the scattering process $\pi \pi \rightarrow KK$ are taken from [23] and for $\pi \pi \rightarrow \eta \eta$ from [24]. The data from [25] are used for the S0-wave scattering process $\pi \pi \rightarrow \eta \eta ^\prime$. A summary of all scattering data is shown in Fig. 11.

Table 1 Number of selected events for all three reactions

Fig. 6

Graphical representation of the most important kinematic variables for the production (a) and decay (b) reference frames. As an example, a scenario corresponding to the ${\bar{p}p}\,\rightarrow \,K^+ K^-\pi ^0$ channel was chosen. The z-axis in a is defined by the flight direction of the antiproton, while the directions of the $x-$ and y-axes are arbitrary and only defined in the laboratory frame by convention (y-axis pointing up in vertical direction). The ${\bar{p}p}$ system then decays to $K^{*+} K^-$, with a further decay of the $K^{*+}$ into $K^+\pi ^0$ (black), or e.g. into $f_0\pi ^0$ with the $f_0$ decaying into $K^+ K^-$ (blue). The angle $\varDelta \phi ^{\bar{p}p}$ is the angle between the planes of these two decay branches. According to Eq. (3) $K^{*+}$ stands for X. In the helicity frame of the $K^{*+}$ depicted in b, the $z'$ axis is defined by the opposite direction of the ${\bar{p}p}$ system or equivalently of the $K^-$ particle. The $x'-z'$ plane is given by the production plane, spanned by the flight directions of the proton and antiproton. Accordingly, the $y'$ axis is perpendicular to this production plane. $K^{*+}$ corresponds to X, $\pi ^0$ to $s_1$ and $K^+$ to $s_2$ which are given in Eq. (4)

4 Partial wave analysis

4.1 Amplitudes

Description of the ${\bar{p}p}$ annihilation amplitudes: The amplitudes for the individual ${\bar{p}p}$ channels are defined in a similar way as explained in [9]. The various contributing initial ${\bar{p}p}$ states are expressed as an expansion in terms of $I^G\;J^{PC}$ states. It has turned out from semi-classical calculations [26] as well as from data analyses, as described in [9] for example, that only states up to a maximal orbital momentum $L^{max}_{\bar{p}p}$ of the ${\bar{p}p}$ system contribute. The complete reaction chain starting from the ${\bar{p}p}$ annihilation system down to the decay into the final state particles is taken into account. The underlying description is based on the helicity formalism. The considered angles, illustrated in Fig. 6, are the polar and azimuthal angle of the production of the intermediate resonance X in the ${\bar{p}p}$ rest frame with respect to the direction of the ${\bar{p}}$ beam ($\theta ^{{\bar{p}p}}_X, \phi ^{{\bar{p}p}}_X$) and the azimuthal and polar angle of the X decay in its helicity system, in which the y-axis is defined to be parallel to the normal vector of the production plane ($\theta ^X_{s_1},\phi ^X_{s_1}$). X stands either for an isolated single resonance or for a partial wave containing several resonances with defined spin/isospin quantum numbers.

The differential cross section is described in terms of the transition amplitude depending on the helicities of the involved particles, which is subdivided into the ${\bar{p}p}$ initial state amplitude $A^{{\bar{p}p}\rightarrow J^{PC}}_{\lambda _p \; \lambda _{\bar{p}}}$, the production amplitude $B^{ J^{PC} \rightarrow X s_r}_{\lambda _X \lambda _{s_r}}$ and the decay amplitude $C^{ X \rightarrow s_1 s_2}_{\lambda _{s_1} \lambda _{s_2}}$ of the intermediate resonance X. The differential cross section for each of the three ${\bar{p}p}$ annihilation reactions is given by:

$$\begin{aligned} \frac{d\sigma }{d\tau } \propto w= & {} \sum _{\lambda _p \lambda _{\bar{p}}} \Big | \sum _{J^{PC}} A^{{\bar{p}p}\rightarrow J^{PC}}_{\lambda _p \; \lambda _{\bar{p}}} \nonumber \\&\cdot \quad \Big ( \sum _{X} \Big ( \sum _{\lambda _X} B^{J^{PC} \rightarrow X s_r}_{\lambda _X \lambda _{s_r}} \cdot C^{ X \rightarrow s_1 s_2}_{\lambda _{s_1} \lambda _{s_2}} \Big ) \Big ) \Big |^2, \end{aligned}$$

(1)

where $\tau$ stands for the phase space, $s_r$ describes the recoil particle of X and $s_1$, $s_2$ are the decay particles of X. $\sum _{X}$ runs over all waves and resonances in all possible sub-channels, like $(K^-\pi ^0)K^+$, $(K^+K^-)\pi ^0$. This expression is equivalent to summing incoherently over the ${\bar{p}p}$ triplet states ($S_{\bar{p}p}= 1$) and the singlet state ($S_{\bar{p}p}= 0$) [27]. The initial state amplitude $A^{{\bar{p}p}\rightarrow J^{PC}}_{\lambda _p \; \lambda _{\bar{p}}}$ is expandable in LS-states:

$$\begin{aligned} A^{{\bar{p}p}\rightarrow J^{PC}}_{\lambda _p \; \lambda _{\bar{p}}}= & {} \sum _{I} i^{J^{PC}}(I^{J^{PC}}_{\bar{p}p})\nonumber \\&\cdot \left( \sum _{L_{{\bar{p}p}}, S_{{\bar{p}p}}}\right. \langle 1/2 , \lambda _p , 1/2 , -\lambda _{\bar{p}}| S_{\bar{p}p}, \lambda _{\bar{p}p}\rangle \nonumber \\&\left. \cdot \langle L_{{\bar{p}p}}, 0 , S_{\bar{p}p}, \lambda _{\bar{p}p}| J^{PC}, \lambda _{\bar{p}p}\rangle \cdot \alpha ^{{\bar{p}p}\rightarrow J^{PC}}_{L_{{\bar{p}p}}S_{\bar{p}p}} \right) ,\nonumber \\ \end{aligned}$$

(2)

where $i^{J^{PC}}(I^{J^{PC}}_{\bar{p}p})$ represents the isospin contributions $I^{\bar{p}p}$=0 and $I^{\bar{p}p}$=1 for the relevant initial ${\bar{p}p}$ state. The expansion into the LS-scheme is taken into account by the sum over the orbital momenta $L_{\bar{p}p}$ and the spins $S_{\bar{p}p}$ of the ${\bar{p}p}$ system with the Clebsch–Gordan coefficients for the coupling of the antiproton and proton spins to $S_{\bar{p}p}$ and for the coupling of $L_{\bar{p}p}$ and $S_{\bar{p}p}$ to $J^{PC}$. The complex fit parameter $\alpha ^{{\bar{p}p}\rightarrow J^{PC}}_{L_{{\bar{p}p}}S_{\bar{p}p}}$ is proportional to the partial wave amplitude $T^{{\bar{p}p}\rightarrow J^{PC}}_{L_{{\bar{p}p}}S_{\bar{p}p}}$ and includes some additional constant prefactors which are not explicitly specified here.

The production amplitude reads:

$$\begin{aligned} B^{ J^{PC}\rightarrow X s_r}_{\lambda _X \lambda _{s_r}}= & {} D^{J^{PC} *}_{\lambda _{{\bar{p}p}} \, \lambda _X} (\theta ^{{\bar{p}p}}_X, \phi ^{{\bar{p}p}}_X)\nonumber \\&\cdot \,\langle I_X, I_{Xz} , I_{s_r}, I_{s_r z}| I^{J^{PC}}_{{\bar{p}p}}, 0 \rangle \nonumber \\&\cdot \Big ( \sum _{L_{X s_r}\;S_{Xs_r}} B^{L_{X s_r}}(\sqrt{s}, m_X, m_{s_r}) \nonumber \\&\cdot \,\langle J_X, \lambda _X, J_{s_r}, \lambda _{s_r} | S_{X s_r} , \lambda _{X s_r} \rangle \nonumber \\&\cdot \,\langle L_{X s_r}, 0, S_{X s_r}, \lambda _{X s_r} | J^{PC} \lambda _{X s_r} \rangle \nonumber \\&\cdot \, \alpha ^{J^{PC} \rightarrow X s_r}_{L_{X s_r} S_{X s_r}} \Big ), \end{aligned}$$

(3)

where $D^{J^{PC} *}_{\lambda _{{\bar{p}p}}\,\lambda _X}$ denotes the complex conjugate Wigner-D function for the decay of the ${\bar{p}p}$ system to X and $s_r$. It is worth noting that also the imaginary part of the Wigner-D function must be used here. The absolute azimuth angle $\phi ^{{\bar{p}p}}_X$ is not unambiguously defined for unpolarized ${\bar{p}p}$ measurements. However, the difference of this angle between two different particle subsystems is accessible and thus considered by this complex function. The first Clebsch–Gordan coefficient describes the isospin coupling followed by the loop over all possible $L_{X s_r} \, S_{X s_r}$ combinations. $B^{L_{X s_r}}$ describes the orbital momentum dependent Blatt–Weisskopf production barrier factor. X stands for the set of isospin and spin quantum numbers of the selected sub-channel. The complex fit parameter $\alpha ^{J^{PC} \rightarrow X s_r}_{L_{X s_r} S_{X s_r}}$ includes again some additional and not explicitly specified constant prefactors.

The decay amplitude is given by:

$$\begin{aligned} C^{X \rightarrow s_1 s_2}_{\lambda _{s_1} \lambda _{s_2}}= & {} D^{J_X*}_{\lambda _X 0}(\theta ^X_{s_1},\phi ^X_{s_1}) \cdot \langle I_{s_1}, I_{s_1 z} , I_{s_2}, I_{ s_2 z}| I_X, I_{Xz} \rangle \nonumber \\&\cdot F_X^{L_{s_1 s_2}}(m_X, m_{s_1}, m_{s_2}) \cdot \alpha ^{X \rightarrow s_1 s_2}_{L_{s_1 s_2} , 0}, \end{aligned}$$

(4)

here the complex conjugate Wigner D-function $D^{J_X*}_{\lambda _X \, 0}$ depends also on the azimuthal angle $\phi ^X_{s_1}$. $m_X$ is the energy of the two-body sub-channel. Since both final state particles exhibit a total spin of 0 only one LS-combination remains with $L_{s_1 s_2}=J_X$ and $S_{s_1 s_2}=0$, which is included in the parameter $\alpha ^{X \rightarrow s_1s_2}_{L_{s_1s_2} , 0}$. The term $F_X^{L_{s_1 s_2}}(m_X, m_{s_1}, m_{s_2})$ represents the dynamics of the partial wave which is described either by the K-matrix formalism or by the Breit-Wigner parametrization as discussed in more detail in the following Sect. 4.2. Since the complex fit parameters $\alpha ^{{\bar{p}p}\rightarrow J^{PC}}_{L_{{\bar{p}p}}S_{\bar{p}p}}$, $\alpha ^{J^{PC} \rightarrow X s_r}_{L_{X s_r} S_{X s_r}}$, and $\alpha ^{X \rightarrow s_1 s_2}_{L_{s_1 s_2} , 0}$ are not independent of each other a certain subset of them is fixed so that exactly one solution is provided for the fit procedure. For a single channel scenario it must be ensured that each product of these fit parameters exhibits one independent complex parameter. Additional constraints such as fixing one global phase in the coherent terms according to Eq. (1) or the treatment of shared parameters for the coupling of different channels lead to further restrictions in the choice of the set of free fit parameters.

For the channels ${\pi ^0\pi ^0\eta }$ and ${\pi ^0\eta \eta }$ only one isospin component is allowed which is $I = 0$ for ${\pi ^0\pi ^0\eta }$ and $I = 1$ for ${\pi ^0\eta \eta }$. The channel ${K^+K^-\pi ^0}$, however, contains excited kaons such as $K^*(892)^\pm$ and probably also the $(K^\pm \pi ^0)_S$ wave. The reaction chains (sub-channels) containing these intermediate resonances with strange quark content must be treated slightly differently compared to the equations above. These channels do not exhibit a well defined C and G parity and can originate from both isospin components $I_{\bar{p}p}= 0$ and $I_{\bar{p}p}= 1$ of the ${\bar{p}p}$ system. Therefore it is necessary to expand the two particle systems $K^*(892)^\pm K^\mp$ and $(K\pi )_S^\pm K^\mp$ to C and G eigenstates for the relevant $I^G \; J^{PC}$ ${\bar{p}p}$ state and the isospin coupling in Eqs. (2–4) must be replaced by appropriate prefactors for considering C-and G-symmetry.

Description of the $\pi \pi$ scattering amplitudes: As mentioned in Sect. 3.4, scattering data from the model independent calculations from [3] are used for the reaction $\pi \pi \rightarrow \pi \pi$ below $\sqrt{s}\;=\;1.425\,$ $\mathrm {GeV/}c^2$. The remaining $\pi \pi$-scattering amplitudes are derived in the usual way from $\pi N$-scattering measurements [28]. For small 4-momentum transfers t they are nearly independent from t and the s-dependence of the $\pi \pi$ scattering can be extracted in the form of scattering matrices $T_{ij}$. i stands for the initial and j for the final channel, such as $\pi \pi$, $K\bar{K}$, $\eta \eta$ or $\eta \eta ^\prime$. The T-matrix can be parametrized in terms of K-matrix elements (see Sect. 4.2). The scattering data for elastic reactions are provided in terms of phase shifts and inelasticities, while for inelastic channels, like $\pi \pi \rightarrow K\bar{K}$ and $\pi \pi \rightarrow \eta \eta$, the moduli squared of the T-matrix, e.g. $(2J+1) \; \rho _{\pi \pi } \; |T|^2 \; \rho _{K\bar{K}}$, are taken (see Fig. 11).

4.2 Dynamics

It is well known that Breit–Wigner parameterizations are only adequate for descriptions of relatively narrow and isolated resonances located far away from any thresholds and with a strong coupling to not more than one channel [8]. However, many light mesons with the same quantum numbers are broad, overlapping with each other and decaying into several different channels. Thus more sophisticated descriptions are needed for those non-trivial dynamics. The analysis presented here makes use of the K-matrix formalism for the 2-body scattering processes and of the P-vector approach for the ${\bar{p}p}$-channels [29, 30]. The P-vector approach is assumed to provide an effective description not only for the non-trivial production mechanism, but also for the effect of rescattering.

Description of the scattering processes: The S-matrix of a 2-body scattering process can be written as

$$\begin{aligned} S =I + 2i \,\rho ^{1/2} \; T \, \rho ^{1/2} , \end{aligned}$$

(5)

with I being the identity and $\rho$ the phase space diagonal matrix. T is the Lorentz-invariant transition matrix element. For reasons of simplicity a possible dependence on the orbital momentum L is neglected here.

T can be written in terms of the K-matrix:

$$\begin{aligned} T(s) = (I \, + \, K(s) \; C(s))^{-1} \; K(s), \end{aligned}$$

(6)

where s is the squared energy of the two-body system and C(s) is the Chew–Mandelstam matrix which is a diagonal matrix by definition. For the fits presented here the elements of this matrix are calculated by the functions as defined in [7] and are connected to the phase space elements by:

$$\begin{aligned} Im \; C_{ii}(s) \, = \, - \rho _{ii}(s), \end{aligned}$$

(7)

where i represents one specific channel. In case of the decay into two stable particles with masses $m_1$ and $m_2$ and with s being real and above the threshold the phase space element reads:

$$\begin{aligned}&\rho _{ii}(s, m_1, m_2) \nonumber \\&\quad = \sqrt{ \Bigl (1-\frac{(m_1+m_2)^2}{s} \Bigr ) \cdot \Bigl (1-\frac{(m_1-m_2)^2}{s}\Bigr ) }\nonumber \\ \end{aligned}$$

(8)

and is normalized such that $\rho _{ii}(s, m_1, m_2) \rightarrow 1$ as $s \rightarrow \infty$. The K-matrix itself is based on the description in [31]:

$$\begin{aligned} K_{ij}(s)= & {} \frac{s-s_0}{s_{norm}} \cdot \sum _{\alpha } B^L_{\alpha _i}(q_i,q_{\alpha _i}) \nonumber \\&\cdot \left( \frac{g^{bare}_{\alpha _i} \; g^{bare}_{\alpha _j}}{ {m^{bare}_\alpha }^2-s} + \sum _n {\tilde{c}}_{nij} \cdot s^n \right) \nonumber \\&\cdot B^L_{\alpha _j}(q_j,q_{\alpha _j}) \end{aligned}$$

(9)

where i and j stand for the reaction channels. The bare parameters $g^{bare}_{\alpha _i}$ and $m^{bare}_\alpha$ represent the coupling strength to the channel i and the mass of the resonance $\alpha$ in the K-matrix representation, respectively. $B^L_{\alpha _i}(q_i,q_{\alpha _i})$ denote the Blatt–Weisskopf barrier factors with the breakup momentum $q_i$ and the resonance breakup momentum $q_{\alpha _i}$ depending on the orbital decay angular momentum L in the channel i. The s dependent polynomial terms of the order n together with the parameters ${\tilde{c}}_{nij}$ describe background contributions, which are allowed to be added to the K-matrix without violating unitarity. $(s-s_0)/s_{norm}$ represents the Adler zero term where $s_0$ is the Adler zero position for the elastic scattering amplitude. Based on ChPT $s_0$ is set to $m_{\pi ^0}^2/2$ for the $(\pi \pi )_S$-wave with isospin I = 0 [32]. For the parameterization of the $(K\pi )_S$ wave with isospin I = 1/2 $s_0$ = 0.23 $\mathrm {GeV/}c^2$ with $s_{norm}= m_K^2 + m_\pi ^2$ is used [31].

Description of the three-body ${\bar{p}p}$ annihilation channels: Here the dynamics is described in the P-vector approach (see Eq. (4)) by [29]:

$$\begin{aligned} F^p_l \; = \; \sum _j (I \; + \; K(s) \; C(s))_{lj}^{-1} \cdot P^p_j, \end{aligned}$$

(10)

where s is the energy squared of the respective two-body sub-channel. p stands for the production of the wave or resonance. $P^p_j$ represents one element of the P-vector taking into account the production process of the sub-channel X. $\sum _j$ runs over all channels relevant for the partial wave under consideration. l is one of the two-body channels relevant for the respective annihilation channel. The F-vector is equivalent to the T-matrix of the two-body scattering process. The P-vector has to exhibit the same pole structures as the K-matrix and is defined as:

$$\begin{aligned} P^p_i = \sum _{\alpha } \left( \frac{ \beta ^p_{\alpha } \; g^{bare}_{\alpha _i}}{{m^{bare}_\alpha }^2 -s} +\sum _n c^p_{ni} \cdot s^n\right) B^L_{\alpha _i}(q_i,q_{\alpha _i}), \end{aligned}$$

(11)

where $\beta ^p_{\alpha }$ is the complex parameter representing the strength of the production process. The remaining terms describe an eventual energy dependent background term. In the coupled channel fit the minor dependency on the different $\bar{p}p$ annihilation processes is neglected and the same effective production background terms have been used for the different $J^{PC}$ initial $\bar{p}p$ states. The masses and decay couplings are the same as in the scattering case, only the production strengths are parameters to be fitted to the annihilation data. For the specific case of the $a_0$ wave represented by a K-matrix consisting of the resonances $a_0(980)$ and $a_0(1450)$ and the channels $\pi ^0\eta$ and $K^+K^-$ with constant background terms produced via $J^{PC} = 1^{++}$ in the reaction $\bar{p}p \rightarrow a_0 \pi ^0 \rightarrow K^+ K^- \pi ^0$ Eqs. (10) and (11) read:

$$\begin{aligned} F^{1^{++}}_{(K^+ K^-)} \; = \; \sum _{j=(\pi ^0\eta )}^{(K^+K^-)} (I \; + \; K(s) \; C(s))_{{(K^+ K^-)} \; j}^{-1} \; \; P^{1^{++}}_j \end{aligned}$$

(12)

with

$$\begin{aligned} P^{1^{++}}_{(K^+ K^-)} = \sum _{\alpha = a_0(980)}^{a_0(1450)} \left( \frac{ \beta ^{1^{++}}_{\alpha } \; g^{bare}_{\alpha _{K^+K^-}}}{{m^{bare}_\alpha }^2 -s} + \, c_{0 \; (K^+ K^-)} \right) \end{aligned}$$

(13)

and

$$\begin{aligned} P^{1^{++}}_{(\pi ^0\eta )} = \sum _{\alpha = a_0(980)}^{a_0(1450)} \left( \frac{ \beta ^{1^{++}}_{\alpha } \; g^{bare}_{\alpha _{\pi ^0\eta }}}{{m^{bare}_\alpha }^2 -s} + \, c_{0 \; (\pi ^0\eta )} \right) . \end{aligned}$$

(14)

The Blatt–Weisskopf barrier factors are not needed here because only the orbital momentum L = 0 is contributing.

4.3 Fits to data

For the coupled channel fit a minimization function is used that considers all individual channels properly. The ${\bar{p}p}$ data, provided by the full information of each event located in a multidimensional phase space volume, are treated slightly differently from the scattering data which are given by one-dimensional diagrams assigned with errors. For the ${\bar{p}p}$ channels an unbinned maximum likelihood minimization procedure is used. Input for this method are the selected data with the event weights $Q_i$ as well as phase-space distributed Monte Carlo events. For properly taking into account the detector resolution and acceptance the GEANT3 transport code has been used. To consider the correct reconstruction efficiency the Monte Carlo events had to undergo the same reconstruction and selection criteria as applied for data events and described in Sect. 3. The extended likelihood function ${\mathscr {L}}$ for each individual channel k is defined as:

$$\begin{aligned}&{\mathscr {L}}_k \propto n_{data}!\cdot \exp \Big (-\frac{(n_{data}-{\overline{n}})^2}{2n_{data}}\Big )\nonumber \\&\quad \cdot \prod _{i=1}^{n_{data}} \frac{w(\varvec{\tau }_{\mathbf{i}}, \varvec{\alpha }) \, \epsilon (\varvec{\tau }_{\mathbf{i}})}{\int w(\varvec{\tau }, \varvec{\alpha }) \, \epsilon (\varvec{\tau }) \, \mathrm {d}\tau } \end{aligned}$$

(15)

where $n_{data}$ denotes the number of data events in the channel k, $\varvec{\tau }$ the phase-space coordinates, $\varvec{\alpha }$ the complex fit parameter, $\epsilon (\varvec{\tau })$ the acceptance and reconstruction efficiency at the position $\varvec{\tau }$ and ${\overline{n}}=n_{data} \cdot \int w(\varvec{\tau }, \varvec{\alpha }) \, \epsilon (\varvec{\tau }) \, \mathrm {d}\tau / \int \epsilon (\tau )\,\mathrm {d}\tau$. $w(\varvec{\tau }, \varvec{\alpha })$ is the weight as given in Eq. (1). $\alpha$ is the set of parameters, like coupling constants, production strengths and bare resonance parameters. By logarithmizing Eq. (15), approximating the integrals with Monte Carlo events and introducing the weight $Q_i$ for each event, the function to be minimized is then given by:

$$\begin{aligned} -\ln \,{\mathscr {L}}_k\approx & {} -\sum _{i=1}^{n_{data}} Q_i \cdot \ln w(\varvec{\tau }_{\mathbf{i}}, \varvec{\alpha }) \nonumber \\&+\, \Big (\sum _{i=1}^{n_{data}} Q_i\Big ) \, \cdot \, \ln \Big ( \frac{\sum _{j=1}^{n_{MC}} w(\varvec{\tau }_{\mathbf{j}}, \varvec{\alpha })}{n_{MC}} \Big ) \nonumber \\&+ \, \frac{1}{2} \, \cdot \, \Big (\sum _{i=1}^{n_{data}} Q_i\Big ) \, \cdot \, \Big (\frac{\sum _{j=1}^{n_{MC}} w(\varvec{\tau }_{\mathbf{j}}, \varvec{\alpha })}{n_{MC}}-1\Big )^2 ,\nonumber \\ \end{aligned}$$

(16)

where $n_{MC}$ represents the number of selected Monte Carlo events for the channel k.

The scattering data are provided by one dimensional data points with errors for each scattering channel $k^\prime$ and here $\chi ^2$ functions are introduced for the minimization procedure. Due to the fact that the relation between $\chi ^2$ and $-\ln \,{\mathscr {L}}$ can be approximated by $\chi ^2 = -2 \cdot \ln \,{\mathscr {L}}$ the total negative likelihood function to be minimized is finally defined as:

$$\begin{aligned} -\ln \,{\mathscr {L}}_{total}= & {} \sum _{{\bar{p}p}\ channel \; k} -\ln \,{\mathscr {L}}_{k} \nonumber \\&+ \sum _{scatt. \; channel\; k^\prime } 0.5 \cdot \chi ^2_{k^\prime } \end{aligned}$$

(17)

4.4 Choice of the best hypothesis

The analysis was performed in two steps. In the first step, which was not performed with the full machinery as described before, the parameter space was investigated in order to fix reasonable start values for the final analysis.

Phase 1: The starting point was the performance of single channel fits for the three ${\bar{p}p}$ reactions individually. Several different hypotheses have been tested in order to get a first glance on the potentially contributing resonances. Based on the outcome from [9] the maximal orbital momentum of the initial ${\bar{p}p}$ system has been chosen to be $L^{max}_{\bar{p}p}\,=\, 4$ for all fits. Also the production amplitudes have been limited to $L^{max}_{X\,s_r} \,=\, 5$. The dynamics of the scalar S wave has been realized by the K-matrix parameterization with fixed parameters from [28]. The $(K\pi )_S$ wave with isospin $I=1/2$ contributes in ${\bar{p}p}\,\rightarrow \,K^+K^-\pi ^0$. It has been expressed for the single as well as for the coupled channel fits by the K-matrix parameterization from the FOCUS experiment [31] containing only the two channels $K\pi$ and $K\eta ^\prime$ and the resonance pole $K^{*\pm }_0(1430)$. All remaining resonances have been taken into account by Breit-Wigner approximations. In order to achieve meaningful results all masses and widths have been fixed to PDG values. Only the narrow $\phi (1020)$ resonance has been treated slightly differently. To take into account the detector resolution a Voigtian function, a convolution of a Breit-Wigner and a Gaussian parameterization, has been used. The total width of $\phi (1020)$ has been fixed to the very precisely known value of 4.2 MeV$/c^2$ [8] in order to avoid unphysical correlations with the fit parameter representing the description of the detector resolution.

Phase 2: Based on the outcome of these fits with simplified and rudimentary descriptions, more sophisticated coupled channel fits taking into account the relevant scattering data have been started. Apart from few isolated resonances the Breit–Wigner and the scalar S wave parameterizations have been replaced by K-matrix descriptions as specified in Sect. 4.2. The masses, coupling strengths and relevant background terms have been released for all contributing resonances. Only the narrow $\phi (1020)$ resonance, the $K^*(892)^\pm$ and the fixed parametrization for the $(K\pi )_S$-wave have been treated in the same way as done before for the single channel fits.

Table 2 Likelihood values and the number of free parameters for fits with the best and alternative hypotheses. $\varDelta$NLL, $\varDelta$ndf, $\varDelta$BIC and $\varDelta$AIC are the differences of the obtained negative log likelihood values, the number of free parameters as well as the BIC and AIC values between the alternative and the best hypothesis. The fits marked with (*) are taken into account for the estimation of the systematic uncertainties. Exemplarily, the results using the scattering data for the solution ($-\;-\;-$) from [21] are shown

The best fit hypothesis had the following ingredients:

• $f_0$-wave ($I^GJ^{PC}=0^+0^{++}$): 5 K-matrix poles ($f_0(500)$, $f_0(980)$, $f_0(1370)$, $f_0(1500)$, $f_0(1710)$) with 5 channels ($\pi \pi$, $K\bar{K}$, $\eta \eta$, $\eta \eta ^\prime$, $2\pi \; 2\pi$). $2\pi \; 2\pi$ is treated as an effective channel with $m_1 = m_2 = m_\pi +m_\pi$ according to Eq. (8) covering all channels with the decay into four pions.

  Similar descriptions for the $f_0$-wave have been used in two other previous analyses. A complementary K-matrix approach with the same decay channels and the same number of poles has been chosen in [28]. The advantage was that a richer set of data samples was considered. On the other hand the treatment of analyticity was more rudimentary since Chew-Mandelstam functions have not been taken into account. In [33] instead high-accuracy dispersive representations have been applied based on a three channel description only.

• $f_2$-wave ($I^GJ^{PC}=0^+2^{++}$): 4 K-matrix poles ($f_2(1270)$, $f^\prime _2(1525)$, $f_2(1810)$, $f_2(1950)$) with 4 channels ($\pi \pi$, $2\pi \; 2\pi$, $K\bar{K}$, $\eta \eta$).

  The decay mode to $\eta \eta ^\prime$ was not used here, since the relevant resonances are expected to couple only weakly to this channel. Also here $2\pi$ $2\pi$ is used as an effective decay mode.

• $\rho$-wave ($I^GJ^{PC}=1^+1^{{-}{-}}$): 2 K-matrix poles ($\rho (770)$, $\rho (1700)$) with 3 channels ($\pi \pi$, $K\bar{K}$ and $2\pi \; 2\pi$). This wave is only relevant for the ${\bar{p}p}$ annihilation channel to ${K^+K^-\pi ^0}$.

• $a_0$-wave ($I^GJ^{PC}=1^-0^{++}$): 2 K-matrix poles ($a_0(980)$, $a_0(1450)$) with 2 channels ($\pi ^0 \eta$, $K\bar{K}$).

  Only these two channels were directly measurable via the ${\bar{p}}p$-data. No information from $\pi \pi$-scattering data could be used. An effective channel for covering all decay modes into $2\pi \;2\pi$ is not introduced here. Fits with additional free parameters related to such an effective channel lead to unreasonable results since no scattering data and thus no constraints on inelasticities can be used.

• $a_2$-wave ($I^GJ^{PC}=1^-2^{++}$): 2 K-matrix poles ($a_2(1320)$, $a_2(1700)$) with 2 channels ($\pi ^0 \eta$, $K\bar{K}$).

  For the choice of the decay channels the same arguments as before hold.

• $(K\pi )_S$-wave ($I\ J^{P}=1/2\ 0^{+}$): Fixed K-matrix parameterization from the FOCUS experiment [31] with one pole ($K^*_0(1430)$) and 2 channels ($K\pi , K\eta ^\prime$).

• $\pi _1$-wave ($I^GJ^{PC}=1^-1^{-+}$): 1 K-matrix pole with two channels ($\pi \eta , \pi \eta ^\prime$). This description is motivated by the recent analysis of COMPASS data [34], where the observed rapid phase shifts of the $1^{-+}$ wave in $\pi \eta$ and in $\pi \eta ^{\prime }$ can be explained by the presence of only one pole.

• $\phi (1020), \, K^*(892)^\pm$.

  These isolated resonances occurring in the channel${K^+K^-\pi ^0}$ are parametrized by Breit-Wigner functions.

In addition, constant background terms for the K-matrix as well as for the P-vector were needed for the three waves $f_0$, $f_2$ and $\rho$ in order to get consistent good results for the simultaneous description of the ${\bar{p}p}$ and scattering data. All background terms of the effective $2\pi \; 2\pi$ channel for the $f_0$-, $f_2$- and $\rho$-wave have been fixed to zero. For the dynamics of the $a_0$- and $a_2$-wave no background terms have been considered and the $\pi _1$-wave is described by a constant background term only for the $\pi \eta$ channel.

The K-matrix parameters for the $f_0$-, $f_2$- and $\rho$-wave obtained by the best fit are summarized in the supplemental material. The parameterizations for the $a_0$, $a_2$ and $\pi _1$-waves are not listed there since the descriptions are simplified and limited to two channels each.

For the selection of the best fit hypothesis the Bayesian information criterion (BIC) and the Akaike information criterion (AIC) [35, 36] have been used, which are given by

$$\begin{aligned} \mathrm {BIC} = -\ln \,{\mathscr {L}} + \mathrm {ndf} \cdot ln(N) \end{aligned}$$

(18)

and

$$\begin{aligned} \mathrm {AIC} = -\ln \,{\mathscr {L}} + 2 \cdot \mathrm {ndf}, \end{aligned}$$

(19)

with ndf being the number of free fit parameters and N the number of data events. The best fit is characterized by a minimal value. The penalty term related to the number of free parameters is larger in BIC than in AIC. Therefore the exclusive use of AIC generally tends to overfitting, while the more stringent criterion BIC instead favors solutions with less parameters and tends to underfitting. A very significant result is achieved when both criteria prefer the same hypothesis. In Table 2 the BIC- and AIC-values for the best fit and for alternative fits are summarized. The best hypothesis is selected by having the lowest AIC + BIC value. A better BIC value is achieved for the hypothesis with only three $f_2$ poles. However, the worsening based on the $\varDelta$AIC value is considerably larger. Slightly better AIC-values are achieved for the hypothesis by adding the $\rho _3(1690)$ resonance and for the ones by adding the $\phi (1680)$ and a contribution of the $\pi _1$ to the $\pi \eta \eta$ channel, respectively. But due to the additional large number of free parameters the BIC criteria gets dramatically worse compared to the best hypothesis. Alternatively to the $\pi _1$ contribution with one pole also this spin-exotic wave containing two poles was tested but discarded because of worse $\varDelta$BIC- and $\varDelta$AIC values. Also the description of the $\pi _1$-wave with a relativistic Breit-Wigner function led to a significantly worse fit result. In addition fits have been performed by adding one more pole for the $f_0$-, $f_2$-, $a_0$- and $a_2$-waves which are not explicitly listed in Table 2. These fits do not yield significant improvements. In most cases the additional poles move far away from the real axis into the complex energy plane and mimick the slowly varying behavior of the K-matrix background terms.

Fig. 7

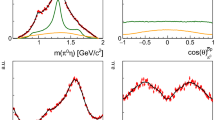
Not acceptance corrected invariant $\pi ^0\pi ^0$ and $\pi ^0\eta$ mass distributions (a, b), acceptance corrected decay angular distributions for the production (c, d) and for the decay (e–h) of the reaction ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$. The data are marked with red and the fit result is illustrated by black dots with error bars

Fig. 8

Not acceptance corrected invariant $\eta \eta$ and $\pi ^0\eta$ mass distributions (a, b), acceptance corrected decay angular distributions for the production (c, d) and for the decay (e–h) of the reaction ${\bar{p}p}\,\rightarrow \,\pi ^0\eta \eta$ . The data are marked with red and the fit result is illustrated by black dots with error bars

Fig. 9

Not acceptance corrected invariant $K^+K^-$ and $K^\pm \pi ^0$ mass distributions (a, b), acceptance corrected decay angular distributions for the production (c, d) and for the decay (e–h) of the reaction ${\bar{p}p}\,\rightarrow \,K^+K^-\pi ^0$ . The data are marked with red and the fit result is illustrated by black dots with error bars

4.5 Comparison of data and fit

4.5.1 Results for ${\bar{p}p}$ data

The fitted mass and decay angular distributions for the reactions ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$ , ${\pi ^0\eta \eta }$ and ${K^+K^-\pi ^0}$ are compared with the data in Figs. 7, 8 and 9, respectively. A good description of the data can be clearly seen for all projections. In Fig. 9c an acceptance hole is clearly visible in the production angular distribution of the $K^\pm \pi ^0$ system for $cos \theta ^{\bar{p}p}_{K^\pm \pi ^0}$ between 0.7 and 1. The loss of acceptance is caused by the limited coverage of the jet drift chamber in the very forward direction. However, this range can be fairly covered by the extrapolation of the fit result.

A goodness of fit test of the obtained probability density function to the data has been performed by utilizing a multivariate analysis based on the concept of statistical energy [37]. The underlying principle is the comparison of the event density distribution in the phasespace volume between the reconstructed data sample and a set of Monte Carlo samples which are generated with the obtained fit parameters and different random seeds each. This powerful binning free approach makes use of the distance between the events in the multidimensional phase-space volume. The p-value is calculated from the number of the comparative scenarios with energies above the nominal statistical energy $\phi _{fit}$ divided by the number of all scenarios. The general idea behind and all details of the energy test are explained extensively in [37]. As shown in Fig. 10, p-values of 0.388, 0.414 and 0.854 demonstrate the good description of the data for all three channels ${\pi ^0\pi ^0\eta }$ , ${\pi ^0\eta \eta }$ and ${K^+K^-\pi ^0}$ , respectively. Furthermore this outcome reveals that the model selection based on the BIC and AIC values is a good choice for the extraction of the best fit hypothesis.

The reliability of the fit procedure has also been tested by an input-output check. Based on the parameter file obtained by the best fit to the data (called reference fit), Monte Carlo samples for the individual channels have been generated. The reliability has been checked by performing fits where the start parameters were randomized within 15 $\sigma$ for the amplitude and 10 $\sigma$ for the resonance parameters. After the fitting procedure the obtained physical quantities are compared with the outcome of the reference fit. The agreement is good and the deviations of all relevant quantities, i.e. differential cross sections, masses, widths, partial widths and spin density matrix elements, are less than $3\sigma$ of the statistical uncertainties.

4.5.2 Results for scattering data

The outcome of the simultaneous fit for the scattering data is summarized in Fig. 11. Apart from some systematic discrepancies, appearing in Fig. 11e, h, the agreement is good. It should be emphasized that in particular a good consistency is achieved for the phase shifts based on the model independent parameterizations with small uncertainties below $\sqrt{s} < 1.425 \;$ $\mathrm {GeV/}c^2$. Figure 12 shows the resulting Argand diagrams for the individual waves.

Fig. 10

Goodness of fit. Statistical energy $\phi$ distribution and corresponding p-value for $\bar{p}p\,\rightarrow \,$ a ${\pi ^0\pi ^0\eta }$, b ${\pi ^0\eta \eta }$ and c ${K^+K^-\pi ^0}$. The red dashed line marks the position of the nominal statistical energy $\phi _{fit}$ and the gray area illustrates the number of scenarios with energies above $\phi _{fit}$

4.6 Comparison to other measurements

One striking feature of the best selected fit is the agreement of the obtained phase difference between the $a_2$ and the $\pi _1$ wave compared to previously published data for $\eta \pi$- and $\eta ^\prime \pi$ production in diffractive $\pi ^- p$ scattering at 191 GeV/c, studied by the COMPASS collaboration [38]. Figure 13 shows the P-wave versus the D-wave phase motion resulting from an $\eta \pi$ partial wave analysis [38], overlayed with the present result extracted from the best fit. It should be stressed that Fig. 13 merely shows a comparison with no subsequent fitting.

5 Extracted properties

For the extraction of all properties the chosen $\pi \pi \rightarrow \pi \pi$ scattering data in the high energy range between $\sqrt{s} \; > \; 1.425$ $\mathrm {GeV/}c^2$ and $\sqrt{s} \; < \; 1.9$ $\mathrm {GeV/}c^2$ are the solution labeled with ($-\;-\;-$) from [22] for the D0- and P1-wave and from [21] for the S0-wave. Since these solutions might be not unambiguous, further alternative fits have been performed by replacing these data by the ones based on the solutions labeled with ($-\;+\;-$) in [22] and [21] for the S0-, D0- and P1-wave and with ($-\;-\;-$) in [22] for the S0-wave, respectively. All of these fit results and the ones marked with (*) in Table 2 are taken into account for the estimation of the systematic uncertainties. Since exchanging the scattering data in the high mass region has a large influence on the resonances in that region, asymmetric uncertainties for the parameters of the $f_0(1710)$, $f_2(1810)$, $f_2(1950)$ and $\rho (1700)$ are determined. Additionally, whenever asymmetries are observed for the deviation of resonance parameters from the respective values of the best fit, these are reflected by asymmetric systematic uncertainties in Table 4, as e.g. for the $f_0(1500)$, $a_2(1700)$ and $\pi _1$.

5.1 Contributions of different waves

The contributions of the individual waves have been determined according to the prescription in [39] by calculating the absolute square of the amplitudes of the relevant wave only, and dividing it by the absolute square of the incoherent and coherent sums of all amplitudes as defined in Eq. (1). As the waves can interfere with each other the sum of all fractions is not necessarily unity. In Table 3 the fractions are listed for each wave and each annihilation channel individually. The total sum of 135.0 ± 1.2 (stat.) ± 8.7 (sys.) $\%$ for the ${\pi ^0\pi ^0\eta }$, 101.2 ± 2.4 (stat.) ± 11.7 (sys.) $\%$ for the ${\pi ^0\eta \eta }$ and 107.8 ± 1.9 (stat.) ± 12.5 (sys.) $\%$ for the ${K^+K^-\pi ^0}$ channel show interference effects which are small enough to believe that the fit result relies on a reasonable physics description. For the resonances described with the K-matrices it is not straightforward to disentangle the individual contributions of different resonances and background terms [39]. Therefore, only the contributions of the partial waves described by the K-matrix are summarized in Table 3. The dominant contributions with more than 20 $\%$ are the $a_0 \, \pi ^0$, $a_2 \, \pi ^0$ and $f_2 \, \eta$ components for the ${\pi ^0\pi ^0\eta }$, the $f_0 \, \pi ^0$, $f_2 \, \pi ^0$ and $a_0 \, \pi ^0$ waves for the ${\pi ^0\eta \eta }$ and the $K^*(892)^\pm \, K^\mp$ reaction for the ${K^+K^-\pi ^0}$ channel. It is worth mentioning that the spin exotic component $\pi _1$ exhibits a fraction of almost 20 $\%$ in ${\pi ^0\pi ^0\eta }$. Figures 14, 15 and 16 show the invariant mass spectra with the contributions of the individual waves for the channels ${\pi ^0\pi ^0\eta }$, ${\pi ^0\eta \eta }$ and ${K^+K^-\pi ^0}$, respectively.

Fig. 11

Results for scattering data. a, b for S wave $\pi \pi \,\rightarrow \,\pi \pi$ inelasticity and phase shift, c–e for $|T|^2$-values of processes $\pi \pi \,\rightarrow \,\eta \eta ,\eta \eta ',KK$ in S wave. f, g for D wave $\pi \pi \,\rightarrow \,\pi \pi$ inelasticity and phase shift. h, i for $|T|^2$-values of processes $\pi \pi \,\rightarrow \,KK, \eta \eta$, j, k for P1 wave $\pi \pi \,\rightarrow \,\pi \pi$ inelasticity and phase shift. The data considered in the best fit are given by red points with error bars which includes the solution ($-\;-\;-$) from [21] (a, b), and solution ($-\;-\;-$) from [22] (f, g, j, k). Data sets from multiple solutions are taken into account as alternative fits. Data points for solution ($-\;+\;-$) from [21] are labeled with magenta stars (a, b), and data points for the solution($-\;-\;-$) and solution ($-\;+\;-$) from [22] are labeled with blue triangles (a, b) and blue squares (a, b, f, g, j, k). The black line represents the fit result, the tiny yellow bands illustrate the statistical uncertainty and the gray bands stand for the systematic uncertainty obtained from the alternative fits. The references for the individual scattering data sets are listed in Sect. 3.4

Fig. 12

Argand plots for the projection $\pi \pi \,\rightarrow \,\pi \pi$ of the waves S0   (a), D0   (b), P1   (c). The numbers along the lines denote the masses at these positions. Exemplarily, the results using the scattering data for the solution ($-\;-\;-$) from [21] for the S0-wave and from [21] [22] for D0- and P1-wave the are shown

Fig. 13

Phase difference between the $a_2$ and the $\pi _1$ wave in $\pi \eta$. The red dots with error bars show the COMPASS data for the P- and D-wave of the $\eta \pi$ system in diffractive $\pi ^- p$ scattering [38]. The corresponding result for the $\pi \eta$ channel extracted from the $a_2$ and the $\pi _1$ scattering matrices $T_{\pi \eta \rightarrow \pi \eta }$ obtained from the best fit in ${\bar{p}p}$ annihilation is represented by the black line. For comparative purposes the obtained phase difference is shifted by an offset of 180$^\circ$. The gray shaded area represents the systematic uncertainty obtained from the alternative fits listed in Table 2 and the yellow band illustrates the statistical uncertainty based on the covariance error matrix from the MINUIT2 fit. Note that this figure does not show a fit to the COMPASS data but merely a comparison

For the reaction ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$ the contributions are comparable with the outcome of the former Crystal Barrel analysis [2]. An obvious difference is that the spin-exotic wave has not been seen in the old analysis. However, an evident contribution of this wave has been found in ${\bar{p}p}$ annihilation data at rest with liquid deuterium and gaseous hydrogen targets [11, 12]. The individual fractions for the channels ${\pi ^0\eta \eta }$ and ${K^+K^-\pi ^0}$ show slight differences compared to former Crystal Barrel analyses [2, 40]. However, the two contributions $\phi (1020) \pi ^0$ and $K^*(892)^\pm K^\mp$ which are of special interest here and where the intermediate resonances are isolated and parameterized by Breit–Wigner functions, are in good agreement with [40]. For most of the remaining resonances, which are described by K-matrices in this work, it is not straightforward to compare the contributions to those obtained from Breit–Wigner based fits.

5.2 Pole and Breit–Wigner parameters

The dynamics of the isolated resonances $K^*(892)^\pm$ and $\phi (1020)$ are described by relativistic Breit–Wigner approximations. The corresponding masses and widths are treated as free parameters so that these properties including their statistical uncertainties can directly be obtained from the outcome of the fit. However, the parameters of the resonances described by the K-matrices must be determined from the pole positions in the complex energy plane of the T-matrix on the Rieman sheet located next to the physical sheet. A detailed description of the classification of poles and their occurrence on the different sheets can be found in [41], for example. Therefore the pole position properties are not direct fit parameters. The scan of the complex energy plane is realized here by a minimization procedure where the real and imaginary parts of the pole in the complex T-matrix plane are the free parameters. The extraction of the statistical errors is based on this fit method as well and makes use of a numerical approach by taking into account the covariance error matrix obtained by the coupled channel fit. Due to the fact that the $f_0(980)$ and $a_0(980)$ resonances are located very close to the $K\bar{K}$ threshold their pole positions have been extracted from the two relevant sheets below and above this threshold. The masses, widths and pole positions obtained for both sheets are listed in Table 4. The systematic uncertainties were derived as described before in Sect. 5.1. It turned out that the statistical errors in particular for the masses and widths provided by the minimization tool MINUIT2 are systematically too small. Therefore the likelihood profiling method [42] has been used for some specific resonances. The obtained uncertainties based on this procedure are larger by a factor of between 2 and 5 compared to the outcome from MINUIT2. However, the uncertainties for the positions of all poles with a significant contribution to the $\bar{p} p$ channels are dominated by the systematics and thus the statistical errors are negligible.

Most of the obtained quantities are in good agreement with other measurements [8]. It should be noted that the $f_0(500)$ exhibits a larger mass and width. This is probably related to the chosen K-matrix approach. The description chosen here does not take into account properly crossing symmetries and other sophisticated constraints for the low $\pi \pi$ mass region, as for example used in [3]. The pole mass of the $a_0(1450)$ meson is measured to be 1302.1 $\mathrm {MeV/}c^2$ , a significantly lower value compared to the PDG average [8]. It is, however, comparable with the old Crystal Barrel analysis [2] and several other measurements collected in [8]. It should be noted that the obtained pole parameters of the $f_0$, $f_2$ and $\rho$ resonances with a non negligible coupling to ${\pi \pi }$ are mainly driven by the used scattering data. Since old analyses are also based on these data and their measurements already contribute to the PDG world average the quantities obtained here are not completely independent. However, the $\pi _1$-, $a_0$- and $a_2$-waves are exclusively contributing in the ${\bar{p}p}$ data samples. Therefore the measurements of the pole positions related to these waves can be claimed to be independent.

Table 3 Contributions in $\%$ of the individual waves for the three channels ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$ , ${\pi ^0\eta \eta }$ and ${K^+K^-\pi ^0}$

5.3 Partial decay widths

Due to the fact that the K-matrix ansatz chosen here fulfills unitarity and analyticity it is for some specific resonances even possible to extract not only the pole positions but also the coupling strengths and thus the partial widths for the individual decay channels. The widths can be extracted via the residues of the scattering matrix T with the projection to the relevant decay channel k on the sheet closest to the physical one. The residues are determined by calculating the integral along a closed contour $C_{z_{\tilde{\alpha }}}$ around the pole $\tilde{\alpha }$ (cf. [8]):

$$\begin{aligned} Res^{\tilde{\alpha }}_{k \rightarrow k} = \frac{1}{2\pi i} \; \oint _{C_{z_{\tilde{\alpha }}}} \; \sqrt{\rho _k} \, \cdot \, T_{k \rightarrow k} (z) \, \cdot \, \sqrt{\rho _k} \; dz \end{aligned}$$

(20)

where $z_{\tilde{\alpha }}$ denotes the pole position of the resonance $\tilde{\alpha }$ in the complex energy plane. This integral has been numerically estimated by making use of the Laurent expansion as described in [43], for example. By determining the Laurent coefficient $a^k_{-1}$ numerically via

$$\begin{aligned} \frac{1}{a^k_{-1}} \; = \; \frac{\partial }{\partial z} \, \Big |_{z=z_{\tilde{\alpha }}} \; \frac{1}{\sqrt{\rho _k} \cdot T_{k \rightarrow k} \cdot \sqrt{\rho _k} } \; \approx \; \frac{1}{Res^{\tilde{\alpha }}_{k \rightarrow k} }, \end{aligned}$$

(21)

one approximates the partial width $\varGamma _k$ for the decay channel k by:

$$\begin{aligned} \varGamma _k \; \approx \; 2\, \cdot \, \Big | \, a^k_{-1} \, \Big |. \end{aligned}$$

(22)

This method is numerically stable because the inverse T-matrix exhibits a value of zero at the pole position. In addition no integration is needed and thus the calculation is fast. This procedure simplifies the extraction of the statistical uncertainties where the calculation must be redone several times.

Fig. 14

Efficiency corrected invariant $\pi ^0\pi ^0$-(left) and $\pi ^0\eta$-mass (right) for the reaction ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$ . The overall result is marked in black, while the individual contributions are visualized by different colors

Fig. 15

Efficiency corrected invariant $\eta \eta$-(left) and $\pi ^0\eta$-mass (right) for the reaction ${\bar{p}p}\,\rightarrow \,\pi ^0\eta \eta$ . The overall result is marked in black, while the individual contributions are visualized by different colors

Fig. 16

Efficiency corrected invariant $K^{+}K^{-}$-(left) and $K^\pm \pi ^0$-mass (right) for the reaction ${\bar{p}p}\,\rightarrow \,K^+K^-\pi ^0$ . The overall result is marked in black, while the individual contributions are visualized by different colors

Table 4 lists the partial widths for the $f_2(1270)$, $f_{2}^{\prime }(1525)$, $\rho (770)$ and $\rho (1700)$ resonances. These quantities are not extracted for the decay channel to $2\pi \, 2\pi$ which is not directly accessible and is only treated as an effective channel to consider unitarity. The partial widths are in good agreement with all other measurements [8]. It should be noted that the obtained quantities for the $\rho (770)$ are only based on the fit to the scattering data. This vector meson does not couple to the ${\bar{p}p}$ channels analyzed here. The absolute coupling strengths for the $a_0$ and $a_2$ resonances have not been determined because the K-matrices are only described by the two channels $\pi \eta$ and $K\bar{K}$. Since further relevant decay modes like 3$\pi$ or $\omega \pi \pi$ are not considered, the extraction would result in unreliable values for these coupling strengths. Instead, the ratios $\varGamma _{\pi \eta } / \varGamma _{K\bar{K}}$ have been determined for these resonances which should deliver more reasonable results.

Due to the fact that the numerical method based on the Laurent expansion is only a trustful approximation for resonances located not too far from the real axis and not too close to thresholds the coupling strengths have not been extracted for the $f_2(1810)$, $f_2(1950)$ and for all $f_0$ resonances. The relevant K-matrix of the $(\pi \pi )_S$-wave is very complex and is characterized by 5 channels and 5 poles. These poles are in fact located far from the real axis or close to specific thresholds.

5.4 Production cross sections and spin density matrix elements for $\phi (1020)$, $K^*(892)^\pm$ and the $\pi ^0_1$-wave

The differential production cross sections and the SDM elements for the resonances $\phi (1020)$, $K^*(892)^\pm$ in the reaction ${\bar{p}p}\,\rightarrow \,K^+K^-\pi ^0$ and for the spin-exotic wave $\pi _1$ in the reaction ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$ derived from the final fit result are discussed in the following. Due to the fact that the information on the beam luminosity is not accessible anymore, only the relative cross sections could be extracted. Absolute values were determined by normalization to the measured total cross sections at the beam momentum of 900 MeV, 347 ± 37 $\mu$b for the channel ${\bar{p}p}\,\rightarrow \,K^+K^-\pi ^0$ [40] and 83.3 ±4.9 $\mu$b for the reaction ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$ with $\eta \rightarrow \gamma \gamma$ [44].

Table 4 Masses and widths for the individual resonances. The values of the Breit-Wigner parameterization are listed for the isolated resonances $K^*$(892) and $\phi (1680)$. The $\phi (1020)$ has been described by a Voigtian. For the $\pi _1$ and all $f_0$, $f_2$, $a_0$, $a_2$ and $\rho$-states the pole positions are extracted from the T-matrix. Absolute and relative branching fractions are extracted for the $f_2(1270)$, $f_{2}^{\prime }(1525)$, $\rho (770)$, $\rho (1570)$ and for the $a_0$ and $a_2$ resonances, respectively. The quantities for the $a_0(980)$ and $f_0(980)$ mesons are determined on the two relevant sheets below and above the $K\bar{K}$ threshold individually. The sheets of the complex plane are characterized and also defined by the signs (+ and −) of the imaginary part of the channel momenta. The order of the channels for the $f_0(980)$ resonance is $\pi \; \pi$, $2\pi \; 2\pi$, $K\;\bar{K}$, $\eta \; \eta$ and $\eta \; \eta ^\prime$ and for the $a_0(980)$ resonance is $\pi \; \eta$ and $K\;\bar{K}$. The statistical uncertainty is given by the first and the systematic uncertainty is provided by the second error. Each resonance is assigned to the data samples which are contributing significantly to the extraction of the resonance properties (${\bar{p}p}$ data (${\bar{p}p}$) or scattering data (scat) or both (${\bar{p}p}$ + scat))

The SDM elements for the three vector mesons have been extracted in a similarly way as already done for the $\omega$ in the reaction ${\bar{p}p}\,\rightarrow \,\omega \pi ^0$ [9]. Since interference effects are not negligible in particular for the contributions $K^*(892)^\pm K^\mp$ and $\pi ^0_1 \pi ^0$, the extraction of these quantities is more challenging compared to the $\omega \pi ^0$ case which is characterized by an isolated narrow resonance. The traditional way, also called Schilling method [45], cannot be utilized for the decay topology here. This method uses only the decay angles and it is therefore mandatory that no interference effects rise up in connection with the resonance of interest. Instead, the SDM elements have been determined here by using the relevant production amplitudes obtained by the fit which contain the full information on these quantities. This method has already been applied successfully for the reaction $\gamma p \; \rightarrow \; \omega p$ [19] and later on for the ${\bar{p}p}$ annihilation process ${\bar{p}p}\,\rightarrow \,\omega \pi ^0$ [9]. The individual $\rho$-elements can be extracted from the initial ${\bar{p}p}$ and production amplitudes via [46]:

$$\begin{aligned} \rho _{\lambda _i\lambda _j}= & {} \frac{1}{N}\sum _{\lambda _{{\bar{p}}},\lambda _{p}} \Big ( A^{{\bar{p}p}\rightarrow J^{PC}}_{\lambda _p \; \lambda _{{\bar{p}}}} B^{J^{PC} \rightarrow X s_r}_{\lambda _i \; 0} \Big )^* \nonumber \\&\cdot \Big ( A^{{\bar{p}p}\rightarrow J^{PC}}_{\lambda _p \; \lambda _{{\bar{p}}}} B^{J^{PC} \rightarrow X s_r}_{\lambda _j \; 0} \Big ), \end{aligned}$$

(23)

where $\lambda _i$ denotes the helicity of the vector meson and N is the normalization factor:

$$\begin{aligned} N =\sum _{\lambda _{{\bar{p}}},\lambda _{p},\lambda _X} \Big |A^{{\bar{p}p}\rightarrow J^{PC}}_{\lambda _p \; \lambda _{{\bar{p}}}} B^{J^{PC} \rightarrow X s_r}_{\lambda _X \; 0}\Big |^2 \end{aligned}$$

(24)

According to Eq. (3) the SDM elements are slightly depending on the invariant mass of the two-body subsystem X which is caused by the production barrier factor $B^{L_{X s_r}}(\sqrt{s}, m_X, m_{s_r})$. In oder to suppress the impact of this model dependent factor the elements have been extracted within the range of $\pm 20$ $\mathrm {MeV/}c^2$ around the obtained mass values for all 3 vector mesons. This limitation ensures that the fluctuations related to the invariant mass values are small and thus negligible compared with other uncertainties.

The spin density matrix elements averaged over the complete production angle have also been calculated via:

$$\begin{aligned} {\overline{\rho }}_{ij} \; = \; \frac{\int \nolimits _{-1}^{1} \frac{d\sigma }{dcos \; \theta ^{\bar{p}p}} \; \rho _{ij}(cos \; \theta ^{\bar{p}p}) \; dcos \; \theta ^{\bar{p}p}}{ \int \nolimits _{-1}^{1} \frac{d\sigma }{dcos \; \theta ^{\bar{p}p}} \; dcos \; \theta ^{\bar{p}p}} \end{aligned}$$

(25)

5.4.1 ${\bar{p}p}\,\rightarrow \,\phi (1020)\pi ^0$

The differential cross section for the produced $\phi (1020)$ is shown in Fig. 17a. It is clearly visible that this vector meson is produced strongly in the forward and backward direction and is symmetric in $cos\theta ^{{\bar{p}p}}_{\phi }$, as expected according to the underlying strong interaction process. Based on this outcome and the one from [40] the total cross section for the reaction ${\bar{p}p}\,\rightarrow \,\phi (1020)\pi ^0$ at a beam momentum of 900 MeV/c is determined to be $\sigma ({\bar{p}p}\,\rightarrow \,\phi (1020)\pi ^0)$ = 17.5 ± 1.9 (stat.) ± 2.1  (exp.) ± 1.9 (ext.) $\mu$b. The first error is the statistical and the second one the systematic uncertainty from this analysis. The third error represents the uncertainty for the total cross section of the reaction ${\bar{p}p}\,\rightarrow \,K^+K^-\pi ^0$ extracted from [40].

The SDM elements for $\phi (1020)$ in its respective helicity system are shown in Fig. 17b–d. All matrix elements exhibit a strong oscillatory dependence on the production angle $cos \; \theta ^{\bar{p}p}_{\phi }$. This oscillatory behavior was already observed in the SDM elements of the $\omega (782)$ [9]. The integrated elements averaged over the complete production angle are consistent with no spin alignment (Table 5) which means that all diagonal elements are in agreement with ${\overline{\rho }}_{ii} = 1/3$.

Fig. 17

Differential production cross section (a) and spin density matrix elements $\rho _{00}$ (b), $\mathfrak {R}\rho _{10}$ (c) and $\rho _{1 -1}$ (d) of the $\phi (1020)$ in ${\bar{p}p}\,\rightarrow \,\phi (1020)\pi ^0$. All elements are shown in the helicity system of the $\phi (1020)$. The yellow and the gray bands stand for the statistical and systematic uncertainty, respectively

Fig. 18

Differential production cross section (a) and spin density matrix elements $\rho _{00}$ (b), $\mathfrak {R}\rho _{10}$ (c) and $\rho _{1 -1}$ (d) of the $K^{*}(892)^-$ in ${\bar{p}p}\,\rightarrow \,K^*(892) K$. All elements are shown in the helicity system of the $K^{*-}$. The yellow and the gray bands stand for the statistical and systematic uncertainty, respectively

5.4.2 ${\bar{p}p}\,\rightarrow \,K^*(892) K$

In contrast to the $\phi (1020)$ the cross section of the $K^*(892)^-$ is characterized by a very significant asymmetric dependence on the production angle (Fig. 18a) . The production of the $K^*(892)^+$ is directly related to the one of the $K^*(892)^-$ by

$$\begin{aligned} \frac{d\sigma }{dcos\theta ^{\bar{p}p}_{K^{*-}}} (cos\theta ^{\bar{p}p}_{K^{*-}})\; = \; \frac{d\sigma }{dcos\theta ^{\bar{p}p}_{K^{*+}}}(-cos\theta ^{\bar{p}p}_{K^{*+}}) \end{aligned}$$

(26)

and thus the corresponding histograms are not explicitly shown here. The reaction ${\bar{p}p}\,\rightarrow \,K^*(892)^- K^+$ exhibits very similar characteristics like ${\bar{p}p}\,\rightarrow \,K^-K^+$ measured by a spark chamber experiment for 20 incident ${\bar{p}}$ momenta between 0.8 and 2.4 $\mathrm {GeV/}c$ [47]. There the forward peak becomes stronger by increasing beam momenta and it has been suggested that this observed s-dependence might be caused by Regge exchange effects [48, 49]. It might be possible that similar underlying processes are also relevant for the charged $K^*(892)^\pm$ production in this energy region. The total cross section for the reaction ${\bar{p}p}\,\rightarrow \,K^*(892)^- K^+$ at a beam momentum of 900 MeV/c is determined to be $\sigma (\bar{p}p \, \rightarrow \, K^*(892)^{\pm }K^{\mp })$ = 474.5 ± 14.1 (stat.)  ± 116.0 (exp.) ± 50.6 (ext.) $\mu$b. Also here the third error is due to the uncertainty of the total cross section for the reaction ${\bar{p}p}\,\rightarrow \,K^+K^-\pi ^0$ [40].

Table 5 Spin density matrix elements averaged over the whole production cross section for the $\phi (1020)$, $K^*(892)^+$ and $\pi _1^0$ vector mesons in their respective helicity system. The errors give the statistical and the systematic uncertainties. Due to symmetry reasons the elements $\mathfrak {R}\,{\overline{\rho }}_{1\;0}$ for $\phi (1020)$ and $\pi _1^0$ are exactly 0 and therefore not listed here

The SDM elements for $K^{*}(892)^-$ in its respective helicity system are shown in Fig. 18b–d. Similar to the $\phi (1020)$ and $\omega (782)$ case all matrix elements exhibit a strong oscillatory dependence on the production angle $cos \; \theta ^{\bar{p}p}_{K^{*-}}$. Also here the integrated elements averaged over the complete production angle are consistent with no spin alignment (Table 5).

5.4.3 $\bar{p}p\,\rightarrow \,\pi _1^0 \pi ^0$

The differential production cross sections and the SDM elements for the $\pi _1^0$-wave are summarized in Fig. 19. In comparison to the $\phi (1020)$ case the forward and backward peak is similarly pronounced and the SDM element ${\overline{\rho }}_{00}$ averaged over the production angle exhibit a value of $66.7\%$. The total cross section for the reaction ${\bar{p}p}\rightarrow \pi _1^0 \pi ^0$ with the decay $\pi _1^0 \rightarrow \eta \pi ^0$ at a beam momentum of 900 MeV/c is calculated to be $\sigma ({\bar{p}p}\rightarrow \pi _1^0 \pi ^0, \pi _1^0 \rightarrow \eta \pi ^0)$ = 36.1 ± 1.0 (stat.)  ± 6.5 (exp.) ± 2.1 (ref.) $\mu$b. The third error represents the uncertainty of the total cross section for the reaction ${\bar{p}p}\,\rightarrow \,\pi ^0\pi ^0\eta$ extracted from [44].

Fig. 19

Differential production cross section of $\bar{p}p\,\rightarrow \,\pi _1^0 \pi ^{0}$ with $\pi _1^0 \,\rightarrow \,\pi ^{0}\eta$ (a) and spin density matrix elements $\rho _{00}$ (b), $\mathfrak {R}\rho _{10}$ (c) and $\rho _{1 -1}$ (d) of the $\pi _1^0$ in $\bar{p}p\,\rightarrow \,\pi _1^0 \pi ^0$. All elements are shown in the helicity system of the $\pi _1^0$. The yellow and the gray bands stand for the statistical and systematic uncertainty, respectively

6 Summary

A coupled channel analysis of ${\bar{p}p}$ annihilation to ${\pi ^0\pi ^0\eta }$,${\pi ^0\eta \eta }$ and ${K^+K^-\pi ^0}$ at a beam momentum of 900 MeV/c has been performed by considering $\pi \pi$-scattering data for the S0-, D0- and P1-waves. The usage of the K-matrix approach for the description of the dynamics ensures a sufficient fulfillment of unitarity and analyticity conditions. It was demonstrated, that it is possible to extract the properties of all contributing resonances in a simultaneous fit to all data. In lots of analyses in the past, part of the properties were taken from previous fits to a sub-set of data and are not treated as free parameters. All data are reproduced reasonably well by the simultaneous fit. The dominant contributions in the three ${\bar{p}p}$ channels are the $a_2 \, \pi ^0$, and $f_2 \, \eta$ components for ${\pi ^0\pi ^0\eta }$, the $f_0 \, \pi ^0$ and $a_2 \, \eta$ waves for ${\pi ^0\eta \eta }$ and the $K^*(892)^\pm \, K^\mp$ reaction for ${K^+K^-\pi ^0}$. Masses and widths obtained from the Breit-Wigner paramerterizations for isolated resonances and pole positions extracted from the K-matrix descriptions have been determined and are within the ballpark of other individual measurements. In the channel ${\pi ^0\pi ^0\eta }$ a significant contribution of the spin exotic $I^G=1^-$ $J^{PC}=1^{-+}$ wave decaying to $\pi ^0 \eta$ has been observed. By choosing the K-matrix approach with one pole and two decay channels ($\pi \eta$, $\pi \eta ^\prime$) for the description of the dynamics, a mass of (1404.7 ± 3.5 (stat.) $^{+9.0}_{-17.3}$ (sys.)) $\mathrm {MeV/}c^2$ and a width of (628.3 ± 27.1 (stat.) $^{+35.8}_{-138.2}$ (sys.)) MeV are obtained. An analysis explicitly focused on this spin-exotic wave will be presented in a forthcoming paper. Partial decay widths for the $f_2(1270)$, $f_{2}^{\prime }(1525)$, $\rho (770)$ and $\rho (1700)$ states and ratios of these properties for the $a_0$ and $a_2$ resonances have been retrieved via the residues of the pole positions. The differential production cross section and the spin-density-matrix elements for the $\phi (1020)$ and the $K^*(892)^\pm$ have been extracted. While the $\phi (1020)$ vector meson is produced strongly in the forward and backward direction, the $K^*(892)^-$ instead, is characterized by a very significant asymmetric dependence on the production angle. No spin-alignment effects are observed for both vector mesons but the individual spin-density matrix elements exhibit an oscillatory dependence on the production angle. The SDM elements have also been determined for the spin-exotic wave $\pi _1^0$ with an averaged value of ${\overline{\rho }}_{00} =66.7\%$.