Abstract
Conventional approaches to describe dark matter phenomenology at collider and (in)direct detection experiments in the form of dark matter effective field theory or simplified models suffer in general from drawbacks regarding validity at high energies and/or generality, limiting their applicability. In order to avoid these shortcomings, we propose a hybrid framework in the form of an effective theory, including, however, both the dark matter states and a mediator connecting the former to the Standard Model fields. Since the mediation can be realized through rather light new dynamical fields allowing for non-negligible collider signals in missing energy searches, the framework remains valid for the phenomenologically interesting parameter region, while retaining correlations dictated by gauge symmetry. Moreover, a richer new-physics sector can be consistently included via higher-dimensional operators. Interestingly, for fermionic and scalar dark matter with a (pseudo-)scalar mediator, the leading effects originate from dimension-five operators, allowing to capture them with a rather small set of new couplings. We finally examine the correlations between constraints from reproducing the correct relic density, direct-detection experiments, and mono-jet and Higgs + missing energy signatures at the LHC and point out new cancellation patterns in direct-detection, emerging non-trivially in the effective theory.
Similar content being viewed by others
1 Introduction and setup
The origin of the dark matter (DM) observed in the universe is one of the biggest mysteries in physics. A multitude of experiments, which are probing very diverse energies, are currently running or in preparation to address this question. Experiments aiming for a direct detection of DM particles via nuclear recoil typically probe collision energies in the keV range, while collider experiments, trying to produce DM particles, feature momentum transfers exceeding the TeV scale.
Combining the results from all kinds of experiments in a single, consistent, yet general framework is important in order to resolve the nature of DM. Bounds from direct detection experiments are usually interpreted in an effective field theory (EFT) approach [1,2,3,4,5], removing the mediator that couples the DM particles to the Standard Model (SM) as an explicit dynamical degree of freedom at low energies. This is possible, if the mediator is assumed to be much heavier than the scale of the experiments, and its effects can thus be described by generic EFT operators, consisting only of the SM and DM fields.
On the other hand, collider experiments such as the LHC run at much larger energies, and it turns out that the momentum transfers lie typically at (or above) interesting mass ranges for the mediator, to which the analyses are sensitive (unless the model is very strongly coupled [6]). Thus, the EFT description becomes invalid since the mediator is missing in the spectrum [7, 8]. Furthermore, achieving the correct relic abundance via the freeze-out mechanism (as assumed here) requires problematically low cutoff scales – an issue which is solved by including a relatively light mediator. In consequence, collider searches are typically interpreted in terms of simplified models [9,10,11,12,13,14], where the mediator is not removed and its interactions with the SM and the DM are simply parametrized by \(D\le 4\) operators. For the sake of flexibility, the simplest implementations do not require gauge-invariance and are thus not well behaved at large energies. A further drawback of this approach is that they are still rather specific models that do not allow for a maximally general description of the dark sector. In the end, one suffers either from a lack of generality or, even worse, from a lack of validity.
In this article, we want to propose a hybrid framework, which can alleviate the above problems: We will consider the minimal amount of additional dynamical degrees of freedom – a DM particle and a mediator – which is able to generate the correct DM abundance and allows for testability at TeV scale energies, while retaining the generality and consistency of the EFT framework.
We will, thus, consider the SM extended by a SM-singlet particle, \(\mathcal{D}\), that is stable on cosmological scales, and a mediator, \(\mathcal{M}\), that couples it to the SM, as well as higher-dimensional EFT operators, consisting of these fields. We will start by assuming the DM to be a fermion, \(\mathcal{D}=\chi \), and the mediator a (pseudo)scalar, \(\mathcal{M} = \mathcal{S} (\tilde{\mathcal{S}})\), and then move on to consider also the case of scalar DM. In these setups, the leading EFT effects will be at the level of \(D=5\) operators, and their inclusion allows to parametrize physics of the dark sector beyond the single DM particle and the mediator.Footnote 1
In fact, while the inclusion of the latter particles makes the theory valid at collider energies, the augmentation with \(D=5\) operators accounts for the fact that the dark/new sector is likely to be non-minimal. Indeed, there is no stringent reason to believe that the sector related with the DM consists only of very few particles, while the SM has a very rich structure. On the other hand, it is conceivable that a few of the new particles (the DM particle and the mediator) are considerably lighter than the rest of the new physics (NP). For example, the mediator could be a (pseudo-)Goldstone boson of a spontaneously broken global symmetry.Footnote 2 The goal of this article is to provide the theoretical framework of this extended DM EFT (eDMeft) approach, demonstrating its strength in phenomenological analyses, as well as pointing out emerging synergies and generic correlations between observables, which are retained in the EFT approach.
1.1 Fermionic DM with a scalar or pseudoscalar mediator
The effective Lagrangian of the model described above, with a fermion singlet, \(\chi \), and a (CP even) scalar, \(\mathcal{S}\), including operators up to \(D=5\) (following normalisations of Ref. [19]) readsFootnote 3

Here \(Q_{\mathrm {L}}^i\) and \(L_{\mathrm {L}}^i\) are the i-th generation left-handed \(\mathrm {SU}(2)_{\mathrm {L}}\) quark and lepton doublets, resp., \(d^j_{\mathrm {R}}\), \(u^j_{\mathrm {R}}\), and \(\ell _{\mathrm {R}}^j\) are the right-handed singlets for generation j, and H is the Higgs doublet. The latter develops a vacuum expectation value (vev), \(|\langle H \rangle | \equiv v/\sqrt{2} \simeq 174\) GeV, triggering electroweak symmetry breaking (EWSB). In unitary gauge, the Higgs field is expanded around the vev as \(H \simeq 1/\sqrt{2} (0, v + h)^T\). Here, h is the physical Higgs boson, with mass \(m_h \approx 125\) GeV. We assume a stabilizing symmetry preventing \(\chi \) to act as a right-handed neutrino. Moreover, while we consider Dirac fermion DM, switching to Majorana nature would not change the discussion conceptually. Finally, we assume that the mediator does not develop a vev and have, thus, included a linear term in \(\mathcal S\) that is fixed such that \(\langle \mathcal{S \rangle } =0\) is satisfied.
Besides the SM couplings, there are several new interactions, both at the renormalisable \((D=4)\) level and in the form of effective \(D=5\) operators. In the scalar sector, the cubic and quartic terms in the singlet potential are parametrized by the couplings \(\lambda ^\prime _{S}\) and \(\lambda _{S}\), resp., while the Higgs-portal couplings involving one or two singlets are denoted by \(\lambda ^\prime _{HS}\) and \(\lambda _{HS}\), resp. Note that, after EWSB, the latter coupling provides a contribution to the mediator mass, which is given by
In addition, there is a Yukawa coupling between the scalar mediator, \(\mathcal S\), and the DM fermions, \(\chi \), denoted by \(y_S\). At the \(D=5\) level, all interactions are suppressed by one power of the scale of heavy NP, \(\Lambda \), which mediates contact interactions between the various fields. In the pure scalar sector, gauge invariant terms feature four (\(c_{\lambda H}\)), two (\(c_{HS}\)), or zero (\(c_{\lambda S}\)) Higgs fields. In order to couple the mediator to SM fermions, the presence of a Higgs doublet is required, allowing for \(D=5\) Yukawa-like couplings, \(\sim (y^S_d)^{ij}\!,(y^S_u)^{ij}\!,(y^S_\ell )^{ij}\). Scalar couplings to the DM fermions at the \(D=5\) level, on the other hand, involve either two scalar singlets or two doublets, due to gauge invariance, parametrized by \(y_S^{(2)}\) and \(y_H^{(2)}\), respectively. Finally, there are effective couplings of \(\mathcal {S}\) to the \(\mathrm {U}(1)_Y\), \(\mathrm {SU}(2)_{\mathrm {L}}\), and \(\mathrm {SU}(3)_{\mathrm {c}}\) field strengths squared, denoted by \(c_B^S\), \(c_W^S\), and \(c_G^S\). In the following, we assume the interactions with \(\mathcal{S}\) to conserve CP, and thus all coefficients in the Lagrangian of Eq. (1) are real.
We conclude this discussion noting that, if the new sector residing at the scale \(\Lambda \) is governed by a coupling \(g_*\), the effective coefficients above can be assigned a certain scaling in this coupling (see e.g. Refs. [22,23,24,25]), which in our case (without assuming the Higgs to be a pseudo-Goldstone state) reads \(c_{\lambda S} \sim c_{H S} \sim c_{\lambda H} \sim g_*^3,\ y_f^S \sim y_f g_*,\ y_{S,H}^{(2)} \sim g_*^2, c_V^S \sim g_*\). This allows to order the operators according to their expected importance in a certain coupling regime and can for example be used to reduce the number of \(D=6\) operators to be considered to leading approximation in the case of a vector mediator.Footnote 4
The eDMeft Lagrangian, Eq. (1), allows to describe phenomena relevant for collider searches for DM as well as for direct (and indirect) detection experiments, as we will now explore in more detail. For example, for a non-negligible \((y_q^S)^{ij}/\Lambda \), the operators \(S \bar{Q}_L^i H q_R^j\) can mediate interactions of DM with a nucleus, coupling the mediator to the DM via the \(S {\bar{\chi }} \chi \) interaction, see the upper panel of Fig. 1, where the scalar mediator is depicted by double-dashed lines, while the fermionic DM is represented by faint double-lines. The same combination of operators induces, on the other hand, DM signals at the LHC in two different, but correlated, incarnations. Mono-jet and Higgs+missing transverse energy  signatures are generated, radiating off a gluon from the (initial state) quarks and considering the physical Higgs within H in the \(S \bar{Q}_L^i H q_R^j\) operator, resp., while the \(S \rightarrow {\bar{\chi }} \chi \) transition is responsible for the
signatures are generated, radiating off a gluon from the (initial state) quarks and considering the physical Higgs within H in the \(S \bar{Q}_L^i H q_R^j\) operator, resp., while the \(S \rightarrow {\bar{\chi }} \chi \) transition is responsible for the  , as shown in the lower panel of Fig. 1.Footnote 5
, as shown in the lower panel of Fig. 1.Footnote 5
Relevant diagrams contributing to nuclear interaction with fermionic DM (first row) and corresponding DM observables at hadron colliders (monojet and Higgs , second row), turning on the interactions \(\sim (y_q^S)^{ij}\) and \(\sim y_S\). The diagrams are similar for scalar and pseudo-scalar mediators, where for the latter case, the operator coefficients in Eq. (1) are to be replaced by the corresponding (tilded) coefficients in Eq. (3). See text for details
, second row), turning on the interactions \(\sim (y_q^S)^{ij}\) and \(\sim y_S\). The diagrams are similar for scalar and pseudo-scalar mediators, where for the latter case, the operator coefficients in Eq. (1) are to be replaced by the corresponding (tilded) coefficients in Eq. (3). See text for details
Note that, since the Yukawa-like couplings \(\sim (y_q^S)^{ij}\) can feature flavour-changing neutral currents (FCNCs), a flavour-protection mechanism like minimal flavour violation could be thought of, which would lead to a suppressed coupling to the light valence quarks and thus small effects at colliders at the tree level (see also Ref. [28]). In an agnostic approach, however, all couplings could be treated as free, and some ad hoc Yukawa structure could be allowed, considering only ‘direct’ experimental constraints, which would permit considerable effects for valence quarks. Finally note that, in case light-quark contributions were suppressed, the operators could still induce a coupling to gluons at the one-loop level, via heavy-quark triangle diagrams.
If other \(D=5\) operators (as well as the portal couplings, \(\lambda _{HS}^\prime \) and \(\lambda _{HS}\)) are set to zero for the moment, all three processes above scale in terms of effective coefficients as \(y_S (y_q^S)^{ij}/\Lambda \), and we can explore the complementarity and combined information of both types of experiments in one framework. We will examine this in more detail in the next section. As an alternative option, we will also consider the coupling of the mediator to the proton/nucleus via the \(\mathcal{S} G^{a\mu \nu }G_{\mu \nu }^a\) operator, trading \((y_q^S)^{ij}\) for \(c_G^S\), which allows for the production of DM in gluon fusion. The corresponding diagrams for the processes discussed above are shown in Fig. 2, where similar correlations can be explored (with the Higgs-associated production now being absent at leading order).
In the same context, another interesting opportunity is to produce the mediator in weak-boson fusion (WBF), by turning on \(c_W^S\) or \(c_B^S\), as depicted by the diagrams in the last row of Fig. 8 and commented on further below.
Relevant diagrams contributing to nuclear interaction with fermionic DM (first row) and corresponding DM observables at hadron colliders (monojet, second row), turning on the interactions \(\sim c_G^S\) and \(\sim y_S\). The diagrams are similar for pseudo-scalar mediators, employing the corresponding tilded coefficients
On the other hand, the Higgs boson might play a crucial role in coupling the DM to quarks and gluons. First, it can provide a portal to the mediator, via the couplings \(\lambda _{HS}, \lambda ^\prime _{HS}\), connecting the SM to the dark sector. In particular if the second operator is present, the mediator can be produced in gluon-fusion Higgs production via mixing with the Higgs field connecting then to the DM via \(y_S\). The corresponding diagrams are given in Fig. 3, where again unavoidably the Higgs channel is present, fixed by gauge invariance. Finally, the operators in Eq. (1) also allow for interactions of DM with hadrons mediated directly by Higgs exchange, if the coefficient \(y_H^{(2)}\) is non-vanishing. Turning on this single coupling provides an instantaneous link between the Higgs field and the DM via a contact interaction, inducing all processes discussed before, with the diagrams given in Fig. 4. Once more, the Higgs
channel is present, fixed by gauge invariance. Finally, the operators in Eq. (1) also allow for interactions of DM with hadrons mediated directly by Higgs exchange, if the coefficient \(y_H^{(2)}\) is non-vanishing. Turning on this single coupling provides an instantaneous link between the Higgs field and the DM via a contact interaction, inducing all processes discussed before, with the diagrams given in Fig. 4. Once more, the Higgs channel is induced by gauge invariance.
channel is induced by gauge invariance.
Relevant diagrams contributing to nuclear interaction with fermionic DM (first row) and corresponding DM observables at hadron colliders (monojet and Higgs , second row), turning on the interactions \(\sim \lambda _{HS}^\prime \) and \(\sim y_S\). Note that the corresponding diagrams are not present for pseudo-scalar mediators
, second row), turning on the interactions \(\sim \lambda _{HS}^\prime \) and \(\sim y_S\). Note that the corresponding diagrams are not present for pseudo-scalar mediators
Let us conclude this discussion by emphasizing again that the Lagrangian of Eq. (1) allows to consistently combine various processes and to include information from different kinds of sources. For example, DM might be produced by a combination of different mechanisms, e.g. via the mediator \(\mathcal{S}\) (triggered by \((y_q^S)^{ij}\), \(c_G^S\), or a portal), but also via direct Higgs exchange – due to the effective \(y_H^{(2)}\), even without \(H- \mathcal S\) mixing – where each contribution leads to characteristic correlations between LHC physics and direct (as well as indirect) detection experiments. We note that the direct Higgs couplings also enter in invisible Higgs decays constraining their size, while resonance searches are directly sensitive to the properties of the mediator. The eDMeft allows to describe and combine all these different phenomena in a general (inclusive) and consistent way including resonance searches for the mediator particle, which would not be possible in a simple DM EFT or a simplified-model approach. Yet, it is simple enough to keep predictivity and to be straightforwardly implemented into tools for automated event generation and implementation of constraints. Finally, matching UV complete models to the eDMeft will also allow to interpret experimental results obtained in the latter framework in terms of such explicit models, without the need to repeat the analysis for numerous different setups.
To explicitly demonstrate that the eDMeft can lead to a better validity of LHC limits compared to the conventional DM EFT, we confront in Fig. 5 the bounds on the cutoff scale \(\Lambda \) of the two setups following from an LHC monojet analysis [29] (depicted as black lines), in the latter EFT (left) and the eDMeft (right) framework. The constraints are derived employing the program CheckMATE [30] after implementing the Lagrangian (1) for the eDMeft via the FeynRules [31, 32] package. For concreteness we consider quark-induced production, where the relevant coefficients in (1) are set to \((y_u^S)^{11}=y_S=1\), while we take \(m_\chi =1\) GeV, \(m_S=80\) GeV as a benchmark with a relatively light mediator that is not integrated out, leaving the cutoff as the free parameter to be compared with that of the DM EFT, where only the light DM \(\chi \) with \(m_\chi =1\) GeV is kept. Here, the operator that would match to the above combination after removing the mediator would be \(\mathrm{D}_1 \equiv \frac{1}{\Lambda ^2} {\bar{\chi }} \chi {\bar{q}} q \) (with \(q=u\)), where again we set the dimensionless coefficient to \(C_\mathrm{D1}=1\) in the numerics. In the plots we indicate, as colored stripes, the various bins in  used in the analysis of Ref. [29]. The red-colored bins lead to an exclusion of the parameter point considered at the \(95\,\%\) CL, whereas the shades of the green bins depict how close they are to a potential exclusion. This is parameterized by the ratio r, which corresponds to the actual cross section over the excluded one, see the plot legend. Thus, the darker the green the closer the cross section in the corresponding bin is to the experimental limit.
used in the analysis of Ref. [29]. The red-colored bins lead to an exclusion of the parameter point considered at the \(95\,\%\) CL, whereas the shades of the green bins depict how close they are to a potential exclusion. This is parameterized by the ratio r, which corresponds to the actual cross section over the excluded one, see the plot legend. Thus, the darker the green the closer the cross section in the corresponding bin is to the experimental limit.
Comparison of limits on the cutoff scale \(\Lambda \) from an LHC monojet analysis [29], depicted as black lines, in the conventional DM EFT (left) and the eDMEFT (right), with (considering quark-induced production) \(C_\mathrm{D1}=1\), \((y_u^S)^{11}\!=\!1\!=\!y_S\), \(m_\chi =1\) GeV, and \(m_S=80\) GeV. The red regions indicate those bins (in  ) that lead to an exclusion at the \(95\,\%\) CL level, while the darker the green the closer the corresponding cross section is to the experimental bound, see text for details. As can be observed, the limits in the DM EFT are driven by the most energetic bins, above the derived cutoff, thereby invalidating the EFT approach to obtain them (see also [7]). On the other hand, the bounds in the eDMeft including a light mediator stem from much lower bins, which makes them much more robust
) that lead to an exclusion at the \(95\,\%\) CL level, while the darker the green the closer the corresponding cross section is to the experimental bound, see text for details. As can be observed, the limits in the DM EFT are driven by the most energetic bins, above the derived cutoff, thereby invalidating the EFT approach to obtain them (see also [7]). On the other hand, the bounds in the eDMeft including a light mediator stem from much lower bins, which makes them much more robust
The validity of the exclusion is then estimated by the gap between the red bins and the black line and is increasing with its size (the larger \(\Lambda \) the better – see, e.g., [7, 33]). One can clearly observe that, first of all, due to the presence of the mediator the limit on \(\Lambda \) is significantly higher in the eDMeft, reaching \(\Lambda \gtrsim 2\) TeV. Beyond that, here the bound is driven from lower bins with  GeV, while in the conventional DM EFT the limit stems from the high-energy tail with
GeV, while in the conventional DM EFT the limit stems from the high-energy tail with  TeV, surpassing the cutoff of the EFT which is here \(\Lambda \sim 1\,\) TeV, invalidating the limit (see also [7]). This makes the eDMeft much more solid for collider searches.Footnote 6
TeV, surpassing the cutoff of the EFT which is here \(\Lambda \sim 1\,\) TeV, invalidating the limit (see also [7]). This makes the eDMeft much more solid for collider searches.Footnote 6
Before exploring in more detail the LHC and direct-detection phenomenology in the eDMeft approach, we will now turn to the remaining scenarios of DM coupled to the SM via a potentially light mediator, which can be analyzed in a similar way. First, we will consider the case of a CP-odd scalar, \(\tilde{\mathcal{S}}\), which has several interesting features. On the one hand, direct detection bounds with a CP-odd scalar mediator are much weaker due to momentum suppression of the cross section [34, 35]. Moreover, besides the \(D=5\) pure scalar interactions, the portal with a single mediator vanishes, which automatically avoids the mixing between the scalars. The Lagrangian now becomes

Here, the contact interactions with gauge bosons feature dual field strength tensors, while all terms can be interpreted analogously as in the CP-even scalar case. In particular, the very same discussion as before on generic correlations between different observables can be performed. Note, however, that due to the vanishing single-mediator portal, no production via the Higgs is possible at the level of \(D \le 4\) interactions, which makes the (extended) EFT terms \(\sim y_q^{{\tilde{S}}}, c_{G\!,B\!,W}, y_H^{(2)}\) even more interesting. We will again assume no new sources of CP violation, and the coefficients in the Lagrangian in Eq. (3) are real.
1.2 Scalar DM with a scalar mediator
We finally move to the case of (singlet) scalar DM, denoted by \(\mathcal{D} = \chi _s\), still considering a scalar mediator, \(\mathcal{M} = \mathcal{S}\). The Lagrangian for this setup, at the \(D=5\) level, reads

We assume again that the mediator, \(\mathcal S\), does not develop a vev, while a \(Z_2\) symmetry assures stability of \(\chi _s\).
For pseudo-scalar, \(\mathcal{M}=\tilde{\mathcal{S}}\), the terms in the last two square brackets are replaced similarly as before (Eq. (1) \(\rightarrow \) Eq. (3)). However, all other contributions with an odd number of \(\mathcal{S}\) are absent, and further dynamics would be required for s-channel mediation between the DM and SM fields, and therefore, we do not consider this scenario here.
Crucial (new) terms in Eq. (4) are the portal-like interactions connecting the DM to the mediator, \(\lambda _{S \chi _s}\), \(\lambda ^\prime _{S \chi _s}\) (and the corresponding \(D=5\) operators, containing odd powers of \(\mathcal{S}\) and even powers of \(\chi _s\), i.e., the terms \(\sim c_{S \chi _s},c_{\lambda \chi _s}, c_{H \chi _s}\)), replacing \(y_S/y_{{\tilde{S}}}\) of the fermionic DM case. Furthermore, there is a new direct \(D=4\) portal to the DM via the Higgs field, given by \(\lambda _{H \chi _s}\), instead of the corresponding term \(\sim y_H^{(2)}\) for fermionic DM, as well as a quartic DM self-interaction \(\sim \lambda _{\chi _s}\). The corresponding diagrams inducing the processes considered in the next section will be referenced along with the ones for the fermionic DM case and can be found in Figs. 12, 13, 14 and 15 in Appendix B.
2 Complementary constraints within one framework: \(\text {eDMEFT}\)
We will now explore phenomenological aspects of the framework making use of the correlations predicted in our eDMeft approach, as anticipated before. For clarity, we will concentrate on the model with fermionic DM and scalar mediator; the treatment can be straightforwardly extended to the other model frameworks described above. In particular, we will address the question of how many events in DM searches at the LHC can be expected, given limits from direct detection experiments, without restricting to an explicit NP model. The presence of the mediator in our EFT will ensure the validity of the analysis for collider searches.Footnote 7
As main observables, we consider the direct-detection cross section for the scattering of DM off a nucleus, N,
and the cross sections for monojet and Higgs+ signals at the 14 TeV LHC
signals at the 14 TeV LHC


By deriving the expected maximal values for last two observables, given the limits from direct detection, LHC results could potentially rule out certain DM incarnations very generally or support/constrain them in synergy with direct-detection experiments. In that context, note that the currently most stringent direct detection constraint corresponds to \(N = \mathrm{Xe}\) and is given by XENON1T [36, 37].
Here, our goal is to pinpoint interesting benchmark scenarios with minimal amount of NP couplings turned on each time; we will leave a more comprehensive study of the parameter space and of the correlations between different operators for future work.
First, we turn on only one \(D=5\) operator at a time, where we consider on the one hand the coupling of the mediator to SM quarks, via the \(D=5\) Yukawa-type interaction, or to gluons, and on the other the direct coupling of DM to the Higgs, \(y_H^{(2)}\). Another possibility would be DM production via Higgs mixing with the mediator, which however has been studied extensively elsewhere, see e.g. Refs. [38,39,40,41], and is significantly constrained from direct-detection experiments. In consequence, we omit it here and defer a short discussion to Appendix A.
In these cases with just one \(D=5\) operator, we only study the mass hierarchy \(m_{\chi }>m_S\): if \(m_{\chi }<m_S\) the DM annihilation cross section is dominated by the s-channel process to SM quarks via the \(D=5\) operator and the cross section is proportional the same combination appearing in the direct-detection cross section such that values avoiding overabundance are disfavoured by experiments. For concreteness, we consider the benchmark values \(m_S=400\) GeV, \(m_\chi =500\) GeV for this first scenario.
For a viable setup in the other hierachy, \(m_{\chi }<m_S\), more than one \(D=5\) operator must be turned on simultaneously (or additional mixing between the mediator and the Higgs is needed), which we will explore further below, in Sect. 2.4, by combining pairs of the operators mentioned above for the values \(m_S=140\) GeV, \(m_\chi =65\) GeV. These two scenarios allow us to illustrate the interesting features of the framework, and serve as a basis for a more complete study.
As mentioned, the requirement to generate the correct relic abundance implies further constraints on the same operators that are entering DM–SM scattering and thus direct detection. Note that for the latter, the limits for a subdomimant DM component are weaker, since the direct detection experiments assume a one-component DM with the observed relic abundance. Therefore, in order to correctly compare with the limits, the produced DM abundance must always be estimated.
Another source of constraints arises from DM annihilations potentially producing an excess of e.g. gamma rays over the galactic background. The most stringent current limits come from the Fermi-LAT satellite experiment [42] constraining the canonical thermal cross section up to \(\sim 100\) GeV DM masses. However, for fermionic DM with scalar mediator, the annihilation cross section is velocity suppressed leading to negligible indirect-detection signals. We therefore do not consider indirect-detection bounds further here.
2.1 Quark-induced production
We start by considering the production of the mediator, \(\mathcal{M}=\mathcal S\), in \(q{\bar{q}}\) annihilation and subsequent decay to DM (as well as the crossed process leading to \(\mathcal{D}-N\) scattering), see Figs. 1 and 12.
For fermionic DM, \(\mathcal{D}=\chi \), the relevant couplings for a CP-even mediator, \(\mathcal S\), are \((y_q^S)^{ij}/\Lambda \) and \(y_S\), see Eq. (1). The former allows the production of \(\mathcal{S}\) via a gauge-invariant coupling to SM quarks and the latter its decays to DM. The corresponding Feynman diagram is given in the upper left corner of Fig. 1. At low energies relevant for direct-detection experiments, the mediator can be integrated out leading to the diagram in the upper right corner, which governs \(\mathcal{D}-N\) scattering at low momenta. For simplicity, we here focus on \((y_u^S)^{11}\) (and \((y_d^S)^{33}\)), although the analysis can easily be extended to include all quark flavours.
For a CP-odd mediator, \(\mathcal{{\tilde{S}}}\), the couplings above are replaced by the corresponding tilded coefficients in Eq. (3). However, in this case, the tree-level interactions with nuclei are momentum suppressed, and this scenario is out of the reach of current direct detection experiments (and thus LHC cross sections are basically unconstrained). Nevertheless, as discussed in Ref. [43], future experiments will start probing it as well. Scenarios with CP-odd mediator have also been considered recently in e.g. Refs. [44,45,46]. Here, we concentrate on a CP-even mediator, and leave the phenomenology of CP-odd mediators, utilizing the full strength of the eDMeft approach, for future work.
The cross section for the DM scattering off nuclei, in terms of eDMeft couplings, now reads [41]
where \(f^q_N\) is the form factor defined by \(\langle N|m_q \bar{q}q|N\rangle \equiv m_N f^q_N\),
is the reduced mass of the DM-nucleon system, and \(m_N=(m_p+m_n)/2\) is the average nucleon mass.
We calculate the running of the matrix elements \(\langle N|y^S_{q}\bar{q}q|N\rangle \) from the EW scale (where we define our couplings) down to direct-detection energies and the corresponding threshold effects from integrating out the heavy quark flavours following Refs. [47, 48] (see also Refs. [49, 50]). While for the gluon-induced production, discussed later, this will lead to non-trivial effects, for the case with only \((y_u^S)^{11}\) non-zero, this effect is trivial (and for the bottom quark one simply employs \(f^b_N=2/27 f_G\), see below, working in the three-flavour scheme).
We fix \(y_S\) such that we obtain the fraction \({f_{\mathrm {rel}}\equiv \Omega _{\chi }/\Omega _{\mathrm {DM}}}\) of the total dark matter abundance. In the direct-detection limits, a single component DM with \(f_{\mathrm {rel}}=1\) is assumed, and thus we require \(f_{\mathrm {rel}}\sigma _N\le \sigma _{\mathrm {X1T}}\) when we compare with the limits for XENON1T.
As noted above, if \(m_{\chi }<m_S\) and no further NP couplings are at work, the DM annihilation cross section is dominated by the s-channel process to SM quarks via the \(D=5\) operator and the cross section is thus proportional to \(y_S^2 [(y_u^S)^{11}]^2\), which is severely limited by the direct-detection cross section such that values avoiding overabundance are disfavoured. Therefore, we concentrate on the mass range \(m_{\chi }>m_S\) for the case at hand, where the dominant annihilation channel is \(\chi \chi \rightarrow SS\) and will return to the other mass hierarchy later. The annihilation cross section can thus be estimated (neglecting subleading \(m_S\) contributions, which are considered in the numerical results) by [43]
We fix \(y_S\) as a function of \(f_{\mathrm {rel}}\) by comparing this to the standard thermal cross section \(\langle \sigma {\mathrm{v}}\rangle _0=3\cdot 10^{-26}\ \mathrm {cm}^3 \mathrm {s}^{-1}\) and using \(\Omega h^2\propto \langle \sigma {\mathrm{v}}\rangle ^{-1}\) to scale this with \(f_{\mathrm {rel}}\).
The latest limit [37] then leads to the bound
Attaching on the other hand a gluon to the initial state quarks or emitting a Higgs boson – possible directly via the contact interaction \(\sim (y_q^S)^{ij}\) – leads to final states considered in LHC searches for DM, i.e. monojet and Higgs signatures. The corresponding diagrams are given in the lower panel of Fig. 1. We calculate the maximal cross sections for these processes at the LHC at 14 TeV center-of-mass energy using MadGraph [51] and employing the direct-detection limit, Eq. (11), for the benchmark scenario \((m_S=400\, \mathrm {GeV}, m_{\chi }=500\, \mathrm {GeV})\). Requiring \(p_T>200\,\)GeV for the jet, we arrive at (fixing for simplicity \(f_{\mathrm {rel}}=1\))
signatures. The corresponding diagrams are given in the lower panel of Fig. 1. We calculate the maximal cross sections for these processes at the LHC at 14 TeV center-of-mass energy using MadGraph [51] and employing the direct-detection limit, Eq. (11), for the benchmark scenario \((m_S=400\, \mathrm {GeV}, m_{\chi }=500\, \mathrm {GeV})\). Requiring \(p_T>200\,\)GeV for the jet, we arrive at (fixing for simplicity \(f_{\mathrm {rel}}=1\))


These cross sections are tiny, but serve here as reference values for this utterly simplified scenario with only two additional couplings compared to the SM turned on. We will therefore defer a more realistic analysis, using CheckMATE, to the case of two \(D=5\) operators being active simultaneously, discussed in Sect. 2.4. Allowing for heavy quark flavours to couple to the mediator already increases the cross sections; changing the up quark to bottom, they read


which is still very small, but could become interesting once combined with other operators, see below.
2.2 Gluon-fusion production
We now turn to the case of coupling the mediator to a gg state, allowing its production in gluon-gluon fusion, which is complementary to the case of external \(q {\bar{q}}\) states. Since the coupling to the DM is still assumed to be induced by \(y_S\), we only replace \({(y_u^S)^{11}}\) by \(c_G^S\) to couple the mediator to gluons. The relevant diagrams are given in Figs. 2 and 13. Note that, due to the absence of the Higgs contact interaction in the NP sector, the Higgs channel is significantly suppressed with respect to the monojet signature, requiring a GGh interaction, induced in the SM via a top loop, and we do not consider that here.
channel is significantly suppressed with respect to the monojet signature, requiring a GGh interaction, induced in the SM via a top loop, and we do not consider that here.
Starting with the \(\mathcal{S}GG\) interaction at the EW scale will now induce the \(\mathcal{S}\bar{q}q\) couplings at the nuclear energy scale [47, 48]. Therefore, the cross section for scattering off nuclei now becomes

where \(c_G^q\) and \(c_G^g\) account for the running and threshold effects down to the nuclear-energy scale, the gluonic form factor is defined as \({\langle N|-\frac{g_s^2}{16\pi ^2}\,G_{\mu \nu } G^{\mu \nu } |N\rangle \equiv \frac{2}{9} m_N f^g_N}\), and we again employ the results of Refs. [47, 48].
Comparing now with XENON1T results, leads to the bound

The monojet cross section (with \(p_T^{\mathrm{jet}}>200\,\)GeV) is thus constrained for the benchmark scenario \((m_S=400\, \mathrm {GeV}, m_{\chi }=500\, \mathrm {GeV})\)
and \(f_{\mathrm {rel}}=1\) to

This value is significantly higher than in the quark-induced production and would correspond to \(S \approx 20\) signal events, from this simple analysis, at the High-Luminosity LHC (HL-LHC) with \(3000\,\mathrm{fb}^{-1}\) of integrated luminosity. This scenario provides thus some prospects to become testable at (future) colliders, given the strong direct-detection limits.
2.3 Higgs-DM portal
Finally, the DM could also be coupled directly to the SM via the Higgs-DM portal, promoting the SM-like Higgs boson itself to a mediator to the DM sector, simply by turning on the \(D=5\) operator \(\sim y_H^{(2)}\) (or the \(D=4\) portal \(\sim \lambda _{H \chi _s}\) for scalar DM). This corresponds to the traditional SM+singlet DM model well known in the literature; see e.g. Refs. [39, 41, 52,53,54,55].
While the invisible width of the Higgs boson significantly constrains these operators in case the DM is light, \(m_{\chi _{(s)}} < m_h/2\), for heavier DM they might play an important role in DM production. The corresponding Feynman diagrams for the processes at hand are given in Figs. 4 and 15. Again, the Higgs channel is induced at leading order via the second Higgs field required by gauge invariance, see the lower-right diagram.
channel is induced at leading order via the second Higgs field required by gauge invariance, see the lower-right diagram.
For fermionic DM, we obtain the direct detection cross section
We trade \(y_H^{(2)}/\Lambda \) for \(f_{\mathrm {rel}}\) from the thermal \(\bar{\chi }\chi \rightarrow {\bar{t}} t, WW, ZZ, hh\) cross section for fixed \(m_{\chi }\). The dominant contribution corresponds to the t-channel annihilation to hh, which can be obtained using Eq. (10) with substitution \(y_S\rightarrow y_H^{(2)}v/\Lambda \). The direct detection limits constrain the relic abundance to \(f_{\mathrm {rel}}\lesssim 10^{-5}\) in the DM mass range \(m_{\chi }>m_h/2\).
The LHC cross sections for \(p_T^{\mathrm{jet}}>200\,\)GeV are in turn limited to

This scenario could provide another interesting probe for the collider experiments, but is constrained to deliver only a tiny fraction of the DM relic abundance. The latter conclusion could be avoided, once the portal is embedded into a richer dark/NP sector, where it could furnish an important contribution to arrive at the correct DM density, as we will discuss now.
2.4 \(m_{\chi }<m_S\): two \(D=5\) portals at the same time
If the DM is lighter than the mediator, the relic abundance is set by the DM annihilating to SM final states. The \(D=5\) gluon-mediator coupling, \(c_G^S\), contributes with a different sign than the \(D=5\) quark-mediator, \(y_q^S\), or direct Higgs-DM couplings, \(y_H^{(2)}\), to the direct-detection cross section, and thus blind regions due to cancellations can arise. While blind spots are known in the DM literature when combining different types of mediators [56,57,58,59], for example in supersymmetry, here we find a new kind of more subtle blind spot in the EFT context, where it can appear between different operators featuring only one type of mediator. The effect is phenomenologically most relevant near the resonant region, and we will illustrate this in the following turning on two of these couplings simultaneously, fixing \(m_\chi =65\) GeV, \(m_S=140\) GeV and \(\Lambda =1\) TeV. For the first two cases, we set \(y_S=1\), and regarding the quark-mediator couplings we consider the bottom quark only.
We calculate the annihilation cross sections with the micrOMEGAs package [60] and show the XENON1T limits (blue shaded regions) along with the correct relic abundance curves in Fig. 6. The purple shaded regions are excluded due to overabundance. One can clearly inspect that while, in both cases, the presence of a single \(D=5\) portal does not lead to a viable scenario, already turning on two higher dimensional operators can produce the correct relic abundance, while not being excluded by direct detection.
Finally, we note that the parameter-space regions fitting the correct relic density and meeting XENON1T constraints now lead to interesting collider perspectives. We find monojet cross sections at 14 TeV (with \(p_T^{\mathrm{jet}}>200\,\)GeV) of
for the first and second case discussed above, respectively (corresponding to the upper and lower panel in Fig. 6).
Employing CheckMATE and scaling the results of [29] to the HL-LHC we find that the latter (Higgs-portal) case can be probed with more than \(2\,\sigma \), where a dedicated analysis could improve on this. While this is already encouraging, an in-depth survey of the full mass ranges – including lighter DM masses – is expected to allow for still larger LHC cross sections. We show both the current LHC \(2\sigma \) exclusions and the projected \(2\sigma \) sensitivity at HL-LHC as green regions in Fig. 6.
The solid purple curve shows the relic abundance \(f_{\mathrm {rel}}=1\), while the purple shaded region is excluded by overabundance. The blue shaded region shows the direct-detection exclusion by XENON1T. The darker (lighter) green region depicts the monojet \(2\sigma \) exclusion at LHC (projected \(2\sigma \) sensitivity at HL-LHC). We have fixed the masses to \(m_{\chi }=65\) GeV and \(m_S=140\) GeV, while the cutoff is set to \(\Lambda = 1\) TeV and \(y_S=1\)
2.5 Further processes
Although dedicated analyses are left for future work, here we already comment on further interesting applications of the eDMeft framework ranging from the inclusion of loop processes in the EFT, over new production mechanisms, up to analyses of Higgs pair production and collider searches for the mediator.
First we note, however, that the additional scalar particle \(\mathcal{S}\) can also have an interesting impact on the nature of the electroweak phase transition, which in the SM is not first order, such as to allow for electroweak baryogenesis [61, 62]. With the help of a light \(\mathcal{S}\), electroweak baryogenesis can become viable (see, e.g. [63,64,65,66]). In turn, the DM phenomenology will be affected. Including such a scenario in our framework is also left for the future.
2.5.1 Loop mediated processes in eDMeft
While the only loop diagrams we encountered so far contained the SM-like GGh triangle, loops involving \({D=5}\) vertices allow for interesting new means to couple the DM to hadrons. First of all, the Yukawa-like operator \(\sim (y_q^S)^{ij}\) can now be inserted coming with the top quark (\(q=u;\,ij=33\)) and couple the mediator to a gluon pair via a (top-)quark loop, see the left diagram in Fig. 7. This operator is expected to be sizable, featuring no (minimal-flavour-violation-like) flavour suppression. The loop suppression could thus be lifted by the potential enhancement with \(m_t/m_q\), since the operator is basically unconstrained for the top.
Finally, at the two-loop level, DM production via a portal to a pseudo-scalar mediator becomes possible, see the right diagram in Fig. 7. Applied to the case of scalar DM (i.e. replacing \(y_{{\tilde{S}}}^{(2)}/\Lambda \rightarrow \lambda _{{\tilde{S}} \chi _s}\)), this opens the possibility to obtain interesting models with a CP-odd mediator.
Potentially important loop diagrams contributing to DM interactions in the eDMeft, turning on the operators \(\sim (y_q^S)^{ij}\) and \(\sim y_S\), or \(\sim \lambda _{H {\tilde{S}}}\) and \(\sim y_{{\tilde{S}}}^{(2)}\), respectively. The right diagram involves the quartic portal term \(\sim \lambda _{H \tilde{S}}\), which is basically the only relevant term that allows to produce scalar DM via a (pair-produced) pseudo-scalar mediator at the \(D\le 5\) level (via a similar diagrams with \(y_{\tilde{S}}^{(2)}/\Lambda \rightarrow \lambda _{{\tilde{S}} \chi _s}\)). See text for details
2.5.2 Weak-boson fusion
Beyond that, a production of the mediator in weak-boson fusion, as depicted by the last two diagrams in Fig. 8, is interesting regarding ‘monojet’ and Higgs signals. In fact, if the corresponding \(D=5\) operators feature a sizable coupling \(c_{W,B}^S\), DM signals at the LHC can be significant, while limits from direct-detection experiments are met, since the corresponding processes with external quark bi-linears are suppressed by a quark-mass insertion (and a loop factor), see the first (and second) row of Fig. 8.
signals. In fact, if the corresponding \(D=5\) operators feature a sizable coupling \(c_{W,B}^S\), DM signals at the LHC can be significant, while limits from direct-detection experiments are met, since the corresponding processes with external quark bi-linears are suppressed by a quark-mass insertion (and a loop factor), see the first (and second) row of Fig. 8.
Diagrams contributing to nuclear interaction with fermionic DM (first row) and DM observables at hadron colliders, turning on the interactions \(\sim c_W^S\) and \(\sim y_S\). The diagrams are similar for pseudo-scalar mediators, employing the corresponding tilded coefficients, as discussed before. The diagrams for scalar DM are equivalent with replacement \(y_S\rightarrow \lambda _{S \chi _s}^\prime v\). See text for details
2.5.3 Higgs pair 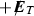
Exploring the production of Higgs pairs in association with missing energy could be an additional interesting probe of dark sectors. Indeed, several operators in the eDMeft allow the production of Higgs pairs along with DM and can be tested in this process. Figure 9 shows sample diagrams that could become important in case the bi-quadratic portal \(\sim \lambda _{HS}\) is weak. Beyond the usual case of the mediator decaying to the DM, they also contain potentially resonant decays of \(\mathcal{M}\) to a Higgs pair, after emission of a DM pair, which could allow to see a peak in the hh invariant mass spectrum and boosted Higgs bosons [67].Footnote 8 Although the cross sections are not expected to be large, non-negligible NP couplings could still feature interesting effects in  production. A dedicated analysis is needed to examine the actual prospects of this process in the light of the expected limited number of events.
production. A dedicated analysis is needed to examine the actual prospects of this process in the light of the expected limited number of events.
Selected diagrams contributing to Higgs pair production in association with  , turning on the interactions \(\sim \lambda _{H S}^\prime , y_{S}^{(2)}\) or \(\sim c_{\lambda H}, y_S\) in the case of fermionic DM (first row) and \(\sim \lambda _{H S}^\prime , c_{H \chi _s}\) in the case of scalar DM (second row). See text for details
, turning on the interactions \(\sim \lambda _{H S}^\prime , y_{S}^{(2)}\) or \(\sim c_{\lambda H}, y_S\) in the case of fermionic DM (first row) and \(\sim \lambda _{H S}^\prime , c_{H \chi _s}\) in the case of scalar DM (second row). See text for details
2.5.4 \(\mathcal{S}\) Resonance search
Finally, one can also search directly for the mediator by looking for a resonant enhancement in the di-jet, \(t {\bar{t}}\), di-lepton, or di-boson spectrum. These processes can also be described consistently in the eDMeft, since the inclusion of the mediator as a dynamical degree of freedom is a defining feature of the setup, and their study can deliver important insight on the nature of DM. Sample diagrams for the first two processes, involving the couplings \(\lambda _{H S}^\prime \) and \((y_q^S)^{ij}\) are shown in Fig. 10.
Note that in the figure, for simplicity, we employ a mass-insertion approximation (MIA), treating the mixing of the Higgs with the new scalar as an interaction marked by a black cross. In the (diagonal) mass basis just the heavy mediator would be exchanged in the s-channel, with its coupling to the \(t {\bar{t}}\) state governed by the Higgs admixture.
Resonance searches are in fact a powerful complementary tool to understand dark sectors and to probe the coupling structure of the mediator even in the case where its production is dominated by a single operator. Being able to combine this information with that of the other DM observables in a single consistent, yet general, framework is a particular strength of the eDMeft.
Resonant contributions of the mediator to di-jet and \(t {\bar{t}}\) final states, turning on the interactions \(\sim \lambda _{H S}^\prime \) and \(\sim (y_q^S)^{ij}\). Replacing the latter by \(c_{W,B,G}^S\) or \((y_\ell ^S)^{ij}\) leads to further interesting contributions to di-boson, di-jet, and di-lepton final states
3 Conclusions
We have presented a new framework to describe DM phenomenology, which can be used to consistently confront limits from direct-detection experiments and the relic abundance with possible collider signatures at high energies, while maintaining a high degree of model-independence. Both the DM and mediator fields remain as propagating degrees of freedom, whereas additional new physics is described in the form of higher-dimensional operators. As an application of the framework, focusing on the level of \(D=5\) operators, we derived possible cross sections in monojet and Higgs+ signatures at the LHC. Considering the limits from direct detection and reproducing the DM relic density, for scalar mediator and a single \(D=5\) coupling turned on, we found that the most promising case for the collider searches is gluon induced production, which could lead to still small, yet non-negligible LHC cross sections. Beyond that, we pointed out that for two \(D=5\) operators being active simultaneously, interesting cancellations can appear in direct-detection cross sections, leading to room for sizable monojet signals. Cases with pseudoscalar mediators are still rather unconstrained by direct-detection experiments, and the eDMeft will reveal its full strength with the future generation of direct-detection facilities. The results presented are valid in a more general context than those derived in conventional (simplified) models and a plethora of possible further applications of the framework is left for the future.
signatures at the LHC. Considering the limits from direct detection and reproducing the DM relic density, for scalar mediator and a single \(D=5\) coupling turned on, we found that the most promising case for the collider searches is gluon induced production, which could lead to still small, yet non-negligible LHC cross sections. Beyond that, we pointed out that for two \(D=5\) operators being active simultaneously, interesting cancellations can appear in direct-detection cross sections, leading to room for sizable monojet signals. Cases with pseudoscalar mediators are still rather unconstrained by direct-detection experiments, and the eDMeft will reveal its full strength with the future generation of direct-detection facilities. The results presented are valid in a more general context than those derived in conventional (simplified) models and a plethora of possible further applications of the framework is left for the future.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study and no experimental data has been listed.]
Notes
The generalization to (fermionic or scalar) DM with a vector mediator calls for the inclusion of \(D=6\) operators and a study of the very rich phenomenology, and we will leave this for future work.
Other ‘UV complete’ DM scenarios that could be straightforwardly matched to the eDMeft are for example the NMSSM with a light singlet and singlino DM, the 2HDM + scalar/pseudoscalar-singlet DM model [15] with a heavy second doublet, the vector-like fermion DM setup of [16, 17], or a Froggatt–Nielsen DM scenario [18], where naturally the new fermions are heavier than the U(1)-breaking scale. An explicit matching to these (and further) scenarios will be explored in a forthcoming work.
We neglect a term \(\bar{\chi }_L \sigma _{\mu \nu } \chi _R B^{\mu \nu }\), which would lead to direct DM interactions with photons and therefore is phenomenologically constrained to be tiny. Moreover, note that the EFT of the SM plus just a scalar singlet \(\mathcal{S}\) has been explored in Refs. [19,20,21].
As shown recently [26], such a counting could also allow to lift the ambiguity in determining masses of new states in an EFT approach.
Note that this is no statement about the fit of the EFT to real data, but just on the internal consistency of the framework in deriving limits at the LHC.
While an analysis of the setup with pseudoscalar mediator would be particularly interesting form the EFT point of view, since here the \(D=4\) Higgs-mediator portal is absent, it leads to a momentum suppressed direct-detection cross section, which is out of the reach of current experiments. In this case indirect detection of dark matter would be a more promising option, which will be left for future work.
Note that, for the given couplings turned on, there are additional (potentially) similar important contributions, attaching the Higgs or mediator lines differently in the diagrams above (including Higgs emissions from SM lines).
References
W. Shepherd, T.M.P. Tait, G. Zaharijas, Phys. Rev. D 79, 055022 (2009). arXiv:0901.2125 [hep-ph]
M. Beltran, D. Hooper, E.W. Kolb, Z.A.C. Krusberg, T.M.P. Tait, JHEP 09, 037 (2010). https://doi.org/10.1007/JHEP09(2010)037. arXiv:1002.4137 [hep-ph]
J. Goodman, M. Ibe, A. Rajaraman, W. Shepherd, T.M.P. Tait, H.-B. Yu, Phys. Lett. B 695, 185 (2011). https://doi.org/10.1016/j.physletb.2010.11.009. arXiv:1005.1286 [hep-ph]
J. Goodman, M. Ibe, A. Rajaraman, W. Shepherd, T.M.P. Tait, H.-B. Yu, Phys. Rev. D 82, 116010 (2010). https://doi.org/10.1103/PhysRevD.82.116010. arXiv:1008.1783 [hep-ph]
Y. Bai, P.J. Fox, R. Harnik, JHEP 12, 048 (2010). https://doi.org/10.1007/JHEP12(2010)048. arXiv:1005.3797 [hep-ph]
S. Bruggisser, F. Riva, A. Urbano, JHEP 11, 069 (2016). https://doi.org/10.1007/JHEP11(2016)069. arXiv:1607.02475 [hep-ph]
G. Busoni, A. DeSimone, E. Morgante, A. Riotto, Phys. Lett. B 728, 412 (2014). https://doi.org/10.1016/j.physletb.2013.11.069. arXiv:1307.2253 [hep-ph]
M. Bauer, A. Butter, N. Desai, J. Gonzalez-Fraile, T. Plehn, Phys. Rev. D 95, 075036 (2017a). https://doi.org/10.1103/PhysRevD.95.075036. arXiv:1611.09908 [hep-ph]
J. Alwall, P. Schuster, N. Toro, Phys. Rev. D 79, 075020 (2009). https://doi.org/10.1103/PhysRevD.79.075020. arXiv:0810.3921 [hep-ph]
A. DeSimone, G.F. Giudice, A. Strumia, JHEP 06, 081 (2014). https://doi.org/10.1007/JHEP06(2014)081. arXiv:1402.6287 [hep-ph]
M.R. Buckley, D. Feld, D. Goncalves, Phys. Rev. D 91, 015017 (2015). https://doi.org/10.1103/PhysRevD.91.015017. arXiv:1410.6497 [hep-ph]
P. Harris, V.V. Khoze, M. Spannowsky, C. Williams, Phys. Rev. D 91, 055009 (2015). https://doi.org/10.1103/PhysRevD.91.055009. arXiv:1411.0535 [hep-ph]
J. Abdallah et al., Phys. Dark Univ. 9–10, 8 (2015). https://doi.org/10.1016/j.dark.2015.08.001. arXiv:1506.03116 [hep-ph]
A. DeSimone, T. Jacques, Eur. Phys. J. C 76, 367 (2016). https://doi.org/10.1140/epjc/s10052-016-4208-4. arXiv:1603.08002 [hep-ph]
S. Ipek, D. McKeen, A.E. Nelson, Phys. Rev. D 90, 055021 (2014). https://doi.org/10.1103/PhysRevD.90.055021. arXiv:1404.3716 [hep-ph]
J. Fan, S.M. Koushiappas, G. Landsberg, JHEP 01, 111 (2016). https://doi.org/10.1007/JHEP01(2016)111. arXiv:1507.06993 [hep-ph]
S. Gopalakrishna, T.S. Mukherjee, Adv. High Energy Phys. 2017, 8689270 (2017). https://doi.org/10.1155/2017/8689270. arXiv:1702.04000 [hep-ph]
C. Alvarado, F. Elahi, N. Raj, Phys. Rev. D 96, 075002 (2017). https://doi.org/10.1103/PhysRevD.96.075002. arXiv:1706.03081 [hep-ph]
A. Carmona, F. Goertz, A. Papaefstathiou, Phys. Rev. D 95, 095022 (2017). https://doi.org/10.1103/PhysRevD.95.095022. arXiv:1606.02716 [hep-ph]
R. Franceschini, G.F. Giudice, J.F. Kamenik, M. McCullough, F. Riva, A. Strumia, R. Torre, JHEP 07, 150 (2016). https://doi.org/10.1007/JHEP07(2016)150. arXiv:1604.06446 [hep-ph]
B. Gripaios, D. Sutherland, JHEP 08, 103 (2016). https://doi.org/10.1007/JHEP08(2016)103. arXiv:1604.07365 [hep-ph]
M.A. Luty, Phys. Rev. D 57, 1531 (1998). https://doi.org/10.1103/PhysRevD.57.1531. arXiv:hep-ph/9706235 [hep-ph]
A.G. Cohen, D.B. Kaplan, A.E. Nelson, Phys. Lett. B 412, 301 (1997). https://doi.org/10.1016/S0370-2693(97)00995-7. arXiv:hep-ph/9706275 [hep-ph]
G.F. Giudice, C. Grojean, A. Pomarol, R. Rattazzi, JHEP 06, 045 (2007). https://doi.org/10.1088/1126-6708/2007/06/045. arXiv:hep-ph/0703164 [hep-ph]
M. Chala, G. Durieux, C. Grojean, L. de Lima, O. Matsedonskyi, JHEP 06, 088 (2017). https://doi.org/10.1007/JHEP06(2017)088. arXiv:1703.10624 [hep-ph]
F. Goertz, JHEP 05, 090 (2019). https://doi.org/10.1007/JHEP05(2019)090. arXiv:1711.03162 [hep-ph]
A. Rajaraman, W. Shepherd, T.M.P. Tait, A.M. Wijangco, Phys. Rev. D 84, 095013 (2011). https://doi.org/10.1103/PhysRevD.84.095013. arXiv:1108.1196 [hep-ph]
F. Goertz, Phys. Rev. Lett. 113, 261803 (2014). https://doi.org/10.1103/PhysRevLett.113.261803. arXiv:1406.0102 [hep-ph]
ATLAS-CONF-2017-060, type Tech. Rep. number ATLAS-CONF-2017-060 ( institution CERN, address Geneva, 2017) https://cds.cern.ch/record/2273876
D. Dercks, N. Desai, J.S. Kim, K. Rolbiecki, J. Tattersall, T. Weber, Comput. Phys. Commun. 221, 383 (2017). https://doi.org/10.1016/j.cpc.2017.08.021. arXiv:1611.09856 [hep-ph]
A. Alloul, N.D. Christensen, C. Degrande, C. Duhr, B. Fuks, Comput. Phys. Commun. 185, 2250 (2014). https://doi.org/10.1016/j.cpc.2014.04.012. arXiv:1310.1921 [hep-ph]
N.D. Christensen, P. de Aquino, C. Degrande, C. Duhr, B. Fuks, M. Herquet, F. Maltoni, S. Schumann, Eur. Phys. J. C 71, 1541 (2011). https://doi.org/10.1140/epjc/s10052-011-1541-5. arXiv:0906.2474 [hep-ph]
R. Contino, A. Falkowski, F. Goertz, C. Grojean, F. Riva, JHEP 07, 144 (2016). https://doi.org/10.1007/JHEP07(2016)144. arXiv:1604.06444 [hep-ph]
C. Boehm, M.J. Dolan, C. McCabe, M. Spannowsky, C.J. Wallace, JCAP 1405, 009 (2014). https://doi.org/10.1088/1475-7516/2014/05/009. arXiv:1401.6458 [hep-ph]
C. Arina, E. DelNobile, P. Panci, Phys. Rev. Lett. 114, 011301 (2015). https://doi.org/10.1103/PhysRevLett.114.011301. arXiv:1406.5542 [hep-ph]
E. Aprile etal. (XENON), (2018). arXiv:1805.12562 [astro-ph.CO]
E. Aprile etal. (XENON), Phys. Rev. Lett. 119, 181301 (2017). https://doi.org/10.1103/PhysRevLett.119.181301. arXiv:1705.06655 [astro-ph.CO]
K. Petraki, A. Kusenko, Phys. Rev. D 77, 065014 (2008). https://doi.org/10.1103/PhysRevD.77.065014. arXiv:0711.4646 [hep-ph]
L. Lopez-Honorez, T. Schwetz, J. Zupan, Phys. Lett. B 716, 179 (2012). https://doi.org/10.1016/j.physletb.2012.07.017. arXiv:1203.2064 [hep-ph]
M.A. Fedderke, J.-Y. Chen, E.W. Kolb, L.-T. Wang, JHEP 08, 122 (2014). https://doi.org/10.1007/JHEP08(2014)122. arXiv:1404.2283 [hep-ph]
T. Alanne, K. Tuominen, V. Vaskonen, Nucl. Phys. B 889, 692 (2014). https://doi.org/10.1016/j.nuclphysb.2014.11.001. arXiv:1407.0688 [hep-ph]
M. Ackermann et al. (Fermi-LAT), Phys. Rev. Lett. 115, 231301 (2015). https://doi.org/10.1103/PhysRevLett.115.231301. arXiv:1503.02641 [astro-ph.HE]
G. Arcadi, M. Dutra, P. Ghosh, M. Lindner, Y. Mambrini, M. Pierre, S. Profumo, F.S. Queiroz, (2017a) arXiv:1703.07364 [hep-ph]
Y. Mambrini, G. Arcadi, A. Djouadi, Phys. Lett. B 755, 426 (2016). https://doi.org/10.1016/j.physletb.2016.02.049. arXiv:1512.04913 [hep-ph]
G. Arcadi, M. Lindner, F.S. Queiroz, W. Rodejohann, S. Vogl, (2017b). arXiv:1711.02110 [hep-ph]
M. Bauer, M. Klassen, V. Tenorth, (2017b). arXiv:1712.06597 [hep-ph]
R.J. Hill, M.P. Solon, Phys. Rev. D 91, 043505 (2015). https://doi.org/10.1103/PhysRevD.91.043505. arXiv:1409.8290 [hep-ph]
F. D’Eramo, J. de Vries, P. Panci, JHEP 05, 089 (2016). https://doi.org/10.1007/JHEP05(2016)089. arXiv:1601.01571 [hep-ph]
F. Bishara, J. Brod, B. Grinstein, J. Zupan, JHEP 11, 059 (2017a). https://doi.org/10.1007/JHEP11(2017)059. arXiv:1707.06998 [hep-ph]
F. Bishara, J. Brod, B. Grinstein, J. Zupan, (2017b). arXiv:1708.02678 [hep-ph]
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, H.S. Shao, T. Stelzer, P. Torrielli, M. Zaro, JHEP 07, 079 (2014). https://doi.org/10.1007/JHEP07(2014)079. arXiv:1405.0301 [hep-ph]
J. McDonald, Phys. Rev. D 50, 3637 (1994a). https://doi.org/10.1103/PhysRevD.50.3637. arXiv:hep-ph/0702143 [HEP-PH]
C.P. Burgess, M. Pospelov, T. ter Veldhuis, Nucl. Phys. B 619, 709 (2001). https://doi.org/10.1016/S0550-3213(01)00513-2. arXiv:hep-ph/0011335 [hep-ph]
Y.G. Kim, K.Y. Lee, Phys. Rev. D 75, 115012 (2007). https://doi.org/10.1103/PhysRevD.75.115012. arXiv:hep-ph/0611069 [hep-ph]
J.M. Cline, K. Kainulainen, P. Scott, C. Weniger, Phys. Rev. D 88, 055025 (2013). https://doi.org/10.1103/PhysRevD.92.039906, https://doi.org/10.1103/PhysRevD.88.055025. (Erratum: Phys. Rev.D92,no.3,039906(2015)). arXiv:1306.4710 [hep-ph]
C. Cheung, L.J. Hall, D. Pinner, J.T. Ruderman, JHEP 05, 100 (2013). https://doi.org/10.1007/JHEP05(2013)100. arXiv:1211.4873 [hep-ph]
P. Huang, C.E.M. Wagner, Phys. Rev. D 90, 015018 (2014). https://doi.org/10.1103/PhysRevD.90.015018. arXiv:1404.0392 [hep-ph]
A. Berlin, S. Gori, T. Lin, L.-T. Wang, Phys. Rev. D 92, 015005 (2015). https://doi.org/10.1103/PhysRevD.92.015005. arXiv:1502.06000 [hep-ph]
A. Choudhury, K. Kowalska, L. Roszkowski, E.M. Sessolo, A.J. Williams, Proceedings, Varying Constants and Fundamental Cosmology (VARCOSMOFUN’16): Szczecin, Poland, September 11-17, 2016, Universe 3, 41 (2017). https://doi.org/10.3390/universe3020041. arXiv:1705.04230 [hep-ph]
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, Comput. Phys. Commun. 185, 960 (2014). https://doi.org/10.1016/j.cpc.2013.10.016. arXiv:1305.0237 [hep-ph]
K. Kajantie, M. Laine, K. Rummukainen, M.E. Shaposhnikov, Phys. Rev. Lett. 77, 2887 (1996). https://doi.org/10.1103/PhysRevLett.77.2887. arXiv:hep-ph/9605288 [hep-ph]
K. Rummukainen, M. Tsypin, K. Kajantie, M. Laine, M.E. Shaposhnikov, Nucl. Phys. B 532, 283 (1998). https://doi.org/10.1016/S0550-3213(98)00494-5. arXiv:hep-lat/9805013 [hep-lat]
G.W. Anderson, L.J. Hall, Phys. Rev. D 45, 2685 (1992). https://doi.org/10.1103/PhysRevD.45.2685
J.R. Espinosa, M. Quiros, Phys. Lett. B 305, 98 (1993). https://doi.org/10.1016/0370-2693(93)91111-Y. arXiv:hep-ph/9301285 [hep-ph]
J. Choi, R.R. Volkas, Phys. Lett. B 317, 385 (1993). https://doi.org/10.1016/0370-2693(93)91013-D. arXiv:hep-ph/9308234 [hep-ph]
J. McDonald, Phys. Lett. B 323, 339 (1994b). https://doi.org/10.1016/0370-2693(94)91229-7
Z. Kang, P. Ko, J. Li, Phys. Rev. Lett. 116, 131801 (2016). https://doi.org/10.1103/PhysRevLett.116.131801. arXiv:1504.04128 [hep-ph]
Acknowledgements
We are grateful to Giorgio Arcadi, Martin Bauer, Farinaldo Queiroz, Valentin Tenorth, and Stefan Vogl for useful discussions and comments.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Higgs-mediator portal
Here we will present, for completeness, the option of coupling the DM to the SM via the Higgs-mediator portal \(\sim \lambda _{HS}^\prime \), turning on this interaction in addition to \(y_S\). This allows for a SM-like production of the scalar mediator via its mixing with the Higgs field, while its coupling to the DM remains as in the cases discussed above. The relevant diagrams are given in Figs. 3 and 14. Note that in the figure we show again the MIA, while in the numerical analysis below we instead diagonalize the \(H-\mathcal{S}\) system. Moreover, the Higgs channel receives the contribution from the second Higgs field present in the portal, as depicted by the lower-right diagram.
channel receives the contribution from the second Higgs field present in the portal, as depicted by the lower-right diagram.
We diagonalise the Higgs-\(\mathcal{S}\) system via a rotation
with the angle, \(\alpha \), given by
Further, we trade \(\lambda _H\) (the coefficient of the quartic Higgs operator) and \(\mu _S^2\) for the masses of the eigenstates, \(m_h\) and \(m_H\), the lighter of which we identify with the 125-GeV Higgs boson.
Focusing again on fermionic DM, we finally obtain
For the relic density calculation, we include the \(\bar{t}t\) channel mediated by the Higgs doublet. We focus on \(m_{\chi }>m_t\) and use the estimate [43]
For the scalar channels, we use Eq. (10) after scaling the couplings with the appropriate mixing coefficients given in Eq. (A1).
Comparing now with XENON1T results, leads to the bounds shown in Fig. 11, and the LHC cross sections (with \(p_T^{\mathrm{jet}}>200\,\)GeV) are constrained due to the direct detection limit as

where we employed \(f_{\mathrm{rel}}=1\) and \(m_H=400\) GeV.
Limits from the direct-detection experiments for the coupling \(\lambda _{HS}^{\prime }\) as a function of the DM mass for the Higgs-mediator portal scenario with fermionic DM and a mass of the heavy scalar eigenstate of 400 GeV. The solid (dashed) line corresponds to \(f_{\mathrm {rel}}=1\) (\(f_{\mathrm {rel}}=0.1\))
Although these processes are not observable in this restricted scenario, the portal contribution could become relevant in a combined analysis with more operators turned on.
Appendix B: Diagrams for Scalar DM
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Alanne, T., Goertz, F. Extended dark matter EFT. Eur. Phys. J. C 80, 446 (2020). https://doi.org/10.1140/epjc/s10052-020-7999-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-7999-2







 , second row), turning on the interaction
, second row), turning on the interaction 



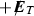




 , second row), turning on the interactions
, second row), turning on the interactions 

 , second row), turning on the interactions
, second row), turning on the interactions 
 , second row), turning on the interaction
, second row), turning on the interaction