1 Introduction

Moving cable systems carrying inertia elements such as rigid-body masses are applied in many engineering systems. In some applications the length of ropes and cables vary during the motion, which results in non-stationary behaviour of the system. For example in elevator and mine lifting installations, the length of the cable varies during the moving with some speed. As a result the variation of natural frequencies of the system can be observed [1]. The host structures are often subjected to external dynamic loads such as wind or earthquakes [2]. This causes the excitation of the structural system and corresponding response of the cable that can be described by using the deterministic models. On the other hand, because of nondeterministic nature of wind load or earthquakes, these systems should be considered with stochastic methods [3,4,5]. The wind action can be assumed as a wide-band random process, however, due to the damping effect inside the system the response of the structure can be regarded as narrow-band random process.

In this paper two models of a cable–mass system are presented: the nonlinear deterministic model under harmonic excitation and corresponding stochastic model with the excitation represented as a narrow-band process mean-square equivalent to the harmonic process. The horizontal displacements of main mass are constrained by applying an auxiliary spring-damper-mass combination to act as a tuned mass damper (TMD) [6]. TMD is used to reduce the negative effects of the resonance phenomenon [7]. It is very difficult to consider the behaviour of this type of structure by applying the analytical methods due to the non-stationarity and non-linearity of the process [8]. Therefore the numerical techniques should by used.

In paper [6] an approximated linear model was expanded by neglecting the non-linear terms in original set of equations of motion. This paper presents different approach, where the equivalent linearization technique is used to replace the nonlinear system by an equivalent linear one, whose coefficients are obtained from the conditions of mean-square minimization of the error between both systems and are given by the terms of expectations of nonlinear functions of the response process.

The statistical linearization technique has been applied to consideration of many various nonlinear stochastic problems since using by Caughey [9]. Other examples of this method can be found e.g. in [10,11,12,13]. This technique was also applied to problems of non-Gaussian excitations such as non-linear system under a Poisson impulse excitation e.g. [14,15,16] or in combination of various advanced method of stochastic dynamics e.g. [17,18,19,20,21].

In this paper the mean values and variances are calculated for different values of auxiliary damping filter ratio. The expected values of particular random state variables are compared with the deterministic results obtained for original nonlinear system subjected to harmonic excitation.

2 Non-linear model

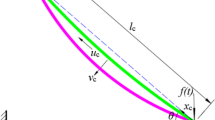
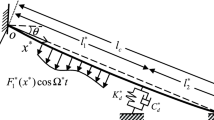
In the model presented in Fig. 1 the main mass M moves downwards at the transport speed denoted as V, and is suspended by a metallic elastic cable of length \(L=L(t)\) which is varying over time. The total height of the host structure is \(Z_0\). The characteristic values of the cable such as cross-sectional area, modulus of elasticity, mass per unit length and mean quasi-static tension are denoted as A, E, m and \(T^i\), respectively. The tension magnitude can be obtained by using the following expression

$$\begin{aligned} T^i=[M+m_d+m(L-x)](g-a), \end{aligned}$$
(1)

where \(m_d\) is a small auxiliary mass attached to the main mass by a spring-dashpot system with the coefficients of stiffness and viscous damping assumed as \(k_d\) and \(c_d\), respectively. The horizontal displacement of auxiliary mass is denoted as \(z_d\). The main mass M is constrained in the lateral direction by a spring of the coefficient of stiffness k. The horizontal and vertical displacements of main mass are assumed as \(u_M(t)\) and \(v_M(t)\). The lateral time-dependent displacements of the cable v(x, t) are coupled with the longitudinal vibrations u(x, t).

Fig. 1
figure 1

Schematic model of cable–mass system: a undeformed setting, b deformed setting

Full size image

The Hamilton’s principle expressed in terms of the kinetic energy and the potential energy of the system and external work of nonconservative forces yields the partial differential equations of motion in the following form

$$\begin{aligned}&m\frac{{\mathrm {D}}^2u}{{\mathrm {D}}t^2}- EA\varepsilon _x=0 \\&m\frac{{\mathrm {D}}^2v}{{\mathrm {D}}t^2}- Tv_{xx}+m(g-a)(xv_{xx}+v_x)-EA(\varepsilon v_x)_x=0 \\&M\ddot{v}_M + T^i(L)v_x|_{x=L}+k\triangle -k_d(z_d-v_M)-c_d(\dot{z}_d-\dot{v}_M) \\&\quad +EA\varepsilon |_{x=L}v_x|_{x=L}=0 \\&m_d\ddot{z}_d + k_d(z_d-v_M)+c_d(\dot{z_d}-\dot{v}_M)=0 \\&(M+m_d)\ddot{u}_M+EA\varepsilon |_{x=L}=0. \end{aligned}$$
(2)

where the cable axial strain is given by the expression \(\displaystyle {\varepsilon =u_x+v_x^2/2}\) and its quasi-static tension is assumed as \(T=(M+m_d+mL)(g-a)\). The symbol \(\varDelta\) denotes the deformation of the spring with the stiffness coefficient k. The partial derivatives with respect to x and time t are denoted as \((\cdot )_x\) and \((\cdot )_t\), respectively, while the total derivatives are expressed by the following equations

$$\begin{aligned} \frac{{\mathrm {D}}^2(\,\,)}{{\mathrm {D}}t^2}&= (\,\,)_{tt}+2V(\,\,)_{xt}+V^2(\,\,)_{xx}+a(\,\,)_x, \\ \frac{{\mathrm {D}}(\,\,)}{{\mathrm {D}}t}&= (\,\,)_{t}+V(\,\,)_{x}. \end{aligned}$$
(3)

For metallic cables the lateral frequencies are much lower than the longitudinal frequencies and the excitation frequencies are considered to be much smaller of the fundamental longitudinal frequencies, so that the longitudinal inertia of the cable in the first equation in (2) can be neglected in further considerations. Integrating this equation and using the boundary conditions \(u(0,t)=0\) and \(u(L,t)=u_M(t)\) leads to the following expression

$$\begin{aligned} u_x=e(t)-\frac{1}{2}v_x^2 \end{aligned}$$
(4)

where e(t) is the quasi-static axial strain in the cable.

The external loads such as strong dynamic wind actions can cause the structure to sway. This results in cable vibration of high amplitudes and low frequencies. The red dashed lines presented on Fig. 1 denotes the bending deformations of the host structure caused by the base excitation due to the sway, which are approximated by the polynomial shape function \(\varPsi (\eta ) = 3\eta ^2 - 2\eta ^3\). The variable \(\displaystyle {\eta =z/Z_0}\) denotes the ratio of coordinate measured from the ground level z and the total height of the entire system \(Z_0\). As a consequence of the bending deformations harmonic motion \(v_0(t)\) occurs at the top end of the cable with the frequency \(\varOmega _0\) and amplitude \(A_0\). The overall time dependent lateral displacements of the cable–mass system can be expressed as

$$\begin{aligned} v(x,t)=\bar{v}(x,t)+\bigg (1+\frac{\varPsi _L-1}{L}x\bigg )v_0(t) \end{aligned}$$
(5)

where the \(\varPsi _L\) is given as

$$\begin{aligned} \varPsi _L=\varPsi \big (\frac{Z_0-L}{Z_0}\big ) \end{aligned}$$
(6)

Due to the fact that the variation of L(t) over a period \(T_0\) corresponding to the fundamental frequency of the system \(f_0\) is small in comparison to the total length of the cable [3], the length of the cable can be considered as a function of the slow time scale defined as \(\tau =\epsilon t\). The small parameter \(\epsilon<<1\) is given by the equation \(\epsilon =\dot{L}(t_0)/f_0L_0\) [22], where \(t_0\) denotes a given time instant, \(f_0\) is the lowest natural frequency that corresponds to \(L_0=L(t_0)\). The relative lateral displacements related to \(L=L(\tau )\) can be expressed by the finite series in the following form

$$\begin{aligned} \bar{v}(x,t;\tau )=\sum _{n=1}^N\varPhi _n[x;L(\tau )]q_n(t) \end{aligned}$$
(7)

with orthogonal trial functions assumed as

$$\begin{aligned} \varPhi _n[x,L(\tau )]=\mathrm {sin}[\lambda _n(L(\tau ))x],\,\,n=1,2,...,N \end{aligned}$$
(8)

where N is the number of considered modes. The eigenvalues \(\lambda _n(\tau )\) are slow varying and are determined from the frequency equation given as

$$\begin{aligned}&\bigg (k-\frac{M}{m}T_{Md}\lambda _n^2\bigg )sin(\lambda _nL)+ T_{Md}\lambda _n cos(\lambda _nL)=0 \\&T_{Md}\equiv T^i(L)=(M+m_d)(g-a) \end{aligned}$$
(9)

By using Eqs. (5–8) in (2) a set of differential equations of motion results as follows [6]

$$\begin{aligned}&m_r\ddot{q}_r+k_rq_r+\sum _{i=1}^{N}K_{rn}q_n-[k_d(z_d-\bar{v}_M)+c_d(\dot{z}_d-\dot{\bar{v}}_M)] \\&\quad \times \varPhi _r(L)- EA\bar{e}\bigg [\sum _{i=1}^{N}\varGamma _{rn}q_n-\frac{\varPsi _L-1}{L}\varPhi _r(L)v_0\bigg ]=Q_r \\&\quad m_d\ddot{z}_d+k_d(z_d-\bar{v}_M)+c_d(\dot{z}_d-\dot{\bar{v}}_M)=Z_d \\&\quad (M+m_d)\ddot{u}_M+EA\bar{e}(t;\tau )=0 \end{aligned}$$
(10)

where

$$\begin{aligned} \bar{v}_M&= \sum _{i=1}^{N}\varPhi _n[L(\tau )]q_n(t),\\ Q_r&= \beta _r^{(0)}(\tau )v_0(t)+\beta _r^{(1)}(\tau )\dot{v}_0(t)+\beta _r^{(2)}(\tau )\ddot{v}_0(t), \\ \beta ^{(0)}_{r}&= \frac{2g}{r\pi }\frac{\varPsi _{L}-1}{L(\tau )} \big [(-1)^r-1\big ],\\ \beta ^{(1)}_{r}&= \frac{4V}{r\pi }\frac{\varPsi _{L}-1}{L(\tau )}\big [(-1)^r-1\big ],\\ \beta ^{(2)}_{r}&= \frac{2}{r\pi }[(-1)^r\varPsi _{L}-1],\\ Z_d&= k_d\varPsi _Lv_0+c_d\varPsi _L\dot{v}_0\\ K_{rn}&= m[g\varPsi _{rn}+(g-a)(\varTheta _{rn}-L\varUpsilon _{rn})],\\ \varTheta _{rn}&= \int _0^L x\varPhi _n^{''}\varPhi _r{\mathrm {d}}x,\,\,\varPsi _{rn}=\int _0^L \varPhi _n^{\prime}\varPhi _r{\mathrm {d}}x,\\ \varUpsilon _{rn}&= \int _0^L \varPhi _n^{''}\varPhi _r{\mathrm {d}}x,\,\,k_r=m_r\omega _r^2,\\ \omega _r&= \lambda _r\sqrt{\frac{T_{Md}}{m}},\, m_r=m\int _0^L\varPhi _r^2{\mathrm {d}}x+M\varPhi _r^2(L), \\ \kappa _{ij}&= \int _0^L\varPhi _i^{\prime}\varPhi _j^{\prime}{\mathrm {d}}x, \,\, \alpha _i=\varPhi _i(L), \\ \varGamma _{rn}&= \varUpsilon _{rn}-\varPhi _n^{\prime}(L)\varPhi _r(L). \end{aligned}$$

Considering a single-mode approximation and taking into account the rth mode the following equations of motion are obtained [6]

$$\begin{aligned}&m_r\ddot{q}_r+\tilde{c}_r\dot{q}_r+\tilde{k}_r q_r-\{k_d[z_d-\varPhi _r(L)q_r]+c_d[\dot{z}_d \\&\quad -\varPhi _r(L)\dot{q}_r]\}\varPhi _r(L)-EA\bar{e}_r\bigg [\varGamma _{rn}q_r-\frac{\varPsi _L-1}{L}\varPhi _r(L)v_0\bigg ]=Q_r \\&\quad m_d\ddot{z}_d+k_d[z_d-\varPhi _r(L)q_r]+c_d[\dot{z}_d-\varPhi _r(L)\dot{q}_r]=Z_d(t,\tau ) \\&\quad (M+m_d)\ddot{u}_M+EA\bar{e}_r=0 \end{aligned}$$
(11)

where \(\tilde{k}_r=k_r+K_{rr}\), \(\tilde{c}_r=2m_r\zeta _r\tilde{\omega }_r\) and \(\tilde{\omega }_r=\sqrt{\frac{\tilde{k}_r}{m_r}}\). The quasi-static axial strain in the cable is given then by the equation

$$\begin{aligned} \bar{e}_r&= \frac{u_{M}(t)}{L(\tau )}+\frac{1}{2}\bigg [\frac{1}{L}\kappa _{rr}(\tau )q_r^2(t)+2v_0(t)\frac{\varPsi _L-1}{L(\tau )}\alpha _r(\tau )q_r(t) \\&+\bigg (\frac{\varPsi _L-1}{L(\tau )}\bigg )^2v_0^2(t)\bigg ]. \end{aligned}$$
(12)

Derivation of the above formulae originates from [6], where the problem of stochastic analysis was also considered. In that paper the linearized problem was solved by neglecting the non-linear terms. In the considerations presented here the equivalent linearization technique is used to replace the original nonlinear system with an equivalent system given by the set of linear differential equations.

3 Stochastic approach

In deterministic nonlinear solution the motion \(v_0(t)\) is assumed to be in form of harmonic vibrations with the amplitude \(A_0\) and frequency \(\varOmega _0\). However the external excitation such as a wind load is of stochastic nature, and can be considered as a narrow-band random process mean-square equivalent to the mentioned harmonic process. Therefore the motion \(v_0\) must satisfy two conditions: be continuous and twice differentiable. These can be fulfilled by assuming that \(v_0\) is the response of the second-order auxiliary filter to the process X(t) which is in turn the response of the first-order filter to the Gaussian white noise excitation \(\xi (t)\) [4]. The stochastic governing equations are given in the following form

$$\begin{aligned}&\ddot{v}_0(t)+2\zeta _{f}\varOmega _0\dot{v}_0(t)+\varOmega _0^2 v_0(t)=X(t) \\&\dot{X}(t)+\alpha X(t)=\alpha \sqrt{2\pi S_{0}}\xi (t) \end{aligned}$$
(13)

where the filter variable \(\alpha\) is expressed by

$$\begin{aligned} \alpha =\varOmega _0\bigg (-\zeta _f+\sqrt{\zeta _f^2+\frac{\zeta _f\varOmega _0^3 A_0^2}{\pi S_0-\zeta _f\varOmega _0^3 A_0^2}}\bigg ), \end{aligned}$$
(14)

while \(S_0\) and \(\zeta _f\) denote the constant level of the white noise power spectrum and damping ratio, respectively. To convert the second-order differential equations into the first-order differential one, the presented formula is used

$$\begin{aligned} d\mathbf {Y}(t)=\mathbf {c}(\mathbf {Y}(t),t)dt+\mathbf {b}(t)dW(t) \end{aligned}$$
(15)

where the standard Wiener process, drift vector and diffusion vector are denoted respectively as W(t), \(\mathbf {c}(\mathbf {Y}(t),t)\) and \(\mathbf {b}(t)\). Equation (15) is expressed in terms of the augmented state vector that is given in following form

$$\begin{aligned} \mathbf {Y}(t)=[\begin{array}{lllllllll} q_r&\dot{q}_r&z_d&\dot{z}_d&u_{M}&\dot{u}_{M}&v_0&\dot{v}_0&X \end{array}]^\mathrm {T}. \end{aligned}$$
(16)

The elements of drift vector are defined as

$$\begin{aligned} c_1(\mathbf {Y}(t))&= \dot{q}_{r}(t), \\ c_2(\mathbf {Y}(t))&= \frac{1}{m_r}\bigg \{ -\tilde{c}_r\dot{q}_r(t)-\tilde{k}_r q_r(t)+\{k_d[z_d(t)-\varPhi _r(L)q_r(t)] \\&+\,c_d[\dot{z}_d(t)-\varPhi _r(L)\dot{q}_r(t)]\}\varPhi _r(L) \\&+\,EA\bigg [\frac{u_{M}(t)}{L(\tau )}\varGamma _{rn}(\tau )q_r(t)-\frac{u_{M}(t)}{L(\tau )}\frac{\varPsi _L-1}{L}\varPhi _r(L)v_0(t)\bigg ] \\&+\,EA\frac{1}{2}\bigg [\frac{1}{L}\kappa _{rr}(\tau )\varGamma _{rn}(\tau )q_r^3(t)-\bigg (\frac{\varPsi _L-1}{L(\tau )}\bigg )^3\varPhi _r(L)v_0^3(t)\bigg ] \\&+\,EA\frac{\varPsi _L-1}{L(\tau )}\varPhi _r(L)\bigg [\varGamma _{rn}(\tau )-\frac{1}{2}\frac{1}{L}\kappa _{rr}(\tau )\bigg ]q_r^2(t)v_0(t) \\&+\,EA\bigg (\frac{\varPsi _L-1}{L(\tau )}\bigg )^2\bigg [\frac{1}{2}\varGamma _{rn}(\tau )-\varPhi _r^2(L)\bigg ]v_0^2(t)q_r(t) \\&+\,\beta _r^{(0)}(\tau )v_0(t)+\beta _r^{(1)}(\tau )\dot{v}_0(t)+\beta _r^{(2)}(\tau )(X(t) \\&-\,2\zeta _{f}\varOmega _0\dot{v}_0(t)-\varOmega _0^2 v_0(t))\bigg \}, \\ c_3(\mathbf {Y}(t))&= \dot{z}_{d}(t), \\ c_4(\mathbf {Y}(t))&= \frac{1}{m_d}\bigg \{-k_d[z_d(t)-\varPhi _r(L)q_r(t)]-c_d[\dot{z}_d(t)-\varPhi _r(L)\dot{q}_r(t)] \\&+\,k_d\varPsi _Lv_0(t)+c_d\varPsi _L\dot{v}_0(t)\bigg \}, \\ c_5(\mathbf {Y}(t))&= \dot{u}_{M}(t), \\ c_6(\mathbf {Y}(t))&= \frac{EA}{M+m_d}\bigg \{-\frac{u_{M}(t)}{L(\tau )}-\frac{1}{2}\bigg [\frac{1}{L}\kappa _{rr}(\tau )q_r^2(t) \\ &+ 2v_0(t)\frac{\varPsi _L-1}{L(\tau )}\varPhi _r(L)q_r(t)+\bigg (\frac{\varPsi _L-1}{L(\tau )}\bigg )^2v_0^2(t)\bigg ]\bigg \}, \\ c_7(\mathbf {Y}(t))&= \dot{v}_{0}(t), \\ c_8(\mathbf {Y}(t))&= X(t)-2\zeta _{f}\varOmega _0\dot{v}_0(t)-\varOmega _0^2 v_0(t), \\ c_9(\mathbf {Y}(t))&= -\alpha X(t). \end{aligned}$$
(17)

4 Implementation of equivalent linearization technique

To convert the original nonlinear set of differential equation into the linear one by using the equivalent linearization technique, the augmented state vector must be transformed to the centralized state vector

$$\begin{aligned} \mathbf {Y}^0(t)=\big [ \begin{array}{lllllllll} Y_1^0&Y_2^0&Y_3^0&Y_4^0&Y_5^0&Y_6^0&Y_7^0&Y_8^0&Y_9^0 \end{array}\big ] ^\mathrm{T}\end{aligned}$$
(18)

in accordance with the following expressions

$$\begin{aligned} Y_1^0(t)&= q_r(t)-\mu _{q_r}(t),\quad Y_2^0(t)=\dot{q}_r(t)-\mu _{\dot{q}_r}(t), \\ Y_3^0(t)&= z_d(t)-\mu _{z_d}(t),\quad Y_4^0(t)=\dot{z}_d(t)-\mu _{\dot{z}_d}(t), \\ Y_5^0(t)&= u_{M}(t)-\mu _{u_{M}}(t),\quad Y_6^0(t)=\dot{u}_{M}(t)-\mu _{\dot{u}_{M}}(t), \\ Y_7^0(t)&= v_0(t)-\mu _{v_0}(t),\quad Y_8^0(t)=\dot{v}_0(t)-\mu _{\dot{v}_0}(t), \\ Y_9^0(t)&= X(t)-\mu _{X}(t). \end{aligned}$$
(19)

The Equation (15) can be then rewritten in the following form

$$\begin{aligned} d\mathbf {Y}^0(t)=\mathbf {c}^0\big (\mathbf {Y}^0(t),t\big )dt+\mathbf {b}(t)dW(t) \end{aligned}$$
(20)

where the centralized drift vector is given by

$$\begin{aligned} \mathbf {c}^0(\mathbf {Y}^0(t),t)=\mathbf {c}\big (\mathbf {Y}^0(t),t\big ) -\mathrm {E}\big [\mathbf {c}(\mathbf {Y}^0(t),t)\big ]. \end{aligned}$$
(21)

The diffusion vector is assumed to be independent of the state vector and defined as

$$\begin{aligned} \mathbf {b}(t)=\big [\begin{array}{llllllllll} 0&0&0&0&0&0&0&0&\alpha \sqrt{2\pi S_{0}} \end{array}\big ]^\mathrm{T} \end{aligned}$$
(22)

The elements of vector \(\mathbf {c}^0(\mathbf {Y}^0(t),t)\) are obtained in following form

$$\begin{aligned} c_1^0(\mathbf {Y}^0(t))&= Y_2^0, \\ c_2^0(\mathbf {Y}^0(t))&= \frac{1}{m_r}\bigg \{-\tilde{c}_rY_2^0-\tilde{k}_r Y_1^0+\{k_d[Y_3^0-\varPhi _r(L)Y_1^0] \\&+\,c_d[Y_4^0-\varPhi _r(L)Y_2^0]\}\varPhi _r(L)+EA\frac{1}{L(\tau )}\varGamma _{rn}(Y_5^0Y_1^0 \\&-\,\mathrm {E}[Y_5^0Y_1^0]+Y_1^0\mu _{u_{M}}+Y_5^0\mu _{{q}_{r}}) \\&-\,EA\frac{1}{L(\tau )}\frac{\varPsi _L-1}{L}\varPhi _r(L)(Y_5^0Y_7^0-\mathrm {E}[Y_5^0Y_7^0] \\&+\,Y_7^0\mu _{u_{M}}+Y_5^0\mu _{v_0}) \\&+\,EA\frac{1}{2L}\kappa _{rr}\varGamma _{rn}\bigg [(Y_1^0)^3+3(Y_1^0)^2\mu _{{q}_{r}} \\&-\,3\mathrm {E}[(Y_1^0)^2]\mu _{{q}_{r}}+3Y_1^0\mu _{{q}_{r}}^2\bigg ] \\&-\,EA\frac{1}{2}\bigg (\frac{\varPsi _L-1}{L(\tau )}\bigg )^3\varPhi _r(L) \\&\times \bigg [(Y_7^0)^3+3(Y_7^0)^2\mu _{v_0}-3\mathrm {E}[(Y_7^0)^2]\mu _{v_0}+3Y_7^0\mu _{v_0}^2\bigg ] \\&+\,EA\frac{\varPsi _L-1}{L(\tau )}\varPhi _r(L)\bigg [\varGamma _{rn}-\frac{1}{2}\frac{1}{L}\kappa _{rr}\bigg ] \\&\times \bigg [Y_7^0(Y_1^0)^2+2Y_7^0Y_1^0\mu _{{q}_{r}}-2\mathrm {E}[Y_7^0Y_1^0]\mu _{{q}_{r}} \\&+\,Y_7^0\mu _{{q}_{r}}^2+(Y_1^0)^2\mu _{v_0}-\mathrm {E}[(Y_1^0)^2]\mu _{v_0}+2Y_1^0\mu _{{q}_{r}}\mu _{v_0}\bigg ] \\&+\,EA\bigg (\frac{\varPsi _L-1}{L(\tau )}\bigg )^2\bigg [\frac{1}{2}\varGamma _{rn}-\varPhi _r^2(L)\bigg ] \\&\times \bigg [(Y_7^0)^2Y_1^0+(Y_7^0)^2\mu _{{q}_{r}}\!\!-\mathrm {E}[(Y_7^0)^2]\mu _{{q}_{r}}+2Y_7^0Y_1^0\mu _{v_0} \\&-\, 2\mathrm {E}[Y_7^0(t)Y_1^0]\mu _{v_0}\!\!+2Y_7^0\mu _{v_0}\mu _{{q}_{r}}\!\!+Y_1^0\mu _{v_0}^2\bigg ]\!\!+\beta _r^{(0)}Y_7^0 \\&+\, \beta _r^{(1)}Y_8^0+\beta _r^{(2)}\big [Y_9^0-2\zeta _{f}\varOmega _0Y_8^0-\varOmega _0^2 Y_7^0\big ]\bigg \}, \\ c_3^0(\mathbf {Y}^0(t))&= Y_4^0, \\ c_4^0(\mathbf {Y}^0(t))&= \frac{1}{m_d}\bigg \{-k_d[Y_3^0-\varPhi _r(L)Y_1^0]-c_d[Y_4^0-\varPhi _r(L)Y_2^0], \\&+\,k_d\varPsi _L(Y_7^0)+c_d\varPsi _L(Y_8^0)\bigg \}, \\ c_5^0(\mathbf {Y}^0(t))&= Y_6^0, \\ c_6^0(\mathbf {Y}^0(t))&= \frac{EA}{M+m_d}\bigg \{-\frac{Y_5^0}{L(\tau )}-\frac{1}{2}\bigg [\frac{1}{L}\kappa _{rr}((Y_1^0)^2 \\&-\,\mathrm {E}[(Y_1^0)^2]+2Y_1^0\mu _{q_{r}})+2\frac{\varPsi _L-1}{L(\tau )}\varPhi _r(L)(Y_1^0Y_7^0 \\&-\,\mathrm {E}[Y_1^0Y_7^0]+Y_7^0\mu _{q_{r}}+Y_1^0\mu _{v_{0}}) \\&+\,\bigg (\frac{\varPsi _L-1}{L(\tau )}\bigg )^2\!\!\!((Y_7^0)^2-\mathrm {E}[(Y_7^0)^2]+2Y_7^0\mu _{v_{0}})\bigg ]\!\bigg \}, \\ c_7^0(\mathbf {Y}^0(t))&= Y_8^0, \\ c_8^0(\mathbf {Y}^0(t))&= Y_9^0-2\zeta _{f}\varOmega _0Y_8^0-\varOmega _0^2Y_7^0, \\ c_9^0(\mathbf {Y}^0(t))&= -\alpha Y_9^0. \end{aligned}$$
(23)

The original nonlinear system given by Eq. (20) is replaced in further consideration by the linear system defined as

$$\begin{aligned} d\mathbf {Y}^0(t)=\mathbf {B}\mathbf {Y}^0(t)dt+\mathbf {b}(t)dW(t), \end{aligned}$$
(24)

where the centralized drift terms are adopted as a linear form of the state variables

$$\begin{aligned} c^0_{i,eq}\big (\mathbf {Y}^0(t)\big )=B_{im}Y^0_{m} \end{aligned}$$
(25)

and components \(B_{im}\) are obtained as

$$\begin{aligned} B_{im}\kappa _{mj}=\mathrm {E}\big [Y^0_{j}c^0_{i}(\mathbf {Y}^0)\big ], \end{aligned}$$
(26)

which in the matrix form is as follows

$$\begin{aligned} \mathbf {B}\mathbf {\kappa }(t)=\mathrm {E}\big [\mathbf {c}^0\big (\mathbf {Y}^0(t)\big ) {\mathbf {Y}^0}^{\mathrm {T}}\big ]. \end{aligned}$$
(27)

Due to the assumption about the jointly Gaussian distribution of the state variables \(\mathbf {Y}^0(t)\), the presented relationship for zero-mean Gaussian random vector \(\mathbf {X}\) [23] is taken into account

$$\begin{aligned} \mathrm {E}\big [\mathbf {X}f(\mathbf {X})\big ]=\mathrm {E}\big [\mathbf {X}\mathbf {X}^\mathrm {T}\big ]\mathrm {E}\big [\nabla f(\mathbf {X})\big ], \end{aligned}$$
(28)

where \(f(\mathbf {X})\) denotes the non-linear function and \(\nabla\) is defined as \(\nabla =\bigg [\frac{\partial }{\partial X_1},\frac{\partial }{\partial X_2},\ldots , \frac{\partial }{\partial X_n}\bigg ]^\mathrm {T}\). Transposing both sides of Eq. (27) and using Eq. (28) yields

$$\begin{aligned} \mathbf {\kappa }(t)\mathbf {B}^\mathrm {T} =\mathbf {\kappa }(t)\mathrm {E}\big [\nabla {\mathbf {c}^0}^{\mathrm {T}} (\mathbf {Y}^0(t))\big ]. \end{aligned}$$
(29)

That defines the components of matrix \(\mathbf {B}\) as

$$\begin{aligned} \mathbf {B}^\mathrm {T}=\mathrm {E}\big [\nabla {\mathbf {c}^0}^{\mathrm {T}}(\mathbf {Y}^0(t))\big ]. \end{aligned}$$
(30)

Using Eq. (30) and the elements of centralized drift vector given by Eqs. (23) the unknown matrix is obtained in the form

$$\begin{aligned} \mathbf {B}=\left[ \begin{array}{lllllllll} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ p^{(1)}_{r} & p^{(2)}_{r}& \frac{k_d\varPhi _r}{m_r}& \frac{c_d\varPhi _r}{m_r}& p^{(3)}_r & 0 & p^{(4)}_{r}& p^{(5)}_{r}& \frac{\beta _r^{(2)}}{m_r}\\ 0 & 0 & 0 & 1 & 0 & 0 & 0& 0 & 0 \\ \frac{k_d\varPhi _r}{m_d}& \frac{c_d\varPhi _r}{m_d} & -\frac{k_d}{m_d}& -\frac{c_d}{m_d}& 0& 0 & \frac{k_d\varPsi _L}{m_d}& \frac{c_d\varPsi _L}{m_d} & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ p^{(6)}_{r} & 0 & 0 & 0 & p^{(7)}_{r}& 0 & p^{(8)}_{r}& 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -\varOmega _0^2 & -2\zeta _f\varOmega _0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -\alpha \\ \end{array} \right] \end{aligned}$$

where

$$\begin{aligned} p^{(1)}_{r}&= \frac{1}{m_r}\bigg \{-\tilde{k}_r-k_d\varPhi _r^2+EA\frac{1}{L}\varGamma _{rn}\mu _{u_{M}} \\&+\, EA\frac{3}{2L}\kappa _{rr}\varGamma _{rn}\bigg [\mathrm {E}[(Y_1^0)^2]+\mu _{{q}_{r}}^2\bigg ] \\&+\, 2EA\frac{\varPsi _L-1}{L}\varPhi _r\bigg [\varGamma _{rn}-\frac{1}{2}\frac{1}{L}\kappa _{rr}\bigg ]\bigg [\mathrm {E}[Y_7^0Y_1^0]+\mu _{{q}_{r}}\mu _{v_0}\bigg ] \\&+\, EA\bigg (\frac{\varPsi _L-1}{L}\bigg )^2\bigg [\frac{1}{2}\varGamma _{rn}-\varPhi _r^2\bigg ]\bigg [\mathrm {E}[(Y_7^0)^2]+\mu _{v_0}^2\bigg ]\bigg \}, \\ p^{(2)}_{r}&= \frac{-\tilde{c}_r-c_d\varPhi _r^2}{m_r}, \\ p^{(3)}_r&= \frac{EA}{m_rL}\big (\varGamma _{rn}\mu _{{q}_{r}}-\frac{\varPsi _L-1}{L}\varPhi _r\mu _{v_0}\big ), \\ p^{(4)}_{r}&= \frac{1}{m_r}\bigg \{EA\frac{\varPsi _L-1}{L}\bigg [-\frac{1}{L(\tau )}\varPhi _r\mu _{u_{M}} \\&- \,\frac{3}{2}\bigg (\frac{\varPsi _L-1}{L(\tau )}\bigg )^2\varPhi _r(L)\bigg (\mathrm {E}[(Y_7^0)^2]+\mu _{v_0}^2\bigg ) \\&+\, \varPhi _r(L)\bigg [\varGamma _{rn}-\frac{1}{2}\frac{1}{L}\kappa _{rr}\bigg ]\bigg (\mathrm {E}[(Y_1^0)^2]+\mu _{{q}_{r}}^2\bigg ) \\&+\, 2\bigg (\frac{\varPsi _L-1}{L}\bigg )\bigg [\frac{1}{2}\varGamma _{rn}- \varPhi _r^2(L)\bigg ]\bigg (\mathrm {E}[Y_7^0Y_1^0]+\mu _{v_0}\mu _{{q}_{r}}\bigg )\bigg ] \\&+\, \beta _r^{(0)}-\beta _r^{(2)}\varOmega _0^2\bigg \}, \\ p^{(5)}_{r}&= \frac{\beta _r^{(1)}-2\beta _r^{(2)}\zeta _{f}\varOmega _0}{m_r}, \\ p^{(6)}_{r}&= -\frac{EA}{M+m_d}\bigg [\frac{1}{L}\kappa _{rr}\mu _{q_{r}}+\frac{\varPsi _L-1}{L}\varPhi _r\mu _{v_{0}}\bigg ], \\ p^{(7)}_{r}&= -\frac{EA}{L(M+m_d)},\\ p^{(8)}_{r}&= -\frac{EA}{M+m_d}\bigg \{\frac{\varPsi _L-1}{L}\varPhi _r\mu _{q_{r}}+\bigg (\frac{\varPsi _L-1}{L}\bigg )^2\mu _{v_{0}}\bigg \}. \end{aligned}$$
(31)

To obtain the covariance matrix \(\mathbf {R_{\mathbf {Y^0Y^0}}}=\mathrm {E}[\mathbf {Y^0}\mathbf {Y^0}^\mathrm {T}]\) and the differential equations governing the second-order statistical moments of the state vector \(\mathbf {Y^0}(t)\), the following differential equation

$$\begin{aligned} \frac{d}{dt}\mathbf {R_{\mathbf {Y^0Y^0}}} =\mathbf {B}\mathbf {R_{\mathbf {Y^0Y^0}}}+\mathbf {R_{\mathbf {Y^0Y^0}}} \mathbf {B}^{\mathrm {T}}+\mathbf {d}\mathbf {d}^{\mathrm {T}} \end{aligned}$$
(32)

should be solved together with the differential equations for mean values defined as

$$\begin{aligned} \frac{d}{dt}\mathbf {\mu }(t)=\mathrm {E}\big [\mathbf {c}(\mathbf {Y}^0(t))\big ], \end{aligned}$$
(33)

where

$$\begin{aligned} \mathbf {\mu }(t)=\mathrm {E}[\mathbf {Y}(t)]. \end{aligned}$$
(34)

The higher-order joint statistical moments of the state vector \(\mathbf {Y^0}(t)\) can be then easily obtained.

5 Numerical results

In the numerical analysis the main mass \(M=6768\) kg is moving downwards with the transport speed \(V=2.5\) m/s. The total height of the entire system and initial length of the cable are assumed as \(Z_0=261.86\) m and \(L(0)=58.66\) m, respectively. The main mass is attached at the lower end of a cable made by \(n_r=6\) steel wire ropes. The parameters of every rope are: mass per unit length \(m=2.18\) kg/m and longitudinal stiffness \(EA=22.889\) MN. The horizontal displacement of main mass is constrained by the spring with the stiffness \(k=2.8\) kN/m and auxiliary small mass \(m_d\). The frequency of the sway and the amplitude at the top point of the host structure are assumed as \(\varOmega _0=0.105\) Hz and \(A_0=0.1\) m, respectively. The parameters of TMD system were selected to mitigate the effects of transition through the fundamental lateral resonance of the system which is observed for the length of suspension rope \(L=161\) m. Using the mass ratio \(\mu =m_d\varPhi ^2_r(L)/m_r=0.05\) and the optimal damping ratio \(\zeta _d=\sqrt{3\mu /(8(1+\mu )^3)}=0.13\), the particular TMD parameters are obtained as \(m_d=382.85\) kg, \(k_d=m_d(\tilde{\omega }_r/(1+\mu ))^2=150.20\) N/m and \(c_d=2m_d\zeta _d\omega _d=61.04\) Ns/m.

The model was treated twice, first by using the nonlinear deterministic analysis with the structural damping ratio \(\zeta _r=\zeta _1=0.01\), and then by using the equivalent linearization technique for different values of damping ratio of the auxiliary filter \(\zeta _f\). The comparison of the results obtained from the two methods (see. Fig. 2) shows that the smaller the value of \(\zeta _f\) is taken into the analysis the smaller differences between the deterministic and expected values for particular random state variables is obtained. As we can see, the best match between the response curves can be observed at the early stage of motion. After the system enters into the resonance area the differences become more significant, especially for the vertical displacement of main mass \(u_M\), as can bee seen on Fig. 2c. However for very small values \(\zeta _f\) the lines of generalized coordinates and horizontal displacements of auxiliary mass are almost identical (Fig. 2a–b).

Figure 3 presents the percentage differences between the expected values obtained for various \(\zeta _f\) and deterministic solution of nonlinear system under harmonic excitation. As it can be seen for small value of \(\zeta _f\) the observed result is under 5\(\%\). The largest deviation of the expected values from the non-linear solution can be observed for the case of vertical displacement of the main mass (Fig. 3c), but it may be caused by very low values of these displacements in comparison with generalized coordinates or horizontal displacements of an auxiliary mass.

Fig. 2
figure 2

Comparison of deterministic results and expected values obtained by the equivalent linearization technique: a \(q_r\), b \(z_d\), c \(u_M\)

Full size image
Fig. 3
figure 3

Percentage difference between the deterministic results and expected values obtained by the equivalent linearization technique: a \(q_r\), b \(z_d\), c \(u_M\)

Full size image

The application of the equivalent linearization technique leads to obtaining not only the expected values of every random state variable but also their variances and the mutual covariances. Figure 4 shows the relationship between the value of coefficient \(\zeta _f\) that was included into the analysis and the variance of selected variables of the system (\(q_r\), \(z_d\) and \(v_0\)). As it can be seen for the lowest values of \(\zeta _f\), for which the best comparison between the stochastic and deterministic results were obtained (see Figs. 2 and 3), the values of variances received by equivalent linearization technique are comparable. On the other hand for the higher value of \(\zeta _f\) the differences between the graphs are significant. This confirms that for this cable–mass system the ratio of damping auxiliary filter should be selected between 0.001 and 0.005.

Fig. 4
figure 4

Variances of particular random state variables obtained by equivalent linearization technique

Full size image

6 Concluding remarks

The equations of motion of a vertical mass-cable moving at speed within a tall host structure should include the nonlinear effects due to the rope stretching. Because of their slenderness high-rise buildings and civil structures are subjected to vibrations caused by external dynamic loads. The excitation due to these loads result in bending deformation of the host structure which in turn leads to the excitation of structural part of internal equipment such as elastic cables and ropes. To reduce their dynamic response the properly designed TMD can be applied. To select the parameters and implement the tuned mass damper action the mode corresponding to the main mass motion should be considered. Because of its nondeterministic nature, the problem should be examined by using stochastic methods. The results presented in this paper bring a conclusion that the random excitation model can be represented as a narrow-band process mean-square equivalent to the harmonic process and can be implemented by using approximation.

The equivalent linearization technique results in replacing the original system governed by non-linear differential equations by an equivalent system governed by linear differential equations, that are expressed in terms of the moments and of the expectations of the non-linear functions of the response process. As a result the covariance matrix of the state variables is obtained. That gives relevant and necessary information that should be taken into account when designing the system.

The nonlinearity and non-stationarity of the process require the application of numerical techniques. The presented procedure shows that the equivalent linearization technique can be effectively used in the analysis. An undoubtful advantage of this approach is shorter time of calculation in comparison to other statistical methods.