1 Introduction

Conformal mapping has been applied to the study of the visual cortex. Frederick and Schwartz [1] presented the conformal mapping of retina as a case of identification of a single point (the representation of the blind spot, or optic disk) in the eye. They mapped one half of the retina conformally to the half unit disk, which conformally is mapped to a unit disk preserving the point in the half disk that mapped to the origin of the target disk as a parameter of this mapping. Finally, the unit disk is mapped conformally to an arbitrary 2D region, the flattened data. More applications can be found in [2, 3].

Explicit formulae for conformal mappings of multiply circular regions onto canonical slit regions in terms of Schottky–Klein prime function and their applications are described in [4,5,6]. Numerical conformal mappings of general multiply connected regions onto canonical slit regions have been described in [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. The obtained boundary integral equation methods in [16,17,18,19,20, 23,24,25] were discretized by the Nyström method with trapezoidal rule to obtain a dense and nonsymmetric linear system. Gauss elimination method of order \(O((M+1)^3n^3)\) operations was used for solving the obtained linear system, where \(M+ 1\) refers to the multiplicity of the multiply connected region and n stands for the number of nodes in the discretization of each boundary component. Hence, it is very expensive to solve the linear system for very large values of M and n.

This paper illustrates a new integral equation method using the adjoint generalized Neumann and Neumann-type kernels for conformal mapping and its inverse of a bounded multiply connected region onto a disk and annulus with circular slits, extending the work presented in Sangawi et al. [16, 17]. Unlike the methods presented in [16, 17] which require solving three integral equations, the method shown in this paper requires only two integral equations. Discretization of the integral equation yields a system of linear equations which are solved by an iterative method based on the restarted version of the generalized minimal residual (GMRES) method of Saad and Schultz [26].

The GMRES method will converge significantly faster without the need to use preconditioning for solving our linear system. See [27,28,29,30,31] for details on FMM operation and memory requirement. This paper is an improvement of the methods presented in [16, 17]. The matrix–vector product function can be computed using the function gmres. The function zfmm2dpart in the MATLAB toolbox FMMLIB2D developed by Greengard and Gimbutas [32] is then used for the matrix–vector product function for the coefficient matrix of our linear system. Thus, the obtained linear system can be solved in \(O((M+1)n)\) operations. We then apply the proposed method to brain medical image processing which gives high-quality information that helps in diagnosing diseases and making the treatment easier.

The disposition of this paper is as follows: Sect. 2 presents some auxiliary materials. Section 3 discusses an integral equation method to calculate the modulus of conformal mapping function f. Derivations of integral equations related to \(f'\) for canonical regions of type disk with circular slits \(\varOmega _1\) and annulus with circular slits \(\varOmega _2\) are given in Sects. 4 and 5 . Section 6 presents a method to compute the inverse mapping functions from the canonical slits region onto the original region. Section 7 describes the fast numerical implementation. Section 8 provides examples to illustrate the effectiveness of proposed method. Section 9 applies the proposed method to brain medical image processing. Finally, Sect. 10 concludes the findings of this paper.

2 Notations and Auxiliary Materials

Let \(\varOmega \) be a bounded multiply connected region of connectivity \(M+1\). The boundary \(\varGamma \) consists of \(M+1\) smooth Jordan curves \(\varGamma _{j}, j=0, 1, \ldots , M\) as shown in Fig. 1.

Fig. 1
figure 1

Mappings of the bounded multiply connected region onto a disk \(\varOmega _1\) and annulus with circular slits \(\varOmega _2\)

Full size image

The curves \(\varGamma _{j}\) are parametrized by \(2 \pi \)-periodic twice continuously differentiable complex functions \(z_{j}(t)\) with non-vanishing first derivatives

$$\begin{aligned} z'_{j}(t)={\mathrm{d}z_{j}(t)}/{\mathrm{d}t} \ne 0, \quad t \in J_{j}=\left[ 0, 2 \pi \right] , \quad j=0, 1, \ldots , M. \end{aligned}$$

The total parameter domain J is the disjoint union of \(M+1\) intervals \(J_{0}, \ldots , J_{M}\). We define a parametrization z(t) of the whole boundary \(\varGamma \) on J by

$$\begin{aligned} z(t)= z_{j}(t),\quad t \in J_{j}. \end{aligned}$$
(1)

Let \(H^*\) be the space of all real Hölder continuous \(2 \pi \)-periodic functions \(\omega (t)\) such that

$$\begin{aligned} \omega (t)= \omega _{j}(t),\quad t \in J_{j}. \end{aligned}$$

Suppose that b(z) and H(z) are complex-valued functions defined on \(\varGamma \) such that \(b(z)\ne 0\), \(H(z)\ne 0\) and \(\overline{H(z)}/T(z)^2\) satisfies the Hölder condition on \(\varGamma \). Then, the interior relationship is defined as follows:

A complex-valued function P(z) is said to satisfy the interior relationship if P(z) is analytic in \(\varOmega \) and satisfies the non-homogeneous boundary relationship

$$\begin{aligned} P(z)= {\frac{b(z)\overline{T(z)}}{\overline{G(z)}}\overline{P(z)}}+\overline{H(z)}, \quad z \in \varGamma , \end{aligned}$$
(2)

where G(z) is analytic in \(\varOmega \), Hölder continuous on \(\varGamma \), and \(G(z)\ne 0\) on \(\varGamma \). The boundary relationship (2) also has the following equivalent form:

$$\begin{aligned} G(z)= {\overline{b(z)}T(z)}\frac{P(z)^2}{\left| P(z)\right| ^2}+\frac{G(z) H(z)}{\overline{P(z)}}, \quad z \in \varGamma . \end{aligned}$$
(3)

The following theorem from [18] gives an integral equation for an analytic function satisfying the interior non-homogeneous boundary relationship (2) or (3).

Theorem 1

[18, Theorem 3.1] If the function P(z) satisfies the interior non-homogeneous boundary relationship (2) or (3), then

$$\begin{aligned}&T(z)P(z)+\int _{\varGamma }N_T(z,w)T(w)P(w)|\mathrm{d}w|+ {b(z)}\left[ \sum _{a_j {{\mathrm{inside}}} \varGamma }\mathop {\mathrm {Res}}\limits _{w=a_j}\frac{{P(w)}}{({w}-{z}){G(w)}} \right] ^{{{\mathrm{conj}}}}\nonumber \\&\quad =-\overline{L_{R}^{-}(z)},\quad z\in \varGamma , \end{aligned}$$
(4)

where

$$\begin{aligned} N_T(z,w)= & {} \left\{ \begin{array}{ll} \displaystyle \frac{1}{2\pi {\mathrm{i}}} \left[ \frac{T(z)}{z-w}-\frac{b(z)}{b(w)}\frac{\overline{T(w)}}{\overline{z} -\overline{w}}\right] , &{}\quad \displaystyle z\ne w\\ \displaystyle -\frac{1}{2\pi {\mathrm{i}} |z'(t)|}\left[ \frac{\overline{Q'(z(t))}}{\overline{Q(z(t))}} + \frac{c'(z(t))}{c(z(t))} \right] \displaystyle ,&{}\quad z=w \end{array} \right. , \end{aligned}$$
(5)
$$\begin{aligned} L_{R}^{-}(z)= & {} \frac{-1}{2}\frac{H(z)}{T(z)}+\mathrm {PV} \frac{1}{2\pi {\mathrm{i}}}\int _{\varGamma }\frac{\overline{b(z)}H(w)}{\overline{b(w)}(w-z)}|\mathrm{d}w|. \end{aligned}$$
(6)

The symbol “conj” in the superscript denotes complex conjugate, while the minus sign in the superscript denotes limit from the exterior. The sum in (4) is over all those zeros \(a_{1}, a_{2}, \ldots , a_{M}\) of G that lie inside \(\varOmega \) . If G has no zeros in \(\varOmega \) , then the term containing the residue in (4) will not appear.

3 Compute the Piecewise Real Function \(h_j\)

Let A(t) be a complex continuously differentiable \(2 \pi \)-periodic function for all \(t \in J\). The generalized Neumann kernel formed with A is defined by [13, 18]

$$\begin{aligned} N(t,s)=\left\{ \begin{array}{ll} \displaystyle \frac{1}{\pi }\text {Im} \left( \frac{\hat{A}(t)}{\hat{A}(s)} \frac{z'(s)}{z(s)-z(t)} \right) , &{}\quad t\ne s\\ \displaystyle \frac{1}{\pi }\left( \frac{1}{2}\text {Im} \frac{z''(t)}{z'(t)} -\text {Im} \frac{A'(t)}{A(t)} \right) ,&{}\quad t=s \end{array} \right. , \end{aligned}$$

The adjoint function to the function \({\tilde{A}}\) is given by

$$\begin{aligned} {\tilde{A}}(t)=\frac{z'(t)}{A(t)}. \end{aligned}$$

The generalized Neumann kernel \({\tilde{N}}(s,t)\) formed with \({\tilde{A}}\) is given by

$$\begin{aligned} {\tilde{N}}(t,s)=\frac{1}{\pi }\text {Im} \left( \frac{{\tilde{A}}(t)}{{\tilde{A}}(s)}\frac{z'(s)}{z(s)-z(t)} \right) . \end{aligned}$$

Then

$$\begin{aligned} {\tilde{N}}(s, t)=- N^{*}(s, t), \end{aligned}$$

where \(N^*(s, t) = N(t, s)\) is the adjoint kernel of the generalized Neumann kernel N(s, t) (see [13] for more details). Define the Fredholm integral operator \(\mathbf{N}^{*}\) by

$$\begin{aligned} \mathbf{N }^{*}\psi (t)=\int _{J} N^*(t, s)\psi (s) ds, \quad t \in J. \end{aligned}$$

It is known that \(\lambda =1\) is an eigenvalue of the kernel N with multiplicity 1 and \(\lambda =-1\) is an eigenvalue of the kernel N with multiplicity M [13]. The eigenfunctions of N corresponding to the eigenvalue \(\lambda = -1\) are \(\left\{ \chi ^{[0]}, \chi ^{[1]}, \ldots , \chi ^{[M]} \right\} \), where

$$\begin{aligned} \chi ^{[j]}(\xi )=\left\{ \begin{array}{ll} \displaystyle 1, &{}\quad \displaystyle \xi \in \varGamma _{j},\\ \displaystyle 0, &{}\quad \displaystyle {\mathrm{otherwise}}, \end{array} \right. \quad j=0, 1, \ldots , M. \end{aligned}$$

Define the space S by

$$\begin{aligned} S={{\mathrm{span}}}\{ \chi ^{[0]}, \chi ^{[1]}, \ldots , \chi ^{[M]}\} \end{aligned}$$
(7)

and define an integral operator \(\mathbf{J }\) by (see [16])

$$\begin{aligned} \mathbf{J }\upsilon =\int _{J} \frac{1}{2 \pi } \sum _{j=0}^{M} \chi ^{[j]}(s) \chi ^{[j]}(t) \upsilon (s) ds. \end{aligned}$$
(8)

The following theorem from [16] is useful in upcoming sections.

Theorem 2

[16] Suppose that the function \(\gamma \in H^*\) and functions \(h, \mu \in S\) such that

$$\begin{aligned} A{\tilde{g}}=\gamma +h+{\mathrm{i}}\mu \end{aligned}$$
(9)

are boundary values of an analytic function \({\tilde{g}}(z)\) in \(\varOmega \). Then, the function \(h=(h_0,h_1,\ldots ,h_M)\) is given by

$$\begin{aligned} h_{j}=(\gamma ,\phi ^{[j]})=\frac{1}{2\pi }\int _{\varGamma } \gamma (t)\phi ^{[j]}(t) \mathrm{d}t, \end{aligned}$$
(10)

where \(\phi ^{[j]}\) are solutions of the following integral equations

$$\begin{aligned} ({{\mathrm{I}}}+{{\mathrm{N}}}^{*}+{{\mathrm{J}}})\phi ^{[j]}=-\chi ^{[j]},\quad j=0, 1, \ldots , M. \end{aligned}$$
(11)

4 Disk with Circular Slit Region

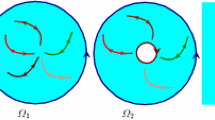
Assume that an analytic function \(w=f(z)\) maps \(\varOmega \) conformally onto a disk with circular slits \(\varOmega _1\) (see Fig. 1b). This canonical region \(\varOmega _1\) consists of the disk \(\left| w\right| \le \mu _0\) slit along M arcs of circles \(\left| w\right| = \mu _j, j = 1, \ldots ,M.\) We assume that \(w = f(z)\) maps \(\varGamma _0\) onto the circle \(\left| w\right| = \mu _0\) , and the curves \(\varGamma _1, \ldots , \varGamma _M\) onto the arcs of circles \(\left| w\right| = \mu _j, j = 1, \ldots ,M\), where \(\mu _0\) is known, and \(\mu _j, j = 1, \ldots ,M,\) are unknowns and have to be determined.The function is uniquely determined by prescribing that \(f(a)=0\) and \(f'(a)>0\). The boundary values of f can be represented in the form

$$\begin{aligned} f(z_{j}(t))= \mu _{j} e^{{{\mathrm{i}}} \theta _{j}(t)},\quad \varGamma _{j}:z=z_{j}(t),\quad 0 \le t \le \beta _{j},\quad j=0,1, \ldots ,M, \end{aligned}$$
(12)

where \(\theta _{j}\) are the boundary correspondence functions of \(\varGamma _{j}\) and \(\mu _{j}\) are the radii of the circular slits. The unit tangent to \(\varGamma \) at z(t) is denoted by \(\displaystyle T(z(t))=\frac{z'(t)}{\left| z'(t) \right| }\). Thus, it can be shown from (12) that

$$\begin{aligned} f(z_{j}(t))=\frac{\mu _{j}}{{{\mathrm{i}}}} T(z_{j}(t)) \frac{\theta _{j}{'}(t)}{\left| \theta _{j}{'}(t) \right| } \frac{f'(z_{j}(t))}{\left| f'(z_{j}(t)) \right| },\quad z_{j} \in \varGamma _{j},\quad j=0, 1, \ldots ,M. \end{aligned}$$
(13)

Note that for \(j=0\), \(\theta _{j}{'} >0\) and for \(j=1, 2, \ldots , M\), \(\theta _{j}{'} \) may be positive or negative since each circular slit \(f(\varGamma _{j})\) is traversed twice (see Fig. 1c). Thus \(\displaystyle \frac{\theta _{j}{'}(t)}{\left| \theta _{j}{'}(t) \right| }= \pm 1\). Squaring both sides of (13), we get

$$\begin{aligned} f(z)^{2}=-{\left| f(z) \right| ^{2}} T(z)^{2} \frac{f'(z)^{2}}{\left| f'(z) \right| ^{2}}, \quad z \in \varGamma . \end{aligned}$$
(14)

The mapping function can also be expressed as [11, 16]

$$\begin{aligned} f(z)=c(z-a) e^{(z-a) {\hat{h}}(z)}, \end{aligned}$$
(15)

where \({\hat{h}}(z)\) is an analytic function and \(c=f'(a)\) is an undetermined real constant. From (14) and (15), we obtain the boundary relationship

$$\begin{aligned} c^2 (z-a)e^{2(z-a){\hat{h}}(z)}=-\frac{{\left| f(z) \right| ^{2}} T(z)^{2}}{z-a} \frac{f'(z)^{2}}{\left| f'(z) \right| ^{2}}, \quad z \in \varGamma . \end{aligned}$$
(16)

By taking logarithm on both sides of (15), we obtain

$$\begin{aligned} \log (f(z(t))=\ln c + \log (z(t)-a) + (z(t)-a){\hat{h}}(z(t)) \end{aligned}$$
(17)

which implies

$$\begin{aligned} \begin{array}{llll} \displaystyle (z(t)-a){\hat{h}}(z(t))&{}=&{}\displaystyle \ln \left( \frac{\mu }{c}\right) - \ln {|z(t)-a|}-\mathrm{i}\arg {(z(t)-a)}+{\mathrm{i}}\theta \\ &{}=&{}\displaystyle \gamma (t)+h(t)+{\mathrm{i}}\upsilon (t), \end{array} \end{aligned}$$
(18)

where \(\displaystyle \gamma (t)= - \ln {|z(t)-a|}\), \(\displaystyle h(t)=\ln \left( \frac{\mu }{c}\right) \), \(\mu =\left( \mu _0, \mu _1, \ldots , \mu _M\right) \). Let \( A(t)=z(t)-a\). By obtaining \(h_j,~~j=0,1, \ldots , m\), from (10), we obtain

$$\begin{aligned} c=e^{-h_0}, \end{aligned}$$
(19)

and

$$\begin{aligned} \mu _j=c e^{h_j},\quad j=1, 2, \ldots , m. \end{aligned}$$
(20)

Comparison of (16) and (3) leads to a choice of \(P(z)=f'(z)\), \(\displaystyle b(z)=\frac{-|f(z)|^2\overline{T(z)}}{\overline{z-a}}\), \(G(z)=c^2(z-a)e^{2(z-a){\hat{h}}(z)}\), \(H(z)=0\). Theorem 1 yields

$$\begin{aligned}&T(z)f'(z)+{{\mathrm{PV}}}\int _{\varGamma } N_T(z,w)T(w)f'(w)\left| \mathrm{d}w\right| \nonumber \\&\quad =\frac{|f(z)|^2\overline{T(z)}}{\overline{(z-a)}} \left[ \sum _{a_j {{\mathrm{inside}}} \varGamma }\mathop {\mathrm {Res}}\limits _{w=a_j}\frac{{f'(w)}}{({w}-{z})c^2(w-a) e^{2(w-a){\hat{h}}(w)}}\right] ^{{{\mathrm{conj}}}},\quad z\in \varGamma , \end{aligned}$$
(21)

where

$$\begin{aligned} N_T(z,w)=\left\{ \begin{array}{ll} \displaystyle \frac{1}{2\pi {{\mathrm{i}}}}\left[ \frac{T(z)}{z-w} -\frac{\overline{(w-a)}|f(z)|^2\overline{T(z)}}{\overline{(z-a)}|f(w)|^2(\overline{z} -\overline{w})}\right] \displaystyle , &{}\quad z\ne w\\ \displaystyle \frac{1}{2\pi \left| z'(t)\right| }\mathop {\mathrm {Im}}\frac{z''(t)}{z'(t)} +\frac{1}{2\pi {\mathrm{i}}\left| z'(t)\right| }\overline{\left( \frac{z'(t)}{z(t)-a}\right) } \displaystyle , &{}\quad z=w \end{array} \right. , \end{aligned}$$
(22)

Note that a is a pole of order one for \(\displaystyle \frac{{f'(w)}}{({w}-{z})c^2(w-a)e^{2(w-a){\hat{h}}(w)}}\). Hence,

$$\begin{aligned} \mathop {\mathrm {Res}}\limits _{w=a}\frac{{f'(w)}}{({w}-{z})c^2(w-a) e^{2(w-a){\hat{h}}(w)}}=\frac{1}{c(a-z)}. \end{aligned}$$
(23)

Combining the integral equation (21) and (23), we get

$$\begin{aligned} T(z)f'(z)+{{\mathrm{PV}}}\int _{\varGamma } N_T(z,w)T(w)f'(w)\left| \mathrm{d}w\right| -\frac{|f(z)|^2\overline{T(z)}}{c\overline{(z-a)^2}}, \quad z\in \varGamma . \end{aligned}$$
(24)

Write the integral equation (24) as

$$\begin{aligned} f'(z)T(z)+\int _{\varGamma } N_T(z,w)f'(w)T(w)\left| \mathrm{d}w\right| =-\frac{|f(z)|^2\overline{T(z)}}{c\overline{(z-a)^2}},\quad z\in \varGamma , \end{aligned}$$
(25)

By using single-valuedness of the mapping function f leads to the following conditions

$$\begin{aligned} \frac{1}{2\pi }\int _{-\varGamma _q} f'(w)T(w)\left| \mathrm{d}w\right| = 0,\quad q=1, 2, \ldots , M. \end{aligned}$$
(26)

Thus, the integral equation (25) with condition (26) should give a unique solution provided the parameters c and \(|f(z_q)|=\mu _{q}, {\ }q=1, 2, \ldots , M\) that appear in (25) are known.

By solving the integral equation (11), we get \(\phi ^{[j]}\), \(j=0, 1, \ldots , M\), which gives \(h_{j}\) through (10) which in turn gives c and \(\mu _{j}\) through (19) and (20). By solving (25) with (26) and the known values of c and \(\mu _{j}\), we get the values of \(f'\). Then, the boundary values of \({\hat{h}}(z)\) are given by

$$\begin{aligned} {\hat{h}}(z)=\frac{1}{2(z-a)}\log \left[ -\frac{|f(z)|^2T(z)^2}{c^2(z-a)^2}\frac{f'(z)^2}{|f'(z)|^2}\right] , \quad z\in \varGamma . \end{aligned}$$
(27)

The logarithm in (27) indicates complex logarithm which define as

$$\begin{aligned} \log (z) = \ln |z|+{{\mathrm{i}}} {\mathrm{Arg}}(z). \end{aligned}$$

In This paper, we define the range of \({\mathrm{Arg}}(z)\) as \([0,2\pi )\) to avoid the multiple value of \({\mathrm{Arg}}(z)\). Finally, the approximate boundary values of f(z) are obtained from (15), i.e.,

$$\begin{aligned} f(z)=c(z-a) e^{(z-a){\hat{h}}(z)}, \quad z\in \varGamma . \end{aligned}$$
(28)

The approach presented here is an improvement over [16]. Unlike [16], no integral equation for \(\theta '(t)\) is required here for the computation of f(z).

Note that if \(\varOmega \) is a simply connected region, then (25) reduced to

$$\begin{aligned} f'(z)T(z)+\int _{\varGamma } N_T(z,w)f'(w)T(w)\left| \mathrm{d}w\right| =-\frac{\overline{T(z)}}{c\overline{(z-a)^2}},\quad z\in \varGamma , \end{aligned}$$
(29)

where

$$\begin{aligned} N_T(z,w)=\left\{ \begin{array}{ll} \displaystyle \frac{1}{2\pi {{\mathrm{i}}}}\left[ \frac{T(z)}{z-w}-\frac{\overline{(w-a)}\overline{T(z)}}{\overline{(z-a)}(\overline{z}-\overline{w})}\right] \displaystyle , &{}\quad z\ne w\\ \displaystyle \frac{1}{2\pi \left| z'(t)\right| }\mathop {\mathrm {Im}}\frac{z''(t)}{z'(t)}+\frac{1}{2\pi \mathrm{i}\left| z'(t)\right| }\overline{\left( \frac{z'(t)}{z(t)-a}\right) } \displaystyle , &{}\quad z=w \end{array} \right. . \end{aligned}$$
(30)

For simply connected region, we can just solve integral equation (22) for \(f'(z(t))\) and compute f(z(t)) using (14).

5 Annulus with Circular Slit Region

Let \(w=f(z)\) be the analytic function which maps \(\varOmega \) conformally onto an annulus with circular slits \(\varOmega _2\) (see Fig. 1c). This canonical region \(\varOmega _2\) consists of a circular annulus \(\mu _M\le \left| w\right| \le \mu _0\) slit along \(M-1\) arcs of circles \(\left| w\right| = \mu _j, j = 1, \ldots ,M-1\). We assume that \(w = f(z)\) maps \(\varGamma _0\) onto the circle \(\left| w\right| = \mu _0\), \(\varGamma _M\) onto the circle \(\left| w\right| = \mu _M\) and the curves \(\varGamma _1, \ldots , \varGamma _{M-1}\) onto the arcs of circles \(\left| w\right| = \mu _j , j = 1, \ldots ,M - 1\), where \(\mu _0\) is known, and \(\mu _j, j = 1, \ldots ,M,\) are unknowns and have to be determined. The boundary values of f can be represented in the form

$$\begin{aligned} f(z_{j}(t))= \mu _{j} e^{{{\mathrm{i}}} \theta _{j}(t)},\quad \varGamma _{j}:z=z_{j}(t),\quad 0 \le t \le \beta _{j},\quad j=0, 1, \ldots ,M, \end{aligned}$$
(31)

where \(\theta _{j}\) are the boundary correspondence functions of \(\varGamma _{j}\) and \(\mu _{j}\) are the radii of the circular slits. The mapping function can be expressed as [11, 17]

$$\begin{aligned} f(z)=\frac{c(b-z)}{b} e^{z {\hat{h}}(z)}, \end{aligned}$$
(32)

where \({\hat{h}}(z)\) is an analytic function and let \(0 \in \varOmega \) and b be an interior point in \(\varGamma _M\). The mapping is made uniquely determined by prescribing that \(f(b)=0\) and \(c=f(0)>0\) where c is an undetermined real constant. From (32), we get

$$\begin{aligned} f'(z)=f(z)\left[ z{\hat{h}}'(z)+{\hat{h}}(z)-\frac{1}{b-z}\right] , \end{aligned}$$
(33)

which implies

$$\begin{aligned} \frac{f'(0)}{{\hat{h}}(0)-\frac{1}{b}}=f(0)=c>0. \end{aligned}$$
(34)

The above equation means either both \(f'(0)\) and \(\displaystyle {\hat{h}}(0)-\frac{1}{b}\) are reals or both pure imaginary complex numbers. The representation (31) also satisfy the boundary relationship (14). Multiplying both sides of (14) by z gives the following boundary relationship

$$\begin{aligned} z f(z)^2=-z\left| f(z) \right| ^{2} T(z)^{2} \frac{f'(z)^{2}}{\left| f'(z) \right| ^{2}}, \quad z \in \varGamma . \end{aligned}$$
(35)

Comparison of (35) and (3) leads to a choice of \(P(z)=f'(z)\), \(\displaystyle b(z)=-\overline{z}|f(z)|^2\overline{T(z)}\), \(\displaystyle G(z)=zf(z)^2\), \(H(z)=0\). Theorem 1 yields

$$\begin{aligned}&T(z)f'(z)+{{\mathrm{PV}}}\int _{\varGamma } N_T(z,w)T(w)f'(w)\left| \mathrm{d}w\right| \nonumber \\&\quad \overline{z}|f(z)|^2\overline{T(z)} \left[ \sum _{a_j {{\mathrm{inside}}} \varGamma }\mathop {\mathrm {Res}}\limits _{w=a_j}\frac{{f'(w)}}{({w}-{z})wf(w)^2} \right] ^{{{\mathrm{conj}}}}, \quad z\in \varGamma , \end{aligned}$$
(36)

where

$$\begin{aligned} N_T(z,w)=\left\{ \begin{array}{ll} \displaystyle \frac{1}{2\pi {{\mathrm{i}}}}\left[ \frac{T(z)}{z-w} -\frac{\overline{z}|f(z)|^2\overline{T(z)}}{\overline{w}|f(w)|^2(\overline{z} -\overline{w})}\right] , &{}\quad z\ne w\\ \displaystyle \frac{1}{2\pi \left| z'(t)\right| }\mathop {\mathrm {Im}}\frac{z''(t)}{z'(t)}-\frac{1}{2\pi \mathrm{i}\left| z'(t)\right| }\overline{\left( \frac{z'(t)}{z(t)}\right) } , &{}\quad z=w \end{array} \right. . \end{aligned}$$
(37)

Note that zero is a pole of order one for \(\displaystyle \frac{{f'(w)}}{({w}-{z})wf(w)^2}\). Hence

$$\begin{aligned} \mathop {\mathrm {Res}}\limits _{w=0}\frac{{f'(w)}}{({w}-{z})wf(w)^2}=\frac{f'(0)}{-c^2z}. \end{aligned}$$
(38)

Thus, integral equation, (36) after dividing both sides by \(f'(0)\), becomes

$$\begin{aligned} \frac{f'(z)T(z)}{f'(0)}+\int _{\varGamma } N_T(z,w)\frac{f'(w)T(w)}{f'(0)}\left| \mathrm{d}w\right| =-\frac{|f(z)|^2\overline{T(z)}}{c^2},\quad z\in \varGamma . \end{aligned}$$
(39)

By using single-valuedness of the mapping function, f leads to the following conditions

$$\begin{aligned} \frac{1}{2\pi }\int _{-\varGamma _q} \frac{f'(w)T(w)}{f'(0)}\left| \mathrm{d}w\right| = 0,\quad q=1, 2, \ldots , M, \end{aligned}$$
(40)

and

$$\begin{aligned} \frac{1}{2\pi {\mathrm{i}}}\int _{\varGamma } \frac{wf'(w)T(w)}{f'(0)}\left| \mathrm{d}w\right| = 0. \end{aligned}$$
(41)

Thus, the integral equation (39) with conditions (40) and (41) should give a unique solution provided the parameters c and \(|f(z_q)|=\mu _{q}, {\ }q=1, 2, \ldots , M\) that appear in (39) are known.

The values of \(\mu \) can be computed by using the integral equation (11), (10), (19) and (20) with \(\displaystyle \gamma (t)= \ln {\left| {b}\right| }- \ln {\left| {b-z(t)}\right| }\) and \(A(t)=z(t)\). By solving (39) with the known values of c and \(\mu \), we get the boundary values of \(f'\). Then, the following equation gives the values of \({\hat{h}}(z)\) if \(f'(0)\) is real

$$\begin{aligned} {\hat{h}}(z)=\frac{1}{2 z}\log \left[ -\frac{b^2|f(z)|^2T(z)^2}{c^2(b-z)^2}\frac{f'(z)^2}{|f'(z)|^2}\right] ,\quad z \in \varGamma . \end{aligned}$$
(42)

The logarithm in (42) indicates complex logarithm. Section 4 (after 27) explained the definition of complex algorithm and range of argument to avoid multiple computation. If \(f'(0)\) and \(({\hat{h}}(0)-\frac{1}{b})\) are both pure imaginary, then the boundary values of \({\hat{h}}(z)\) are given by

$$\begin{aligned} {\hat{h}}(z)=\frac{1}{2 z}\log \left[ \frac{b^2|f(z)|^2T(z)^2}{c^2(b-z)^2}\frac{f'(z)^2}{|f'(z)|^2}\right] ,\quad z \in \varGamma . \end{aligned}$$
(43)

Finally, the approximate boundary values of f(z) are given by

$$\begin{aligned} f(z)=\frac{c(b-z)}{b} e^{z{\hat{h}}(z)}, \quad z\in \varGamma . \end{aligned}$$
(44)

6 Computing Values of Mapping Functions Interior and Inverse Mapping Functions

The approximate interior values of the function f(z) for both canonical slits regions are calculated by the Cauchy integral formula in the form of

$$\begin{aligned} f(z)= \frac{\int _{\varGamma }\frac{f(w)}{w-z}\mathrm{d}w}{\int _{\varGamma }\frac{1}{w-z}\mathrm{d}w}, \quad z \in \varOmega , \end{aligned}$$
(45)

numerically where \( \displaystyle \int _{\varGamma }\frac{1}{w-z}\mathrm{d}w = 1\), the integral in the numerator has the advantage that the denominator in this formula compensates for the error in the numerator (see [33]). The integrals in (45) are approximated by the trapezoidal rule.

For computing the inverse maps, note that the mapping function \(f^{-1}(w)=z\) is analytic in the respective canonical slits region. Then by means of Cauchy’s integral formula, we obtain \(z\in \varOmega \) by

$$\begin{aligned} z=\frac{1}{ 2\pi \mathrm{i}}\int _{J}\frac{z(t)}{f(z(t))-w}f'(z(t))z'(t)\mathrm{d}t. \end{aligned}$$
(46)

7 Numerical Implementation

Since the functions \(z_{j}(t)\) are \(2\pi \)-periodic, a reliable procedure for solving the integral equations (11), (25) and (39) numerically is by using the Nyström’s method with the trapezoidal rule [34]. The trapezoidal rule is the most accurate method for integrating periodic functions numerically [35, pp. 134–142]. The details for solving integral equation (11) is given in [36, 37].

7.1 Solving Integral Equation with Neumann-Type Kernel for Conformal Mapping onto Unit Disk with Circular Slits

For solving integral equation (25), multiplying both sides by \(|z'(t)|\) gives

$$\begin{aligned} f'(z)z'(t)+\int _{\varGamma } N_T(z,w)f'(w)|z'(t)|T(w)\left| \mathrm{d}w\right| =-\frac{|f(z)|^2\overline{z'(t)}}{c\overline{(z-a)^2}},\quad z\in \varGamma . \end{aligned}$$
(47)

We choose n equidistant collocation points for \(\varGamma _j\)

$$\begin{aligned} t_{{\tilde{j}}}=\frac{(({\tilde{j}}-1){{\mathrm{mod}}} n)2\pi }{n},\quad {\tilde{j}}=1,2, \ldots , n (M+1). \end{aligned}$$

Using the parametric representation z(t) on \(\varGamma \) and discretize integral equation (47) and (26) gives

$$\begin{aligned}&\displaystyle f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}}) \displaystyle +\frac{1}{n {\mathrm{i}}}\sum _{\begin{array}{c} {\tilde{j}}=1 \\ {\tilde{k}}\ne {\tilde{j}} \end{array}}^{(M+1)n} \left[ \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}})-z(t_{{\tilde{j}}})} -\frac{\overline{(z(t_{{\tilde{j}}})-a)}|\overline{z'(t_{{\tilde{k}}})}}{\overline{(z(t_{{\tilde{k}}})-a)}|(\overline{z(t_{{\tilde{k}}})} -\overline{z(t_{{\tilde{j}}})})}\right. \nonumber \\&\quad \displaystyle \times \left. \frac{|f(z(t_{{\tilde{k}}}))|^2}{|f(z(t_{{\tilde{j}}}))|^2}\right] f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})\displaystyle + \sum _{{\tilde{k}}=1}^{(M+1)n} \left( \frac{1}{n}\mathop {\mathrm {Im}}\frac{z''(t_{{\tilde{k}}})}{z'(t_{{\tilde{k}}})}+\frac{1}{n {\mathrm{i}}}\overline{\left( \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}})-a}\right) }\right) \nonumber \\&\quad \displaystyle f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}}) =-\frac{|f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})}}{c\overline{(z(t_{{\tilde{k}}})-a)^2}}, \end{aligned}$$
(48)
$$\begin{aligned}&\frac{1}{n}\sum _{{\tilde{j}}=n+1}^{(M+1)n} f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}}) = 0. \end{aligned}$$
(49)

We define vector hpx as

$$\begin{aligned} hpx_{{\tilde{j}}}=\left\{ \begin{array}{ll} \displaystyle 0, &{}\quad \displaystyle {\tilde{j}}=1,2, \ldots , n\\ \displaystyle f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}}), &{}\quad \displaystyle {\tilde{j}}=n+1,n+2, \ldots , (M+1)n \end{array} \right. . \end{aligned}$$
(50)

Then, (49) can be written as

$$\begin{aligned} \frac{1}{n}\sum _{{\tilde{j}}=1}^{(M+1)n} hpx_{{\tilde{j}}} = 0. \end{aligned}$$
(51)

Adding (51) and (48) gives

$$\begin{aligned}&\displaystyle f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}}) +\frac{1}{n}\sum _{{\tilde{j}}=1}^{(M+1)n} hpx_{{\tilde{j}}} \displaystyle +\frac{1}{n {\mathrm{i}}}\sum _{\begin{array}{c} {\tilde{j}}=1 \\ {\tilde{k}} \ne {\tilde{j}} \end{array}}^{(M+1)n} \left[ \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}})-z(t_{{\tilde{j}}})} -\frac{\overline{(z(t_{{\tilde{j}}})-a)}}{\overline{(z(t_{{\tilde{k}}})-a)}}\right. \nonumber \\&\quad \displaystyle \times \left. \frac{|f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})}}{|f(z(t_{{\tilde{j}}}))|^2(\overline{z(t_{{\tilde{k}}})} -\overline{z(t_{{\tilde{j}}})})}\right] f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}}) \displaystyle + \sum _{{\tilde{k}}=1}^{(M+1)n}\left( \frac{1}{n}\mathop {\mathrm {Im}}\frac{z''(t_{{\tilde{k}}})}{z'(t_{{\tilde{k}}})}+\frac{1}{n {\mathrm{i}}}\right. \nonumber \\&\quad \displaystyle \times \left. \overline{\left( \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}})-a}\right) }\right) f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}}) =-\frac{|f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})}}{c\overline{(z(t_{{\tilde{k}}})-a)^2}}. \end{aligned}$$
(52)

Rearrange (52) yields

$$\begin{aligned}&\displaystyle f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}})+\frac{1}{n} \sum _{{\tilde{j}}=1}^{(M+1)n} hpx_{{\tilde{j}}} \displaystyle +\frac{1}{n {\mathrm{i}}}\sum _{\begin{array}{c} {\tilde{j}}=1 \\ {\tilde{k}} \ne {\tilde{j}} \end{array}}^{(M+1)n} \left[ \frac{f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})}{z(t_{{\tilde{k}}})-z(t_{{\tilde{j}}})}\right] z'(t_{{\tilde{k}}})\nonumber \\&\quad \displaystyle - \frac{1}{n {\mathrm{i}}}\sum _{\begin{array}{c} {\tilde{j}}=1 \\ {\tilde{k}} \ne {\tilde{j}} \end{array}}^{(M+1)n}\left[ \frac{f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}}) \overline{(z(t_{{\tilde{j}}})-a)}}{|f(z(t_{{\tilde{j}}}))|^2 (\overline{z(t_{{\tilde{k}}})}-\overline{z(t_{{\tilde{j}}})})}\right] \frac{|f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})}}{\overline{(z(t_{{\tilde{k}}})-a)}} + \sum _{{\tilde{k}}=1}^{(M+1)n} \left( \frac{1}{n}\right. \nonumber \\&\quad \displaystyle \times \left. \mathop {\mathrm {Im}}\frac{z''(t_{{\tilde{k}}})}{z'(t_{{\tilde{k}}})} +\frac{1}{n {\mathrm{i}}}\overline{\left( \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}}) -a}\right) }\right) f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}}) =-\frac{|f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})}}{c\overline{(z(t_{{\tilde{k}}})-a)^2}}. \end{aligned}$$
(53)

Let E and G be \(n\times n\) matrices with the elements

$$\begin{aligned} (E)_{{\tilde{k}}{\tilde{j}}}=\left\{ \begin{array}{ll} \displaystyle \frac{1}{\overline{z(t_{{\tilde{k}}})} -\overline{z(t_{{\tilde{j}}})}} \displaystyle ,&{}\quad {\tilde{k}}\ne {\tilde{j}}\\ \displaystyle 0 \displaystyle ,&{}\quad {\tilde{k}}={\tilde{j}} \end{array} \right. , \end{aligned}$$
(54)

and

$$\begin{aligned} (G)_{{\tilde{k}}{\tilde{j}}}=\left\{ \begin{array}{ll} \displaystyle \frac{1}{z(t_{{\tilde{k}}})-z(t_{{\tilde{j}}})} ,&{}\quad {\tilde{k}}\ne {\tilde{j}}\\ \displaystyle 0 &{}\quad {\tilde{k}}={\tilde{j}} \end{array} \right. , \end{aligned}$$
(55)

Take \(\mathbf{t }\) to be the vector with element \(t_{{\tilde{k}}}\), where \({\tilde{k}}=1,2,\ldots ,(M+1)n\), \(\mathbf{a }\) be \((M+1)n \times 1\) vector with element a and

$$\begin{aligned} \mathbf{y }=\frac{1}{n}\sum _{{\tilde{j}}=1}^{(M+1)n} hpx_{{\tilde{j}}}. \end{aligned}$$

Then, (53) can be written in matrix form as

$$\begin{aligned}&\displaystyle f'(z(\mathbf{t }))z'(\mathbf{t })+ \mathbf{y } +\frac{1}{n {\mathrm{i}}}\left[ G f'(z(\mathbf{t }))z'(\mathbf{t })\right] z'(\mathbf{t }) - \frac{1}{n {\mathrm{i}}}\left[ \frac{Ef'(z(\mathbf{t }))z'(\mathbf{t }) \overline{(z(\mathbf{t })-\mathbf{a })}}{|f(z(\mathbf{t }))|^2}\right] \nonumber \\&\quad \displaystyle \times \frac{|f(z(\mathbf{t }))|^2\overline{z'(\mathbf{t })}}{\overline{(z(\mathbf{t })-\mathbf{a })}}+ \left( \frac{1}{n}\mathop {\mathrm {Im}}\frac{z''(\mathbf{t })}{z'(\mathbf{t })}+\frac{1}{n {\mathrm{i}}} \overline{\left( \frac{z'(\mathbf{t })}{z(\mathbf{t })-a}\right) } \right) f'(z(\mathbf{t }))z'(\mathbf{t })\nonumber \\&\quad =-\frac{|f(z(\mathbf{t }))|^2\overline{z'(\mathbf{t })}}{c\overline{(z(\mathbf{t })-\mathbf{a })^2}}. \end{aligned}$$
(56)

From (56), multiplication of matrix G by a vector can be done by FMM of order \(O((M + 1)n)\) operations. Let the \((M + 1)n\times 1\) vector \(\mathbf{p }\) be the vector \(f'(z(\mathbf{t }))z'(\mathbf{t })\) and the \((M + 1)n\times 1\) vector \(\mathbf{q }\) be the vector \(\displaystyle \frac{f'(z(\mathbf{t }))z'(\mathbf{t })\overline{(z(\mathbf{t })-\mathbf{a })}}{|f(z(\mathbf{t }))|^2}\). Let also b and c be \(2\times (M + 1)n\) real vectors

$$\begin{aligned} \mathbf{b }= \left( \begin{array}{cccc} {\text {R}}{\text {e}}(\overline{z(\mathbf{t })})^T\\ {\text {I}}{\text {m}}(\overline{z(\mathbf{t })})^T \end{array}\right) \end{aligned}$$
(57)

and

$$\begin{aligned} \mathbf{c }= \left( \begin{array}{cccc} {\text {R}}{\text {e}}(z(\mathbf{t }))^T\\ {\text {I}}{\text {m}}(z(\mathbf{t }))^T \end{array}\right) . \end{aligned}$$
(58)

Hence the products \(E\mathbf{p }\) and \(G\mathbf{q }\) can be computed by using the MATLAB function zfmm2dpart as follows [32]:

$$\begin{aligned} E\mathbf{p }=\texttt {zfmm2dpart}(iprec, n, \mathbf{b }, \mathbf{p }^T, 1) \end{aligned}$$
(59)

and

$$\begin{aligned} G\mathbf{q }=\texttt {zfmm2dpart}(iprec, n, \mathbf{c }, \mathbf{q }^T, 1). \end{aligned}$$
(60)

In this paper, we take \(iprec = 4\), which implies the tolerance of the FMM is \(0.5\times 10^{-12}\). The solution of the system (56) can be solve by using GMRES method. We use the MATLAB function gmres to solve the system (56) with relative residual \(<10^{-12}\) as the stopping criteria. Once the solution \(\displaystyle \frac{f'(z(t))z'(t)}{f'(0)}\) has been computed, the mapping function f(z(t)) is computed, by the formulas (27) and (28). The computation of interior values and inverse value via Cauchy integral formula (45) and (46) is referred to Nasser [37]. For computing Cauchy integral formula, we also discretized integrals using Nyström method with trapezoidal rule. The summation can be done by using FMM.

7.2 Solving Integral Equation with Neumann-Type Kernel for Conformal Mapping onto the Annulus with Circular Slits

For solving integral equation (39), multiplying both sides of equation (39) by \(|z'(t)|\) gives

$$\begin{aligned} \frac{f'(z)z'(t)}{f'(0)}+\int _{\varGamma } N_T(z,w)\frac{f'(w)T(w)|z'(t)|}{f'(0)}\left| \mathrm{d}w\right| =-\frac{|f(z)|^2 \overline{z'(t)}}{c^2},\quad z\in \varGamma . \end{aligned}$$
(61)

We choose n equidistant collocation points by choosing the same equidistant collocation points as in previous subsection. Using the parametric representation z(t) on \(\varGamma \) and discretizing integral equations (61), (40) and (41) gives

$$\begin{aligned}&\displaystyle \frac{f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}})}{f'(0)} \displaystyle +\frac{1}{n {\mathrm{i}}}\sum _{\begin{array}{c} {\tilde{j}}=1 \\ {\tilde{k}} \ne {\tilde{j}} \end{array}}^{(M+1)n} \left[ \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}}) -z(t_{{\tilde{j}}})}-\frac{\overline{z(t_{{\tilde{k}}})}|f(z(t_{{\tilde{k}}})) |^2\overline{z'(t_{{\tilde{k}}})}}{\overline{z(t_{{\tilde{j}}})} |f(z(t_{{\tilde{j}}}))|^2(\overline{z(t_{{\tilde{k}}})} -\overline{z(t_{{\tilde{j}}})})}\right] \nonumber \\&\quad \frac{f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})}{f'(0)} \displaystyle + \sum _{{\tilde{k}}=1}^{(M+1)n} \left( \frac{1}{n} \mathop {\mathrm {Im}}\frac{z''(t_{{\tilde{k}}})}{z'(t_{{\tilde{k}}})}+\frac{1}{n {\mathrm{i}}} \overline{\left( \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}})}\right) }\right) \frac{f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}})}{f'(0)} \nonumber \\&\quad =-\frac{|f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})}}{c^2}, \end{aligned}$$
(62)
$$\begin{aligned}&\frac{1}{n}\sum _{{\tilde{j}}=n+1}^{(M+1)n} \frac{f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})}{f'(0)} = 0, \end{aligned}$$
(63)

and

$$\begin{aligned} \frac{1}{n{\mathrm{i}}}\sum _{{\tilde{j}}=1}^{(M+1)n} \frac{z(t_{{\tilde{j}}})f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})}{f'(0)} = 0. \end{aligned}$$
(64)

We define vector hp as

$$\begin{aligned} hp_{{\tilde{j}}}=\left\{ \begin{array}{ll} \displaystyle 0, &{}\quad \displaystyle {\tilde{j}}=1,2, \ldots , n\\ \displaystyle \frac{f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})}{f'(0)} &{} \displaystyle ,\quad {\tilde{j}}=n+1,n+2, \ldots , (M+1)n \end{array} \right. . \end{aligned}$$
(65)

Then, (49) can be written as

$$\begin{aligned} \frac{1}{n}\sum _{{\tilde{j}}=1}^{(M+1)n} hp_{{\tilde{j}}} = 0. \end{aligned}$$
(66)

Adding (66), (64) and (62) gives

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}})}{f'(0)} +\frac{1}{n}\sum _{{\tilde{j}}=1}^{(M+1)n} hp_{{\tilde{j}}}+\frac{1}{n{\mathrm{i}}}\sum _{{\tilde{j}}=1}^{(M+1)n} \frac{z(t_{{\tilde{j}}})f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})}{f'(0)}\\ \displaystyle \quad +\frac{1}{n {\mathrm{i}}}\sum _{\begin{array}{c} {\tilde{j}}=1 \\ {\tilde{k}} \ne {\tilde{j}} \end{array}}^{(M+1)n} \left[ \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}})-z(t_{{\tilde{j}}})}-\frac{\overline{z(t_{{\tilde{k}}}) }|f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})}}{\overline{z(t_{{\tilde{j}}})}|f(z(t_{{\tilde{j}}}))|^2(\overline{z(t_{{\tilde{k}}})} -\overline{z(t_{{\tilde{j}}})})}\right] \frac{f'(z(t_{{\tilde{j}}})) z'(t_{{\tilde{j}}})}{f'(0)}\\ \displaystyle \quad + \sum _{{\tilde{k}}=1}^{(M+1)n} \left( \frac{1}{n}\mathop {\mathrm {Im}}\frac{z''(t_{{\tilde{k}}})}{z'(t_{{\tilde{k}}})}+\frac{1}{n {\mathrm{i}}} \overline{\left( \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}})}\right) }\right) \frac{f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}})}{f'(0)} =-\frac{|f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})}}{c^2}. \end{array} \end{aligned}$$
(67)

Rearrange (67) yields

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}})}{f'(0)} +\frac{1}{n}\sum _{{\tilde{j}}=1}^{(M+1)n} hp_{{\tilde{j}}}+\frac{1}{n{\mathrm{i}}}\sum _{{\tilde{j}}=1}^{(M+1)n} \frac{z(t_{{\tilde{j}}})f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})}{f'(0)}\\ \displaystyle \quad +\frac{1}{n {\mathrm{i}}}\sum _{\begin{array}{c} {\tilde{j}}=1 \\ {\tilde{k}}\ne {\tilde{j}} \end{array}}^{(M+1)n} \left[ \frac{f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})/f'(0)}{z(t_{{\tilde{k}}}) -z(t_{{\tilde{j}}})}\right] z'(t_{{\tilde{k}}})\\ \displaystyle \quad - \frac{1}{n {\mathrm{i}}}\sum _{\begin{array}{c} {\tilde{j}}=1 \\ {\tilde{k}}\ne {\tilde{j}} \end{array}}^{(M+1)n}\left[ \frac{f'(z(t_{{\tilde{j}}})) z'(t_{{\tilde{j}}})/f'(0)}{\overline{z(t_{{\tilde{j}}})}|f(z(t_{{\tilde{j}}}))|^2 (\overline{z(t_{{\tilde{k}}})} -\overline{z(t_{{\tilde{j}}})})}\right] \overline{z(t_{{\tilde{k}}})} |f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})} \\ \displaystyle \quad + \sum _{{\tilde{k}}=1}^{(M+1)n} \left( \frac{1}{n}\mathop {\mathrm {Im}}\frac{z''(t_{{\tilde{k}}})}{z'(t_{{\tilde{k}}})}+\frac{1}{n \mathrm{i}}\overline{\left( \frac{z'(t_{{\tilde{k}}})}{z(t_{{\tilde{k}}})}\right) }\right) \frac{f'(z(t_{{\tilde{k}}}))z'(t_{{\tilde{k}}})}{f'(0)} =-\frac{|f(z(t_{{\tilde{k}}}))|^2\overline{z'(t_{{\tilde{k}}})}}{c^2}. \end{array} \end{aligned}$$
(68)

Let E and G be \((M+1)n\times (M+1)n\) matrices as in (54) and (55), take \(\mathbf{t }\) be vector with element \(t_k\), where \(k=1,2,\ldots ,(M+1)n\) and

$$\begin{aligned} \mathbf{s }=\frac{1}{n}\sum _{{\tilde{j}}=1}^{(M+1)n} hp_{{\tilde{j}}}+\frac{1}{n{\mathrm{i}}}\sum _{{\tilde{j}}=1}^{(M+1)n} \frac{z(t_{{\tilde{j}}})f'(z(t_{{\tilde{j}}}))z'(t_{{\tilde{j}}})}{f'(0)}. \end{aligned}$$

Then, (68) can be written in matrix form as

$$\begin{aligned}&\displaystyle \frac{f'(z(\mathbf{t }))z'(\mathbf{t })}{f'(0)}+ \mathbf{s }+\frac{1}{n {\mathrm{i}}}\left[ G \frac{f'(z(\mathbf{t }))z'(\mathbf{t })}{f'(0)}\right] z'(\mathbf{t })- \frac{1}{n {\mathrm{i}}}\left[ E \frac{f'(z(\mathbf{t }))z'(\mathbf{t })/f'(0)}{\overline{z(\mathbf{t })} |f(z(\mathbf{t }))|^2}\right] \nonumber \\&\quad \displaystyle \times \overline{z(\mathbf{t })}|f(z(\mathbf{t }))|^2 \overline{z'(\mathbf{t })} + \left( \frac{1}{n}\mathop {\mathrm {Im}}\frac{z''(\mathbf{t })}{z'(\mathbf{t })}+\frac{1}{n {\mathrm{i}}}\overline{\left( \frac{z'(\mathbf{t })}{z(\mathbf{t })}\right) }\right) \frac{f'(z(\mathbf{t }))z'(\mathbf{t })}{f'(0)}\nonumber \\&\quad =-\frac{|f(z(\mathbf{t }))|^2\overline{z'(\mathbf{t })}}{c^2}. \end{aligned}$$
(69)

Let the \((M+1)n\times 1\) vector \(\mathbf{p }\) be the vector \(\displaystyle |\frac{f'(z(\mathbf{t }))z'(\mathbf{t })}{f'(0)}\) and the \((M+1)n\times 1\) vector \(\displaystyle \mathbf{q }\) be the vector \(\displaystyle \frac{f'(z(\mathbf{t }))z'(\mathbf{t })/f'(0)}{\overline{z(\mathbf{t })}|f(z(\mathbf{t }))|^2}\). Let also b and c be \(2\times (M+1)n\) real vectors as given in (57) and (58). The products \(E\mathbf{p }\) and \(G\mathbf{q }\) can be computed by using the MATLAB function zfmm2dpart according to (59) and (60), respectively. We take \(iprec = 4\), which implies the tolerance of the FMM is \(0.5\times 10^{-12}\). The solution of the system (69) can be solved by using GMRES method. We use the MATLAB function gmres to solve the system (69) with relative residual \(<10^{-12}\) as the stopping criteria. Once the solution \(\displaystyle \frac{f'(z(t))z'(t)}{f'(0)}\) has been computed, the mapping function f(z(t)) is computed, by the formulas (42), (43) and (44). The computation of interior values and inverse value via Cauchy integral formula (45) and (46) is referred to Nasser [37]. For computing Cauchy integral formula, we also discretized integrals using Nyström method with trapezoidal rule. The summation arising from discretization can be done by using FMM.

Fig. 2
figure 2

Mapping a region bounded by unit circle onto a disk for Example 1

Full size image
Fig. 3
figure 3

Inverse image of the disk for Example 1

Full size image
Fig. 4
figure 4

Mappings of circular frame with \(c=0.3, \rho =0.1, \sigma =0.50, \mu = e^{-2\sigma }\)

Full size image
Fig. 5
figure 5

Inverse images of the canonical slits regions onto original region for Example 2

Full size image
Fig. 6
figure 6

Mappings a region bounded by an ellipse and two circles onto a disk \(\varOmega _1\) and annulus with circular slits region \(\varOmega _2\) for Example 3

Full size image
Fig. 7
figure 7

Inverse images of the canonical slits regions onto original region for Example 3

Full size image
Fig. 8
figure 8

Mappings a region of connectivity fifteen onto a disk \(\varOmega _1\) and annulus with circular slits region \(\varOmega _2\) for Example 4

Full size image
Fig. 9
figure 9

Inverse images of the canonical slits regions onto original region for Example 4

Full size image
Fig. 10
figure 10

Mappings a region of connectivity ninety-two onto a disk \(\varOmega _1\) and annulus with circular slits region \(\varOmega _2\) for Example 5

Full size image
Fig. 11
figure 11

Inverse images of the canonical slits regions onto original region for Example 5

Full size image

8 Numerical Examples

For numerical experiments, we have used some test regions of connectivity one, two and fifteen. All the computations were done using MATLAB 7.12.0.635(R2011a). The number of points used in the discretization of each boundary component \(\varGamma _{j}\) is n. The test regions and their corresponding images are shown in Figs. 2, 3, 4, 5, 3, 7, 8, 9, 10 and 11.

Example 1

Consider a region \(\varOmega \) bounded by the unit circle

$$\begin{aligned} \varGamma : {\{}z(t)= & {} e^{{\mathrm{i}}t}{\}},\quad 0 \le t \le 2\pi ,\quad a = 0.3+0.3{{\mathrm{i}}}. \end{aligned}$$

Then, the exact mapping function is given by [8, p. 340]

$$\begin{aligned} {g(z)=\frac{z-a}{1-\overline{a}z},\quad \mu =1.} \end{aligned}$$
(70)

See Figs. 2, 3 and Table 1 for numerical results.

Example 2

Circular Frame :

Consider a pair of circles [38]

$$\begin{aligned} \varGamma _{0}: {\{}z(t)= & {} e^{{\mathrm{i}}t}{\}},\\ \varGamma _{1}: {\{}z(t)= & {} c + \rho e^{-{\mathrm{i}}t}{\}},\quad t: 0 \le t \le 2\pi , \quad b=0.3, \end{aligned}$$

such that the region \(\varOmega \) bounded by \(\varGamma _{0}\) and \(\varGamma _{1}\) is the region between a unit circle and a circle center at c with radius \(\rho \). Since \(\theta _{4}(\pi \tau {\mathrm{i}}/2) = 0\) and \({{\tilde{r}}}=q=e^{-\pi \tau }\) where \(\theta _{4}\) is the Jacobi Theta-functions [39], this implies \(\tau = \displaystyle \frac{\ln ({{\tilde{r}}})}{-\pi }\) and \(a = \displaystyle \frac{\lambda -e^{-2\sigma }}{1-\lambda e^{-2\sigma }}\). We choose a real number \(\sigma \) such that \(0< \sigma < \pi \tau /2.\) Then, the exact mapping function is given by [40]

$$\begin{aligned} g(z)=e^{2\sigma }\displaystyle \frac{\theta _{4}\left( \displaystyle \frac{1}{2\mathrm{i}}\log p(z)+ \displaystyle \frac{{\mathrm{i}}\pi \tau }{2}-{\mathrm{i}} \sigma \right) }{\theta _{4}\left( \displaystyle \frac{1}{2{\mathrm{i}}}\log p(z) + \displaystyle \frac{{\mathrm{i}}\pi \tau }{2}+{\mathrm{i}} \sigma \right) },\quad 0<\sigma < \frac{\pi \tau }{2}, \end{aligned}$$
(71)

where \(p(z)=(z-\lambda )/(\lambda z-1)\) with

$$\begin{aligned} \lambda= & {} \displaystyle \frac{2c}{1+(c^2-\rho ^2)+\sqrt{(1-(c-\rho )^2)(1-(c+\rho )^2)}},\\ {{\tilde{r}}}= & {} \displaystyle \frac{2\rho }{1-(c^2-\rho ^2)+\sqrt{(1-(c-\rho )^2) (1-(c+\rho )^2)}}, \end{aligned}$$

maps \(\varGamma _0\) onto the unit circle and \(\varGamma _1\) onto a circle of radius \({\tilde{r}}\). See Figs. 2, 3 and Tables 2, 3 for numerical results.

Table 1 Error norm (unit circle) for Example 1
Full size table
Table 2 Error norm (circular frame onto disk) for Example 2
Full size table
Table 3 Error norm (circular frame onto annulus) for Example 2
Full size table

Example 3

Ellipse with Two Circles:

Let \(\varOmega \) be the region bounded by [41, 42]

$$\begin{aligned} \varGamma _{0}: {\{}z(t)= & {} 2\cos t + {\mathrm{i}} \sin t{\}},\\ \varGamma _{1}: {\{}z(t)= & {} 0.5\left( \cos t - {\mathrm{i}} \sin t\right) {\}},\\ \varGamma _{2}: {\{}z(t)= & {} 1.2+0.3\left( \cos t - {\mathrm{i}} \sin t\right) {\}},\quad 0 \le t \le 2\pi , a=0 , b=1. \end{aligned}$$

This example is also discussed in Reichel [41] and Kokkinos et al. [42] which allows for comparison of the radii \(\mu _{1}\), \(\mu _{2}\). Since our condition problem is different from them, we should multiply our radii by 2.5 to compare with the result of Reichels and Kokkinos et al. We choose the symbols \(\mu _{1R}\) and \(\mu _{2R}\) for the radii in Reichel [41] and \(\mu _{1K}\) and \(\mu _{2K}\) for the radii in Kokkinos et al. [42]. Figures 6 and 7 show the region and its images based on our method. See Tables 4, 5 and 6 for comparisons between our computed values of \(\mu _{1}\) and \(\mu _{2}\) with those computed values of Reichel [41] and Kokkinos et al. [42] and computed values of \(c_D\), \(c_A\), \(\mu _{A1}\) and \(\mu _{A2}\).

Table 4 Radii comparison for Example 3 for disk with slits \(\varOmega _1\)
Full size table
Table 5 Radii comparison for Example 3 for disk with slits \(\varOmega _1\)
Full size table
Table 6 Numerical values of \(c_{D}\), \(c_{A}\), \(\mu _{Ai}\), \(i= 1,2\) for Example 3
Full size table

Example 4

Consider the region \(\varOmega \) of connectivity fifteen [43],

$$\begin{aligned} z_j(t)=\xi _j+e^{{\mathrm{i}}\sigma _j}(a_j\cos t+{\mathrm{i}}b_j\sin t),~j=0,1,\ldots ,14, \end{aligned}$$
(72)

where \(a=-0.5-{\mathrm{i}}0.5\), \(b=-0.833-{\mathrm{i}}2.165\) and the values of the complex constants \(\xi _j\) and the real constants \(a_j\), \(b_j\) and \(\sigma _j\) are as in Table 7. We chose the symbols \(\mu _{Dj}\) and \(\mu _{Aj}\) for radii in previous two canonical slits regions, respectively. The numerical results are presented in Figs. 8 and 9. See Table 8 for our computed values of \(c_D\), \(c_A\), \(\mu _\mathrm{Di}\) and \(\mu _\mathrm{Ai},~i=1, 2,\ldots , 14\).

Table 7 Values of constants \(a_j\), \(b_j\), \(\xi _j\) and \(\sigma _j\) for Example 4
Full size table
Table 8 Numerical values of \(\mu _\mathrm{Di}\), \(\mu _\mathrm{Ai}\), \(i=0, 1, \ldots , 14\) for Example 4
Full size table
Table 9 Values of constants \(\xi _j\) for Example 5
Full size table

Example 5

Consider a region \(\varOmega \) with complicated boundaries,

$$\begin{aligned} \varGamma _{0}: {\{}z(t)= & {} 0.2-{\mathrm{i}}0.5+6 e^{({\mathrm{i}}t)}{\}},\\ \varGamma _{ i}: {\{}z(t)= & {} \xi _{i}+ 0.303\left( 0.3\cos t - {\mathrm{i}} \sin t\right) {\}},\quad i=1, 3, \ldots , 17,\\ \varGamma _{{\hat{i}}}: {\{}z(t)= & {} \xi _{{\hat{i}}}+ 0.303 e^{(-{\mathrm{i}}t)}{\}}, \quad {\hat{i}}=2, 4, \ldots , 18,\\ \varGamma _{j}: {\{}z(t)= & {} \xi _{j}+ (0.24+0.08\cos (2t))e^{(-{\mathrm{i}}t)}{\}}, \quad j=19, 20, \ldots , 22,\\ \varGamma _{k}: {\{}z(t)= & {} \xi _{k}+ (0.24+0.08\cos (4t))e^{(-{\mathrm{i}}t)}{\}}, \quad k=23, 24, \ldots , 30,\\ \varGamma _{l}: {\{}z(t)= & {} \xi _{l}+ (0.24+0.08\cos (6t))e^{(-{\mathrm{i}}t)}{\}}, \quad l=31, 32, \ldots , 45,\\ \varGamma _{m}: {\{}z(t)= & {} \xi _{m}+ (0.24+0.08\cos (8t))e^{(-{\mathrm{i}}t)}{\}}, \quad m=46, 47, \ldots , 90,\\ \varGamma _{91}: {\{}z(t)= & {} 5.4419 + {\mathrm{i}}0.6903+ (0.24+0.08\cos (8t))e^{(-{\mathrm{i}}t)}{\}},\quad 0 \le t \le 2\pi , \end{aligned}$$

where \(a=3.9+{\mathrm{i}}0.2\) and \(b=-4.6871 - {\mathrm{i}}1.3355\) and the values of the complex constants \(\xi _j\) are as in Table 9. Mapping function from the original region onto the disk and annulus with slits region and the inverse mapping functions from the disk and annulus with slits region onto the original region. The numerical results are presented in Figs. 10 and 11.

9 Medical Image Processing Applications

Medical image processing has experienced a dramatic expansion. Experts from applied mathematics, engineering, computer sciences, biology and medicine have been attracted by biomedical research. One of the important parts of clinical routine is computer analytic processing. Image processing is a very important process for analyzing images and gives high-quality information that helps in diagnosing diseases and making treatment easier.

A conformal mapping is a one-one and onto transformation \(w=f(z)\) that preserves both local angles and shape of infinitesimal small figures but not necessarily their size which is necessary factor in medical image processing.

Conformal mapping can be effectively applied in the field of brain surface mapping. Parameterization of anatomical surfaces in brain imaging is valuable to help analyze anatomical shape. Conformal mapping involving slits has been applied by Wang et al. [3] to study the difference in cortical surface of the brain. It helps in disease diagnosis related to cortical surface such as Alzheimer’s disease. Conformal mapping can be used to map an irregular surface onto a disk and annulus while preserving the angle, which is useful for visualization of magnetic resonance imaging (MRI). MRI is a tomographic imaging procedure which uses strong magnetic fields and radio-waves to create images of internal physical and chemical characteristics of an object. An MRI scanner is shown in Fig. 12.

Fig. 12
figure 12

Shahid Aso Hospital MR imaging process

Full size image

The conformal mapping method of a simply and multiply connected region is applied to a brain surface image onto a disk and annulus with circular slit regions. The results based on our method are presented in Figs. 13 and 14 . Different values of a has the same effect as “warping” and “zooming” to get better and clearer pictures of different parts of the brain. Since conformal mappings are one-to-one, no information is lost. One is able to see how the zoomed part of the brain relates with the other parts. Thus conformal maps help preserve some essential features of visual information of the brain.

Fig. 13
figure 13

Application of the proposed method on the human brain. Computation times with \(n=2^{12}\) are b 2.239811 s, c 2.260020 s, d 2.270281 s, e 2.258278 s, f 2.262168 s

Full size image
Fig. 14
figure 14

Original image and the transformed images based on conformal mapping by choosing different point in the original image. Computation times with \(n=2^{14}\) are b 11.409960 s, c 11.714795 s, d 16.170715 s, e 16.219867 s, f 16.323288 s

Full size image

For our test experiments, we have considered real MR test brain image of a patient from Shahid Aso Hospital, to help diagnose diseases and treatment by obtaining better quality information. The results based on our method are presented in Figs. 15 and 16 .

Fig. 15
figure 15

Original MR image and the transformed images based on conformal mapping by choosing different point in the original image. Computation times with \(n=2^{12}\) are b 2.470122 s, c 2.515067 s, d 2.313659 s, e 2.414645 s, f 2.563450 s

Full size image
Fig. 16
figure 16

Original MR image and the transformed images based on conformal mapping by choosing different point in the original image. Computation times with \(n=2^{14}\) are b 16.915156 s, c 16.106628 s, d 15.326305 s, e 45.435839 s, f 42.948651 s

Full size image

10 Conclusions

In this paper, we have constructed new boundary integral equations for conformal mapping of bounded multiply connected regions onto the disk and annulus with circular slits regions. The advantage of the proposed method is that the boundary integral equations are all linear. Also in contrast to the boundary integral equation used in Nasser [10, 11], the right-hand sides of newly constructed boundary integral equations are much simpler and do not contain any singular operator. Moreover, several mappings of the test regions of connectivity one, two, three, fifteen and ninety-two were computed numerically using the proposed method. After computing the boundary values of the mapping function, the interior values of the mapping function and its inverse were calculated by means of Cauchy integral formula. The numerical examples presented have illustrated that the innovative boundary integral equation method has high accuracy. Luckily, this rate of accuracy is highly vital for medical application of image analysis. This paper used MATLAB functions graythresh, imfill, bwareaopen and bwboundaries to recognize and extract object boundary from medical images reproducibly and accurately. Consequently, this led to the achievement of better and clearer images. In the end, one should bear this in mind that such results were achieved after applying the proposed method to the medical image objective that helps in diagnosing diseases and making treatment easier.