Effect of non-cytolytic cure and saturation response: An in silico study to instigate the viral spread inhibition

Abstract

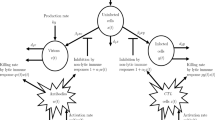
The non-cytolytic cure of infected cells is an imperative mechanism that maintains the healthy state in the host body by reducing the level of infection. The primary purpose of humoral immune response, i.e., the B cell response, is to neutralize the extracellular virions present in the body. To explore the impact of infected cells and virus particle-mediated saturation response on the viral spread dynamics under the influence of these critical factors, we propose a viral infection model incorporating the coupling effect of non-cytolytic cure mechanism and saturation response in the presence of humoral immune responses. Through parameter variation experimentation, we obtain that under the exposure of a weak humoral response, the saturation response effectively reduces the level of virions, whereas it has a less significant effect on viral infection dynamics in the presence of a strong humoral response or non-cytolytic cure mechanism. We observe that the strength of humoral immune response depends on the number of activated B cells present in the body rather than the rate at which it neutralizes the viruses. Further, we demonstrate that the non-cytolytic cure mechanism plays a vital role in restoring the no infection phase in the host body in the presence of a high infection coefficient. Moreover, a case study of HCV-infected human hepatic Huh7.5.1 cell lines has been presented to describe the HCV infection dynamics in a real-life scenario using model prediction technique.

Graphic Abstract

Appendices

Appendix A: Proof of Theorem 1

Proof

From the system of equations (1), we have $\frac{dT(t)}{dt}|_{T(t)= 0} = A + \alpha I(t)$, $\frac{dI(t)}{dt}|_{I(t)= 0} = \frac{\beta T(t) V(t)}{1 + nV(t)}$ and $\frac{dV(t)}{dt}|_{V(t)= 0} = kI(t)$.

If possible, let us suppose that for some $t >0$, the system (1) fails to satisfy the condition $\frac{dV(t)}{dt}|_{V(t)= 0} \ge 0$. Then, there must exist some $t_V > 0$ such that

$$\begin{aligned} t_{V} = \inf \left\{ t | V(t) = 0, \frac{dV(t)}{dt} < 0, t> 0\right\} . \end{aligned}$$

Therefore, $\frac{dV(t_{V})}{dt}|_{V(t_{V})= 0} = kI(t_{V}) < 0$, i.e., $I(t_{V}) < 0$.

Then, there must exist a $t_{I} > 0$ such that $t_{I} = \inf \{t | I(t) = 0, \frac{dI(t)}{dt} < 0, t> 0\}$.

It is evident that $t_{I} < t_{V}$. Now, since $V(t_{I}) > 0$, the condition $\frac{dI(t_{I})}{dt}|_{I(t_{I})= 0} = \frac{T(t_{I}) V(t_{I})}{1 + nV(t_{I})} < 0$ implies $T(t_{I}) < 0$.

Now, let us consider

$$\begin{aligned} t_{T} = \inf \left\{ t | T(t) = 0, \frac{dT(t)}{dt} < 0, t> 0\right\} . \end{aligned}$$

Then, it follows the condition $t_{T}< t_{I} < t_{V}$. Further, $\frac{dT(t_{T})}{dt}|_{T(t_{T})= 0} = A + \alpha I(t_{T}) > 0$, since $I(t_{T}) > 0$. This contradicts the definition of $t_{T}$ itself.

Therefore, $\frac{dV(t)}{dt}|_{V(t)= 0} \ge 0$, and thus, $V(t) \ge 0$, $\forall$$t > 0$. Hence, $I(t) \ge 0$ as well as $T(t) \ge 0$ for all $t > 0$.

Moreover, by the last equation of the system (1), we have $W(t) = W(0) \mathrm{e}^{\int _{0}^{t} (gV(x) - h)dx} \ge 0$, $\forall$$t \ge 0$. This confirms the nonnegativity of solutions of the system (1) initiating in ${\mathbb {R}}_{+}^{4}$.

To prove the boundedness of solutions to the system (1), let us define two new variables $N_1(t) = T(t) + I(t)$ and $N_2(t) = V(t) + \frac{p}{g}W(t)$.

Taking the derivative, we have $\frac{dN_1(t)}{dt} = A - dT(t) - aI(t) \le A - d_{n_1}N_1(t)$, $d_{n_1} = \min \{d, a\}$. This implies $\lim \nolimits _{t\rightarrow \infty } \sup N_1(t) \le \frac{A}{d_{n_1}}$ which gives $T(t) \le \frac{A}{d_{n_1}}$ and $I(t) \le \frac{A}{d_{n_1}}$.

Also, $\frac{dN_{2}}{dt} = kI(t) - \mu V(t) - \frac{ph}{g}W(t) \le kI(t) - d_{n_2}N_{2}(t)$, $d_{n_2} = \min \{\mu , h\}$.

Therefore, $\lim \nolimits _{t\rightarrow \infty } \sup N_{2}(t) \le \frac{A k}{d_{n_1} d_{n_2}}$ which returns $V(t) \le \frac{A k}{d_{n_1} d_{n_2}}$ and $W(t) \le \frac{A g k}{p d_{n_1} d_{n_2}}$.

Therefore, the solutions for the system (1) with initial values in ${\mathbb {R}}_{+}^{4}$ are ultimately bounded with positive invariant set

$$\begin{aligned}&{\mathcal {D}} = \left\{ \left( T(t), I(t), V(t), W(t)\right) \in {\mathbb {R}}^{3}_{+} : 0 \le T(t), I(t) \le \frac{A}{d_{n_1}}, 0 \le V(t) \le \frac{A k}{d_{n_1} d_{n_2}},\right. \\&\qquad \qquad \left. 0 \le W(t) \le \frac{A g k}{p d_{n_1} d_{n_2}}\right\} . \end{aligned}$$

Moreover, the first equation of the system (1) implies

$$\begin{aligned} \frac{dT(t)}{dt}&\ge A - dT(t) - \frac{\beta T(t) V(t)}{1 + nV(t)}\\&\ge A - \left( d + \frac{\beta V_{u}}{1 + nV_{l}}\right) T(t), \text { for large }t, \end{aligned}$$

where $V_{u} = \frac{A k}{\mu d_{1}}$ is the upper bound of V(t) and $V_{l}$ is the lower bound of V(t).

Thus, $\lim \nolimits _{t\rightarrow \infty } \inf T(t) \ge \frac{A (1 + nV_{l})}{ d + (\beta V_{u} + ndV_{l})}$. Hence, there exists a $\delta > 0$ such that $\lim \nolimits _{t\rightarrow \infty } \inf T(t) \ge \delta$. $\square$

Appendix B: Derivation of basic reproduction number

The equations concerning infection are

$$\begin{aligned} \begin{aligned} \frac{dI}{dt}&= \frac{\beta T V}{1 + nV} - aI - \alpha I = F_{1} - V_{1}\\ \frac{dV}{dt}&= kI - \mu V - pVW = F_{2} - V_{2} \end{aligned} \end{aligned}$$

where $F_{1} = \frac{\beta T V}{1 + nV}$, $V_{1} = aI + \alpha I$, $F_{2} = 0$, $V_{2} = \mu V + pVW - kI$. Thus,

$$\begin{aligned} \mathcal {F}= & {} \begin{pmatrix} \frac{\partial F_{1}}{\partial I}|_{{\small E_{0}}} &{} \frac{\partial F_{1}}{\partial V}|_{{\small E_{0}}} \\ \frac{\partial F_{2}}{\partial I}|_{{\small E_{0}}} &{} \frac{\partial F_{2}}{\partial V}|_{{\small E_{0}}} \end{pmatrix} = \begin{pmatrix} 0 &{} \frac{\beta A}{d} \\ 0 &{} 0 \end{pmatrix},\\ \mathcal {V}= & {} \begin{pmatrix} \frac{\partial V_{1}}{\partial I}|_{{\small E_{0}}} &{} \frac{\partial V_{1}}{\partial V}|_{{\small E_{0}}} \\ \frac{\partial V_{2}}{\partial I}|_{{\small E_{0}}} &{} \frac{\partial V_{2}}{\partial V}|_{{\small E_{0}}} \end{pmatrix} = \begin{pmatrix} a + \alpha &{} 0 \\ -k &{} \mu \end{pmatrix} \end{aligned}$$

According to the definition of basic reproduction number, $R_{0} = \rho (\mathcal {F} \mathcal {V}^{-1})$, where $\rho (C)$ is the spectral radius of the matrix C. Hence, in this case, it can be written as

$$\begin{aligned} R_{0} = \frac{A \beta k}{\mu d (a + \alpha )}. \end{aligned}$$

Appendix C: Proof of global stability analysis

1.1 C.1 Proof of Theorem 2

Proof

Let us define a Lyapunov function $L_0$ as

$$\begin{aligned} L_{0} = T - T_{0} -T_{0}\ln \frac{T}{T_{0}} + I + \frac{\beta T_{0}}{\mu }V + \frac{\beta p T_{0}}{\mu g}W + \frac{\alpha }{2(d + a)T_{0}}[(T - T_{0}) + I]^{2}. \end{aligned}$$

Note that $\alpha (1 - \frac{T_{0}}{T})I = - \alpha I \frac{(T- T_{0})^{2}}{TT_{0}} + \frac{\alpha }{T_{0}}(T - T_{0})I$.

Then, the time derivative of $L_0$ along the solutions of the system (1) and the relation $T_0 = \frac{A}{d}$ give

$$\begin{aligned} \frac{dL_{0}}{dt}= & {} -\left( dT_{0} + \alpha I + \frac{\alpha d T}{d + a}\right) \frac{(T - T_{0})^{2}}{TT_{0}} - \frac{\alpha a I^{2}}{(d + a) T_{0}} \\&- \frac{n\beta T_{0} V^2}{1 + nV} -\frac{\beta hpT_{0}W}{\mu g} + ( a + \alpha )I(R_{0} - 1). \end{aligned}$$

Thus, $\frac{dL_{0}}{dt} \le 0$ for $R_{0} \le 1$. Let $M_{0}$ be the largest invariant set $\{(T, I, V, W)|\frac{dL_{0}}{dt} = 0\}$. Then, following the condition $\frac{dL_{0}}{dt} = 0$ if and only if $T = T_{0}$ and $I = V = W = 0$, we obtain $M_{0} = \{E_{0}\}$. Hence, the LaSalle invariance principle affirms that the infection-free equilibrium $E_0$ is globally asymptotically stable for $R_0 \le 1$. $\square$

1.2 C.2 Proof of Theorem 3

Proof

Let us define a Lyapunov function $L_1$ as

$$\begin{aligned} L_{1}= & {} T - T_{1} -T_{1}\ln \frac{T}{T_{1}} + I - I_{1} -I_{1}\ln \frac{I}{I_{1}} \\&+ \frac{\beta T_{1} V_{1}}{kI_{1}(1+nV_1)}\left( V - V_{1} -V_{1}\ln \frac{V}{V_{1}}\right) + \frac{\beta p T_{1} V_{1}}{gkI_{1}(1+nV_1)} W \\&+ \frac{\alpha }{2(d + a)T_{1}}\left[ (T - T_{1}) + (I - I_{1})\right] ^{2} \end{aligned}$$

At $E_{1}$, we have $A = dT_{1} + aI_{1}$, $\beta T_{1} V_{1} = (a + \alpha )I_{1}(1+nV_1)$ and $\mu = \frac{kI_{1}}{V_{1}}$.

Further, $\alpha (I - I_{1})(1 - \frac{T_{1}}{T}) = - \alpha (I - I_{1}) \frac{(T- T_{1})^{2}}{TT_{1}} + \frac{\alpha }{T_{1}}(T - T_{1})(I - I_{1})$.

Then, the time derivative of $L_1$ along the solution of the system (1) gives

$$\begin{aligned} \frac{dL_1}{dt}= & {} - \left[ dT_1 + \alpha (I - I_1) + \frac{\alpha d T}{d + a}\right] \frac{(T - T_1)^{2}}{TT_1} \\&- \frac{a\alpha }{d + a}(I - I_1)^{2} - \frac{(a + \alpha )nI_1(V - V_{1})^2}{V_1(1 + nV)(1+nV_1)} \\&+ (a + \alpha )I_1\left( 4 - \frac{T_1}{T} - \frac{IV_1}{I_1V} -\frac{1 + nV}{1 + nV_1} - \frac{TI_1V}{T_1IV_1}\frac{1 + nV_1}{1 + nV} \right) \\&+ \frac{\beta p h T_1 V_1}{gkI_1 (1+nV_1)} [R_1 -1]W. \end{aligned}$$

From the AM-GM inequality, we have

$$\begin{aligned} 4 - \frac{T_1}{T} - \frac{IV_1}{I_1V} - \frac{TI_1V}{T_1IV_1}\frac{1 + nV_1}{1 + nV}-\frac{1 + nV}{1 + nV_1} \le 0. \end{aligned}$$

Thus, $\frac{dL_{1}}{dt} \le 0$ if $R_{1} \le 1$ and $dT_1 - \alpha I_1 \ge 0$. Let $M_{1}$ be the largest invariant set $\{(T, I, V, W)|\frac{dL_{1}}{dt} = 0\}$. Thus, following the condition $\frac{dL_{1}}{dt} = 0$ if and only if $T = T_{1}$, $I = I_{1}$, $V = V_{1}$ and $W = 0$, we have $M_{1} = \{E_{1}\}$. Further, since the equilibrium $E_{1}$ exists for $R_{0} > 1$, the LaSalle invariance principle confirms the global asymptotic stability of $E_1$ whenever $R_{1} \le 1 < R_{0}$ and $dT_1 - \alpha I_1 \ge 0$. $\square$

1.3 C.3 Proof of Theorem 4

Proof

Let us define a Lyapunov function $L^*$ as

$$\begin{aligned} L^*= & {} T - T^* -T^*\ln \frac{T}{T^*} + I - I^* -I^*\ln \frac{I}{I^*} \\&+ \frac{\beta T^* V^*}{kI^*(1+nV^*)}\left( V - V^* -V^*\ln \frac{V}{V^*}\right) \\&+ \frac{\beta p T^* V^*}{gkI^*(1+nV^*)} \left( W - W^* -W^*\ln \frac{W}{W^*}\right) \\&+ \frac{\alpha }{2(d + a)T^*}\left[ (T - T^*) + (I - I^*)\right] ^{2} \end{aligned}$$

At $E^*$, we have $A = dT^* + aI^*$, $\beta T^* V^* = (a + \alpha )I^*(1+nV^*)$ and $\mu = \frac{kI^*}{V^*} - pW^*$.

Further, $\alpha (I - I^{*})(1 - \frac{T^{*}}{T}) = - \alpha (I - I^{*}) \frac{(T- T^{*})^{2}}{TT^{*}} + \frac{\alpha }{T^{*}}(T - T^{*})(I - I^{*})$.

Then, the time derivative of $L^*$ along the solution of the system (1) gives

$$\begin{aligned} \frac{dL^*}{dt}= & {} - \left[ dT^* + \alpha (I - I^*) + \frac{\alpha d T}{d + a}\right] \frac{(T - T^*)^{2}}{TT^*} \\&- \frac{a\alpha }{d + a}(I - I^*)^{2} - \frac{(a + \alpha )nI^*(V - V_{1})^2}{V^*(1 + nV)(1+nV^*)}\\&+ (a + \alpha )I^*\left( 4 - \frac{T^*}{T} - \frac{IV^*}{I^*V} -\frac{1 + nV}{1 + nV^*} - \frac{TI^*V}{T^*IV^*}\frac{1 + nV^*}{1 + nV} \right) . \end{aligned}$$

From the AM-GM inequality, we have

$$\begin{aligned} 4 - \frac{T^*}{T} - \frac{IV^*}{I^*V} -\frac{1 + nV}{1 + nV^*} - \frac{TI^*V}{T^*IV^*}\frac{1 + nV^*}{1 + nV} \le 0. \end{aligned}$$

Thus, $\frac{dL^*}{dt} \le 0$ whenever $dT^* - \alpha I^* \ge 0$. Let $M^*$ be the largest invariant set $\{(T, I, V, W)|\frac{dL^{*}}{dt} = 0\}$. Thus, following the condition $\frac{dL^*}{dt} = 0$ if and only if $T = T^{*}$, $I = I^{*}$, $V = V^{*}$ and $W = W^{*}$, we obtain $M^* = \{E^{*}\}$. Moreover, since the equilibrium $E^*$ exists for $R_{1} > 1$, the LaSalle invariance principle affirms the global asymptotic stability of $E^*$ provided $R_{1} > 1$ and $(dT^{*} - \alpha I^{*}) \ge 0$. $\square$