Skip to main content
SpringerLink
Log in

Nonlinear Galerkin finite element methods for fourth-order Bi-flux diffusion model with nonlinear reaction term

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

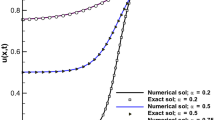
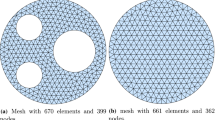
A fourth-order diffusion model is presented with a nonlinear reaction term to simulate some special chemical and biological phenomenon. To obtain the solutions to those problems, the nonlinear Galerkin finite element method under the framework of the Hermite polynomial function for the spatial domain is utilized. The Euler backward difference method is used to solve the equation in the temporal domain. Subject to the Dirichlet and Navier boundary conditions, the numerical experiments for Bi-flux Fisher–Kolmogorov model present excellent convergence, accuracy and acceleration behavior. Also, the numerical solutions to the Bi-flux Gray–Scott model, subject to no flux boundary conditions, show excellent convergence, accuracy and symmetry.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Akrivis G (1996) High-order finite element methods for the Kuramoto–Sivashinsky equation. ESAIM M M Num Anal 30(2):157–183

    MathSciNet  MATH  Google Scholar 

  • Araujo ALA (2014) Periodic solutions for extended Fisher–Kolmogorov and Swift–Hohenberg equations obtained using a continuation theorem. Nonlinear Anal 94:100–106

    MathSciNet  MATH  Google Scholar 

  • Bevilacqua L, Galeão ACNR, Costa FP (2011) On the significance of higher order terms in diffusion processes. J Braz Soc Mech Sci Eng 34(2):166–175

    Google Scholar 

  • Bevilacqua L, Galeão ACNR, Simas JG, Doce APR (2013) A new theory for anomalous diffusion with a bimodal flux distribution. J Braz Soc Mech Sci Eng 35(4):431–440

    Google Scholar 

  • Bevilacqua L, Jiang M, Silva Neto AJ, Galeão ACNR (2016) An evolutionary model of bi-flux diffusion processes. J Braz Soc Mech Sci Eng 38(5):1421–1432

    Google Scholar 

  • Chunk SK, Pani AK (2001) Numerical methods for the Rosenau equation. Appl Anal 77(3–4):351–369

    MathSciNet  Google Scholar 

  • Danumjaya P, Pani KA (2005) Orthogonal cubic spline collocation method for the extended Fisher–Kolmogorov equation. J Comput Appl Math 174(1):101–117

    MathSciNet  MATH  Google Scholar 

  • Dee GT, Saarloos W (1988) Bistable systems with propagating fronts leading to pattern formation. Phys Rev Lett 60:2641

    Google Scholar 

  • Dettopri L, Gottlieb D, Temam R (1995) A nonlinear Galerkin method: the two-level Fourier-collocation case. J Sci Comput 10(4):371–389

    MathSciNet  MATH  Google Scholar 

  • Doelman A, Kaper TJ, Zegeling P (1997) Pattern formation in 1D Gray–Scott model. Nonlinearity 10:523–563

    MathSciNet  MATH  Google Scholar 

  • Dubois T, Jauberteau F, Temam R (1998) Incremental unknowns, multilevel methods and the numerical simulation of turbulence. Com Met A Mech Eng 159(1–2):123–189

    MathSciNet  MATH  Google Scholar 

  • Dubois T, Jauberteau F, Temam R (1999) Dynamic multilevel methods and the numerical simulation of turbulence. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  • Dubois T, Jauberteau F, Temam R (2004) Multilevel methods in turbulence. Encyclopedia of computational mechanics. Wiley, New York

    Google Scholar 

  • Elliott CM, French DA (1987) Numerical studies of the Cahn-Hilliard equation for the phase seperation. IMA J Appl Math 38(2):97–128

    MathSciNet  MATH  Google Scholar 

  • Elliott CM, Zheng S (1986) On the Cahn–Hilliard equation Arch. Rat Mech Anal 96:399

    Google Scholar 

  • Hobbs RE (1981) Pipeline buckling caused by axial loads. J Constr Steel Res 1(2):2–10

    Google Scholar 

  • Jiang M (2017) The fourth order diffusion model for bi-flux mass transfer. PhD. dissertation, Federal University of Rio de Janeiro

  • Jiang M, Bevilacqua L, Silva Neto AJ, Galeão ACNR, Zhu J (2018) Bi-flux theory applied to the dispersion of particles in anisotropic substratum. Appl Math Model 64:121–134

    MathSciNet  MATH  Google Scholar 

  • Khiari N, Omrani K (2011) Finite difference discretization of the extended Fisher–Kolmogorov equation in two dimensions. Comput Math Appl 62(11):4151–4160

    MathSciNet  MATH  Google Scholar 

  • Laminie J, Pascal F, Temam R (1993) Implementation of finite element nonlinear Galerkin methods using hierarchical bases. Comput Mech 11(5–6):384–407

    MathSciNet  MATH  Google Scholar 

  • Lee KJ, McCormick WD, Pearson JE, Swinney HL (1994) Experimental observation of self-replicating spots in a reaction–diffusion system. Nature 369:215–218

    Google Scholar 

  • Liu R, Wang W, Yan S (2013) Pipeline buckling caused by axial loads. J Cent South Univ 20(1):236–245

    Google Scholar 

  • Marion M, Temam R (1989) Nonlinear Galerkin methods SIAM. J Numer Anal 26(5):1139–1157

    MathSciNet  MATH  Google Scholar 

  • Marion M, Temam R (1990) Nonlinear Galerkin methods: the finite elements case Numer. Mathematics 57(1):205–226

    MATH  Google Scholar 

  • Marion M, Xu J (1995) Error estimates on a new nonlinear Galerkin method based on two-grid finite elements SIAM. J Numer Anal 32(4):1170–1184

    MathSciNet  MATH  Google Scholar 

  • Pearson JE (1993) Complex patterns in a simple system. Science 261:189–192

    Google Scholar 

  • Peletier LA (1996) Chaotic spatial patterns described by the extended Fisher–Kolmogorov equation. J Differ Equ 129(2):458–508

    MathSciNet  MATH  Google Scholar 

  • Peletier LA, Troy WC (1996) Spatial patterns described by the extended Fisher–Kolmogorov equation: periodic solutions. J Math Anal 28(6):1317–1353

    MathSciNet  MATH  Google Scholar 

  • Qiang DU, Nicolaides RA (1991) Numerical analysis of continuum model of phase transition. SIAM J Numer Anal 28(5):1310–1322

    MathSciNet  MATH  Google Scholar 

  • Turing AM (1952) The chemical basis of morphogenesis. Philos Trans R Soc Lond B 237:37–72

    MathSciNet  MATH  Google Scholar 

  • Zhang R, Zhu J, Loula AFD, Yu X (2016) A new nonlinear Galerkin finite element method for the computation of reaction diffusion equations. J Math Anal Appl 434(1):136–148

    MathSciNet  MATH  Google Scholar 

  • Zhang J, Zhu J, Zhang R, Yang D, Loula AFD (2017) A combined discontinuous Galerkin finite element method for miscible displacement problem. J Comput Appl Math 309(1):44–55

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

Jiang Zhu’s work was partially supported by the National Council for Scientific and Technological Development of Brazil (CNPq). Xijun Yu’s work was supported partially by the National Natural Science Foundation of China (Grant No. 11571002, 11772067, 11702028) and CAEP Foundation of China (Grant No. CX2019032). Luiz Bevilacqua’s work was supported partially by CNPq/TWAS Grant, the COPPE/CAPES Grant 001, and the USP/IEA visiting research program. Maosheng Jiang’s work was supported partially by CNPq/TWAS Grant.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Qingdao University, Qingdao, 266071, China

    Maosheng Jiang

  2. Alberto Luiz Coimbra Institute Graduate School of Engineering (COPPE), Federal University of Rio de Janeiro, Rio de Janeiro, Brazil

    Luiz Bevilacqua

  3. Laboratório Nacional de Computação Científica, MCTIC, Avenida Getúlio Vargas 333, Petrópolis, RJ, 25651-075, Brazil

    Jiang Zhu

  4. Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing, 100088, China

    Xijun Yu

  5. Institute for Advanced Studies, University of São Paulo, São Paulo, Brazil

    Luiz Bevilacqua

Authors
  1. Maosheng Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luiz Bevilacqua
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jiang Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xijun Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Luiz Bevilacqua.

Additional information

Communicated by Abimael Loula.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, M., Bevilacqua, L., Zhu, J. et al. Nonlinear Galerkin finite element methods for fourth-order Bi-flux diffusion model with nonlinear reaction term. Comp. Appl. Math. 39, 143 (2020). https://doi.org/10.1007/s40314-020-01168-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-020-01168-w

Keywords

Mathematics Subject Classification

Search

Navigation