Abstract
A brief general review is presented of the theory of information transmission capacities of quantum communication channels, which is a development of the classical Shannon theory. Unlike a classical communication channel, a quantum channel is characterised by a whole set of different capacities, which depend on the type of transmitted information (classical or quantum) and on additional resources used during transmission. The main characteristics of a quantum channel are considered: classical capacity, capacity assisted by entanglement between the channel input and output, quantum capacity and secret classical capacity. The unique role of the quantum entanglement property, which manifests itself, in particular, in a nonclassical phenomenon of capacity superadditivity, is emphasised.
Export citation and abstract BibTeX RIS
1. Introduction
Quantum information theory is a scientific discipline that studies the laws of transmission and transformation of information in systems obeying the rules of quantum mechanics. This review addresses only one, but very important topic, i.e. the coding theorem for quantum communication channels, and emphasises a special role played by the quantum entanglement property. The concept of channel capacity is central to Shannon's classical theory. In the quantum case, this concept splits into several categories, giving rise to a whole range of informational characteristics of a quantum channel.
Quantum information theory is a source of a number of physically motivated mathematical problems that are often formulated quite simply, but difficult to solve (or still unsolved). Its main mathematical apparatus is linear algebra and the theory of operators in a Hilbert space, which is, as a rule, finite-dimensional. A detailed, more in-depth presentation of the issues in question, including numerous examples, can be found in books [1, 2], as well as in the course of lectures [3]. However, we should emphasise that since the time these books were written, progress has been made in solving some problem, which is reflected in this work.
2. Randomisation, entanglement and information
To understand the difference between classical systems and quantum systems from an information point of view, we consider the following statement:
Principle (C). Introduction of additional independent noise into observations cannot increase the amount of information about the observed system. This principle seems reasonable and is indeed valid when it comes to classical systems. We refine it by giving a mathematical formulation. Let the observed classical system be described by a random variable Y. The uncertainty of the state of this system is described by another random variable X, correlated with Y. The entropy of the distribution {px} of a random variable X can serve as a measure of uncertainty:

The amount of information about the system state, contained in observation Y, is expressed by Shannon's formula
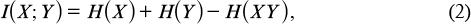
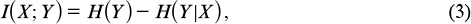
where H(XY) is the entropy of the joint distribution of random variables X and Y; and H(Y|X) = H(XY) − H(Y) is the conditional entropy. Suppose that, in addition to Y, independent noise Y0 is observed. Then, the amount of information about the system state, contained in observation YY0, is I(X;YY0). A simple calculation using formulae (1) and (2) shows that

This is a quantitative expression of the above principle (C) for classical systems. The introduction of additional independent noise in the observation is called randomisation. Note that in classical statistics there are other situations (of a gaming nature, when an unknown state is chosen in the worst way for the observer) in which the probabilistic choice of a decision is on average beneficial. In the considered situation of simple observation, this principle seems obvious, if not trivial. However, it ceases to be valid when it comes to quantum systems.
Statement (Q). Introduction of additional independent quantum noise into observations (quantum randomisation) can increase the amount of information about the observed system. To give an exact formulation, we recall the basic elements of the mathematical description of quantum systems. In quantum theory,
Download figure:
Standard imageDownload figure:
Standard image–the system is described by a Hilbert space  ;
;
–the states of the system are described by unit vectors  ;
;
–the measurement (ideal) with outcomes y corresponds to an orthonormal basis {ey} = E in  ; and
; and
–the probability of the outcome y in measuring E in the state ψ is

Let us now consider a quantum analogue of the situation of simple observation. The observed quantum system is described by a Hilbert space  ; the uncertainty of its state is expressed by specifying a family of unit vectors
; the uncertainty of its state is expressed by specifying a family of unit vectors  , where x are the values of the random variable X. Thus, this uncertainty has a classical character. If we perform a measurement {ey} = E over the system
, where x are the values of the random variable X. Thus, this uncertainty has a classical character. If we perform a measurement {ey} = E over the system  , then the conditional probability of the outcome y, provided that the state of the system is ψx, according to the statistical postulate, will take the form
, then the conditional probability of the outcome y, provided that the state of the system is ψx, according to the statistical postulate, will take the form

Together with the distribution of X, this conditional probability determines the joint distribution of x and y values, which allows one to apply formula (2) to find the amount of information about the state of the system, obtained by this measurement, which we denote as I(X,E).
Quantum noise is another system that is described by a Hilbert space  with a fixed state vector
with a fixed state vector  To describe the totality of the observed system and noise, it is necessary to make use of the following postulate of quantum theory.
To describe the totality of the observed system and noise, it is necessary to make use of the following postulate of quantum theory.
The composite system  ,
,  is described by the tensor product of Hilbert spaces
is described by the tensor product of Hilbert spaces  ; the vector ψ ⊗ ψ0 describes a state in which the subsystems are independent, the first being in state ψ and the second in state ψ0.
; the vector ψ ⊗ ψ0 describes a state in which the subsystems are independent, the first being in state ψ and the second in state ψ0.
Consider measurements over a composite system including an additional independent quantum noise, which are described by orthonormal bases  in the space
in the space  , and the corresponding amount of information
, and the corresponding amount of information  . The exact formulation of statement (Q) is that a strict inequality
. The exact formulation of statement (Q) is that a strict inequality
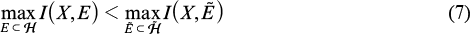
is possible.
The simplest example, in which such an inequality does hold, is given by a two-level quantum system with a family of three equally probable states with equiangular vectors {ψ0, ψ1, ψ2} (Fig. 1). It is assumed that the vectors lie in a real subspace; for example, these can be polarisation vectors of coherent monochromatic laser radiation. It was shown in [4] that for such a system
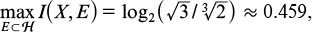
whereas
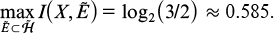
Figure 1. Information optimum for three equiangular state vectors.
Download figure:
Standard imageBoth maximisation problems are mathematically nontrivial, and we present here only the results. The first maximum is reached on the basis E consisting of two vectors located symmetrically with respect to any pair of vectors {ψ0, ψ1, ψ2}. To describe the solution to the second problem, we note that it can be reformulated as the maximisation problem for all possible overcomplete systems in the space  of the observed system. A family of vectors
of the observed system. A family of vectors  that satisfies the condition
that satisfies the condition
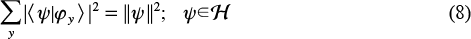
is called an overcomplete system.
This condition is similar to the condition of completeness of the basis, but the system {φy} does not need to be orthonormal or even linearly independent. Accordingly, every vector is decomposed via the components of an overcomplete system, but the decomposition may not be unique. It can be proved that every overcomplete system is obtained by projection P onto  of an orthonormal basis
of an orthonormal basis  in some extension
in some extension  of the original Hilbert space
of the original Hilbert space  ; this statement is a special case of the classical theorem of M.A. Naimark (1940) on the extension of a generalised spectral measure. Moreover, the extension can always be chosen so that
; this statement is a special case of the classical theorem of M.A. Naimark (1940) on the extension of a generalised spectral measure. Moreover, the extension can always be chosen so that  , with
, with  being identified with the subspace
being identified with the subspace  (see [1]). Then the conditional probability of the outcome y in measuring
(see [1]). Then the conditional probability of the outcome y in measuring  is
is  , and the difference between the left- and right-hand sides of (7) is that in the first case the maximum is taken over all orthonormal bases, while in the second, over all overcomplete systems in
, and the difference between the left- and right-hand sides of (7) is that in the first case the maximum is taken over all orthonormal bases, while in the second, over all overcomplete systems in  . An optimal overcomplete system consists of three equiangular vectors {φ0, φ1, φ2} of length
. An optimal overcomplete system consists of three equiangular vectors {φ0, φ1, φ2} of length  , orthogonal to the corresponding state vectors (see Fig. 1). Sasaki et al. [5] experimentally demonstrated an optimal measurement of
, orthogonal to the corresponding state vectors (see Fig. 1). Sasaki et al. [5] experimentally demonstrated an optimal measurement of  for three states of a plane-polarised photon using the polarisation of reference field as an auxiliary system
for three states of a plane-polarised photon using the polarisation of reference field as an auxiliary system  .
.
Thus, the phenomenon (Q) does hold for quantum systems. It is based on (unusual from the classical point of view) properties of composite quantum systems, which are described by the tensor product of subsystems. The tensor product of Hilbert spaces, along with vectors of the form ψ ⊗ ψ0, contains all possible linear combinations (superpositions) of  . The states of a composite system, defined by vectors of the first kind, are called nonentangled, while all the other states, not reducible to such vectors, are called entangled. Entanglement is a purely quantum property, partly related to classical correlation, but not reducible to it. The presence of entangled states makes it possible not only theoretically, but also experimentally to refute the hypothesis of hidden parameters, i.e., the possibility of a classical probabilistic description of quantum systems satisfying the physically motivated condition of locality. A large chapter of the modern quantum information theory is the quantitative theory of entanglement of states, a kind of combinatorial geometry of tensor products of finite-dimensional Hilbert spaces (see, for example, [6]).
. The states of a composite system, defined by vectors of the first kind, are called nonentangled, while all the other states, not reducible to such vectors, are called entangled. Entanglement is a purely quantum property, partly related to classical correlation, but not reducible to it. The presence of entangled states makes it possible not only theoretically, but also experimentally to refute the hypothesis of hidden parameters, i.e., the possibility of a classical probabilistic description of quantum systems satisfying the physically motivated condition of locality. A large chapter of the modern quantum information theory is the quantitative theory of entanglement of states, a kind of combinatorial geometry of tensor products of finite-dimensional Hilbert spaces (see, for example, [6]).
Dually, there are measurements in the composite quantum systems described by bases consisting of entangled vectors. Only these measurements make information inequality (7) possible in a situation when the state of the observed system and noise are not entangled. More generally, consider two quantum systems  and
and  , which are in an indefinite nonentangled state. Let I1, I2 and I12 be the maximum amounts of information about the state, obtained from measurements on systems 1, 2 and composite system 12, respectively. Then, in the general case, I12 > I1 + I2. This phenomenon of strict information superadditivity occurs and plays an important role in the theory of quantum communication channel capacity.
, which are in an indefinite nonentangled state. Let I1, I2 and I12 be the maximum amounts of information about the state, obtained from measurements on systems 1, 2 and composite system 12, respectively. Then, in the general case, I12 > I1 + I2. This phenomenon of strict information superadditivity occurs and plays an important role in the theory of quantum communication channel capacity.
3. Shannon's theorem
Before considering quantum channels, recall the concept of capacity in the classical information theory. The central role is played by coding theorems, which establish the possibility of asymptotically error-free transmission of information through a noisy channel at transmission rates not exceeding a certain threshold value, which is called capacity [7].
Mathematically, a noisy channel is specified by the conditional probability p(y|x) of receiving a signal (letter) y at the output, provided that the signal x is at the input. If a long message is transmitted, x(n) = (x1, . . ., xn), and each letter is transmitted independently (a memoryless channel), then the probability of a message at the output is p(y(n)|x(n)) = p(y1|x1) . . . p(yn|xn). Information transfer can be displayed as follows:
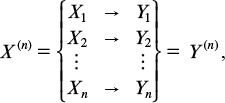
where Xi and Yi denote random variables at the channel input and output, respectively (i = 1, . . ., n). The capacity of such a channel is given by Shannon's formula

where the maximum is taken over all possible distributions of the input signal. Defining a similar quantity C(n) maxX(n)I(X(n);Y(n)) for messages of length n, we have C(n) = nC. This property of capacity additivity indicates absence of memory, or correlations between consecutive uses of a channel.
Encoding messages at the input involves a special choice of transmitted messages, in which messages at the output corresponding to different messages at the input are as distinguishable as possible. The coding theorem states that the number of messages of length n, which can be transmitted asymptotically (at n → ∞) without errors, is N ∼ 2nC. In other words, nC is the number of binary digits (bits) necessary and sufficient for asymptotically error-free transmission, with the optimal choice of messages at the input and their optimal discrimination at the output.
4. Quantum coding theorem
Quantum states, which are described by unit vectors of a Hilbert space, are pure states. It is convenient for the pure state to denote by Pψ the orthogonal projector onto the corresponding vector ψ. Quantum statistics also considers mixed states. Such a state is a statistical mixture of several pure states Pψi, taken with probabilities pi, and is represented by the density operator ρ = ∑i pi Pψi. The density operator is characterised by two properties: 1) ρ is a Hermitian positive operator; and 2) ρ has a unit trace, Trρ = 1. Thus, the eigenvalues of the density operator form a probability distribution. The entropy of this distribution is called entropy of the state ρ, or (in the operator form)
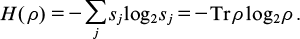
The simplest quantum communication channel is specified by a family of quantum states {ρx}, where x is the input signal. This channel is called a classical-quantum channel with a classical input and a quantum output. The mapping x → ρx in compressed form contains a description of the process that generates the state ρx. For example, let x = 0, 1, where ρ1 is the coherent state of the laser beam and ρ0 is the vacuum state; then we have a classical-quantum channel with two pure nonorthogonal states. At the channel output, a quantum measurement is performed, which is described in general by an overcomplete system {φy} = E, so that the conditional probability of the outcome y under the condition of the input signal x has the form  .
.
If letters of a message of length n are transmitted independently, then the transmission is described by a diagram
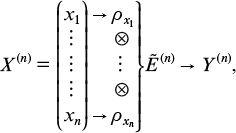
where ρxl ⊗ ··· ⊗ ρxn is the output density operator in the tensor product of the spaces  , corresponding to a message (x1, . . ., xn). Let the input messages have some distribution corresponding to a random variable X(n). The measurement
, corresponding to a message (x1, . . ., xn). Let the input messages have some distribution corresponding to a random variable X(n). The measurement  generating a random outcome Y(n) is performed at the output. Denoting the amount of information corresponding to the measurement
generating a random outcome Y(n) is performed at the output. Denoting the amount of information corresponding to the measurement  , as
, as  , we find
, we find
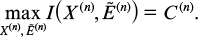
Unlike in the case of a classical channel, a strict inequality

is possible i.e. for quantum memoryless channels, the transmitted classical information can be strictly superadditive, which, of course, is due to the existence of entangled measurements at the channel output. For this reason, we cannot assert that the capacity is equal to C(1) as in the classical case; instead we define it as

Remarkably, however, that for a quantity defined in this way there is an explicit expression
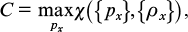
where
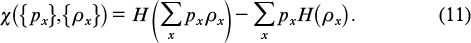
This statement represents the content of quantum coding theorem. The inequality «⩽» follows from the entropy bound which was proven in 1973 [8]. The attainability of this bound was established in 1996 (for more details on the history of the proof of the coding theorem, see Ref. [1]). Note that χ can be considered as a quantum analogue of the expression H(Y) − H(Y|X) for Shannon's information.
By calculating the C(1) and C values for some specific channels, we can verify that C(1) < C and, therefore, inequality (10) does hold for sufficiently large n. For example, for a channel with two pure states ψ0, ψ1
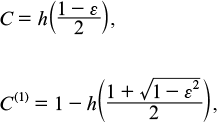
where ε = |⟨ψ0|ψ1⟩|, and
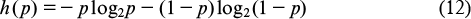
is the binary entropy. Indeed, C(1) < C for 0 < ε < 1; in particular, limε → 1C/C(1) = ∞.
Both in case C and in case C(1), the maximising distribution ascribes equal probabilities 1/2 to signal states, and the information-optimal measurement in case C(1) is given by the basis {e0, e1} located symmetrically with respect to these states.
For a channel with three pure symmetric states (see Fig. 1), C = 1, i.e., such a channel is asymptotically ideal! Of course, as in the classical information theory, the coding theorem only indicates the existence of optimal coding and decoding, which allows one to reach a maximum capacity, but does not provide a way to construct them. For such a channel, C(1) = 0.645, and the maximum of information is achieved when two of the three states are selected with probabilities 1/2, and the measurement is information-optimal for these two states [9]. Since we are dealing with the transmission of classical information, the quantity C is called the classical capacity of a quantum channel.
5. Additivity problem
Let us now consider the classical capacity of a channel with both a quantum output and a quantum input. Such a channel is given by a linear completely positive mapping Φ, which transfers the states at the input to the states at the output,  . The property of complete positivity means that the trivial extension of the channel by means of an ideal channel (defined by the identity mapping Id) of any finite dimension remains a positive mapping and, therefore, is also a channel,
. The property of complete positivity means that the trivial extension of the channel by means of an ideal channel (defined by the identity mapping Id) of any finite dimension remains a positive mapping and, therefore, is also a channel,

A definition and a detailed discussion of this property can be found in [1]. It guarantees the preservation of positivity for the tensor product of any channels. The transmission of classical information through the channel  will then be expressed as:
will then be expressed as:
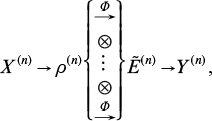
where coding means the selection of some quantum states  at the channel input Φ⊗n with probabilities px, and
at the channel input Φ⊗n with probabilities px, and  is some measurement at the output. Note that for fixed input states we obtain a (block) channel with a classical input, considered in Section 4. Applying the quantum coding theorem, we have the following expression for the classical channel capacity Φ:
is some measurement at the output. Note that for fixed input states we obtain a (block) channel with a classical input, considered in Section 4. Applying the quantum coding theorem, we have the following expression for the classical channel capacity Φ:

where
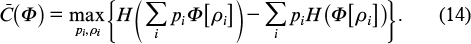
There arises the following fundamental additivity hypothesis: Is it true that for arbitrary quantum channels Φ1, Φ2 the equality
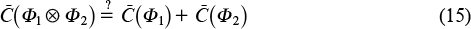
holds [note that the validity of (15) with the sign «⩾» is obvious]. If this hypothesis were valid, it would mean that the use of entangled states at the input, in contrast to entangled measurements at the output, does not allow the amount of transmitted classical information to be increased:  . This question remained open until 2008, when Hastings [10], relying on the property of asymptotic concentration of measure [11] and the previous results by Winter and Hayden, showed that in very high dimensions there exist random unitary channels exhibiting strict superadditivity with high probability. The practical significance of this result, however, remains unclear, since so far no constructive example has been presented.
. This question remained open until 2008, when Hastings [10], relying on the property of asymptotic concentration of measure [11] and the previous results by Winter and Hayden, showed that in very high dimensions there exist random unitary channels exhibiting strict superadditivity with high probability. The practical significance of this result, however, remains unclear, since so far no constructive example has been presented.
At the same time, the additivity property was established for a number of important classes of quantum channels [12 – 14]. A significant achievement was the solution of the long-standing problem of Gaussian optimisers and the additivity of capacity for bosonic Gaussian communication channels [15, 16]. Such channels are (irreversible) transformations of systems with 'continuous variables', such as a set of quantum oscillators that approximately describes electromagnetic radiation. For a wide class of 'phase-insensitive' bosonic Gaussian channels, including attenuators, amplifiers and classical noise channels, the optimality of coherent input states and the additivity of the minimum output entropy are proved. This made it possible to establish that the classical capacity of such channels is also additive and is achieved with Gaussian coding, as a result of which explicit expressions were given for the fundamental limits of the information transmission rate for the most usable classes of quantum channels in quantum optics (see, for example, [17, 18]).
6. Using entanglement between the input and the output
Suppose that there are two spatially separated quantum systems A and B, described by the entangled state ρAB. Such states can be prepared experimentally and are of great interest in relation with a direct verification of quantum theory: the correlations between A and B predicted by the theory do not fit into the framework of any acceptable classical model. It is known that the presence of entanglement alone does not make it possible to transmit information from A to B. However, if A and B are additionally connected by a quantum channel Φ, then the presence of entanglement allows one to increase its classical capacity. If Φ = Id is an ideal channel, then the gain in capacity provided by the so-called superdense coding is twofold [2]. This is achieved by using for encoding the maximally entangled states of the orthonormal basis in the AB system, which B can obtain due to the presence of the quantum channel Φ.
The stronger the channel differs from the ideal one, the greater the gain, and in the limit of channels with very large noise, it can tend to infinity. Generalising the superdense coding protocol, it is not difficult to give a mathematical definition of classical capacity using entanglement assistance, for which there is a remarkable formula obtained by Bennett, Shor, Smolin and Thapliyal [19]*

where I(ρ, Φ) is the quantum mutual information between A and B, given by the formula
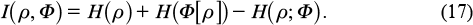
Here H(ρ) and H(Φ[ρ]) are the entropies of the input and output states, respectively; and H(ρ; Φ) is the so-called entropy exchange. To define the latter, we need introduce the concept of purification of a quantum state. Namely, for any density operator ρA in the Hilbert space  there is a pure state, i.e., the one-dimensional projector Pρ in the space
there is a pure state, i.e., the one-dimensional projector Pρ in the space  , where
, where  is the space of the reference system such that the partial trace of Pρ in the space
is the space of the reference system such that the partial trace of Pρ in the space  coincides with ρA. Moreover, the partial trace of Pρ in the space
coincides with ρA. Moreover, the partial trace of Pρ in the space  , i.e., the state of the reference system, has the same entropy as ρA. Entropy exchange is defined as
, i.e., the state of the reference system, has the same entropy as ρA. Entropy exchange is defined as
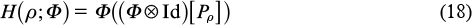
and can be interpreted as an analogue of the joint entropy of A and B. Then formula (17) is an analogue of the expression I(X;Y) = H(X) + H(Y) − H(XY) for Shannon's information. Quantum mutual information has a number of natural properties, similar to those of Shannon's information; in particular, it is subadditive with respect to the tensor product of the channels. Hence, the capacity Cea(Φ) is additive.
The practical realisation of the above protocol involves the spatial distribution of entanglement, which is currently an engineering challenge. Possible approaches to solving this problem are discussed in [20].
7. Quantum capacity
When classical information is transmitted over a quantum channel, it is recorded into a quantum state, which, therefore, represents an information resource. The peculiarity of this resource consists in the fact that the entirety of its information content (sometimes called quantum information) cannot be reduced to a classical message. This is due to the fact that the quantum state contains information about the statistics of all possible, including mutually exclusive (complementary), measurements over the system. A simple argument based on the linearity of the equations of quantum evolution shows that, unlike classical information, there is no 'quantum Xerox machine', that is, a physical device that allows one to copy quantum information.
Thus, the transformation of the quantum state ρ → Φ[ρ] can be considered as the transfer of quantum information. It is natural to raise the question of asymptotically (for n → ∞) error-free transmission by the channel Φ⊗n:
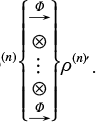
Quantum capacity Q(Φ) is determined by the maximum dimension of the subspace of the input space vectors [∼2nQ(Φ)] for which the states corresponding to them are transmitted asymptotically without errors, i.e., almost reversibly. For Q(Φ) there is an expression using coherent information

namely
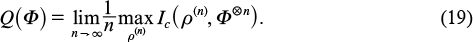
The concept of quantum capacity and its relationship with coherent information at the heuristic level were discussed by Lloyd [21], who proposed the formula

based on the assumption of additivity of coherent information, which, however, was soon refuted. An exact definition of quantum capacity is given by Barnum et al. [22], who also proved the inequality with the ⩽ sign in (19). The question of equality remained open until 2003, when Shor gave a sketch of the proof clarifying Lloyd's arguments, and Devetak [23] presented a completely different proof based on the parallel between a quantum channel and a classical channel [7], and in the quantum case, the role the eavesdropper is played by the environment of the open system in question.
Nevertheless, the quantum capacity remains the least studied of the whole variety of capacities of a quantum communication channel. Formula (19), due to its asymptotic nature, is hardly suitable for calculation, but it is known that for the so-called degradable channels [24] it is simplified to expression (20).
Smith and Yard [25] constructed an example of the remarkable phenomenon of superactivation when the inequality Q(Φ1 ⊗ Φ2) > 0 holds for two quantum channels Φ1, Φ2 with zero quantum capacity. Shirokov [26] showed that a similar phenomenon can occur for quantum zero-error capacity. This can be considered as an extreme manifestation of the capacity superadditivity, which is based on the unusual geometric properties of the tensor product of channels that improve the 'reversibility' of some transmitted states.
8. Secret classical capacity
Consider the transmission of classical information in which there are three participants: the sender A, the receiver B, and the eavesdropper E. A quantum channel subject to eavesdropping ΦBE is defined by isometric mapping of the space A into the space BE. Suppose A selects states  } with probabilities {px}; then participants B and E receive the states
} with probabilities {px}; then participants B and E receive the states  and
and  , respectively; the upper bounds of Shannon's information for B and E are the quantities
, respectively; the upper bounds of Shannon's information for B and E are the quantities  and
and  where χ is defined by formula (11). By analogy with a classical eavesdropping channel [7], the 'secrecy' of transmission can be characterised by the quantity
where χ is defined by formula (11). By analogy with a classical eavesdropping channel [7], the 'secrecy' of transmission can be characterised by the quantity
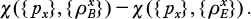
Assuming that the input states  are pure, and denoting the average state of the input ensemble as
are pure, and denoting the average state of the input ensemble as  , we obtain the key relation
, we obtain the key relation
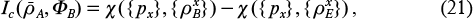
which reveals an important relationship between coherent information and secret classic capacity (defined below); the relation also indicates a way of proving direct coding theorem for quantum capacity through consideration of an eavesdropping channel.
The exact upper bound of the achievable transmission rates, provided that the mutual information between A and E asymptotically disappears, is called the secret classic capacity Cp (ΦBE) of the eavesdropping channel. This capacity is expressed as
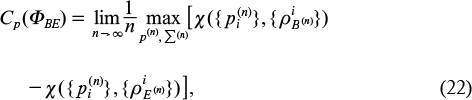
where the maximum is taken over all finite sets of states  in
in  and probability distributions
and probability distributions  (we use the notations
(we use the notations  and
and  ).
).
Relations (19), (21) and (22) yield an important inequality between the quantum and classical secret capacities:
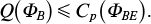
This inequality follows from the fact that in calculating Cp(ΦBE), all ensembles of states are taken into account, and in calculating Q(ΦB), only ensembles of pure states for A are considered. In general, a strict inequality is possible; therefore, of particular interest is the following statement: If the channel B is degradable [24], then
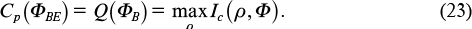
This makes it possible to explicitly calculate the capacities Cp and Q in a number of interesting cases (see [1] for more details).
At the end of the brief discussion of eavesdropping channels, we mention a vast field of quantum cryptography, which is an independent and far developed chapter of quantum information science (see, for example, reviews [27, 28]).
9. Conclusions
We have considered the main capacities of quantum communication channels. Further development of the theory leads to the study of multiple-user quantum channels ("quantum Internet") [29]. A large part of quantum information science is devoted to the study of systems with continuous variables based on the principles of quantum optics, as well as hybrid optical-atomic systems. Many experiments and protocols of quantum information theory, carried out at the laboratories of a number of developed countries, are implemented on such systems.




